Cascading Failure Analysis on Shanghai Metro Networks: An Improved Coupled Map Lattices Model Based on Graph Attention Networks
Abstract
:1. Introduction
2. Literature Review
2.1. Topology Analysis of Metro Networks
2.2. Cascading Failure
2.3. Graph Neural Network
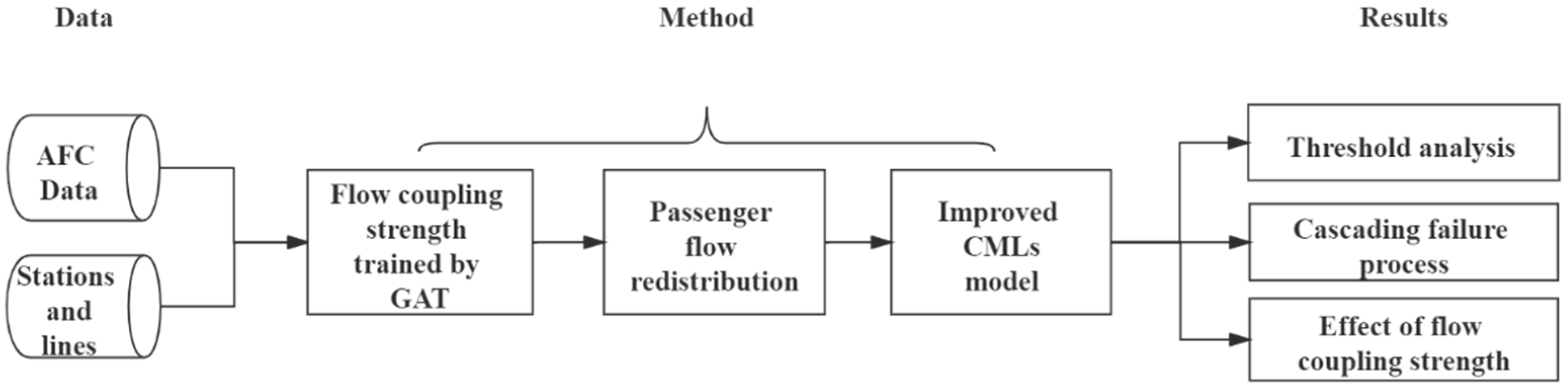
3. Data and Methods
3.1. Data Description of Shanghai Metro
3.2. Model Specification
3.2.1. Flow Coupling Strength Trained by GAT
3.2.2. Passenger Flow Redistribution
3.2.3. An Improved CMLs Model
- The correlation between the scale of cascading failures and the external perturbation under different attacks;
- The speed of cascading failures in a discrete time series under different attacks;
- The difference between this improved model and existing CMLs model.
4. Results and Discussions
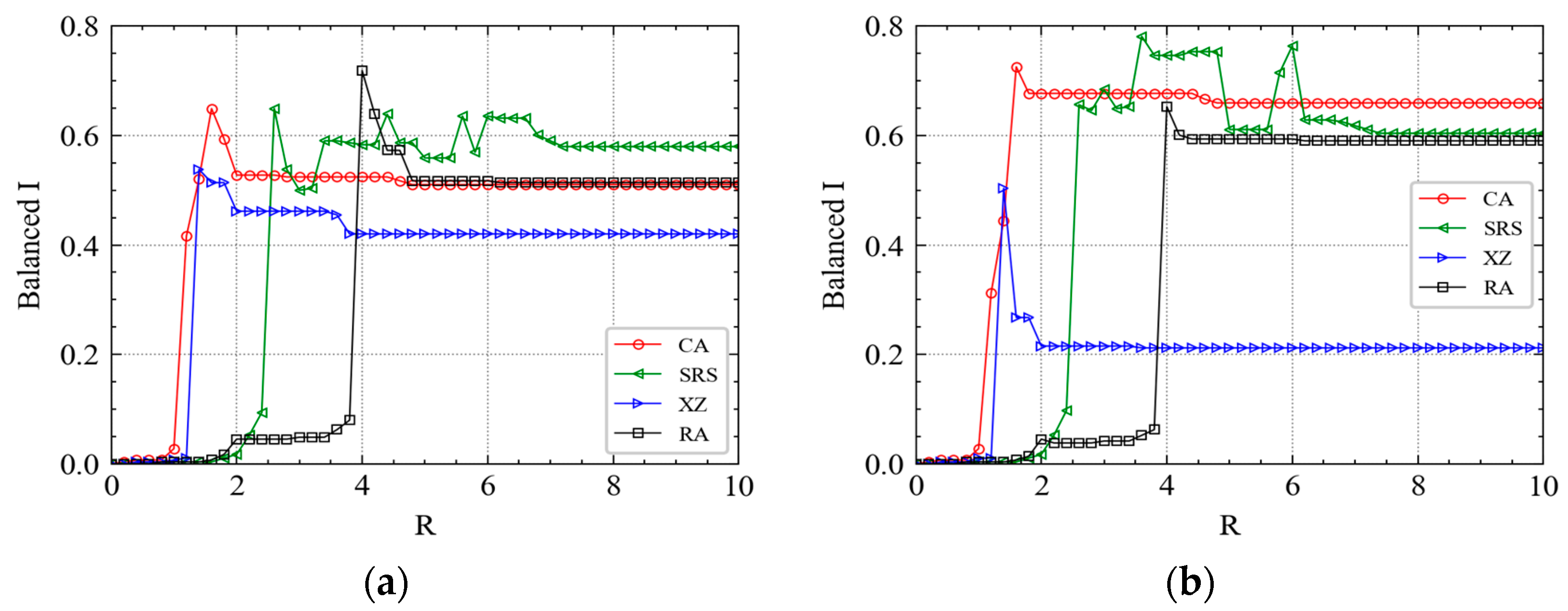
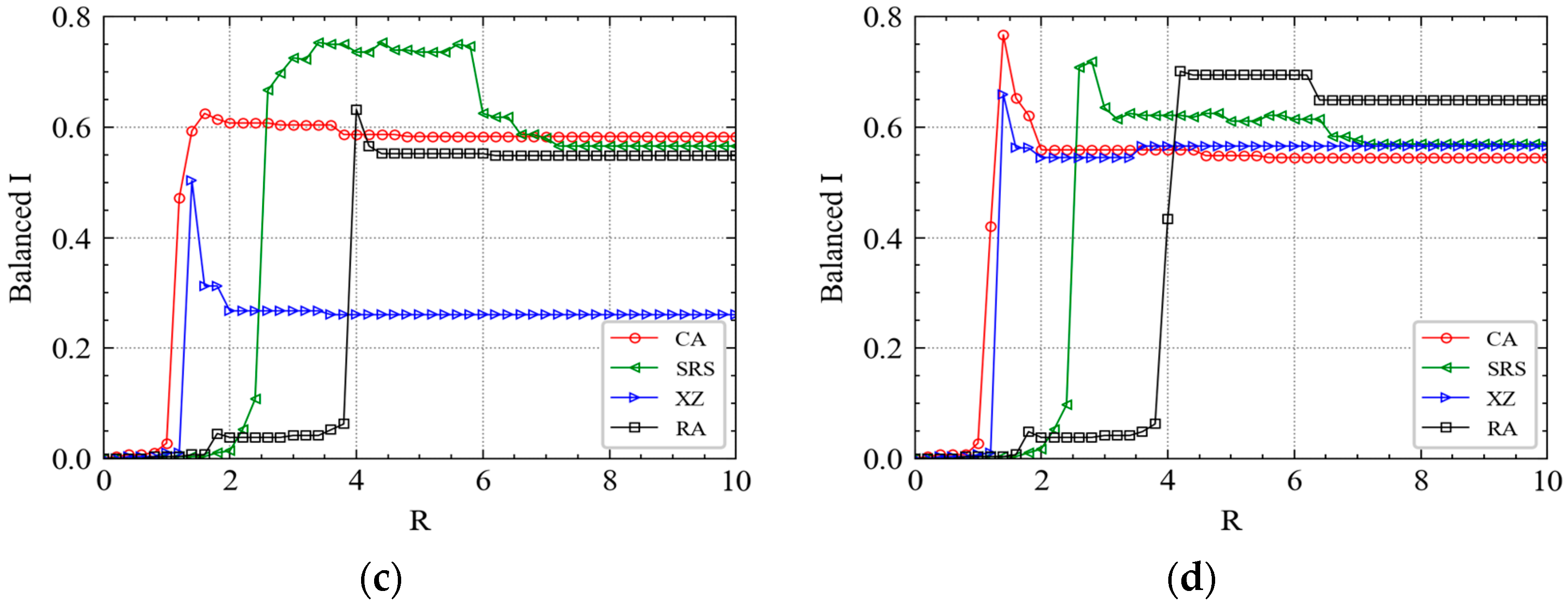
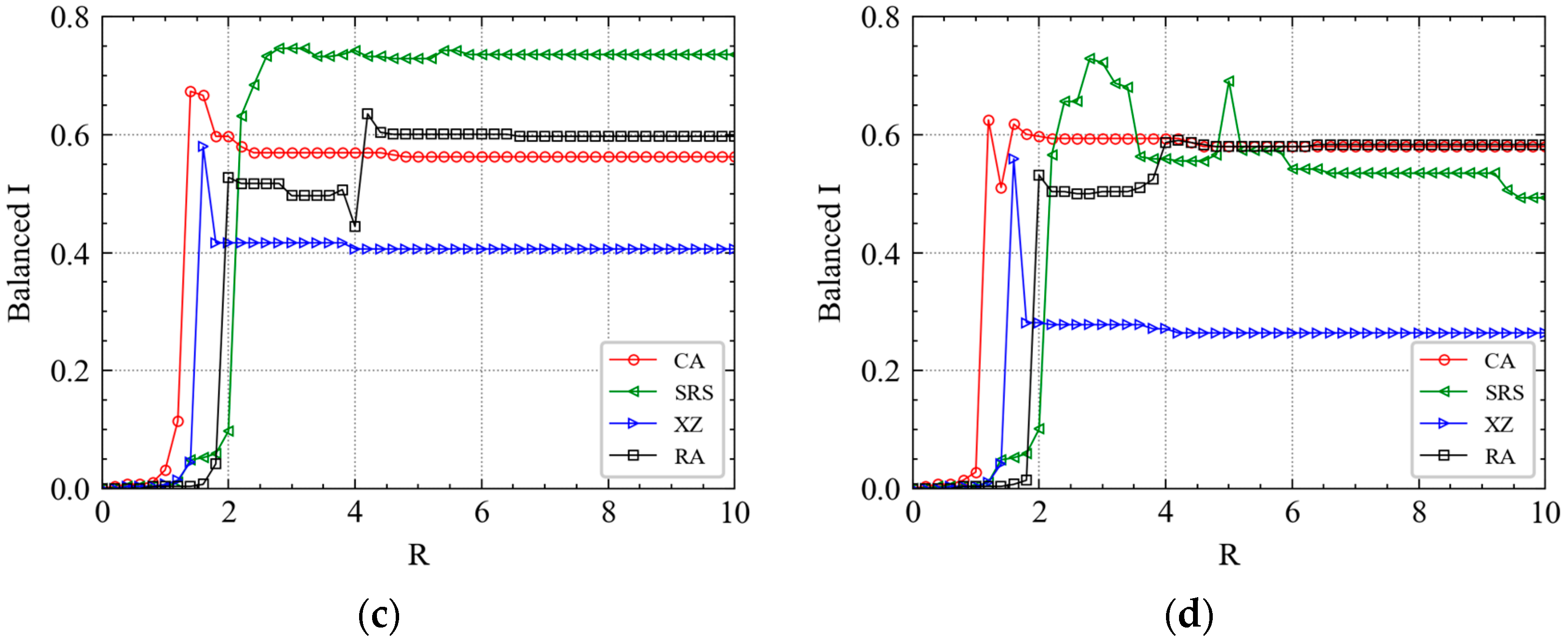
4.1. Threshold Analysis for Cascading Failure
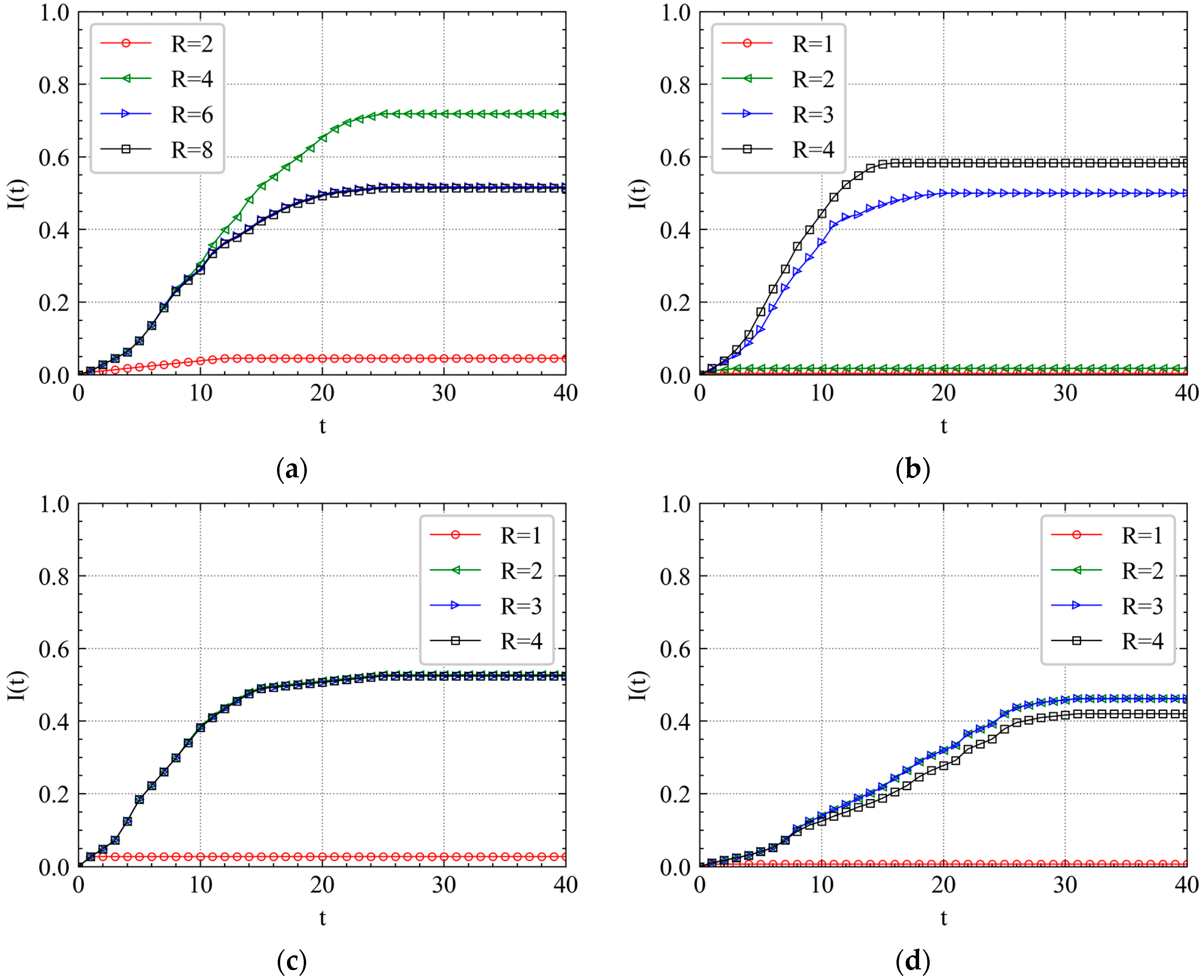
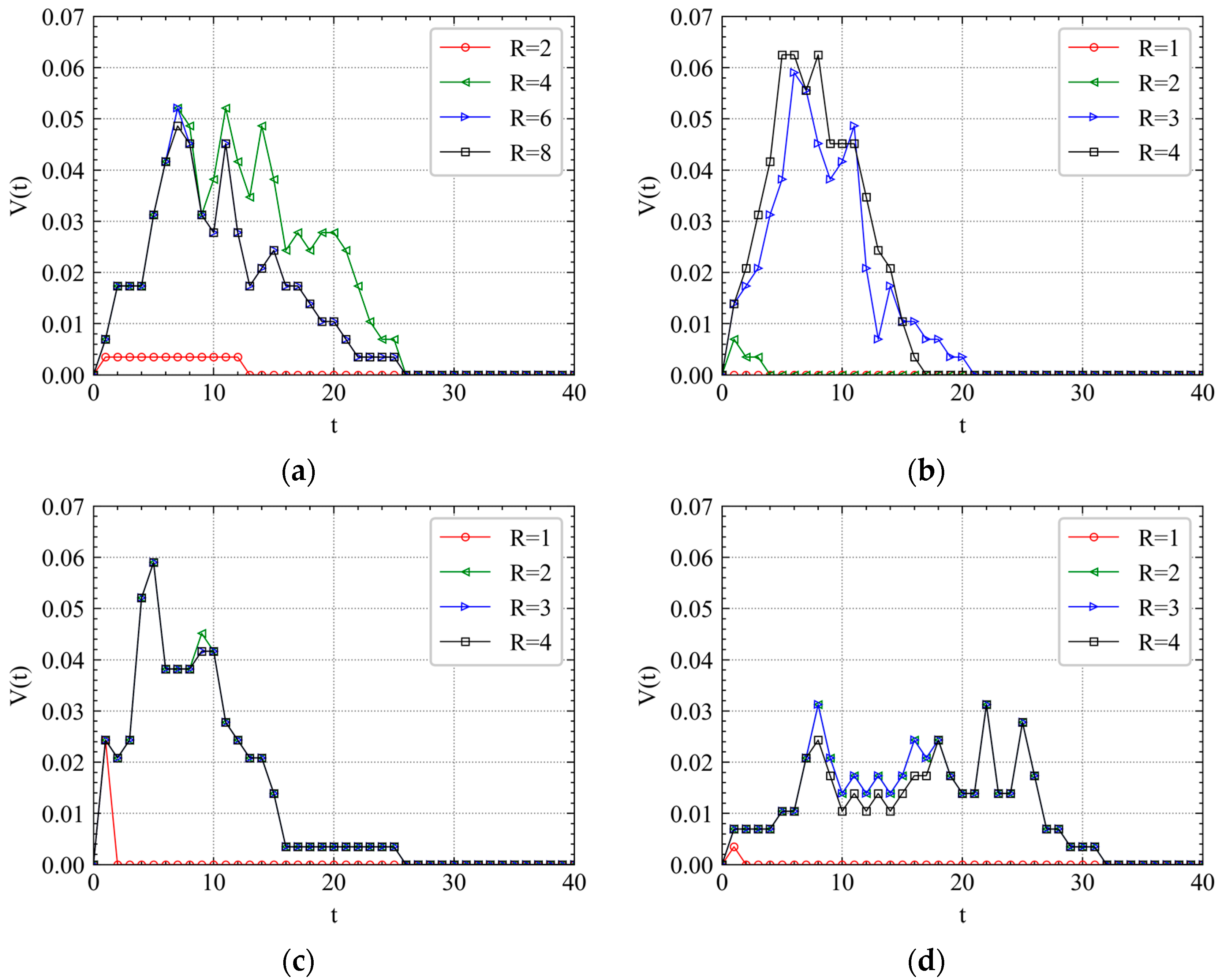
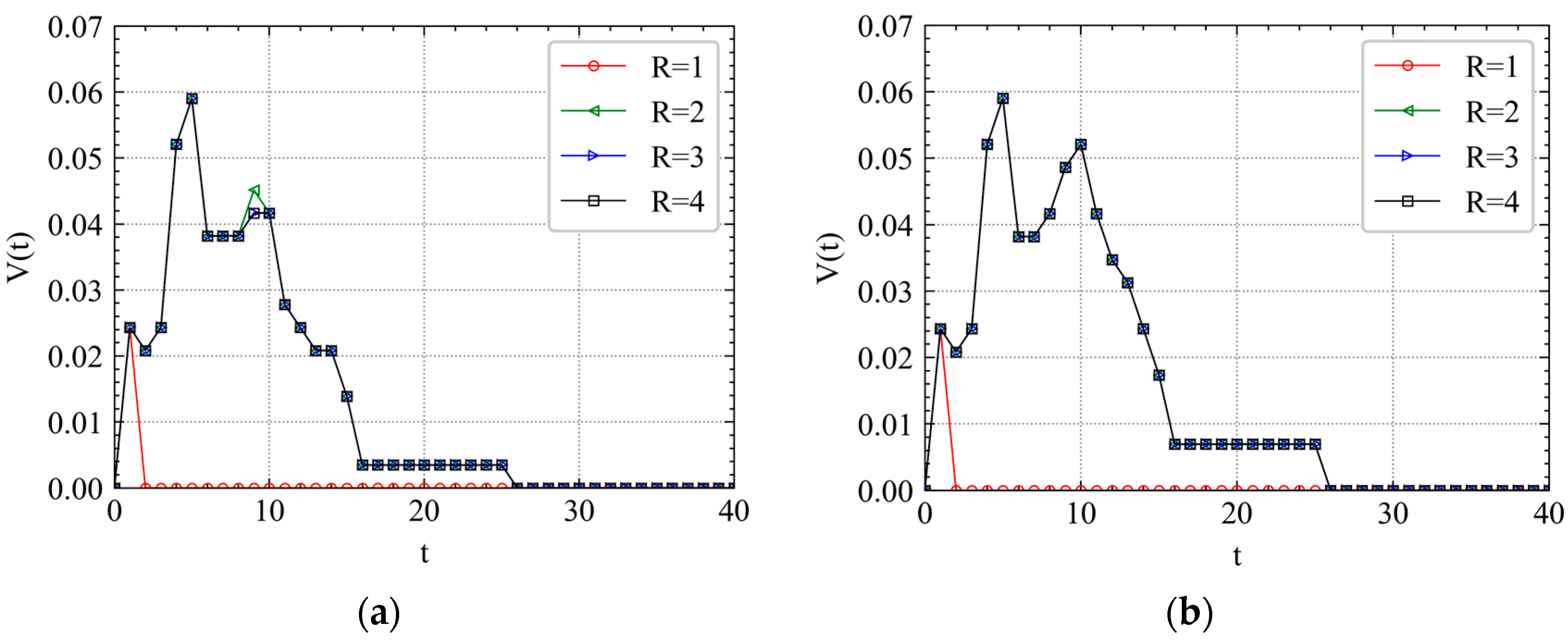
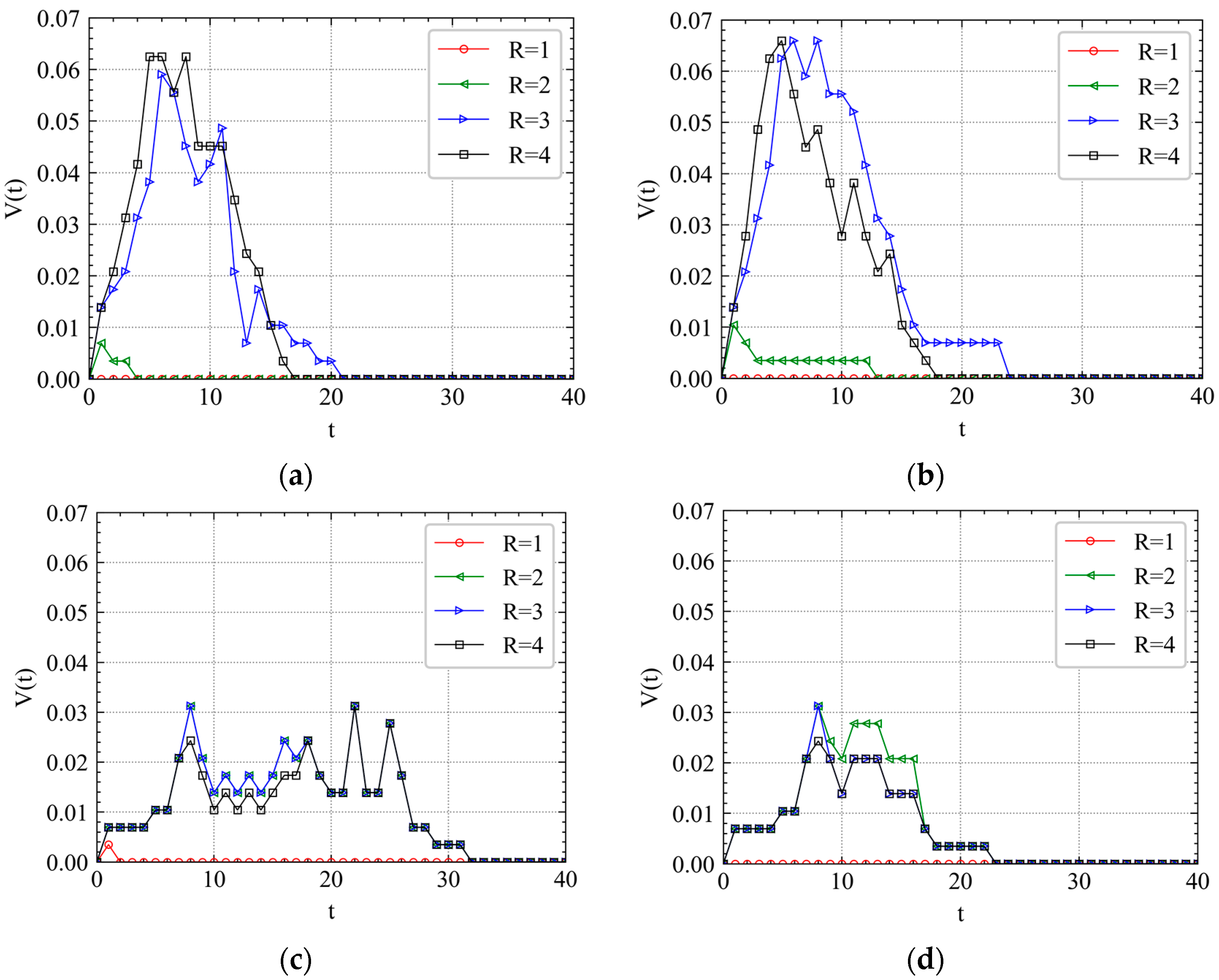
4.2. Cascading Failure Process
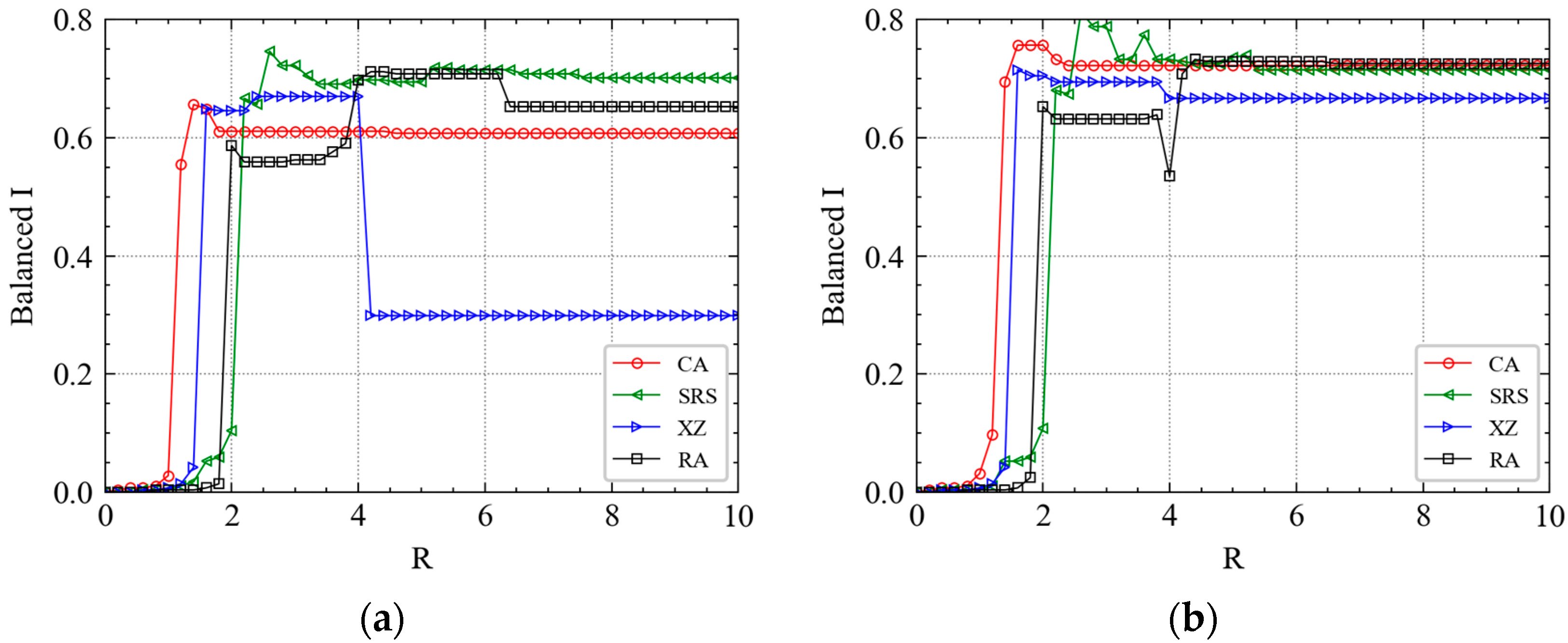
4.3. Effect of Coupling Strength
4.3.1. Comparison of GAT and Classical Baseline GCN
4.3.2. Difference between CMLs Based on GAT and CMLs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, D.M.; Du, F.; Huang, H.W.; Zhang, F.; Ayyub, B.M.; Beer, M. Resiliency assessment of urban rail transit networks: Shanghai metro as an example. Saf. Sci. 2018, 106, 230–243. [Google Scholar] [CrossRef]
- Wang, J.W.; Rong, L.L.; Zhang, L. Effect of Attack on Scale-Free Networks Due to Cascading Failure. Mod. Phys. Lett. B 2011, 23, 1577–1587. [Google Scholar] [CrossRef]
- Lister, T.; Burrows, E.; Dewan, A.S. Petersburg Metro Explosion: At Least 11 Dead in Russia Blast. Available online: https://edition.cnn.com/2017/04/03/europe/st-petersburg-russia-explosion (accessed on 3 April 2017).
- Wang, X.; Xu, J. Cascading failures in coupled map lattices. Phys. Rev. Stat. Nonl. Soft Matt. Phys. 2004, 70, 056113. [Google Scholar] [CrossRef]
- Velikovi, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Musso, A.; Vuchic, V. Characteristics of Metro Networks and Methodology for Their Evaluation; National Research Council, Transportation Research Board: Washington, DC, USA, 1988; pp. 22–33. [Google Scholar]
- Scott, D.; Novak, D.; Aultman-Hall, L.; Guo, F. Network Robustness Index: A new method for identifying critical links and evaluating the performance of transportation networks. J. Trans. Geogr. 2006, 14, 215–227. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Is the Boston subway a small-world network? Phys. Stat. Mech. Appl. 2002, 314, 109–113. [Google Scholar] [CrossRef] [Green Version]
- Seaton, K.A.; Hackett, L.M. Stations, trains and small-world networks. Phys. Stat. Mech. Appl. 2004, 339, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.Q.; Song, R. Reliability analysis of Guangzhou rail transit with complex network theory. J. Trans. Syst. Eng. Inf. Technol. 2010, 10, 194–200. [Google Scholar]
- Zhang, J.; Xu, X.; Hong, L.; Wang, S.; Fei, Q. Networked analysis of the Shanghai subway network, in China. Phys. Stat. Mech. Appl. 2011, 390, 4562–4570. [Google Scholar] [CrossRef]
- Angeloudis, P.; Fisk, D. Large subway systems as complex networks. Phys. Stat. Mech. Appl. 2006, 367, 553–558. [Google Scholar] [CrossRef]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. Stat. Mech. Appl. 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhou, M.; Li, F.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing Subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Y.; Huang, Y.; Yao, L. Vulnerability Assessment of Urban Rail Transit based on Multi-static Weighted Method:A Case Study of Beijing, China. Trans. Res. Part Pol. Pract. 2016, 108, 12–24. [Google Scholar] [CrossRef]
- Chen, P.; Chen, F.; Hu, Y.; Li, X.; Wang, Z. On Urban Rail Transit Network Centrality Using Complex Network Theory. Complex Syst. Complex. Sci. 2017, 14, 97–102. [Google Scholar]
- Zio, E.; Golea, L.R.; Sansavini, G. Optimizing protections against cascades in network systems: A modified binary differential evolution algorithm. Reliab. Eng. Syst. Saf. 2012, 103, 72–83. [Google Scholar] [CrossRef] [Green Version]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. 2002, 66, 065102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.M.; Pang, S.P.; Zou, X.Q. An LCOR model for suppressing cascading failure in weighted complex networks. Chin. Phys. 2013, 22, 058901. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Ran, B. Analysis of cascading failure induced by load fluctuation and robust station capacity assignment for metros. Transportmetrica 2021, 18, 1–22. [Google Scholar] [CrossRef]
- Gade, P.; Hu, C.-K. Synchronous chaos in coupled map lattices with small-world interactions. Phys. Rev. Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 6409–6413. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Guan, S. Measuring vulnerability of urban metro network from line operation perspective. Transp. Res. Pol. Pract. 2016, 94, 348–359. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Ran, B. Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: A case study of Nanjing, China. Transportation 2021, 48, 537–553. [Google Scholar] [CrossRef]
- Lei, W.; Li, A.; Gao, R.; Hao, X.; Deng, B. Simulation of pedestrian crowds’ evacuation in a huge transit terminal subway station. Phys. Stat. Mech. Appl. 2012, 391, 5355–5365. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Q.; Xu, R. Simulation on the Dynamic Distribution of Passenger Flow in Urban Rail Transit. Urban Rail Transit. Res. 2006, 4, 70–73. [Google Scholar]
- Xu, R.; Luo, Q.; Gao, P. Passenger Flow Distribution Model and Algorithm for Urban Rail Transit Network Based on Multi-route Choice. J. China Rail. Soc. 2009, 2, 110–114. [Google Scholar]
- Hong, L.; Gao, J.; Xu, R. Calculation Method of Emergency Passenger Flow in Urban Rail Network. J. Tongji Univ. Nat. Sci. 2011, 39, 1485–1489. [Google Scholar]
- Yang, Z.; Li, J.; Shi, F.; He, J. Modeling of passenger travel choice affected by urban rail train delay. Urban Rail. Transit. 2020, 29, 60–64. [Google Scholar]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 2, pp. 729–734. [Google Scholar]
- Micheli, A. Neural Network for Graphs: A Contextual Constructive Approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Bruna, J.; Zaremba, W.; Szlam, A.; Lecun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Henaff, M.; Bruna, J.; Lecun, Y. Deep Convolutional Networks on Graph-Structured Data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Levie, R.; Monti, F.; Bresson, X.; Bronstein, M.M. CayleyNets: Graph Convolutional Neural Networks with Complex Rational Spectral Filters. IEEE Trans. Signal Proc. 2018, 67, 97–109. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Wang, S.K.; Ren, Y.B.; Wang, C.; Gao, P.; Chen, G. Predicting Station-Level Short-Term Passenger Flow in a Citywide Metro Network Using Spatiotemporal Graph Convolutional Neural Networks. ISPRS Int. J. Geo-Inf. 2019, 8, 243. [Google Scholar] [CrossRef] [Green Version]
- Gilmer, J.; Schoenholz, S.; Riley, P.; Vinyals, O.; Dahl, G. Neural Message Passing for Quantum Chemistry. arXiv 2017, arXiv:1704.01212. [Google Scholar]
- Hamilton, W.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. arXiv 2017, arXiv:1706.02216. [Google Scholar]
- Zhang, K.; He, F.; Zhang, Z.C.; Lin, X.; Li, M. Graph attention temporal convolutional network for traffic speed forecasting on road networks. Transportmetrica 2021, 9, 153–171. [Google Scholar] [CrossRef]
- Barabino, B.; Lai, C.T.; Olivo, A. Fare evasion in public transport systems: A review of the literature. Publ. Trans. 2020, 12, 27–88. [Google Scholar] [CrossRef]
- Huang, A.L.; Zhang, H.M.; Guan, W.; Yang, Y.; Zong, G.Q. Cascading Failures in Weighted Complex Networks of Transit Systems Based on Coupled Map Lattices. Math Probl. Eng. 2015, 2015, 1–16. [Google Scholar] [CrossRef]



| ID | Date | Time | Node | Vehicle | Cost | Discount |
|---|---|---|---|---|---|---|
| 3002779092 | 1 April 2015 | 07:23:50 | L3, ZhongTanRoad | metro | 0.0 | no |
| 3002779092 | 1 April 2015 | 07:44:36 | L4, BaoShanRoad | metro | 4.0 | no |
| Symbols | Definition |
|---|---|
| represents the characteristic information of metro station i (e.g., passenger flow or time). | |
| means that the current metro system doubles its passenger flow. | |
| means that there is an edge between node and ; otherwise, . | |
| , , | is the passenger flow through node . represents the in-flow of node , represents the out-flow of node . |
| , , | denotes the degree of node which is defined as the number of edges incident to node . denotes the in-degree of station and denotes the out-degree of station . |
| indicates the correlation between node i and node j. | |
| , , | is the coupling strength of topological structure. is the coupling strength of topological structure and is that of passenger flow. |
| , | is the topology coupling strength of the directed edge from node to node , is the passenger flow coupling strength of the directed edge from node to node . |
| , | represents the topology coupling strength mean of node and represents the topology coupling strength mean of node . |
| the passenger flow volume from station to station . | |
| denotes the state of node i at the t-th time step, | |
| defines the cumulative failure proportion of the network before the t-th time step. | |
| Balanced I | Balanced I is the stable as R increases. |
| represents the instant failure proportion. |
| Morning-1 | Morning-2 | Morning-3 | Morning-4 | Evening-1 | Evening-2 | Evening-3 | Evening-4 | |
|---|---|---|---|---|---|---|---|---|
| XZ | 4.0 | 3.6 | 3.5 | 3.5 | 4.2 | 4.0 | 4.0 | 4.2 |
| CA | 5.0 | 4.7 | 3.7 | 4.5 | 4.6 | 5.3 | 4.7 | 4.7 |
| SRS | 7.0 | 6.5 | 7.2 | 7.0 | 7.6 | 5.4 | 5.8 | 9.5 |
| RA | 6.0 | 6.2 | 6.2 | 6.3 | 6.3 | 6.5 | 6.5 | 6.3 |
| Station | p | p | p |
|---|---|---|---|
| SRS | 0.90 | 0.47 | 0.95 |
| CA | 0.82 | 0.84 | 0.84 |
| XZ | 0.59 | 0.59 | 0.58 |
| Method | MAE | MAPE | RMSE |
|---|---|---|---|
| GAT | 25.08 | 0.52 | 47.82 |
| GCN | 30.64 | 0.49 | 60.22 |
| Station | ||
|---|---|---|
| XZ | 1/2, 1/2 | 0.48, 0.52 |
| SRS | 1/4, 1/4, 1/4, 1/4 | 0.25, 0.24, 0.26, 0.25 |
| CA | 1/7, 1/7, 1/7, 1/7, 1/7, 1/7, 1/7 | 0.14, 0.14, 0.14, 0.14, 0.14, 0.15, 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, H.; Luo, X. Cascading Failure Analysis on Shanghai Metro Networks: An Improved Coupled Map Lattices Model Based on Graph Attention Networks. Int. J. Environ. Res. Public Health 2022, 19, 204. https://doi.org/10.3390/ijerph19010204
Ye H, Luo X. Cascading Failure Analysis on Shanghai Metro Networks: An Improved Coupled Map Lattices Model Based on Graph Attention Networks. International Journal of Environmental Research and Public Health. 2022; 19(1):204. https://doi.org/10.3390/ijerph19010204
Chicago/Turabian StyleYe, Haonan, and Xiao Luo. 2022. "Cascading Failure Analysis on Shanghai Metro Networks: An Improved Coupled Map Lattices Model Based on Graph Attention Networks" International Journal of Environmental Research and Public Health 19, no. 1: 204. https://doi.org/10.3390/ijerph19010204
APA StyleYe, H., & Luo, X. (2022). Cascading Failure Analysis on Shanghai Metro Networks: An Improved Coupled Map Lattices Model Based on Graph Attention Networks. International Journal of Environmental Research and Public Health, 19(1), 204. https://doi.org/10.3390/ijerph19010204






