Shallow Failure of Weak Slopes in Bayan Obo West Mine
Abstract
:1. Introduction
2. Analysis on the Deformation Mechanism of the Shallow Layer of Soft Rock Slope
2.1. Analysis of Blasting-Damage Layer
- (1)
- Fracture extension range
- (2)
- Parameter modification
2.2. Determination of Key Mechanical Parameters of Rock Mass
2.3. Calculation of Rock Mechanics Parameters
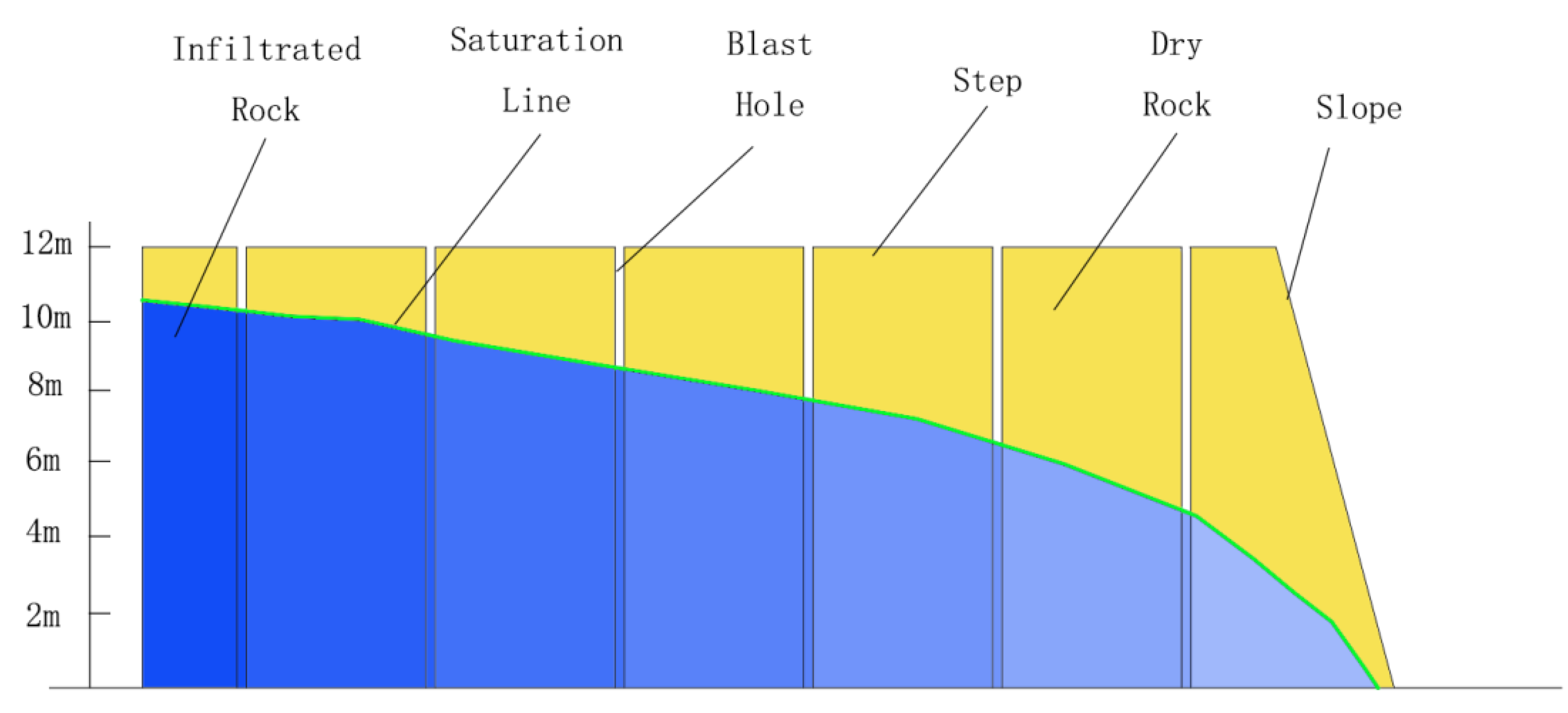
2.4. Analysis of Water Content in Slope
3. Slope Stability Analysis
3.1. Mechanical Parameters of Shallow Rock Mass
3.2. Deformation Analysis of Shallow Rock Mass on Weak Rock Slope
3.3. Slope Surface Displacement Monitoring
3.4. Case Analysis of Shallow Failure
4. Conclusions
- (1)
- After disturbance, the mechanical strength parameters of the shallow rock mass of the weak rock slope in West Mine are obviously inferior to intact rock.
- (2)
- The shallow failure of the weak rock slope in the West Mine experienced such a process where the slope body first underwent large deformation and displacement along the slope toe; then, the slope rock mass began to collapse, and finally, the creep at the bottom of the step pulled the top apart to form a shallow collapse. This deformation and failure mode conforms to the creep–crack mode.
- (3)
- The numerical simulation was carried out by using the parameter-assigning method for weak rock slope layer by layer. The simulation results were very close to the real slope slide failure, which shows the scientificity of this method.
- (4)
- The rule of cumulative displacement and deformation of the soft rock slope of the West Mine is that the toe of the slope is 3–5 times that of the top of the slope.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, H.; Li, C.; Zhou, J.-Q.; Gu, X.; Duan, Y.; Liao, L.; Chen, W.; Zhu, Y.; Long, J. A large-scale obliquely inclined bedding rockslide triggered by heavy rainstorm on the 8th of July 2020 in Shiban Village, Guizhou, China. Landslides 2022, 19, 1119–1130. [Google Scholar]
- Zhou, M.; Li, J.; Luo, Z.; Sun, J.; Xu, F.; Qiao Jiang, Q.; Deng, H. Impact of water–rock interaction on the pore structures of red-bed soft rock. Sci. Rep. 2021, 11, 97–104. [Google Scholar]
- Song, Y.; Chen, L.; Zhang, X.; Zhao, Q.; Yu, L.; Xu, J. Experimental investigation on the deformation and failure mechanism of slope with interbedding soft and hard rocks under rainfall infiltration. E3S Web Conf. 2020, 194, 04056. [Google Scholar]
- Bao, C.; Zhan, L.; Xia, Y.; Huang, Y.; Zhao, Z. Development Trend and Stability Analysis of Creep Landslide with Obvious Slip Zone Under Rainfall-Taking Xinchang Xiashan Basalt Slope as an Example. Front. Earth Sci. 2022, 9, 184–192. [Google Scholar]
- JLuo, J.; Zhu, W.; Xiao, C.; Ouyang, J.; Feng, Z.; Shuai, Q.; Zhang, Z.; Zhong, W. Detection of a Weak Structural Stratum and Stability Analysis of the Slope in an Intensely Weathered Open-pit Mine. IOP Conf. Series: Earth Environ. Sci. 2021, 861, 022044. [Google Scholar]
- Lou, C.; Yan, G.X. Dynamic response law and instability mechanism of steep inclined soft-hard interphase bedding slope under strong earthquakes. Ferroelectrics 2021, 580, 129–142. [Google Scholar]
- Zhan, J.W.; Wang, Q.; Zhang, W.; Shangguan, Y.; Song, S.; Chen, J. Soil-engineering properties and failure mechanisms of shallow landslides in soft-rock materials. Catena 2019, 181, 301–315. [Google Scholar]
- Wu, T.Y. Stability analysis for high-steep slope subjected to repeated blasting vibration. Arab. J. Geosci. 2020, 13, 826–828. [Google Scholar]
- Yang, J.H. Discussion on blasting vibration monitoring for rock damage control in rock slope excavation. Earthq. Eng. Eng. Vib. 2022, 21, 53–65. [Google Scholar]
- Li, H.; Zhong, D.W.; Liu, Y.H.; Song, K.; Jiang, N. Prediction of Bench Blasting Vibration on Slope and Safety Threshold of Blasting Vibration Velocity to Undercrossing Tunnel. Shock. Vib. 2021, 2021, 9939361. [Google Scholar]
- Mariantonietta, C.; Settimio, F.; Vito, F.; Clorinda, M.M.; Nicola, M. Landslide Susceptibility Analysis by Applying TRIGRS to a Reliable Geotechnical Slope Model. Geosciences 2021, 12, 18. [Google Scholar]
- Chen, G.Q.; Li, H.W.; Wei, T.; Zhu, J. Searching for multistage sliding surfaces based on the discontinuous dynamic strength reduction method. Eng. Geol. 2021, 286, 826–828. [Google Scholar]
- Raina, A.K. Influence of Joint Conditions and Blast Design on Pre-split Blasting Using Response Surface Analysis. Rock Mech. Rock Eng. 2019, 52, 826–828. [Google Scholar]
- Seyedkhoei, A.; Akbari, R.; Maalek, S.; Karinski, Y.S. Earthquake-Induced Domino-Type Progressive Collapse in Regular, Semiregular, and Irregular Bridges. Shock. Vib. 2019, 13, 826–828. [Google Scholar]
- Lai, J.; Wang, Y.C.; Liu, Y. Blasting Excavation Induced Damage Caused to the Rock Mass Surrounding Tunnels. In Proceedings of the 2021 5th International Conference on Sustainable Energy Engineering (ICSEE 2021), Singapore, 3–5 February 2021; Volume 2021, pp. 100–102. [Google Scholar]
- Lin, Y.; Wei, W.; Hong, J. Analysis on Deformation Control Technology for Large-Span Subway Tunnels from High-Narrow Channel. In Proceedings of the 6th International Conference on Environmental Science and Civil Engineering (ESCE 2020), Hanoi, Vietnam, 28–30 December 2020; pp. 1322–1330. [Google Scholar]
- Wang, D.J.; Wu, X.G.; Wang, L. Safety Analysis of the Tunnel Excavation Blasting and the Supporting. In Proceedings of the 2019 International Conference on Energy, Environmental and Civil Engineering(EECE 2019), Wuhan, China, 23 June–24 June 2020; Volume 2019, pp. 237–244. [Google Scholar]
- Raina, A.K. Importance and Sensitivity of Variables Defining the Performance of Pre-split Blasting Using Artificial Neural Networks. Metall. Explor. 2021, 38, 826–828. [Google Scholar]
- Wang, W.D.; Zhang, Y.; Jiang, H.T. Low cost quasi presplit blasting technology in side slope rock excavation. Chin. J. Sci. Instrum. 2021, 34, 293–296. [Google Scholar]
- Dai, J. Calculation of rock crushing circle and fracture circle in cylindrical charge blasting. J. Liaoning Tech. Univ. (Nat. Sci.) 2001, 20, 144–147. [Google Scholar]
- Yang, R.S. A fractal study on blasting damage of an eccentric decouple charge structure. J. Vib. Shock. 2020, 39, 129–134. [Google Scholar]
- Zhang, S.L. Damage Zone Test of Jointed Rock Slope under Pre-split Blasting. Blasting 2020, 37, 74–77,94. [Google Scholar]
- Wang, Z.G.; Zhao, W.B. Study on Effective Influence Range of Permeability Enhancement by Double Hole Presplitting Blasting in Low Permeability Coal Seam. Blasting 2020, 37, 75–80. [Google Scholar]
- Huang, Y.P.; Wang, Z.L.; Bi, C.C. Simulation analysis of blast-induced damage scope and its distribution characteristics of rocks. Hydro-Sci. Eng. 2018, 2018, 95–102. [Google Scholar]
- Dai, J. Rock Dynamic Characteristics and Blasting Theory; Metallurgical Industry Press: Beijing, China, 2013. [Google Scholar]
- Wu, S.C. Rock Mechanics, 1st ed.; Higher Education Press: Beijing, China, 2021. [Google Scholar]
- Sánchez, L.K.; Emery, X.; Séguret, S.A. Geostatistical modeling of Rock Quality Designation (RQD) and geotechnical zoning accounting for directional dependence and scale effect. Eng. Geol. 2021, 293, 826–828. [Google Scholar]
- Jun, Z.; Yang, X.J.; Lü, Q.; Yu, Z.; Deng, J.H.; Ding, Z.J. A new perspective for the directivity of Rock Quality Designation (RQD) and an anisotropy index of jointing degree for rock masses. Eng. Geol. 2018, 240, 81–94. [Google Scholar]
- Chakraborty, A.K.; Choudhury, P.B.; Ramulu, M.R. Development of Models for Fragmentation Prediction Based on Digital Image Analysis of Muck Piles in Large Opencast Coal Mines in India. In Proceedings of the Seventh International Symposium on Rock Fragmentation by Blasting, Beijing, China, 12 August 2002; Volume 2002, pp. 271–277. [Google Scholar]
- Du, S.G.; Xu, S.F.; Yang, S.F. Application of Rock Quality Designation (RQD) to Engineering Classification of Rocks. J. Eng. Geol. 2020, 2000, 351–356. [Google Scholar]
- Zhao, B.Y.; Li, Y.F.; Huang, W.; Wang, X.P.; Chen, C. Experimental study on mechanical properties of shale rock and its strength criterion. Arab. J. Geosci. 2021, 14, 264. [Google Scholar]
- Li, D.L.; Liu, X.R.; Li, X.W.; Liu, Y.Q. The Impact of Microearthquakes Induced by Reservoir Water Level Rise on Stability of Rock Slope. Shock. Vib. 2016, 2016, 7583108. [Google Scholar]
- Wang, Z.D. Testing Method for the Range of Fracture Zone of Rock Slope under Blasting Load. Shock. Vib. 2020, 2020, 5574696. [Google Scholar]
- Luo, Z.S. Research on the Influence of Moisture Condition on the Mechanical Properties and Microstructure of Sandstone. Shock. Vib. 2021, 2021, 4850650. [Google Scholar]
- He, C.L.; Yang, J. Experimental and numerical investigations of dynamic failure process in rock under blast loading. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2019, 83, 552–564. [Google Scholar]
- Chen, B.B.; Liu, C.Y.; Yang, J.X.; Russo, S. Design and Application of Blasting Parameters for Presplitting Hard Roof with the Aid of Empty-Hole Effect. Shock. Vib. 2018, 2018, 8749415. [Google Scholar]
- Alrammahi, F.S.; Abbas, S.A.; Khassaf, S.I.; Madhloom, H.M.; Aljaradin, M. Earthen slope stability using dimensional analysis. J. Phys. Conf. Ser. 2021, 1895, 826–828. [Google Scholar]
- Ez Eldin, M.A.M.; Tang, H.; Xu, Y.; Xiong, C.; Ge, Y. Engineering Geological and Geophysical Assessment of the 2009 Jiwei Shan Rockslide, Wulong, China. In Proceedings of the 2013 International Conference on Geology and Geophysics (ICGG 2013), Beijing, China, 16–18 June 2013; pp. 63–73. [Google Scholar]
- Wu, Z. Experimental Study on the Application of Rigid-framed Minipile in Landslide Reinforcement. In Proceedings of the 2012 2nd International Conference on Advanced Materials and Information Technology Processing (AMITP 2012), Taipei, Taiwan, 17–18 October 2012; Volume 33, pp. 365–369. [Google Scholar]
- Technical Code for Non-Coal Open Pit Mine Slope Engineering; China Planning Press: Beijing, China, 2015; pp. 88–89.
- Wei, W.B.; Cheng, Y.M.; Li, L. Three-dimensional slope failure analysis by the strength reduction and limit equilibrium methods. Comput. Geotech. 2009, 36, 70–80. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yan, Y.; Qu, Y.; Wang, P. Shallow Failure of Weak Slopes in Bayan Obo West Mine. Int. J. Environ. Res. Public Health 2022, 19, 9755. https://doi.org/10.3390/ijerph19159755
Wang W, Yan Y, Qu Y, Wang P. Shallow Failure of Weak Slopes in Bayan Obo West Mine. International Journal of Environmental Research and Public Health. 2022; 19(15):9755. https://doi.org/10.3390/ijerph19159755
Chicago/Turabian StyleWang, Wencai, Yongfu Yan, Yue Qu, and Pengfei Wang. 2022. "Shallow Failure of Weak Slopes in Bayan Obo West Mine" International Journal of Environmental Research and Public Health 19, no. 15: 9755. https://doi.org/10.3390/ijerph19159755
APA StyleWang, W., Yan, Y., Qu, Y., & Wang, P. (2022). Shallow Failure of Weak Slopes in Bayan Obo West Mine. International Journal of Environmental Research and Public Health, 19(15), 9755. https://doi.org/10.3390/ijerph19159755




