Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts
Abstract
:1. Introduction
2. Literature Review
2.1. Literature Review on Previous Research Efforts Analyzing Rear-End Crashes
2.2. Literature Review on Approaches for Unobserved Heterogeneity
3. Data Description
4. Methodology
5. Transferability Tests
6. Results and Discussion
6.1. Driver Characteristics
6.2. Vehicle Characteristics
6.3. Roadway Characteristics
6.4. Environmental Characteristics
6.5. Temporal Characteristics
6.6. Spatial Characteristics
6.7. Traffic Characteristics
6.8. Crash Characteristics
6.9. Random Parameters and Heterogeneity in Means and Variances
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable Description | 2014–2015 G2 | 2016–2017 G2 | 2018–2019 G2 | |||
|---|---|---|---|---|---|---|
| Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | |
| No Injury/Minor Injury/Severe Injury | 0.705/0.183/0.112 | 0.685/0.188/0.127 | 0.700/0.182/0.118 | 0.667/0.206/0.127 | 0.649/0.233/0.118 | 0.625/0.250/0.125 |
| Driver characteristics | ||||||
| Safety (1 if speeding, 0 otherwise) | 0.682 (0.471) | 0.675 (0.415) | 0.413 (0.492) | 0.712 (0.453) | 0.425 (0.494) | 0.443 (0.497) |
| Safety (1 if improper action, 0 otherwise) | 0.265 (0.268) | 0.221 (0.343) | 0.497 (0.434) | 0.285 (0.451) | 0.372 (0.345) | 0.357 (0.397) |
| Vehicle characteristics | ||||||
| Vehicle type (1 if passenger car, 0 otherwise) | 0.698 (0.499) | 0.871 (0.335) | 0.573 (0.495) | 0.715 (0.512) | 0.517 (0.500) | 0.793 (0.826) |
| Vehicle type (1 if minibus, 0 otherwise) | 0.045 (0.208) | 0.079 (0.314) | 0.012 (0.111) | 0.033 (0.177) | 0.027 (0.162) | 0.073 (0.291) |
| Vehicle type (1 if bus, 0 otherwise) | 0.006 (0.075) | 0.009 (0.096) | 0.012 (0.111) | 0.033 (0.177) | 0.013 (0.111) | 0.017 (0.128) |
| Vehicle type (1 if van, 0 otherwise) | 0.003 (0.059) | 0.003 (0.058) | 0 | 0.013 (0.115) | 0.011 (0.103) | 0.005 (0.069) |
| Vehicle type (1 if truck, 0 otherwise) | 0.309 (0.256) | 0.007 (0.086) | 0.341 (0.474) | 0.177 (0.382) | 0.392 (0.488) | 0.535 (0.499) |
| Vehicle type (1 if heavy truck, 0 otherwise) | 0.187 (0.390) | 0.133 (0.339) | 0.088 (0.283) | 0.267 (0.443) | 0.041 (0.160) | 0.035 (0.183) |
| Roadway characteristics | ||||||
| : Radius of the plane curve of front section (103 m) | 384.2 (481.9) | 406.3 (486.8) | 444.4 (493.1) | 441.2 (492.5) | 407.5 (487.2) | 381.3 (481.2) |
| : Radius of the horizontal curve (103 m) | 347.5 (471.5) | 369.0 (477.9) | 321.9 (462.2) | 353.1 (473.1) | 357.7 (474.6) | 426.4 (490.5) |
| Radius of the plane curve of back section (103 m) | 479.6 (496.2) | 441.364 (492.708) | 438.9 (492.3) | 444.3 (492.9) | 444.9 (493.0) | 460.15 (482.76) |
| : Length of the plane curve of front section (103 m) | 1.158 (0.733) | 1.195 (0.711) | 1.225 (0.720) | 1.220 (0.721) | 1.202 (0.698) | 1.592 (0.687) |
| : Length of the horizontal curve (103 m) | 1.605 (0.681) | 1.627 (0.671) | 1.611 (0.616) | 1.631 (0.612) | 1.632 (0.668) | 1.267 (0.761) |
| : Length of the plane curve of back section (103 m) | 1.278 (0.815) | 1.258 (0.785) | 1.185 (0.700) | 1.206 (0.737) | 1.183 (0.726) | 1.372 (0.738) |
| : Minimum longitudinal grade of current section (%) | 0.132 (0.355) | 0.131 (0.476) | 0.002 (0.449) | 0.012 (0.448) | 0.002 (0.456) | 0.016 (0.425) |
| : Length of the longitudinal slope corresponding to the minimum grade (m) | 749.314 (288.8) | 746.233 (270.1) | 736.906 (277.3) | 610.020 (218.2) | 759.360 (283.7) | 680.480 (325.1) |
| : Maximum longitudinal grade of current section (%) | 0.129 (1.064) | 0.113 (0.495) | 0.014 (1.116) | 0.008 (1.112) | 0.041 (1.107) | 0.006 (1.074) |
| : Length of the longitudinal slope corresponding to the maximum grade (m) | 657.368 (276.365) | 641.553 (259.8) | 630.817 (199.4) | 610.025 (218.2) | 627.570 (252.1) | 567.532 (274.3) |
| Environmental characteristics | ||||||
| Weather (1 if fine, 0 otherwise) | 0.219 (0.324) | 0.213 (0.424) | 0.271 (0.444) | 0.155 (0.331) | 0.251 (0.434) | 0.287 (0.452) |
| Weather (1 if cloudy, 0 otherwise) | 0.307 (0.461) | 0.385 (0.484) | 0.544 (0.498) | 0.373 (0.484) | 0.509 (0.488) | 0.397 (0.491) |
| Weather (1 if rainy, 0 otherwise) | 0.216 (0.412) | 0.346 (0.469) | 0.107 (0.309) | 0.357 (0.479) | 0.177 (0.267) | 0.278 (0.368) |
| Weather (1 if foggy, 0 otherwise) | 0.013 (0.115) | 0.045 (0.135) | 0.017 (0.128) | 0.049 (0.215) | 0.013 (0.111) | 0.029 (0.167) |
| Weather (1 if snowy, 0 otherwise) | 0.086 (0.280) | 0.011 (0.163) | 0.058 (0.234) | 0.066 (0.249) | 0.061 (0.239) | 0.012 (0.109) |
| Road surface condition (1 if icy, 0 otherwise) | 0.013 (0.115) | 0.021 (0.142) | 0.045 (0.207) | 0.032 (0.176) | 0.023 (0.151) | 0.015 (0.104) |
| Road surface condition (1 if wet, 0 otherwise) | 0.331 (0.456) | 0.326 (0.361) | 0.217 (0.412) | 0.214 (0.382) | 0.164 (0.318) | 0.227 (0.312) |
| Temporal characteristics | ||||||
| Time of week (1 if Monday, 0 otherwise) | 0.116 (0.320) | 0.116 (0.320) | 0.125 (0.330) | 0.112 (0.331) | 0.127 (0.333) | 0.109 (0.312) |
| Time of week (1 if Tuesday, 0 otherwise) | 0.097 (0.295) | 0.153 (0.360) | 0.101 (0.302) | 0.110 (0.313) | 0.131 (0.337) | 0.140 (0.347) |
| Time of week (1 if Wednesday, 0 otherwise) | 0.131 (0.337) | 0.157 (0.364) | 0.139 (0.346) | 0.142 (0.349) | 0.109 (0.312) | 0.129 (0.335) |
| Time of week (1 if Thursday, 0 otherwise) | 0.178 (0.383) | 0.159 (0.366) | 0.176 (0.381) | 0.183 (0.386) | 0.154 (0.361) | 0.135 (0.342) |
| Time of week (1 if Friday, 0 otherwise) | 0.170 (0.376) | 0.121 (0.327) | 0.166 (0.372) | 0.153 (0.360) | 0.172 (0.378) | 0.167 (0.373) |
| Time of week (1 if Saturday, 0 otherwise) | 0.176 (0.381) | 0.170 (0.376) | 0.137 (0.344) | 0.168 (0.374) | 0.177 (0.382) | 0.187 (0.390) |
| Time of week (1 if Sunday, 0 otherwise) | 0.132 (0.339) | 0.123 (0.329) | 0.157 (0.363) | 0.118 (0.322) | 0.124 (0.329) | 0.133 (0.339) |
| Time of day (1 if early morning (24:00–05:59), 0 otherwise) | 0.339 (0.473) | 0.703 (0.457) | 0.256 (0.437) | 0.272 (0.446) | 0.278 (0.448) | 0.287 (0.452) |
| Time of day (1 if morning (06:00–11:59), 0 otherwise) | 0.221 (0.415) | 0.121 (0.296) | 0.251 (0.434) | 0.1764 (0.381) | 0.260 (0.439) | 0.226 (0.418) |
| Time of day (1 if afternoon (12:00–17:59), 0 otherwise) | 0.290 (0.454) | 0.097 (0.296) | 0.267 (0.442) | 0.176 (0.381) | 0.303 (0.460) | 0.287 (0.452) |
| Time of day (1 if evening (18:00–23:59), 0 otherwise) | 0.150 (0.358) | 0.079 (0.269) | 0.190 (0.392) | 0.178 (0.382) | 0.159 (0.366) | 0.200 (0.400) |
| Season of year (1 if spring, 0 otherwise) | 0.410 (0.492) | 0.041 (0.199) | 0.438 (0.496) | 0.356 (0.479) | 0.314 (0.464) | 0.117 (0.322) |
| Season of year (1 if summer, 0 otherwise) | 0.263 (0.440) | 0.161 (0.367) | 0.194 (0.395) | 0.216 (0.411) | 0.228 (0.419) | 0.054 (0.226) |
| Season of year (1 if autumn, 0 otherwise) | 0.150 (0.358) | 0.473 (0.499) | 0.184 (0.388) | 0.248 (0.432) | 0.247 (0.432) | 0.011 (0.103) |
| Season of year (1 if winter, 0 otherwise) | 0.117 (0.382) | 0.325 (0.469) | 0.184 (0.388) | 0.181 (0.385) | 0.211 (0.408) | 0.007 (0.084) |
| Spatial characteristics | ||||||
| Location type (1 if crash occurred in the interchange, 0 otherwise) | 0.103 (0.459) | 0.155 (0.362) | 0.094 (0.292) | 0.112 (0.315) | 0.125 (0.331) | 0.294 (0.456) |
| Location type (1 if crash occurred on the bridge, 0 otherwise) | 0.301 (0.459) | 0.271 (0.445) | 0.284 (0.451) | 0.277 (0.448) | 0.301 (0.459) | 0.236 (0.424) |
| Traffic characteristics | ||||||
| AADT: Average annual daily traffic volume | 51700.6 (11314) | 50816.7 (11165) | 50983.9 (11426) | 52443.2 (10985) | 51476.5 (11512) | 52332.3 (10690) |
| Crash characteristics | ||||||
| EMS (Emergency Medical Service: 1 if arrive time is <20 min, 0 otherwise) | 0.048 (0.213) | 0.064 (0.244) | 0.041 (0.199) | 0.038 (0.190) | 0.038 (0.190) | 0.004 (0.060) |
| EMS (1 if arrive time is 20–60 min, 0 otherwise) | 0.566 (0.496) | 0.559 (0.497) | 0.596 (0.491) | 0.550 (0.498) | 0.529 (0.499) | 0.045 (0.208) |
| EMS (1 if arrive time is >60 min, 0 otherwise) | 0.386 (0.487) | 0.378 (0.497) | 0.363 (0.481) | 0.412 (0.492) | 0.434 (0.496) | 0.951 (0.216) |
| Variable Description | 2014–2015 G25 | 2016–2017 G25 | 2018–2019 G25 | |||
|---|---|---|---|---|---|---|
| Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | |
| No Injury/Minor Injury/Severe Injury | 0.643/0.227/0.130 | 0.620/0.250/0.130 | 0.619/0.248/0.134 | 0.589/0.277/0.134 | 0.575/0.298/0.127 | 0.549/0.315/0.136 |
| Driver characteristics | ||||||
| Safety (1 if speeding, 0 otherwise) | 0.315 (0.465) | 0.407 (0.491) | 0.166 (0.372) | 0.578 (0.493) | 0.403 (0.402) | 0.573 (0.495) |
| Safety (1 if improper action, 0 otherwise) | 0.622 (0.485) | 0.549 (0.498) | 0.723 (0.448) | 0.417 (0.493) | 0.527 (0.446) | 0.423 (0.494) |
| Vehicle characteristics | ||||||
| Vehicle type (1 if passenger car, 0 otherwise) | 0.218 (0.413) | 0.845 (0.361) | 0.297 (0.417) | 0.760 (0.427) | 0.465 (0.499) | 0.218 (0.413) |
| Vehicle type (1 if minibus, 0 otherwise) | 0.059 (0.236) | 0.055 (0.229) | 0.008 (0.089) | 0.036 (0.186) | 0.024 (0.153) | 0.059 (0.236) |
| Vehicle type (1 if bus, 0 otherwise) | 0.016 (0.125) | 0.043 (0.204) | 0.004 (0.063) | 0.032 (0.176) | 0.133 (0.366) | 0.016 (0.125) |
| Vehicle type (1 if van, 0 otherwise) | 0.212 (0.409) | 0.047 (0.212) | 0.343 (0.475) | 0.012 (0.108) | 0.037 (0.189) | 0.212 (0.409) |
| Vehicle type (1 if truck, 0 otherwise) | 0.231 (0.415) | 0.206 (0.404) | 0.186 (0.389) | 0.184 (0.387) | 0.201 (0.401) | 0.231 (0.415) |
| Vehicle type (1 if heavy truck, 0 otherwise) | 0.264 (0.429) | 0.213 (0.410) | 0.162 (0.368) | 0.064 (0.244) | 0.140 (0.347) | 0.264 (0.429) |
| Roadway characteristics | ||||||
| : Radius of the plane curve of front section (103 m) | 368.867 (481.4) | 350.781 (357.2) | 518.916 (498.8) | 371.343 (481.2) | 350.864 (475.8) | 373.050 (482.3) |
| : Radius of the horizontal curve (103 m) | 380.175 (483.6) | 347.131 (353.2) | 346.3 (473.6) | 465.208 (496.0) | 432.974 (492.8) | 464.845 (496.7) |
| Radius of the plane curve of back section (103 m) | 390.358 (452.2) | 363.0 (368.3) | 444.0 (495.8) | 327.936 (467.0) | 398.9 (488.2) | 330.004 (468.5) |
| : Length of the plane curve of front section (103 m) | 1.029 (0.794) | 1.024 (0.521) | 1.057 (0.632) | 1.051 (0.629) | 1.097 (0.729) | 1.025 (0.701) |
| : Length of the horizontal curve (103 m) | 1.268 (0.687) | 1.543 (0.718) | 1.175 (0.714) | 1.134 (0.693) | 1.419 (0.622) | 1.212 (0.629) |
| : Length of the plane curve of back section (103 m) | 1.027 (0.716) | 1.023 (0.697) | 0.989 (0.494) | 1.112 (0.624) | 1.015 (0.617) | 1.054 (0.627) |
| : Minimum longitudinal grade of current section (%) | 0.061 (0.428) | 0.022 (0.414) | 0.033 (0.515) | 0.028 (0.995) | −0.045 (0.540) | 0.026 (0.552) |
| : Length of the longitudinal slope corresponding to the minimum grade (m) | 662.286 (394.9) | 534.471 (428.3) | 712.380 (309.1) | 769.987 (306.8) | 753.042 (314.2) | 771.994 (306.8) |
| : Maximum longitudinal grade of current section (%) | 0.039 (1.194) | 0.122 (1.082) | −0.021 (1.478) | −0.072 (2.238) | −0.048 (1.215) | −0.041 (1.235) |
| : Length of the longitudinal slope corresponding to the maximum grade (m) | 616.312 (340.8) | 525.743 (370.9) | 560.618 (237.3) | 577.305 (270.1) | 754.493 (341.5) | 784.358 (277.5) |
| Environmental characteristics | ||||||
| Weather (1 if fine, 0 otherwise) | 0.103 (0.304) | 0.059 (0.236) | 0.308 (0.462) | 0.226 (0.418) | 0.127 (0.334) | 0.124 (0.329) |
| Weather (1 if cloudy, 0 otherwise) | 0.410 (0.492) | 0.455 (0.498) | 0.406 (0.462) | 0.563 (0.496) | 0.467 (0.499) | 0.548 (0.499) |
| Weather (1 if rainy, 0 otherwise) | 0.487 (0.500) | 0.486 (0.500) | 0.172 (0.378) | 0.212 (0.323) | 0.405 (0.491) | 0.327 (0.469) |
| Weather (1 if foggy, 0 otherwise) | 0 | 0 | 0.114 (0.316) | 0 | 0 | 0 |
| Weather (1 if snowy, 0 otherwise) | 0 | 0 | 0 | 0 | 0 | 0 |
| Road surface condition (1 if icy, 0 otherwise) | 0.013 (0.150) | 0 | 0 | 0 | 0 | 0 |
| Road surface condition (1 if wet, 0 otherwise) | 0.348 (0.464) | 0.314 (0.411) | 0.484 (0.500) | 0.517 (0.512) | 0.595 (0.491) | 0.672 (0.469) |
| Temporal characteristics | ||||||
| Time of week (1 if Monday, 0 otherwise) | 0.095 (0.293) | 0.134 (0.341) | 0.111 (0.314) | 0.179 (0.384) | 0.111 (0.314) | 0.142 (0.349) |
| Time of week (1 if Tuesday, 0 otherwise) | 0.154 (0.361) | 0.158 (0.365) | 0.139 (0.346) | 0.135 (0.342) | 0.138 (0.345) | 0.150 (0.357) |
| Time of week (1 if Wednesday, 0 otherwise) | 0.130 (0.337) | 0.126 (0.333) | 0.116 (0.319) | 0.131 (0.338) | 0.115 (0.319) | 0.130 (0.336) |
| Time of week (1 if Thursday, 0 otherwise) | 0.123 (0.328) | 0.142 (0.349) | 0.136 (0.342) | 0.135 (0.342) | 0.134 (0.341) | 0.116 (0.320) |
| Time of week (1 if Friday, 0 otherwise) | 0.158 (0.365) | 0.162 (0.368) | 0.156 (0.362) | 0.166 (0.372) | 0.158 (0.365) | 0.156 (0.363) |
| Time of week (1 if Saturday, 0 otherwise) | 0.189 (0.392) | 0.158 (0.365) | 0.143 (0.349) | 0.148 (0.356) | 0.142 (0.350) | 0.150 (0.357) |
| Time of week (1 if Sunday, 0 otherwise) | 0.150 (0.358) | 0.1119 (0.323) | 0.199 (0.399) | 0.105 (0.306) | 0.202 (0.401) | 0.156 (0.363) |
| Time of day (1 if early morning (24:00–05:59), 0 otherwise) | 0.158 (0.365) | 0.221 (0.415) | 0.188 (0.390) | 0.238 (0.426) | 0.186 (0.389) | 0.148 (0.355) |
| Time of day (1 if morning (06:00–11:59), 0 otherwise) | 0.328 (0.469) | 0.268 (0.443) | 0.270 (0.443) | 0.262 (0.440) | 0.269 (0.444) | 0.272 (0.445) |
| Time of day (1 if afternoon (12:00–17:59), 0 otherwise) | 0.296 (0.456) | 0.344 (0.475) | 0.363 (0.481) | 0.321 (0.467) | 0.360 (0.480) | 0.358 (0.480) |
| Time of day (1 if evening (18:00–23:59), 0 otherwise) | 0.217 (0.413) | 0.166 (0.372) | 0.179 (0.383) | 0.179 (0.384) | 0.186 (0.389) | 0.216 (0.412) |
| Season of year (1 if spring, 0 otherwise) | 0.154 (0.361) | 0.217 (0.413) | 0.311 (0.462) | 0.188 (0.391) | 0.316 (0.465) | 0.170 (0.376) |
| Season of year (1 if summer, 0 otherwise) | 0.178 (0.383) | 0.252 (0.434) | 0.239 (0.426) | 0.308 (0.462) | 0.237 (0.426) | 0.166 (0.372) |
| Season of year (1 if autumn, 0 otherwise) | 0.351 (0.478) | 0.292 (0.455) | 0.246 (0.430) | 0.336 (0.473) | 0.245 (0.430) | 0.400 (0.490) |
| Season of year (1 if winter, 0 otherwise) | 0.316 (0.465) | 0.237 (0.426) | 0.204 (0.402) | 0.168 (0.374) | 0.202 (0.401) | 0.264 (0.441) |
| Spatial characteristics | ||||||
| Location type (1 if crash occurred in the interchange, 0 otherwise) | 0.391 (0.488) | 0.328 (0.469) | 0.323 (0.467) | 0.297 (0.457)) | 0.320 (0.467) | 0.234 (0.424) |
| Location type (1 if crash occurred on the bridge, 0 otherwise) | 0.051 (0.221) | 0.071 (0.257) | 0.088 (0.283) | 0.153 (0.360) | 0.087 (0.282) | 0.060 (0.238) |
| Traffic characteristics | ||||||
| AADT: Average annual daily traffic volume | 50267.1 (11217) | 49486.2 (11928) | 51592.7 (11247) | 51497.4 (10947) | 48908.6 (11671) | 53621.1 (10514) |
| Crash characteristics | ||||||
| EMS (Emergency Medical Service: 1 if arrive time is <20 min, 0 otherwise) | 0.040 (0.167) | 0.213 (0.410) | 0.104 (0.304) | 0.105 (0.306) | 0.103 (0.304) | 0.172 (0.378) |
| EMS (1 if arrive time is 20–60 min, 0 otherwise) | 0.391 (0.413) | 0.336 (0.472) | 0.575 (0.446) | 0.434 (0.496) | 0.227 (0.448) | 0.324 (0.457) |
| EMS (1 if arrive time is >60 min, 0 otherwise) | 0.569 (0.517) | 0.451 (0.497) | 0.621 (0.485) | 0.461 (0.499) | 0.621 (0.486) | 0.504 (0.497) |
| Model Estimation Results | MNL | RPL | RPLM | RPLMV | ||||
|---|---|---|---|---|---|---|---|---|
| Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | |
| G2 2014–2015 | ||||||||
| Number of parameters (K) | 7 | 7 | 10 | 9 | 11 | 9 | 12 | 9 |
| Number of samples (n) | 703 | 695 | 703 | 695 | 703 | 695 | 703 | 695 |
| ) | −587.810 | −565.757 | −587.810 | −565.757 | −587.810 | −565.757 | −587.810 | −565.757 |
| ) | −188.954 | −182.628 | −182.471 | −171.658 | −179.547 | −167.984 | −174.842 | −164.797 |
| 0.679 | 0.677 | 0.690 | 0.697 | 0.695 | 0.703 | 0.703 | 0.709 | |
| Akaike information criterion (AIC) | 391.908 | 379.256 | 384.942 | 361.316 | 381.094 | 353.968 | 373.684 | 347.594 |
| Bayesian information criterion (BIC) | 423.795 | 411.063 | 430.496 | 402.211 | 431.203 | 394.863 | 428.348 | 388.489 |
| test | MNL vs. RPLMV 28.224(5) [>99.99%] | RPL vs. RPLMV 15.258(2) [>99.99%] | RPLM vs. RPLMV 9.41(1) [99.98%] | MNL vs. RPLMV 35.662(2) [>99.99%] | RPL vs. RPLMV - 1 | RPLM vs. RPLMV - | ||
| G2 2016–2017 | ||||||||
| Number of parameters (K) | 11 | 11 | 13 | 13 | 14 | 14 | 15 | 14 |
| Number of samples (n) | 739 | 768 | 739 | 768 | 739 | 768 | 739 | 768 |
| ) | −637.195 | −649.617 | −637.195 | −649.617 | −637.195 | −649.617 | −637.195 | −649.617 |
| ) | −243.704 | −241.628 | −236.584 | −234.957 | −223.628 | −226.947 | −219.704 | −222.689 |
| 0.618 | 0.628 | 0.629 | 0.638 | 0.649 | 0.651 | 0.655 | 0.657 | |
| Akaike information criterion (AIC) | 509.408 | 505.256 | 499.168 | 495.914 | 475.256 | 481.894 | 469.408 | 473.378 |
| Bayesian information criterion (BIC) | 560.066 | 556.338 | 559.037 | 556.283 | 539.730 | 546.907 | 538.487 | 538.391 |
| test | MNL vs. RPLMV 48.000(4) [>99.99%] | RPL vs. RPLMV 33.754(2) [>99.99%] | RPLM vs. RPLMV 7.848(1) [99.67%] | MNL vs. RPLMV 37.878(3) [>99.99%] | RPL vs. RPLMV 24.536(1) [>99.99%] | RPLM vs. RPLMV - | ||
| G2 2018–2019 | ||||||||
| Number of parameters (K) | 9 | 6 | 10 | 7 | 10 | 7 | 10 | 7 |
| Number of samples (n) | 822 | 829 | 822 | 829 | 822 | 829 | 822 | 829 |
| ) | −736.823 | −745.853 | −736.823 | −745.853 | −736.823 | −745.853 | −736.823 | −745.853 |
| ) | −267.627 | −235.574 | −254.157 | −221.628 | −252.628 | −218.957 | −249.874 | −215.903 |
| 0.637 | 0.684 | 0.655 | 0.703 | 0.657 | 0.706 | 0.661 | 0.711 | |
| Akaike information criterion (AIC) | 553.254 | 483.148 | 528.314 | 457.256 | 525.256 | 451.914 | 519.748 | 445.806 |
| Bayesian information criterion (BIC) | 595.660 | 511.469 | 575.431 | 490.298 | 572.373 | 484.956 | 566.865 | 478.848 |
| test | MNL vs. RPLMV 35.506(1) [>99.99%] | RPL vs. RPLMV - | RPLM vs. RPLMV - | MNL vs. RPLMV 39.342(1) [>99.99%] | RPL vs. RPLMV - | RPLM vs. RPLMV - | ||
| G25 2014–2015 | ||||||||
| Number of parameters (K) | 9 | 7 | 11 | 9 | 12 | 10 | 13 | 10 |
| Number of samples (n) | 515 | 589 | 515 | 589 | 515 | 589 | 515 | 589 |
| ) | −514.189 | −601.854 | −514.189 | −601.854 | −514.189 | −601.854 | −514.189 | −601.854 |
| ) | −188.628 | −203.628 | −189.257 | −198.547 | −184.628 | −191.584 | −178.076 | −187.494 |
| 0.633 | 0.662 | 0.632 | 0.670 | 0.641 | 0.682 | 0.654 | 0.688 | |
| Akaike information criterion (AIC) | 395.256 | 421.256 | 400.514 | 415.094 | 393.256 | 403.168 | 382.152 | 394.988 |
| Bayesian information criterion (BIC) | 433.454 | 451.905 | 447.200 | 454.500 | 444.186 | 446.952 | 437.326 | 438.772 |
| test | MNL vs. RPLMV 21.104(4) [>99.99%] | RPL vs. RPLMV 22.362(2) [>99.99%] | RPLM vs. RPLMV 13.104(1) [99.98%] | MNL vs. RPLMV 32.268(3) [>99.99%] | RPL vs. RPLMV 8.180(1) [99.78%] | RPLM vs. RPLMV - | ||
| G25 2016–2017 | ||||||||
| Number of parameters (K) | 8 | 7 | 9 | 9 | 10 | 9 | 10 | 9 |
| Number of samples (n) | 561 | 632 | 561 | 632 | 561 | 632 | 561 | 632 |
| ) | −549.624 | −621.594 | −549.624 | −621.594 | −549.624 | −621.594 | −549.624 | −621.594 |
| ) | −219.517 | −229.541 | −215.261 | −218.629 | −206.817 | −211.561 | −197.603 | −206.393 |
| 0.601 | 0.631 | 0.608 | 0.648 | 0.624 | 0.660 | 0.640 | 0.668 | |
| Akaike information criterion (AIC) | 455.034 | 473.082 | 448.522 | 455.258 | 433.634 | 441.122 | 415.216 | 430.786 |
| Bayesian information criterion (BIC) | 489.672 | 504.224 | 487.489 | 495.298 | 476.931 | 481.162 | 458.513 | 470.826 |
| test | MNL vs. RPLMV 43.828(2) [>99.99%] | RPL vs. RPLMV 35.316(1) [>99.99%] | RPLM vs. RPLMV - | MNL vs. RPLMV 46.296(2) [>99.99%] | RPL vs. RPLMV - | RPLM vs. RPLMV - | ||
| G25 2018–2019 | ||||||||
| Number of parameters (K) | 10 | 11 | 12 | 14 | 12 | 15 | 12 | 16 |
| Number of samples (n) | 621 | 712 | 621 | 712 | 621 | 712 | 621 | 712 |
| ) | −613.978 | −664.739 | −613.978 | −664.739 | −613.978 | −664.739 | −613.978 | −664.739 |
| ) | −234.847 | −261.254 | −228.517 | −252.629 | −221.594 | −248.957 | −214.273 | −243.155 |
| 0.617 | 0.607 | 0.628 | 0.620 | 0.639 | 0.625 | 0.651 | 0.634 | |
| Akaike information criterion (AIC) | 489.694 | 544.508 | 481.034 | 533.258 | 467.188 | 527.914 | 452.546 | 518.31 |
| Bayesian information criterion (BIC) | 534.007 | 594.757 | 534.210 | 597.211 | 520.364 | 596.435 | 505.722 | 591.399 |
| test | MNL vs. RPLMV 41.148 (2) [>99.99%] | RPL vs. RPLMV - | RPLM vs. RPLMV - | MNL vs. RPLMV 36.198 (5) [>99.99%] | RPL vs. RPLMV 18.948 (2) [>99.99%] | RPLM vs. RPLMV 11.604 (1) [>99.99%] | ||
| Variable | 2014–2015 G2 | 2016–2017 G2 | 2018–2019 G2 | |||
|---|---|---|---|---|---|---|
| Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | |
| Random parameter (normally distributed) | ||||||
| [NI] Constant | −0.582 (−2.87) | 3.017 (3.40) | 2.105 (3.58) | −3.057 (−6.54) | ||
| Standard deviation | 0.228 (2.19) | 0.221 (2.33) | 1.067 (2.07) | 2.657 (2.58) | ||
| [MI] Constant | 1.067 (2.19) | −1.262 (−2.32) | ||||
| Standard deviation | 1.049 (2.08) | 1.931 (2.90) | ||||
| [SI] Constant | −1.672 (−2.52) | −3.818 (−3.31) | ||||
| Standard deviation | 1.179 (2.28) | 2.092 (2.83) | ||||
| [NI] Time of week (1 if Tuesday, 0 otherwise) | 1.298 (2.20) | |||||
| Standard deviation | −1.128 (−2.17) | |||||
| [SI] Season of year (1 if spring, 0 otherwise) | −3.506 (−2.87) | |||||
| Standard deviation | 1.911 (2.62) | |||||
| [SI] AADT: Average annual daily traffic volume | −0.000130 (−2.83) | |||||
| Standard deviation | 0.000504 (2.58) | |||||
| Heterogeneity in the means of random parameter | ||||||
| [NI] Time of week (1 if Tuesday, 0 otherwise): Safety (1 if speeding, 0 otherwise) | 1.136 (2.18) | |||||
| [SI] Season of year (1 if spring, 0 otherwise): Time of day (1 if evening (18:00–23:59), 0 otherwise) | 2.136 (2.89) | |||||
| Heterogeneity in the variances of random parameter | ||||||
| [NI] Time of week (1 if Tuesday, 0 otherwise): Time of day (1 if early morning (24:00–05:59), 0 otherwise) | −1.304 (−2.97) | |||||
| [SI] Season of year (1 if spring, 0 otherwise): Weather (1 if rainy, 0 otherwise) | −1.628 (−2.18) | |||||
| [NI] Constant | 6.977 (5.13) | |||||
| [MI] Constant | −1.354 (−2.78) | |||||
| [SI] Constant | −0.583 (−2.37) | −4.079 (−5.56) | ||||
| Driver characteristics | ||||||
| [NI] Safety (1 if speeding, 0 otherwise) | −0.529 (−2.21) | |||||
| Vehicle characteristics | ||||||
| [NI] Vehicle type (1 if truck, 0 otherwise) | −1.947 (−3.46) | |||||
| [SI] Vehicle type (1 if truck, 0 otherwise) | 2.092 (2.61) | |||||
| [MI] Vehicle type (1 if heavy truck, 0 otherwise) | 6.689 (2.69) | |||||
| Roadway characteristics | ||||||
| : Length of the plane curve of front section (103 m) | 1.061 (2.70) | |||||
| : Radius of the horizontal curve (103 m) | −0.172 (−3.28) | −0.246 (−2.08) | ||||
| : Length of the horizontal curve (103 m) | −0.421 (−2.33) | |||||
| : Length of the horizontal curve (103 m) | 0.444 (2.71) | |||||
| : Length of the horizontal curve (103 m) | 0.654 (2.25) | |||||
| : Length of the longitudinal slope corresponding to the maximum grade (m) | 0.00223 (2.52) | |||||
| : Length of the longitudinal slope corresponding to the minimum grade (m) | 0.00401 (3.55) | |||||
| Environmental characteristics | ||||||
| [NI] Weather (1 if fine, 0 otherwise) | 1.006 (2.32) | |||||
| [MI] Weather (1 if fine, 0 otherwise) | −1.874 (−2.45) | |||||
| [MI] Weather (1 if cloudy, 0 otherwise) | 1.179 (2.52) | |||||
| Temporal characteristics | ||||||
| [SI] Time of week (1 if Monday, 0 otherwise) | 2.489 (2.63) | |||||
| [NI] Time of week (1 if Tuesday, 0 otherwise) | −1.042 (−2.79) | |||||
| [SI] Time of week (1 if Tuesday, 0 otherwise) | 2.589 (2.39) | |||||
| [NI] Time of week (1 if Saturday, 0 otherwise) | −2.252 (−2.76) | |||||
| [SI] Time of week (1 if Saturday, 0 otherwise) | 2.336 (2.62) | |||||
| [NI] Time of day (1 if early morning (24:00–05:59), 0 otherwise) | −0.904 (−2.47) | −0.639 (−1.99) | −0.628 (−3.67) | |||
| [MI] Time of day (1 if early morning (24:00–05:59), 0 otherwise) | 0.691 (2.79) | |||||
| [SI] Time of day (1 if afternoon (12:00–17:59), 0 otherwise) | −1.978 (−2.51) | |||||
| [NI] Time of day (1 if evening (18:00–23:59), 0 otherwise) | −2.013 (−2.57) | |||||
| [SI] Time of day (1 if evening (18:00–23:59), 0 otherwise) | 2.770 (4.06) | |||||
| [SI] Season of year (1 if spring, 0 otherwise) | −2.591 (−2.02) | |||||
| [MI] Season of year (1 if winter, 0 otherwise) | 0.713 (2.61) | |||||
| Spatial characteristics | ||||||
| [MI] Location type (1 if crash occurred on the bridge, 0 otherwise) | −7.261 (−2.51) | |||||
| [SI] Location type (1 if crash occurred on the bridge, 0 otherwise) | 1.006 (2.17) | |||||
| Traffic characteristics | ||||||
| [NI] AADT: Average annual daily traffic volume | 0.000589 (4.02) | 0.000141 (2.95) | ||||
| [SI] AADT: Average annual daily traffic volume | −0.000131 (−2.83) | −0.000321 (−2.82) | ||||
| Crash characteristics | ||||||
| [SI] Emergency Medical Service (1 if arrive time is 20–60 min, 0 otherwise) | −1.737 (−2.11) | |||||
| Number of parameters (K) | 12 | 9 | 15 | 14 | 10 | 7 |
| Number of samples (n) | 703 | 695 | 739 | 768 | 822 | 829 |
| ) | −587.810 | −565.757 | −637.195 | −649.617 | −736.823 | −745.853 |
| ) | −174.842 | −164.797 | −219.704 | −222.689 | −249.874 | −215.903 |
| 0.703 | 0.709 | 0.655 | 0.657 | 0.661 | 0.711 | |
| Akaike information criterion (AIC) | 373.684 | 347.594 | 469.408 | 473.378 | 519.748 | 445.806 |
| Bayesian information criterion (BIC) | 428.348 | 388.489 | 538.487 | 538.391 | 566.865 | 478.848 |
| Variable | 2014–2015 G25 | 2016–2017 G25 | 2018–2019 G25 | |||
|---|---|---|---|---|---|---|
| Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | Two-Vehicle | Multi-Vehicle | |
| Random parameter (normally distributed) | ||||||
| [NI] Constant | 1.734 (5.60) | 0.720 (3.08) | 0.245 (2.51) | |||
| Standard deviation | 0.558 (2.66) | 0.283 (2.17) | 0.687 (2.35) | |||
| [MI] Constant | −0.431 (−2.70) | −0.794 (−2.43) | ||||
| Standard deviation | 2.227 (2.59) | 0.730 (2.38) | ||||
| [SI] Constant | −3.685 (−4.88) | −6.294 (−2.50) | −4.080 (−3.92) | −3.679 (−4.02) | ||
| Standard deviation | 2.355 (3.31) | 2.227 (2.09) | 2.607 (2.40) | 2.156 (2.15) | ||
| [NI] Weather (1 if rainy, 0 otherwise) | 0.736 (2.18) | |||||
| Standard deviation | 0.836 (2.62) | |||||
| [MI] Time of day (1 if evening (18:00–23:59), 0 otherwise) | −0.666 (−2.96) | |||||
| Standard deviation | 3.33 (2.03) | |||||
| : Length of the longitudinal slope corresponding to the minimum grade (m) | −0.476 (−2.13) | |||||
| Standard deviation | 0.635 (2.69) | |||||
| [MI] Location type (1 if crash occurred on the bridge, 0 otherwise) | 0.892 (2.28) | |||||
| Standard deviation | 0.598 (2.16) | |||||
| Heterogeneity in the means of random parameter | ||||||
| [NI] Weather (1 if rainy, 0 otherwise): Safety (1 if speeding, 0 otherwise) | −1.325 (−2.98) | |||||
| [MI] Time of day (1 if evening (18:00–23:59), 0 otherwise): Time of week (1 if Sunday, 0 otherwise) | −0.591 (−2.47) | |||||
| : Length of the longitudinal slope corresponding to the minimum grade (m): Weather (1 if rainy, 0 otherwise) | −0.000231 (−3.97) | |||||
| [MI] Location type (1 if crash occurred on the bridge, 0 otherwise): Weather (1 if rainy, 0 otherwise) | 0.768 (2.01) | |||||
| Heterogeneity in the variances of random parameter | ||||||
| [NI] Weather (1 if rainy, 0 otherwise): Vehicle type (1 if passenger car, 0 otherwise | 1.035 (2.17) | |||||
| [MI] Time of day (1 if evening (18:00–23:59), 0 otherwise): Safety (1 if speeding, 0 otherwise) | 1.306 (2.01) | |||||
| [MI] Constant | 1.025 (2.12) | 1.610 (4.28) | ||||
| [SI] Constant | −3.457 (−5.90) | |||||
| Vehicle characteristics | ||||||
| [NI] Vehicle type (1 if passenger car, 0 otherwise) | 0.420 (2.14) | |||||
| [MI] Vehicle type (1 if passenger car, 0 otherwise) | −1.273 (−2.35) | |||||
| [MI] Vehicle type (1 if truck, 0 otherwise) | −0.396 (−2.26) | |||||
| [SI] Vehicle type (1 if truck, 0 otherwise) | 2.353 (3.01) | |||||
| [SI] Vehicle type (1 if heavy truck, 0 otherwise) | 1.923 (2.21) | 2.655 (2.03) | 0.948 (2.48) | |||
| Roadway characteristics | ||||||
| : Radius of the plane curve of front section (103 m) | −0.00137 (−2.65) | |||||
| : Length of the horizontal curve (103 m) | −0.119 (−2.58) | |||||
| : Length of the horizontal curve (103 m) | 0.663 (2.45) | |||||
| Environmental characteristics | ||||||
| [NI] Weather (1 if cloudy, 0 otherwise) | −0.533 (−2.69) | |||||
| [MI] Weather (1 if cloudy, 0 otherwise) | 0.563 (2.03) | |||||
| [MI] Weather (1 if rainy, 0 otherwise) | 0.422 (2.39) | 0.185 (2.63) | ||||
| Temporal characteristics | ||||||
| [MI] Time of week (1 if Monday, 0 otherwise) | 2.310 (2.40) | |||||
| [SI] Time of week (1 if Monday, 0 otherwise) | 0.651 (2.38) | |||||
| [SI] Time of week (1 if Thursday, 0 otherwise) | 1.987 (2.50) | |||||
| [MI] Time of week (1 if Saturday, 0 otherwise) | −0.892 (−2.25) | |||||
| [MI] Time of week (1 if Sunday, 0 otherwise) | 0.279 (2.72) | |||||
| [MI] Time of day (1 if early morning (24:00–05:59), 0 otherwise) | 0.501 (2.03) | |||||
| [SI] Time of day (1 if early morning (24:00–05:59), 0 otherwise) | 1.602 (2.71) | 2.289 (2.63) | 0.363 (2.59) | |||
| [NI] Season of year (1 if summer, 0 otherwise) | −0.403 (−2.22) | |||||
| [NI] Season of year (1 if autumn, 0 otherwise) | −0.152 (−2.20) | |||||
| [SI] Season of year (1 if winter, 0 otherwise) | 1.721 (2.30) | |||||
| Spatial characteristics | ||||||
| [SI] Location type (1 if crash occurred in the interchange, 0 otherwise) | −2.201 (−2.74) | |||||
| Traffic characteristics | ||||||
| [NI] AADT: Average annual daily traffic volume | 0.000158 (2.68) | 0.000267 (3.16) | 0.000249 (2.67) | |||
| [SI] AADT: Average annual daily traffic volume | −0.000368 (−2.37) | |||||
| Crash characteristics | ||||||
| [MI] Emergency Medical Service (1 if arrive time is <20 min, 0 otherwise) | 1.356 (2.96) | 1.178 (2.74) | ||||
| [MI] Emergency Medical Service (1 if arrive time is 20–60 min, 0 otherwise) | 0.894 (3.36) | 1.100 (2.37) | ||||
| [SI] Emergency Medical Service (1 if arrive time is >60 min, 0 otherwise) | 1.522 (2.02) | |||||
| Number of parameters (K) | 13 | 10 | 10 | 9 | 12 | 16 |
| Number of samples (n) | 515 | 589 | 561 | 632 | 621 | 712 |
| ) | −514.189 | −601.854 | −549.624 | −621.594 | −613.978 | −664.739 |
| ) | −178.076 | −187.494 | −197.608 | −206.393 | −214.273 | −243.155 |
| 0.654 | 0.688 | 0.640 | 0.668 | 0.651 | 0.634 | |
| Akaike information criterion (AIC) | 382.152 | 394.988 | 415.216 | 430.786 | 452.546 | 518.310 |
| Bayesian information criterion (BIC) | 437.326 | 438.772 | 458.513 | 470.826 | 505.722 | 591.399 |
| Variable | 2014–2015 G2 | 2016–2017 G2 | 2018–2019 G2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NI | MI | SI | NI | MI | SI | NI | MI | SI | |
| Driver characteristics | |||||||||
| Safety (1 if speeding, 0 otherwise) | – (–) | – (–) | – (–) | –0.0282 * (–) | 0.0203 (–) | 0.0079 (–) | – (–) | – (–) | – (–) |
| Vehicle characteristics | |||||||||
| Vehicle type (1 if truck, 0 otherwise) | – (−0.0183) | – (0.0129) | – (0.0054) | – (–) | – (–) | – (–) | – (−0.0648) | – (−0.0017) | – (0.0665) |
| Vehicle type (1 if heavy truck, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | –0.0468 (–) | 0.0491 (–) | –0.0023 (–) |
| Roadway characteristics | |||||||||
| – (–) | – (–) | – (–) | – (−0.0300) | – (−0.0029) | – (0.0329) | – (–) | – (–) | – (–) | |
| – (–) | – (–) | – (–) | 0.0259 (0.0188) | 0.0029 (0.0069) | –0.0288 (−0.0257) | – (–) | – (–) | – (–) | |
| –0.0667 (–) | –0.0099 (–) | 0.0766 (–) | –0.0554 (−0.0547) | 0.0406 (0.0561) | 0.0149 (−0.0013) | – (–) | – (–) | – (–) | |
| – (–) | – (–) | – (–) | 0.0877 (–) | –0.0544 (–) | –0.0332 (–) | – (–) | – (–) | – (–) | |
| – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | –0.0668 (–) | 0.0821 (–) | –0.0153 (–) | |
| Environmental characteristics | |||||||||
| Weather (1 if fine, 0 otherwise) | – (–) | – (–) | – (–) | – (0.0060) | – (−0.0062) | – (0.0002) | – (–) | – (–) | – (–) |
| Weather (1 if cloudy, 0 otherwise) | – (−0.0187) | – (0.0210) | – (−0.0024) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Temporal characteristics | |||||||||
| Time of week (1 if Monday, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | –0.0185 (–) | –0.0005 (–) | 0.0190 (–) |
| Time of week (1 if Tuesday, 0 otherwise) | – (–) | – (–) | – (–) | −0.0156 (−0.0108) | −0.0022 (0.0075) | 0.0178 (0.0033) | – (−0.0065) | – (0.0052) | – (0.0013) |
| Time of week (1 if Thursday, 0 otherwise) | – (–) | – (–) | – (–) | –0.0163 (−0.0127) | 0.0123 (−0.0010) | 0.0040 (0.0137) | – (–) | – (–) | – (–) |
| Time of week (1 if Saturday, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | –0.0227 (−0.0095) | –0.0007 (0.0071) | 0.0234 (0.0024) |
| Time of day (1 if early morning (24:00–05:59)) | – (−0.0520) | – (0.0301) | – (0.0219) | –0.0151 (−0.0547) | 0.0109 (0.0561) | 0.0042 (−0.0014) | – (−0.0175) | – (0.0142) | – (0.0033) |
| Time of day (1 if afternoon (12:00–17:59), 0 otherwise) | – (–) | – (–) | – (–) | 0.0058 (–) | 0.0008 (–) | –0.0066 (–) | – (–) | – (–) | – (–) |
| Time of day (1 if evening (18:00–23:59), 0 otherwise) | –0.0214 (–) | –0.0024 (–) | 0.0238 (–) | – (–) | – (–) | – (–) | – (−0.0085) | – (0.0062) | – (0.0023) |
| Season of year (1 if spring, 0 otherwise) | 0.0277 (–) | −0.0198 (–) | −0.0079 (–) | – (0.0049) | – (0.0007) | – (−0.0056) | 0.0120 (–) | 0.0007 (–) | −0.0127 (–) |
| Season of year (1 if winter, 0 otherwise) | – (−0.0119) | – (0.0129) | – (−0.0010) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Spatial characteristics | |||||||||
| Location type (1 if crash occurred in the bridge, 0 otherwise) | –0.0197 (–) | –0.0027 (–) | 0.0224 (–) | – (–) | – (–) | – (–) | 0.0151 (–) | –0.0155 (–) | 0.0004 (–) |
| Traffic characteristics | |||||||||
| AADT: Average annual daily traffic volume | 0.0720 (0.0624) | –0.0468 (−0.0379) | –0.0152 (−0.0245) | – (0.0612) | – (0.0052) | – (−0.0664) | 0.0717 (–) | 0.0251 (–) | –0.0968 (–) |
| Crash characteristics | |||||||||
| EMS (1 if arrive time is >60 min, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | – (0.0096) | – (0.0002) | – (−0.0098) |
| Variable | 2014–2015 G25 | 2016–2017 G25 | 2018–2019 G25 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NI | MI | SI | NI | MI | SI | NI | MI | SI | |
| Vehicle characteristics | |||||||||
| Vehicle type (1 if passenger car, 0 otherwise) | – (–) | – (–) | – (–) | – (0.0714) | – (−0.0840) | – (0.0126) | – (0.0253) | – (–0.0238) | – (−0.0015) |
| Vehicle type (1 if truck, 0 otherwise) | −0.0096 (0.0280) | −0.0157 (−0.0337) | 0.0253 * (0.0057) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Vehicle type (1 if heavy truck, 0 otherwise) | –0.0024 (–) | –0.0033 (–) | 0.0057 (–) | – (−0.0136) | – (−0.0063) | – (0.0199) | – (−0.0071) | – (−0.0063) | – (0.0134) |
| Roadway characteristics | |||||||||
| – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | – (−0.0235) | – (−0.0210) | – (0.0445) | |
| – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | 0.0281 (−0.0195) | –0.0287 (−0.0173) | 0.0006 (0.0368) | |
| – (–) | – (–) | – (–) | –0.0170 (–) | 0.0163 (–) | 0.0007 (–) | – (–) | – (–) | – (–) | |
| Environmental characteristics | |||||||||
| Weather (1 if cloudy, 0 otherwise) | −0.0356 (–) | 0.0375 (–) | –0.0019 (–) | −0.0355 (–) | 0.0338 (–) | 0.0017 (–) | – (–) | – (–) | – (–) |
| Weather (1 if rainy, 0 otherwise) | – (−0.0382) | – (0.0458) | – (−0.0076) | – (–) | – (–) | – (–) | –0.0178 (−0.0314) | 0.0232 (0.0471) | –0.0054 (−0.0157) |
| Temporal characteristics | |||||||||
| Time of week (1 if Monday, 0 otherwise) | – (–) | – (–) | – (–) | – (−0.0355) | – (0.0370) | – (−0.0015) | –0.0013 (–) | –0.0008 (–) | 0.0021 (–) |
| Time of week (1 if Thursday, 0 otherwise) | – (–) | – (–) | – (–) | – (−0.0077) | – (−0.0027) | – (0.0104) | – (–) | – (–) | – (–) |
| Time of week (1 if Saturday, 0 otherwise) | – (0.0258) | – (−0.0314) | – (0.0056) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Time of week (1 if Sunday, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | –0.0098 (–) | 0.0100 (–) | –0.0002 (–) |
| Time of day (1 if early morning (24:00–05:59)) | – (–) | – (–) | – (–) | –0.0058 (−0.0093) | –0.0050 (−0.0033) | 0.0108 (0.0126) | –0.0123 (−0.0027) | 0.0126 (−0.0024) | –0.0003 (0.0051) |
| Time of day (1 if evening (18:00–23:59)) | 0.0220 (–) | –0.0242 (–) | 0.0022 (–) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Season of year (1 if summer, 0 otherwise) | – (–) | – (–) | – (–) | –0.0201 (–) | 0.0192 (–) | 0.0009 (–) | – (–) | – (–) | – (–) |
| Season of year (1 if autumn, 0 otherwise) | – (−0.0543) | – (0.0655) | – (−0.0112) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Season of year (1 if winter, 0 otherwise) | –0.0066 (–) | –0.0125 (–) | 0.0191 (–) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) |
| Spatial characteristics | |||||||||
| Location type (1 if crash occurred in the interchange, 0 otherwise) | – (−0.0461) | – (0.0548) | – (−0.0087) | – (–) | – (–) | – (–) | – (0.0032) | – (0.0030) | – (−0.0062) |
| Traffic characteristics | |||||||||
| AADT: Average annual daily traffic volume | – (0.0369) | – (−0.0172) | – (−0.0197) | 0.0487 (–) | −0.0298 (–) | −0.0189 (–) | 0.0435 (0.0748) | 0.0249 (−0.0364) | –0.0684 (−0.0384) |
| Crash characteristics | |||||||||
| Emergency Medical Service (1 if arrive time is <20 min, 0 otherwise) | –0.0230 (–) | 0.0266 (–) | –0.0036 (–) | – (–) | – (–) | – (–) | –0.0500 (–) | 0.0512 (–) | –0.0012 (–) |
| Emergency Medical Service (1 if arrive time is 20–60 min, 0 otherwise) | –0.0713 (–) | 0.0773 (–) | –0.0060 (–) | – (–) | – (–) | – (–) | –0.0821 (–) | 0.0841 (–) | –0.0020 (–) |
| Emergency Medical Service (1 if arrive time is >60 min, 0 otherwise) | – (–) | – (–) | – (–) | – (–) | – (–) | – (–) | – (−0.0047) | – (−0.0043) | – (0.0090) |
References
- World Health Organization. Global Status Report on Road Safety; World Health Organization: Geneva, Switzerland, 2018; ISBN 978-92-4-156568-4. [Google Scholar]
- Yan, X.; Radwan, E.; Abdel-Aty, M. Characteristics of rear-end accidents at signalized intersections using multiple logistic regression model. Accid. Anal. Prev. 2005, 37, 983–995. [Google Scholar] [CrossRef] [PubMed]
- Singh, S. Driver Attributes and Rear-End Crash Involvement Propensity; NHTSA Report DOT-HS-809-540; U.S. Department of Transportation: Washington, DC, USA, 2003. [Google Scholar]
- National Safety Council. National Safety Council Injury Facts 2020 Edition; National Safety Council: Itasca, IL, USA, 2020; Available online: https://injuryfacts.nsc.org/motor-vehicle/overview/type-of-crash/ (accessed on 1 June 2022).
- Traffic Management Bureau of the Ministry of Public Security. Statistics of Road Traffic Accidents in People’s Republic of China (2017); Traffic Management Bureau of the Ministry of Public Security: Beijing, China, 2018. [Google Scholar]
- Wang, C.; Chen, F.; Zhang, Y.; Wang, S.; Yu, B.; Cheng, J. Temporal stability of factors affecting injury severity in rear-end and non-rear-end crashes: A random parameter approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2022, 35, 100219. [Google Scholar] [CrossRef]
- Yu, M.; Zheng, C.; Ma, C. Analysis of injury severity of rear-end crashes in work zones: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2020, 27, 100126. [Google Scholar] [CrossRef]
- Zhang, K.; Hassan, M. Identifying the factors contributing to injury severity in work zone rear-end crashes. J. Adv. Transp. 2019, 2019, 1163. [Google Scholar] [CrossRef]
- Jung, S.; Jang, K.; Yoon, Y.; Kang, S. Contributing factors to vehicle to vehicle crash frequency and severity under rainfall. J. Saf. Res. 2014, 50, 1–10. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Tarefder, R.; Ma, J.; Wei, H.; Guan, H. A multinomial logit model-Bayesian network hybrid approach for driver injury severity analyses in rear-end crashes. Accid. Anal. Prev. 2015, 80, 76–88. [Google Scholar] [CrossRef]
- Qi, Y.; Srinivasan, R.; Teng, H.; Baker, R. Analysis of the frequency and severity of rear-end crashes in work zones. Traffic Inj. Prev. 2013, 14, 61–72. [Google Scholar] [CrossRef]
- Mannering, F.; Shankar, V.; Bhat, C. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Alnawmasi, N.; Mannering, F. A statistical assessment of temporal instability in the factors determining motorcyclist injury severities. Anal. Methods Accid. Res. 2019, 22, 100090. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. The temporal stability of factors affecting driver-injury severities in single-vehicle crashes: Some empirical evidence. Anal. Methods Accid. Res. 2015, 8, 7–32. [Google Scholar] [CrossRef]
- Yan, X.; He, J.; Zhang, C.; Liu, Z.; Wang, C.; Qiao, B. Temporal analysis of crash severities involving male and female drivers: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2021, 30, 100161. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. Determinants of bicyclist injury severities in bicycle-vehicle crashes: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2017, 16, 35–47. [Google Scholar] [CrossRef]
- Milton, J.; Shankar, V.; Mannering, F. Highway accident severities and the mixed logit model: An exploratory empirical analysis. Accid. Anal. Prev. 2008, 40, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, F.; Zhang, Y.; Cheng, J. Spatiotemporal instability analysis of injury severities in truck-involved and non-truck-involved crashes. Anal. Methods Accid. Res. 2022, 34, 100214. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Yang, J.; Milton, J.C. An explanatory analysis of driver injury severity in rear-end crashes using a decision table/Naive Bayes (DTNB) hybrid classifier. Accid. Anal. Prev. 2016, 90, 95–107. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. Time-of-day variations and temporal instability of factors affecting injury severities in large-truck crashes. Anal. Methods Accid. Res. 2019, 23, 100102. [Google Scholar] [CrossRef]
- Wang, H.; Sun, X.; He, Y. Effects of geometric features of rear-end crash accidents on mountainous two-lane highways. J. Beijing Univ. Technol. 2010, 36, 1236–1241. [Google Scholar]
- Yan, X.; Radwan, E. Analyses of rear-end crashes based on classification tree models. Traffic Inj. Prev. 2006, 7, 276–282. [Google Scholar] [CrossRef]
- Das, A.; Abdel-Aty, M. A combined frequency–severity approach for the analysis of rear-end crashes on urban arterials. Saf. Sci. 2011, 49, 1156–1163. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q.; Yan, X. Analysis of work zone rear-end crash risk for different vehicle-following patterns. Accid. Anal. Prev. 2014, 72, 449–457. [Google Scholar] [CrossRef]
- Mannering, F.; Bhat, C.; Shankar, V.; Abdel-aty, M. Big data, traditional data and the tradeoffs between prediction and causality in highway-safety analysis. Anal. Methods Accid. Res. 2020, 25, 100113. [Google Scholar] [CrossRef]
- Mannering, F. Temporal instability and the analysis of highway accident data. Accid. Anal. Prev. 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Islam, M.; Mannering, F. A temporal analysis of driver-injury severities in crashes involving aggressive and non-aggressive driving. Anal. Methods Accid. Res. 2020, 27, 100128. [Google Scholar] [CrossRef]
- Mannering, F.; Bhat, C. Analytic methods in accident research: Methodological frontier and future directions. Anal. Methods Accid. Res. 2014, 1, 1–22. [Google Scholar] [CrossRef]
- Yan, X.; He, J.; Zhang, C.; Liu, Z.; Wang, C.; Qiao, B. Spatiotemporal instability analysis considering unobserved heterogeneity of crash-injury severities in adverse weather. Anal. Methods Accid. Res. 2021, 32, 100182. [Google Scholar] [CrossRef]
- Chiou, Y.; Fu, C. Modeling crash frequency and severity with spatiotemporal dependence. Anal. Methods Accid. Res. 2015, 5, 43–58. [Google Scholar] [CrossRef]
- Xiao, D.; Xu, X.; Duan, L. Spatial-Temporal Analysis of Injury Severity with Geographically Weighted Panel Logistic Regression Model. J. Adv. Transp. 2019, 2019, 8521649. [Google Scholar] [CrossRef]
- Liu, J.; Hainen, A.; Li, X.; Nie, Q.; Nambisan, S. Pedestrian injury severity in motor vehicle crashes: An integrated spatio-temporal modeling approach. Accid. Anal. Prev. 2019, 132, 105272. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Abdelwahab, H. Modeling rear-end collisions including the role of driver’s visibility and light truck vehicles using a nested logit structure. Accid. Anal. Prev. 2004, 36, 447–456. [Google Scholar] [CrossRef]
- Truong, L.T.; Kieu, L.M.; Vu, T.A. Spatiotemporal and random parameter panel data models of traffic crash fatalities in Vietnam. Accid. Anal. Prev. 2016, 94, 153–161. [Google Scholar] [CrossRef]
- Meng, Q.; Weng, J. Evaluation of rear-end crash risk at work zone using work zone traffic data. Accid. Anal. Prev. 2011, 43, 1291–1300. [Google Scholar] [CrossRef] [PubMed]
- Ghasemzadeh, A.; Ahmed, M. Exploring factors contributing to injury severity at work zones considering adverse weather conditions. IATSS Res. 2019, 43, 131–138. [Google Scholar] [CrossRef]
- Malyshkina, N.; Mannering, F. Markov switching multinomial logit model: An application to accident-injury severities. Accid. Anal. Prev. 2009, 41, 829–838. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, A.; Jahangiri, A.; Berardi, V.; Machiani, S.G. Crash severity analysis of rear-end crashes in California using statistical and machine learning classification methods. J. Transp. Saf. Secur. 2018, 12, 522–546. [Google Scholar] [CrossRef]
- Champahom, T.; Jomnonkwao, S.; Chatpattananan, V.; Karoonsoontawong, A.; Ratanavaraha, V. Analysis of Rear-End Crash on Thai Highway: Decision Tree Approach. J. Adv. Transp. 2019, 2019, 2568978. [Google Scholar] [CrossRef]
- Washington, S.; Karlaftis, M.; Mannering, F. Statistical and Econometric Methods for Transportation Data Analysis, 2nd ed.; Taylor and Francis: Abingdon, UK; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Seraneeprakarn, P.; Huang, S.; Shankar, V.; Mannering, F.; Venkataraman, N.; Milton, J. Occupant injury severities in hybrid-vehicle involved crashes: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2017, 15, 41–55. [Google Scholar] [CrossRef]
- McFadden, D.; Train, K. Mixed MNL models for discrete response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, R.; King, M.; Shi, Q.; He, J.; Hu, Z. Spatiotemporal analysis of crash severity on rural highway: A case study in Anhui, China. Accid. Anal. Prev. 2022, 165, 106538. [Google Scholar] [CrossRef]
- Fountas, G.; Anastasopoulos, P.; Abdel-aty, M. Analysis of accident injury-severities using a correlated random parameters ordered probit approach with time variant covariates. Anal. Methods Accid. Res. 2018, 18, 57–68. [Google Scholar] [CrossRef]
- Yan, X.; He, J.; Wu, G.; Zhang, C.; Wang, C.; Ye, Y. Differences of overturned and hit-fixed-object crashes on rural roads accompanied by speeding driving: Accommodating potential temporal shifts. Anal. Methods Accid. Res. 2022, 35, 100220. [Google Scholar]
- Huang, H.; Siddiqui, C.; Abdel-Aty, M. Indexing crash worthiness and crash aggressivity by vehicle type. Accid. Anal. Prev. 2011, 43, 1364–1370. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Gu, W.; Zhang, X.; Wen, H.; Lee, J.; Hao, W. Analyzing freeway crash severity using a bayesian spatial generalized ordered logit model with conditional autoregressive priors. Accid. Anal. Prev. 2019, 127, 87. [Google Scholar] [CrossRef] [PubMed]
- The Ministry of Transport of People’s Republic of China (MTPRC). Specifications for Highway Safety Audit (JTG B05-2015); The Ministry of Transport of People’s Republic of China: Beijing, China, 2015. [Google Scholar]
- Sarhan, M.; Hassan, Y. Three-dimensional, probabilistic highway design: Sight distance application. Transp. Res. Rec. J. Transp. Res. Board 2008, 2060, 10–18. [Google Scholar] [CrossRef]
- Mortazavi, A.; Eskandarian, A.; Sayed, R. Effects of drowsiness on driving performance variables of commercial vehicle drivers. Int. J. Automot. Technol. 2009, 10, 391–404. [Google Scholar] [CrossRef]
- Wang, C.; Chen, F.; Zhang, Y.; Cheng, J. Analysis of injury severity in rear-end crashes on an expressway involving different types ofvehicles using random-parameters logit models with heterogeneity in means and variances. Transp. Lett. 2022, 1–12. [Google Scholar] [CrossRef]
- Yu, H.; Li, Z.; Zhang, G.; Liu, P. A latent class approach for driver injury severity analysis in highway single vehicle crash considering unobserved heterogeneity and temporal influence. Anal. Methods Accid. Res. 2019, 24, 100110. [Google Scholar] [CrossRef]
- Cheng, W.; Gill, G.; Sakrani, T.; Dasu, M.; Zhou, J. Predicting motorcycle crash injury severity using weather data and alternative Bayesian multivariate crash frequency models. Accid. Anal. Prev. 2017, 108, 172–180. [Google Scholar] [CrossRef]
- Yu, M.; Ma, C.; Shen, J. Temporal stability of driver injury severity in single-vehicle roadway departure crashes: A random thresholds random parameters hierarchical ordered probit approach. Anal. Methods Accid. Res. 2021, 29, 100144. [Google Scholar] [CrossRef]
- Li, Y.; Song, L.; David, W. Day-of-the-week variations and temporal instability of factors influencing pedestrian injury severity in pedestrian-vehicle crashes: A random parameters logit approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2021, 29, 100152. [Google Scholar] [CrossRef]
- Hou, Q.; Huo, X.; Leng, J.; Mannering, F. A note on out-of-sample prediction, marginal effects computations, and temporal testing with random parameters crash-injury severity models. Anal. Methods Accid. Res. 2022, 33, 100191. [Google Scholar] [CrossRef]
- Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Vehicle occupant injury severity on highways: An empirical investigation. Accid. Anal. Prev. 2010, 42, 1606–1620. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Abdel-Aty, M. Analyzing crash injury severity for a mountainous freeway incorporating real-time traffic and weather data. Safe Sci. 2014, 63, 50–56. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, M.; Cai, Q.; Wang, L. Effects of emergency medical services times on traffic injury severity: A random-effects ordered probit approach. Traffic Inj. Prev. 2018, 19, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Wen, H.; Huang, H. The interactive effect on injury severity of driver-vehicle units in two-vehicle crashes. J. Saf. Res. 2016, 59, 105–111. [Google Scholar] [CrossRef]
| Variable Names | Findings |
|---|---|
| Driver characteristics | |
| Gender | Inconsistent findings have been demonstrated about the effects of gender on the injury severity in different types of crashes [12,15,20]. However, a limited body of studies exclusively analyzed the effects of rear-end crashes on injury severity. For instance, Zhang and Hassan [8] indicated that male drivers increased the possibility of fatal rear-end crashes compared to female drivers. |
| Age | In the research efforts of Chen et al. [10] and Chen et al. [19], age showed statistically insignificance in rear-end crashes, whereas Zhang and Hassan [8] demonstrated that young drivers are related to fatal outcomes in rear-end crashes. Yu et al. [7] illustrated that young (<25) and middle-aged (25–60) drivers tend to cause less severe injuries in rear-end crashes in work zones. |
| Alcohol or medicine | The involvement of alcohol or medicine significantly increased the frequency of more severe injuries in rear-end crashes [7,11]. |
| Vehicle characteristics | |
| Vehicle type | Heavy vehicles were found to be associated with more severe injury outcomes. For example, the involvement of trucks increased the possibility of more severe injury outcomes [10,11]. Heavy trucks were also found to be significant in predicting drivers’ fatalities [19]. Passenger cars increased the possibility of injury, whereas sports utility vehicles only increased the possibility of property damage [7]. |
| Number of vehicles | Previous studies also indicated inconsistences on the effects of the number of vehicles. Two-vehicle crashes are identified as the most common rear-end type causing fatalities [19], while Yu et al. [7] reported that two-vehicle collisions lead to a lower possibility of severe-injury outcomes in the rear-end crashes. |
| Roadway characteristics | |
| Roadway geometry | More severe injury severity outcomes occurred on the curved segments [8]. The probability of rear-end crashes is related to the length of the longitudinal slope [21]. |
| Speed limit | Speeding was statistically significant in fatal crashes in work zones, whereas the higher speed limit was related to severe outcomes in rear-end crashes [8]. Yu et al. [7] also reported that the speed limit is positively related to injury and possible injury possibility. |
| Number of lanes | Two-lane roadways were positively related to the fatalities in rear-end crashes [19]. |
| Environmental characteristics | |
| Weather condition | As expected, rainfall conditions increase the severity levels of rear-end crashes [9], and windy weather is related to more severe injury outcomes for occupants in rear-end crashes [10,19]. However, foggy weather tends to mitigate the injury severity in work zone rear-end crashes [8]. |
| Pavement condition | A counterintuitive finding was reported by Qi et al. [11], in which the authors demonstrated that rear-end collisions occurring on slippery roadways caused less severe outcomes. |
| Temporal characteristics | |
| Time of day | The propensity of daytime rear-end crashes is distinctly higher than that during the night [2,22]. The dusk and dawn time tends to decrease slightly the likelihood of injury [10]. |
| Weekdays | Driving at night on weekends was strongly associated with injury and fatal outcomes in rear-end collisions [8]. |
| Traffic characteristics | |
| Traffic volume | The average daily traffic volumes significantly affect the occurrences of urban rear-end crashes [23]. Weng et al. [24] also reported that greater traffic volume will increase the risk propensity of work zone rear-end crashes. Wang et al. [6] illustrated that the average annual daily traffic volumes are positively related to severe and fatal rear-end crashes. |
| Methodological Approaches | Previous Research |
|---|---|
| Statistical methods | |
| Nested logit model | Abdel-Aty and Abdelwahab [33] |
| Stepwise regression | Meng and Weng [35] |
| Ordered probit model | Ghasemzadeh and Ahmed [36] |
| Random-parameters ordered probit model | Zhang and Hassan [8] |
| Mixed probit model | Weng et al. [24] |
| Markov switching multinomial logit model | Malyshkina and Mannering [37] |
| Random-parameters logit with heterogeneity in means and variances | Yu et al. [7] |
| Data-driven methods | |
| Binary classification tree and logistic regression models | Yan et al. [22] |
| Decision table/Naïve Bayes (DTNB) hybrid classifier | Chen et al. [19] |
| Support vector machine and mixed logit model | Ahmadi et al. [38] |
| Decision Tree Approach | Champahom et al. [39] |
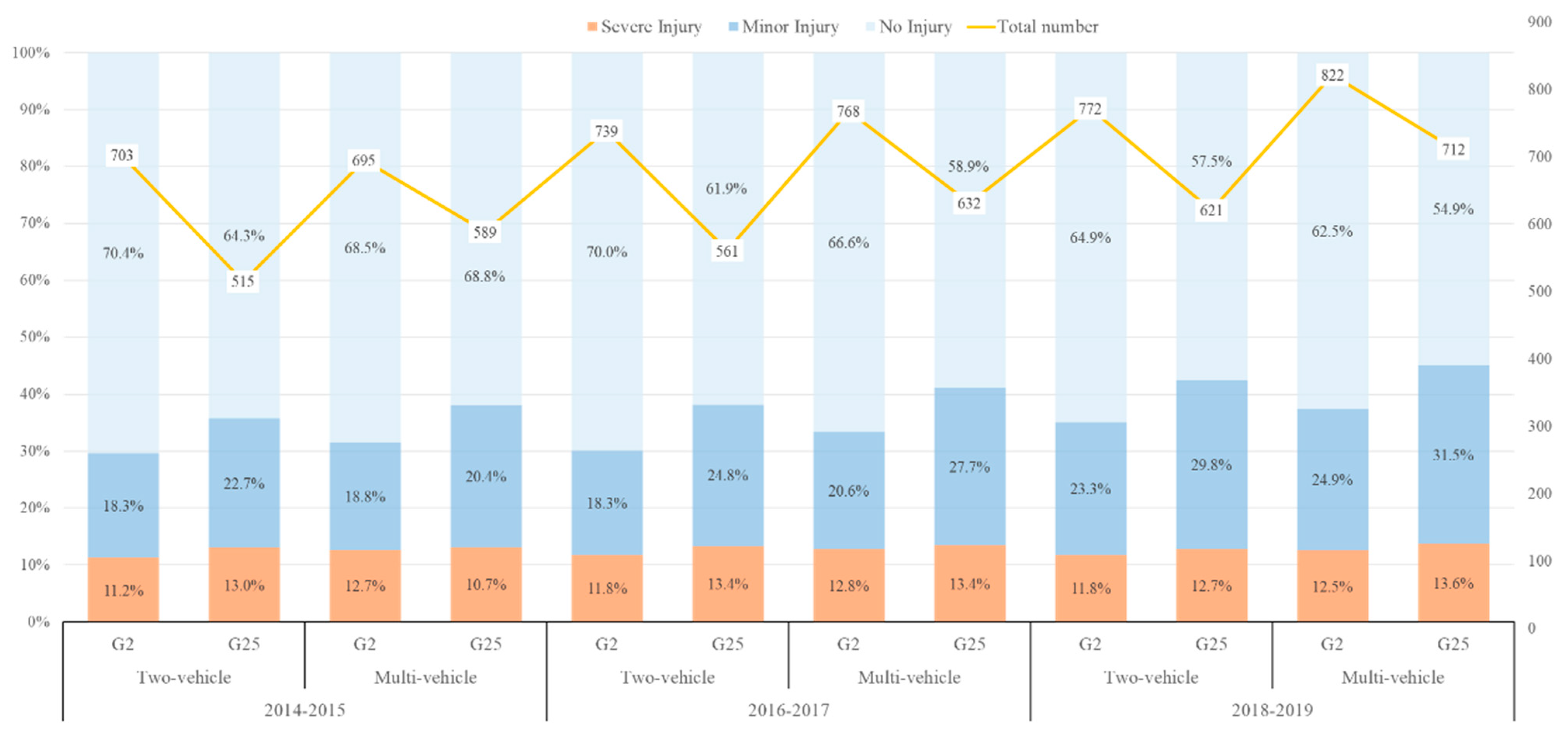
| Subgroup | Severe Injury | Minor Injury | No Injury | Total | |||||
|---|---|---|---|---|---|---|---|---|---|
| G2 | G25 | G2 | G25 | G2 | G25 | G2 | G25 | ||
| 2014–2015 | Two-Vehicle | 79 | 67 | 129 | 117 | 495 | 331 | 703 | 515 |
| Multi-Vehicle | 88 | 77 | 131 | 147 | 476 | 365 | 695 | 589 | |
| 2016–2017 | Two-Vehicle | 87 | 75 | 135 | 139 | 517 | 347 | 739 | 561 |
| Multi-Vehicle | 98 | 85 | 158 | 175 | 512 | 372 | 768 | 632 | |
| 2018–2019 | Two-Vehicle | 91 | 79 | 180 | 185 | 501 | 357 | 772 | 621 |
| Multi-Vehicle | 103 | 97 | 205 | 224 | 514 | 391 | 822 | 712 | |
| y1 | y2 | ||
|---|---|---|---|
| 2014–2015 | 2016–2017 | 2018–2019 | |
| 2014–2015 | – | 82.20 (15) [>99.99%] | 112.39 (10) [>99.99%] |
| 2016–2017 | 145.05 (12) [>99.99%] | – | 91.74 (10) [>99.99%] |
| 2018–2019 | 135.49 (12) [>99.99%] | 206.01 (15) [>99.99%] | – |
| y1 | y2 | ||
|---|---|---|---|
| 2014–2015 | 2016–2017 | 2018–2019 | |
| 2014–2015 | – | 85.64 (14) [>99.99%] | 66.37 (7) [>99.99%] |
| 2016–2017 | 160.78 (9) [>99.99%] | – | 168.66 (7) [>99.99%] |
| 2018–2019 | 297.63 (9) [>99.99%] | 426.85 (14) [>99.99%] | – |
| y1 | y2 | ||
|---|---|---|---|
| 2014–2015 | 2016–2017 | 2018–2019 | |
| 2014–2015 | – | 102.90 (10) [>99.99%] | 110.33 (12) [>99.99%] |
| 2016–2017 | 108.56 (13) [>99.99%] | – | 124.83 (12) [>99.99%] |
| 2018–2019 | 144.84 (13) [>99.99%] | 135.62 (10) [>99.99%] | – |
| y1 | y2 | ||
|---|---|---|---|
| 2014–2015 | 2016–2017 | 2018–2019 | |
| 2014–2015 | – | 121.28 (9) [>99.99%] | 104.96 (16) [>99.99%] |
| 2016–2017 | 74.94 (10) [>99.99%] | – | 79.71 (16) [>99.99%] |
| 2018–2019 | 147.83 (10) [>99.99%] | 119.47 (9) [>99.99%] | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Xia, Y.; Chen, F.; Cheng, J.; Wang, Z. Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts. Int. J. Environ. Res. Public Health 2022, 19, 10282. https://doi.org/10.3390/ijerph191610282
Wang C, Xia Y, Chen F, Cheng J, Wang Z. Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts. International Journal of Environmental Research and Public Health. 2022; 19(16):10282. https://doi.org/10.3390/ijerph191610282
Chicago/Turabian StyleWang, Chenzhu, Yangyang Xia, Fei Chen, Jianchuan Cheng, and Zeng’an Wang. 2022. "Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts" International Journal of Environmental Research and Public Health 19, no. 16: 10282. https://doi.org/10.3390/ijerph191610282
APA StyleWang, C., Xia, Y., Chen, F., Cheng, J., & Wang, Z. (2022). Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts. International Journal of Environmental Research and Public Health, 19(16), 10282. https://doi.org/10.3390/ijerph191610282







