3D Co-Seismic Surface Displacements Measured by DInSAR and MAI of the 2017 Sarpol Zahab Earthquake, Mw7.3
Abstract
:1. Introduction
2. Materials and Methods
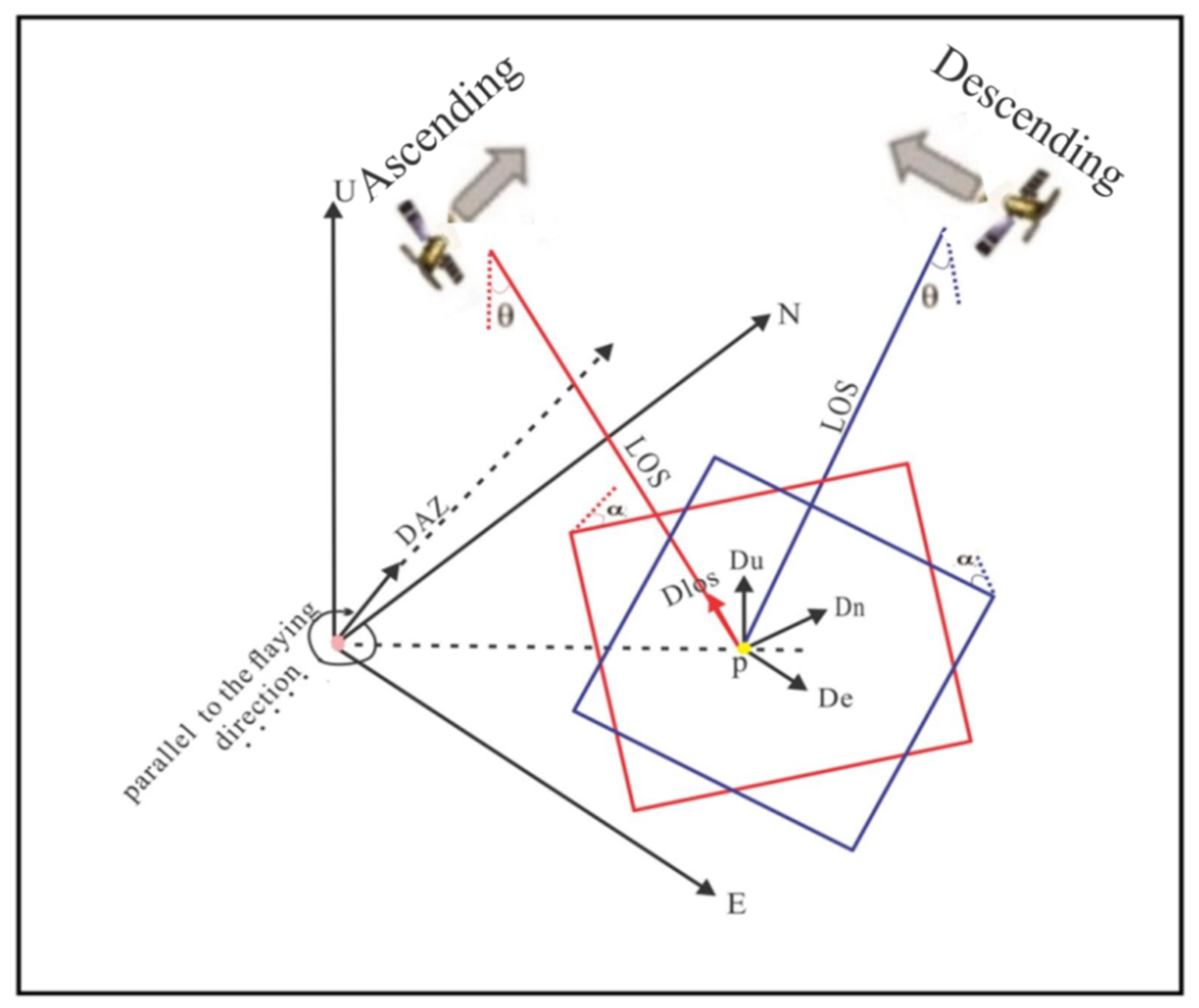
3. Results
3.1. Co-Seismic Deformation along the Line-of-Sight
3.2. Along-Track Co-Seismic Deformation (Azimuth)
3.3. 3D Co-Seismic Deformation
3.4. Co-Seismic Faults and Slip Inversion
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Masson, F.; Chéry, J.; Hatzfeld, D.; Martinod, J.; Vernant, P.; Tavakoli, F.; Ghafory-Ashtiani, M. Seismic versus aseismic deformation in Iran inferred from earthquakes and geodetic data. Geophysical. J. Int. 2004, 160, 217–226. [Google Scholar] [CrossRef]
- Talebian, M.; Jackson, J. Offset on the Main Recent Fault of NW Iran and implications for the late Cenozoic tectonics of the Arabia-Eurasia collision zone. Geophys. J. Int. 2002, 150, 422–439. [Google Scholar] [CrossRef] [Green Version]
- Blanc, E.-P.; Allen, M.B.; Inger, S.; Hassani, H. Structural styles in the Zagros simple folded zone, Iran. J. Geol. Soc. 2003, 160, 401–412. [Google Scholar] [CrossRef]
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abbassi, M.R.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ashtiani, A.; Bayer, R.; et al. present-day crustal deformation and plate kinematics in the Middle East constrained by GPS measurements in Iran and northern Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef] [Green Version]
- Vergés, J.; Saura, E.; Casciello, E.; FERNÀNDEZ, M.; Villasenor, A.; Jiménez-Munt, I.; Garcia-Castellanos, D. Crustal-scale cross-sections across the NW Zagros belt implications for the Arabian margin reconstruction. Geol. Mag. 2011, 148, 739–761. [Google Scholar] [CrossRef] [Green Version]
- McQuarrie, N. Crustal scale geometry of the Zagros fold-thrust belt, Iran. J. Struct. Geol. 2004, 26, 519–535. [Google Scholar] [CrossRef]
- Beydoun, Z. Arabian Plate Hydrocarbon Geology and Potential—A Plate Tectonic Approach; American Association of Petroleum Geologists: Tulsa, OK, USA, 1991; pp. 1–77. [Google Scholar]
- Sharland, P.R.; Archer, R.; Casey, D.M.; Davies, R.B.; Hall, S.H.; Heward, A.P.; Horbury, A.D.; Simmons, M.D. Arabian plate sequence stratigraphy. GeoArabia J. Middle East Pet. Geosci. 2013, 18, 4. [Google Scholar]
- Al-Qayim, B.A.; Baziany, M.M.; Ameen, B.M. Mesozoic Tethyan Radiolarite age determination, Zagros suture zone, Kurdistan, NE Iraq. Iraqi Geol. J. 2018, 51, 17–33. Available online: https://www.researchgate.net/publication/325498597 (accessed on 12 March 2018).
- Al-Qayim, B.; Omer, A.; Koyi, H. Tectonostratigraphic overview of the Zagros suture zone, Kurdistan region, Northeast Iraq. GeoArabia 2012, 17, 109–156. [Google Scholar] [CrossRef]
- Trasatti, E.T.; Kyriakopoulos, C.; Chini, M. Finite element inversion of DInSAR data from the Mw 6.3 L’Aquila earthquake, 2009 (Italy). Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.-J.; Li, Z.; Ding, X.; Jian-Jun, Z.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Joa, M.-J.; Jung, H.-S.; Chae, S.-H. Advances in three-dimensional deformation mapping from satellite radar observations: Application to the 2003 Bam earthquake. Geomat. Nat. Hazards Risk 2018, 9, 678–690. [Google Scholar] [CrossRef] [Green Version]
- Tatar, M.; Ghaemaghamian, M.; Yamini-Fard, F.; Hesami-Azar, K.; Ansari, A.; Firoozi, E. Sarpol-e Zahab Earthquake Report-Seismology Aspects; IIEES: Tehran, Iran, 2017. [Google Scholar]
- Durmuş, H.; Utkucu, M. Coseismic slip distributions and stress interactions of the November 12, 2017, Sarpole-Zahab (Western Iran) earthquake (MW = 7.3) and its aftershocks: Seismotectonic implications. Arab. J. Geosci. 2021, 14, 1188. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Weston, J.; Ferreira, A.M.; Funning, G.J. Systematic comparisons of earthquake source models determined using InSAR and seismic data. Tectonophysics 2012, 532, 61–81. [Google Scholar] [CrossRef]
- Gonzalez, P.J.; Fernandez, J.; Camacho, A.G. Coseismic three-dimensional displacements determined using SAR data: Theory and an application test. Pure Appl. Geophys. 2009, 166, 1403–1424. [Google Scholar] [CrossRef]
- Bechor, N.; Zebker, H. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Wegnüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 Support in the GAMMA Software. Procedia Comput. Sci. 2016, 100, 1305–1312. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.; Werner, C. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.-S.; Yun, S.-H.; Jo, M.-J. An Improvement of the Performance of Multiple-Aperture SAR Interferometry (MAI). Earth Obs. Remote Sens. 2015, 8, 4952–4960. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, R.; Wang, X.; Liu, G. Retrieving Three-Dimensional Co-Seismic Deformation of the 2017 Mw7.3 Iraq Earthquake by Multi-Sensor SAR Images. Remote Sens. 2018, 10, 857. [Google Scholar] [CrossRef] [Green Version]
- Jo, M.-J.; Jung, H.-S.; Won, J.-S.; Poland, M.P.; Miklius, A.; Lu, Z. Measurement of slow-moving along-track displacement from an efficient multiple-aperture SAR interferometry (MAI) stacking. J. Geod. 2015, 89, 411–425. [Google Scholar] [CrossRef]
- Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Peter, C.; Murray, M.H.; Segall, P.; Aoki, Y.; Kato, T. Estimating source parameters from deformation data, with an application to the March 1997 earthquake swarm off the Izu Peninsula, Japan. J. Geophys. Res. Solid Earth 2001, 11, 217–237. [Google Scholar] [CrossRef]
- Barnhart, D.; Brengman, C.M.; Li, S.; Peterson, K.E. Ramp-flat basement structures of the Zagros Mountains inferred from co-seismic slip and afterslip of the 2017 Mw 7.3 Darbandikhan, Iran/Iraq earthquake. Earth Planet. Sci. Lett. 2018, 496, 96–107. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Almeida, R.; Yassaghi, A.; Li, J.; Qiu, Q.; Li, P.; Zheng, W. Geodetic constraints of the 2017 Mw7. 3 Sarpol Zahab, Iran earthquake, and its implications on the structure and mechanics of the northwest Zagros thrust-fold belt. Geophys. Res. Lett. 2018, 45, 6853–6861. [Google Scholar] [CrossRef]








| Sensor | Orbit Path | Acquisition Data | Incidence Angle | Perpendicular Baseline | Heading Angle (°) |
|---|---|---|---|---|---|
| ALOS-2 | ascending | 9August 2016 14 November 2017 | 47.2 | 70 m | 91 |
| Descending | 4 October 2017 15 November 2017 | 47.2 | 186.3 m | 170 | |
| Sentinel-1A | ascending | 11 November 2017 23 November 2017 | 39.2 | 62.2m | 167 |
| descending | 7 November 2017 19 November 2017 | 39.2 | 70.2 | 167 |
| Parameter | Strike (◦) | Dip (◦) | Rake (◦) | Length (km) | Width (km) | Depth (km) | Slip (m) | Longitude (◦) | Latitude (◦) |
|---|---|---|---|---|---|---|---|---|---|
| USGS 1 | 352 | 16 | 137 | 1.5 | - | −19 | 3.26 | 45.956 | 34.905 |
| Global MT 2 | 351 | 11 | 140 | - | - | 18.0 | - | 45.84 | 34.83 |
| Barnhart et al., (2018) 3 [28] | 350 | 15 | 128 a | - | - | 15.0 | - | 45.87 b | 34.65 b |
| Feng et al., (2018) 3 [29] | 353.5 | 14.5 | 135.6 a | - | - | 14.5 | - | 45.86 b | 34.73 b |
| This study (InSAR) 3 | 337.5 | 11.2 | 130.1 a | 30 | 30 | -8.5 | 5 | 45.6 b | 34.6 b |
| 337.5 | 11.2 | 135 a | 30 | 30 | 10.5 | 5.3 | 45.7 b | 34.8 b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; Wu, X.; Chen, Q.; Elubid, B.A.; Dafalla, D.S.; Kamran, M.; Aldoud, A.A. 3D Co-Seismic Surface Displacements Measured by DInSAR and MAI of the 2017 Sarpol Zahab Earthquake, Mw7.3. Int. J. Environ. Res. Public Health 2022, 19, 9831. https://doi.org/10.3390/ijerph19169831
Ali R, Wu X, Chen Q, Elubid BA, Dafalla DS, Kamran M, Aldoud AA. 3D Co-Seismic Surface Displacements Measured by DInSAR and MAI of the 2017 Sarpol Zahab Earthquake, Mw7.3. International Journal of Environmental Research and Public Health. 2022; 19(16):9831. https://doi.org/10.3390/ijerph19169831
Chicago/Turabian StyleAli, Randa, Xiyong Wu, Qiang Chen, Basheer A. Elubid, Dafalla S. Dafalla, Muhammad Kamran, and Abdelmottaleb A. Aldoud. 2022. "3D Co-Seismic Surface Displacements Measured by DInSAR and MAI of the 2017 Sarpol Zahab Earthquake, Mw7.3" International Journal of Environmental Research and Public Health 19, no. 16: 9831. https://doi.org/10.3390/ijerph19169831







