Optimization of Emission Reduction Target in the Beijing–Tianjin–Hebei Region: An Atmospheric Transfer Coefficient Matrix Perspective
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source
2.3. Methods
2.3.1. WRF/CALPUFF Model
2.3.2. Optimization Model
Transfer Coefficient Matrixes of Pollutants
Optimization Model
2.3.3. Comparative Analysis Method of Optimization Results
2.3.4. Calculation Method of GDP after Emission Reduction
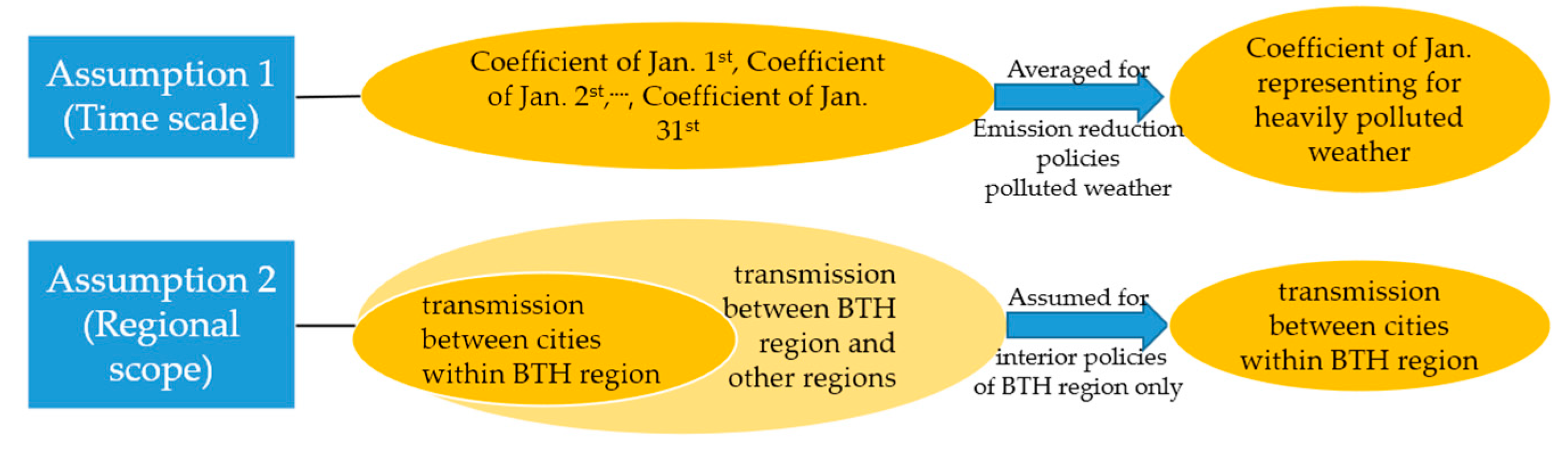
2.4. Assumptions of This Research Study
- (1)
- Assumption 1 is about the time scale of this study. We chose the most severe season in one of the most polluted years (i.e., January 2016) in the Beijing–Tianjin–Hebei region. This assumption was mainly used in the WRF/CALPUFF model and the optimization model (Section 3.1, Section 3.2 and Section 3.3). The transmission coefficient of each city constantly changes, depending on natural conditions such as topography and meteorology, for the relationship between pollutant emission and concentration is affected by many complex physical and chemical mechanisms. However, this study mainly analyzed the optimization of emission reduction responsibility from the perspective of management and took the average results of the transmission coefficient of each city as the optimization parameters.
- (2)
- Assumption 2 is about the scope of the study area. We only considered emissions from the Beijing–Tianjin–Hebei region, excluding other regions. It was mainly used in the WRF/CALPUFF model setup (Section 3.1 and Section 3.2). Although the surrounding areas have a certain impact on the atmospheric environmental quality of Beijing, Tianjin, and Hebei, the impact of cities inside the Beijing–Tianjin–Hebei region is greater. Moreover, when making policies, the Chinese government often considers the Beijing–Tianjin–Hebei region as a whole, without considering the surrounding provinces. Therefore, the results of the interaction between Beijing–Tianjin–Hebei region and its surrounding areas were not the main basis for formulating the emission responsibility of the 13 cities in this paper.
3. Results
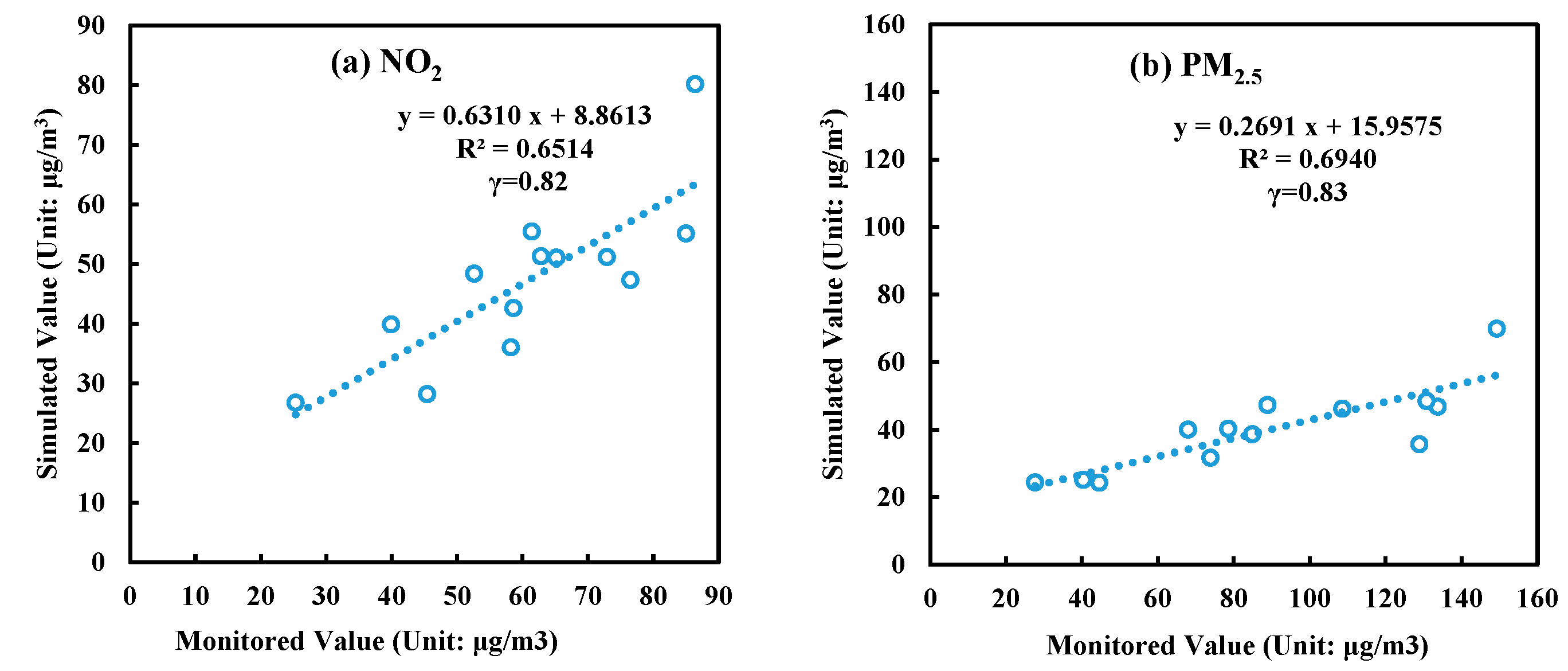
3.1. Validation of the WRF/CALPUFF Model
3.2. Pollutant Transfer Coefficients
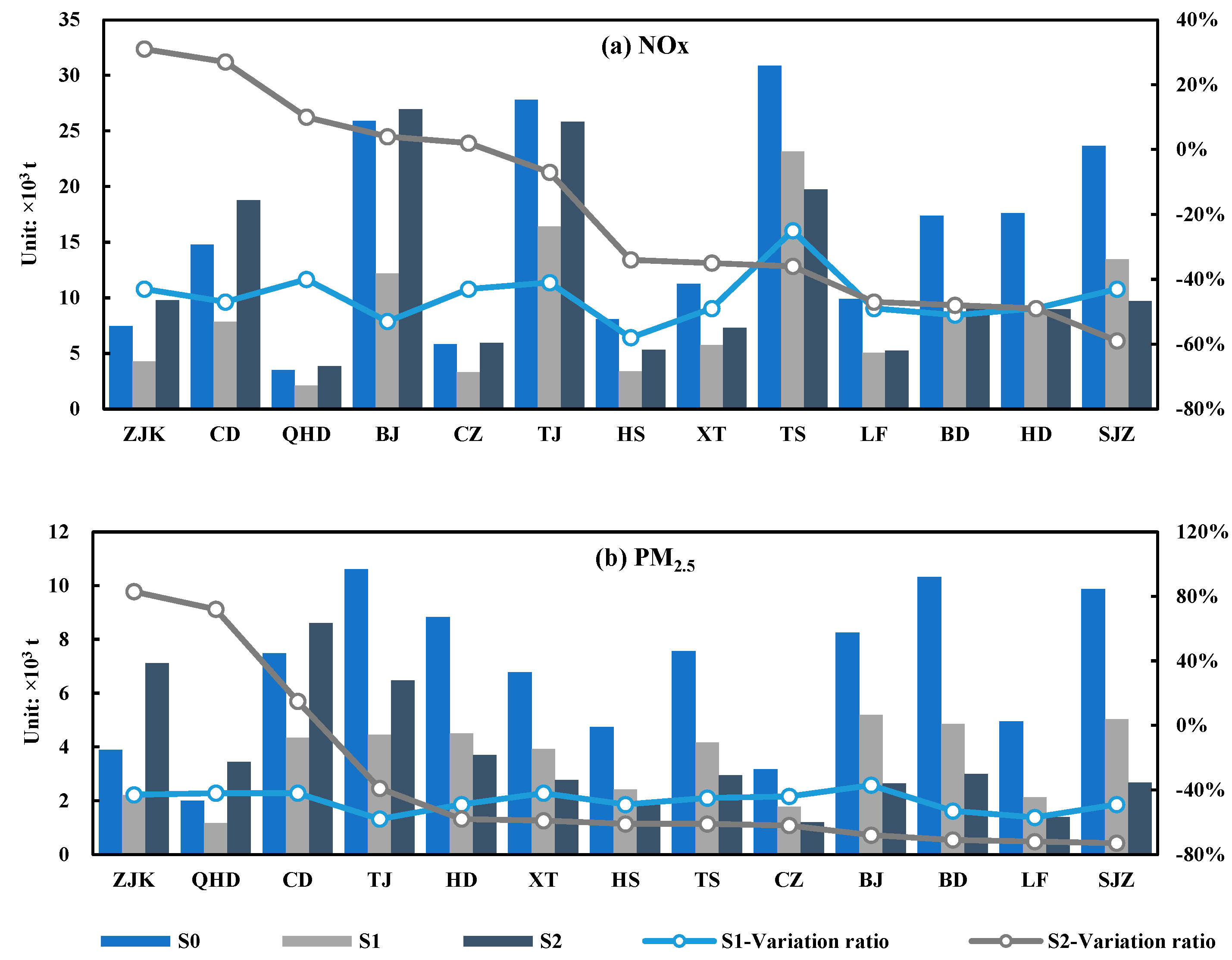
3.3. Maximum Allowable Emissions
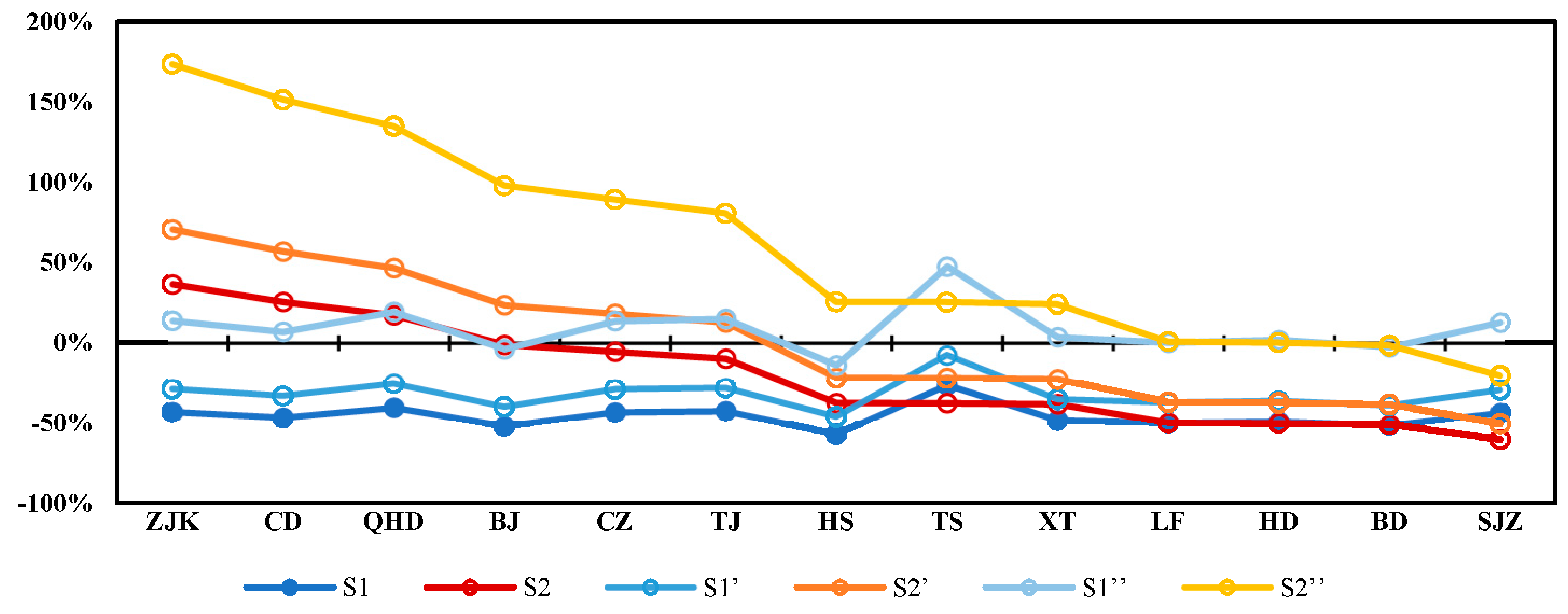
3.4. Impact of Emission Changes on Economy (GDP)
3.5. Impact of Emission Intensity Changes on GDP
3.6. Discussion
4. Conclusions and Suggestions
4.1. Conclusions
- (1)
- For those cities with smaller transfer coefficients, such as Zhangjiakou (with a transfer coefficient of 0.64 × 10−3 μg/m3·t to Baoding), even if the emission of these cities increased, the impact on the local and surrounding atmospheric environment quality would be relatively small; for cities with larger transfer coefficients, such as Shijiazhuang (with a transfer coefficient of 49.74 × 10−3 μg/m3·t to Baoding), reducing emissions would not only be beneficial to the local atmospheric environment quality, but it could also improve the atmospheric environment quality of other cities and reduce the pressure of emission reduction in other cities. It is also an important aspect of joint air defense and control work to make full use of the emission reduction optimization brought by atmospheric transmission.
- (2)
- This study tried to provide a new perspective of regional air pollution prevention and control, that is, to optimize emission reduction targets according to the natural spatial differences between emissions and atmospheric environmental quality. If cities adopted the traditional and unified emission reduction ratio policy (scenario S1), the maximum allowable emissions of NOx and PM2.5 in the Beijing–Tianjin–Hebei region would be 114,330.72 t and 46,186.69 t, respectively. Considering the regional air pollution transmission and joint prevention and control with the optimization method (scenario S2), the maximum allowable emissions of NOx and PM2.5 in this region would be 156,407.33 t and 47,824.49 t, respectively. The concentration of NOx and PM2.5 under these two scenarios could both meet the national air quality secondary standard, but the latter is easier and more economical.
- (3)
- In general, the reduction measures of pollutants would lead to the deceleration or loss of the economy. However, from the perspective of regional air pollution joint prevention and control, and economic development, emissions cannot be required to fall in all cities. On the premise of insisting on improving emission reduction technology, we assessed the economic impact of pollutant reduction, optimized the emission reduction proportion of each city instead of simply setting the emission reduction ratio based on the principle of anti-degradation of air quality (any city’s pollutant emissions are not allowed to increase), and reduced the negative impact of pollution reduction on the economy. In scenario S1, the average GDP in the Beijing–Tianjin–Hebei region was 2.87 USD USD. In scenario S2, the average GDP of the Beijing–Tianjin–Hebei region was 4.72 USD USD, which is much higher than that of scenario S1.
4.2. Suggestions
- (1)
- When making local policies, it is suggested that policy makers allow cities with a great impact on regional air quality to reduce emissions more and allow cities with a small impact on regional air quality to pursue less emission reduction or even increase emissions. In this way, the overall pressure of emission reduction would be reduced, and the impact on the economy would also be mitigated.
- (2)
- Local governments are advised to improve air quality without affecting economic development by reducing pollutant emission intensity. They are suggested to adjust the industrial structure, eliminate backward enterprises, control the amount of coal consumption, find clean and efficient energy varieties, and seek better energy management methods.
- (3)
- Pollutant emission reduction can depend not only on the reduction in industrial source emissions, but also on the reduction in the emissions of residents and traffic sources. Residents are advised to use clean heating and reduce the amount of coal burning in winter. In order to reduce the emissions of traffic source pollutants, the proportion of electric vehicles should be increased.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Zhou, C.; Wang, Z.; Feng, K.; Hubacek, K. The characteristics and drivers of fine particulate matter (PM2.5) distribution in China. J. Clean. Prod. 2017, 142, 1800–1809. [Google Scholar] [CrossRef]
- Xing, J.; Wang, S.; Chatani, S.; Zhang, C.Y.; Wei, W.; Hao, J.; Klimont, Z.; Cofala, J.; Amann, M. Projections of air pollutant emissions and its impacts on regional air quality in China in 2020. Atmos. Chem. Phys. 2011, 11, 3119–3136. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, S.; Liu, H.; Xu, J.; Fu, K.; Klimont, Z.; Hao, J.; He, K.; Cofala, J.; Amann, M. NOx emissions in China: Historical trends and future perspectives. Atmos. Chem. Phys. 2013, 13, 9869–9897. [Google Scholar] [CrossRef]
- Anwar, A.; Younis, M.; Ullah, I. Impact of urbanization and economic growth on CO2 emission: A case of far east asian countries. Int. J. Env. Res. Public Health 2020, 17, 2531. [Google Scholar] [CrossRef]
- Perera, F. Pollution from Fossil-Fuel Combustion is the leading environmental threat to global pediatric health and equity: Solutions exist. Int. J. Environ. Res. Public Health 2018, 15, 16. [Google Scholar] [CrossRef]
- Tian, H.; Xu, R.; Canadell, J.; Thompson, R.; Winiwarter, W.; Suntharalingam, P.; Davidson, E.; Ciais, P.; Jackson, R.; Janssens-Maenhout, G.; et al. A comprehensive quantification of global nitrous oxide sources and sinks. Nature 2020, 586, 248–256. [Google Scholar] [CrossRef]
- Burke, M.; Hsiang, E.; Miguel, E. Global non-linear effect of temperature on economic production. Nature 2015, 527, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Li, X.; Zhang, Q.; Jiang, X.; Lin, J.; Peters, G.; Li, M.; Geng, G.; Zheng, B.; Huo, H.; et al. Effects of atmospheric transport and trade on air pollution mortality in China. Atmos. Chem. Phys. 2017, 17, 10367–10381. [Google Scholar] [CrossRef]
- Zhou, Y.; Levy, J.; Hammitt, J.; Evans, J. Estimating population exposure to power plant emissions using CALPUFF: A case study in Beijing, China. Atmos. Environ. 2003, 37, 815–826. [Google Scholar] [CrossRef]
- Wu, D.; Xu, Y.; Zhang, S. Will joint regional air pollution control be more cost-effective? An empirical study of China’s Beijing-Tianjin-Hebei region. J. Environ. Manag. 2015, 149, 27–36. [Google Scholar] [CrossRef]
- Yan, D.; Lei, Y.; Shi, Y.; Zhu, Q.; Li, L.; Zhang, Z. Evolution of the spatiotemporal pattern of PM2.5 concentrations in China—A case study from the Beijing-Tianjin-Hebei region. Atmos. Environ. 2018, 183, 225–233. [Google Scholar] [CrossRef]
- Lin, J.; Pan, D.; Davis, S.; Zhang, Q.; He, K.; Wang, C.; Streets, D.; Wuebbles, D.; Guan, D. China’s international trade and air pollution in the United States. Proc. Natl. Acad. Sci. USA 2014, 111, 1736–1741. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Tong, D.; Davis, S.; Ni, R.; Tan, X.; Pan, D.; Zhao, H.; Lu, Z.; Streets, D.; Feng, D.; et al. Global climate forcing of aerosols embodied in international trade. Nat. Geosci. 2016, 9, 790–794. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, X.; Tong, D.; Davis, S.; Zhao, H.; Geng, G.; Feng, T.; Zheng, B.; Lu, Z.; Streets, D.; et al. Transboundary health impacts of transported global air pollution and international trade. Nature 2017, 543, 705. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Wang, S.; Zhao, B.; Xing, J.; Liu, X.; Wei, L.; Song, Y.; Wu, W.; Cai, S.; Zheng, H.; et al. Contributions of inter-city and regional transport to PM2.5 concentrations in the Beijing-Tianjin-Hebei region and its implications on regional joint air pollution control. Sci. Total Environ. 2019, 660, 1191–1200. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Qiao, Z.; Lu, Y. Inter-city air pollutant transport in The Beijing-Tianjin-Hebei urban agglomeration: Comparison between the winters of 2012 and 2016. J. Environ. Manag. 2019, 250, 109520. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Q.; Kurokawa, J.; Woo, J.; He, K.; Lu, Z.; Ohara, T.; Song, Y.; Streets, D.G.; Carmichael, G.R.; et al. MIX: A mosaic Asian anthropogenic emission inventory under the international collaboration framework of the MICS-Asia and HTAP. Atmos. Chem. Phys. 2017, 17, 935–963. [Google Scholar] [CrossRef]
- Elkamel, A.; Fatehifar, E.; Taheri, M.; Al-Rashidi, M.; Lohi, A. A heuristic optimization approach for Air Quality Monitoring Network design with the simultaneous consideration of multiple pollutants. J. Environ. Manag. 2008, 88, 507–516. [Google Scholar] [CrossRef]
- Turrini, E.; Carnevale, C.; Finzi, G.; Volta, M. A non-linear optimization programming model for air quality planning including co-benefits for GHG emissions. Sci. Total Environ. 2018, 621, 980–989. [Google Scholar] [CrossRef]
- Qin, X.; Huang, G.; Liu, L. A genetic-algorithm-aided Stochastic optimization model for regional air quality management under uncertainty. J. Air Waste Manag. 2010, 60, 63–71. [Google Scholar] [CrossRef]
- Kojić, M.; Schlüter, S.; Mitića, P.; Hanić, A. Economy-environment nexus in developed European countries: Evidence from multifractal and wavelet analysis. Chaos Solitons Fractals 2022, 160, 112189. [Google Scholar] [CrossRef]
- Wang, J.; Pan, X. Application of linear programming in the allocation of environmental capacity resources. Environ. Sci. 2005, 26, 197–200. (In Chinese) [Google Scholar] [CrossRef]
- Du, Y.; Sun, T.; Peng, J.; Fang, K.; Liu, Y.; Yang, Y.; Wang, Y. Direct and spillover effects of urbanization on PM2.5 concentrations in China’s top three urban agglomerations. J. Clean Prod. 2018, 190, 72–83. [Google Scholar] [CrossRef]
- Fang, C.; Yu, D. China’s New Urbanization; China Science Publishing & Media Ltd.: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Ye, W.; Ma, Z.; Ha, X. Spatial-temporal patterns of PM (2.5) concentrations for 338 Chinese cities. Sci. Total Environ. 2018, 631–632, 524–533. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, S.; Zhu, L.; Xu, R.; Li, J. Characteristics of primary pollutants of air quality in cities along the Taihang Mountains in Beijing-Tianjin-Hebei region during 2014–2016. Environ. Sci. 2018, 39, 4422–4429. (In Chinese) [Google Scholar] [CrossRef]
- Jia, H.; Yin, T.; Qu, X.; Cheng, N.; Cheng, B.; Wang, J.; Wang, W.; Meng, F.; Chai, F. Characteristics and source simulation of ozone in Beijing and its surrounding areas in 2015. China Environ. Sci. 2017, 37, 1231–1238. (In Chinese) [Google Scholar]
- Urban Social and Economic Investigation Department of the National Bureau of Statistics. China Urban Statistical Yearbook in 2016; China Statistics Press: Beijing, China, 2017. [Google Scholar]
- Wang, Z.; Li, J.; Wang, Z.; Yang, W.; Tang, X.; Ge, B.; Yan, P.; Zhu, L.; Chen, X.; Chen, H.; et al. Modeling study of regional severe hazes over mid-eastern China in January 2013 and its implications on pollution prevention and control. Sci. China Earth Sci. 2014, 57, 3–13. [Google Scholar] [CrossRef]
- Itahashi, S.; Uno, I.; Osada, K.; Kamiguchi, Y.; Yamamoto, S.; Tamura, K.; Wang, Z.; Kurosaki, Y.; Kanaya, Y. Nitrate transboundary heavy pollution over East Asia in winter. Atmos. Chem. Phys. 2017, 17, 3823–3843. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, Q.; Wang, Z.; Fu, P.; Li, J.; Yang, T.; Yin, Y. Investigation of the sources and evolution processes of severe haze pollution in Beijing in January 2013. J. Geophys. Res.-Atmos. 2014, 119, 4380–4398. [Google Scholar] [CrossRef]
- Mo, Z.; Wang, Z.; Mao, G.; Pan, X.; Wu, L.; Xu, P.; Chen, S.; Wang, A.; Zhang, Y.; Luo, J. Characterization and health risk assessment of PM 2.5-bound polycyclic aromatic hydrocarbons in 5 urban cities of Zhejiang Province, China. China Sci. Rep. 2019, 9, 7296. [Google Scholar] [CrossRef]
- Jin, J.; Miller, N. Sensitivity Study of Four Land Surface Schemes in the WRF Model. Adv. Meteorol. 2010, 2010, 185–194. [Google Scholar] [CrossRef]
- Scire, J.; Robe, F.; Fernau, M.; Yamartino, R. A User’s Guide for the CALMET Meteorological Model (Version 5). Available online: https://www.researchgate.net/publication/225089751_A_user%27s_guide_for_the_CALMET_meteorological_model_Version_5 (accessed on 28 September 2019).
- MEPC. China City Statistical Yearbook; China Statistics Press: Beijing, China, 2017; Available online: http://navi.cnki.net/KNavi/YearbookDetail?pcode=CYFD&pykm=YZGCA&bh= (accessed on 28 January 2022).
- Zhang, X.; Zhao, X.; Jiang, Z.; Shao, S. How to achieve the 2030 CO2 emission-reduction targets for China’s industrial sector: Retrospective decomposition and prospective trajectories. Glob. Environ. Change 2017, 44, 83–97. [Google Scholar] [CrossRef]
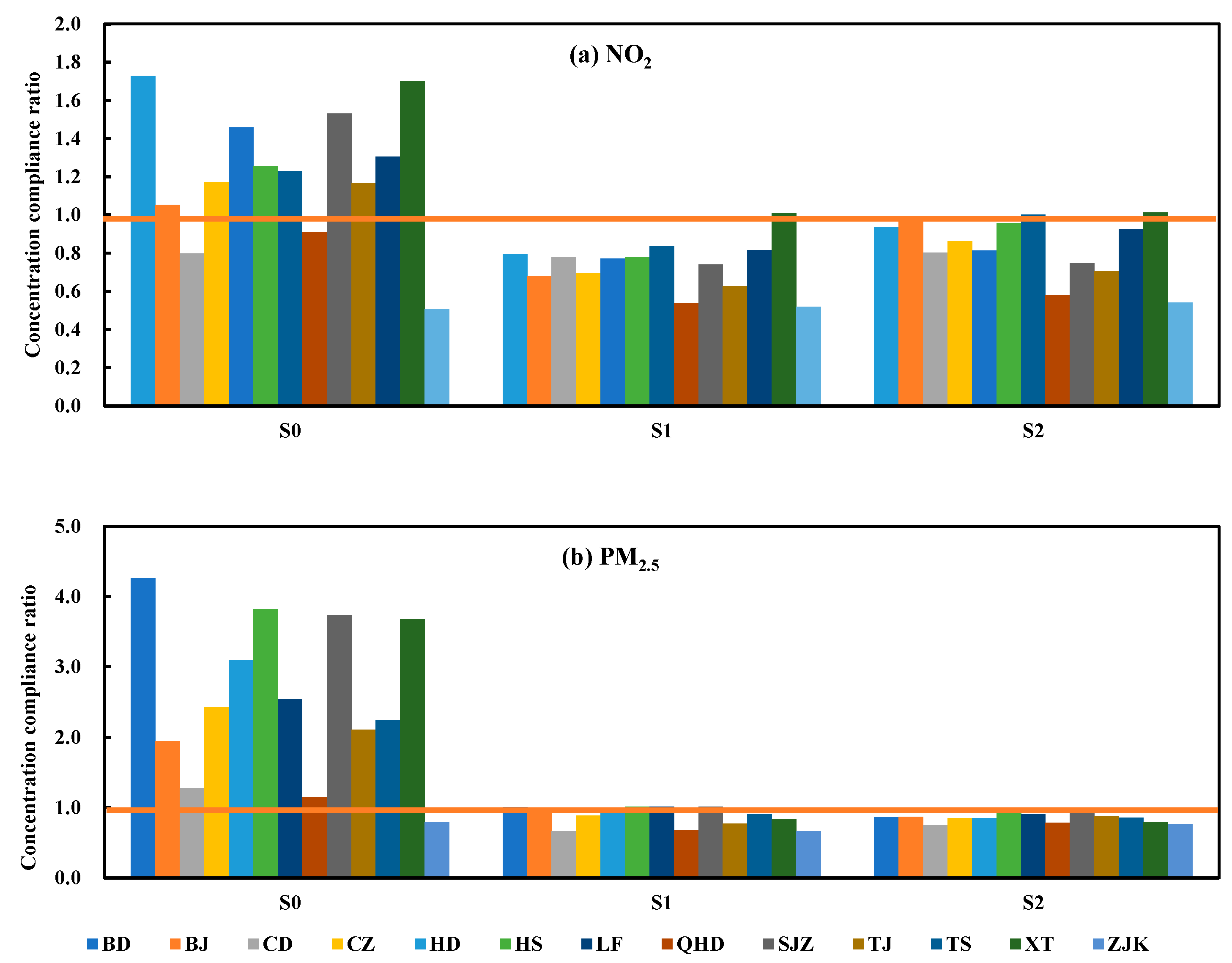

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Pan, Z.; Li, Y.; Lu, Y.; Dong, Y.; Ping, L. Optimization of Emission Reduction Target in the Beijing–Tianjin–Hebei Region: An Atmospheric Transfer Coefficient Matrix Perspective. Int. J. Environ. Res. Public Health 2022, 19, 13512. https://doi.org/10.3390/ijerph192013512
Wang Y, Pan Z, Li Y, Lu Y, Dong Y, Ping L. Optimization of Emission Reduction Target in the Beijing–Tianjin–Hebei Region: An Atmospheric Transfer Coefficient Matrix Perspective. International Journal of Environmental Research and Public Health. 2022; 19(20):13512. https://doi.org/10.3390/ijerph192013512
Chicago/Turabian StyleWang, Yuan, Zhou Pan, Yue Li, Yaling Lu, Yiming Dong, and Liying Ping. 2022. "Optimization of Emission Reduction Target in the Beijing–Tianjin–Hebei Region: An Atmospheric Transfer Coefficient Matrix Perspective" International Journal of Environmental Research and Public Health 19, no. 20: 13512. https://doi.org/10.3390/ijerph192013512
APA StyleWang, Y., Pan, Z., Li, Y., Lu, Y., Dong, Y., & Ping, L. (2022). Optimization of Emission Reduction Target in the Beijing–Tianjin–Hebei Region: An Atmospheric Transfer Coefficient Matrix Perspective. International Journal of Environmental Research and Public Health, 19(20), 13512. https://doi.org/10.3390/ijerph192013512





