Evolutionary Game Analysis of Government and Residents’ Participation in Waste Separation Based on Cumulative Prospect Theory
Abstract
1. Introduction
- (1)
- Behavior of waste separation: The behavior of waste separation is one of the earliest issues that received academic attention, and domestic and international research on waste-separation behavior has focused on the factors influencing separation behavior [8,9,10,11,12,13], source separation [14,15,16,17], and participant intent [2,12,18,19], and some other scholars have conducted research in the Chinese context.
- (2)
- Waste-separation strategies: With the gradual systematization of behavioral research on waste separation, strategy research on waste separation has also been emphasized by domestic and foreign scholars, with foreign studies focusing on hazardous-waste-separation methods [20,21], waste-separation policy utility [22,23,24], and correctness of waste separation [25,26], among others.
- (3)
- Mechanism of waste separation: The mechanism research of waste separation is an inevitable stage of waste-separation research, and domestic and foreign studies mainly focus on waste-separation management mechanism [27,28,29,30], waste-separation and recycling user mechanism [31,32,33], and construction waste-separation and disposal mechanisms [34,35].
- (4)
- Waste-separation spillover: Studies are more comprehensive regarding waste separation and related studies, but the relationship between waste separation and its external subjects in the supply chain has not been studied much. Domestic and foreign studies have focused more on the relationship between waste separation and the environment [36], economy [37,38,39], rural revitalization [30], etc., and have studied the relationship between waste separation and the external subjects of its supply chain to a lesser extent.
2. Modeling
2.1. Model Assumptions
- (1)
- Behavioral choice: Assume that two subjects—residents and government—are involved in waste separation at the moment. Assume that the participation strategy set of residents is (participation, non-participation), and the participation strategy set of government is {participation, non-participation}. When both residents and government choose to participate, the waste separation is successful. It produces direct transformation to obtain total benefits, which residents and government share, with the sharing ratio of β and 1 − β (0 < β < 1), respectively. At the same time, the implementation of waste separation will lead to the improvement of resource utilization efficiency and the original ecological environment in addition to the provision of public services required by society for waste separation and minimization and resource utilization and the potential benefits gained by the government in investment attraction, talent attraction, environmental management, pharmaceutical R&D, etc., due to the improved environment. When residents decide not to participate, and the government decides not to participate, both parties still do not gain the benefits from waste separation. However, the government still needs to bear the management costs of participating in waste separation.
- (2)
- Participation benefits: If residents choose the “non-participation” strategy, they can obtain the general utility U1. If the government decides on “non-participation”, they can obtain the available utility U2. Suppose both residents and the government choose the “participation” strategy. In that case, they can obtain the total benefit of K, which residents and the government share; the use obtained by residents is βK, and the benefit received by the government is (1 − β)K.
- (3)
- Participation cost: It is assumed that residents’ participation in waste separation requires input cost T (T > 0), including residents’ labor cost for waste separation and the cost of waste-separation tools, etc. The government’s participation in waste separation requires an input management fee of C (C > 0), including labor, device, and management costs necessary for waste separation.
- (4)
- Prospective gains and losses: When residents choose to participate, and the government decides to participate, the government will gain potential profits P (P > 0) due to investment attraction, talent attraction, and urban governance after environmental improvement; at the same time, residents need to bear the opportunity cost of opportunity cost M (M > 0) that may come from participation in waste separation.
- (5)
- Participation probability: the probability of residents taking the “participation” strategy is x, and the possibility of taking the “non-participation” strategy is 1 − x, where 0 ≤ x ≤ 1; the probability of the government taking the “participation” strategy is y, and the possibility of taking the “non-participation” strategy is 1 − y, where 0 ≤ y ≤ 1.
2.2. Constructing the Expected Return Function
2.3. Solving the Replicated Dynamic Equation
3. Model Discussion
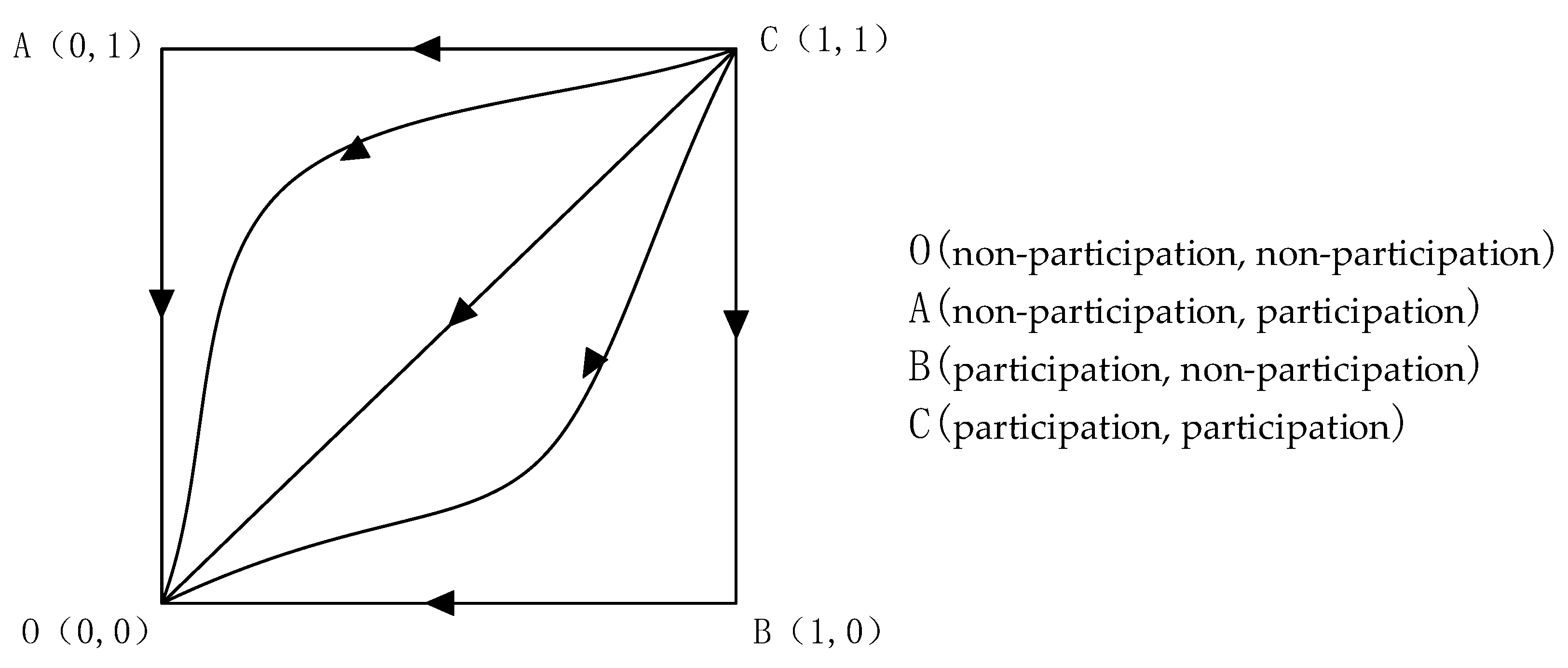
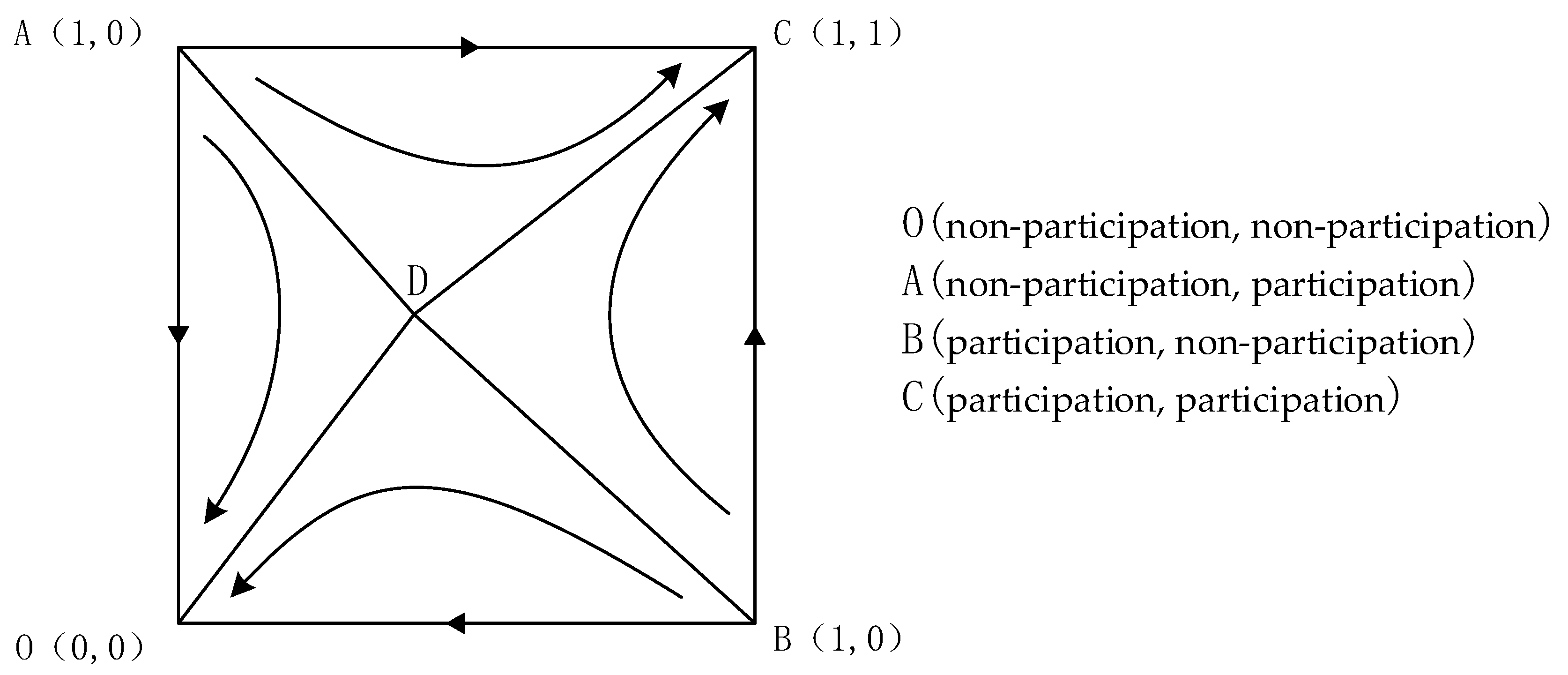
3.1. Equilibrium Strategy Stability Analysis
3.2. Evolutionary Game Analysis Based on Cumulative Prospect Theory
3.2.1. Cost–Benefit Function Based on Cumulative Prospect Theory
- M = π(P1)V(m) + π(1 − P1)V(0)
- and since V(0) = 0, M = π(P1)V(m)
- K = π(P2)V(k) + π(1 − P2)V(0)
- and since V(0) = 0, K = π(P2)V(k)
- P = π(P2)V(p) + π(1 − P2)V(0)
- and since V(0) = 0, P = π(P2)V(p)
3.2.2. Analysis of Evolutionary Stabilization Strategies Based on Cumulative Prospect Theory
- (1)
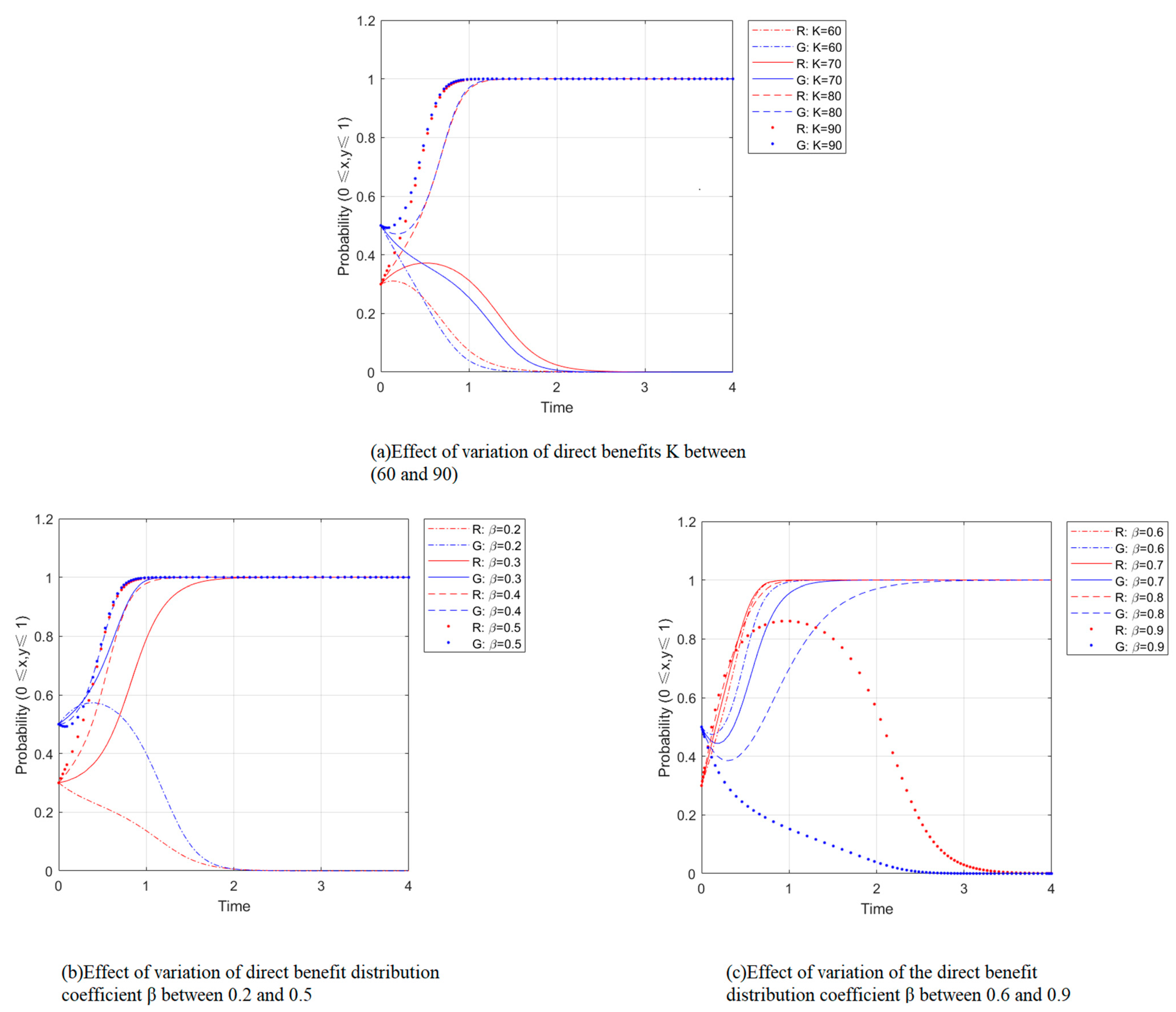
- Impact of revenue: The premise of the direct benefits of waste separation is that residents and the government participate in waste separation, with residents putting out waste in the first stage and the government disposing of waste in the second stage and realizing the direct benefits through recycling of recyclable materials and special treatment of hazardous waste. Residents usually underestimate the probability P2 of immediate benefits after participating in waste separation, i.e., π(P2) < P2, so that K = π(P2)V(k) < P2V(k), and the actual direct benefits are more significant than the expected immediate benefits.
- (2)
- Impact of cost: The government can reduce the time cost T by raising residents’ awareness of waste separation through preliminary publicity and education and effectively reduce the management cost by optimizing the waste-separation process. However, due to traditional waste-disposal methods, residents are unwilling to participate in waste separation because of the hassle. Residents and the government overestimate the difficulty of completing waste separation, time cost T, and management cost C. The actual costs incurred in time cost (T1 < T) and management cost (C1 < C) are smaller than the expected costs incurred.
- (3)
- Impact of prospective gains and losses: The characteristic of limited rationality of the waste-separation participant overestimates the possibility of opportunity costs occurring and underestimates the chance of potential profits arising. They tend to overestimate the probability of missing other gains P1, i.e., π(P1) > P1, so that M = π(P1)V(m) > P1V(m), and they underestimate the probability of potential gains from participation in waste separation, i.e., π(P2) < P2, so that P = π(P2)V(p) < P2V(p), so the real opportunity cost is smaller than the expected opportunity cost, and the actual potential gain is larger than the expected potential gain.
- βK – M − T = βπ(P2)V(k) − π(P1)V(m) − T < βP2k − P1m − T1
- (1 − β)K + P − C = (1 − β)π(P2)V(k) + π(P2)V(p) − C<(1-β)P2k + P2p − C1
4. Numerical Analysis
4.1. Setting Parameters
4.2. Sensitivity Analysis
4.2.1. Direct Income and Its Distribution Factor
4.2.2. Time Costs and Management Costs
4.2.3. Opportunity Costs and Potential Benefits
5. Discussion
- (1)
- There are two stable evolutionary strategies in the system. Due to the influence of limited rationality, there are two evolutionary strategies, i.e., {non-participation, non-participation} and {participation, participation}, for waste separation even when the gained benefit for residents is greater than the sum of time cost and opportunity cost. The sum of direct and potential uses for the government is greater than the management cost it pays. Participating agents prefer loss avoidance and forgo immediate benefits rather than bear the potential opportunity costs. In participating in waste separation, participating subjects are more inclined to underestimate the probability of occurrence of direct and potential benefits and overestimate the likelihood of event of opportunity costs, making the system still likely to evolve toward the {non-participation, non-participation} strategy.
- (2)
- Residents are sensitive to participation benefits and participation cost changes. While participation in waste separation benefits residents, it also requires them to bear certain costs or losses. The greater the benefits of participation, the smaller the costs, and the easier it is to participate. The participation cost of residents mainly includes material costs and time costs. Residents need to buy specific waste-separation containers for the project, i.e., material cost; they need to identify and sort the waste before putting it out, i.e., time cost. The government’s participation cost is mainly the human and material cost in the management process, i.e., the management cost. Therefore, by rationalizing and optimizing the design of the waste-separation process, the government can promote residents’ participation in waste separation; reduce the participation cost of both residents and the government, mainly the time cost T and the management cost C; and actively increase the participation rate of waste separation.
- (3)
- The allocation coefficient of direct benefits of participation significantly impacts strategy choice—the distribution coefficient (0 ≤ β ≤ 1) needs to be found between 0 and 1. Simulation results show that too high or too low a distribution coefficient may change the evolutionary strategy from {participation, participation} to {non-participation, non-participation}, thus failing to achieve the goal of both residents and government participation in waste separation. Therefore, the functional departments should design the direct benefit distribution coefficients through legislation or introduce management methods that meet the local conditions to effectively increase the willingness of residents and local governments to participate in waste separation at the same time and realize the purpose of both residents and governments to participate in waste separation at the same time.
- (4)
- The opportunity cost of residents has a significant role in promoting strategy choice. In participation in waste separation, the opportunity cost for residents and the potential gain for the government are both uncertain future losses and gains. The research results show that residents are more sensitive to the performance of opportunity costs. In contrast, the potential gain is not significant to the strategic choice of both participating subjects, which is consistent with the characteristics of cumulative prospect theory. Small-probability events are given larger weights, while medium- and high-probability events are given smaller ones. In the case of participation in waste separation, the resident’s involvement in the waste-separation process causing them to miss other benefits is a small-probability event. The simulation results show that some minor changes make the residents sensitive due to being given larger weights by limited, rational people.
6. Conclusions
- (1)
- Raising the level of environmental awareness among residents: The choice of both residents and the government to participate in waste separation is a very complex issue that depends on individual residents’ attitudes and level of environmental awareness. Agreeing to participate does not necessarily mean fully supporting household waste separation. Participation in waste separation is essential, as is the quality of individual residents’ waste separation. Many scholars have studied promoting waste separation and analyzed government educational efforts. Therefore, the government should improve the environmental awareness cultivation system by starting from both school and non-school systems, establishing a top-down waste-separation education model, and striving to create an excellent ecological awareness atmosphere in the whole society to effectively improve the level of environmental awareness of individual residents and their family members, thus achieving the goal of both increasing the willingness to participate in waste separation and enhancing the quality of individual residents’ waste separation.
- (2)
- Strengthen government support policies and programs: As residents are sensitive to participation benefits and cost changes, participating subjects are more inclined to loss avoidance. The government should thoroughly investigate the ratio of benefits to costs of participating topics in waste classification, actively give a certain amount of reasonable financial subsidy plan to fully ensure that the benefits of participating subjects in waste classification are more significant than the costs, and at the same time optimize the waste-classification management chain, redesign the local unreasonable places, and strive to reduce the government. At the same time, we encourage the government to optimize the waste-separation management chain, redesign the local irrationalities, and try to reduce the management costs.
- (3)
- Continuous and in-depth research on garbage sorting: In this paper, we combine the cumulative prospect theory and evolutionary game to consider the influence of the psychological changes of the participating subjects on their willingness to participate in waste separation. Moreover, due to the time limitation, current research conditions, and the number of participants, we cannot thoroughly examine the characteristics of individual residents. We intend to conduct specific research on individual residents’ factors in the subsequent studies, such as the study of residents’ waste-separation behavior based on the theory of planned behavior, the survey of residents’ waste-separation behavior under the environmental behavior model, and the study of psychological empowerment cognition on residents’ waste-separation behavior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, Z.; Zhao, Y.; Zhu, Y.; Zhang, M.; Yu, Y.; Guo, Y.; Zhou, T. Efficient treatment of mature landfill leachate with a novel composite biological trickle reactor developed using refractory domestic waste and aged refuse. J. Clean. Prod. 2021, 305, 127194. [Google Scholar] [CrossRef]
- Zhang, B.; Lai, K.-H.; Wang, B.; Wang, Z. From intention to action: How do personal attitudes, facilities accessibility, and government stimulus matter for household waste sorting? J. Environ. Manag. 2019, 233, 447–458. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yue, G.; Xinquan, G.; Yingmei, Y.; Hua, C.; Jianping, H.; Jian, Z. Exploring the residents’ intention to separate MSW in Beijing and understanding the reasons: An explanation by extended VBN theory. Sustain. Cities Soc. 2018, 37, 637–648. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, L.; Huang, J.; Li, W.; Chen, Y.; Qiu, W. Evolutionary Game Analysis on Behavioral Strategies of Government and Residents in Municipal Household Waste Separation. Sustainability 2021, 13, 11421. [Google Scholar] [CrossRef]
- Soltani, A.; Sadiq, R.; Hewage, K. Selecting sustainable waste-to-energy technologies for municipal solid waste treatment: A game theory approach for group decision-making. J. Clean. Prod. 2016, 113, 388–399. [Google Scholar] [CrossRef]
- Chen, F.; Chen, H.; Guo, D.; Han, S.; Long, R. How to achieve a cooperative mechanism of MSW source separation among individuals—An analysis based on evolutionary game theory. J. Clean. Prod. 2018, 195, 521–531. [Google Scholar] [CrossRef]
- Zhou, G.H.; Zhang, Y.; Yan-Laib, L.I. Evolutionary Game Analysis of the Behavior of Construction Safety Management Based on Prospect Theory. J. Syst. Manag. 2012, 04, 501–509. [Google Scholar]
- Ekere, W.; Mugisha, J.; Drake, L. Factors influencing waste separation and utilization among households in the Lake Victoria crescent, Uganda. Waste Manag. 2009, 29, 3047–3051. [Google Scholar] [CrossRef]
- Bernstad, A. Household food waste separation behavior and the importance of convenience. Waste Manag. 2014, 34, 1317–1323. [Google Scholar] [CrossRef]
- Xu, D.Y.; Lin, Z.Y.; Gordon, M.P.R.; Robinson, N.K.L.; Harder, M.K. Perceived key elements of a successful residential food waste sorting program in urban apartments: Stakeholder views. J. Clean. Prod. 2016, 134, 362–370. [Google Scholar] [CrossRef]
- Stoeva, K.; Alriksson, S. Influence of recycling programmes on waste separation behaviour. Waste Manag. 2017, 68, 732–741. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Si, H.; Yu, L.; Si, H. Factors Influencing Young People’s Intention toward Municipal Solid Waste Sorting. Int. J. Environ. Res. Public Health 2019, 16, 1708. [Google Scholar] [CrossRef]
- Leeabai, N.; Suzuki, S.; Jiang, Q.; Dilixiati, D.; Takahashi, F. The effects of setting conditions of trash bins on waste collection performance and waste separation behaviors; distance from walking path, separated setting, and arrangements. Waste Manag. 2019, 94, 58–67. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, G.; Yin, X.; Gong, Q. Residents’ Waste Separation Behaviors at the Source: Using SEM with the Theory of Planned Behavior in Guangzhou, China. Int. J. Environ. Res. Public Health 2015, 12, 9475–9491. [Google Scholar] [CrossRef]
- Boonrod, K.; Towprayoon, S.; Bonnet, S.; Tripetchkul, S. Enhancing organic waste separation at the source behavior: A case study of the application of motivation mechanisms in communities in Thailand. Resour. Conserv. Recycl. 2015, 95, 77–90. [Google Scholar] [CrossRef]
- Rousta, K.; Bolton, K.; Lundin, M.; Dahlén, L. Quantitative assessment of distance to collection point and improved sorting information on source separation of household waste. Waste Manag. 2015, 40, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, J.; Wen, Z.-G.; Chen, Y.-X. College students’ municipal solid waste source separation behavior and its influential factors: A case study in Beijing, China. J. Clean. Prod. 2017, 164, 444–454. [Google Scholar] [CrossRef]
- Fan, B.; Yang, W.; Shen, X. A comparison study of ‘motivation–intention–behavior’ model on household solid waste sorting in China and Singapore. J. Clean. Prod. 2018, 211, 442–454. [Google Scholar] [CrossRef]
- Massarutto, A.; Marangon, F.; Troiano, S.; Favot, M. Moral duty, warm glow or self-interest? A choice experiment study on motivations for domestic garbage sorting in Italy. J. Clean. Prod. 2018, 208, 916–923. [Google Scholar] [CrossRef]
- Musee, N.; Lorenzen, L.; Aldrich, C. New methodology for hazardous waste classification using fuzzy set theory: Part I. Knowledge acquisition. J. Hazard. Mater. 2008, 154, 1040–1051. [Google Scholar] [CrossRef]
- Musee, N.; Aldrich, C.; Lorenzen, L. New methodology for hazardous waste classification using fuzzy set theory: Part II. Intelligent decision support system. J. Hazard. Mater. 2008, 157, 94–105. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, S. Waste separation at home: Are Japanese municipal curbside recycling policies efficient? Resour. Conserv. Recycl. 2010, 55, 325–334. [Google Scholar] [CrossRef]
- Xu, L.; Ling, M.; Lu, Y.; Shen, M. Understanding Household Waste Separation Behaviour: Testing the Roles of Moral, Past Experience, and Perceived Policy Effectiveness within the Theory of Planned Behaviour. Sustainability 2017, 9, 625. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.; Ma, J.; Yang, Y.; Liu, G.-J. An Exploration of the Impacts of Compulsory Source-Separated Policy in Improving Household Solid Waste-Sorting in Pilot Megacities, China: A Case Study of Nanjing. Sustainability 2018, 10, 1327. [Google Scholar] [CrossRef]
- Rousta, K.; Ekström, K.M. Assessing Incorrect Household Waste Sorting in a Medium-Sized Swedish City. Sustainability 2013, 5, 4349–4361. [Google Scholar] [CrossRef]
- Liu, H.; Yao, Z. Research on Mixed and Classification Simulation Models of Medical Waste—A Case Study in Beijing, China. Sustainability 2018, 10, 4226. [Google Scholar] [CrossRef]
- Barletta, I.; Larborn, J.; Mani, M.; Johannson, B. Towards an Assessment Methodology to Support Decision Making for Sustainable Electronic Waste Management Systems: Automatic Sorting Technology. Sustainability 2016, 8, 84. [Google Scholar] [CrossRef]
- Meng, X.; Tan, X.; Wang, Y.; Wen, Z.; Tao, Y.; Qian, Y. Investigation on decision-making mechanism of residents’ household solid waste classification and recycling behaviors. Resour. Conserv. Recycl. 2018, 140, 224–234. [Google Scholar] [CrossRef]
- Liu, W.; Cui, M.; Shen, Y.; Zhu, G.; Luo, L.; Li, M.; Li, J. Waste cigarette filter as nanofibrous membranes for on-demand immiscible oil/water mixtures and emulsions separation. J. Colloid Interface Sci. 2019, 549, 114–122. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L. Research and Countermeasure of Rural Waste Classification under Rural Revitalization Strategy. In Proceedings of the 2019 4th International Social Sciences and Education Conference (ISSEC 2019), Xiamen, China, 27–28 June 2019; p. 4. [Google Scholar]
- Eklund, J.; Kihlstedt, A.; Engkvist, I.-L. Sorting and disposing of waste at recycling centres—A users perspective. Appl. Ergon. 2010, 41, 355–361. [Google Scholar] [CrossRef]
- Ordoñez, I.; Harder, R.; Nikitas, A.; Rahe, U. Waste sorting in apartments: Integrating the perspective of the user. J. Clean. Prod. 2015, 106, 669–679. [Google Scholar] [CrossRef]
- Struk, M. Distance and incentives matter: The separation of recyclable municipal waste. Resour. Conserv. Recycl. 2017, 122, 155–162. [Google Scholar] [CrossRef]
- Yuan, H.; Lu, W.; Hao, J.J. The evolution of construction waste sorting on-site. Renew. Sustain. Energy Rev. 2013, 20, 483–490. [Google Scholar] [CrossRef]
- Hossain, U.; Wu, Z.; Poon, C.S. Comparative environmental evaluation of construction waste management through different waste sorting systems in Hong Kong. Waste Manag. 2017, 69, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Tadesse, T. Environmental concern and its implication to household waste separation and disposal: Evidence from Mekelle, Ethiopia. Resour. Conserv. Recycl. 2009, 53, 183–191. [Google Scholar] [CrossRef]
- Xu, L.; Ling, M.; Wu, Y. Economic incentive and social influence to overcome household waste separation dilemma: A field intervention study. Waste Manag. 2018, 77, 522–531. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, X.; Ling, M. Spillover effects of household waste separation policy on electricity consumption: Evidence from Hangzhou, China. Resour. Conserv. Recycl. 2018, 129, 219–231. [Google Scholar] [CrossRef]
- Tianlun, L. From Policy to Practice: Historical Experience, Difficulty Avoidance and Governance Strategy of Waste Classification Policy in the New Era. In Proceedings of the 2019 International Conference on Emerging Researches in Management, Business, Finance and Economics (ERMBFE 2019), Shanghai, China, 15–16 October 2019; p. 11. [Google Scholar]
- Chen, F.; Chen, H.; Liu, S.; Li, W.; Li, Q.; Long, R. Formation and recurrence mechanism of residents’ waste separation behavior under the intervention of an information interaction. Resour. Conserv. Recycl. 2020, 162, 105027. [Google Scholar] [CrossRef]
- Chen, F.; Chen, H.; Jin, Y.; Wang, F.; Long, R. Impact of cognition on waste separation behavior-Nonlinear moderating effect by trustworthiness for links. J. Clean. Prod. 2021, 296, 126525. [Google Scholar] [CrossRef]
- Chen, F.; Hou, J.; Gu, X.; Hou, J.; Pan, Q.; Tang, Z. Research on temporal and spatial evolution of public’s response to the mandatory waste separation policy based on big data mining. Sustain. Prod. Consum. 2022, 31, 236–248. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Friedman, D. Evolutionary Games in Economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef]

| Government | Participation (y) | Non-Participation (1 − y) | |
|---|---|---|---|
| Residents | |||
| Participation (x) | U1 + βK − M − T U2 + (1 − β)K − C + P | U1 − M − T U2 | |
| Non-participation (1 − x) | U1 U2 − C | U1 U2 | |
| Equilibrium Point | ∣Je∣ | trJe | Results |
|---|---|---|---|
| (0, 0) | + | - | ESS |
| (0, 1) | - | + | Instability point |
| (1, 0) | - | + | Instability point |
| (1, 1) | + | + | Saddle point |
| Equilibrium Point | ∣Je∣ | trJe | Results |
|---|---|---|---|
| (0, 0) | + | - | ESS |
| (0, 1) | + | + | Instability point |
| (1, 0) | + | + | Instability point |
| (1, 1) | + | - | ESS |
| + | 0 | Saddle point |
| Parameters | Meaning | Value | Parameters | Meaning | Value |
|---|---|---|---|---|---|
| x | Probability of resident participation | 0.3 | M | Resident opportunity cost | 1 |
| y | Probability of government involvement | 0.5 | T | Resident time cost | 3 |
| β | The direct benefit allocation factor | 0.5 | P | Potential government benefits | 3 |
| K | Direct benefits | 90 | C | Government management costs | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Jiang, Y.; Wu, J. Evolutionary Game Analysis of Government and Residents’ Participation in Waste Separation Based on Cumulative Prospect Theory. Int. J. Environ. Res. Public Health 2022, 19, 14589. https://doi.org/10.3390/ijerph192114589
Zhang L, Jiang Y, Wu J. Evolutionary Game Analysis of Government and Residents’ Participation in Waste Separation Based on Cumulative Prospect Theory. International Journal of Environmental Research and Public Health. 2022; 19(21):14589. https://doi.org/10.3390/ijerph192114589
Chicago/Turabian StyleZhang, Lichi, Yanyan Jiang, and Junmin Wu. 2022. "Evolutionary Game Analysis of Government and Residents’ Participation in Waste Separation Based on Cumulative Prospect Theory" International Journal of Environmental Research and Public Health 19, no. 21: 14589. https://doi.org/10.3390/ijerph192114589
APA StyleZhang, L., Jiang, Y., & Wu, J. (2022). Evolutionary Game Analysis of Government and Residents’ Participation in Waste Separation Based on Cumulative Prospect Theory. International Journal of Environmental Research and Public Health, 19(21), 14589. https://doi.org/10.3390/ijerph192114589






