Model-Based Biomechanical Exoskeleton Concept Optimization for a Representative Lifting Task in Logistics
Abstract
1. Introduction
1.1. Musculoskeletal Disorders and Exoskeletons
1.2. Objective
2. Methods
2.1. Workflow Overview
2.2. Test Subjects and Experimental Setup
2.3. Experimental Procedures
2.4. Biomechanical Modeling of the Motion Sequences
2.5. Motion Sequence Evaluation and Selection
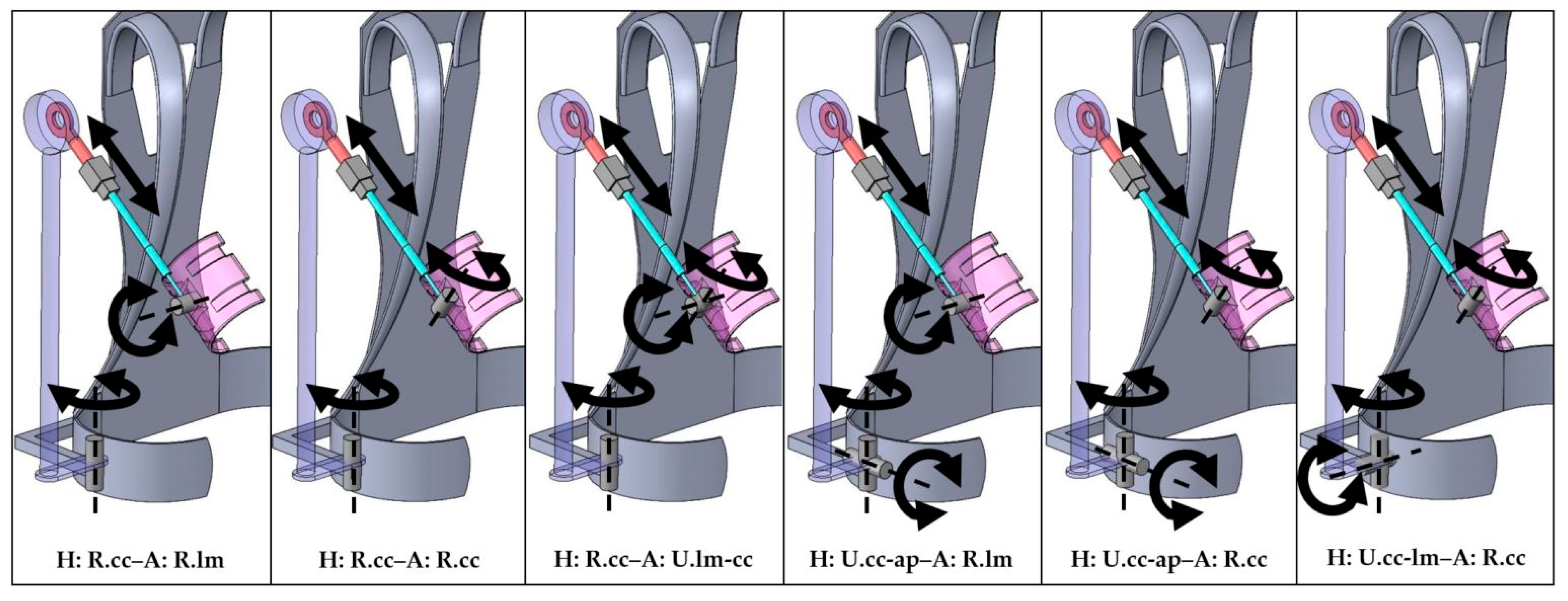
2.6. Exoskeleton Concepts
2.7. Modeling of the Exoskeleton-Human System and Interaction
2.8. Exoskeleton Concepts Analysis
3. Results
3.1. Motion Sequence Evaluation and Selection
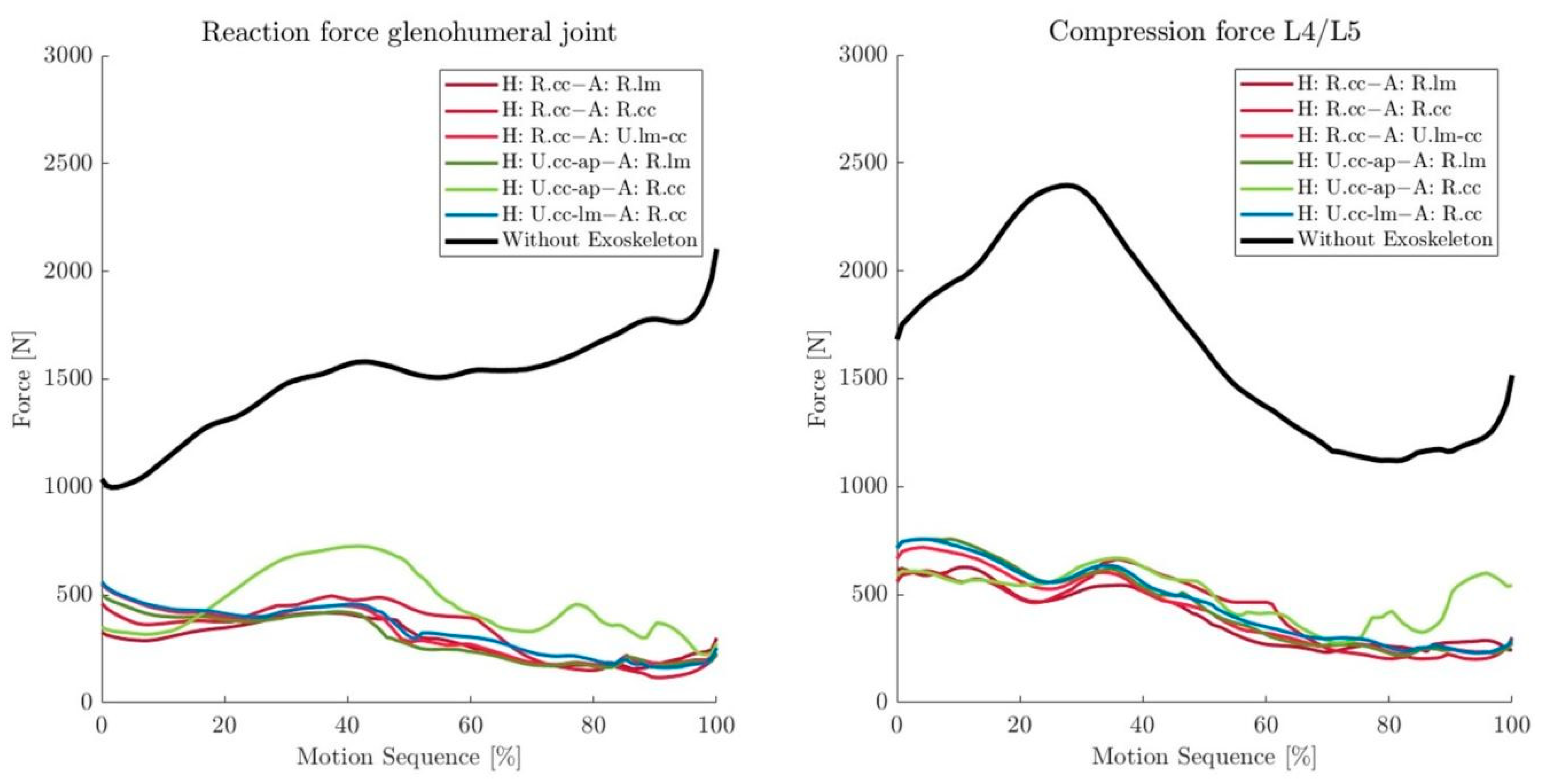
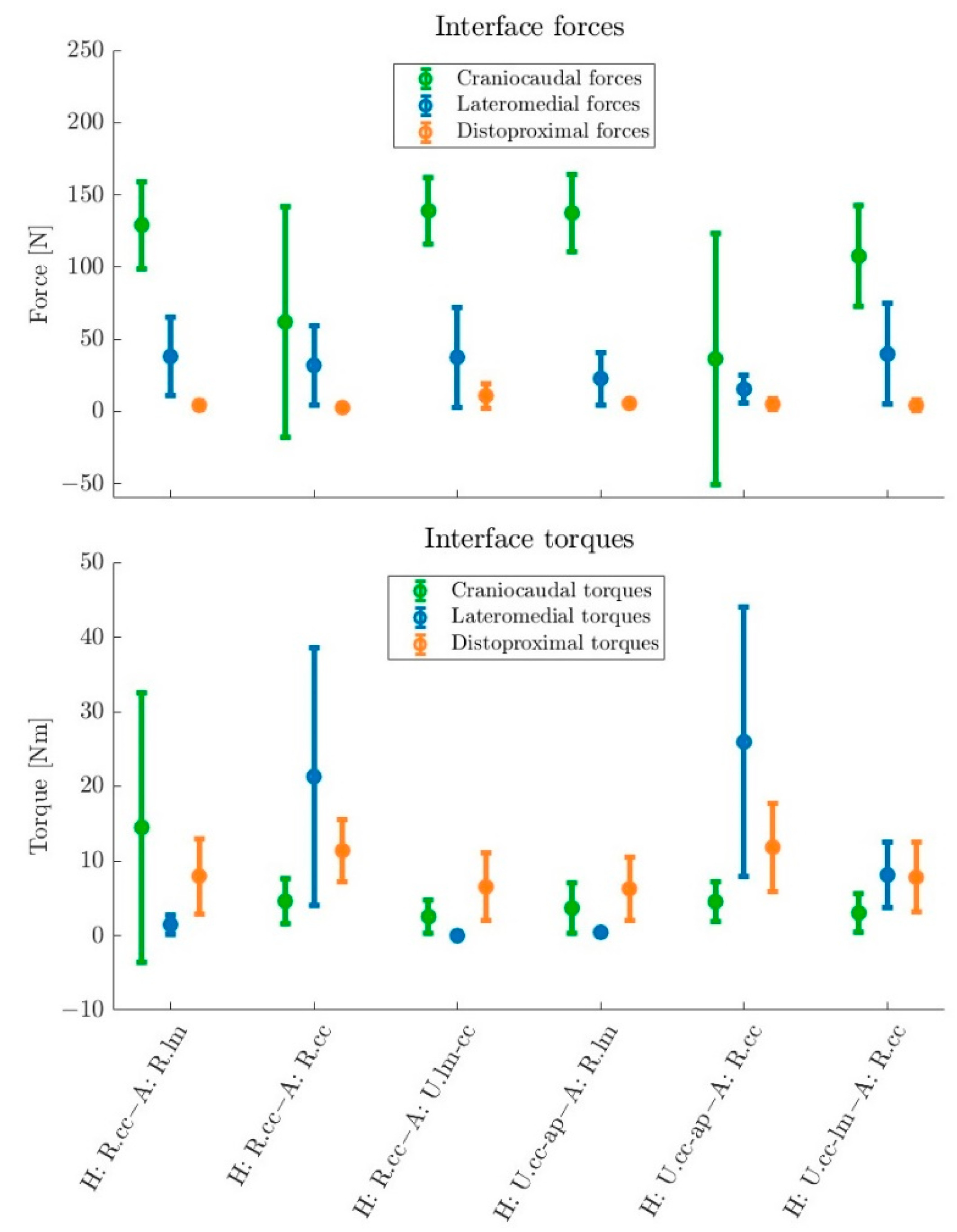
3.2. Exoskeleton Concepts Analysis
4. Discussion
4.1. Motion Sequence Evaluation and Selection
4.2. Exoskeleton Concepts Analysis
5. Conclusions
- A linear DOF (prismatic joint) in the arm longitudinal direction in front of the arm interface to reduce shear loads.
- A rotational joint in the connection to the arm interface allowing for forward/backward tilting of the arm bracing and minimizing lateromedial torques.
- A universal joint in the hip connection allowing for rotation parallel to the body axis and tilting outward/inward of the exoskeleton structures at the hip, thereby reducing lateromedial forces and improving the range of motion.
- A combination of these that allows for sound biomechanical unloading of the shoulders and back while parasitic forces and torques are effectively reduced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Kok, J.; Vroonhof, P.; Snjiders, J.; Roullis, G.; Clarke, M.; Peereboom, K.; van Dorst, P.; Isusi, I. Work-Related Musculoskeletal Disorders: Prevalence, Costs and Demographics in the EU: European Risk Observatory Report; European Agency for Safety and Health at Work: Luxembourg, 2019.
- Luttmann, A.; Jäger, M.; Griefahn, B.; Caffier, G.; Liebers, F. Factors to be considered in prevention. In Preventing Musculoskeletal Disorders in the Workplace, 1st ed.; Kortum-Margot, E., Ed.; World Health Organization: Geneva, Switzerland, 2003; pp. 12–14. [Google Scholar]
- Monica, L.; Sara Anastasi, S.; Francesco Draicchio, F. Occupational Exoskeletons: Wearable Robotic Devices To Prevent Work-Related Musculoskeletal Disorders in the Workplace of the Future; European Agency for Safety and Health at Work: Bilbao, Spain, 2020. [Google Scholar]
- Theurel, J.; Desbrosses, K. Occupational Exoskeletons: Overview of Their Benefits and Limitations in Preventing Work-Related Musculoskeletal Disorders. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 264–280. [Google Scholar] [CrossRef]
- Agrawal, A.; Dube, A.N.; Kansara, D.; Shah, S.; Sheth, S. Exoskeleton: The Friend of Mankind in context of Rehabilitation and Enhancement. Indian J. Sci. Technol. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Bogue, R. Robotic exoskeletons: A review of recent progress. Ind. Robot Int. J. 2015, 42, 5–10. [Google Scholar] [CrossRef]
- Gopura, R.; Bandara, D.; Kiguchi, K.; Mann, G. Developments in hardware systems of active upper-limb exoskeleton robots: A review. Robot. Auton. Syst. 2016, 75, 203–220. [Google Scholar] [CrossRef]
- Gull, M.A.; Bai, S.; Bak, T. A Review on Design of Upper Limb Exoskeletons. Robotics 2020, 9, 16. [Google Scholar] [CrossRef]
- Rupal, B.S.; Rafique, S.; Singla, A.; Singla, E.; Isaksson, M.; Virk, G.S. Lower-limb exoskeletons. Int. J. Adv. Robot. Syst. 2016, 14, 18–24. [Google Scholar] [CrossRef]
- Yang, C.-J.; Zhang, J.-F.; Chen, Y.; Dong, Y.-M.; Zhang, Y. A Review of exoskeleton-type systems and their key technologies. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1599–1612. [Google Scholar] [CrossRef]
- Young, A.J.; Ferris, D.P. State of the Art and Future Directions for Lower Limb Robotic Exoskeletons. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 171–182. [Google Scholar] [CrossRef]
- Skelex 360-XFR. Available online: https://www.skelex.com/skelex-360-xfr/ (accessed on 28 October 2022).
- ekso EVO. Available online: https://eksobionics.com/de/ekso-evo-de/ (accessed on 28 October 2022).
- Ottobock Shoulder: Overhead Work Redefined. Available online: https://ottobockexoskeletons.com/obs/?lang=en (accessed on 28 October 2022).
- MATE-XT Exoskeleton. Available online: https://mate.comau.com/ (accessed on 28 October 2022).
- BESK. Available online: https://en.cyberhs.eu/besk (accessed on 28 October 2022).
- ShivaExo. Available online: https://www.shivaexo.fr/en/ (accessed on 28 October 2022).
- AIRFRAME®—Fatigue Has a New Enemy. Available online: https://www.levitatetech.com/airframe/ (accessed on 28 October 2022).
- V3 ShoulderX. Available online: https://www.suitx.com/shoulderx (accessed on 28 October 2022).
- AGADEXO Shoulder. Available online: https://agade-exoskeletons.com/en/agade-eng/ (accessed on 28 October 2022).
- Shoulder exoskeleton S700. Available online: https://www.exoiq.com/schulter-exoskelett-s700 (accessed on 16 August 2022).
- Ottobock Back: The Exoskeleton for the Relief of the Back. Available online: https://ottobockexoskeletons.com/paexo-back/?lang=en (accessed on 28 October 2022).
- HAL Lumbar Type for Labor Support. Available online: https://www.cyberdyne.jp/english/products/Lumbar_LaborSupport.html (accessed on 16 August 2022).
- Discover New Dimensions in Human Augmentation. Available online: https://www.germanbionic.com/ (accessed on 28 October 2022).
- Muscle Suit. Available online: https://innophys.jp/en/product/standard/ (accessed on 28 October 2022).
- Flex Lift. Available online: https://kineticedgeinc.com/ (accessed on 28 October 2022).
- Wearable Chest and Back Support. Available online: https://www.laevo-exoskeletons.com/en/laevo-v2-1 (accessed on 28 October 2022).
- Exoback. Available online: https://www.rb3d.com/en/exosquelettes/exoback (accessed on 16 August 2022).
- V3 BackX. Available online: https://www.suitx.com/backx (accessed on 28 October 2022).
- Federal Institute for Occupational Safety and Health (BAuA). MEGAPHYS—Mehrstufige Gefährdungsanalyse Physischer Belastungen am Arbeitsplatz; Federal Institute for Occupational Safety and Health (BAuA): Dortmund, Germany, 2019. [Google Scholar]
- Andersen, J.H.; Haahr, J.P.; Frost, P. Risk factors for more severe regional musculoskeletal symptoms: A two-year prospective study of a general working population. Arthritis Rheum. 2007, 56, 1355–1364. [Google Scholar] [CrossRef]
- Harkness, E.F.; Macfarlane, G.J.; Nahit, E.S.; Silman, A.J.; McBeth, J. Mechanical and psychosocial factors predict new onset shoulder pain: A prospective cohort study of newly employed workers. Occup. Environ. Med. 2003, 60, 850–857. [Google Scholar] [CrossRef]
- Beach, J.; Senthilselvan, A.; Cherry, N. Factors affecting work-related shoulder pain. Occup. Med. 2012, 62, 451–454. [Google Scholar] [CrossRef] [PubMed][Green Version]
- De Bock, S.; Ghillebert, J.; Govaerts, R.; Elprama, S.A.; Marusic, U.; Serrien, B.; Jacobs, A.; Geeroms, J.; Meeusen, R.; De Pauw, K. Passive Shoulder Exoskeletons: More Effective in the Lab than in the Field? IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 29, 173–183. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, L. Model-Based Comparison of Passive and Active Assistance Designs in an Occupational Upper Limb Exoskeleton for Overhead Lifting. IISE Trans. Occup. Ergon. Hum. Factors 2021, 9, 167–185. [Google Scholar] [CrossRef] [PubMed]
- Crea, S.; Beckerle, P.; de Looze, M.; De Pauw, P.; Grazi, L.; Kermavnar, T.; Masood, J.; O’Sullivan, L.W.; Pacifico, I.; Rodriguez-Guerrero, C.; et al. Occupational exoskeletons: A roadmap toward large-scale adoption. Methodology and challenges of bringing exoskeletons to workplaces. Wearable Technol. 2021, 2, E11. [Google Scholar] [CrossRef]
- Agarwal, P.; Narayanan, M.S.; Lee, L.-F.; Mendel, F.; Krovi, V.N. Simulation-Based Design of Exoskeletons Using Musculoskeletal Analysis. In Volume 3: 30th Computers and Information in Engineering Conference, Parts A and B, Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; ASMEDC: New York, NY, USA, 2010; pp. 1357–1364. ISBN 978-0-7918-4411-3. [Google Scholar]
- Molz, C.; Yao, Z.; Sänger, J.; Gwosch, T.; Weidner, R.; Matthiesen, S.; Wartzack, S.; Miehling, J. A Musculoskeletal Human Model-Based Approach for Evaluating Support Concepts of Exoskeletons for Selected Use Cases. Proc. Des. Soc. 2022, 2, 515–524. [Google Scholar] [CrossRef]
- Tröster, M.; Schneider, U.; Bauernhansl, T.; Rasmussen, J.; Andersen, M. Simulation Framework for Active Upper Limb Exoskeleton Design Optimization Based on Musculoskeletal Modeling. In Technische Unterstützungssysteme, Die Die Menschen Wirklich Wollen: Dritte Transdisziplinäre Konferenz: Hamburg 2018, 1st ed.; Weidner, R., Karafillidis, A., Eds.; Helmut-Schmidt-Universität: Hamburg, Deutschland, 2018; pp. 345–353. ISBN 978-3-86818-246-0. [Google Scholar]
- Zhou, L.; Li, Y.; Bai, S. A human-centered design optimization approach for robotic exoskeletons through biomechanical simulation. Robot. Auton. Syst. 2017, 91, 337–347. [Google Scholar] [CrossRef]
- Fritzsche, L.; Galibarov, P.E.; Gärtner, C.; Bornmann, J.; Damsgaard, M.; Wall, R.; Schirrmeister, B.; Gonzalez-Vargas, J.; Pucci, D.; Maurice, P.; et al. Assessing the efficiency of exoskeletons in physical strain reduction by biomechanical simulation with AnyBody Modeling System. Wearable Technol. 2021, 2, e6. [Google Scholar] [CrossRef]
- Seiferheld, B.E.; Andersen, M.S.; Frost, J.; Krog, M.; Skals, S. Biomechanical investigation of a passive upper-extremity exoskeleton for manual material handling—A computational parameter study and modelling approach. IJHFMS 2022, 7, 275–300. [Google Scholar] [CrossRef]
- Koelewijn, A.D.; Heinrich, D.; van den Bogert, A.J. Metabolic cost calculations of gait using musculoskeletal energy models, a comparison study. PLoS ONE 2019, 14, e0222037. [Google Scholar] [CrossRef]
- Shourijeh, M.S.; Jung, M.; Damsgaard, M. Metabolic Energy Consumption in a Box-Lifting Task: A Parametric Study on the Assistive Torque. In Wearable Robotics: Challenges and Trends; González-Vargas, J., Ibáñez, J., Contreras-Vidal, J.L., van der Kooij, H., Pons, J.L., Eds.; Springer International Publishing: Cham, Germany, 2017; pp. 143–148. ISBN 978-3-319-46531-9. [Google Scholar]
- Tröster, M.; Budde, S.; Maufroy, C.; Andersen, M.S.; Rasmussen, J.; Schneider, U.; Bauernhansl, T. Biomechanical Analysis of Stoop and Free-Style Squat Lifting and Lowering with a Generic Back-Support Exoskeleton Model. IJERPH 2022, 19, 9040. [Google Scholar] [CrossRef]
- Tröster, M.; Wagner, D.; Müller-Graf, F.; Maufroy, C.; Schneider, U.; Bauernhansl, T. Biomechanical Model-Based Development of an Active Occupational Upper-Limb Exoskeleton to Support Healthcare Workers in the Surgery Waiting Room. IJERPH 2020, 17, 5140. [Google Scholar] [CrossRef] [PubMed]
- Gneiting, E.; Schiebl, J.; Tröster, M.; Kopp, V.; Maufroy, C.; Schneider, U. Model-Based Biomechanics for Conceptual Exoskeleton Support Estimation Applied for a Lifting Task. In Wearable Robotics: Challenges and Trends; Moreno, J.C., Masood, J., Schneider, U., Maufroy, C., Pons, J.L., Eds.; Springer International Publishing: Cham, Germany, 2022; pp. 395–399. ISBN 978-3-030-69546-0. [Google Scholar]
- Hichert, M.; Güttes, M.; Bäuerle, I.; Ziegenspeck, N.; Bölke, N.; Schiebl, J. Exoskeletons for Military Logistics and Maintenance. In Wearable Robotics: Challenges and Trends; Moreno, J.C., Masood, J., Schneider, U., Maufroy, C., Pons, J.L., Eds.; Springer International Publishing: Cham, Germany, 2022; pp. 525–528. ISBN 978-3-030-69546-0. [Google Scholar]
- AnyBody Technology. The AnyMoCap Framework. Available online: https://anyscript.org/ammr-doc/anymocap/index.html (accessed on 22 October 2022).
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; de Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Aurbach, M.; Špička, J.; Süß, F.; Vychytil, J.; Havelková, L.; Ryba, T.; Dendorfer, S. Torus obstacle method as a wrapping approach of the deltoid muscle group for humeral abduction in musculoskeletal simulation. J. Biomech. 2020, 109, 109864. [Google Scholar] [CrossRef]
- Skals, S.; Jung, M.K.; Damsgaard, M.; Andersen, M.S. Prediction of ground reaction forces and moments during sports-related movements. Multibody Syst Dyn 2017, 39, 175–195. [Google Scholar] [CrossRef]
- Balser, F.; Desai, R.; Ekizoglou, A.; Bai, S. A Novel Passive Shoulder Exoskeleton Designed With Variable Stiffness Mechanism. IEEE Robot. Autom. Lett. 2022, 7, 2748–2754. [Google Scholar] [CrossRef]
- Grazi, L.; Trigili, E.; Proface, G.; Giovacchini, F.; Crea, S.; Vitiello, N. Design and Experimental Evaluation of a Semi-Passive Upper-Limb Exoskeleton for Workers With Motorized Tuning of Assistance. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2276–2285. [Google Scholar] [CrossRef]
- van der Have, A.; Rossini, M.; Rodriguez-Guerrero, C.; van Rossom, S.; Jonkers, I. The Exo4Work shoulder exoskeleton effectively reduces muscle and joint loading during simulated occupational tasks above shoulder height. Appl. Ergon. 2022, 103, 103800. [Google Scholar] [CrossRef]
- van Engelhoven, L.; Kazerooni, H. Design and Intended Use of a Passive Actuation Strategy for a Shoulder Supporting Exoskeleton. In Proceedings of the 2019 Wearable Robotics Association Conference (WearRAcon), Scottsdale, AZ, USA, 25–27 March 2019; pp. 7–12. [Google Scholar]
- Kutzner, I.; Heinlein, B.; Graichen, F.; Bender, A.; Rohlmann, A.; Halder, A.; Beier, A.; Bergmann, G. Loading of the knee joint during activities of daily living measured in vivo in five subjects. J. Biomech. 2010, 43, 2164–2173. [Google Scholar] [CrossRef]
- Kotzar, G.M.; Davy, D.T.; Goldberg, V.M.; Heiple, K.G.; Berilla, J.; Brown, R.H.; Burstein, A.H. Telemeterized in vivo hip joint force data: A report on two patients after total hip surgery. J. Orthop. Res. 1991, 9, 621–633. [Google Scholar] [CrossRef]
- Jäger, M. Die „Revidierten Dortmunder Richtwerte“. Zbl Arb. 2019, 69, 271–289. [Google Scholar] [CrossRef]
- Westerhoff, P.; Graichen, F.; Bender, A.; Halder, A.; Beier, A.; Rohlmann, A.; Bergmann, G. In vivo measurement of shoulder joint loads during activities of daily living. J. Biomech. 2009, 42, 1840–1849. [Google Scholar] [CrossRef]
- Jarrassé, N.; Morel, G. Connecting a Human Limb to an Exoskeleton. IEEE Trans. Robot. 2012, 28, 697–709. [Google Scholar] [CrossRef]
- Georgarakis, A.-M.; Stampfli, R.; Wolf, P.; Riener, R.; Duarte, J.E. A Method for Quantifying Interaction Forces in Wearable Robots. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 789–794. [Google Scholar]
- Lund, M.E.; de Zee, M.; Andersen, M.S.; Rasmussen, J. On validation of multibody musculoskeletal models. Proc. Inst. Mech. Eng. H 2012, 226, 82–94. [Google Scholar] [CrossRef] [PubMed]
- Bassani, T.; Stucovitz, E.; Qian, Z.; Briguglio, M.; Galbusera, F. Validation of the AnyBody full body musculoskeletal model in computing lumbar spine loads at L4L5 level. J. Biomech. 2017, 58, 89–96. [Google Scholar] [CrossRef]
- Chander, D.S.; Böhme, M.; Andersen, M.S.; Rasmussen, J.; Zentner, J.; Cavatorta, M.P. A comparison of different methods for modelling the physical human-exoskeleton interface. IJHFMS 2022, 7, 204–230. [Google Scholar] [CrossRef]
- Andersen, M.S.; de Zee, M.; Damsgaard, M.; Nolte, D.; Rasmussen, J. Introduction to Force-Dependent Kinematics: Theory and Application to Mandible Modeling. J. Biomech. Eng. 2017, 139, 091001. [Google Scholar] [CrossRef] [PubMed]
- Mallat, R.; Khalil, M.; Venture, G.; Bonnet, V.; Mohammed, S. Human-Exoskeleton Joint Misalignment: A Systematic Review. In Proceedings of the 2019 Fifth International Conference on Advances in Biomedical Engineering (ICABME), Tripoli, Lebanon, 17–19 October 2019; pp. 1–4. [Google Scholar]
- Schiele, A. Ergonomics of exoskeletons: Subjective performance metrics. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 480–485. [Google Scholar]

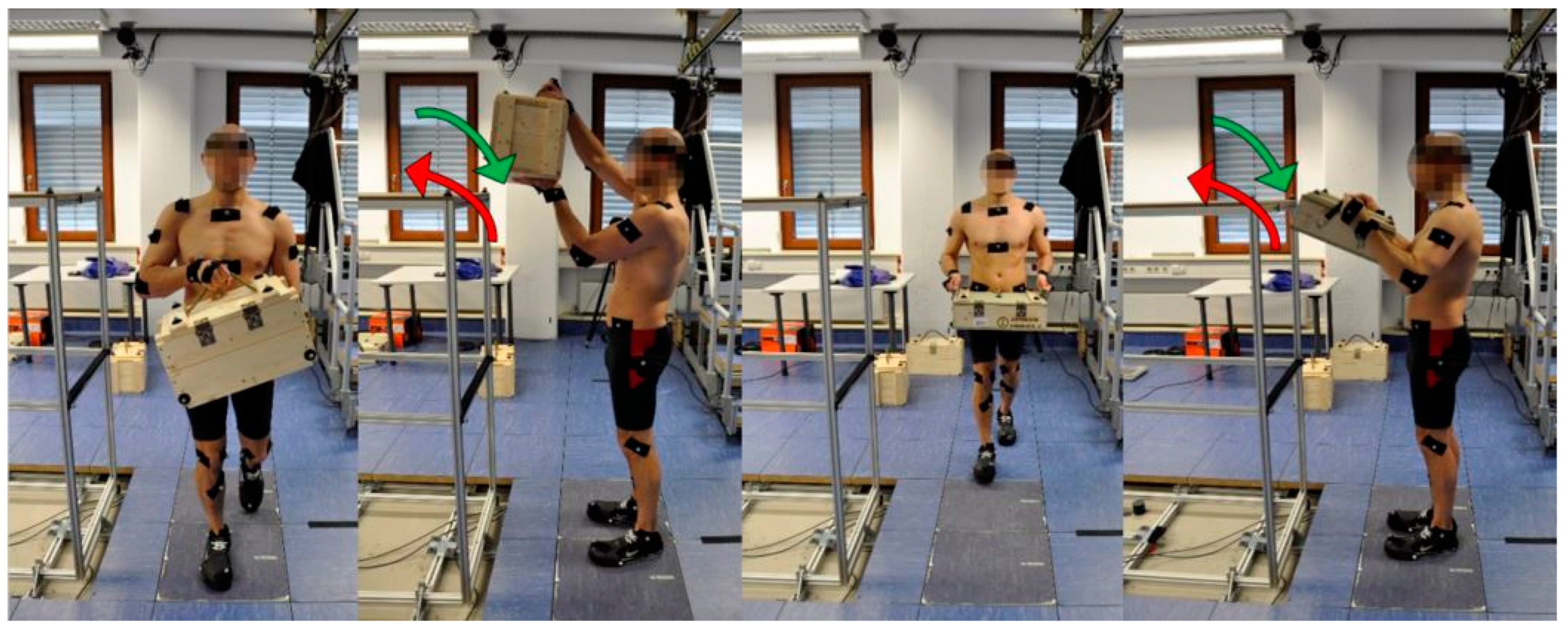


| Motion Sequence | ||||||
|---|---|---|---|---|---|---|
| Biomechanical Stress Criteria | T1 | T2 | T3 | T4 | T5 | T6 |
| Muscle activities (MAs) [%s] | ||||||
| Whole body | 78 ± 6 | 82 ± 21 | 54 ± 16 | 72 ± 3 | 90 ± 13 | 45 ± 12 |
| Lower extremities | 28 ± 5 | 23 ± 8 | 15 ± 6 | 26 ± 4 | 22 ± 3 | 11 ± 1 |
| Abdomen | 27 ± 4 | 39 ± 10 | 30 ± 7 | 25 ± 1 | 36 ± 3 | 21 ± 4 |
| Lower back | 24 ± 3 | 37 ± 9 | 29 ± 9 | 22 ± 1 | 35 ± 3 | 21 ± 3 |
| Neck | 13 ± 3 | 19 ± 9 | 12 ± 2 | 17 ± 1 | 24 ± 12 | 11± 3 |
| Shoulders | 47 ± 16 | 62 ± 27 | 41 ± 17 | 27 ± 2 | 56 ± 15 | 23 ± 10 |
| Arms | 78 ± 7 | 72 ± 16 | 50 ± 14 | 72 ± 3 | 87 ± 7 | 44 ± 11 |
| Joint forces (JFs) [kN] | ||||||
| Knee | 3.8 ± 0.5 | 3.7 ± 0.5 | 2.8 ± 0.8 | 3.4 ± 0.4 | 4.3 ± 1.6 | 2.8 ± 0.6 |
| Hip | 4 ± 1.2 | 3.1 ± 0.7 | 3 ± 0.5 | 4.3 ± 0.7 | 4.2 ± 0.2 | 3.3 ± 1.2 |
| Glenohumeral | 1.9 ± 0.5 | 2.7 ± 1.1 | 1.9 ± 0.2 | 1.4 ± 0.2 | 3.7 ± 1.8 | 1.8 ± 0.4 |
| Elbow | 1.2 ± 0.1 | 1.4 ± 0.4 | 1 ± 0.2 | 1.1 ± 0.1 | 1.2 ± 0.4 | 0.9 ± 0.1 |
| Wrist | 1.3 ± 0 | 1.7 ± 0.6 | 1 ± 0.3 | 1.1 ± 0 | 1.7 ± 1.2 | 0.7 ± 0.3 |
| L4/L5 | 2 ± 0.4 | 2.6 ± 0.1 | 2.2 ± 0.2 | 2.1 ± 0.3 | 3.2 ± 0.7 | 2.4 ± 0.4 |
| Overall score | 50 | 63 | 32 | 39 | 70 | 19 |
| Acronym | Hip Connection | Illustr. | Arm Connection | Illustr. |
|---|---|---|---|---|
| H: R.cc–A: R.lm | Revolute joint with craniocaudal axis | 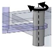 | Revolute joint with lateromedial axis |  |
| H: R.cc–A: R.cc | Revolute joint with craniocaudal axis | 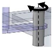 | Revolute joint with craniocaudal axis |  |
| H: R.cc–A: U.lm-cc | Revolute joint with craniocaudal axis | 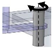 | Universal joint with lateromedial and craniocaudal axis |  |
| H: U.cc-ap–A: R.lm | Universal joint with craniocaudal and anteroposterior axis | 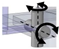 | Revolute joint with lateromedial axis |  |
| H: U.cc-ap–A: R.cc | Universal joint with craniocaudal and anteroposterior axis | 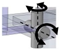 | Revolute joint with craniocaudal axis |  |
| H: U.cc-lm–A: R.cc | Universal joint with craniocaudal and lateromedial axis | 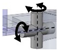 | Revolute joint with craniocaudal axis | 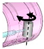 |
| Hip Connection | No Exoskeleton | R.cc | U.cc-ap | U.cc-lm | |||
|---|---|---|---|---|---|---|---|
| Arm Connection | R.lm | R.cc | U.lm-cc | R.lm | R.cc | R.cc | |
| Muscle activities MA [%] | |||||||
| Shoulders | 37.1 | 13.8 | 15.1 | 13.1 | 13.4 | 26.9 | 13.2 |
| Back | 27.9 | 8.9 | 9.2 | 9.0 | 9.5 | 10.3 | 9.6 |
| Joint forces JF [N] | |||||||
| Glenohumeral | 1495.0 | 287.2 | 329.9 | 319.1 | 298.4 | 461.3 | 334.2 |
| L4/L5 | 1665.3 | 401.5 | 429.8 | 432.7 | 448.5 | 502.1 | 460.5 |
| Arm bracing forces [N] | |||||||
| Distoproximal | - | 4.2 | 2.6 | 10.8 | 5.5 | 5.0 | 4.2 |
| Lateromedial | - | 38.1 | 31.9 | 37.5 | 22.7 | 15.4 | 39.7 |
| Arm bracing torques [Nm] | |||||||
| Distoproximal | - | 8.0 | 11.4 | 6.5 | 6.3 | 11.8 | 7.8 |
| Craniocaudal | - | 14.5 | 4.6 | 2.5 | 3.7 | 4.5 | 3.0 |
| Overall rating | - | 25.0 | 28.0 | 22.0 | 24.0 | 39.0 | 30.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiebl, J.; Tröster, M.; Idoudi, W.; Gneiting, E.; Spies, L.; Maufroy, C.; Schneider, U.; Bauernhansl, T. Model-Based Biomechanical Exoskeleton Concept Optimization for a Representative Lifting Task in Logistics. Int. J. Environ. Res. Public Health 2022, 19, 15533. https://doi.org/10.3390/ijerph192315533
Schiebl J, Tröster M, Idoudi W, Gneiting E, Spies L, Maufroy C, Schneider U, Bauernhansl T. Model-Based Biomechanical Exoskeleton Concept Optimization for a Representative Lifting Task in Logistics. International Journal of Environmental Research and Public Health. 2022; 19(23):15533. https://doi.org/10.3390/ijerph192315533
Chicago/Turabian StyleSchiebl, Jonas, Mark Tröster, Wiem Idoudi, Elena Gneiting, Leon Spies, Christophe Maufroy, Urs Schneider, and Thomas Bauernhansl. 2022. "Model-Based Biomechanical Exoskeleton Concept Optimization for a Representative Lifting Task in Logistics" International Journal of Environmental Research and Public Health 19, no. 23: 15533. https://doi.org/10.3390/ijerph192315533
APA StyleSchiebl, J., Tröster, M., Idoudi, W., Gneiting, E., Spies, L., Maufroy, C., Schneider, U., & Bauernhansl, T. (2022). Model-Based Biomechanical Exoskeleton Concept Optimization for a Representative Lifting Task in Logistics. International Journal of Environmental Research and Public Health, 19(23), 15533. https://doi.org/10.3390/ijerph192315533







