Disparity and Spatial Heterogeneity of the Correlation between Street Centrality and Land Use Intensity in Jinan, China
Abstract
1. Introduction
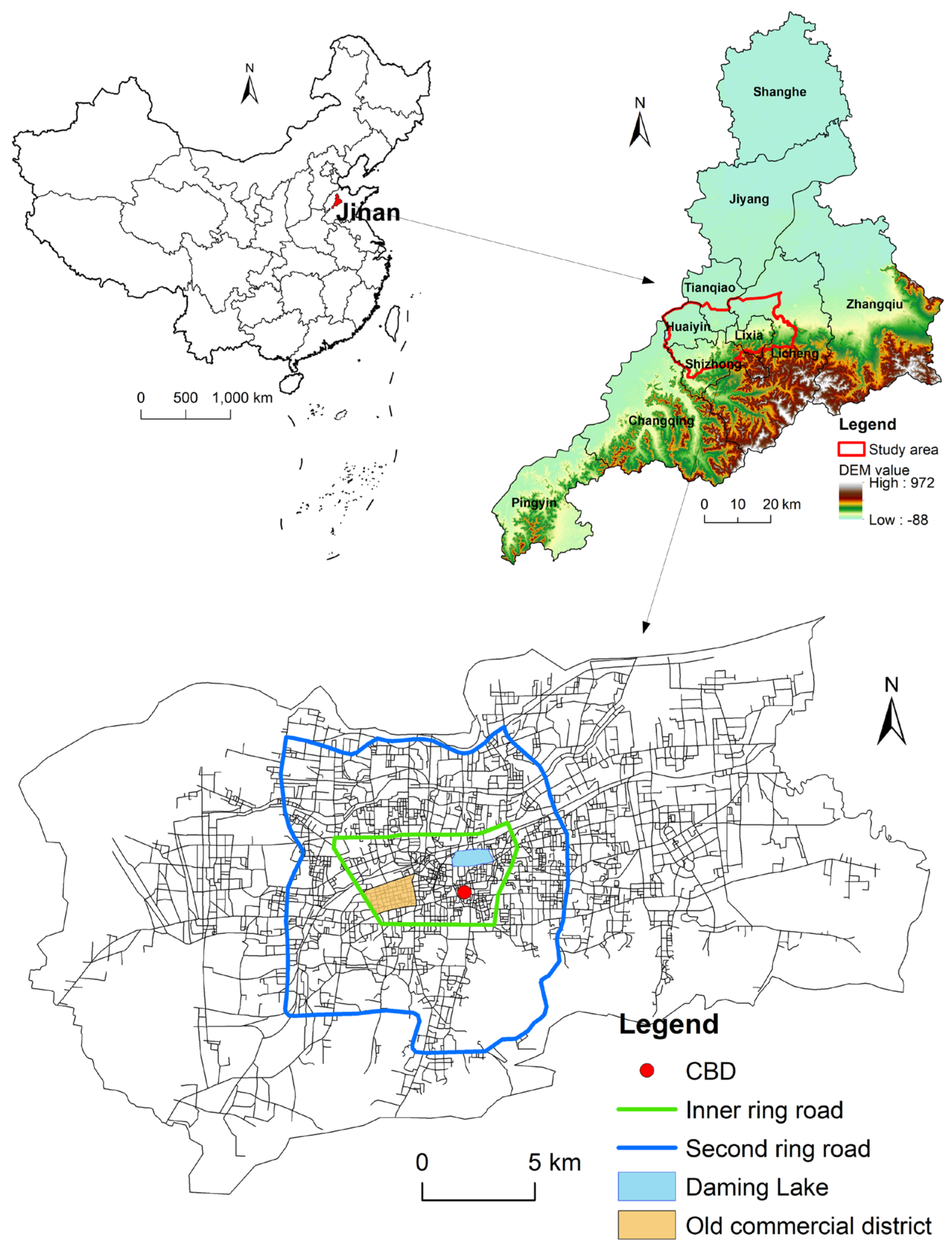
2. Study Area and Date
2.1. Study Area
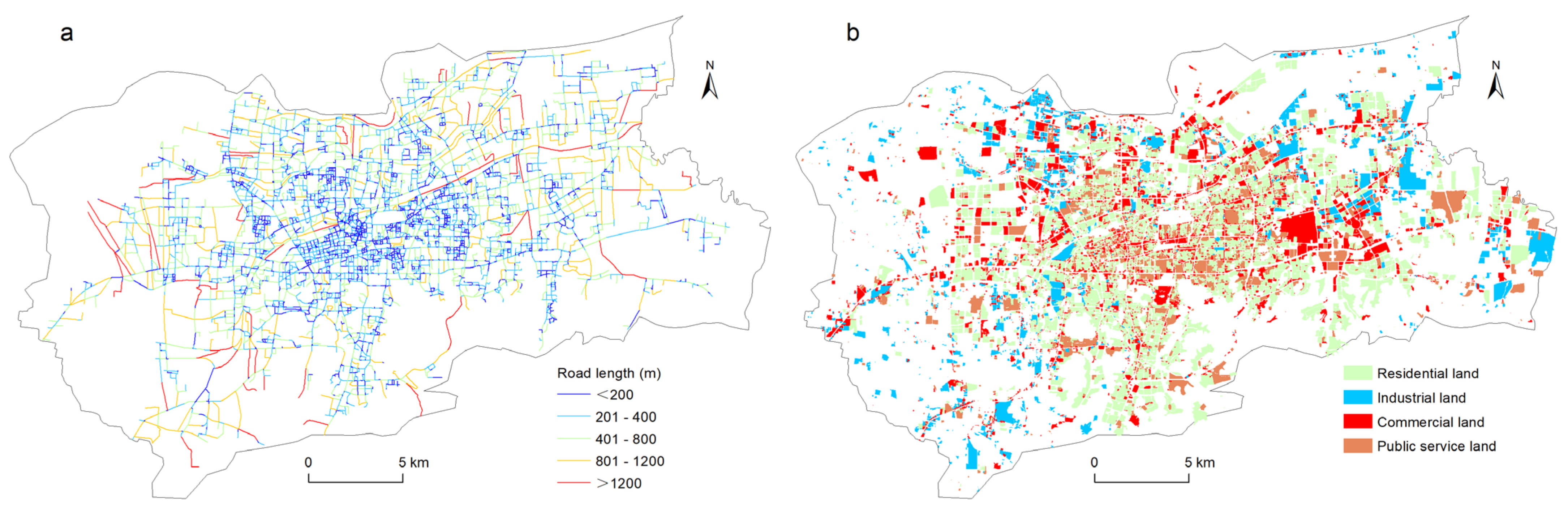
2.2. Street Network and Urban Land Use
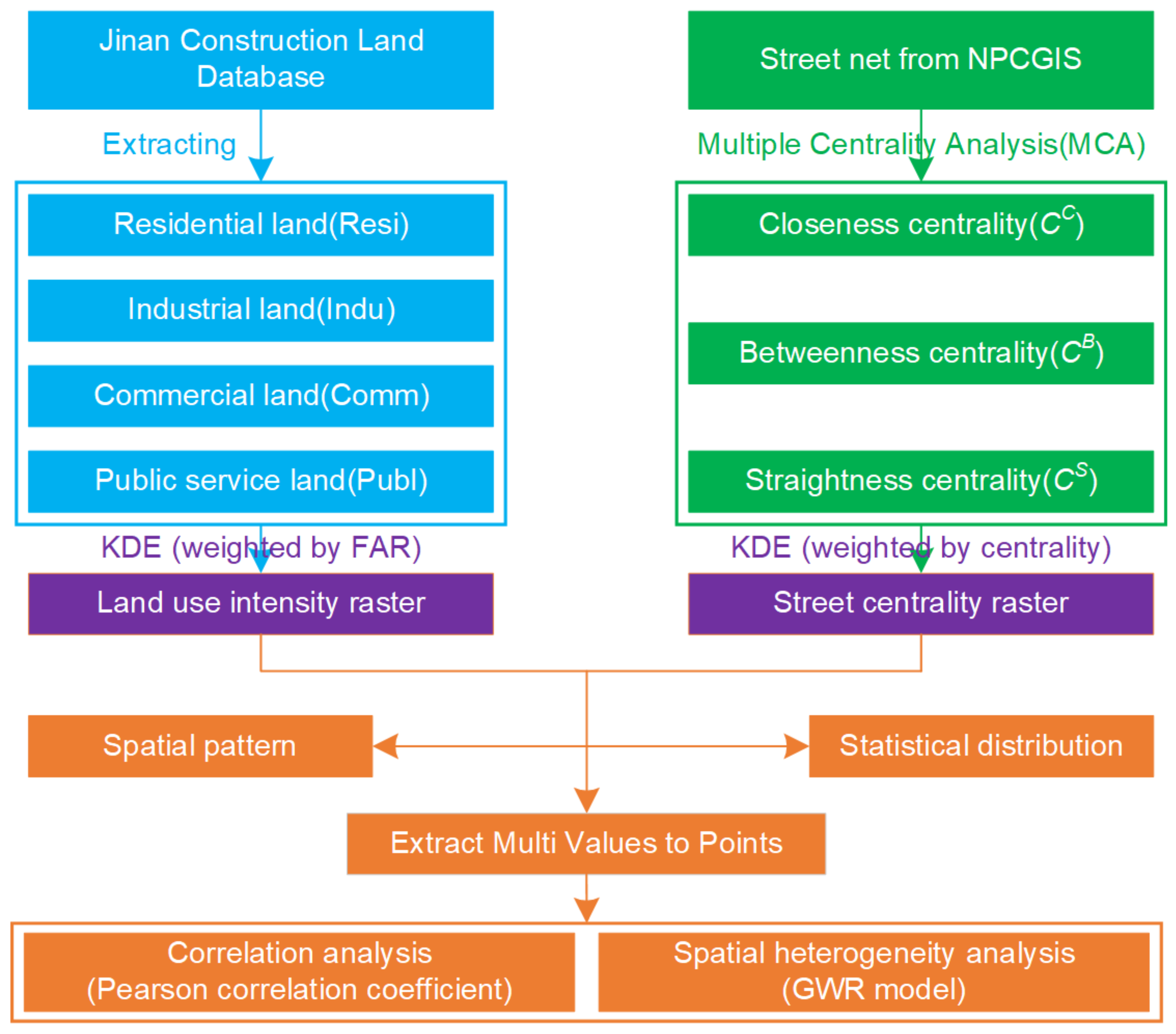
3. Research Methods
3.1. Street Centrality Measures
- (1)
- The closeness centrality (CC) indicated the closeness of a node to all other nodes in the traffic network, as well as the accessibility of the node in the network. It was measured using the shortest road network distance and size from a given node to all nodes. The calculation formula for the closeness centrality of node i waswhere N is the number of traffic network nodes, and dij is the shortest distance between nodes i and j. In short, the closeness centrality was the reciprocal of the average distance from a node to all other nodes. The smaller the average distance was, the stronger the closeness centrality was.
- (2)
- The betweenness centrality (CB) described the importance of node i in the traffic network by calculating the number of times the shortest path between node pairs passed through node i. The betweenness centrality reflected the transfer and connection functions of the nodes in the traffic network. The greater the number of shortest paths passed through a node, the stronger the betweenness centrality was, which meant that the node played the role of a bridge or a hub transfer in the entire traffic network. The calculation of the betweenness centrality of node i waswhere N is the number of traffic network nodes, nik is the number of shortest paths between nodes j and k, and njk(i) is the number of shortest paths passing through node i in the shortest paths between nodes j and k. Unlike the closeness centrality, the betweenness centrality could capture the special attributes of the node position; that is, it was not used as the starting point or destination of travel but rather as a necessary intermediate transition point. The betweenness centrality was an important indicator for measuring the traffic flow of the network nodes.
- (3)
- The straightness centrality (CS) was used to calculate the importance of a node by calculating the average ratio of the shortest path distance over the straight-line distance between node i and the other nodes. The basic principle was that when the network path distance between two nodes was close to their Euclidean distance, the communication between the two nodes was easier. The straightness centrality calculation formula of node i waswhere N is the number of traffic network nodes, is the Euclidean distance between nodes i and j, and dij is the shortest distance between nodes i and j. As an important indicator for measuring the efficiency of traffic networks, straightness centrality is of great significance in spatial network research.
3.2. Kernel Density Estimation (KDE)
3.3. Bivariate Moran’s I
3.4. Geographically Weighted Regression (GWR)
4. Results
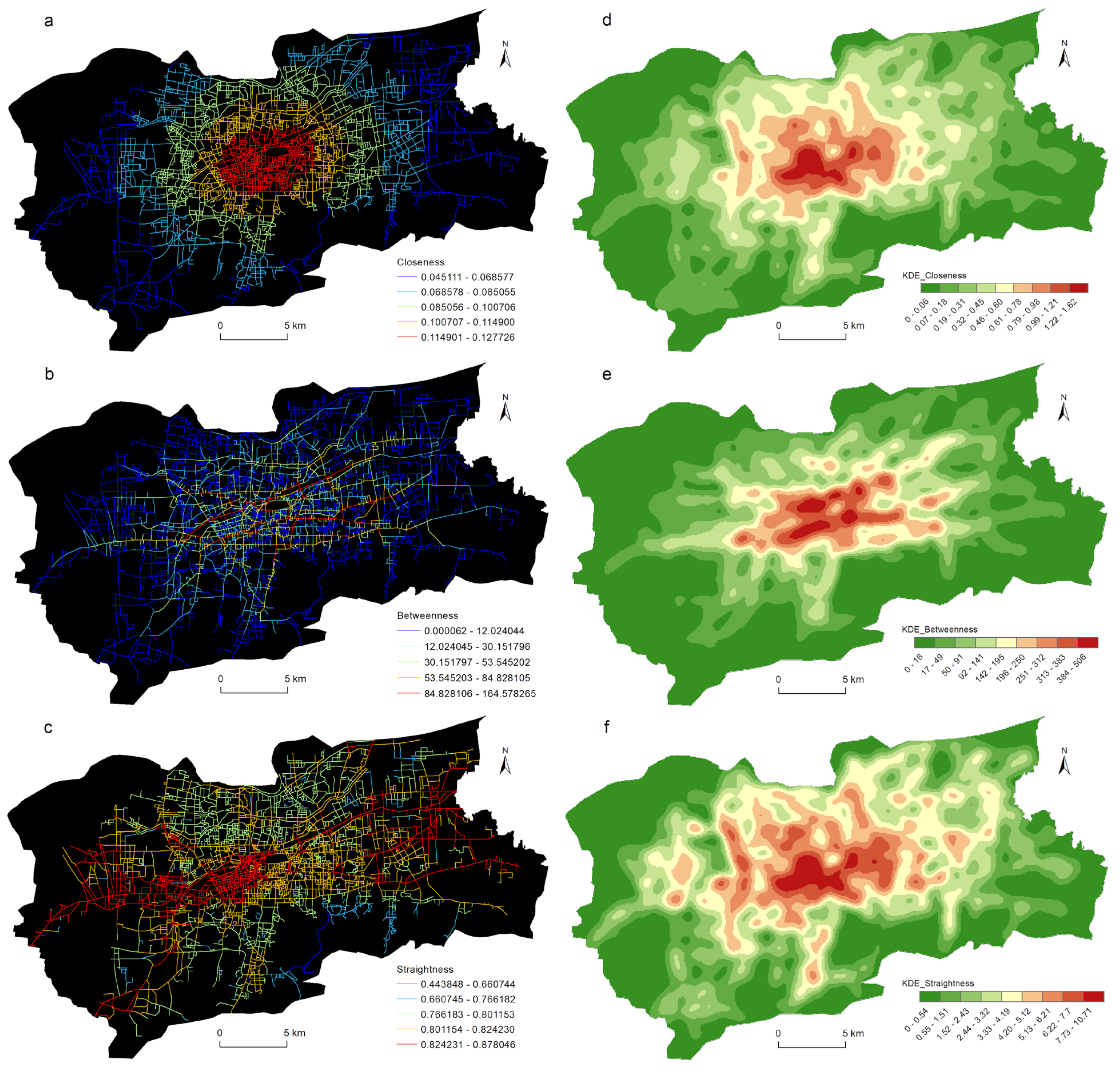
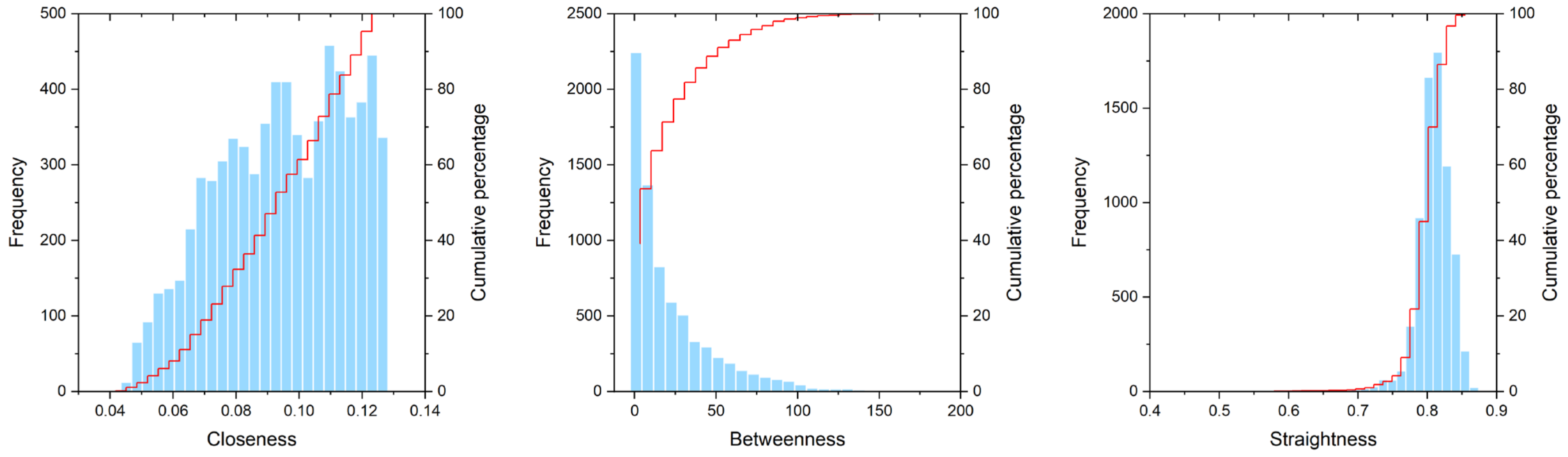
4.1. Spatial Patterns of Street Centrality
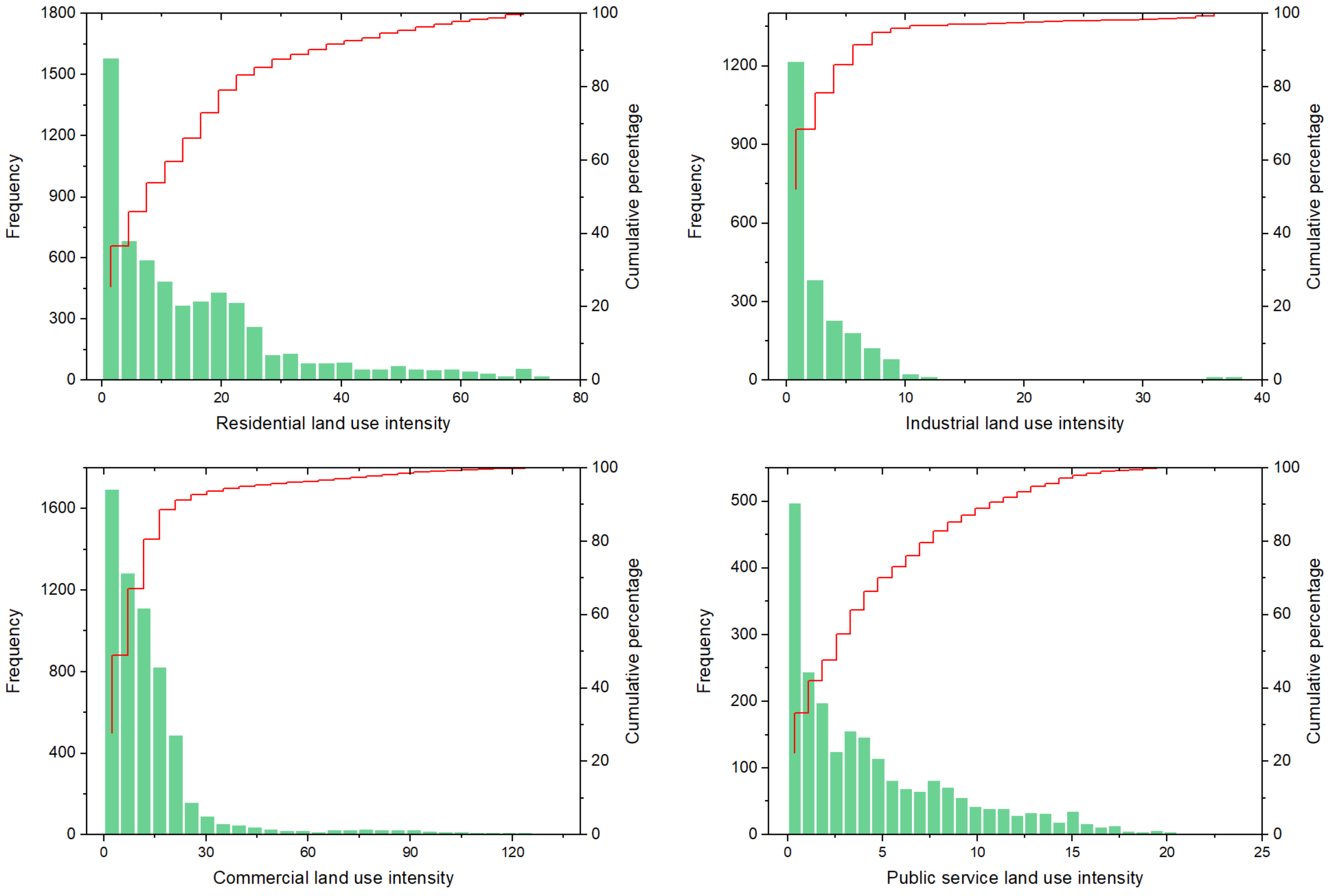
4.2. Spatial Distributions of Urban LUI
4.3. Correlation Analysis
4.4. Spatial Correlation between Street Centrality and Urban LUI
4.5. Spatial Heterogeneity Explored with the GWR Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rui, Y.; Ban, Y. Exploring the relationship between street centrality and land use in Stockholm. Int. J. Geogr. Inf. Sci. 2014, 28, 1425–1438. [Google Scholar] [CrossRef]
- Yin, G.W.; Liu, Y.G.; Wang, F.L. Emerging Chinese new towns: Local government-directed capital switching in inland China. Cities 2018, 79, 102–112. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. A structural approach to the model generalization of an urban street network. Geoinformatica 2004, 8, 157–171. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Radeloff, V.C.; Hammer, R.B.; Clayton, M.K. Road density and landscape pattern in relation to housing density, and ownership, land cover, and soils. Landsc. Ecol. 2005, 20, 609–625. [Google Scholar] [CrossRef]
- Wegener, M. Operational urban models state of the art. J. Am. Plan. Assoc. 1994, 60, 17–29. [Google Scholar] [CrossRef]
- Goncalves, J.A.M.; Portugal, L.D.S.; Nassi, C.D. Centrality indicators as an instrument to evaluate the integration of urban equipment in the area of influence of a rail corridor. Transp. Res. Part A Policy Pract. 2009, 43, 13–25. [Google Scholar] [CrossRef]
- Burgess, E.W. The growth of the city: An introduction to a research project. In The City; Park, R.E., Burgess, E.W., Mackenzie, R.D., Eds.; University of Chicago Press: Chicago, IL, USA, 1925; pp. 1–47. [Google Scholar]
- Hoyt, H. The Structure and Growth of Residential Neighborhoods in American Cities; Federal Housing Administration: Washington, DC, USA, 1940. [Google Scholar]
- Harris, C.D.; Ullman, E.L. The Nature of Cities. Ann. Am. Acad. Political Soc. Sci. 1945, 242, 7–17. [Google Scholar] [CrossRef]
- Park, R.E. The city: Suggestions for the investigation of human behavior in the city environment. Am. J. Sociol. 1915, 20, 577–612. [Google Scholar] [CrossRef]
- Alonso, W. Location and Land Use; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Mills, E.S. Studies in the Structure of the Urban Economy; Johns Hopkins University: Baltimore, MD, USA, 1972. [Google Scholar]
- Muth, R.F. Cities and Housing; University of Chicago: Chicago, IL, USA, 1969. [Google Scholar]
- Casetti, E. Spatial analysis: Perspectives and prospects. Urban Geogr. 1993, 14, 526–537. [Google Scholar] [CrossRef]
- Jiang, B.; Yao, X. Geospatial analysis and modeling of urban structure and dynamics: An overview. In Geospatial Analysis and Modelling of Urban Structure and Dynamics; Jiang, B., Yao, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 3–11. [Google Scholar]
- Levinson, D.M. Network structure and city size. PLoS ONE 2012, 7, e29721. [Google Scholar] [CrossRef]
- Parthasarathi, P.; Hochmair, H.; Levinson, D.M. Network structure and activity spaces. SSRN Electron. J. 2011. [Google Scholar] [CrossRef][Green Version]
- Scellato, S.; Cardillo, A.; Latora, V.; Porta, S. The backbone of a city. Eur. Phys. J. B 2006, 50, 221–225. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, Y. Relationship between morphological characteristics and land-use intensity: Empirical analysis of shanghai development zones. J. Urban Plan. Dev. ASCE 2013, 139, 49–61. [Google Scholar] [CrossRef]
- Lowry, I.S. A Model of Metropolis; Rand Corporation: Santa Monica, CA, USA, 1964. [Google Scholar]
- Garin, R.A. Research note: A matrix formulation of the Lowry model for intrametropolitan activity allocation. J. Am. Plan. Assoc. 1966, 32, 361–364. [Google Scholar] [CrossRef]
- Wang, F.; Guldmann, J. Simulating urban population density with a gravity-based model. Socio-Econ. Plan. Sci. 1996, 30, 245–256. [Google Scholar] [CrossRef]
- Batty, M. Network geography: Relations, interactions, scaling and spatial processes in GIS. In Re-Presenting Geographical Information Systems; Fisher, P., Unwin, D., Eds.; John Wiley and Sons: Chichester, UK, 2003; pp. 149–170. [Google Scholar]
- Batty, M. Whither network science. Environ. Plan. B Plan. Des. 2008, 35, 569–571. [Google Scholar] [CrossRef]
- Miller, H.J. Measuring space-time accessibility benefits within transportation networks: Basic theory and computational procedures. Geogr. Anal. 1999, 31, 187–212. [Google Scholar] [CrossRef]
- Borruso, G. Network density estimation: A GIS approach for analysing point patterns in a network space. Trans. GIS 2008, 12, 377–402. [Google Scholar] [CrossRef]
- Borruso, G. Network density estimation: Analysis of point patterns over a network. In Computational Science and Its Applications-ICCSA 2005; Gervasi, O., Gavrilova, M.L., Kuma, V., Laganà, R., Lee, H.P., Mun, Y., Taniar, D., Tan, C.J.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 126–132. [Google Scholar]
- Okabe, A.; Okunuki, K.; Shiode, S. Sanet: A toolbox for spatial analysis on a network. Geogr. Anal. 2006, 38, 57–66. [Google Scholar] [CrossRef]
- Okabe, A.; Okunuki, K.; Shiode, S. The Sanet toolbox: New methods for network spatial analysis. Trans. GIS 2006, 10, 535–550. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Li, Q.; Zhou, S.; Wen, P. The relationship between centrality and land use patterns: Empirical evidence from five Chinese metropolises. Comput. Environ. Urban Syst. 2019, 78, 101356. [Google Scholar] [CrossRef]
- Cutini, V. Configuration and centrality-some evidence from two Italian case studies. In Proceedings of the Space Syntax 3rd International Symposium, Atlanta, GA, USA, 7–11 May 2001. [Google Scholar]
- Kim, H.K.; Sohn, D.W. An analysis of the relationship between land use density of office buildings and urban street configuration: Case studies of two areas in Seoul by space syntax analysis. Cities 2002, 19, 409–418. [Google Scholar] [CrossRef]
- Scoppa, M.; Peponis, J. Distributed attraction: The effects of street network connectivity upon the distribution of retail frontage in the city of Buenos Aires. Environ. Plan. B-Plan. Des. 2015, 42, 354–378. [Google Scholar] [CrossRef]
- Omer, I.; Goldblatt, R. Spatial patterns of retail activity and street network structure in new and traditional Israeli cities. Urban Geogr. 2016, 37, 629–649. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality in networks of urban streets. Chaos 2006, 16, 15113. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E 2006, 73, 36125. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B-Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. Multiple centrality assessment in Parma: A network analysis of paths and open spaces. Urban Des. Int. 2008, 13, 41–50. [Google Scholar] [CrossRef]
- Al-Saaidy, H.J.E.; Alobaydi, D. Studying street centrality and human density in different urban forms in Baghdad, Iraq. Ain Shams Eng. J. 2021, 12, 1111–1121. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Strano, E.; Cardillo, A.; Scellato, S.; Iacoviello, V.; Messora, R. Street centrality and densities of retail and services in Bologna, Italy. Environ. Plan. B-Plan. Des. 2009, 36, 450–465. [Google Scholar] [CrossRef]
- Wang, F.; Chen, C.; Xiu, C.; Zhang, P. Location analysis of retail stores in Changchun, China: A street centrality perspective. Cities 2014, 41, 54–63. [Google Scholar] [CrossRef]
- Kang, C. Spatial access to pedestrians and retail sales in Seoul, Korea. Habitat Int. 2016, 57, 110–120. [Google Scholar] [CrossRef]
- Lin, G.; Chen, X.; Liang, Y. The location of retail stores and street centrality in Guangzhou, China. Appl. Geogr. 2018, 100, 12–20. [Google Scholar] [CrossRef]
- Ozuduru, B.H.; Webster, C.J.; Chiaradia, A.J.; Yucesoy, E. Associating street-network centrality with spontaneous and planned subcentres. Urban Stud. 2020, 58, 2059–2078. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Cardillo, A.; Belli, E.; Cardenas, F.; Cormenzana, B.; et al. Street centrality and the location of economic activities in barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Wang, F.; Antipova, A.; Porta, S. Street centrality and land use intensity in Baton Rouge, Louisiana. J. Transp. Geogr. 2011, 19, 285–293. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, X.; Jiao, L.; Wang, H. Relationships between street centrality and land use intensity in Wuhan, China. J. Urban Plan. Dev. ASCE 2016, 142, 5015001. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Jiao, L.; Liu, Y.; He, J.; Ai, T. Road centrality and landscape spatial patterns in Wuhan metropolitan area, China. Chin. Geogr. Sci. 2015, 25, 511–522. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Chen, D.; Truong, K. Using multilevel modeling and geographically weighted regression to identify spatial variations in the relationship between place-level disadvantages and obesity in Taiwan. Appl. Geogr. 2012, 32, 737–745. [Google Scholar] [CrossRef]
- Kuai, X.; Zhao, Q. Examining healthy food accessibility and disparity in Baton Rouge, Louisiana. Ann. GIS 2017, 23, 103–116. [Google Scholar] [CrossRef]
- Wang, F. Quantitative Methods and Socio-Economic Applications in GIS, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Quantitative Geography: Perspectives on Spatial Data Analysis; Sage: London, UK, 2000; pp. 146–149. [Google Scholar]
- O’Sullivan, D.; Unwin, D.J. Geographic Information Analysis; John Wiley and Sons: Chichester, UK, 2003; pp. 85–87. [Google Scholar]
- Downs, J.A.; Horner, M.W. Characterising linear point patterns. In Proceedings of the GIS Research UK Annual Conference, Maynooth, Ireland, 27–29 April 2007. [Google Scholar]
- Downs, J.A.; Horner, M.W. Network-based kernel density estimation for home range analysis. In Proceedings of the Ninth International Conference on Geocomputation, Maynooth, Ireland, 3–5 September 2007. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986; p. 76. [Google Scholar]
- Anselin, L. GeoDa Workbook. 2019. Available online: https://geodacenter.github.io/documentation.html (accessed on 15 October 2021).
- Lee, S.H.; Kim, P.-J.; Jeong, H. Statistical Properties of Sampled Networks. Phys. Rev. E 2006, 73, 016102. [Google Scholar] [CrossRef] [PubMed]

| Centralities | Resi | Indu | Comm | Publ | ln(Resi) | ln(Indu) | ln(Comm) | ln(Publ) |
|---|---|---|---|---|---|---|---|---|
| CC | 0.7293 *** | 0.1751 *** | 0.6835 *** | 0.7164 *** | 0.7440 *** | 0.0046 | 0.7158 *** | 0.6966 *** |
| CB | 0.6537 *** | −0.0170 | 0.5474 *** | 0.6414 *** | 0.6693 *** | −0.2397 *** | 0.6060 *** | 0.6252 *** |
| CS | 0.7077 *** | 0.1733 *** | 0.6662 *** | 0.6911 *** | 0.7267 *** | 0.0676 *** | 0.7157 *** | 0.6938 *** |
| ln(CC) | 0.5057 *** | 0.1363 *** | 0.4386 *** | 0.5522 *** | 0.6982 *** | 0.0809 *** | 0.6424 *** | 0.6855 *** |
| ln(CB) | 0.4819 *** | 0.1116 *** | 0.3928 *** | 0.5232 *** | 0.6951 *** | 0.0034 | 0.6225 *** | 0.6869 *** |
| ln(CS) | 0.4584 *** | 0.1170 *** | 0.3893 *** | 0.5003 *** | 0.6302 *** | 0.0873 *** | 0.5799 *** | 0.6306 *** |
| Variables | Bivariate Global Moran’s I | z-Value | p-Value |
|---|---|---|---|
| Closeness and Residential LUI | 0.7263 | 217.6262 | 0.001 |
| Betweenness and Residential LUI | 0.6581 | 198.2794 | 0.001 |
| Straightness and Residential LUI | 0.7020 | 213.8111 | 0.001 |
| Closeness and Industrial LUI | 0.1815 | 32.2781 | 0.001 |
| Betweenness and Industrial LUI | 0.0357 | 6.4741 | 0.001 |
| Straightness and Industrial LUI | 0.1743 | 30.9267 | 0.001 |
| Closeness and Commercial LUI | 0.6797 | 199.9732 | 0.001 |
| Betweenness and Commercial LUI | 0.5516 | 171.3770 | 0.001 |
| Straightness and Commercial LUI | 0.6577 | 195.0182 | 0.001 |
| Closeness and Public service LUI | 0.7110 | 104.1247 | 0.001 |
| Betweenness and Public service LUI | 0.6527 | 98.2945 | 0.001 |
| Straightness and Public service LUI | 0.6776 | 99.7421 | 0.001 |
| Dependent Variable | Explanatory Variables | OLS | GWR | GWR-OLS | |||
|---|---|---|---|---|---|---|---|
| AICc | Adjusted R2 | AICc | Adjusted R2 | AICc | Adjusted R2 | ||
| Residential LUI | CC | 47,542 | 0.53 | 37,790 | 0.90 | −9752 | 0.37 |
| Residential LSU | CB | 48,787 | 0.43 | 35,181 | 0.93 | −13,606 | 0.50 |
| Residential LSU | CS | 47,956 | 0.50 | 39,006 | 0.88 | −8950 | 0.38 |
| Industrial LUI | CC | 14,625 | 0.03 | 10,989 | 0.80 | −3636 | 0.77 |
| Industrial LUI | CB | 14,701 | 0.00 | 8584 | 0.93 | −6117 | 0.93 |
| Industrial LUI | CS | 14,629 | 0.03 | 11,394 | 0.76 | −3252 | 0.73 |
| Commercial LUI | CC | 48,901 | 0.47 | 39,642 | 0.88 | −9259 | 0.41 |
| Commercial LUI | CB | 50,568 | 0.30 | 33,483 | 0.96 | −17,085 | 0.66 |
| Commercial LUI | CS | 49,200 | 0.44 | 39,917 | 0.88 | −9283 | 0.44 |
| Public service LUI | CC | 11,424 | 0.52 | 8763 | 0.86 | −2661 | 0.34 |
| Public service LUI | CB | 11,843 | 0.42 | 7102 | 0.93 | −4741 | 0.51 |
| Public service LUI | CS | 11,596 | 0.48 | 8843 | 0.85 | −2753 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, G.; Liu, T.; Chen, Y.; Hou, Y. Disparity and Spatial Heterogeneity of the Correlation between Street Centrality and Land Use Intensity in Jinan, China. Int. J. Environ. Res. Public Health 2022, 19, 15558. https://doi.org/10.3390/ijerph192315558
Yin G, Liu T, Chen Y, Hou Y. Disparity and Spatial Heterogeneity of the Correlation between Street Centrality and Land Use Intensity in Jinan, China. International Journal of Environmental Research and Public Health. 2022; 19(23):15558. https://doi.org/10.3390/ijerph192315558
Chicago/Turabian StyleYin, Guanwen, Tianzi Liu, Yanbin Chen, and Yiming Hou. 2022. "Disparity and Spatial Heterogeneity of the Correlation between Street Centrality and Land Use Intensity in Jinan, China" International Journal of Environmental Research and Public Health 19, no. 23: 15558. https://doi.org/10.3390/ijerph192315558
APA StyleYin, G., Liu, T., Chen, Y., & Hou, Y. (2022). Disparity and Spatial Heterogeneity of the Correlation between Street Centrality and Land Use Intensity in Jinan, China. International Journal of Environmental Research and Public Health, 19(23), 15558. https://doi.org/10.3390/ijerph192315558







