Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Retrieval and Preprocessing
2.3. Modeling Framework and Model Structure
Ei+1 = Ei − I*i + E*i ⋯ E*ij ~ binom(Sij, πij(SE))
Ii+1 = Ii − R*i + I*i ⋯ I*ij ~ binom(Eij, πj(EI))
Ri+1 = Ri − S*i − R*i ⋯ R*ij ~ binom(Iij, πj(IR))
πi(IR) = 1 − exp(− hiγ(IR))
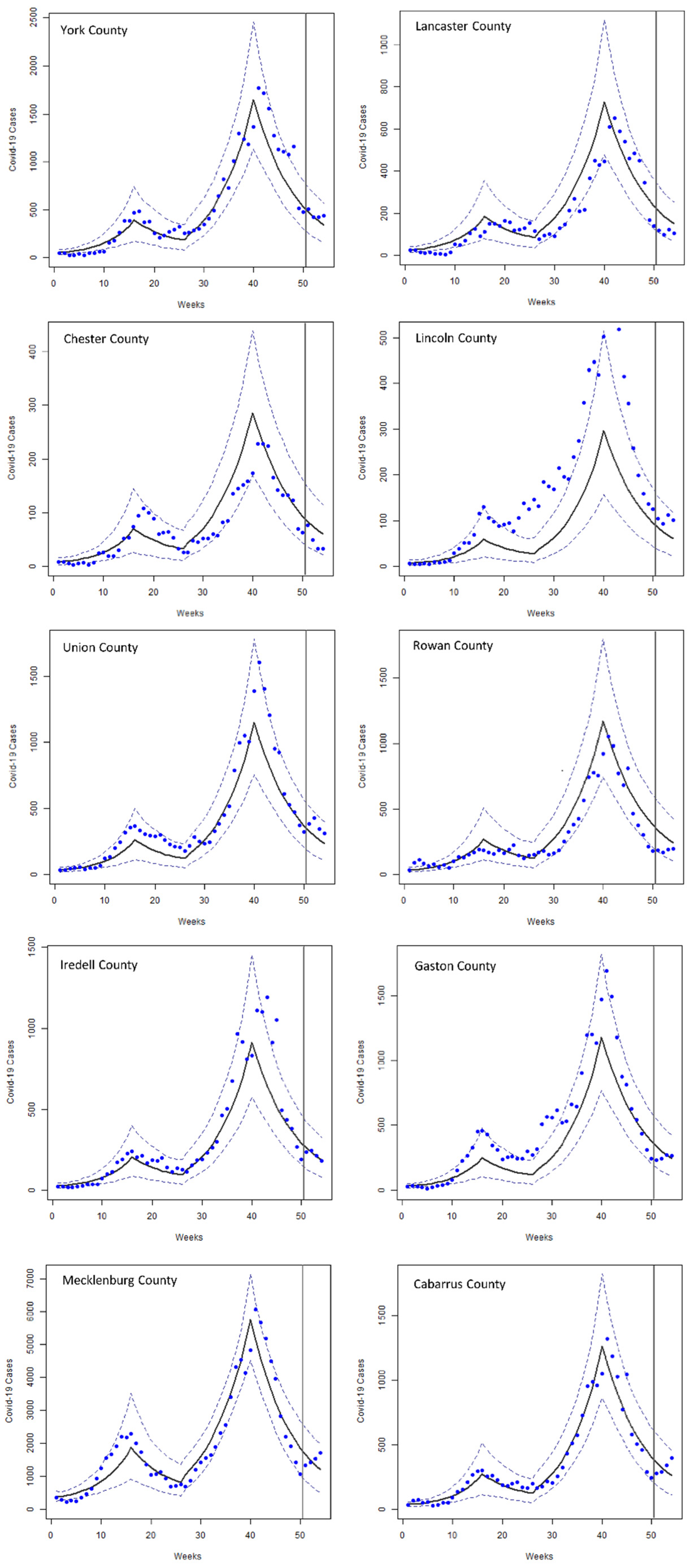
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Verges, F.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A review. Sci. Total Environ. 2020, 739, 140033. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Adeyemi, O.; Ghosh, S.; Pokhrel, K.; Arif, A.A. Dynamics of COVID-19 mortality and social determinants of health: A spatiotemporal analysis of exceedance probabilities. Ann. Epidemiol. 2021, 62, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Arif, A.A.; Adeyemi, O.; Ghosh, S.; Han, D. Progression of COVID-19 from urban to rural areas in the United States: A spatiotemporal analysis of prevalence rates. J. Rural. Health 2020, 36, 591–601. [Google Scholar] [CrossRef]
- Rahman, M.M.; Thill, J.C. Associations between COVID-19 Pandemic, Lockdown Measures and Human Mobility: Longitudinal Evidence from 86 Countries. Int. J. Environ. Res. Public Health 2022, 19, 7317. [Google Scholar] [CrossRef]
- The New York Times. Cases by Region. 2022. Available online: https://www.nytimes.com/interactive/2021/us/covid-cases.html (accessed on 9 February 2022).
- Cramer, E.Y.; Huang, Y.; Wang, Y.; Ray, E.L.; Cornell, M.; Bracher, J.; Brennen, A.; Rivadeneira, A.J.C.; Gerding, A.; House, K.; et al. The United States COVID-19 Forecast Hub dataset. Sci. Data 2021, 9, 462. Available online: https://www.medrxiv.org/content/10.1101/2021.11.04.21265886v1 (accessed on 17 August 2021). [CrossRef] [PubMed]
- Lalmuanawma, S.; Hussain, J.; Chhakchhuak, L. Applications of machine learning and artificial intelligence for COVID-19 (SARS-CoV-2) pandemic: A review. Chaos Solitons Fractals 2020, 139, 110059. [Google Scholar] [CrossRef]
- Shoeibi, A.; Khodatars, M.; Alizadehsani, R.; Ghassemi, N.; Jafari, M.; Moridian, P.; Khadem, A.; Sadeghi, D.; Hussain, S.; Zare, A.; et al. Automated detection and forecasting of covid-19 using deep learning techniques: A review. arXiv 2020, arXiv:2007.10785. [Google Scholar]
- Voutilainen, A.; Tolppanen, A.M.; Vehviläinen-Julkunen, K.; Sherwood, P.R. From spatial ecology to spatial epidemiology: Modeling spatial distributions of different cancer types with principal coordinates of neighbor matrices. Emerg. Themes Epidemiol. 2014, 11, 11. [Google Scholar] [CrossRef] [Green Version]
- Desikan, R.; Padmanabhan, P.; Kierzek, A.M.; van der Graaf, P.H. Mechanistic models of COVID-19: Insights into disease progression, vaccines, and therapeutics. Int. J. Antimicrob. Agents 2022, 60, 106606. [Google Scholar] [CrossRef]
- Friji, H.; Hamadi, R.; Ghazzai, H.; Besbes, H.; Massoud, Y. A generalized mechanistic model for assessing and forecasting the spread of the COVID-19 pandemic. IEEE Access 2021, 9, 13266–13285. [Google Scholar] [CrossRef]
- Brown, G.D.; Oleson, J.J.; Porter, A.T. An empirically adjusted approach to reproductive number estimation for stochastic compartmental models: A case study of two Ebola outbreaks. Biometrics 2016, 72, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Shankar, S.; Mohakuda, S.S.; Kumar, A.; Nazneen, P.S.; Yadav, A.K.; Chatterjee, K.; Chatterjee, K. Systematic review of predictive mathematical models of COVID-19 epidemic. Med. J. Armed Forces India 2021, 77, S385–S392. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2021, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; Duan, M.; Shi, J.; Hong, J.; Chang, Z.; Zhang, Z. Compartmental structures used in modeling COVID-19: A scoping review. Infect. Diseases Poverty 2022, 11, 72. [Google Scholar] [CrossRef]
- Istaiteh, O.; Owais, T.; Al-Madi, N.; Abu-Soud, S. Machine learning approaches for covid-19 forecasting. In Proceedings of the 2020 International Conference on Intelligent Data Science Technologies and Applications (IDSTA), Valencia, Spain, 19–22 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 50–57. [Google Scholar]
- Tian, Y.; Luthra, I.; Zhang, X. Forecasting COVID-19 cases using Machine Learning models. MedRxiv 2020. [Google Scholar] [CrossRef]
- Nikparvar, B.; Rahman, M.; Hatami, F.; Thill, J.C. Spatio-temporal prediction of the COVID-19 pandemic in US counties: Modeling with a deep LSTM neural network. Sci. Rep. 2021, 11, 21715. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef]
- Holmdahl, I.; Buckee, C. Wrong but useful—What COVID-19 epidemiologic models can and cannot tell us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef]
- United States Census Bureau. Annual Estimates of the Resident Population for Counties: April 1, 2020 to July 1, 2021 (CO-EST2021-POP). 2021. Available online: https://www.census.gov/data/tables/time-series/demo/popest/2020s-counties-total.html (accessed on 11 January 2021).
- United States Census Bureau. Annual Resident Population Estimates for States and Counties: April 1, 2010 to July 1, 2019; April 1, 2020; and July 1, 2020 (CO-EST2020). 2021. Available online: https://www.census.gov/programs-surveys/popest/technical-documentation/research/evaluation-estimates/2020-evaluation-estimates/2010s-counties-total.html (accessed on 11 January 2021).
- Bureau of Economic Analysis. CAEMP25N Total Full-Time and Part-Time Employment by NAICS Industry 1/Total Employment (Number of Jobs). 2022. Available online: https://apps.bea.gov/iTable/iTable.cfm?reqid=70&step=1&acrdn=6 (accessed on 10 June 2022).
- United States Census Bureau. LEHD Origin-Destination Employment Statistics Data (2002–2018). 2018. Available online: https://lehd.ces.census.gov/data/ (accessed on 5 April 2021).
- Delmelle, E.C.; Zhou, Y.; Thill, J.C. Densification without growth management? Evidence from local land development and housing trends in Charlotte, North Carolina, USA. Sustainability 2014, 6, 3975–3990. [Google Scholar] [CrossRef] [Green Version]
- City of Charlotte. 2030 Transit Corridor System Plan. 2006. Available online: https://charlottenc.gov/cats/transit-planning/2030-plan/Pages/default.aspx (accessed on 22 June 2022).
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. MMWR Week Fact Sheet. Available online: https://ndc.services.cdc.gov/wp-content/uploads/MMWR_Week_overview.pdf (accessed on 1 April 2022).
- Pergolizzi, J.V., Jr.; Magnusson, P.; LeQuang, J.A.; Breve, F.; Paladini, A.; Rekatsina, M.; Yeam, C.T.; Imani, F.; Saltelli, G.; Taylor, R., Jr.; et al. The current clinically relevant findings on COVID-19 pandemic. Anesthesiol. Pain Med. 2020, 10, e103819. [Google Scholar] [CrossRef] [PubMed]
- SimplyAnalytics Census 2020 Current Estimates Data. 2020. Available online: https://simplyanalytics.com/ (accessed on 8 May 2020).
- Brown, T.S.; Engø-Monsen, K.; Kiang, M.V.; Mahmud, A.S.; Maude, R.J.; Buckee, C.O. The impact of mobility network properties on predicted epidemic dynamics in Dhaka and Bangkok. Epidemics 2021, 35, 100441. [Google Scholar] [CrossRef] [PubMed]
- Ramiadantsoa, T.; Metcalf CJ, E.; Raherinandrasana, A.H.; Randrianarisoa, S.; Rice, B.L.; Wesolowski, A.; Randriatsarafara, F.M.; Rasambainarivo, F. Existing human mobility data sources poorly predicted the spatial spread of SARS-CoV-2 in Madagascar. Epidemics 2022, 38, 100534. [Google Scholar] [CrossRef] [PubMed]
- Aktay, A.; Bavadekar, S.; Cossoul, G.; Davis, J.; Desfontaines, D.; Fabrikant, A.; Gabrilovich, E.; Gadepalli, K.; Gipson, B.; Guevara, M.; et al. Google COVID-19 Community Mobility Reports: Anonymization process description (version 1.1). arXiv 2021, arXiv:2004.04145. [Google Scholar]
- Apple. COVID-19 Mobility Trends Reports. 2021. Available online: https://covid19.apple.com/mobility (accessed on 5 May 2021).
- SafeGraph. Monthly Patterns. 2021. Available online: https://docs.safegraph.com/docs/monthly-patterns (accessed on 5 May 2021).
- SafeGraph. SafeGraph COVID-19 Data Consortium. 2021. Available online: https://www.safegraph.com/academics (accessed on 9 October 2021).
- Grossman, G.; Kim, S.; Rexer, J.M.; Thirumurthy, H. Political partisanship influences behavioral responses to governors’ recommendations for COVID-19 prevention in the United States. Proc. Natl. Acad. Sci. USA 2020, 117, 24144–24153. [Google Scholar] [CrossRef]
- North Carolina State Board of Elections. Voting Results. 2020. Available online: https://er.ncsbe.gov/ (accessed on 17 February 2021).
- South Carolina Election Commissions. Voting results. 2020. Available online: https://www.enr-scvotes.org/SC/106502/Web02-state.264691/#/?undefined (accessed on 21 February 2021).
- North Carolina Department of Health and Human Services. People Vaccinate Demographics. 2021. Available online: https://covid19.ncdhhs.gov/dashboard/data-behind-dashboards (accessed on 11 December 2021).
- North Carolina Government. NC COVID-19 Orders and Directives. 2020. Available online: https://www.nc.gov/covid-19/covid-19-orders-directives#executive-orders--2020-executive-orders-issued-by-gov--roy-cooper (accessed on 21 January 2021).
- United States Census Bureau. Cartographic Boundary Files—Shapefile. 2018. Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/carto-boundary-file.html (accessed on 6 March 2021).
- Brown, G.D.; Porter, A.T.; Oleson, J.J.; Hinman, J.A. Approximate Bayesian computation for spatial SEIR(S) epidemic models. Spat. Spatio-Temporal Epidemiol. 2018, 24, 27–37. [Google Scholar] [CrossRef]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2009, 6, 187–202. [Google Scholar] [CrossRef] [Green Version]
- Ray, E.L.; Wattanachit, N.; Niemi, J.; Kanji, A.H.; House, K.; Cramer, E.Y.; Bracher, J.; Zheng, A.; Yamana, T.K.; Xiong, X.; et al. Ensemble forecasts of coronavirus disease 2019 (COVID-19) in the US. MedRXiv 2022. [Google Scholar] [CrossRef]
- Beaumont, M.A. Approximate Bayesian computation in evolution and ecology. Annu. Rev. Ecol. Evol. Syst. 2010, 41, 379–406. [Google Scholar] [CrossRef]
- Thill, J.-C. Research on urban and regional systems: Contributions from GIS&T, spatial analysis, and location modeling. In Innovations in Urban and Regional Systems—Contributions from GIS&T, Spatial Analysis and Location Modeling; Springer Nature: Cham, Switzerland, 2020; pp. 3–20. [Google Scholar]
- Hou, X.; Gao, S.; Li, Q.; Kang, Y.; Chen, N.; Chen, K.; Rao, J.; Ellenberg, J.S.; Patz, J.A. Intracounty modeling of COVID-19 infection with human mobility: Assessing spatial heterogeneity with business traffic, age, and race. Proc. Natl. Acad. Sci. USA 2021, 118, e2020524118. [Google Scholar] [CrossRef]
- Lawson, A.B.; Kim, J. Space-time covid-19 Bayesian SIR modeling in South Carolina. PLoS ONE 2021, 16, e0242777. [Google Scholar] [CrossRef] [PubMed]
- Chiang, W.H.; Liu, X.; Mohler, G. Hawkes process modeling of COVID-19 with mobility leading indicators and spatial covariates. Int. J. Forecast. 2022, 38, 505–520. [Google Scholar] [CrossRef] [PubMed]
- Kinsey, M.; Tallaksen, K.R.F.O.; Asher, L.; Costello, C.; Kelbaugh, M.; Wilson, S. Bucky Model: A Spatial SEIR Model for Simulating COVID-19 at the County Level; The Johns Hopkins University Applied Physics Laboratory LLC: Laurel, MD, USA, 2020; Available online: https://buckymodel.com/ (accessed on 7 December 2021).
- Macías, R.Z.; Gutiérrez-Pulido, H.; Arroyo EA, G.; González, A.P. Geographical network model for COVID-19 spread among dynamic epidemic regions. Math. Biosci. Eng. 2022, 19, 4237–4259. [Google Scholar] [CrossRef]
- Gopalakrishnan, V.; Pethe, S.; Kefayati, S.; Srinivasan, R.; Hake, P.; Deshpande, A.; Liu, X.; Hoang, E.; Davila, M.; Bianco, S.; et al. Globally local: Hyper-local modeling for accurate forecast of COVID-19. Epidemics 2021, 37, 100510. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Li, H.X. Global Behavior of a Multi–Group Seir Epidemic Model with Spatial Diffusion in a Heterogeneous Environment. Int. J. Appl. Math. Comput. Sci. 2022, 32, 271–283. [Google Scholar]
- Rajuladevi, R.S.; Marathe, M.; Porebski, P.; Venkataramanan, S. Impact of Seeding and Spatial Heterogeneity on Metapopulation Disease Dynamics. In Proceedings of the epiDAMIK 5.0: The 5th International workshop on Epidemiology meets Data Mining and Knowledge discovery at KDD 2022, Washington, DC, USA, 15 August 2022. [Google Scholar]
- Bernardi, M.S.; Sangalli, L.M.; Mazza, G.; Ramsay, J.O. A penalized regression model for spatial functional data with application to the analysis of the production of waste in Venice province. Stoch. Environ. Res. Risk Assess. 2017, 31, 23–38. [Google Scholar] [CrossRef] [Green Version]
- Boehm Vock, L.F.; Reich, B.J.; Fuentes, M.; Dominici, F. Spatial variable selection methods for investigating acute health effects of fine particulate matter components. Biometrics 2015, 71, 167–177. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.; Fahrmeir, L. Spatial Bayesian variable selection with application to functional magnetic resonance imaging. J. Am. Stat. Assoc. 2007, 102, 417–431. [Google Scholar] [CrossRef]

| Variable | Mean | Std. Dev. | Min | Pctl. 25 | Pctl. 75 | Max |
|---|---|---|---|---|---|---|
| Google mobility (change in time spent at workplaces (%)) | −28.835 | 8.118 | −53.714 | −33.893 | −22.714 | −10.429 |
| Population vaccinated with at least one dose | 1028.341 | 2375.554 | 0 | 0 | 306.25 | 13162 |
| Apple mobility (average requests for changing directions) | 130.352 | 24.699 | 53.999 | 119.248 | 148.376 | 180.517 |
| Voting ratio (democrats/republicans) | 0.756 | 0.468 | 0.361 | 0.508 | 0.8 | 2.094 |
| Population density (per mi2) | 515.209 | 551.934 | 55.335 | 273.888 | 579.502 | 2097.705 |
| Wintery temperature | 0.63 | 0.48 | 0 | 0 | 1 | 1 |
| School shutdowns | 0.39 | 0.49 | 0 | 0 | 1 | 1 |
| Face mask intervention policy | 0.28 | 0.45 | 0 | 0 | 1 | 1 |
| Model Specification | Approximate Bayes Factor | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | ||
| Model 1 | Face mask intervention policy School shutdowns Wintery temperature Population density Vaccinated population with at least one dose | 1.0 | 0.2 | 3.1 |
| Model 2 | Face mask intervention policy School shutdowns Wintery temperature Presidential election voting ratio Vaccinated population with at least one dose Percentage change in mobility (Apple Mobility dataset) | 5.6 | 1.0 | 17.3 |
| Model 3 | Face mask intervention policy School shutdowns Wintery temperature Presidential election voting ratio Vaccinated population with at least one dose Change in time spent at work (Google mobility reports dataset) | 0.3 | 0.1 | 1.0 |
| County | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cabarrus | Gaston | Iredell | Lincoln | Mecklenburg | Rowan | Union | Chester | Lancaster | York | ||
| PC Model 1 | W1 | 284 | 251 | 226 | 64 | 1677 | 265 | 299 | 72 | 207 | 454 |
| W2 | 256 | 227 | 204 | 58 | 1515 | 240 | 270 | 65 | 188 | 410 | |
| W3 | 232 | 205 | 184 | 53 | 1372 | 217 | 244 | 59 | 170 | 370 | |
| W4 | 210 | 186 | 167 | 47 | 1241 | 196 | 221 | 53 | 153 | 336 | |
| PC Model 2 | W1 | 364 | 337 | 261 | 85 | 1665 | 338 | 328 | 84 | 209 | 472 |
| W2 | 326 | 301 | 234 | 76 | 1492 | 303 | 294 | 75 | 188 | 423 | |
| W3 | 292 | 270 | 210 | 68 | 1340 | 271 | 263 | 67 | 168 | 379 | |
| W4 | 262 | 243 | 188 | 61 | 1203 | 243 | 236 | 60 | 151 | 340 | |
| PC Model 3 | W1 | 181 | 170 | 132 | 36 | 1661 | 160 | 174 | 41 | 113 | 269 |
| W2 | 162 | 151 | 118 | 32 | 1484 | 143 | 156 | 37 | 101 | 240 | |
| W3 | 144 | 135 | 105 | 29 | 1328 | 127 | 139 | 33 | 90 | 214 | |
| W4 | 130 | 121 | 94 | 26 | 1189 | 114 | 125 | 29 | 81 | 192 | |
| RC | W1 | 277 | 233 | 236 | 104 | 1328 | 184 | 383 | 77 | 120 | 503 |
| W2 | 289 | 245 | 244 | 93 | 1436 | 166 | 424 | 50 | 100 | 419 | |
| W3 | 343 | 270 | 213 | 112 | 1532 | 190 | 346 | 33 | 123 | 420 | |
| W4 | 396 | 268 | 183 | 101 | 1724 | 196 | 313 | 32 | 106 | 440 | |
| County | Cabarrus | Gaston | Iredell | Lincoln | Mecklenburg | Rowan | Union | Chester | Lancaster | York |
|---|---|---|---|---|---|---|---|---|---|---|
| Spatial SEIR—Model 1 | 110 | 54 | 26 | 48 | 311 | 56 | 111 | 18 | 70 | 63 |
| Spatial SEIR—Model 2 | 86 | 60 | 14 | 32 | 326 | 113 | 90 | 26 | 70 | 56 |
| Spatial SEIR—Model 3 | 184 | 115 | 108 | 72 | 332 | 54 | 220 | 19 | 21 | 218 |
| Ensemble | 174 | 92 | 102 | 23 | 882 | 86 | 148 | 18 | 22 | 139 |
| Model 1 | Model 2 | Model 3 | Ensemble | |
|---|---|---|---|---|
| RMSE- average weighted by county population | 172 | 177 | 224 | 440 |
| RMSE- unweighted average | 87 | 87 | 134 | 169 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatami, F.; Chen, S.; Paul, R.; Thill, J.-C. Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model. Int. J. Environ. Res. Public Health 2022, 19, 15771. https://doi.org/10.3390/ijerph192315771
Hatami F, Chen S, Paul R, Thill J-C. Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model. International Journal of Environmental Research and Public Health. 2022; 19(23):15771. https://doi.org/10.3390/ijerph192315771
Chicago/Turabian StyleHatami, Faizeh, Shi Chen, Rajib Paul, and Jean-Claude Thill. 2022. "Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model" International Journal of Environmental Research and Public Health 19, no. 23: 15771. https://doi.org/10.3390/ijerph192315771
APA StyleHatami, F., Chen, S., Paul, R., & Thill, J.-C. (2022). Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model. International Journal of Environmental Research and Public Health, 19(23), 15771. https://doi.org/10.3390/ijerph192315771










