Study on the Decoupling and Interaction Effect between Industrial Structure Upgrading and Carbon Emissions under Dual Carbon Targets
Abstract
:1. Introduction
2. Research Design
2.1. Construction of Indicator System
2.1.1. Measurement of Industrial Structure Upgrading
- (1)
- Advanced industrial structure (SH)
- (2)
- Rational structure of production (TL)
- (3)
- Industrial structure upgrading index (IS)
2.1.2. Measurement of Carbon Emissions
2.2. Research Method
2.2.1. Decoupling Model
2.2.2. Kernel Density Function
2.2.3. Dagum Gini Coefficient
2.2.4. Moran Index
2.3. Data Source and Processing
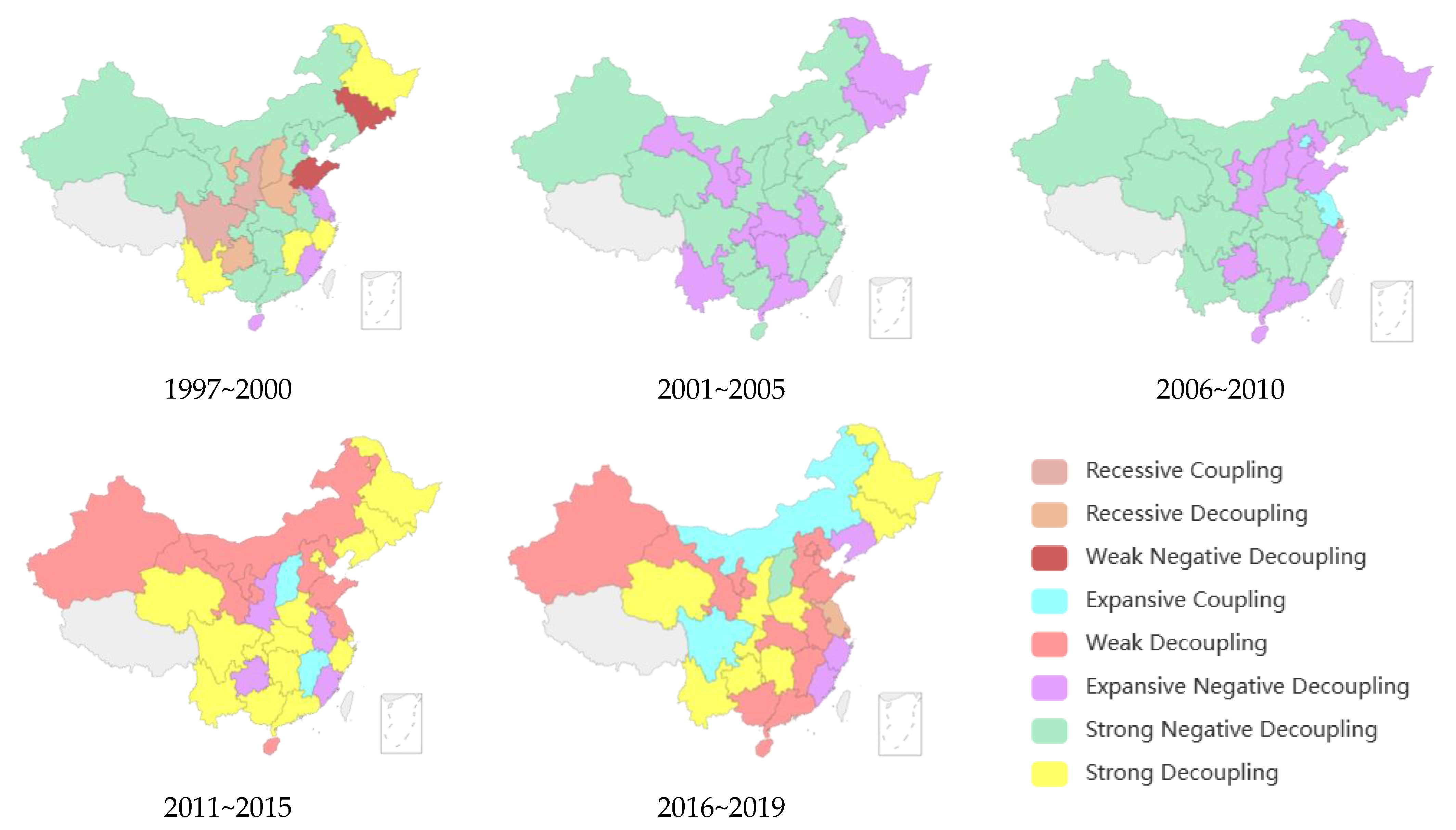
3. Analysis of the Heterogeneity of Decoupling between Industrial Structure and Carbon Emissions
3.1. Analysis of Decoupling Measurement Results
3.2. Analysis of Decoupling Distribution Characteristics Based on Kernel Density Function
3.3. Analysis of Difference Sources Based on Dagum Gini Coefficient Decomposition Method
3.3.1. Overall Differences
3.3.2. Differences within the Region
3.3.3. Differences between Regions
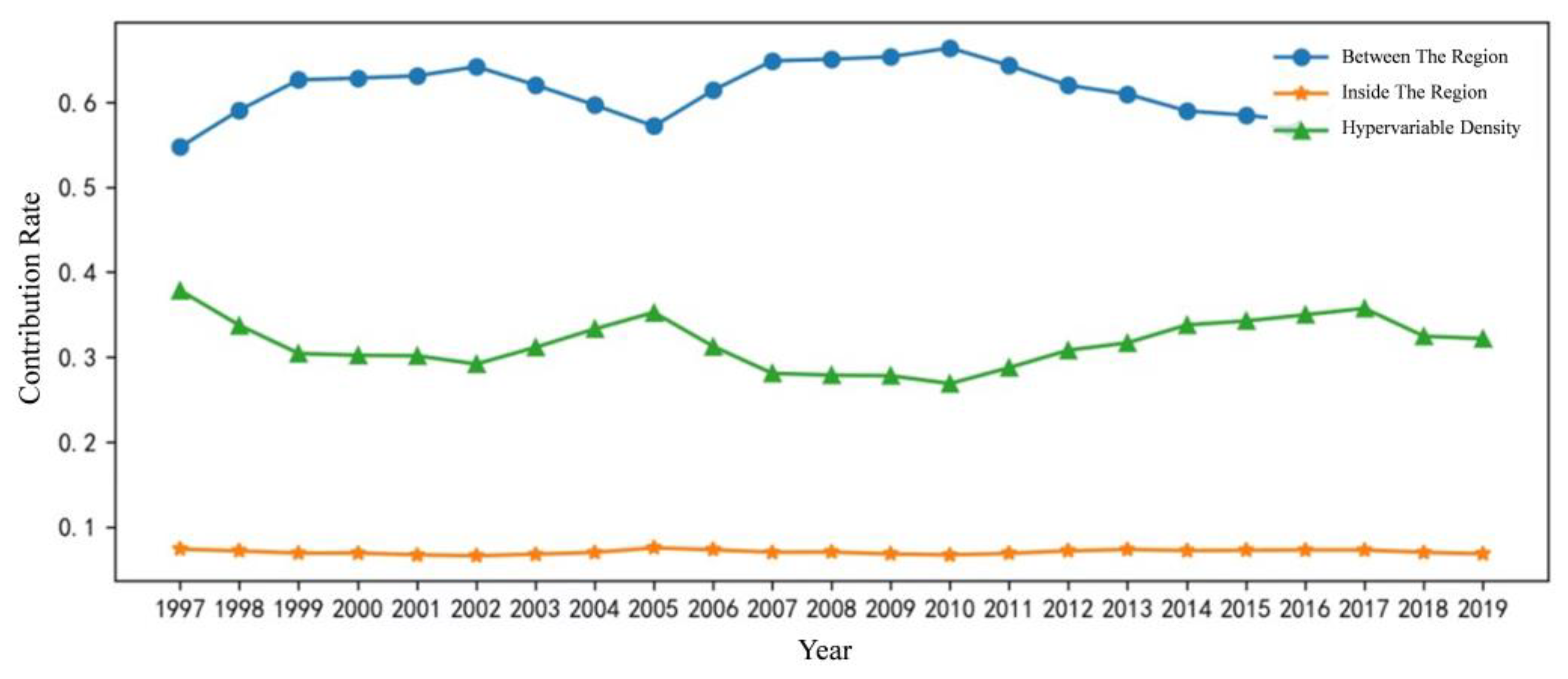
3.4. Source and Contribution of Difference
4. Study on the Synergistic Effect of Industrial Structure and Carbon Emissions
4.1. Spatial Autocorrelation Analysis and Results
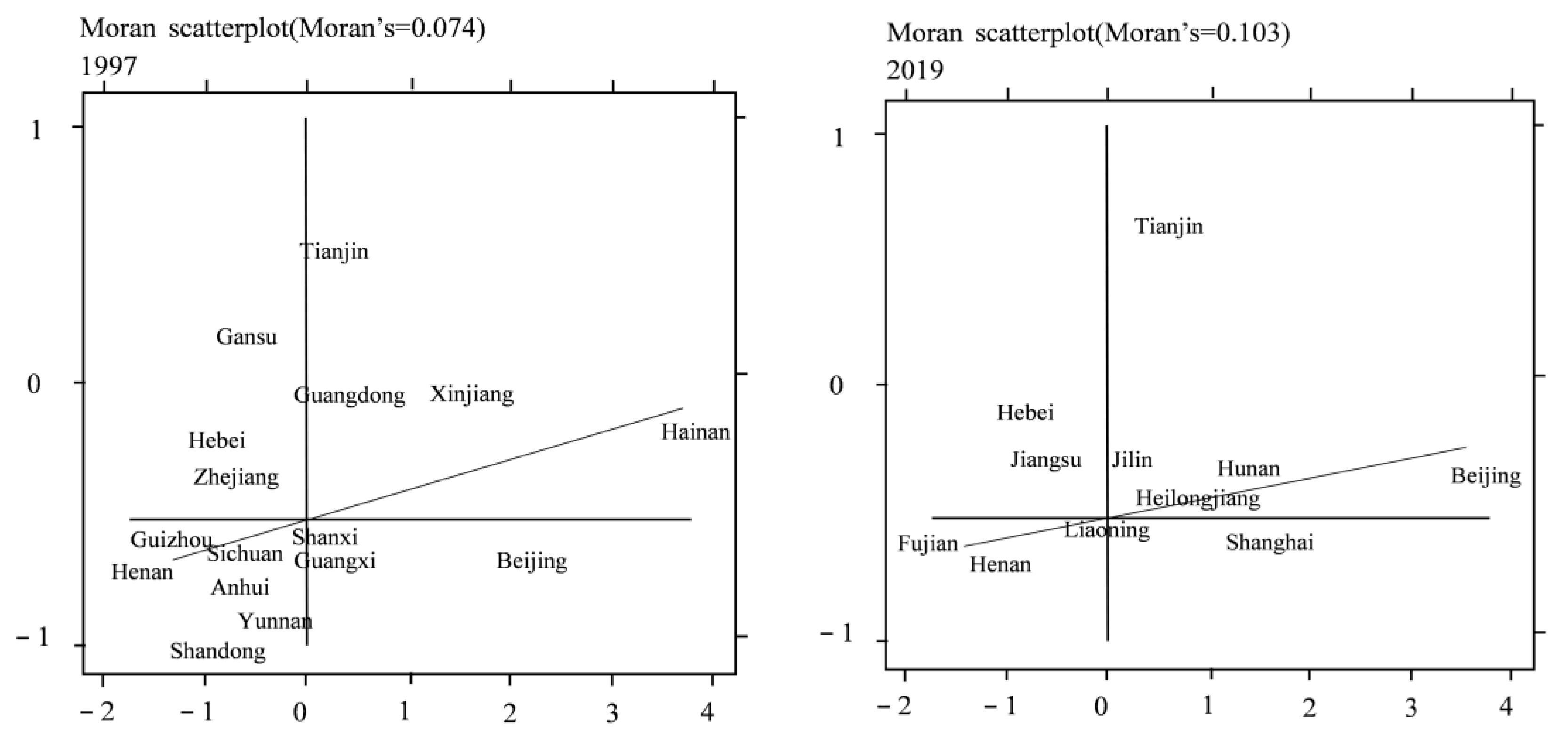
4.1.1. Global Moran Index
4.1.2. Local Moran Index
4.2. Impact of Industrial Structure Upgrading on Carbon Emissions
4.2.1. Impact of China’s Overall Industrial Structure Upgrading on Carbon Emissions
- (1)
- LM inspection
- (2)
- Model comparison
- (3)
- LR inspection
4.2.2. Impact of Industrial Structure Upgrading on Carbon Emissions in Eastern, Central and Western Regions
4.2.3. Analysis of Regression Results of Spatial Econometric Model
5. Conclusions and Policy Implications
5.1. Conclusions
5.2. Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Razzaq, A.; Liu, H.; Xiao, M.; Mehmood, K.; Shahzad, M.A.; Zhou, Y. Analyzing past and future trends in Pakistan’s groundwater irrigation development: Implications for environmental sustainability and food security. Environ. Sci. Pollut. Res. 2022, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Gou, L. The speed measurement, space-time evolution and influencing factors of China’s industrial structure transformation and upgrading. Ind. Tech. Econ. 2022, 41, 59–67. [Google Scholar]
- Wang, X.; Chen, M.; Chen, N. Digital economy, green technology innovation and industrial structure upgrading. Econ. Issues 2023, 19–28. [Google Scholar] [CrossRef]
- Guo, S.; Jin, Z. Research on the spatial spillover effect of digital inclusive finance on the upgrading of regional industrial structure. Econ. Lat. 2023, 1–11. [Google Scholar]
- Liu, H.; Ji, R. Research on the mechanism and effect of digital economy promoting industrial structure upgrading. Sci. Tech. Pro. Cm. 2023, 1–10. [Google Scholar] [CrossRef]
- Chen, F.; Xie, Y. Does the upgrading policy of provincial development zones promote the upgrading of industrial structure? J. Haust. 2023, 1–9. [Google Scholar]
- Wang, G. Human capital upgrading, regional innovation and industrial structure upgrading—Taking Anhui Province as an example. J. Ctgu. 2022, 44, 70–77. [Google Scholar]
- Cui, H. Research on Carbon Emission Measurement and Influencing Factors of Countries along the “the Belt and Road”. J. Green Sci. Technol. 2019, 257–260. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, J.; Wan, L. Measurement of carbon emissions and analysis of influencing factors in Chongqing: 1998∼2008. Explore 2010, 106–110. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, P. Research on the measurement and decoupling elasticity of agricultural carbon emissions—Taking Guizhou Province as an example. Rural Econ. Technol. 2022, 33, 1–3. [Google Scholar]
- Yang, Z.; Li, Z. Research on the dynamic characteristics of carbon emission measurement and driving factors in central China. Eco. Econ. 2022, 38, 13–20. [Google Scholar]
- Yang, X.; Cai, L.; Zhang, J. Research on the relationship between financial innovation, industrial structure upgrading and carbon emissions from a spatial perspective. J. Xust. 2022, 42, 791–799. [Google Scholar]
- Xie, W.; Gao, K.; Yu, J. Digital economy, industrial structure upgrading and carbon emissions. Stats. Dec. 2022, 38, 114–118. [Google Scholar]
- Wu, L.; Sun, L.; Qi, P.; Ren, X.; Sun, X. Energy endowment, industrial structure upgrading, and CO2 emissions in China: Revisiting resource curse in the context of carbon emissions. Res. Pol. 2021, 74, 102329. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Wang, Y.; Qin, Y. Industrial structure, technological progress and CO2 emissions in China: Analysis based on the STIRPAT framework. Nat. Hazards 2017, 88, 1545–1564. [Google Scholar] [CrossRef]
- Gong, M.; Liu, H. China’s two-way FDI coordinated development, industrial structure evolution and environmental pollution. Intl. Trade Issues 2020, 110–124. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, F. Carbon emissions and upgrading of industrial structure—A test based on the perspective of energy consumption. Orient. For. 2022, 29, 39–52. [Google Scholar]
- Dong, B.; Xu, Y.; Fan, X. How to achieve a win-win situation between economic growth and carbon emission reduction: Empirical evidence from the perspective of industrial structure upgrading. Environ. Sci. Pollut. Res. 2020, 27, 43829–43844. [Google Scholar] [CrossRef]
- Zheng, J.; Shao, X.; Liu, W.; Kong, J.; Zuo, G. The impact of the pilot program on industrial structure upgrading in low-carbon cities. J. Clean. Prod. 2021, 290, 125868. [Google Scholar] [CrossRef]
- Gan, C.; Zheng, R.; Yu, D. The impact of China’s industrial structure change on economic growth and volatility. Econ. R. 2011, 5, 16. [Google Scholar]
- Han, Y.; Huang, L.; Wang, X. Has industrial policy promoted the upgrading of local industrial structure—Theoretical explanation and empirical test based on development-oriented local government. Econ. R. 2017, 52, 33–48. [Google Scholar]
- Erfanian, S.; Ziaullah, M.; Tahir, M.A.; Ma, D. How does justice matter in developing supply chain trust and improving information sharing-an empirical study in Pakistan. Int. J. Manuf. Tech. Manag. 2021, 35, 354–368. [Google Scholar] [CrossRef]



| Indicator Type | First-Level Indicators | Second-Level Indicators | Indicator Code |
|---|---|---|---|
| Interpreted variable | Industrial structure upgrading | Advanced industrial structure | |
| Rationalization of industrial structure | |||
| Core explanatory variables | Carbon emission | Total carbon dioxide emissions | |
| Intermediary variable | Energy structure | Total coal consumption | |
| Energy intensity | Proportion of energy consumption | ||
| Control variable | Economic development level | Total GDP | |
| Degree of government intervention | Proportion of fiscal expenditure | ||
| Scientific and technological level | R&D investment | ||
| Income level | Gini index |
| Decoupling State | ||||
|---|---|---|---|---|
| Negative decoupling | Expansive negative decoupling | + | + | (1.2, +∞) |
| Strong negative decoupling | + | − | (−∞, 0) | |
| Weak negative decoupling | − | − | [0, 0.8) | |
| Decoupling | Weak decoupling | + | + | [0, 0.8) |
| Strong decoupling | − | + | (−∞, 0) | |
| Recessive decoupling | − | − | (1.2, +∞) | |
| Coupling | Expansive coupling | + | + | [0.8, 1.2] |
| Recessive coupling | − | − | [0.8, 1.2] | |
| Economic Region | Province |
|---|---|
| Southern coast | Fujian, Guangdong, Hainan |
| Northern coast | Beijing, Tianjin, Hebei, Shandong |
| Northeast China | Liaoning, Jilin, Heilongjiang |
| The middle reaches of the Yangtze River | Anhui, Jiangxi, Hubei, Hunan |
| The middle reaches of the Yellow River | Shanxi, Inner Mongolia, Henan, Shaanxi |
| Southwest China | Guangxi, Chongqing, Sichuan, Guizhou, Yunnan |
| East Coast | Shanghai, Jiangsu, Zhejiang |
| Northwest China | Gansu, Qinghai, Ningxia, Xinjiang |
| Distribution Position | Shape | Kurtosis | |
|---|---|---|---|
| National regions | The overall shift to the right shows that the decoupling index has an upward trend during the review period, and the carbon emission rate is greater than the growth rate of the industrial structure upgrading index | Most years are in a single peak state, indicating that the decoupling index gap between provinces is relatively stable | The peak value reached its maximum in 2013 and then showed a high decline trend, indicating that the distribution difference of decoupling index among provinces first increased and then decreased |
| Eastern region | In 2019, there was a significant bimodal trend, and the polarized camp has strengthened. The left peak was greater than the right peak, indicating that the number of provinces with low decoupling index was more than with high decoupling index | Before 2013, the nuclear density function peak of carbon emissions was relatively low, with the highest peak in 2013; the peak value decreases, indicating that the difference in decoupling index between eastern regions is enlarged | |
| Central region | The overall shift from left to right shows that the decoupling index first decreases and then increases during the review period, and the carbon emission rate is first lower than and then higher than the growth rate of the industrial structure upgrading index | The density function changes from a bimodal state to a unimodal state. The bimodal state has no significant trend, the camp of polarization changes and the regional polarization weakens | In 2013, there was a changing trend from peak to broad peak, indicating that the difference in decoupling index was expanding |
| Western region | The density function shows the multi-peak phenomenon for many years, indicating that the carbon emissions in the western region have a greater two-stage differentiation, the decoupling index varies greatly among provinces and the polarization situation is changing | The peak value was the highest in 2013, followed by 2019, indicating widening and strong polarization of the carbon emissions gap in the western region |
| Particular Year | ||||||
|---|---|---|---|---|---|---|
| Moran’s I | Z Value | p Value | Moran’s I | Z Value | p Value | |
| 1997 | 0.077 | 1.063 | 0.044 | 0.274 | 2.535 | 0.006 |
| 1998 | 0.076 | 1.011 | 0.046 | 0.221 | 2.114 | 0.017 |
| 1999 | 0.092 | 1.222 | 0.011 | 0.266 | 2.501 | 0.006 |
| 2000 | 0.068 | 0.994 | 0.040 | 0.236 | 2.261 | 0.0132 |
| 2001 | 0.075 | 1.048 | 0.047 | 0.266 | 2.509 | 0.006 |
| 2002 | 0.084 | 1.096 | 0.037 | 0.278 | 2.611 | 0.005 |
| 2003 | 0.059 | 0.862 | 0.044 | 0.275 | 2.590 | 0.005 |
| 2004 | 0.055 | 0.817 | 0.007 | 0.279 | 2.653 | 0.004 |
| 2005 | 0.030 | 0.042 | 0.043 | 0.297 | 2.881 | 0.002 |
| 2006 | 0.040 | 0.065 | 0.044 | 0.271 | 2.704 | 0.003 |
| 2007 | 0.024 | 0.123 | 0.041 | 0.249 | 2.498 | 0.006 |
| 2008 | 0.023 | 0.145 | 0.042 | 0.259 | 2.527 | 0.006 |
| 2009 | 0.020 | 0.613 | 0.047 | 0.283 | 2.720 | 0.003 |
| 2010 | 0.058 | 0.040 | 0.049 | 0.301 | 2.827 | 0.002 |
| 2011 | 0.050 | 0.966 | 0.047 | 0.309 | 2.861 | 0.002 |
| 2012 | 0.043 | 0.865 | 0.044 | 0.289 | 2.709 | 0.003 |
| 2013 | 0.038 | 0.826 | 0.044 | 0.276 | 2.820 | 0.002 |
| 2014 | 0.021 | 0.588 | 0.048 | 0.250 | 2.617 | 0.004 |
| 2015 | 0.014 | 0.506 | 0.006 | 0.254 | 2.600 | 0.005 |
| 2016 | 0.036 | 0.709 | 0.039 | 0.226 | 2.346 | 0.009 |
| 2017 | 0.050 | 0.851 | 0.047 | 0.242 | 2.454 | 0.007 |
| 2018 | 0.089 | 1.435 | 0.016 | 0.205 | 2.182 | 0.015 |
| 2019 | 0.107 | 1.592 | 0.046 | 0.195 | 2.068 | 0.019 |
| Test | LM Value | p Value |
|---|---|---|
| LM Lag test | 2.424 | 0.120 |
| Robust LM Lag test | 31.972 | 0.000 |
| LM Error test | 33.748 | 0.000 |
| Robust LM Error test | 63.296 | 0.000 |
| Variable Name | SAR | SEM | SDM |
|---|---|---|---|
| 0.032 ** (2.230) | 0.028 ** (2.010) | 0.023 * (1.640) | |
| −0.294 *** (−17.610) | −0.310 *** (−18.740) | −0.300 *** (−17.150) | |
| 0.260 *** (3.490) | 0.318 *** (4.160) | 0.268 *** (3.420) | |
| 0.162 *** (11.540) | 0.190 *** (12.650) | 0.182 *** (7.450) | |
| 0.016 (1.140) | 0.0158 (1.020) | −0.003 (−0.210) | |
| −4.625 *** (−4.860) | −5.984 *** (−5.340) | −8.387 *** (1.220) | |
| −0.529 ** (−2.430) | −0.634 ** (−2.510) | 0.035 (0.120) | |
| Constant | 1.471 (12.880) | 1.527 (11.530) | 1.017 (5.220) |
| - | - | 0.012 (0.270) | |
| Control variable | - | - | Spatial lag |
| Log−L | 485.531 | 496.183 | 503.608 |
| 0.012 *** | 0.011 *** | 0.011 *** | |
| The goodness of fit | 0.526 | 0.524 | 0.543 |
| Hausman Test | 21.530 ** | 25.220 ** | 27.190 |
| LR test | 36.160 *** | 14.850 | - |
| Eastern Region | Central Region | Western Region | ||
|---|---|---|---|---|
| SAR | Control variable | - | - | - |
| 0.010 *** | 0.005 *** | 0.005 *** | ||
| The goodness of fit | 0.800 | 0.506 | 0.329 | |
| Hausman Test | 137.100 *** | 455.630 *** | 49.230 *** | |
| LR test | 25.820 *** | 43.250 *** | 12.820 * | |
| SEM | Control variable | - | - | - |
| 0.010 *** | 0.005 *** | 0.005 *** | ||
| The goodness of fit | 0.793 | 0.404 | 0.315 | |
| Hausman Test | 137.820 *** | 24.680 ** | 561.860 *** | |
| LR test | 30.010 *** | 39.440 *** | 10.040 | |
| SDM | Control variable | Spatial lag | Spatial lag | Spatial lag |
| 0.009 *** | 0.004 *** | 0.004 *** | ||
| The goodness of fit | 0.817 | 0.571 | 0.467 | |
| Hausman Test | - | - | - | |
| LR test | - | - | - |
| Variable Name | Eastern Region | Central Region | Western Region |
|---|---|---|---|
| −0.169 *** (−5.810) | 0.044 (1.490) | 0.003 (0.220) | |
| −0.309 *** (−14.590) | −0.020 (−0.510) | −0.041 (−1.250) | |
| 0.136 (1.330) | 0.340 *** (1.530) | 0.177 (0.860) | |
| 0.469 *** (12.970) | −0.309 *** (−4.120) | −0.255 ** (−2.570) | |
| −0.028 (−0.660) | 0.145 *** (5.110) | 0.002 (0.130) | |
| −7.438 *** (−5.010) | −5.202 (−2.250) | 3.732 ** (2.170) | |
| −1.308 *** (−2.630) | −0.470 (−1.200) | 0.826 *** (2.840) | |
| Constant | 0.686 ** (2.590) | 1.282 *** (3.540) | 0.226 (0.830) |
| −0.016 (−0.180) | 0.083 (1.250) | 0.010 (0.260) |
| Variable Name | Direct Effect | Indirect Effect | Total Effect |
|---|---|---|---|
| 0.011 (0.840) | −0.107 ** (−2.390) | −0.096 ** (−2.050) | |
| −0.275 *** (−18.290) | 0.128 *** (3.430) | −0.147 *** (−3.730) | |
| 0.082 (1.220) | −0.523 *** (−3.280) | −0.441 *** (−2.620) | |
| −0.191 *** (−4.690) | 0.005 (0.120) | −0.186 *** (−4.010) | |
| −0.088 *** (−5.640) | −0.040 (−1.420) | −0.128 *** (−4.790) | |
| −6.989 *** (−6.380) | 4.660 * c(1.800) | −2.329 (−0.810) | |
| 0.198 (0.650) | 0.877 * (1.640) | 1.075 * (1.750) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Liu, Y.; Yang, Z.; Wang, M.; Zhang, C.; Wang, L. Study on the Decoupling and Interaction Effect between Industrial Structure Upgrading and Carbon Emissions under Dual Carbon Targets. Int. J. Environ. Res. Public Health 2023, 20, 1945. https://doi.org/10.3390/ijerph20031945
Sun Y, Liu Y, Yang Z, Wang M, Zhang C, Wang L. Study on the Decoupling and Interaction Effect between Industrial Structure Upgrading and Carbon Emissions under Dual Carbon Targets. International Journal of Environmental Research and Public Health. 2023; 20(3):1945. https://doi.org/10.3390/ijerph20031945
Chicago/Turabian StyleSun, Yuqing, Yingchao Liu, Zhiwei Yang, Mengyao Wang, Chunying Zhang, and Liya Wang. 2023. "Study on the Decoupling and Interaction Effect between Industrial Structure Upgrading and Carbon Emissions under Dual Carbon Targets" International Journal of Environmental Research and Public Health 20, no. 3: 1945. https://doi.org/10.3390/ijerph20031945
APA StyleSun, Y., Liu, Y., Yang, Z., Wang, M., Zhang, C., & Wang, L. (2023). Study on the Decoupling and Interaction Effect between Industrial Structure Upgrading and Carbon Emissions under Dual Carbon Targets. International Journal of Environmental Research and Public Health, 20(3), 1945. https://doi.org/10.3390/ijerph20031945







