Multi-Objective Optimization of Microalgae Metabolism: An Evolutive Algorithm Based on FBA
Abstract
:1. Introduction
2. Results
3. Discussion
4. Materials and Methods
4.1. Proposed Evolutionary Approach Based on NSGAII
4.1.1. Multi-Objective Optimization Model for FBA
4.1.2. Evolutionary Approach for MOFBA
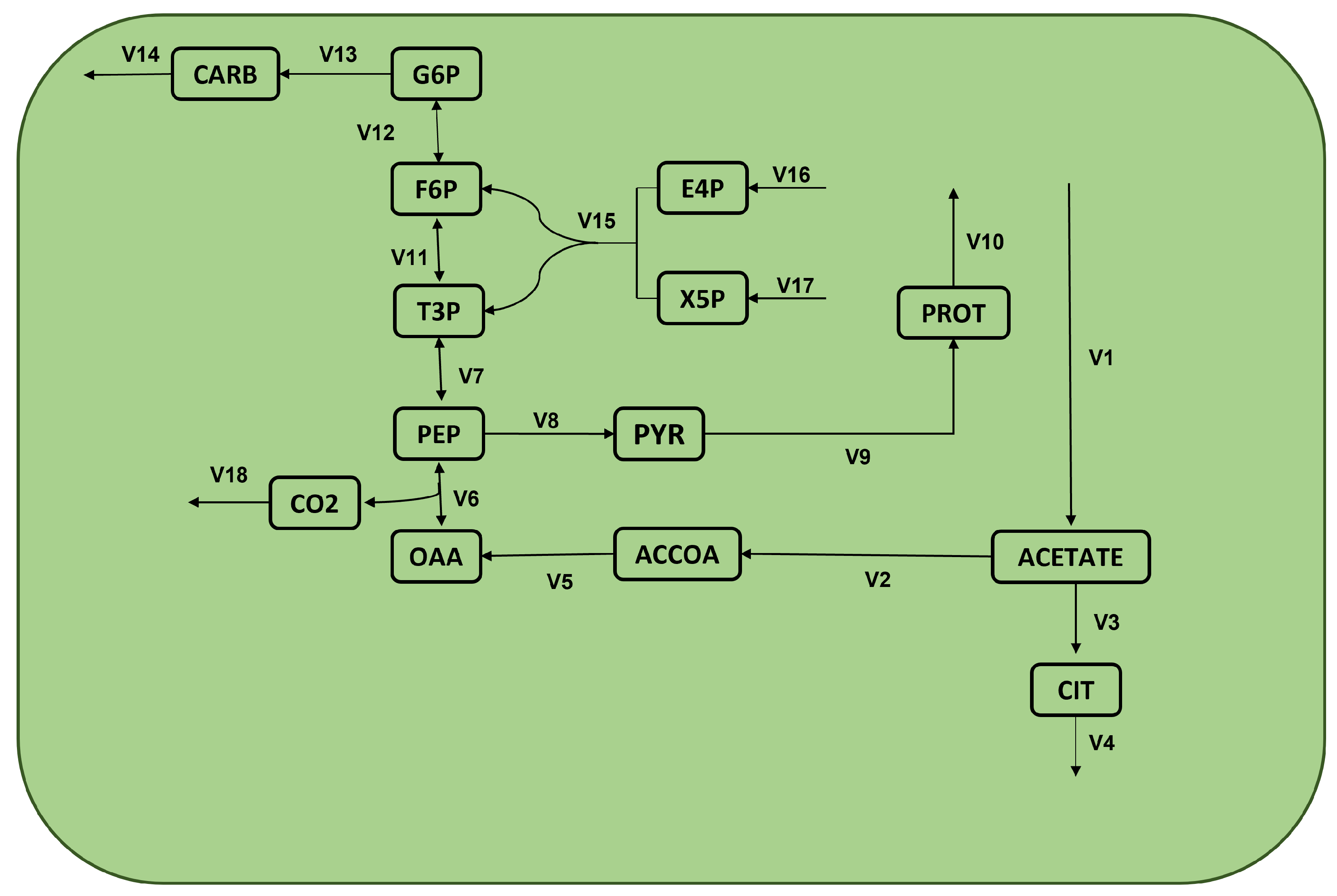
4.2. Case of Study: Metabolic Network of Chlamydomonas reinhardtii
4.3. Experimental Design
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACCOA | Acetyl-coenzyme A |
| CIT | Citrato |
| OAA | Oxaloacetate |
| PEP | Phosphoenol pyruvate |
| T3P | Dihydroxyacetone phosphate and 3-phosphoglycerate |
| PYR | Pyruvate |
| PROT | Protein |
| F6P | Fructose-6-phosphate |
| G6P | Glucose-6-phosphate |
| CARB | Carbohydrates |
| FBA | Fluxes balance analysis |
| CO2 | Carbon dioxide |
| NSGAII | Genetic Algorithm of Non-Dominated Classification |
| MO-FBA | Multi-objective flux balance analysis |
| MO-FVA | Multi-objective flux variability analysis |
| MOEAs | Multi-objective Evolutionary Algorithms |
| SBX | Simulated Binary Crossover |
References
- Vale, M.A.; Ferreira, A.; Pires, J.C.; Gonçalves, A.L. Chapter 17—CO2 capture using microalgae. In Advances in Carbon Capture; Rahimpour, M.R., Farsi, M., Makarem, M.A., Eds.; Woodhead Publishing: Thorston, UK, 2020; pp. 381–405. [Google Scholar] [CrossRef]
- Li, C.T.; Yelsky, J.; Chen, Y.; Zuñiga, C.; Eng, R.; Jiang, L.; Shapiro, A.; Huang, K.W.; Zengler, K.; Betenbaugh, M.J. Utilizing genome-scale models to optimize nutrient supply for sustained algal growth and lipid productivity. NPJ Syst. Biol. Appl. 2019, 5, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuñiga, C.; Levering, J.; Antoniewicz, M.R.; Guarnieri, M.T.; Betenbaugh, M.J.; Zengler, K. Predicting dynamic metabolic demands in the photosynthetic eukaryote Chlorella vulgaris. Plant Physiol. 2018, 176, 450–462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guzmán-Palomino, A.; Aguilera-Vázquez, L.; Hernández-Escoto, H.; García-Vite, P.M. Sensitivity, Equilibria, and Lyapunov Stability Analysis in Droop’s Nonlinear Differential Equation System for Batch Operation Mode of Microalgae Culture Systems. Mathematics 2021, 9, 2192. [Google Scholar] [CrossRef]
- Chowdury, K.H.; Nahar, N.; Deb, U.K. The growth factors involved in microalgae cultivation for biofuel production: A Review. Comput. Water Energy Environ. Eng. 2020, 9, 185–215. [Google Scholar] [CrossRef]
- Zuñiga, C.; Li, C.T.; Huelsman, T.; Levering, J.; Zielinski, D.C.; McConnell, B.O.; Long, C.P.; Knoshaug, E.P.; Guarnieri, M.T.; Antoniewicz, M.R.; et al. Genome-Scale Metabolic Model for the Green Alga Chlorella vulgaris UTEX 395 Accurately Predicts Phenotypes under Autotrophic, Heterotrophic, and Mixotrophic Growth Conditions. Plant Physiol. 2016, 172, 589–602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orth, J.D.; Thiele, I.; Palsson, B.∅. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Raman, K.; Chandra, N. Flux balance analysis of biological systems: Applications and challenges. Brief. Bioinform. 2009, 10, 435–449. [Google Scholar] [CrossRef]
- Lewis, N.; Nagarajan, H.; Palsson, B. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat. Reviews. Microbiol. 2012, 10, 291–305. [Google Scholar] [CrossRef] [Green Version]
- Knoop, H.; Zilliges, Y.; Lockau, W.; Steuer, R. The metabolic network of Synechocystis sp. PCC 6803: Systemic properties of autotrophic growth. Plant Physiol. 2010, 154, 410–422. [Google Scholar] [CrossRef] [Green Version]
- Montagud, A.; Zelezniak, A.; Navarro, E.; de Córdoba, P.F.; Urchueguía, J.F.; Patil, K.R. Flux coupling and transcriptional regulation within the metabolic network of the photosynthetic bacterium Synechocystis sp. PCC6803. Biotechnol. J. 2011, 6, 330–342. [Google Scholar] [CrossRef]
- Vu, T.T.; Hill, E.A.; Kucek, L.A.; Konopka, A.E.; Beliaev, A.S.; Reed, J.L. Computational evaluation of Synechococcus sp. PCC 7002 metabolism for chemical production. Biotechnol. J. 2013, 8, 619–630. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Kim, M.K.; Kumaraswamy, G.K.; Agarwal, A.; Lun, D.S.; Dismukes, G.C. Flux balance analysis of photoautotrophic metabolism: Uncovering new biological details of subsystems involved in cyanobacterial photosynthesis. Biochim. Biophys. Acta (BBA)-Bioenerg. 2017, 1858, 276–287. [Google Scholar] [CrossRef] [PubMed]
- Alagesan, S.; Gaudana, S.B.; Sinha, A.; Wangikar, P.P. Metabolic flux analysis of Cyanothece sp. ATCC 51142 under mixotrophic conditions. Photosynth. Res. 2013, 118, 191–198. [Google Scholar] [CrossRef]
- Boyle, N.R.; Morgan, J.A. Flux balance analysis of primary metabolism in Chlamydomonas reinhardtii. BMC Syst. Biol. 2009, 3, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norena-Caro, D.A.; Zuniga, C.; Pete, A.J.; Saemundsson, S.A.; Donaldson, M.R.; Adams, A.J.; Dooley, K.M.; Zengler, K.; Benton, M.G. Analysis of the cyanobacterial amino acid metabolism with a precise genome-scale metabolic reconstruction of Anabaena sp. UTEX 2576. Biochem. Eng. J. 2021, 171, 108008. [Google Scholar] [CrossRef]
- Juneja, A.; Chaplen, F.W.; Murthy, G.S. Genome scale metabolic reconstruction of Chlorella variabilis for exploring its metabolic potential for biofuels. Bioresour. Technol. 2016, 213, 103–110. [Google Scholar] [CrossRef]
- Wu, C.; Xiong, W.; Dai, J.; Wu, Q. Genome-based metabolic mapping and 13C flux analysis reveal systematic properties of an oleaginous microalga Chlorella protothecoides. Plant Physiol. 2015, 167, 586–599. [Google Scholar] [CrossRef] [Green Version]
- Stiti, N.; Missihoun, T.D.; Kotchoni, S.O.; Kirch, H.H.; Bartels, D. Aldehyde dehydrogenases in Arabidopsis thaliana: Biochemical requirements, metabolic pathways, and functional analysis. Front. Plant Sci. 2011, 2, 65. [Google Scholar] [CrossRef] [Green Version]
- Boyle, N.R.; Sengupta, N.; Morgan, J.A. Metabolic flux analysis of heterotrophic growth in Chlamydomonas reinhardtii. PLoS ONE 2017, 12, e0177292. [Google Scholar] [CrossRef] [Green Version]
- Budinich, M.; Bourdon, J.; Larhlimi, A.; Eveillard, D. A multi-objective constraint-based approach for modeling genome-scale microbial ecosystems. PLoS ONE 2017, 12, e0171744. [Google Scholar] [CrossRef] [Green Version]
- Andrade, R.; Doostmohammadi, M.; Santos, J.; Sagot, M.F.; Mira, N.P.; Vinga, S. MOMO—Multi-objective metabolic mixed integer optimization: Application to yeast strain engineering. BMC Inform. 2020, 21, 69. [Google Scholar] [CrossRef] [Green Version]
- Van Pelt-KleinJan, E.; de Groot, D.H.; Teusink, B. Understanding FBA Solutions under Multiple Nutrient Limitations. Metabolites 2021, 11, 257. [Google Scholar] [CrossRef] [PubMed]
- Zomorrodi, A.R.; Maranas, C.D. OptCom: A Multi-Level Optimization Framework for the Metabolic Modeling and Analysis of Microbial Communities. PLoS Comput. Biol. 2012, 8, e1002363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, K.H. Chapter 19—Multiobjective Optimization and Advanced Topics. In e-Design; Chang, K.H., Ed.; Academic Press: Boston, MA, USA, 2015; pp. 1105–1173. [Google Scholar] [CrossRef]
- Limleamthong, P.; Guillén-Gosálbez, G. Combined Use of Bilevel Programming and Multi-objective Optimization for Rigorous Analysis of Pareto Fronts in Sustainability Studies: Application to the Redesign of the UK Electricity Mix. In Proceedings of the 28th European Symposium on Computer Aided Process Engineering, Graz, Austria, 10–13 June 2018; Friedl, A., Klemeš, J.J., Radl, S., Varbanov, P.S., Wallek, T., Eds.; Computer Aided Chemical Engineering. Elsevier: Amsterdam, The Netherlands, 2018; Volume 43, pp. 1099–1104. [Google Scholar] [CrossRef]
- Zhang, Y.; Boley, D. Nonlinear Multi-Objective Flux Balance Analysis of the Warburg Effect. arXiv 2021, arXiv:2111.12145. [Google Scholar]
- Chang, K.H. Multiobjective optimization and advanced topics. In Design Theory and Methods Using CAD/CAE; Elsevier: Amsterdam, The Netherlands, 2015; pp. 325–406. [Google Scholar]
- Ngatchou, P.; Zarei, A.; El-Sharkawi, A. Pareto multi objective optimization. In Proceedings of the 13th International Conference on, Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 84–91. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Vo-Duy, T.; Duong-Gia, D.; Ho-Huu, V.; Vu-Do, H.C.; Nguyen-Thoi, T. Multi-objective optimization of laminated composite beam structures using NSGA-II algorithm. Compos. Struct. 2017, 168, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Cruz, L.; Fernandez, E.; Gomez, C.; Rivera, G.; Perez, F. Many-Objective Portfolio Optimization of Interdependent Projects with ‘a priori’ Incorporation of Decision-Maker Preferences. Appl. Math. Inf. Sci. 2014, 8, 1517–1531. [Google Scholar] [CrossRef] [Green Version]
- Rivera, G.; Florencia, R.; Guerrero, M.; Porras, R.; Sanchez-Solis, J. Online multi-criteria portfolio analysis through compromise programming models built on the underlying principles of fuzzy outranking. Inf. Sci. 2021, 580, 734–755. [Google Scholar] [CrossRef]
- Vijayakumar, S.; Conway, M.; Lió, P.; Angione, C. Seeing the wood for the trees: A forest of methods for optimization and omic-network integration in metabolic modelling. Briefings Bioinform. 2018, 19, 1218–1235. [Google Scholar] [CrossRef] [Green Version]
- Costanza, J.; Carapezza, G.; Angione, C.; Lió, P.; Nicosia, G. Robust design of microbial strains. Bioinformatics 2012, 28, 3097–3104. [Google Scholar] [CrossRef] [Green Version]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. Optknock: A bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Kliphuis, A.M.; Klok, A.J.; Martens, D.E.; Lamers, P.P.; Janssen, M.; Wijffels, R.H. Metabolic modeling of Chlamydomonas reinhardtii: Energy requirements for photoautotrophic growth and maintenance. J. Appl. Phycol. 2012, 24, 253–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cruz-Reyes, L.; Fernandez, E.; Rangel-Valdez, N. A metaheuristic optimization-based indirect elicitation of preference parameters for solving many-objective problems. Int. J. Comput. Intell. Syst. 2017, 10, 56–77. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Goyal, M. A combined genetic adaptive search (geneas) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Deb, K.; Agrawal, R.B. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Ebrahim, A.; Lerman, J.A.; Palsson, B.O.; Hyduke, D.R. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef] [Green Version]
- Benítez-Hidalgo, A.; Nebro, A.J.; García-Nieto, J.; Oregi, I.; Del Ser, J. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm Evol. Comput. 2017, 12, e0171744. [Google Scholar] [CrossRef] [Green Version]

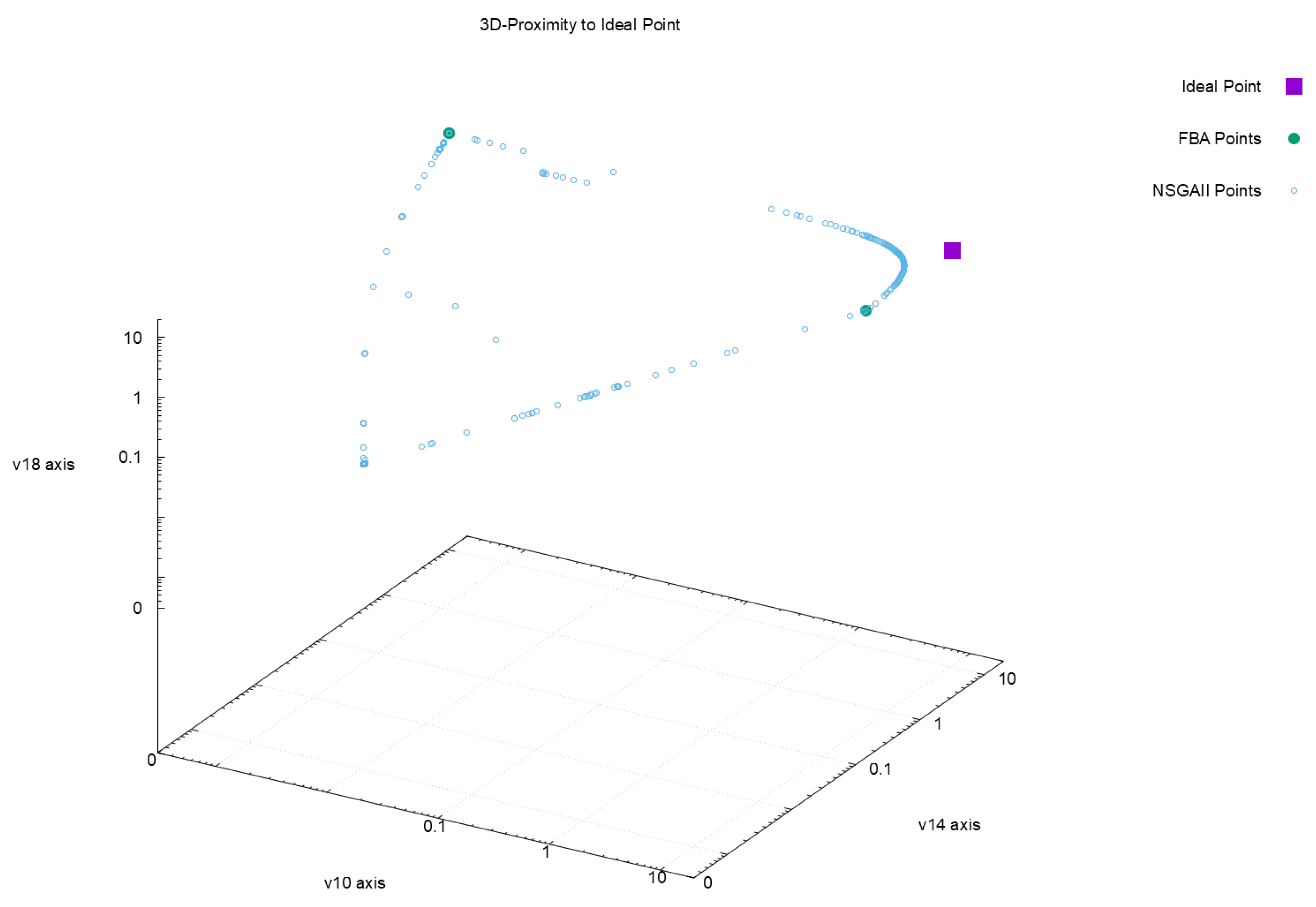

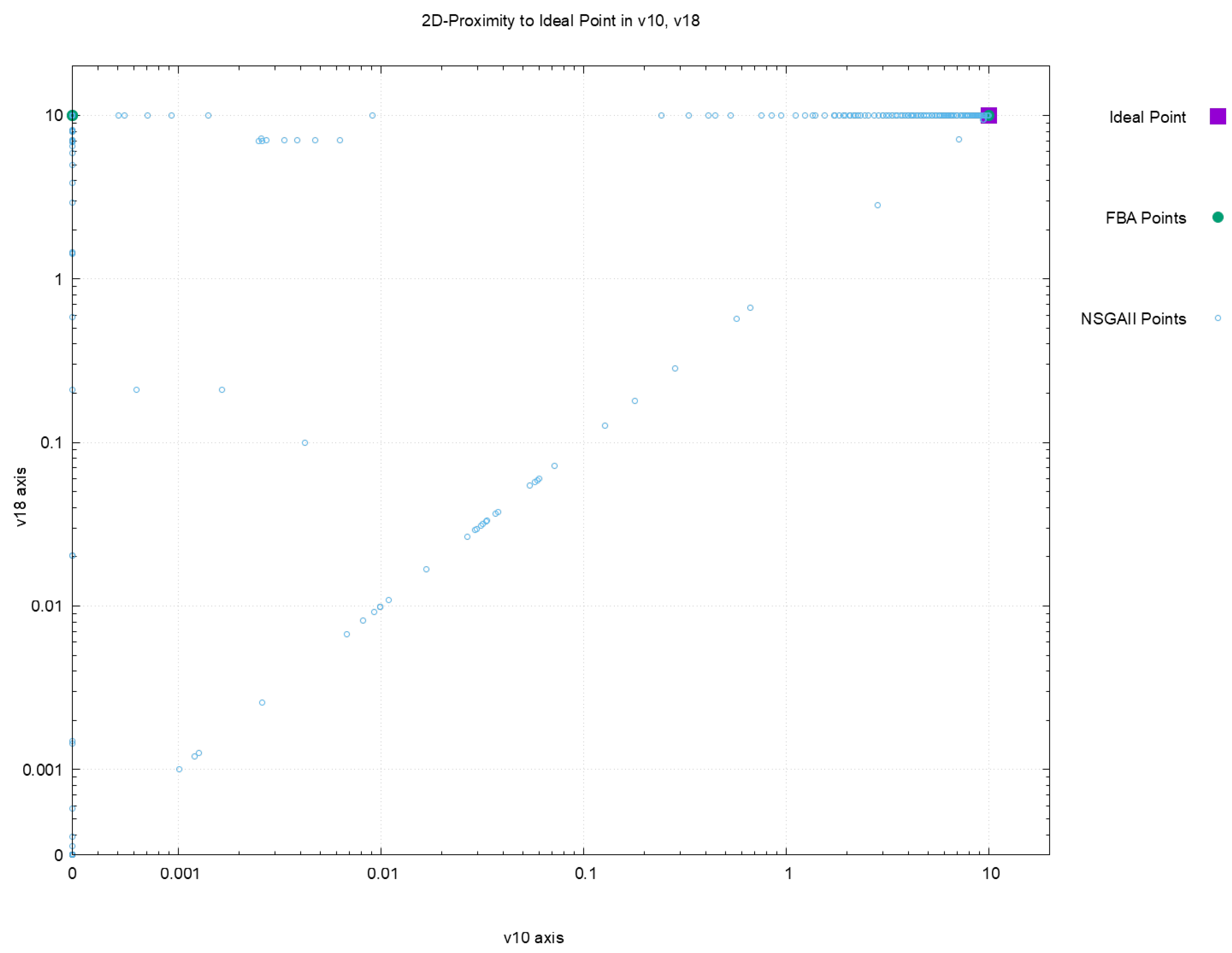


| Euclidean Distance to Ideal Point | |||||
|---|---|---|---|---|---|
| Config. | |||||
| 7.16 | 10.12 | 10 | 10 | 349 | |
| 8.07 | 10.12 | 10 | 10 | 158 | |
| 11.56 | 14.23 | 14.14 | 14.14 | 2501 | |
| 11.56 | 14.23 | 14.14 | 14.14 | 1701 | |
| 7.12 | 10.12 | 10 | 10 | 217 | |
| 8.34 | 10.12 | 10 | 10 | 359 | |
| 8.19 | 14.23 | 10 | 10 | 617 | |
| 10 | 10.12 | 14.14 | 10 | 53 | |
| 10 | 10.12 | 14.14 | 10 | 68 | |
| 10 | 14.27 | 10 | 10 | 147 | |
| 8.25 | 14.31 | 10 | 10 | 397 | |
| 8.24 | 14.31 | 10 | 10 | 279 | |
| 7.13 | 10.12 | 10 | 10 | 218 | |
| 0 | 0 | 0 | 0 | 125 | |
| 8.16 | 10 | 10 | 14.14 | 1821 | |
| 8.16 | 10 | 10 | 14.14 | 1646 | |
| 0 | 0 | 0 | 0 | 189 | |
| 0 | 0 | 0 | 0 | 216 | |
| 9.98 | 10 | 10 | 10 | 160 | |
| 0 | 0 | 0 | 0 | 88 | |
| 0 | 0 | 0 | 0 | 171 | |
| 8.20 | 10.06 | 10.06 | 10 | 202 | |
| 7.13 | 10.12 | 10.12 | 10 | 325 | |
| 7.13 | 10.12 | 10.12 | 10 | 465 | |
| 0 | 0.06 | 0.06 | 0 | 81 | |
| 0 | 0 | 0 | 0 | 125 | |
| 8.17 | 10 | 10 | 14.14 | 1597 | |
| 8.18 | 10 | 10 | 14.14 | 1199 | |
| 0 | 0 | 0 | 0 | 175 | |
| 0 | 0 | 0 | 0 | 280 | |
| 0 | 0 | 0 | 0 | 391 | |
| 8.27 | 10 | 10 | 10 | 276 | |
| 7.17 | 10 | 10 | 10 | 261 | |
| 0 | 0 | 0 | 0 | 122 | |
| 0 | 0 | 0 | 0 | 55 | |
| 0 | 0 | 0 | 0 | 90 | |
| 0 | 0 | 0 | 0 | 25 | |
| BY OBJECTIVE | 0 | 10 | 0 | 0 | 9.99 | 3.93 | 5.099 | |
| 10.12 | 0 | 10 | 10.11 | 0.045 | 6.68 | 5.019 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| EUCLIDEAN | 10.12 | 10 | 10 | 10.119 | 10 | 7.49 | 7.15 | |
| OBJECTIVE | 10 | 0 | 10 | 10 | 6.60 | 4.90 | ||
| 0.48 | 10.6 | 0.6 | 0.48 | 10.55 | 3.91 | 5.58 | ||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||
| FLUXES | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||
| 0 | 10 | 0 | 0 | 9.99 | 3.93 | 5.099 | ||
| 10 | 0 | 10 | 10 | 6.60 | 4.90 | |||
| 10 | 0 | 10 | 10 | 6.60 | 4.90 | |||
| 10 | 0 | 10 | 10 | 6.60 | 4.90 | |||
| 0.24 | 10.3 | 0.3 | 0.24 | 10.27 | 3.65 | 5.34 | ||
| 0.48 | 10.6 | 0.6 | 0.48 | 10.55 | 3.91 | 5.58 | ||
| 0.48 | 10.6 | 0.6 | 0.48 | 10.55 | 3.91 | 5.58 | ||
| 0.48 | 10.6 | 0.6 | 0.48 | 10.55 | 3.91 | 5.58 | ||
| 0.24 | 0.3 | 0.3 | 0.24 | 0.27 | 0.26 | 0.24 | ||
| 0.24 | 0.3 | 0.3 | 0.24 | 0.27 | 0.26 | 0.24 | ||
| 0.24 | 0.3 | 0.3 | 0.24 | 0.27 | 0.26 | 0.24 | ||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Encode Solution w | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Decision Variables | Objectives | ||||||||||
 |  | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 5 | 0.50 | 0 | 0.75 | 2 | 0.80 | 10 | 1.00 | 2.5 | 0.50 | 7.5 | 0.10 |
| Name | Formula | Name | Formula |
|---|---|---|---|
| v1 : | –> acetate | v10 : | PROT –> |
| v2 : | acetate –> ACCOA | v11 : | T3P <=> F6P |
| v3 : | acetate –> CIT | v12 : | F6P <=> G6P |
| v4 : | CIT –> | v13 : | G6P –> CARB |
| v5 : | ACCOA –> OAA | v14 : | CARB –> |
| v6 : | OAA <=> PEP + CO2 | v15 : | E4P + X5P –> F6P + T3P |
| v7 : | PEP <=> T3P | v16 : | –> E4P |
| v8 : | PEP –> PYR | v17 : | –> X5P |
| v9 : | PYR –> PROT | v18 : | CO2–> |
| No. | Configuration | No. | Configuration | No. | Configuration |
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Briones-Baez, M.F.; Aguilera-Vazquez, L.; Rangel-Valdez, N.; Martinez-Salazar, A.L.; Zuñiga, C. Multi-Objective Optimization of Microalgae Metabolism: An Evolutive Algorithm Based on FBA. Metabolites 2022, 12, 603. https://doi.org/10.3390/metabo12070603
Briones-Baez MF, Aguilera-Vazquez L, Rangel-Valdez N, Martinez-Salazar AL, Zuñiga C. Multi-Objective Optimization of Microalgae Metabolism: An Evolutive Algorithm Based on FBA. Metabolites. 2022; 12(7):603. https://doi.org/10.3390/metabo12070603
Chicago/Turabian StyleBriones-Baez, Monica Fabiola, Luciano Aguilera-Vazquez, Nelson Rangel-Valdez, Ana Lidia Martinez-Salazar, and Cristal Zuñiga. 2022. "Multi-Objective Optimization of Microalgae Metabolism: An Evolutive Algorithm Based on FBA" Metabolites 12, no. 7: 603. https://doi.org/10.3390/metabo12070603
APA StyleBriones-Baez, M. F., Aguilera-Vazquez, L., Rangel-Valdez, N., Martinez-Salazar, A. L., & Zuñiga, C. (2022). Multi-Objective Optimization of Microalgae Metabolism: An Evolutive Algorithm Based on FBA. Metabolites, 12(7), 603. https://doi.org/10.3390/metabo12070603








