Integrated Switched Reluctance Starter/Generator for Aerospace Applications: Particle Swarm Optimization for Constant Current and Constant Voltage Control Designs
Abstract
:1. Introduction
2. Research Significance
- Applying the PSO algorithm for fine-tuning the PID parameters of a current-controlled SRG.
- The ability of the proposed controller to generate the required turn-off or turn-on angles for constant output voltage or constant output current loads in aerospace applications.
- The proposed controller system can effectively limit the maximum value of output voltage or output current in the electric aircraft system as a safety precaution.
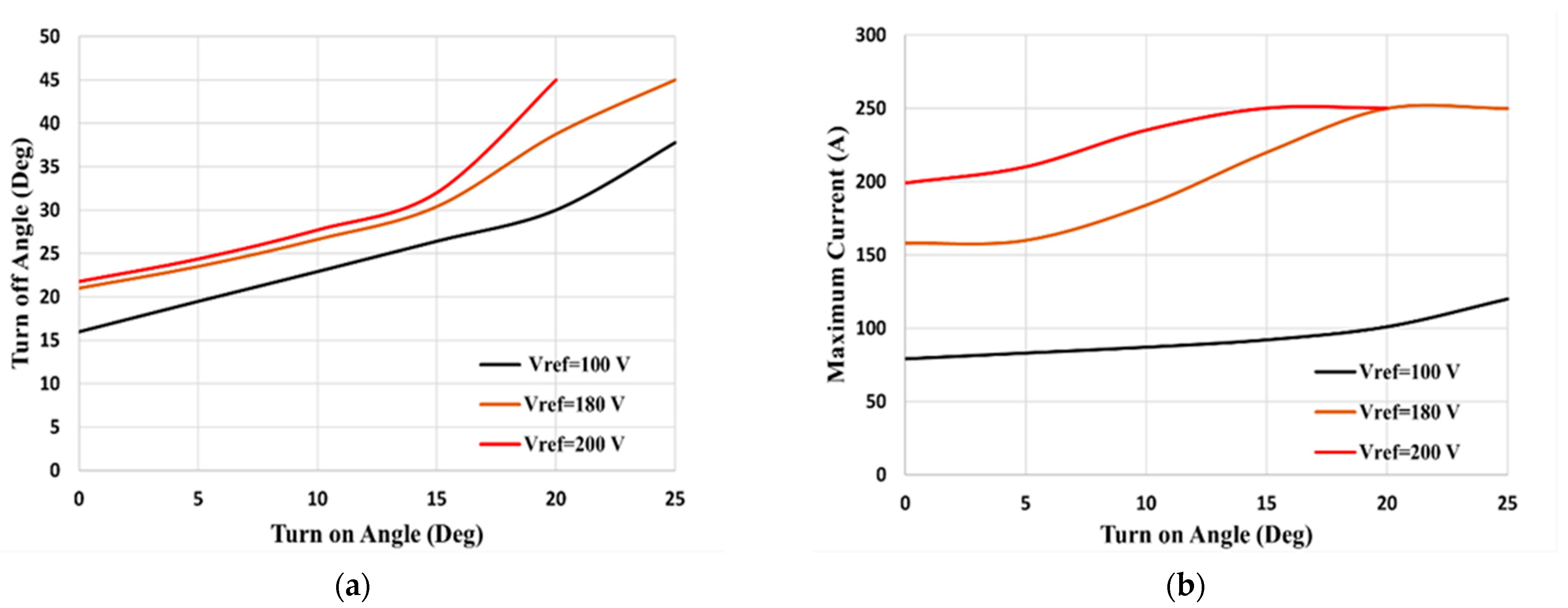
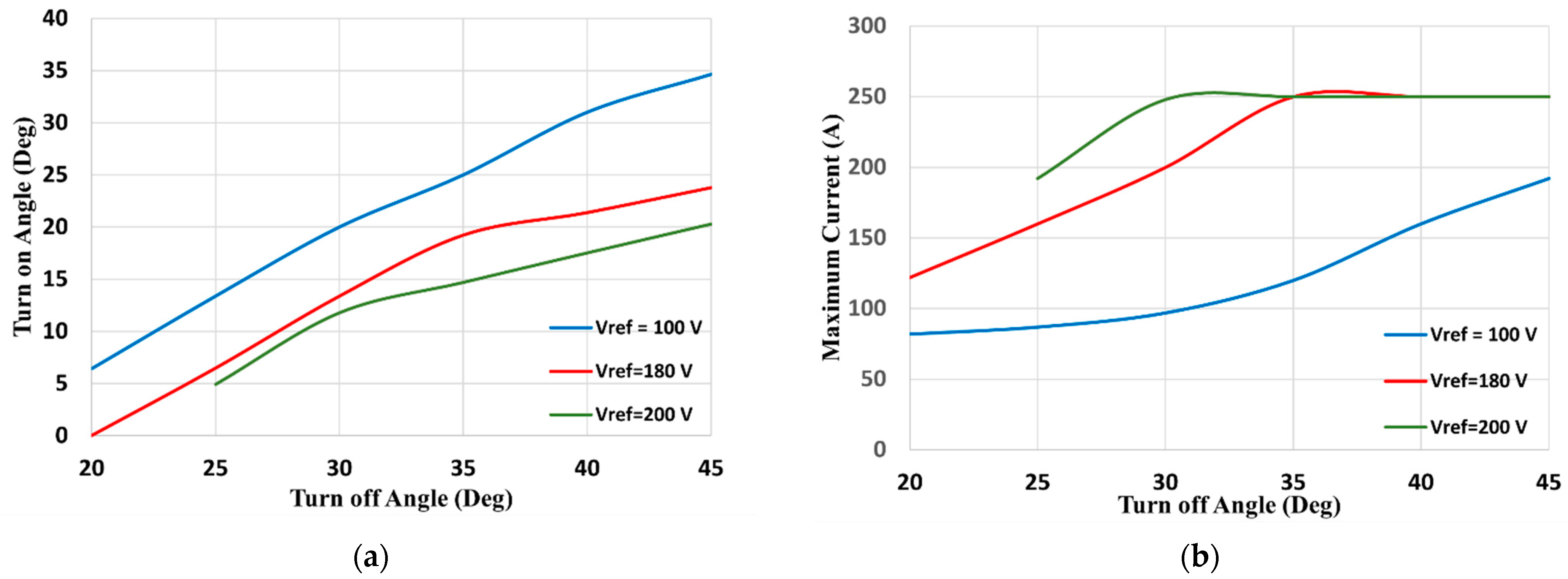
- The trade-off between the turn-on angle and turn-off angle control performance is investigated.
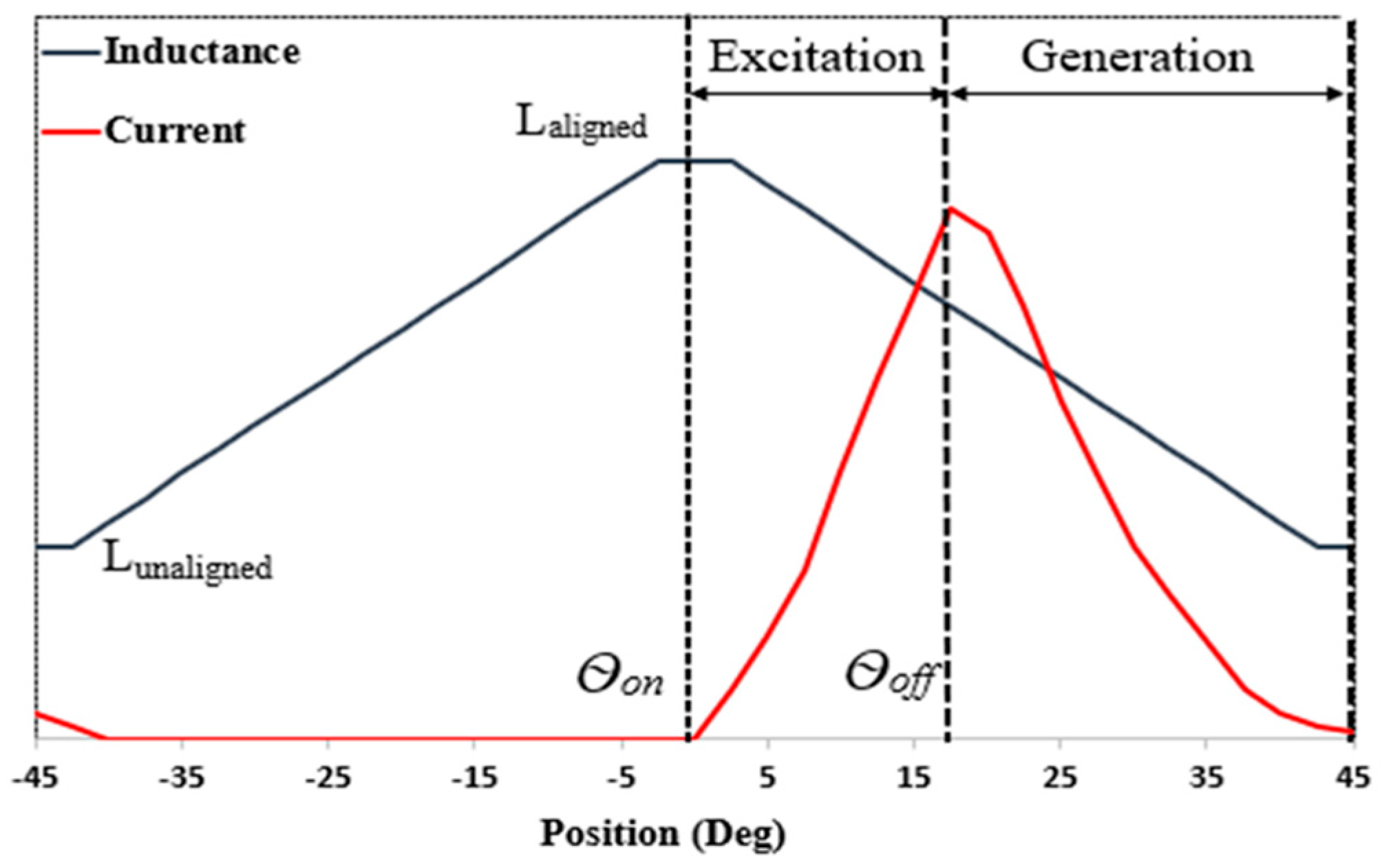
3. A 3 Phase 6/4 SRM Mathematical Model and Operation
4. Particle Swarm Optimization (PSO)
5. SRM Simulation Model
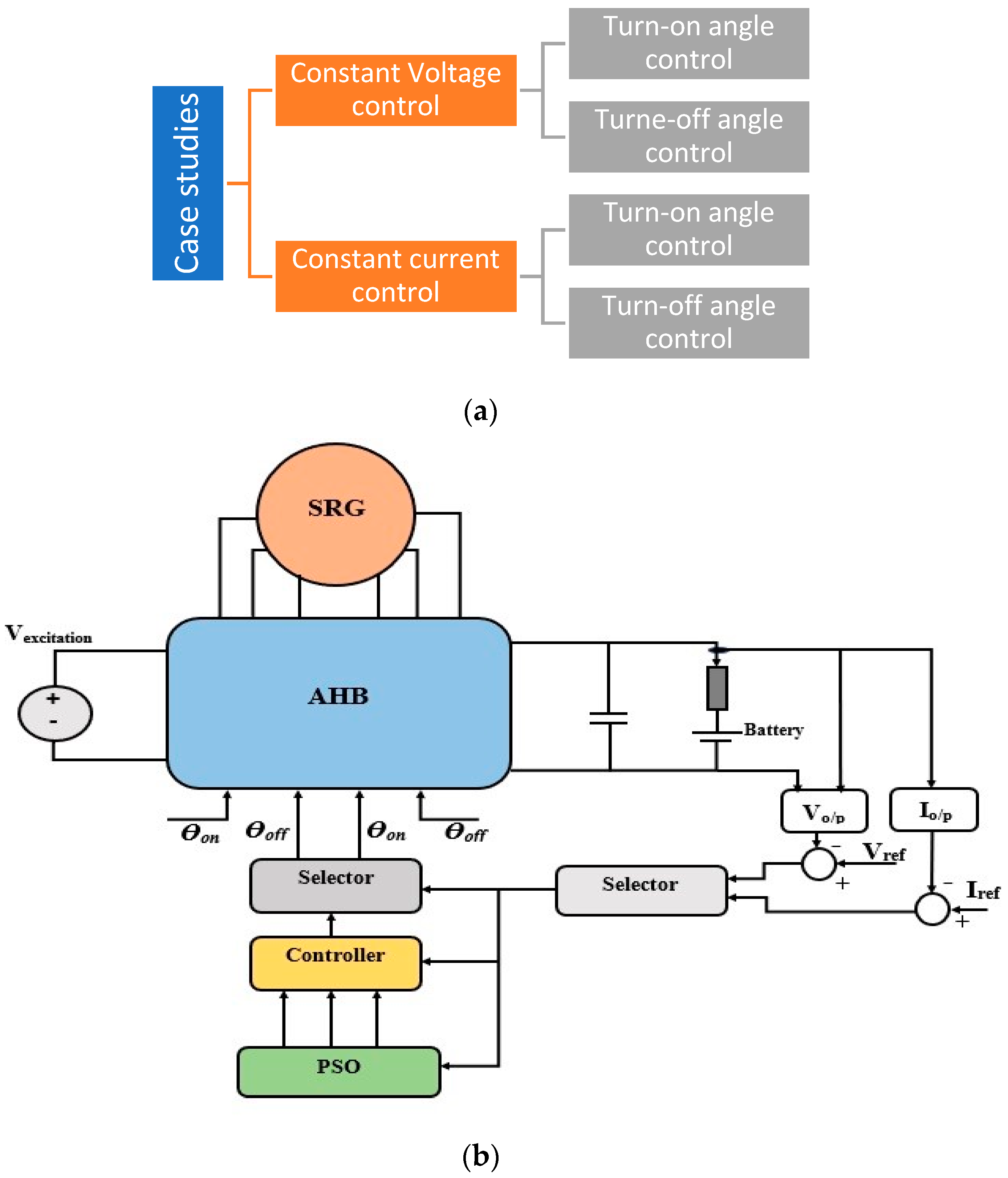
6. Methodology
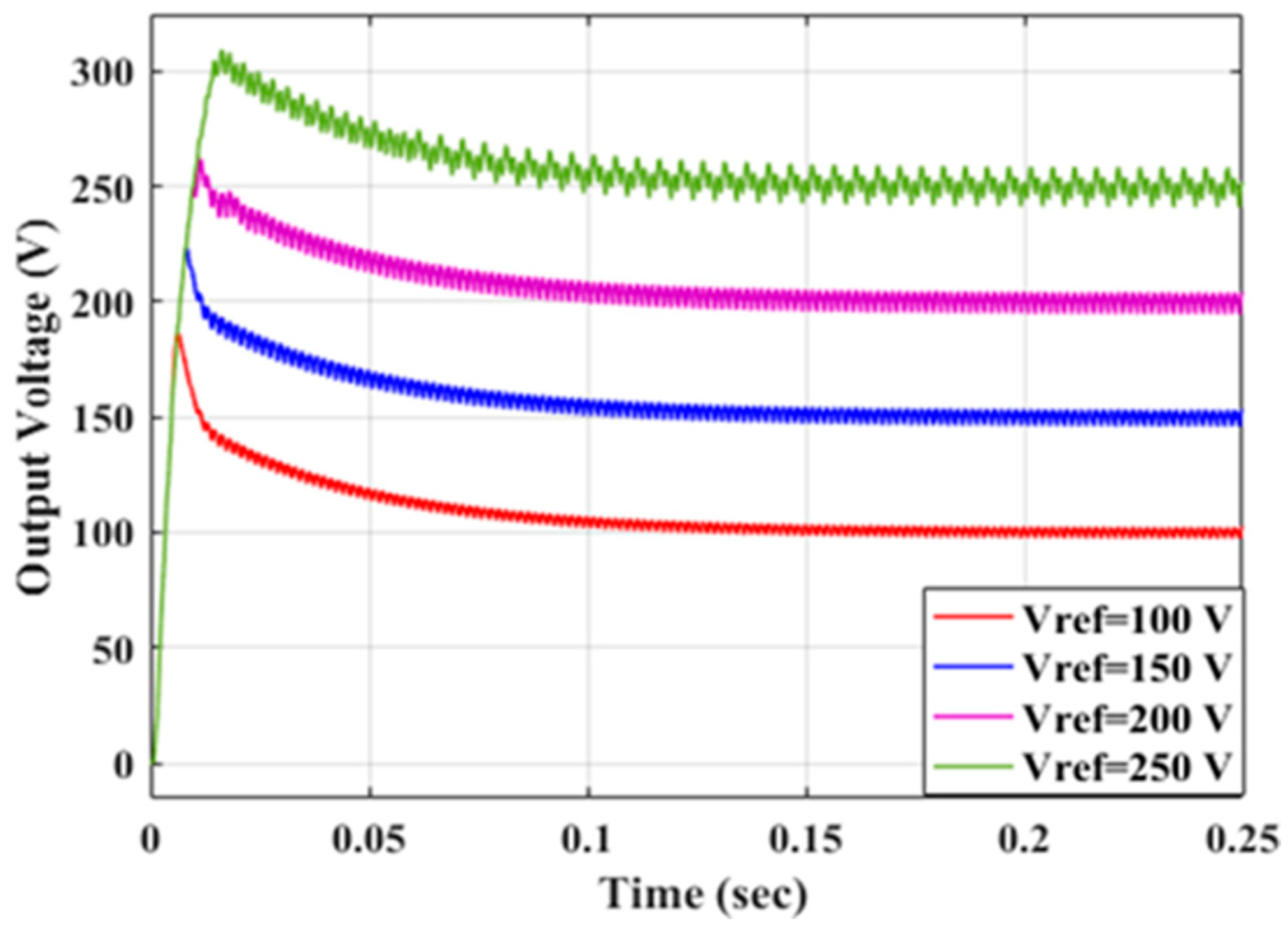
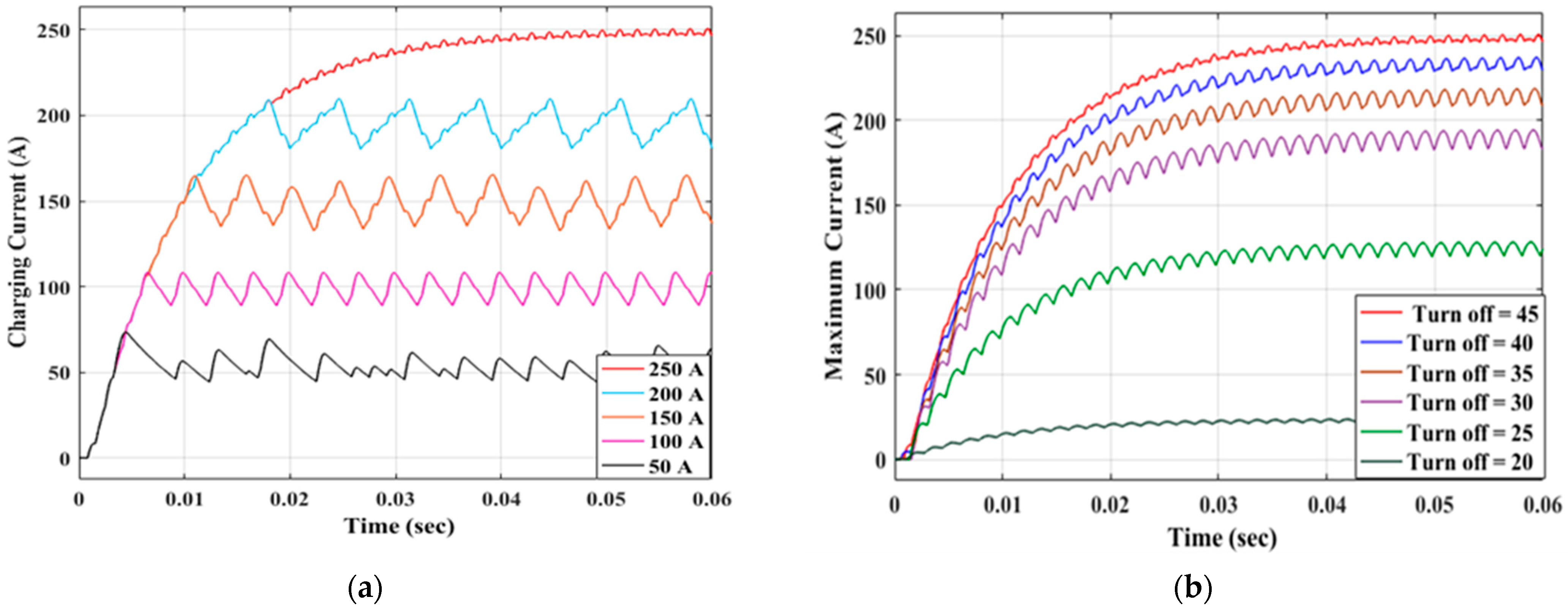
6.1. Case (1): Constant Output Voltage Control
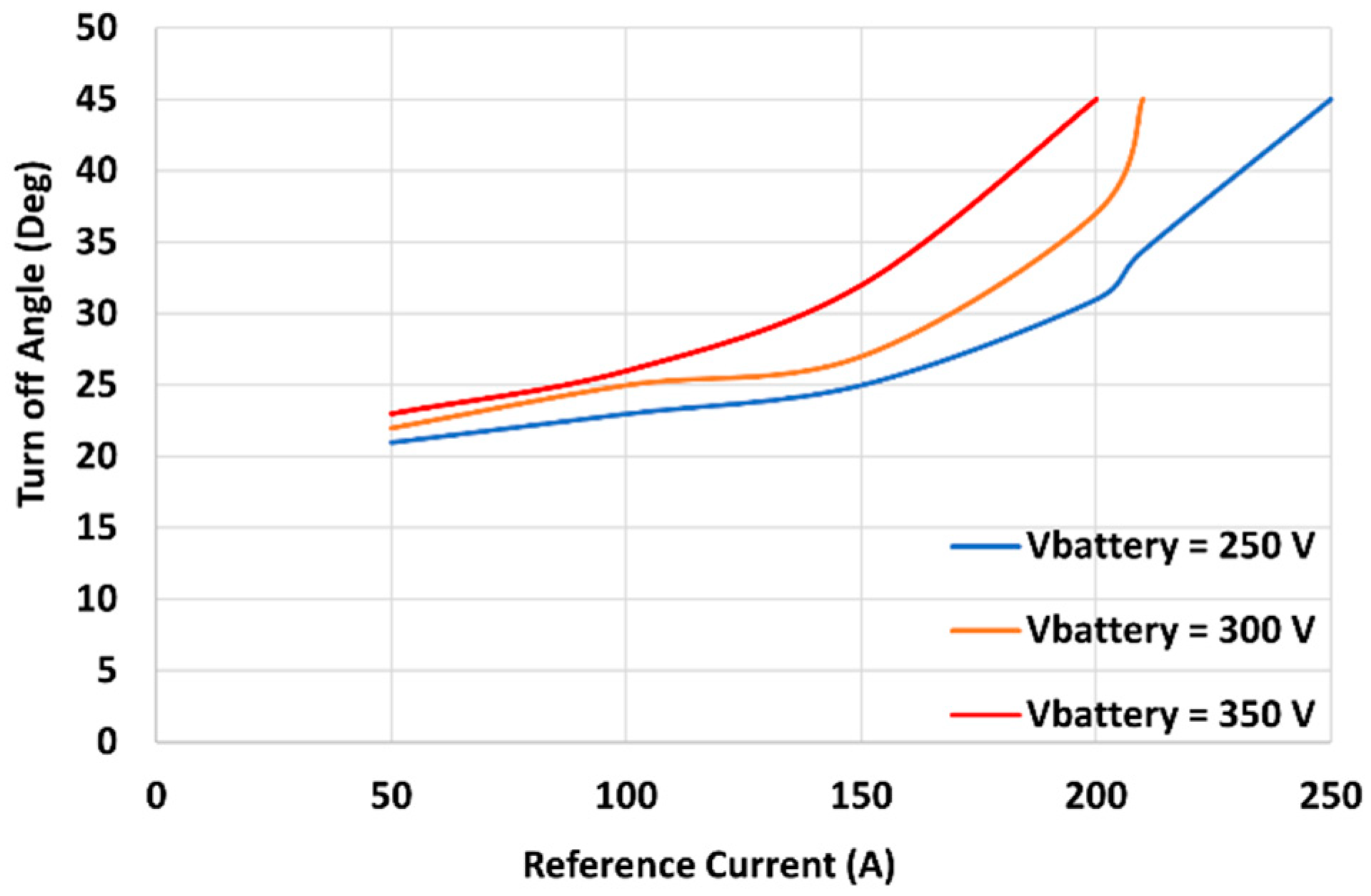
6.1.1. Turn-Off Angle Control
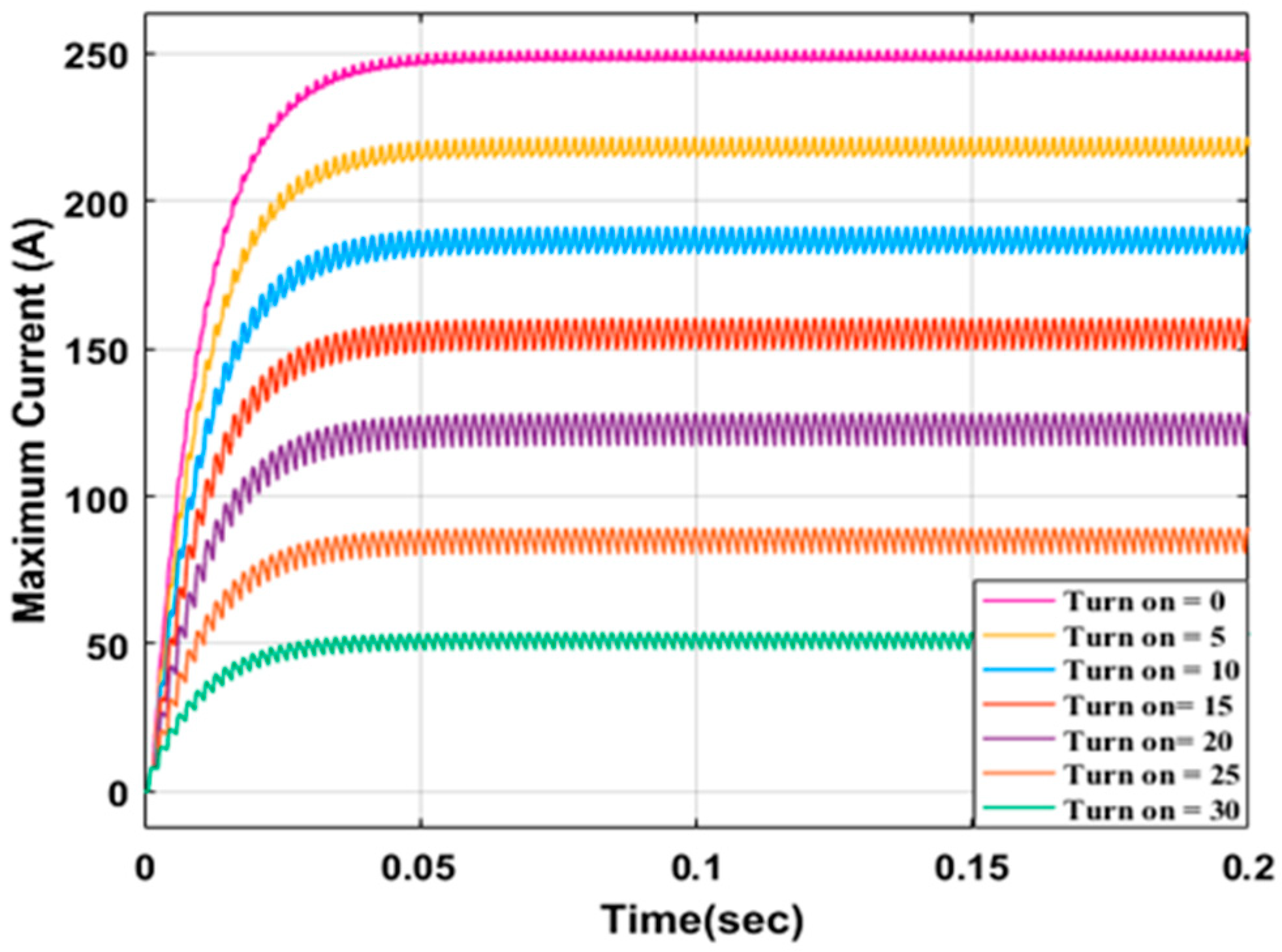
6.1.2. Turn-On Angle Control
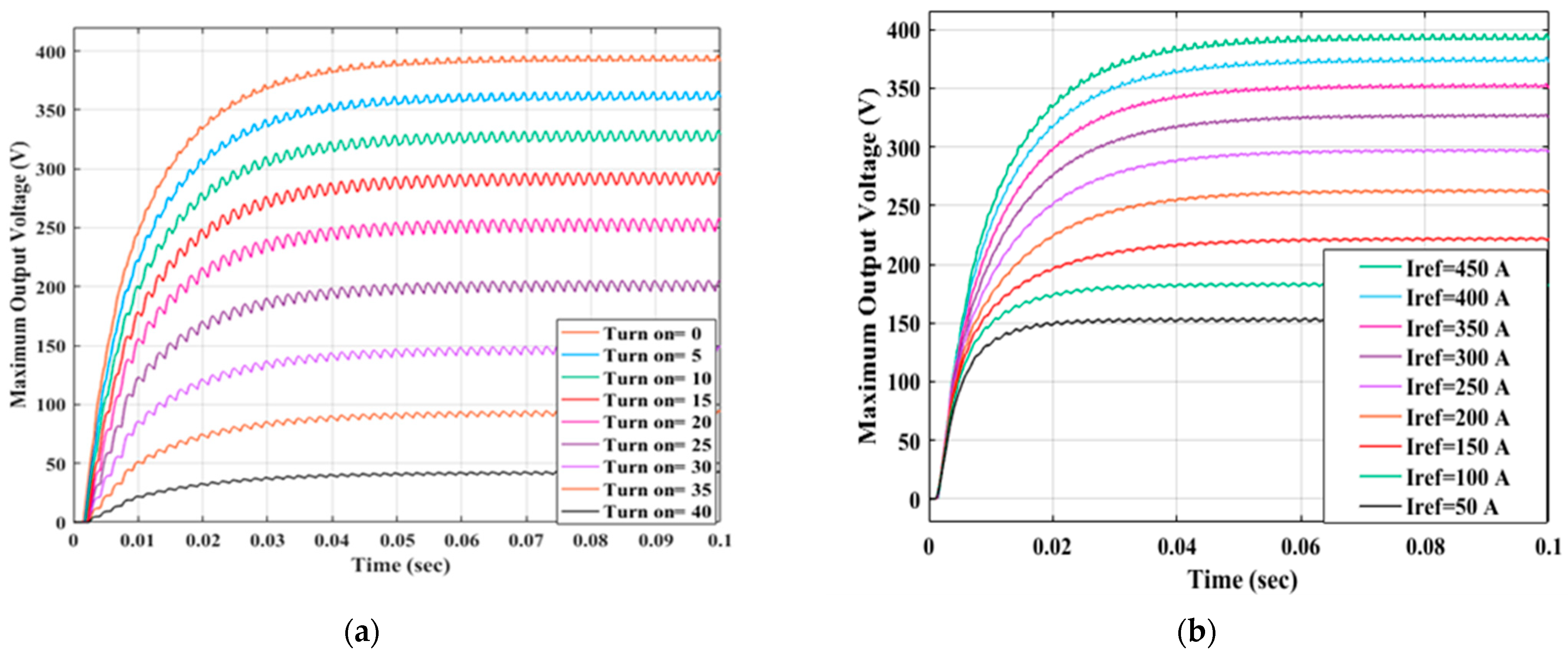
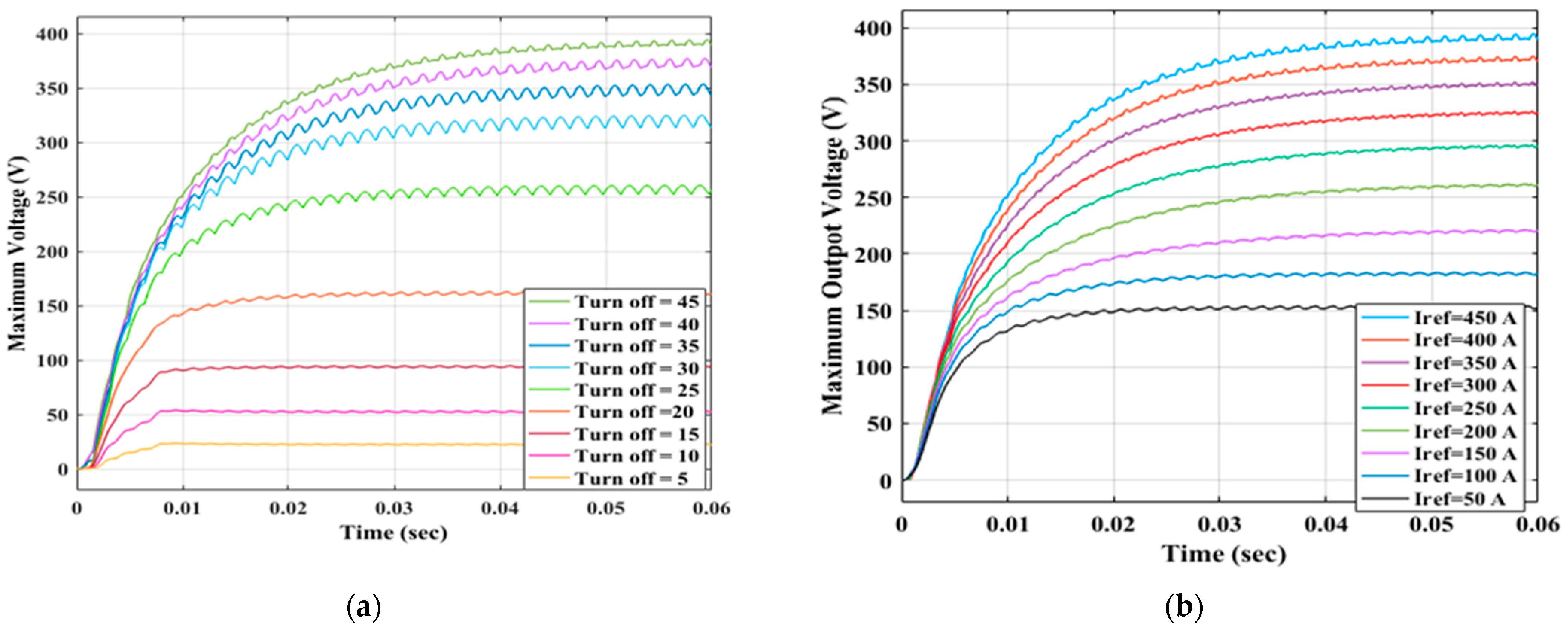
6.2. Case (2): Constant Current Control
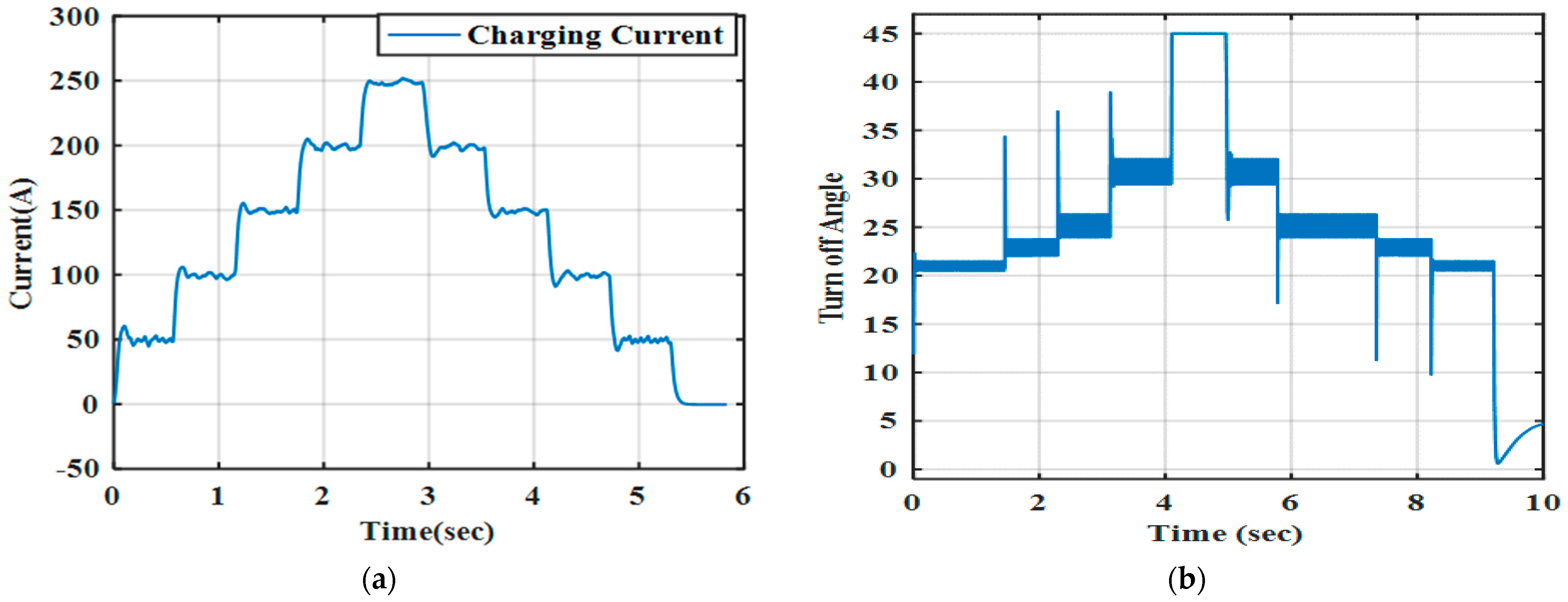
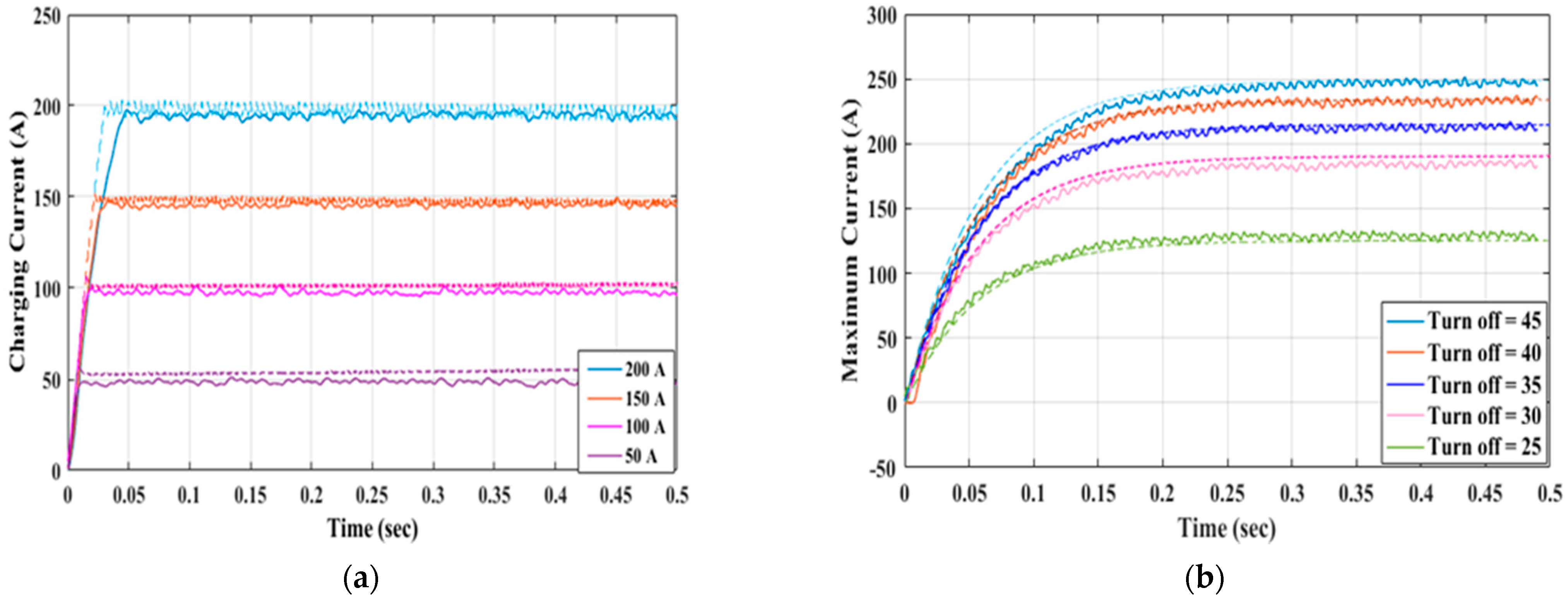
6.2.1. Turn-Off Angle Control
6.2.2. Turn-On Angle Control
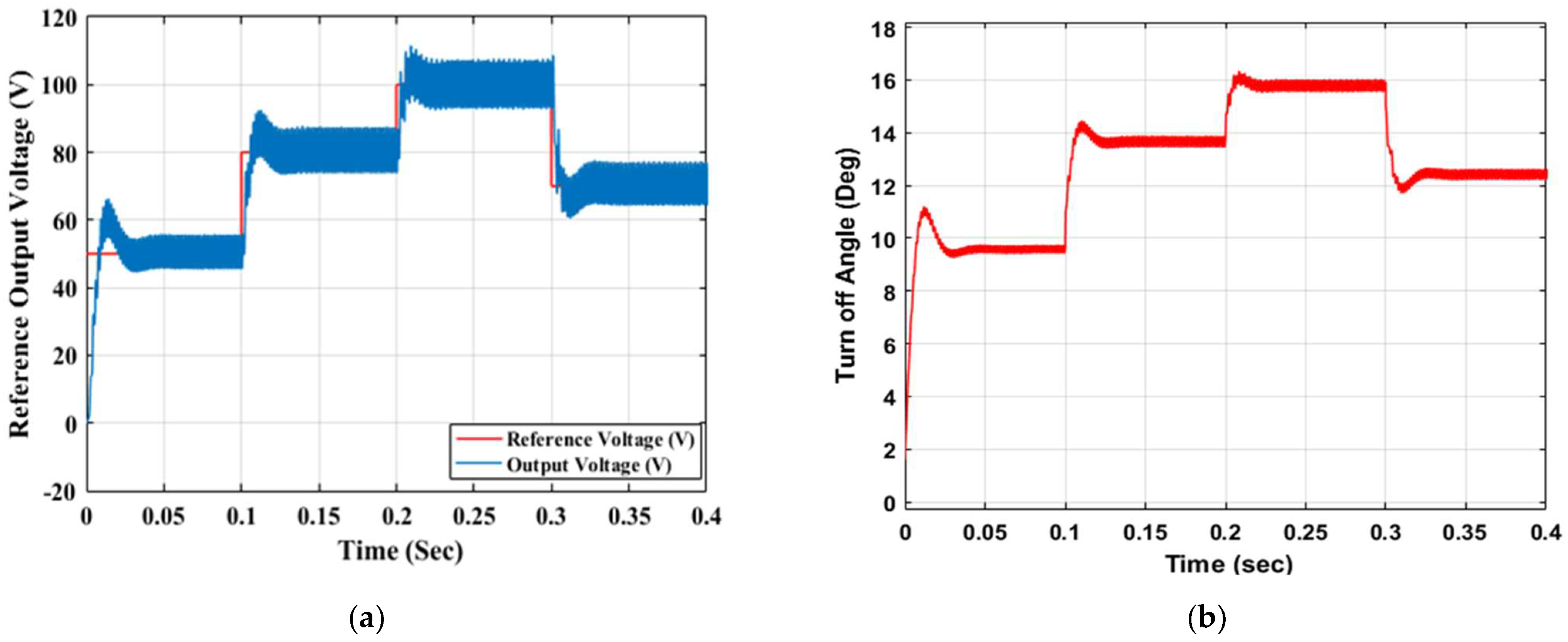
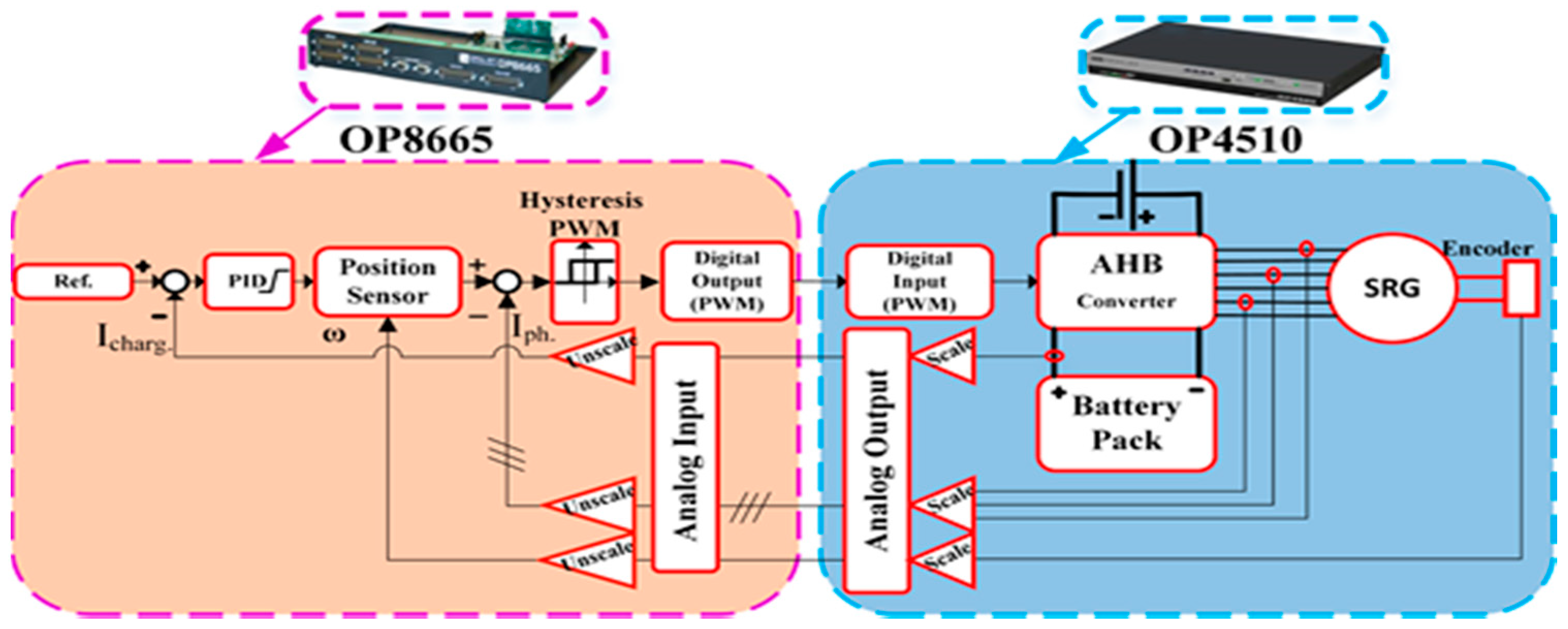
7. Experimental Validation
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartolo, J.B.; Degano, M.; Espina, J.; Gerada, C. Design and initial testing of a high-speed 45-kW switched reluctance drive for aerospace application. IEEE Trans. Ind. Electron. 2016, 64, 988–997. [Google Scholar] [CrossRef]
- Zhao, E.; Song, S.; Ma, Z.; Zhang, X.; Ning, L.; Liu, Y. Design and initial testing of an integrated switched reluctance starter/generator system for unmanned aerial vehicle. CES Trans. Electr. Mach. Syst. 2018, 2, 377–383. [Google Scholar] [CrossRef]
- Wang, Y.; Nuzzo, S.; Zhang, H.; Zhao, W.; Gerada, C.; Galea, M. Challenges and opportunities for wound field synchronous generators in future more electric aircraft. IEEE Trans. Transp. Electrif. 2020, 6, 1466–1477. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, B. Design and analysis of a five-phase fault-tolerant permanent magnet synchronous motor for aerospace starter-generator system. IEEE Access 2019, 7, 135040–135049. [Google Scholar] [CrossRef]
- Nøland, J.K.; Leandro, M.; Suul, J.A.; Molinas, M. High-power machines and starter-generator topologies for more electric aircraft: A technology outlook. IEEE Access 2020, 8, 130104–130123. [Google Scholar] [CrossRef]
- Apostolidou, N.; Papanikolaou, N. Active Power Control of Switched Reluctance Generator in More Electric Aircraft. IEEE Trans. Veh. Technol. 2021, 70, 12604–12616. [Google Scholar] [CrossRef]
- Guo, H.-J.; Yoshida, J.; Ishihara, T. A Simulation Model and New Speed Control Method of Switched Reluctance Generator for Wind-generator Systems. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Chengdu, China, 1–4 August 2021; pp. 191–194. [Google Scholar]
- Cai, S.; Wang, Y.; Chen, H.; Yuan, X.; Yu, L.; Zhang, Z.; Lee, C.H.T. Design and Analysis of a Doubly Salient Wound Field Starter Generator for Cost-Effective Automobile Application. IEEE Trans. Veh. Technol. 2022. [Google Scholar] [CrossRef]
- Raj, E.F.I.; Appadurai, M.; Rani, E.F.I.; Jenish, I. Finite-element design and analysis of switched reluctance motor for automobile applications. Multiscale Multidiscip. Modeling Exp. Des. 2022. [Google Scholar] [CrossRef]
- Zhu, Y. Modeling of SRM Drive System for EV. In The Key Technologies for Powertrain System of Intelligent Vehicles Based on Switched Reluctance Motors; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–36. [Google Scholar]
- Li, Z.; Yu, X.; Qian, Z.; Wang, X.; Xiao, Y.; Sun, H. Generation Characteristics Analysis of Deflection Type Double Stator Switched Reluctance Generator. IEEE Access 2020, 8, 196175–196186. [Google Scholar] [CrossRef]
- Makhad, M.; Zazi, K.; Zazi, M.; Loulijat, A. Adaptive super-twisting terminal sliding mode control and LVRT capability for switched reluctance generator based wind energy conversion system. Int. J. Electr. Power Energy Syst. 2022, 141, 108142. [Google Scholar] [CrossRef]
- Mapa, S.; Bhuvaneswari, G. Suitable Choice of Capacitor for a Self-excited Switched Reluctance Generator Driven by a Roof-Top Wind Turbine at Varying Wind Speeds. Trans. Indian Natl. Acad. Eng. 2022, 7, 259–267. [Google Scholar] [CrossRef]
- Touati, Z.; Pereira, M.; Araújo, R.E.; Khedher, A. Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation. Machines 2022, 10, 103. [Google Scholar] [CrossRef]
- Ahmad, S.S.; Narayanan, G. Modeling of single-pulse operated switched reluctance generator and its verification. IEEE Trans. Ind. Appl. 2020, 56, 4966–4976. [Google Scholar] [CrossRef]
- Ichinokura, O.; Kikuchi, T.; Nakamura, K.; Watanabe, T.; Guo, H.-J. Dynamic simulation model of switched reluctance generator. IEEE Trans. Magn. 2003, 39, 3253–3255. [Google Scholar] [CrossRef]
- Omaç, Z.; Cevahir, C. Control of switched reluctance generator in wind power system application for variable speeds. Ain Shams Eng. J. 2021, 12, 2665–2672. [Google Scholar] [CrossRef]
- Arifin, A.; Al-Bahadly, I.; Mukhopadhyay, S.C. State of the art of switched reluctance generator. Sci. Res. 2012, 4, 447–458. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Zhou, B.; Zhou, X.; Jiang, S.; Wei, J. The output voltage control strategy for DSEG with controlled rectification based on conduction angle estimation. IEEE Trans. Ind. Electron. 2019, 67, 3350–3360. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, H.; Zhang, J. Regenerative braking control strategy for electric vehicles based on optimization of switched reluctance generator drive system. IEEE Access 2020, 8, 76671–76682. [Google Scholar] [CrossRef]
- Catata, E.O.H.; Neto, P.J.D.S.; de Paula, M.V.; Silveira, J.P.C.; Barros, T.A.D.S.; Filho, E.R. In-Loop Adaptive Filters to Improve the Power Quality of Switched Reluctance Generator in WECS. IEEE Access 2021, 10, 2941–2951. [Google Scholar] [CrossRef]
- Rahmanian, E.; Akbari, H.; Sheisi, G.H. Maximum power point tracking in grid connected wind plant by using intelligent controller and switched reluctance generator. IEEE Trans. Sustain. Energy 2017, 8, 1313–1320. [Google Scholar] [CrossRef]
- Verma, A.; Ahmad, S.S.; Narayanan, G. Optimal Switching Angles for Single-Pulse-Operated Switched Reluctance Generator. In Proceedings of the 2021 National Power Electronics Conference (NPEC), Bhubaneswar, India, 15–17 December 2021; pp. 1–6. [Google Scholar]
- Zhi, X.; Xiangjun, D.; Lei, L. MPPT for wind power system with switched reluctance generator. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May 2018–2 June 2018; pp. 1420–1424. [Google Scholar]
- Sun, N.; Choi, D.; Li, J.; Cho, Y. The angle control of switched reluctance generator for maximum output power. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012; pp. 1–4. [Google Scholar]
- Hajiabadi, H.; Farshad, M.; Nejad, M.A.S. Maximum power extraction for switched reluctance generator wind turbine using optimal firing angles control. In Proceedings of the 2019 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Tehran, Iran, 11–12 June 2019; pp. 1–7. [Google Scholar]
- Viajante, G.P.; Sanguino, T.d.M. Design and implementation of a fuzzy control system applied to a 6 × 4 srg. IEEE Trans. Ind. Appl. 2020, 57, 528–536. [Google Scholar] [CrossRef]
- Domínguez-Navarro, J.A.; Artal-Sevil, J.; Pascual, H.; Bernal-Agustín, J.L. Fuzzy-logic strategy control for switched reluctance machine. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–5. [Google Scholar]
- Park, K.; Chen, Z. Self-tuning fuzzy logic control of a switched reluctance generator for wind energy applications. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 357–363. [Google Scholar]
- Li, J.; Li, Y.; Wang, Y. Fuzzy Inference NSGA-III Algorithm-Based Multi-Objective Optimization for Switched Reluctance Generator. IEEE Trans. Energy Convers. 2021, 36, 3578–3581. [Google Scholar] [CrossRef]
- Chen, H.; Nie, R.; Gu, J.; Yan, S.; Zhao, R. Efficiency optimization strategy for switched reluctance generator system with position sensorless control. IEEE/ASME Trans. Mechatron. 2020, 26, 469–479. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Deng, X. Control for power converter of small-scale switched reluctance wind power generator. IEEE Trans. Ind. Electron. 2020, 68, 3148–3158. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Üstün, O.; Önder, M.; Sefa, İ. Identification of mechanical parameters for the switched reluctance motor. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–7. [Google Scholar]
- Scalcon, F.P.; Vieira, R.P.; Gründling, H.A. PSO-Based Fast Mechanical Parameters Estimation of Switched Reluctance Motor Drives. J. Control. Autom. Electr. Syst. 2022, 1–8. [Google Scholar] [CrossRef]
- Mapa, S.; Gurumoorthy, B. Maximum power extraction from a switched reluctance generator based wind power generating system using optimization techniques. Eng. Rep. 2022, 4, e12457. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; el Ouanjli, N.; Quynh, N.V.; Mossa, M.A. A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor. World Electr. Veh. J. 2022, 13, 78. [Google Scholar] [CrossRef]
- Ghith, E.S.; Tolba, F.A.A. Real-Time Implementation of Tuning PID Controller Based on Whale Optimization Algorithm for Micro-robotics System. In Proceedings of the 2022 14th International Conference on Computer and Automation Engineering (ICCAE), Brisbane, Australia, 25–27 March 2022; pp. 103–109. [Google Scholar]
- Kumar, N.K.; Gopi, R.S.; Kuppusamy, R.; Nikolovski, S.; Teekaraman, Y.; Vairavasundaram, I.; Venkateswarulu, S. Fuzzy Logic-Based Load Frequency Control in an Island Hybrid Power System Model Using Artificial Bee Colony Optimization. Energies 2022, 15, 2199. [Google Scholar] [CrossRef]
- Shan, J.; Chu, S.-C.; Weng, S.-W.; Pan, J.-S.; Jiang, S.-J.; Zheng, S.-G. A parallel compact firefly algorithm for the control of variable pitch wind turbine. Eng. Appl. Artif. Intell. 2022, 111, 104787. [Google Scholar] [CrossRef]
- Yalçin, O.; Canli, A.; Yilmaz, A.R.; Erkmen, B. Robust Tuning of PID Controller Using Differential Evolution Algorithm Based on FPGA. In Proceedings of the 2022 9th International Conference on Electrical and Electronics Engineering (ICEEE), Alanya, Turkey, 29–31 March 2022; pp. 180–184. [Google Scholar]
- Sundararaju, N.; Vinayagam, A.; Veerasamy, V.; Subramaniam, G. A Chaotic Search-Based Hybrid Optimization Technique for Automatic Load Frequency Control of a Renewable Energy Integrated Power System. Sustainability 2022, 14, 5668. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Vansompel, H.; Zhang, Z.; Ibrahim, M.N.; Sergeant, P. Comparative Study of Switched Reluctance Generators with Separate Field Current and Circulating Current Excitations. IEEE Trans. Energy Convers. 2021, 37, 1124–1133. [Google Scholar] [CrossRef]
- Scalcon, F.P.; Vieira, R.P.; Gründling, H.A. PSO-Based Performance Optimization Procedure for Current-Controlled Switched Reluctance Generators in Wind Power Applications. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Araujo, W.R.H.; Reis, M.R.C.; Wainer, G.A.; Calixto, W.P. Efficiency Enhancement of Switched Reluctance Generator Employing Optimized Control Associated with Tracking Technique. Energies 2021, 14, 8388. [Google Scholar] [CrossRef]
- Maghfiroh, H.; Saputro, J.; Hermanu, C.; Ibrahim, M.; Sujono, A. Performance Evaluation of Different Objective Function in PID Tuned by PSO in DC-Motor Speed Control. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Philadelphia, PA, USA, 2021; Volume 1096, p. 012061. [Google Scholar]
- Kawata, N.; Chiba, A. Design of switched reluctance generator for competitive energy efficiency in the latest hybrid electric vehicle. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 6461–6467. [Google Scholar]
- Qi, Z.; Shi, Q.; Zhang, H. Tuning of Digital PID Controllers Using Particle Swarm Optimization Algorithm for a CAN-Based DC Motor Subject to Stochastic Delays. IEEE Trans. Ind. Electron. 2020, 67, 5637–5646. [Google Scholar] [CrossRef]
- Verma, B.; Padhy, P.K. Robust Fine Tuning of Optimal PID Controller with Guaranteed Robustness. IEEE Trans. Ind. Electron. 2020, 67, 4911–4920. [Google Scholar] [CrossRef]
- Gaing, Z.-W. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 9, 384–391. [Google Scholar] [CrossRef] [Green Version]









| Parameter | Value | Unit |
|---|---|---|
| number of phases | 3 | |
| number of stator poles | 6 | |
| number of rotor poles | 4 | |
| stator resistance | 0.05 | Ω |
| machine inertia | 0.05 | N m s2/rad |
| friction | 0.02 | N m s/rad |
| unaligned Inductance | 0.67 × 10−3 | H |
| aligned Inductance | 23.6 × 10−3 | H |
| maximum Current | 450 | A |
| maximum Flux Linkage | 0.486 | V s |
| rated Speed | 3000 | RPM |
| kp | ki | kd | |
|---|---|---|---|
| PS1 | 0.382976 | 72.97717 | 0.004077 |
| PS2 | 0.388455 | 74.30645 | 0.004164 |
| PS3 | 0.388088 | 73.30799 | 0.004163 |
| PS4 | 1.405067 | 176.1952 | 0.004016 |
| PS5 | 0.047432 | 100.0567 | 0.003584 |
| PS6 | 0.390093 | 73.22360 | 0.004168 |
| PS7 | 0.701417 | 97.90111 | 0.004426 |
| PS8 | 0.341268 | 47.79083 | 0.004200 |
| PS9 | 0.409198 | 102.9344 | 0.003757 |
| PS10 | 0.338800 | 73.25463 | 0.004200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sedky, M.M.; Abdel-Azim, W.E.; Abdel-Khalik, A.S.; Massoud, A.M. Integrated Switched Reluctance Starter/Generator for Aerospace Applications: Particle Swarm Optimization for Constant Current and Constant Voltage Control Designs. Appl. Sci. 2022, 12, 7583. https://doi.org/10.3390/app12157583
Sedky MM, Abdel-Azim WE, Abdel-Khalik AS, Massoud AM. Integrated Switched Reluctance Starter/Generator for Aerospace Applications: Particle Swarm Optimization for Constant Current and Constant Voltage Control Designs. Applied Sciences. 2022; 12(15):7583. https://doi.org/10.3390/app12157583
Chicago/Turabian StyleSedky, Mohamed M., Wessam E. Abdel-Azim, Ayman S. Abdel-Khalik, and Ahmed M. Massoud. 2022. "Integrated Switched Reluctance Starter/Generator for Aerospace Applications: Particle Swarm Optimization for Constant Current and Constant Voltage Control Designs" Applied Sciences 12, no. 15: 7583. https://doi.org/10.3390/app12157583









