Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity
Abstract
:1. Introduction
2. Materials and Methods
3. Initial and Boundary Conditions
4. Numerical Method
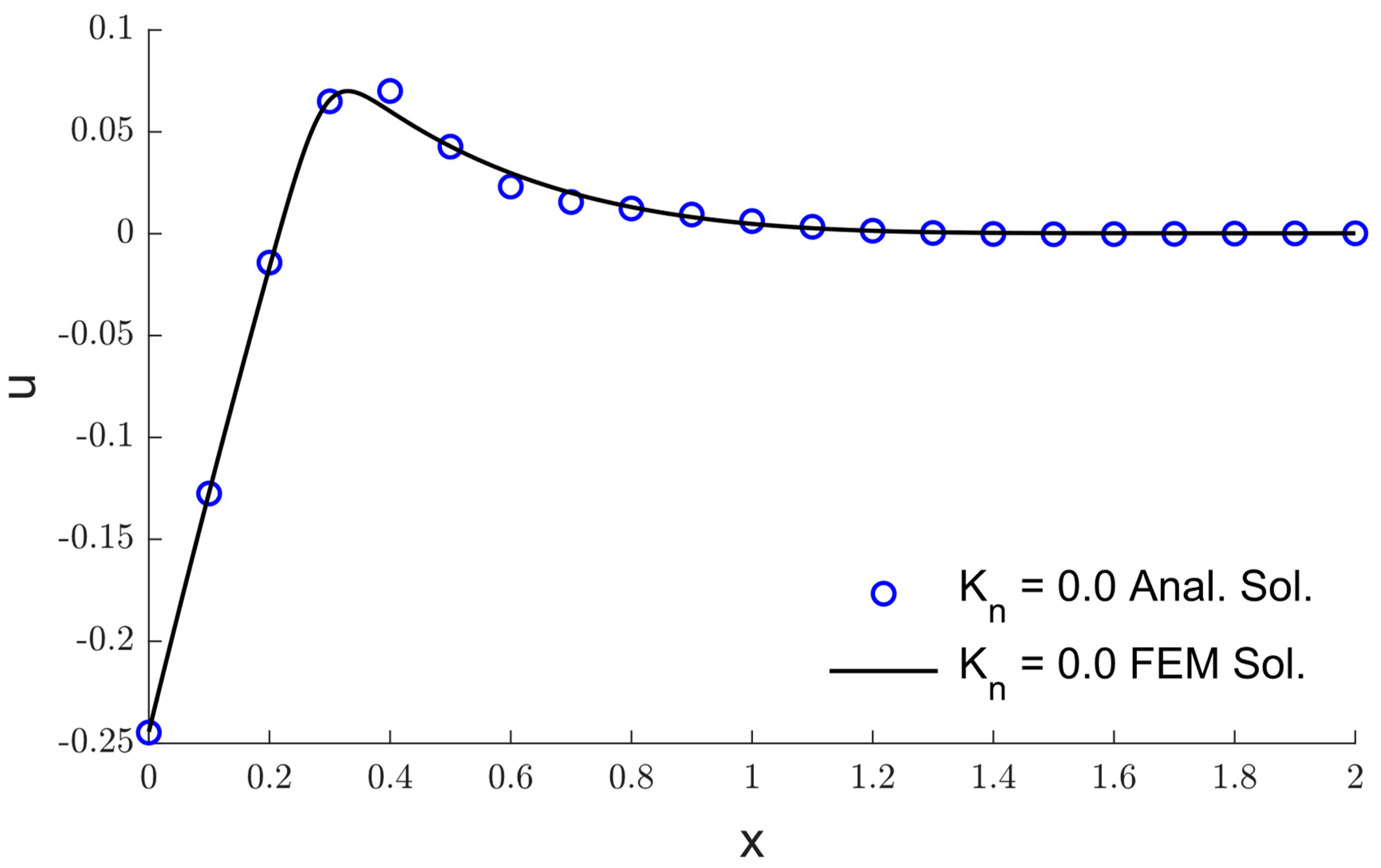
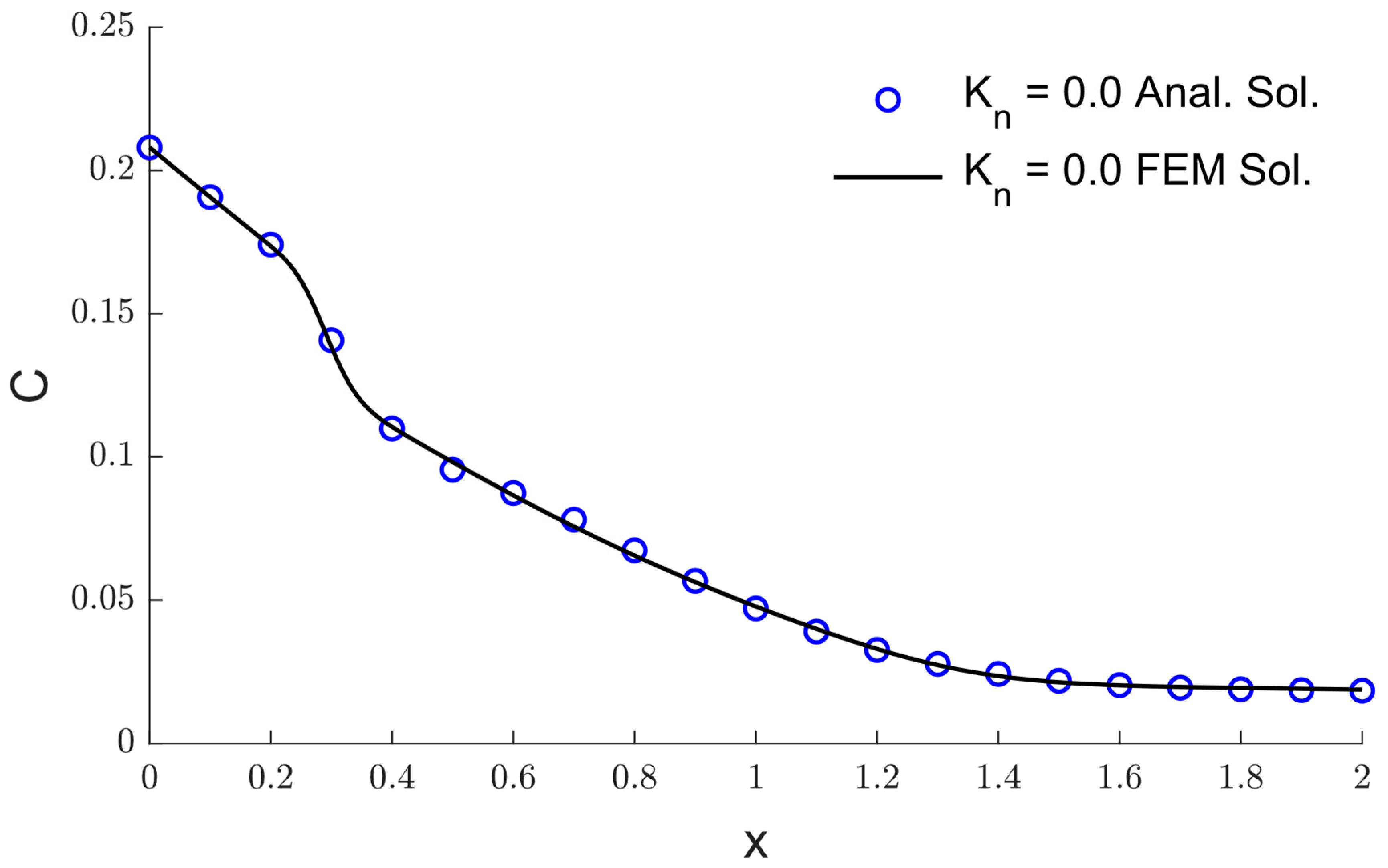
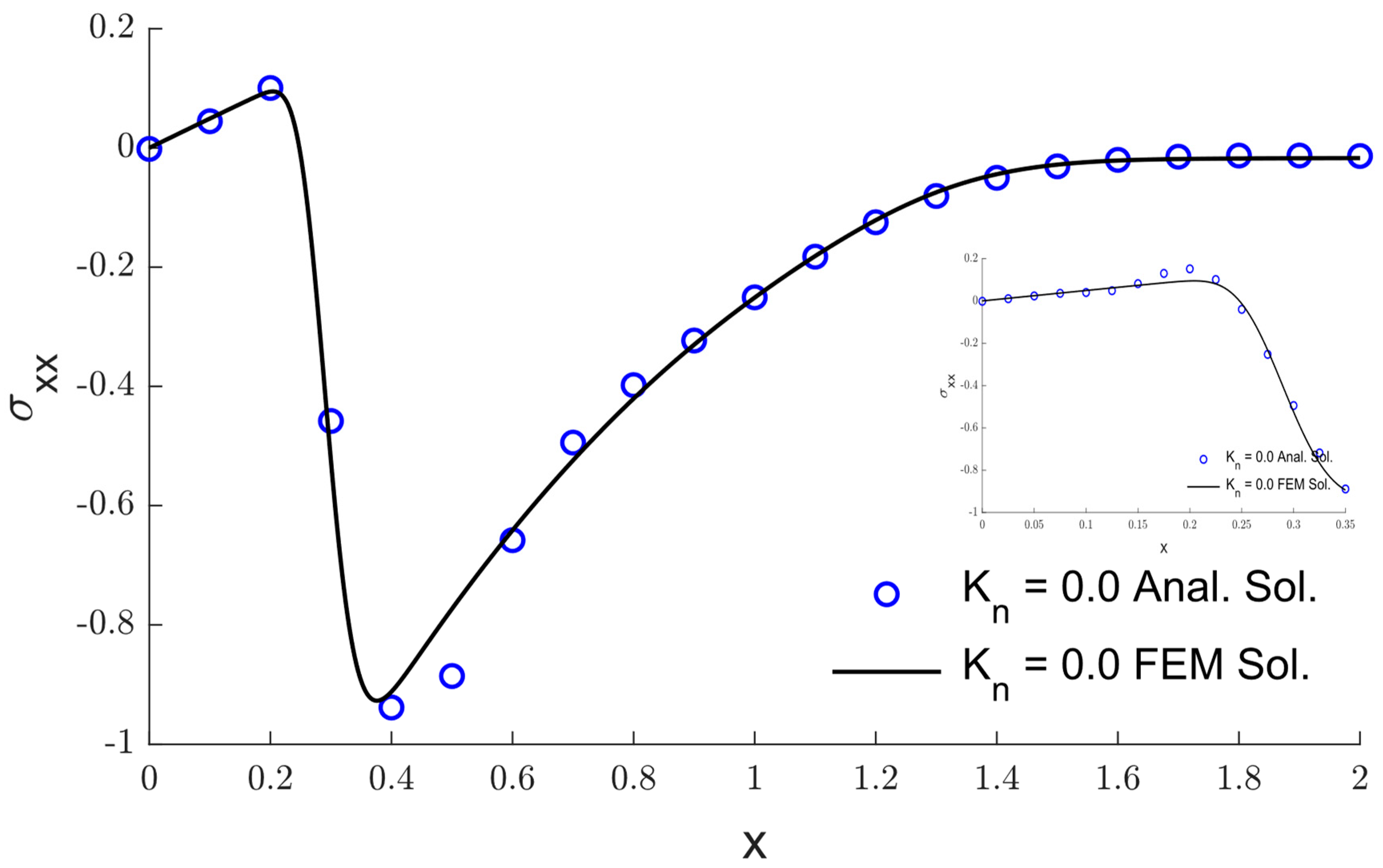
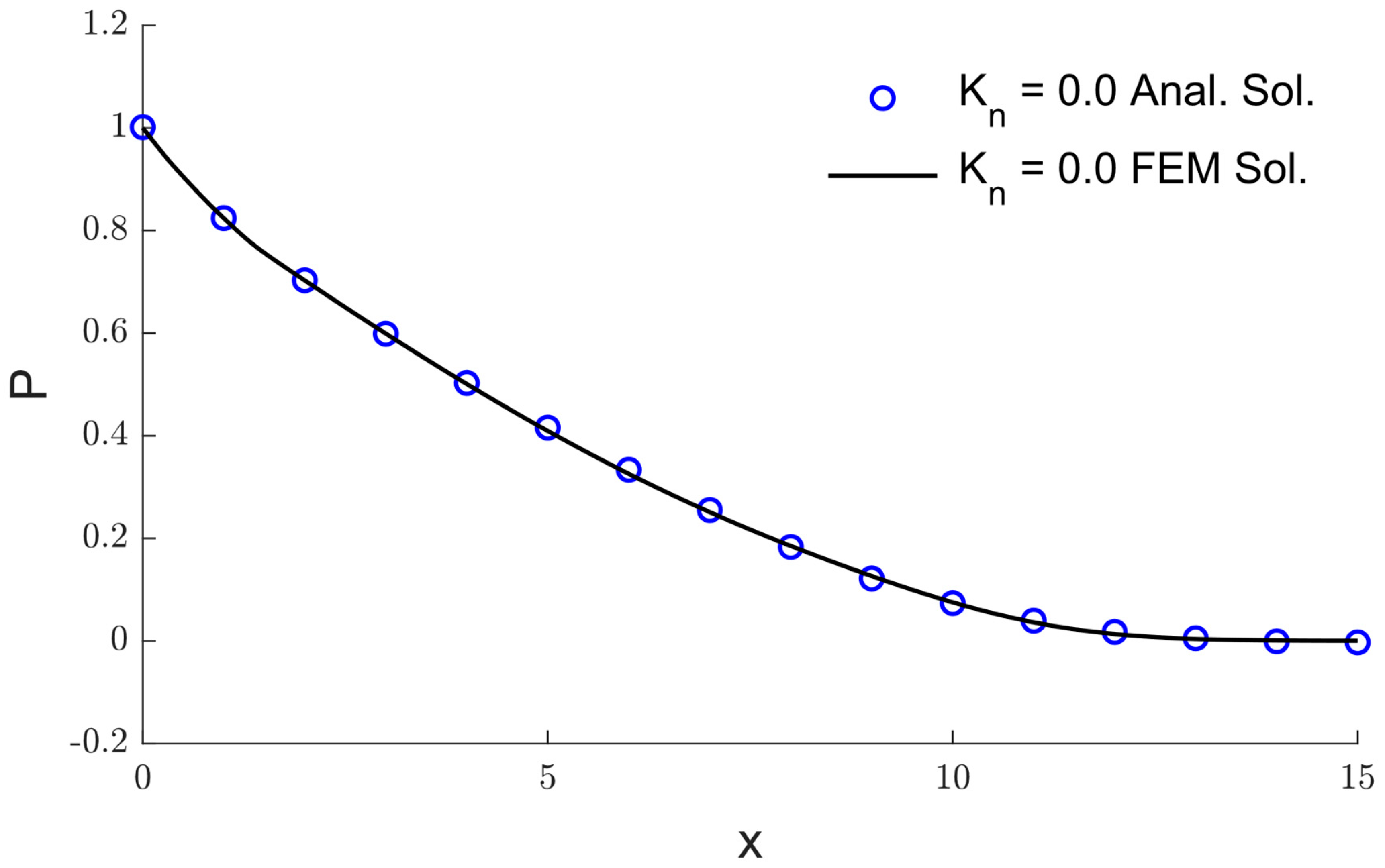
5. The Validation of the Numerical Method
6. Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Youssef, H.M.; El-Bary, A.A. Two-Temperature Generalized Thermoelasticity with Variable Thermal Conductivity. J. Therm. Stress. 2010, 33, 187–201. [Google Scholar] [CrossRef]
- Sherief, H.; Abd El-Latief, A.M. Effect of variable thermal conductivity on a half-space under the fractional order theory of thermoelasticity. Int. J. Mech. Sci. 2013, 74, 185–189. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Wang, Q.; Shu, C. Thermoelastic response of thin plate with variable material properties under transient thermal shock. Int. J. Mech. Sci. 2015, 104, 200–206. [Google Scholar] [CrossRef]
- Li, C.; Guo, H.; Tian, X.; Tian, X. Transient response for a half-space with variable thermal conductivity and diffusivity under thermal and chemical shock. J. Therm. Stress. 2017, 40, 389–401. [Google Scholar] [CrossRef]
- Godfrey, D. A critical review of engineering ceramics relevant to their use in severe thermal environments. In Proceedings of the Conference on Non-Metallic Materials for the Royal Navy, Manadon, Plymouth, UK; 1975. [Google Scholar]
- Hamad, M.A.A.; Uddin, M.J.; Ismail, A.I.M. Investigation of combined heat and mass transfer by Lie group analysis with variable diffusivity taking into account hydrodynamic slip and thermal convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1355–1362. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Nowacki, W. Dynamic problems of diffusion in solids. Eng. Fract. Mech. 1976, 8, 261–266. [Google Scholar] [CrossRef]
- Nowacki, W. Thermodiffusion in Solids. Mech. Teor. I Stosow 1975, 13, 143–158. [Google Scholar]
- Nowacki, W. Dynamical problem of thermodiffusion in solids—1. Bull. Acad. Pol. Sci. Ser. Sci. Technol. 1974, 22, 55–64. [Google Scholar]
- Sherief, H.H.; Hamza, F.A.; Saleh, H.A. The theory of generalized thermoelastic diffusion. Int. J. Eng. Sci. 2004, 42, 591–608. [Google Scholar] [CrossRef]
- Burchuladze, T. Non-stationary problems of generalized elastothermodiffusion for inhomogeneous media. Georgian Math. J. 1994, 1, 587–598. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, N.; Lata, P. Effects of thermal and diffusion phase-lags in a plate with axisymmetric heat supply. Multidiscip. Model. Mater. Struct. 2016, 12, 275–290. [Google Scholar] [CrossRef]
- Sharma, J.N.; Kumari, N.; Sharma, K.K. Diffusion in a generalized thermoelastic solid in an infinite body with a cylindrical cavity. J. Appl. Mech. Technol. Phys. 2013, 54, 819–831. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical Solutions of a Two-Dimensional Generalized Thermoelastic Diffusions Problem Due to Laser Pulse. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 57–71. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Eraki, E.E.M. Generalized magneto-thermoelastic half-space with diffusion under initial stress using three-phase-lag model. Mech. Based Des. Struct. Mach. 2017, 45, 145–159. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Elhagary, M.A.; Soleiman, A.; Khalil, K.M. Generalized thermoelastic-diffusion model with higher-order fractional time-derivatives and four-phase-lags. Mech. Based Des. Struct. Mach. 2022, 50, 897–914. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R.; Chawla, V. Response of thermal source in a transversely isotropic thermoelastic half-space with mass diffusion by using a finite element method. Chin. Phys. 2012, 21, 084601. [Google Scholar] [CrossRef]
- Lotfy, K. Effect of Variable Thermal Conductivity during the Photothermal Diffusion Process of Semiconductor Medium. Silicon 2019, 11, 1863–1873. [Google Scholar] [CrossRef]
- Molla, M.A.K.; Mallik, S.H. Variational principle, uniqueness and reciprocity theorems for higher order time-fractional four-phase-lag generalized thermoelastic diffusion model. Mech. Based Des. Struct. Mach. 2021, 1–16. [Google Scholar] [CrossRef]
- Abbas, I.A.; Singh, B. Finite Element Analysis in a Rotating Thermoelastic Half-Space with Diffusion. J. Comput. Theor. Nanosci. 2014, 11, 2276–2282. [Google Scholar] [CrossRef]
- Bajpai, A.; Sharma, P.K.; Kumar, R. Transient response of a thermo-diffusive elastic thick circular plate with variable conductivity and diffusivity. Acta Mech. 2021, 232, 3343–3361. [Google Scholar] [CrossRef]
- Deswal, S.; Jangra, A.; Punia, B.S. Reflection of plane waves at the free surface of a magneto-thermoelastic medium with variable thermal conductivity and variable mass diffusivity. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Sharma, P.K.; Bajpai, A.; Kumar, R. Analysis of two temperature thermoelastic diffusion plate with variable thermal conductivity and diffusivity. Waves Random Complex Media 2021, 1–19. [Google Scholar] [CrossRef]
- Xue, Z.N.; Yu, Y.J.; Li, X.Y.; Tian, X.G. Study of a generalized thermoelastic diffusion bi-layered structures with variable thermal conductivity and mass diffusivity. Waves Random Complex Media 2019, 29, 34–53. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I.A. Analytical solutions of photo-thermo-elastic waves in a non-homogenous semiconducting material. Results Phys. 2018, 10, 385–390. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time Depend. Mater. 2016, 21, 61–72. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. 2D deformation in initially stressed thermoelastic half-space with voids. Steel Compos. Struct. 2016, 20, 1103–1117. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Nonlinear Transient Thermal Stress Analysis of Temperature-Dependent Hollow Cylinders Using a Finite Element Model. Int. J. Struct. Stab. Dyn. 2014, 14, 1450025. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M.L. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 2019, 31, 715–724. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.; Marin, M. A GL Model on Thermo-Elastic Interaction in a Poroelastic Material Using Finite Element Method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. AIP Adv. 2015, 5, 037113. [Google Scholar] [CrossRef] [Green Version]
- Marin, M. An evolutionary equation in thermoelasticity of dipolar bodies. J. Math. Phys. 1999, 40, 1391–1399. [Google Scholar] [CrossRef]
- Lata, P.; Singh, S. Stoneley wave propagation in nonlocal isotropic magneto-thermoelastic solid with multi-dual-phase lag heat transfer. Steel Compos. Struct. 2021, 38, 141–150. [Google Scholar] [CrossRef]
- Kaur, H.; Lata, P. Effect of thermal conductivity on isotropic modified couple stress thermoelastic medium with two temperatures. Steel Compos. Struct. 2020, 34, 309–319. [Google Scholar] [CrossRef]
- Lata, P.; Kumar, R.; Sharma, N. Plane waves in an anisotropic thermoelastic. Steel Compos. Struct. 2016, 22, 567–587. [Google Scholar] [CrossRef]
- Lataa, P.; Kaur, I. Effect of time harmonic sources on transversely isotropic thermoelastic thin circular plate. Geomach. Eng. 2019, 19, 29–36. [Google Scholar] [CrossRef]
- Marin, M.; Baleanu, D.; Vlase, S. Effect of microtemperatures for micropolar thermoelastic bodies. Struct. Eng. Mech. 2017, 61, 381–387. [Google Scholar] [CrossRef]
- Abbas, I.A.; Alzahrani, F.S.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2018, 29, 328–343. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Li, C.; Guo, H.; Tian, X. Time-domain finite element analysis to nonlinear transient responses of generalized diffusion-thermoelasticity with variable thermal conductivity and diffusivity. Int. J. Mech. Sci. 2017, 131–132, 234–244. [Google Scholar] [CrossRef]
- Abbas, I.A. A two-dimensional problem for a fibre-reinforced anisotropic thermoelastic half-space with energy dissipation. Sadhana 2011, 36, 411–423. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abbas, I.A. LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Appl. Math. Model. 2011, 35, 3759–3768. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Lahiri, A.; Das, B.; Sarkar, S. Eigenvalue approach to thermoelastic interactions in an unbounded body with a spherical cavity. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010; pp. 1881–1886. [Google Scholar]
- Abbas, I.A.; Abdalla, A.-E.-N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stress. 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
- Abbas, I.A. Analytical Solution for a Free Vibration of a Thermoelastic Hollow Sphere. Mech. Based Des. Struct. Mach. 2014, 43, 265–276. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Sherief, H.H.; Saleh, H.A. A half-space problem in the theory of generalized thermoelastic diffusion. Int. J. Solids Struct. 2005, 42, 4484–4493. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Abbas, I. Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity. Mathematics 2022, 10, 2773. https://doi.org/10.3390/math10152773
Hobiny A, Abbas I. Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity. Mathematics. 2022; 10(15):2773. https://doi.org/10.3390/math10152773
Chicago/Turabian StyleHobiny, Aatef, and Ibrahim Abbas. 2022. "Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity" Mathematics 10, no. 15: 2773. https://doi.org/10.3390/math10152773
APA StyleHobiny, A., & Abbas, I. (2022). Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity. Mathematics, 10(15), 2773. https://doi.org/10.3390/math10152773





