What Drives Petrol Price Dispersion across Australian Cities?
Abstract
:1. Introduction
- What determines the price variation between cities in WA?
- What is the correlation between petrol prices and city-specific characteristics?
- Which factors result in cross-sectional price variations?
2. Background and Literature
3. Empirical Framework
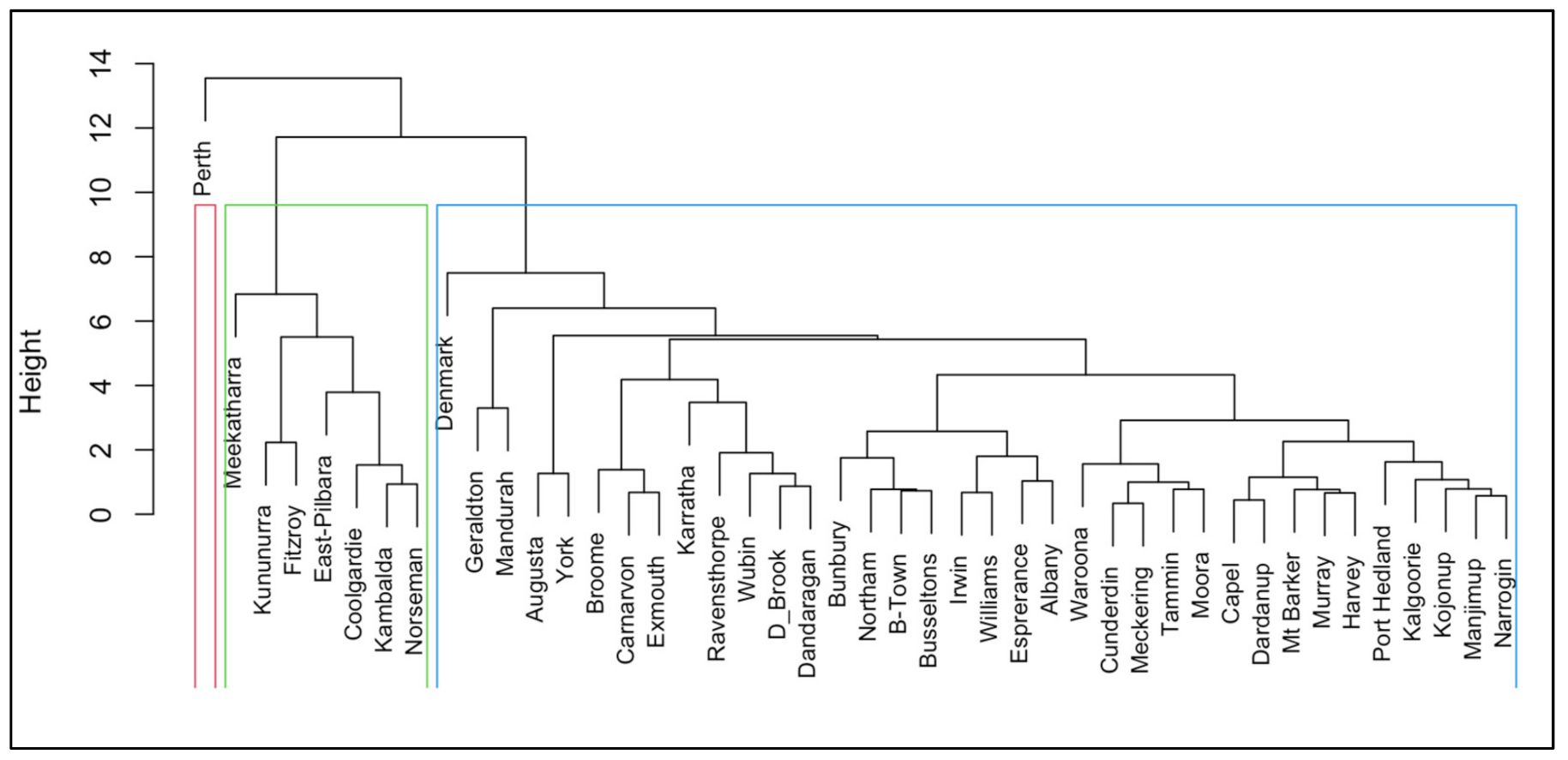
3.1. Cluster Analysis
3.1.1. K-Means Clustering Method
3.1.2. Hierarchical Clustering Method
- Find the smallest element dij remaining in D. The distance between clusters i and j are represented as dij (let cluster i contain ni objects).
- Merge clusters i and j into a single new cluster.
- Compute a new set of distances dkm using the distance equation as follows:
- 4.
- Steps one to three are repeated (N − 1 iterations) until D includes only one cluster that contains all objects.
3.2. ANOVA Test
- Data for all groups are sorted in ascending order.
- Ranks are allocated to the sorted data points.
- The statistic H is estimated as
- 4.
- The critical chi-square value for the (k − 1)th degree of freedom is calculated, where k is the number of groups.
- 5.
- Finally, the decision on whether to reject the null hypothesis is made by comparing the value of H with the critical chi-square value. The null hypothesis is rejected if the H statistic is bigger than the critical chi-square value. The null hypothesis is that the medians are equal. Otherwise, the null hypothesis is not rejected if the H statistic is not bigger than the critical chi-square value [40].
3.3. Regression Analysis
3.4. Determinants of Petrol Prices
3.4.1. Supply-Side Factors
3.4.2. Competition
3.4.3. Demand-Side Factors
3.4.4. City-Specific Characteristics
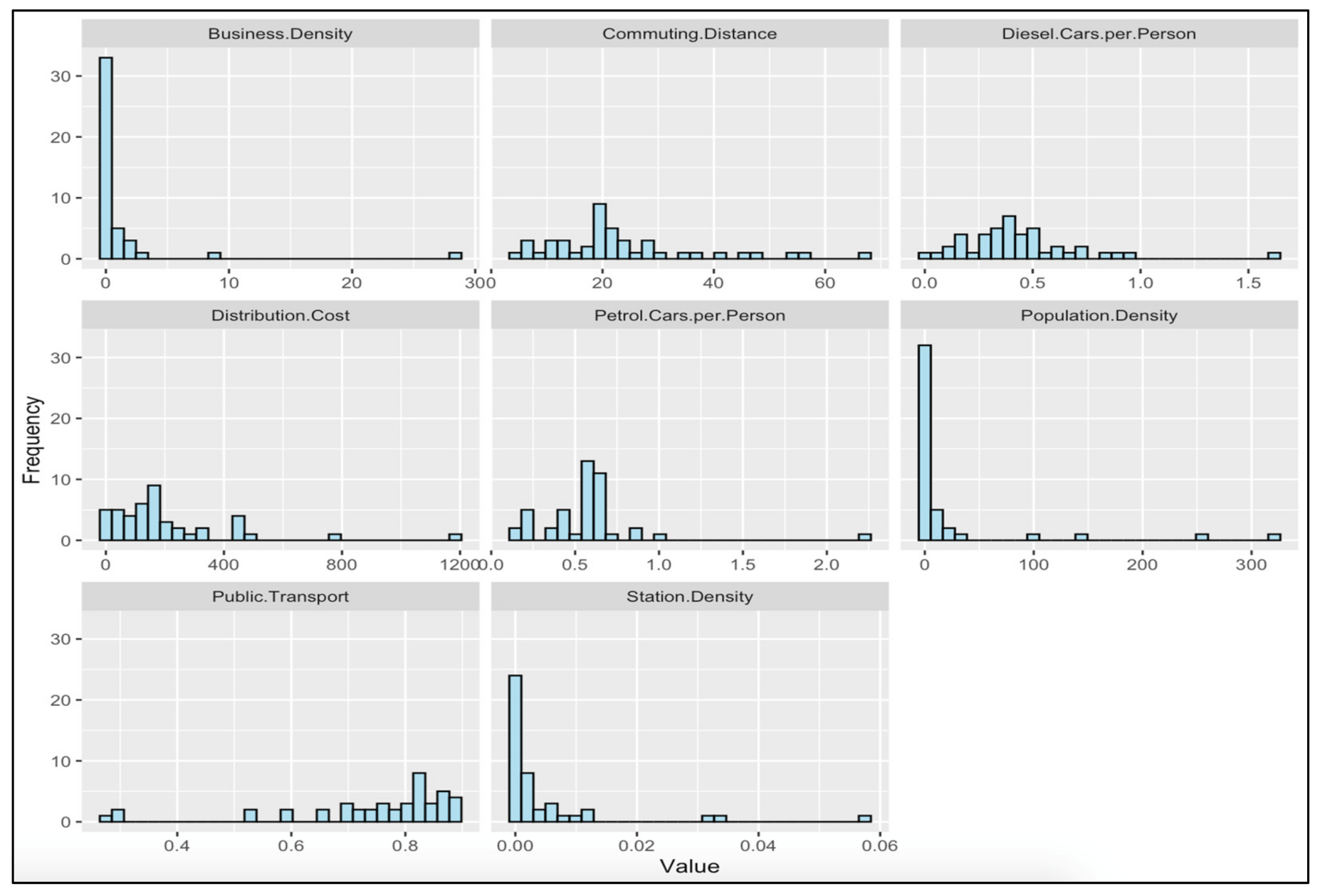
4. Data
5. Results
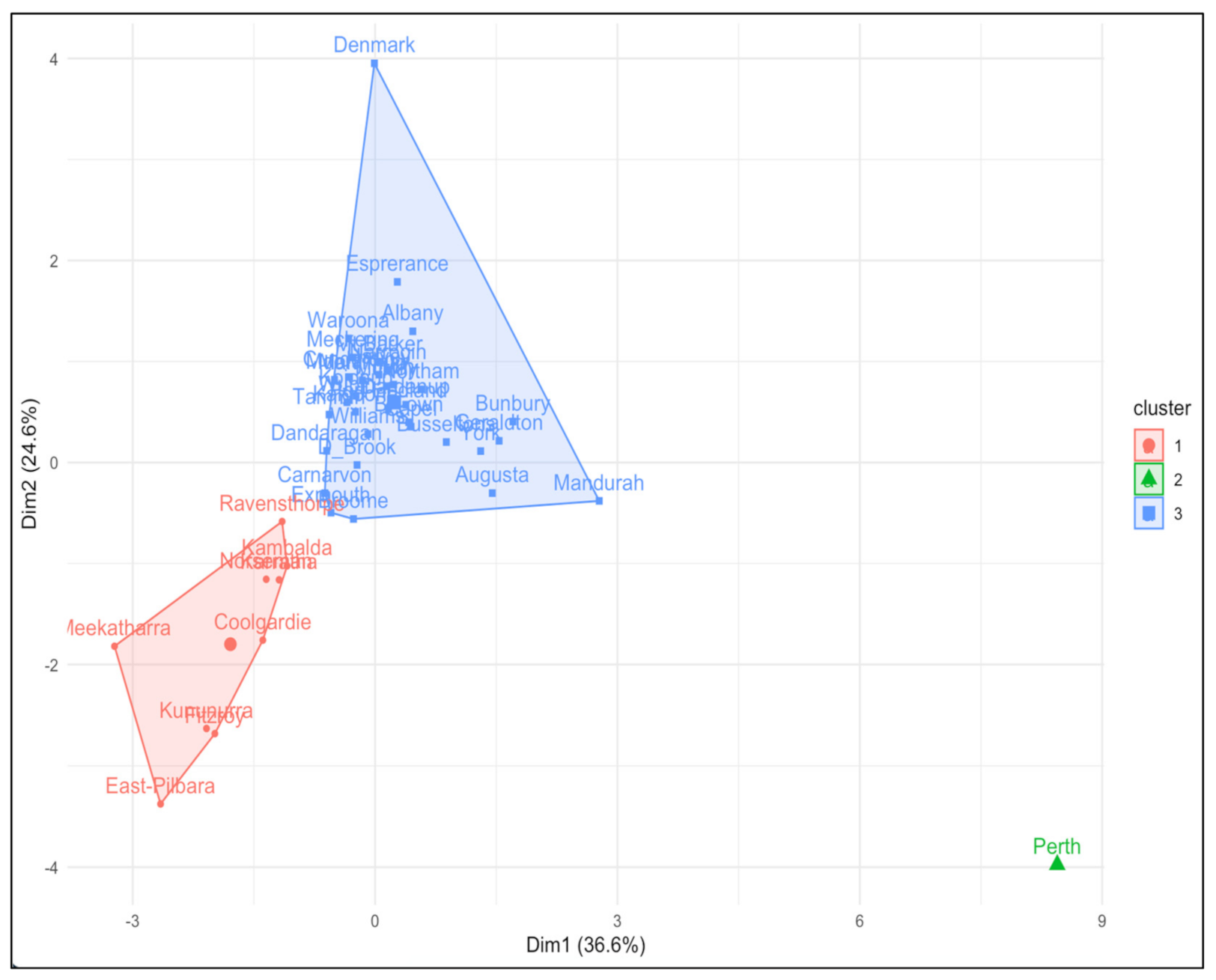
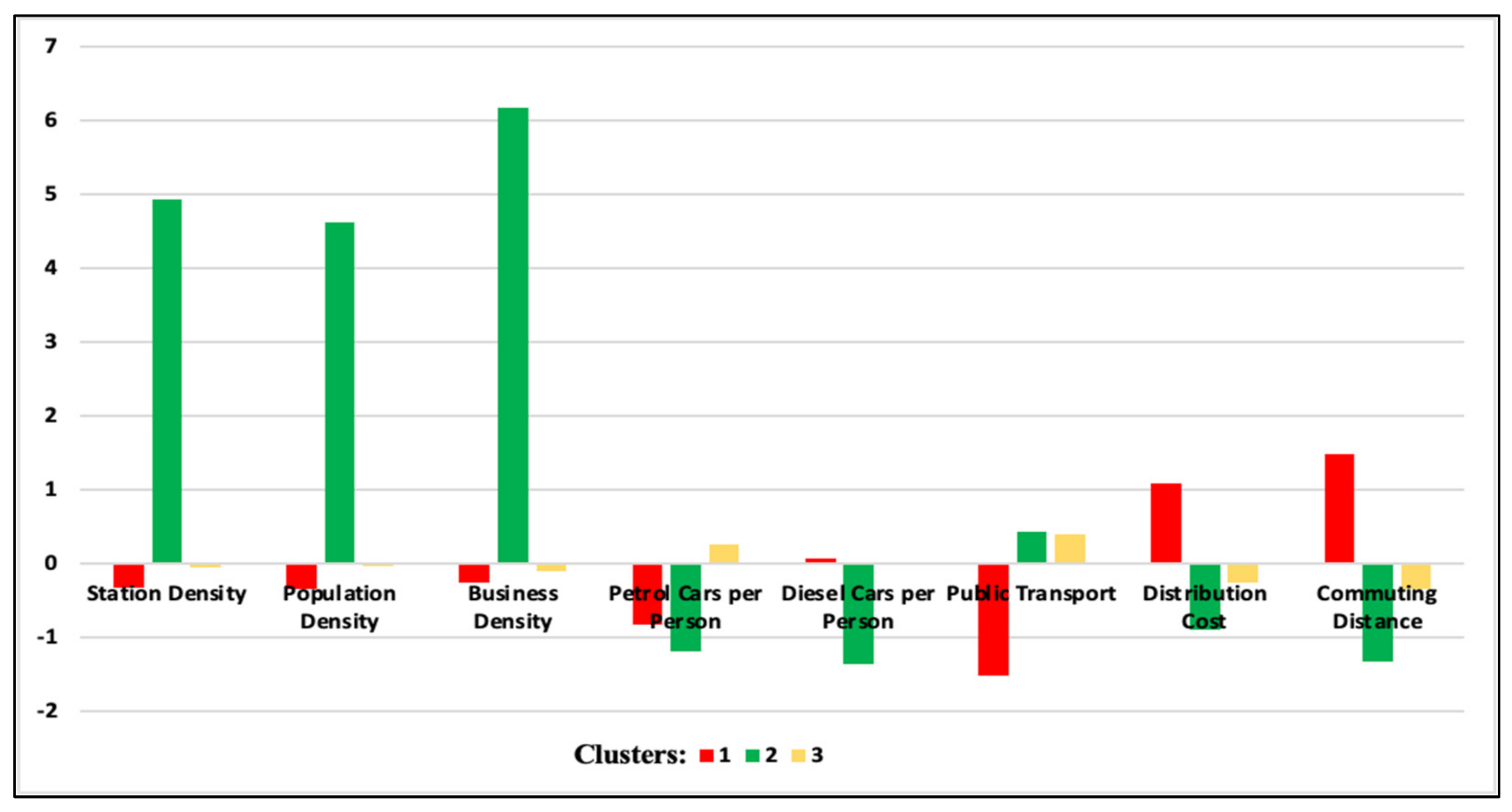
5.1. Cluster Analysis
5.2. Regression Analysis
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Australian Competition and Consumer Commission. Report on the Australian Petroleum Market, December Quarter 2021; ACCC: Canberra, ACT, Australia, 2021. [Google Scholar]
- Australian Competition and Consumer Commission. Report on the Australian Petroleum Market, December Quarter 2019; ACCC: Canberra, ACT, Australia, 2019. [Google Scholar]
- Australian Competition and Consumer Commission. Petrol Prices and Australian Consumers: Report of the ACCC Inquiry into the Price of Unleaded Petrol; ACCC: Canberra, ACT, Australia, 2007. [Google Scholar]
- Australian Competition and Consumer Commission. Fuel in Regional Australia; ACCC: Canberra, ACT, Australia, 2018. [Google Scholar]
- Van Meerbeeck, W. Competition and local market conditions on the Belgian retail gasoline market. Economist 2003, 151, 369–388. [Google Scholar] [CrossRef]
- Hosken, D.; Mcmillan, R.; Taylor, C. Retail gasoline pricing: What do we know? Int. J. Ind. Organ. 2008, 26, 1425–1436. [Google Scholar] [CrossRef]
- Taylor, C.T.; Kreisle, N.M.; Zimmerman, P.R. Vertical relationships and competition in retail gasoline markets: Empirical evidence from contract changes in Southern California: Comment. Am. Econ. Rev. 2010, 100, 1269–1276. [Google Scholar] [CrossRef]
- Ghazanfari, A. Regional Patterns for the Retail Petrol Prices. Int. J. Energy Econ. Policy 2021, 11, 383–397. [Google Scholar] [CrossRef]
- Tappata, M.; Yan, J. Competition in retail petrol markets. Aust. Econ. Pap. 2017, 56, 201–218. [Google Scholar] [CrossRef]
- Kvasnička, M.; Staněk, R.; Krčál, O. Is the retail gasoline market local or national? J. Ind. Compet. Trade 2018, 18, 47–58. [Google Scholar] [CrossRef]
- Valadkhani, A.; Anwar, S.; Ghazanfari, A.; Nguyen, J. Are petrol retailers less responsive to changes in wholesale or crude oil prices when they face lower competition? The case of Greater Sydney. Energy Policy 2021, 153, 112278. [Google Scholar] [CrossRef]
- Australian Competition and Consumer Commission. Petrol Price Cycles in Australia; ACCC: Canberra, ACT, Australia, 2018. [Google Scholar]
- Eckert, A.; West, D.S. Retail gasoline price cycles across spatially dispersed gasoline stations. J. Law Econ. 2004, 47, 245–273. [Google Scholar] [CrossRef]
- Barron, J.M.; Taylor, B.A.; Umbeck, J.R. Number of sellers, average prices, and price dispersion. Int. J. Ind. Organ. 2004, 22, 1041–1066. [Google Scholar] [CrossRef]
- Clemenz, G.; Gugler, K. Locational choice and price competition: Some empirical results for the Austrian retail gasoline market. Empir. Econ. 2006, 31, 291–312. [Google Scholar] [CrossRef]
- Cooper, T.E.; Jones, J.T. Asymmetric competition on commuter routes: The case of gasoline pricing. South. Econ. J. 2007, 17, 483–504. [Google Scholar] [CrossRef]
- Houde, J.-F. Spatial differentiation and vertical mergers in retail markets for gasoline. Am. Econ. Rev. 2012, 102, 2147–2182. [Google Scholar] [CrossRef]
- Pennerstorfer, D. Spatial price competition in retail gasoline markets: Evidence from Austria. Ann. Reg. Sci. 2009, 43, 133–158. [Google Scholar] [CrossRef]
- Zimmerman, R. The competitive impact of hypermarket retailers on gasoline prices. J. Law Econ. 2012, 55, 27–41. [Google Scholar] [CrossRef]
- Ghazanfari, A.; Razmjoo, A. The effect of market isolation on competitive behavior in retail petrol markets. Sustainability 2022, 14, 8102. [Google Scholar] [CrossRef]
- Noel, M.D.; Qiang, H. The role of information in retail gasoline price dispersion. Energy Econ. 2019, 80, 173–187. [Google Scholar] [CrossRef]
- Haucap, J.; Heimeshoff, U.; Siekmann, M. Price Dispersion and Station Heterogeneity on German Retail Gasoline Markets; DICE Discussion Paper; DICE: Düsseldorf, Germany, 2015. [Google Scholar]
- Yilmazkuday, D.; Yilmazkuday, H. Understanding gasoline price dispersion. Ann. Reg. Sci. 2016, 57, 223–252. [Google Scholar] [CrossRef]
- Valadkhani, A.; Chen, G.; Anderson, J. A cluster analysis of petrol profit margins across various regional and urban locations in Australia. Australas. J. Reg. Stud. 2014, 20, 159–184. [Google Scholar]
- Rietveld, P.; van Woudenberg, S. Why fuel prices differ. Energy Econ. 2005, 27, 79–92. [Google Scholar] [CrossRef]
- Burke, J.; Nishitateno, S. Gasoline prices, gasoline consumption, and new-vehicle fuel economy: Evidence for a large sample of countries. Energy Econ. 2013, 36, 363–370. [Google Scholar] [CrossRef]
- Chouinard, H.H.; Perloff, J.M. Gasoline price differences: Taxes, pollution regulations, mergers, market power, and market conditions. BE J. Econ. Anal. Policy 2007, 7, 1–28. [Google Scholar] [CrossRef]
- Bello, A.; Contín-Pilart, I. Taxes, cost and demand shifters as determinants in the regional gasoline price formation process: Evidence from Spain. Energy Policy 2012, 48, 439–448. [Google Scholar] [CrossRef]
- Valadkhani, A.; Babacan, A. Modelling how much extra motorists pay on the road? A cross-sectional study of profit margins of unleaded petrol in Australia. Energy Policy 2014, 69, 179–188. [Google Scholar] [CrossRef]
- Iglesias, F.; Kastner, W. Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies 2013, 6, 579–597. [Google Scholar] [CrossRef]
- Gillingham, K. Identifying the elasticity of driving: Evidence from a gasoline price shock in California. Reg. Sci. Urban Econ. 2014, 47, 13–24. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Wang, H. Short-Term wind speed forecasting based on spectral clustering and optimised echo state networks. Renew. Energy 2015, 78, 599–608. [Google Scholar] [CrossRef]
- Steinhaus, H. Sur la division des corps materiels en parties. Bull. Acad. Polon. Sci 1956, 1, 801. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, a Novel Method of Data Analysis and Pattern Classification; Stanford Research Institute: Menlo Park, CA, USA, 1965. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Guha, P. Application of multivariate-rank-based techniques in clustering of big data. Vikalpa 2018, 43, 179–190. [Google Scholar] [CrossRef]
- Kaur, N.; Sahiwal, J.K.; Kaur, N. Efficient K-Means clustering algorithm using ranking method in data mining. Int. J. Adv. Res. Comput. Eng. Technol. 2012, 1, 85–91. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hoffman, J.I. Biostatistics for Medical and Biomedical Practitioners; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Baltagi, B.H.; Liu, L. The Hausman–Taylor panel data model with serial correlation. Stat. Probab. Lett. 2012, 82, 1401–1406. [Google Scholar] [CrossRef]
- Breusch, T.; Ward, M.B.; Nguyen, H.T.M.; Kompas, T. On the fixed-effects vector decomposition. Political Anal. 2011, 19, 123–134. [Google Scholar] [CrossRef]
- Hausman, J.A.; Taylor, W.E. Panel data and unobservable individual effects. Econom. J. Econom. Soc. 1981, 49, 1377–1398. [Google Scholar]
- Bell, A.; Jones, K. Explaining fixed effects: Random effects modelling of time-series cross-sectional and panel data. Political Sci. Res. Methods 2015, 3, 133–153. [Google Scholar] [CrossRef]
- Schunck, R. Within and between estimates in random-effects models: Advantages and drawbacks of correlated random effects and hybrid models. Stata J. 2013, 13, 65–76. [Google Scholar] [CrossRef]
- Allison, D. Fixed Effects Regression Models; SAGE Publications: New York, NY, USA, 2009; p. 160. [Google Scholar]
- Raudenbush, S.W.; Bryk, A.S. Hierarchical Linear Models: Applications and Data Analysis Methods; SAGE Publications: New York, NY, USA, 2002; Volume 1. [Google Scholar]
- Australian Competition and Consumer Commission. Fuel Facts: What Drives Fuel Prices in Regional Australia; ACCC: Canberra, ACT, Australia, 2012. [Google Scholar]
- Australian Institute of Petroleum. Inquiry into Fuel Prices in Regional Victoria; The Victorian Economic, Education, Jobs and Skills Committee: Canberra, ACT, Australia, 2017. [Google Scholar]
- Australian Bureau of Statistics. Census Data by Geography; Australian Bureau of Statistics: Canberra, ACT, Australia, 2018.
- Australian Bureau of Statistics. Survey of Motor Vehicle Use, Australia; Australian Bureau of Statistics: Canberra, ACT, Australia, 2018.
- Vita, M.G. Regulatory restrictions on vertical integration and control: The competitive impact of gasoline divorcement policies. J. Regul. Econ. 2000, 18, 217–233. [Google Scholar] [CrossRef]
- Alm, J.; Sennoga, E.; Skidmore, M. Perfect competition, urbanization, and tax incidence in the retail gasoline market. Econ. Inq. 2009, 47, 118–134. [Google Scholar] [CrossRef]
- Lee, S.-Y. Spatial Competition in the Retail Gasoline Market: An Equilibrium Approach Using SAR Models; Department of Economics, The Ohio State University: Columbus, OH, USA, 2007. [Google Scholar]
- Li, T.; Sipe, N.; Dodson, J. Social and spatial effects of transforming the private vehicle fleet in Brisbane, Australia. Transp. Res. Part D Transp. Environ. 2017, 51, 43–52. [Google Scholar] [CrossRef]
- Balaguer, J.; Ripollés, J. Do classes of gas stations contribute differently to fuel prices? Evidence to foster effective competition in Spain. Energy Policy 2020, 139, 111315. [Google Scholar] [CrossRef]
- Radchenko, S. Oil price volatility and the asymmetric response of gasoline prices to oil price increases and decreases. Energy Econ. 2005, 27, 708–730. [Google Scholar] [CrossRef]
- Tsuruta, Y. What affects intranational price dispersion? The case of Japanese gasoline prices. Jpn. World Econ. 2008, 20, 563–584. [Google Scholar] [CrossRef]
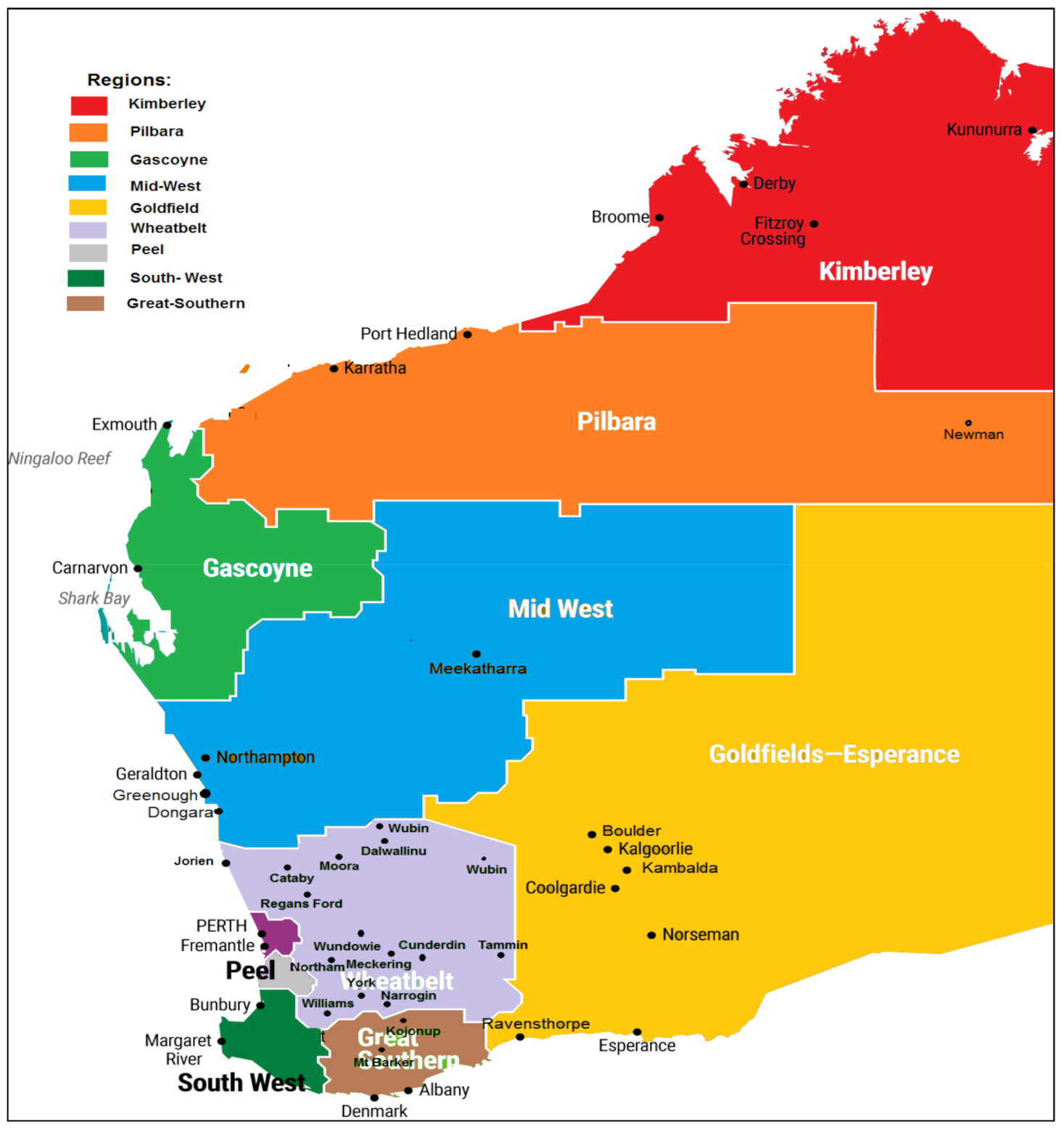
| Region | City/Town |
|---|---|
| Pilbara | East Pilbara, Karratha, Port Hedland |
| Kimberley | Broome, Fitzroy, Kununurra |
| Gascoyne | Carnarvon, Exmouth |
| Midwest | Irwin, Geraldton, Meekatharra |
| Goldfield–Esperance | Kalgoorlie/Builder, Coolgardie, Esperance, Kambalda, Norseman, Ravensthorpe |
| Wheatbelt | Cunderdin, Dalwallinu, Dandaragan, Meckering, Moora, Narrogin, Northam, Tammin, Williams, York |
| Southwest | Bunbury, Manjimup, Bridgetown/Greenbushes, Busselton, Capel, Dardanup, Donnybrook/Balingup, Harvey, Augusta |
| Peel | Murray, Waroona, Mandurah |
| Great Southern | Albany, Denmark, Kojonup, Mt Barker |
| Perth | Perth |
| Variables | Mean | Std Dev | Min | Max | Kurtosis | Skewness | Range |
|---|---|---|---|---|---|---|---|
| Station density | 0.005 | 0.011 | 0.000 | 0.057 | 14.781 | 3.683 | 0.057 |
| Population density | 22.357 | 64.633 | 0.000 | 320.900 | 14.094 | 3.746 | 320.900 |
| Business density | 1.193 | 4.407 | 0.000 | 28.390 | 35.752 | 5.820 | 28.390 |
| Petrol cars/population | 0.570 | 0.322 | 0.174 | 2.257 | 17.350 | 3.311 | 2.083 |
| Diesel cars/population | 0.436 | 0.280 | 0.010 | 1.630 | 6.736 | 1.951 | 1.620 |
| Public transport | 0.034 | 0.069 | 0.000 | 0.335 | 9.475 | 3.041 | 0.335 |
| Distribution cost | 206.202 | 221.329 | 0.400 | 1184.600 | 8.505 | 2.535 | 1184.200 |
| Commuting distance | 23.559 | 13.901 | 5.000 | 67.800 | 1.874 | 1.361 | 62.800 |
| Clusters/Features | 1 | 2 | 3 |
|---|---|---|---|
| Station density | −0.33012 | 4.924333 | −0.05745 |
| Population density | −0.34246 | 4.619029 | −0.0452 |
| Business density | −0.26814 | 6.171106 | −0.11053 |
| Petrol cars per person | −0.83292 | −1.19809 | 0.255716 |
| Diesel cars per person | 0.063911 | −1.35642 | 0.022977 |
| Public transport | −1.51968 | 0.420818 | 0.389892 |
| Distribution cost | 1.079932 | −0.89325 | −0.25959 |
| Commuting distance | 1.485641 | −1.33508 | −0.35399 |
| Kruskal–Wallis Rank Sum Test | ||
|---|---|---|
| Kruskal–Wallis chi-squared = 14.334 | df = 2 | p-value = 0.0007 |
| Cluster | Cities | Region | Mean Petrol Prices | Station Density | Population Density | Business Density | Petrol Vehicles/Pop | Diesel Vehicles/Pop | Public Transport | Commuting Distance | Distribution Cost |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Fitzroy | Kimberley | 164.44 | 0.00007 | 0.1 | 0.002 | 0.192 | 0.132 | 0.523 | 42.1 | 768.8 |
| 1 | Meekatharra | Midwest | 154.75 | 0.00161 | 0 | 0.001 | 0.327 | 1.63 | 0.292 | 54 | 452.9 |
| 1 | Norseman | Goldfield | 154.11 | 0.00012 | 0 | 0 | 0.242 | 0.401 | 0.693 | 56.1 | 180.8 |
| 1 | Ravensthorpe | Goldfield | 146.83 | 0.00011 | 0.2 | 0.026 | 0.568 | 0.397 | 0.532 | 36.1 | 165.8 |
| 1 | East-Pilbara | Pilbara | 145.93 | 0.00518 | 0 | 0 | 0.175 | 0.375 | 0.272 | 67.8 | 450 |
| 1 | Kambalda | Goldfield | 143.36 | 0.00039 | 0 | 0.001 | 0.229 | 0.342 | 0.771 | 48.1 | 290.6 |
| 1 | Kununurra | Kimberley | 142.89 | 0.00001 | 0.1 | 0.006 | 0.364 | 0.185 | 0.587 | 28.5 | 1184.6 |
| 1 | Coolgardie | Goldfield | 138.91 | 0.00002 | 0.1 | 0.004 | 0.174 | 0.182 | 0.585 | 45.7 | 324.8 |
| 3 | Kojonup | Great Southern | 137.04 | 0.00004 | 0.7 | 0.173 | 0.636 | 0.468 | 0.757 | 17.7 | 149.8 |
| 3 | Moora | Wheatbelt | 133.54 | 0.0013 | 0.6 | 0.1 | 0.59 | 0.889 | 0.767 | 20.1 | 148.3 |
| 3 | Dalwallinu | Wheatbelt | 143.04 | 0.0021 | 0.2 | 0.127 | 0.875 | 0.349 | 0.723 | 23.2 | 217.6 |
| 3 | Carnarvon | Gascoyne | 145.97 | 0.00031 | 0.1 | 0.014 | 0.451 | 0.419 | 0.663 | 9.3 | 442.8 |
| 3 | Esperance | Goldfield | 138.95 | 0.00013 | 0.3 | 0.039 | 1.001 | 0.383 | 0.829 | 13.9 | 8.4 |
| 3 | Exmouth | Gascoyne | 158.67 | 0.00004 | 0.4 | 0.043 | 0.436 | 0.257 | 0.652 | 6.1 | 498.1 |
| 3 | Kalgoorlie | Goldfield | 141.73 | 0.00003 | 0.3 | 0.021 | 0.573 | 0.465 | 0.799 | 10.2 | 339.1 |
| 3 | Mt Barker | Great Southern | 134.58 | 0.00038 | 1.1 | 0.149 | 0.641 | 0.405 | 0.878 | 24.4 | 50.6 |
| 3 | Broome | Kimberley | 154.09 | 0.00055 | 0.3 | 0.023 | 0.413 | 0.01 | 0.692 | 7.3 | 462.1 |
| 3 | Irwin | Midwest | 136.12 | 0.00013 | 1.5 | 0.168 | 0.614 | 0.154 | 0.827 | 18.6 | 50 |
| 3 | Port Hedland | Pilbara | 146.16 | 0.00481 | 0.8 | 0.037 | 0.436 | 0.498 | 0.71 | 10.6 | 2.2 |
| 3 | Karratha | Pilbara | 149.89 | 0.00299 | 1.5 | 0.063 | 0.444 | 0.445 | 0.302 | 19.5 | 188.7 |
| 3 | B-Town | Southwest | 137.62 | 0.011 | 3.5 | 0.369 | 0.648 | 0.323 | 0.834 | 19.1 | 200.4 |
| 3 | Manjimup | Southwest | 138.14 | 0.00015 | 1.3 | 0.175 | 0.569 | 0.597 | 0.822 | 15 | 183.3 |
| 3 | Cunderdin | Wheatbelt | 136.13 | 0.00091 | 0.6 | 0.075 | 0.661 | 0.643 | 0.782 | 21 | 127.5 |
| 3 | Meckering | Wheatbelt | 136.13 | 0.00045 | 0.6 | 0.075 | 0.661 | 0.706 | 0.818 | 21 | 107.3 |
| 3 | Tammin | Wheatbelt | 134.67 | 0.0008 | 0.4 | 0.044 | 0.564 | 0.715 | 0.696 | 19.8 | 150 |
| 3 | Narrogin | Wheatbelt | 133.54 | 0.00094 | 3.1 | 0.299 | 0.573 | 0.48 | 0.838 | 10.3 | 152.6 |
| 3 | Williams | Wheatbelt | 134.38 | 0.00054 | 0.4 | 0.076 | 0.601 | 0.115 | 0.75 | 21.3 | 136.2 |
| 3 | Geraldton | Midwest | 138.41 | 0.00534 | 139.1 | 0.062 | 0.199 | 0.583 | 0.856 | 6.6 | 0.4 |
| 3 | Albany | Great Southern | 137.57 | 0.00001 | 8.8 | 0.806 | 0.857 | 0.178 | 0.867 | 20.5 | 1.9 |
| 3 | Denmark | Great Southern | 137.56 | 0.0002 | 3.3 | 0.397 | 2.257 | 0.823 | 0.812 | 19 | 50.1 |
| 3 | Waroona | Peel | 137.17 | 0.00102 | 5 | 0.375 | 0.645 | 0.957 | 0.88 | 27.8 | 69.3 |
| 3 | Mandurah | Peel | 134.41 | 0.00062 | 259 | 8.376 | 0.628 | 0.528 | 0.871 | 25.5 | 33.5 |
| 3 | Murray | Peel | 136.48 | 0.00295 | 10.4 | 0.659 | 0.54 | 0.529 | 0.885 | 28 | 32.4 |
| 3 | Augusta | Southwest | 138.74 | 0.03296 | 7.4 | 0.943 | 0.59 | 0.296 | 0.824 | 14 | 257.3 |
| 3 | Busselton | Southwest | 137 | 0.00951 | 26.8 | 2.748 | 0.581 | 0.312 | 0.854 | 19.2 | 162.1 |
| 3 | Capel | Southwest | 138.07 | 0.00256 | 32.3 | 2.036 | 0.55 | 0.401 | 0.833 | 21.2 | 130.1 |
| 3 | Dardanup | Southwest | 137.16 | 0.00156 | 27.3 | 1.497 | 0.516 | 0.48 | 0.862 | 18.4 | 129.9 |
| 3 | D-Brook | Southwest | 138.15 | 0.00521 | 3.9 | 0.451 | 0.601 | 0.314 | 0.784 | 29.4 | 248.5 |
| 3 | Harvey | Southwest | 135.09 | 0.00015 | 16.1 | 0.913 | 0.604 | 0.597 | 0.858 | 22.6 | 95 |
| 3 | York | Wheatbelt | 133.78 | 0.03091 | 1.7 | 0.186 | 0.743 | 0.206 | 0.824 | 24.3 | 78 |
| 3 | Northam | Wheatbelt | 135.66 | 0.00704 | 7.8 | 0.558 | 0.632 | 0.267 | 0.874 | 19.9 | 77.1 |
| 3 | Bunbury | Southwest | 138.11 | 0.01255 | 95.2 | 1.917 | 0.677 | 0.293 | 0.885 | 13 | 122.4 |
| 3 | Dandaragan | Wheatbelt | 135.93 | 0.00184 | 0.5 | 0.075 | 0.62 | 0.418 | 0.736 | 35.4 | 143.1 |
| 2 | Perth | Perth | 131.39 | 0.05749 | 320.9 | 28.39 | 0.184 | 0.057 | 0.809 | 5 | 8.5 |
| City | αi | βi (xit = Wholesale Price) | AIC | Schwarz Criterion | HQC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | Std. Error | p-Value | Coef. | Std. Error | p-Value | |||||
| Exmouth | 1.728 | 0.065 | 0.000 | 0.678 | 0.013 | 0.000 | 0.687 | −4.642 | −4.634 | −4.639 |
| Fitzroy | 5.208 | 0.005 | 0.000 | 0.017 | 0.001 | 0.000 | 0.320 | −9.996 | −9.982 | −9.991 |
| Coolgardie | 0.621 | 0.049 | 0.000 | 0.900 | 0.010 | 0.000 | 0.866 | −4.629 | −4.621 | −4.626 |
| Esperance | 0.763 | 0.021 | 0.000 | 0.869 | 0.004 | 0.000 | 0.916 | −5.227 | −5.223 | −5.226 |
| Albany | 0.082 | 0.012 | 0.000 | 1.006 | 0.002 | 0.000 | 0.929 | −5.116 | −5.114 | −5.115 |
| Denmark | 0.724 | 0.048 | 0.000 | 0.876 | 0.010 | 0.000 | 0.863 | −4.653 | −4.644 | −4.650 |
| Kojonup | 0.490 | 0.032 | 0.000 | 0.925 | 0.007 | 0.000 | 0.913 | −5.067 | −5.061 | −5.065 |
| Mt Barker | 0.706 | 0.043 | 0.000 | 0.876 | 0.009 | 0.000 | 0.840 | −4.475 | −4.468 | −4.472 |
| Irwin | 1.373 | 0.023 | 0.000 | 0.748 | 0.005 | 0.000 | 0.849 | −4.864 | −4.861 | −4.863 |
| Waroona | 0.686 | 0.024 | 0.000 | 0.870 | 0.005 | 0.000 | 0.943 | −5.634 | −5.628 | −5.631 |
| Augusta | 2.079 | 0.020 | 0.000 | 0.598 | 0.004 | 0.000 | 0.786 | −4.884 | −4.882 | −4.883 |
| B-Town | 0.612 | 0.034 | 0.000 | 0.896 | 0.007 | 0.000 | 0.896 | −4.927 | −4.921 | −4.924 |
| Bunbury | 0.894 | 0.026 | 0.000 | 0.840 | 0.005 | 0.000 | 0.820 | −4.421 | −4.419 | −4.420 |
| Busselton | 1.387 | 0.015 | 0.000 | 0.739 | 0.003 | 0.000 | 0.871 | −5.067 | −5.065 | −5.066 |
| Capel | 0.221 | 0.041 | 0.000 | 0.977 | 0.009 | 0.000 | 0.810 | −4.053 | −4.050 | −4.052 |
| Dardanup | 0.898 | 0.025 | 0.000 | 0.833 | 0.005 | 0.000 | 0.891 | −5.027 | −5.023 | −5.025 |
| D-Brook | 1.235 | 0.023 | 0.000 | 0.769 | 0.005 | 0.000 | 0.913 | −5.436 | −5.431 | −5.434 |
| Manjimup | 0.134 | 0.025 | 0.000 | 0.996 | 0.005 | 0.000 | 0.858 | −4.365 | −4.363 | −4.364 |
| Harvey | 1.132 | 0.028 | 0.000 | 0.787 | 0.006 | 0.000 | 0.836 | −4.661 | −4.658 | −4.660 |
| Cunderdin | 2.596 | 0.078 | 0.000 | 0.483 | 0.016 | 0.000 | 0.591 | −4.373 | −4.358 | −4.367 |
| Meckering | 1.733 | 0.095 | 0.000 | 0.662 | 0.020 | 0.000 | 0.651 | −3.996 | −3.981 | −3.990 |
| Tammin | 2.540 | 0.106 | 0.000 | 0.492 | 0.022 | 0.000 | 0.449 | −3.762 | −3.747 | −3.756 |
| Dandaragan | 1.504 | 0.025 | 0.000 | 0.723 | 0.005 | 0.000 | 0.939 | −5.941 | −5.933 | −5.938 |
| Moora | 0.583 | 0.021 | 0.000 | 0.899 | 0.004 | 0.000 | 0.960 | −5.940 | −5.934 | −5.938 |
| Narrogin | 0.409 | 0.030 | 0.000 | 0.933 | 0.006 | 0.000 | 0.926 | −5.222 | −5.216 | −5.219 |
| Williams | 0.479 | 0.035 | 0.000 | 0.922 | 0.007 | 0.000 | 0.896 | −4.869 | −4.863 | −4.866 |
| York | 0.811 | 0.046 | 0.000 | 0.852 | 0.010 | 0.000 | 0.868 | −4.757 | −4.749 | −4.754 |
| Norseman | 1.314 | 0.018 | 0.000 | 0.776 | 0.004 | 0.000 | 0.973 | −6.647 | −6.639 | −6.644 |
| Broome | 3.929 | 0.008 | 0.000 | 0.009 | 0.000 | 0.000 | 0.852 | −4.113 | −4.109 | −4.112 |
| Meekatharra | 2.621 | 0.024 | 0.000 | 0.504 | 0.005 | 0.000 | 0.845 | −5.616 | −5.610 | −5.613 |
| Karratha | 1.414 | 0.032 | 0.000 | 0.749 | 0.007 | 0.000 | 0.807 | −4.561 | −4.557 | −4.559 |
| Carnarvon | 2.428 | 0.022 | 0.000 | 0.532 | 0.005 | 0.000 | 0.812 | −5.279 | −5.275 | −5.277 |
| Kalgoorlie/Builder | 1.707 | 0.019 | 0.000 | 0.674 | 0.004 | 0.000 | 0.818 | −4.849 | −4.847 | −4.848 |
| Kambalda | 1.117 | 0.081 | 0.000 | 0.800 | 0.017 | 0.000 | 0.788 | −4.305 | −4.290 | −4.299 |
| Ravensthorpe | 2.007 | 0.059 | 0.000 | 0.623 | 0.012 | 0.000 | 0.678 | −4.243 | −4.235 | −4.240 |
| Kununurra | 1.773 | 0.032 | 0.000 | 0.669 | 0.007 | 0.000 | 0.807 | −4.788 | −4.783 | −4.786 |
| Port Hedland | 0.469 | 0.029 | 0.000 | 0.941 | 0.006 | 0.000 | 0.829 | −4.256 | −4.253 | −4.255 |
| East Pilbara | 1.418 | 0.071 | 0.000 | 0.749 | 0.015 | 0.000 | 0.810 | −4.580 | −4.566 | −4.575 |
| Dalwallinu | 1.716 | 0.027 | 0.000 | 0.675 | 0.006 | 0.000 | 0.852 | −5.091 | −5.086 | −5.089 |
| Geraldton | 0.031 | 0.036 | 0.000 | 1.013 | 0.008 | 0.000 | 0.731 | −3.530 | −3.528 | −3.529 |
| Mandurah | 0.550 | 0.055 | 0.000 | 0.906 | 0.012 | 0.000 | 0.480 | −2.674 | −2.672 | −2.673 |
| Murray | 0.550 | 0.065 | 0.000 | 0.906 | 0.014 | 0.000 | 0.480 | −2.674 | −2.671 | −2.673 |
| Northam | 0.558 | 0.017 | 0.000 | 0.904 | 0.003 | 0.000 | 0.983 | −6.790 | −6.782 | −6.787 |
| Perth | 0.730 | 0.021 | 0.000 | 0.868 | 0.004 | 0.000 | 0.449 | −2.634 | −2.633 | −2.634 |
| City | α0 | βi (xit = Crude Oil Price) | AIC | Schwarz Criterion | HQC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | Std. Error | p-Value | Coef. | Std. Error | p-Value | |||||
| Exmouth | 4.023 | 0.014 | 0.000 | 0.242 | 0.003 | 0.000 | 0.810 | −5.143 | −5.135 | −5.140 |
| Fitzroy | 4.293 | 0.020 | 0.000 | 0.187 | 0.005 | 0.000 | 0.355 | −3.613 | −3.609 | −3.611 |
| Coolgardie | 3.273 | 0.019 | 0.000 | 0.385 | 0.004 | 0.000 | 0.862 | −4.598 | −4.589 | −4.595 |
| Esperance | 3.241 | 0.011 | 0.000 | 0.393 | 0.003 | 0.000 | 0.856 | −4.512 | −4.508 | −4.511 |
| Albany | 3.184 | 0.008 | 0.000 | 0.404 | 0.002 | 0.000 | 0.773 | −3.895 | −3.894 | −3.895 |
| Denmark | 3.217 | 0.021 | 0.000 | 0.396 | 0.005 | 0.000 | 0.847 | −4.416 | −4.407 | −4.413 |
| Kojonup | 3.133 | 0.018 | 0.000 | 0.415 | 0.004 | 0.000 | 0.839 | −4.266 | −4.259 | −4.263 |
| Mt Barker | 3.133 | 0.018 | 0.000 | 0.415 | 0.004 | 0.000 | 0.839 | −4.266 | −4.259 | −4.263 |
| Irwin | 3.434 | 0.016 | 0.000 | 0.344 | 0.004 | 0.000 | 0.655 | −3.636 | −3.633 | −3.635 |
| Waroona | 3.600 | 0.055 | 0.000 | 0.306 | 0.013 | 0.000 | 0.241 | −2.077 | −2.071 | −2.074 |
| Augusta | 3.718 | 0.012 | 0.000 | 0.282 | 0.003 | 0.000 | 0.634 | −3.942 | −3.939 | −3.941 |
| B-Town | 3.511 | 0.019 | 0.000 | 0.328 | 0.004 | 0.000 | 0.758 | −4.228 | −4.222 | −4.226 |
| Bunbury | 3.376 | 0.010 | 0.000 | 0.360 | 0.002 | 0.000 | 0.825 | −4.454 | −4.451 | −4.453 |
| Busselton | 3.538 | 0.009 | 0.000 | 0.320 | 0.002 | 0.000 | 0.737 | −4.166 | −4.164 | −4.166 |
| Capel/Colie | 3.394 | 0.015 | 0.000 | 0.356 | 0.003 | 0.000 | 0.775 | −4.160 | −4.156 | −4.158 |
| Dardanup | 3.354 | 0.016 | 0.000 | 0.364 | 0.004 | 0.000 | 0.751 | −3.986 | −3.982 | −3.985 |
| D-Brook | 3.581 | 0.011 | 0.000 | 0.313 | 0.003 | 0.000 | 0.865 | −5.037 | −5.033 | −5.036 |
| Manjimup | 3.295 | 0.014 | 0.000 | 0.379 | 0.003 | 0.000 | 0.702 | −3.654 | −3.652 | −3.653 |
| Harvey | 3.275 | 0.017 | 0.000 | 0.378 | 0.004 | 0.000 | 0.728 | −3.784 | −3.780 | −3.783 |
| Cunderdin | 4.036 | 0.031 | 0.000 | 0.204 | 0.007 | 0.000 | 0.574 | −4.333 | −4.318 | −4.327 |
| Meckering | 3.715 | 0.038 | 0.000 | 0.278 | 0.009 | 0.000 | 0.626 | −3.927 | −3.912 | −3.921 |
| Tammin | 4.036 | 0.042 | 0.000 | 0.201 | 0.010 | 0.000 | 0.409 | −3.692 | −3.678 | −3.687 |
| Dandaragan | 3.416 | 0.055 | 0.000 | 0.347 | 0.013 | 0.000 | 0.377 | −2.472 | −2.464 | −2.469 |
| Moora | 3.310 | 0.014 | 0.000 | 0.368 | 0.003 | 0.000 | 0.872 | −4.779 | −4.773 | −4.777 |
| Narrogin | 3.277 | 0.014 | 0.000 | 0.375 | 0.003 | 0.000 | 0.877 | −4.784 | −4.778 | −4.782 |
| Williams | 3.174 | 0.015 | 0.000 | 0.401 | 0.003 | 0.000 | 0.882 | −4.697 | −4.691 | −4.695 |
| York | 3.289 | 0.025 | 0.000 | 0.373 | 0.006 | 0.000 | 0.779 | −4.088 | −4.080 | −4.085 |
| Norseman | 3.677 | 0.014 | 0.000 | 0.316 | 0.003 | 0.000 | 0.886 | −5.215 | −5.207 | −5.212 |
| Broome | 3.143 | 0.016 | 0.000 | 0.440 | 0.004 | 0.000 | 0.789 | −3.821 | −3.818 | −3.820 |
| Meekatharra | 4.146 | 0.010 | 0.000 | 0.208 | 0.002 | 0.000 | 0.805 | −5.411 | −5.405 | −5.409 |
| Karratha | 3.601 | 0.011 | 0.000 | 0.327 | 0.003 | 0.000 | 0.838 | −4.737 | −4.733 | −4.735 |
| Carnarvon | 4.087 | 0.009 | 0.000 | 0.208 | 0.002 | 0.000 | 0.748 | −5.086 | −5.082 | −5.084 |
| Kalgoorlie/Builder | 3.569 | 0.011 | 0.000 | 0.321 | 0.002 | 0.000 | 0.716 | −4.055 | −4.053 | −4.054 |
| Kambalda | 3.501 | 0.033 | 0.000 | 0.338 | 0.008 | 0.000 | 0.768 | −4.219 | −4.204 | −4.213 |
| Ravensthorpe | 3.889 | 0.026 | 0.000 | 0.255 | 0.006 | 0.000 | 0.601 | −3.996 | −3.988 | −3.993 |
| Kununurra | 4.088 | 0.017 | 0.000 | 0.203 | 0.004 | 0.000 | 0.510 | −4.088 | −4.084 | −4.087 |
| Port Hedland | 3.343 | 0.012 | 0.000 | 0.381 | 0.003 | 0.000 | 0.797 | −4.158 | −4.156 | −4.157 |
| East Pilbara | 4.126 | 0.026 | 0.000 | 0.197 | 0.006 | 0.000 | 0.376 | −3.603 | −3.597 | −3.601 |
| Wubin/Dalwallinu | 3.620 | 0.013 | 0.000 | 0.312 | 0.003 | 0.000 | 0.809 | −4.634 | −4.629 | −4.632 |
| Geraldton | 3.326 | 0.018 | 0.000 | 0.372 | 0.004 | 0.000 | 0.548 | −3.029 | −3.027 | −3.028 |
| Mandurah | 3.300 | 0.022 | 0.000 | 0.371 | 0.005 | 0.000 | 0.436 | −2.582 | −2.580 | −2.582 |
| Murray | 3.299 | 0.073 | 0.000 | 0.372 | 0.017 | 0.000 | 0.441 | −2.596 | −2.581 | −2.590 |
| Northam | 3.246 | 0.036 | 0.000 | 0.386 | 0.008 | 0.000 | 0.635 | −3.313 | −3.304 | −3.310 |
| Perth | 3.288 | 0.008 | 0.000 | 0.374 | 0.002 | 0.000 | 0.480 | −2.746 | −2.745 | −2.746 |
| Variables | Model 1: Fixed Effects | Model 2: Random Effects | Model 3: Hybrid Model | |||
|---|---|---|---|---|---|---|
| Coeff. | S.E. | Coeff. | S.E. | Coeff. | S.E. | |
| Wholesale price | 0.838 *** | 0.0027 | 0.838 *** | 0.0027 | 0.838 *** | 0.003 |
| Mean (wholesale price) | 0.618 *** | 0.168 | ||||
| Station density | −0.220 ** | 0.6173 | −0.433 ** | 0.638 | ||
| Population density | 0.004 * | 0.0100 | 0.006 * | 0.01 | ||
| Business density | 0.007 | 0.0081 | 0.008 | 0.008 | ||
| Petrol vehicles/population | 0.053 * | 0.0312 | 0.05 * | 0.031 | ||
| Diesel vehicles/population | −0.030 * | 0.0141 | −0.024 * | 0.015 | ||
| Public transport | −0.049 * | 0.0224 | −0.059 * | 0.024 | ||
| Distribution cost | 0.004 | 0.0081 | 0.007 | 0.008 | ||
| Commuting distance | 0.007 | 0.0091 | 0.004 | 0.013 | ||
| Adj R2 | 0.78 | 0.78 | 0.86 | |||
| Variables | Model 1: Fixed Effects | Model 2: Random Effects | Model 3: Hybrid Model | |||
|---|---|---|---|---|---|---|
| Coeff. | S.E. | Coeff. | S.E. | Coeff. | S.E. | |
| Wholesale price | 0.332 *** | 0.001 | 0.332 *** | 0.001 | 0.332 *** | 0.001 |
| Mean (wholesale price) | 0.123 *** | 0.015 | ||||
| Station density | −0.040 ** | 0.0119 | −0.04 ** | 0.012 | ||
| Population density | 0.014 * | 0.0116 | 0.015 * | 0.012 | ||
| Business density | 0.011 | 0.0091 | 0.011 | 0.009 | ||
| Petrol vehicles/population | 0.043 * | 0.0350 | 0.043 * | 0.035 | ||
| Diesel vehicles/population | −0.01 * | 0.0151 | −0.01 * | 0.015 | ||
| Public transport | −0.10 * | 0.0253 | −0.11 * | 0.025 | ||
| Distribution cost | 0.011 | 0.0087 | 0.011 | 0.009 | ||
| Commuting distance | 0.07 * | 0.0216 | 0.07 * | 0.022 | ||
| Adj R2 | 0.77 | 0.77 | 0.86 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghazanfari, A. What Drives Petrol Price Dispersion across Australian Cities? Energies 2022, 15, 6025. https://doi.org/10.3390/en15166025
Ghazanfari A. What Drives Petrol Price Dispersion across Australian Cities? Energies. 2022; 15(16):6025. https://doi.org/10.3390/en15166025
Chicago/Turabian StyleGhazanfari, Arezoo. 2022. "What Drives Petrol Price Dispersion across Australian Cities?" Energies 15, no. 16: 6025. https://doi.org/10.3390/en15166025
APA StyleGhazanfari, A. (2022). What Drives Petrol Price Dispersion across Australian Cities? Energies, 15(16), 6025. https://doi.org/10.3390/en15166025





