Predicting the Optimal Performance of a Concentrated Solar Segmented Variable Leg Thermoelectric Generator Using Neural Networks
Abstract
:1. Introduction
- Very few works have combined material segmentation and device geometry modification to form a new device configuration with higher performance. Moreso, these works lack in-depth insights regarding the optimum geometry combinations that can produce maximum power outputs and efficiencies from the device. This study, for the first in time, conducts this optimization analysis, uncovering the best combination of heights and cross-sectional areas needed to manufacture a high-performing, modified device. After this study, the optimization insights drawn from this study will be sent to TEG manufacturing companies, such as Kryotherm, who specialize in producing state-of-the-art thermoelectric modules;
- A means of overcoming the high computational energy and time requirements of traditional, FEM-based multiphysics solvers is introduced by using ANNs. These ANNs ease and speed up the rate at which useful information can be drawn from the performance of the device through data prediction based on successful training. It is expected that the ANNs can predict the device performance much faster than the conventional, time-consuming, FEM-based methods. So far, ANNs have not been used to predict the performance of either segmented or variable area leg thermoelectrics;
- Therefore, the purpose of this research paper is to, first of all, develop a 3-dimensional digital twin model of a modified, segmented variable area leg TEG using ANSYS software. After this, a comprehensive geometry optimization of the different segments is carried out to find the optimum lengths and areas that maximize the new device power and efficiency while considering all temperature-dependent thermoelectric properties and effects. Finally, an ANN model is introduced as a substitute for the computational time- and energy-consuming, traditional, FEM-based multiphysics software. This provides an accurate, faster, and more efficient way of predicting the device performance under different working conditions. In the end, the optimization insights provided by this study will be very useful to TEG manufacturing companies, such as Kryotherm, that specialize in manufacturing next-generation thermoelectric devices.
2. Materials and Methods
2.1. System Description
2.2. Governing Equations
2.3. Data Generation Process
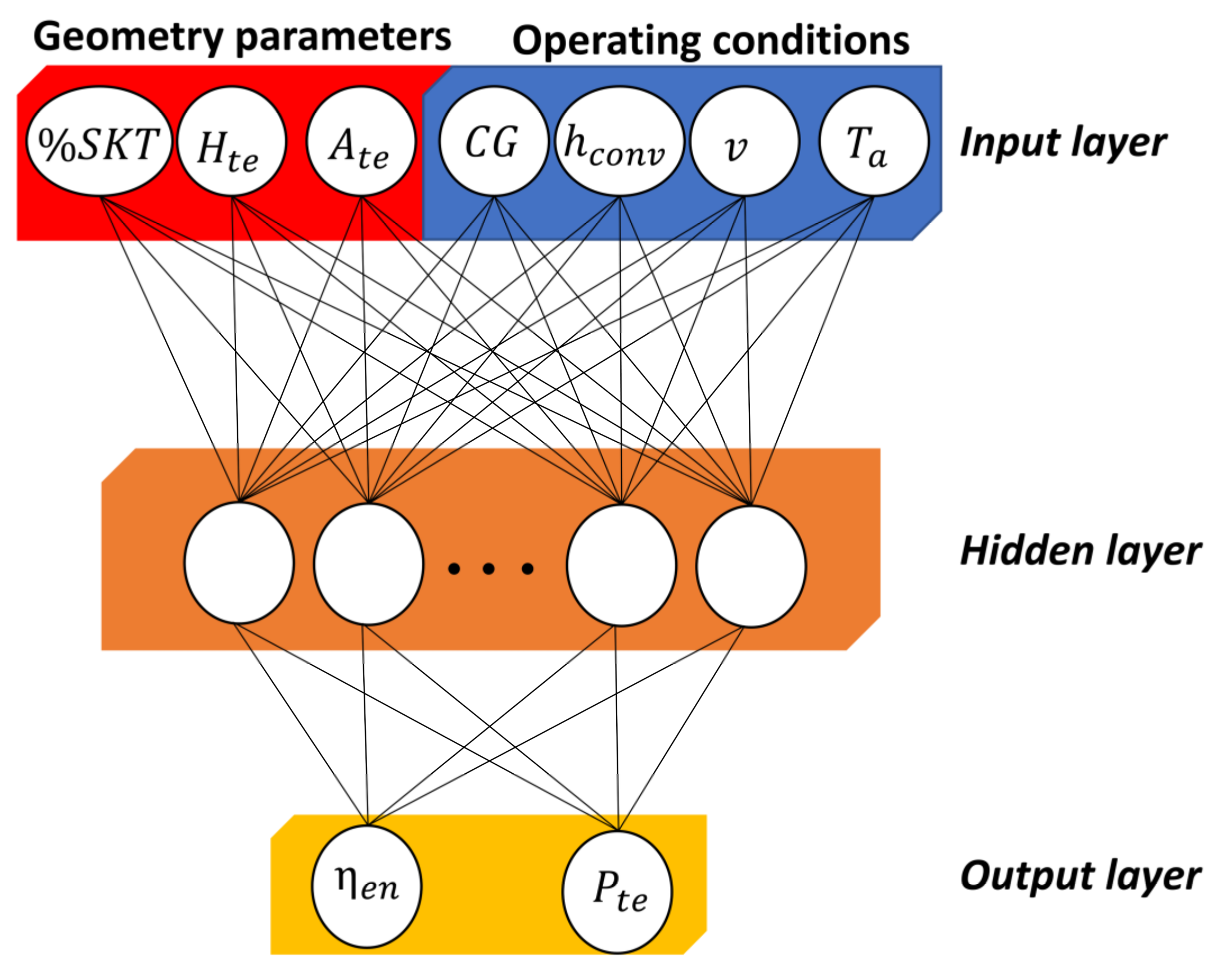
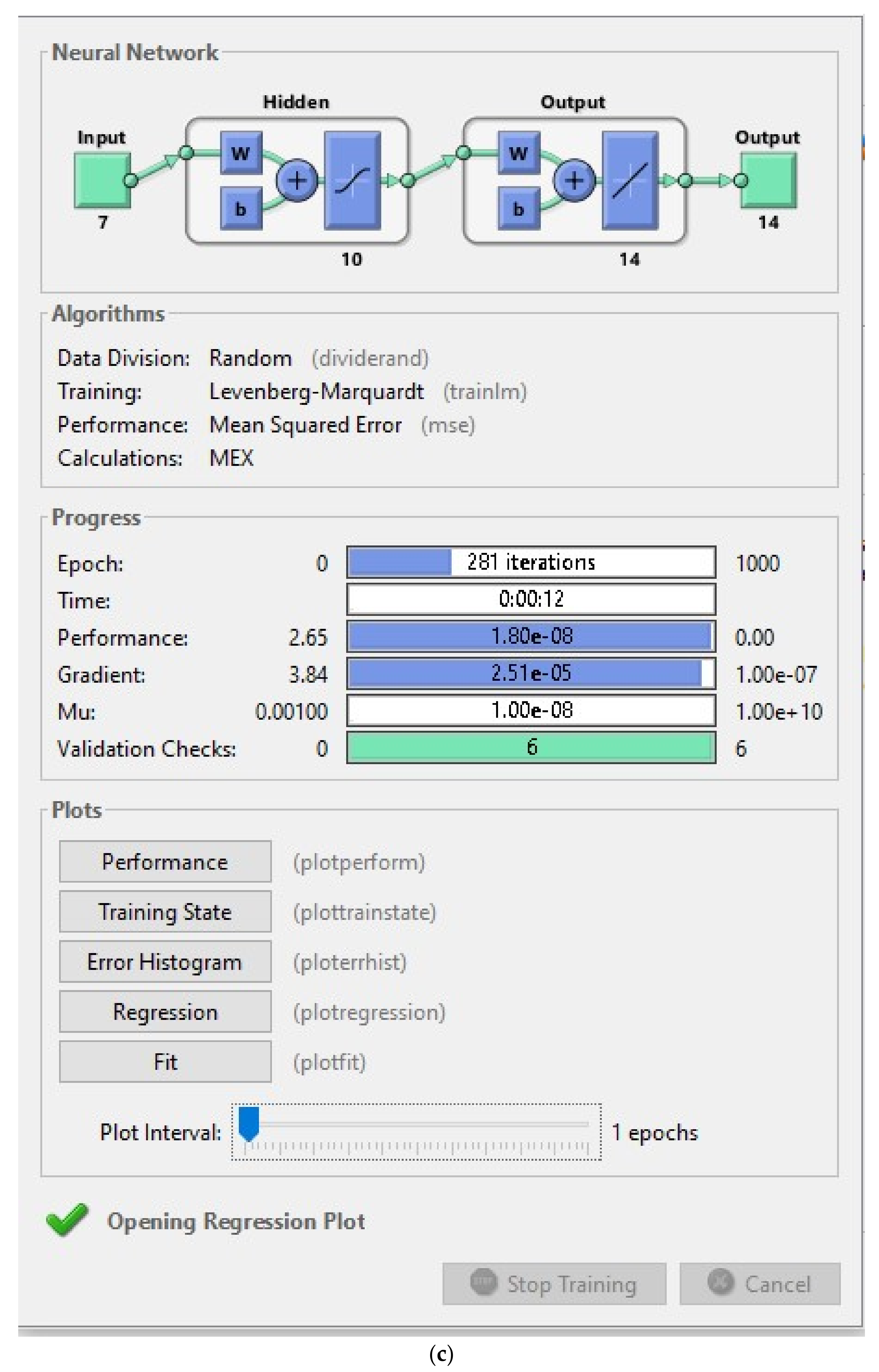
2.4. Configuring the ANN
3. Results
4. Discussion
5. Conclusions
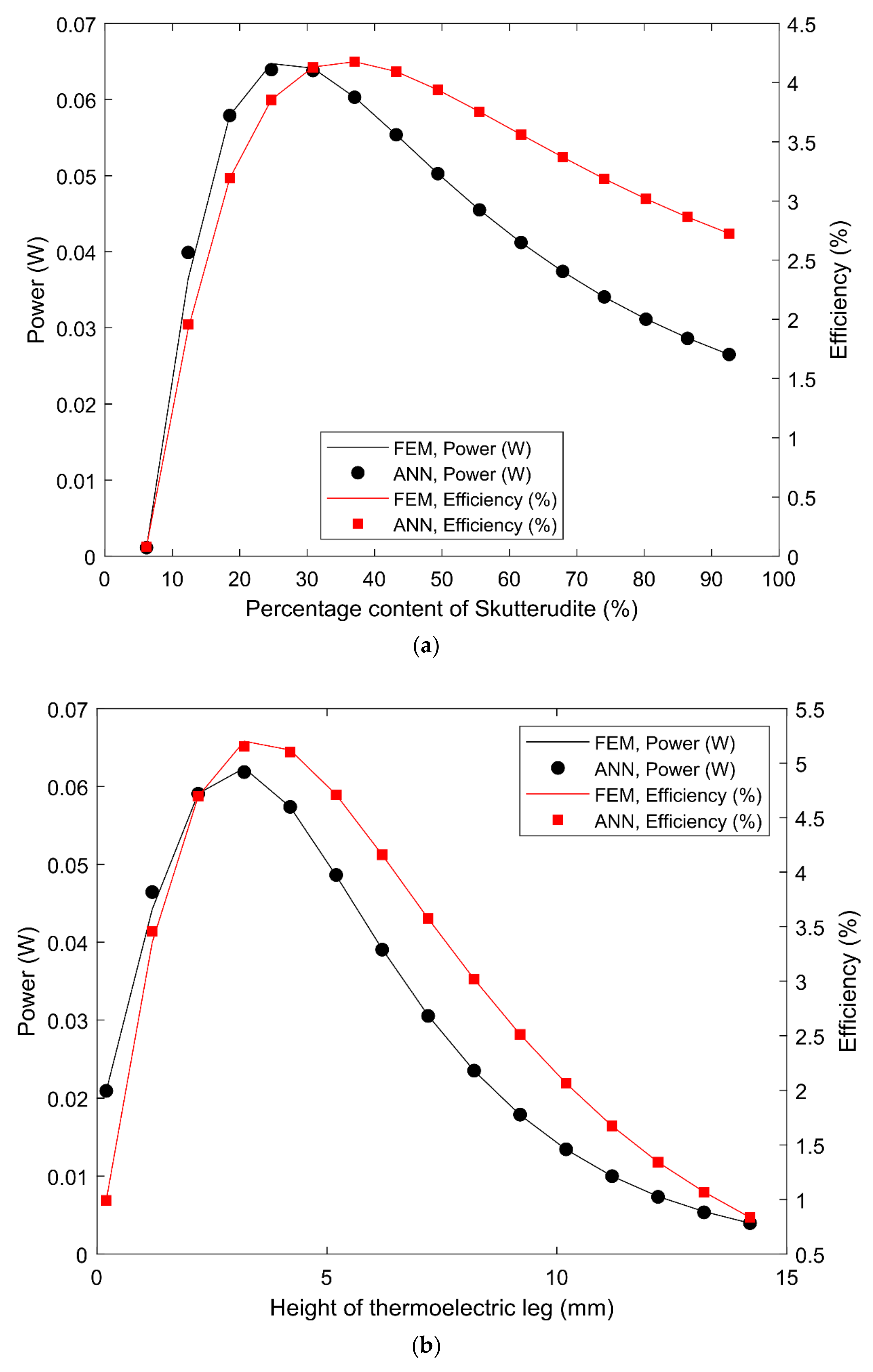
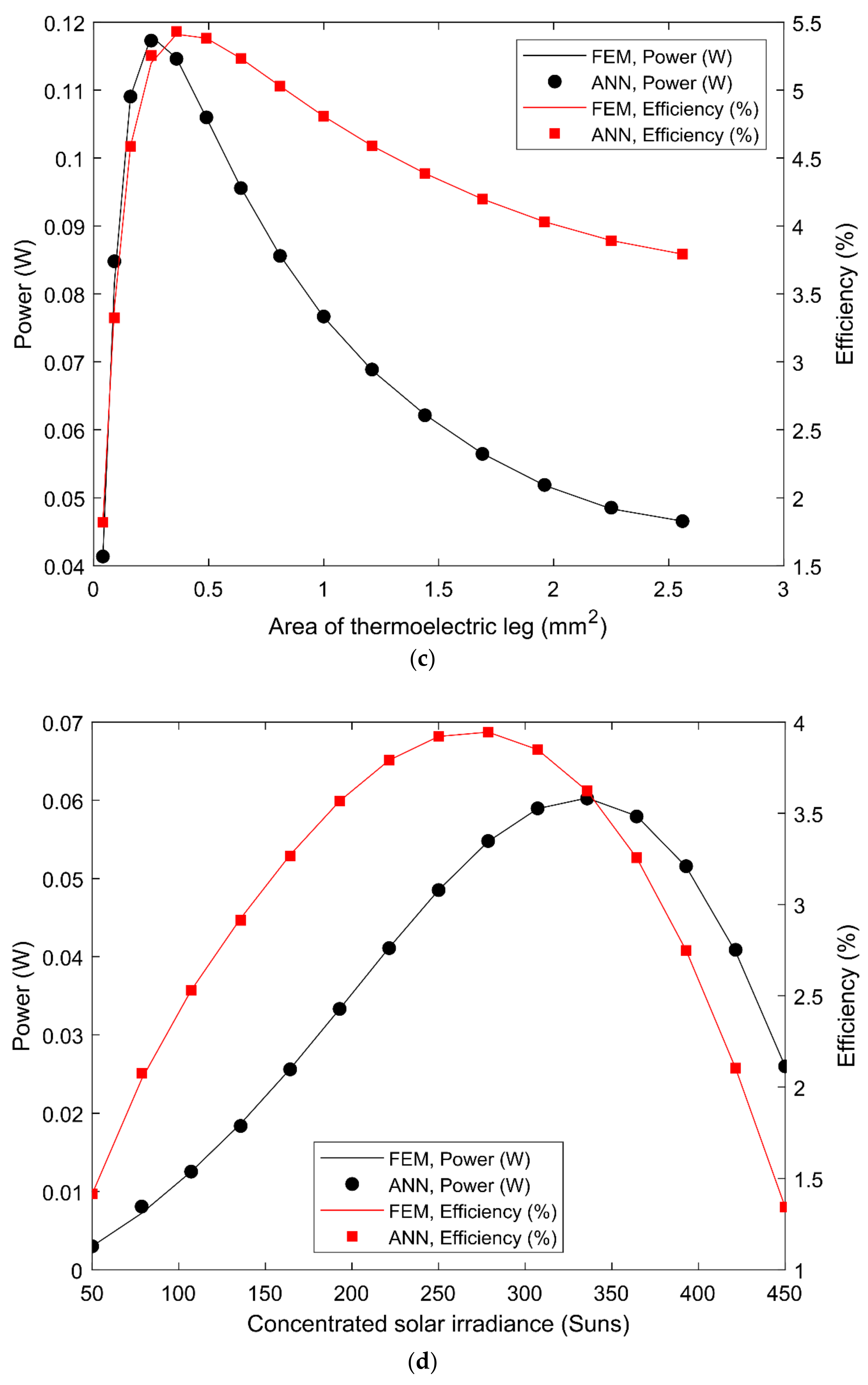
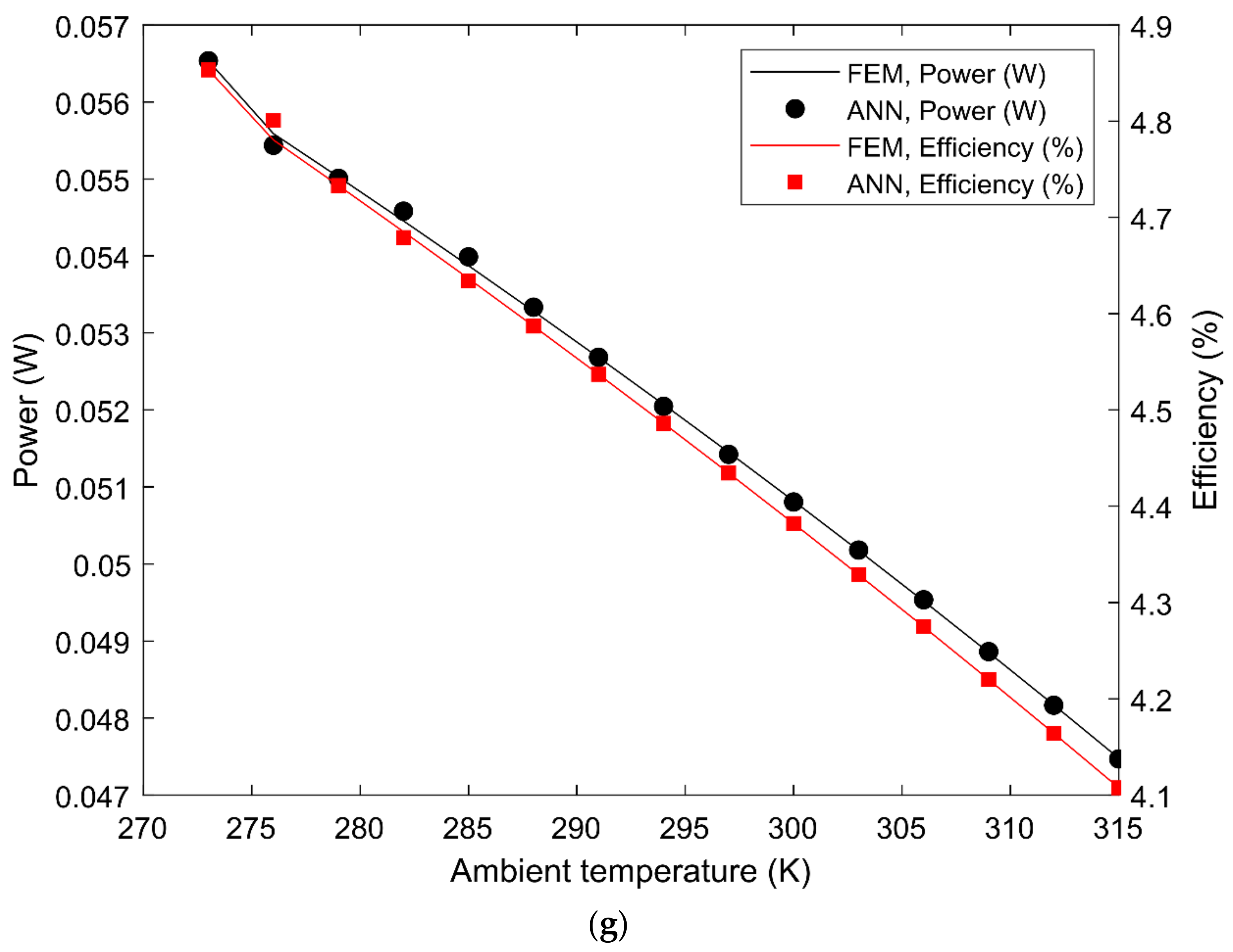
- The optimum parameters for maximum device power and efficiency were calculated and obtained by using a verified finite element method developed in ANSYS. The optimum parameters were very different from the original operating parameters that were specified by the manufacturers and device operators. At the end of the optimization, the performance of the original device and the optimized device were compared, and it was found that the power and efficiency of the optimized device were 3 and 2 higher than that of the original device, respectively;
- The multilayer perceptron regressive artificial neural network built using MATLAB codes was found to be very accurate in learning the data generated by the finite element method. The training, testing, and validation regression were 100%, 100%, and 99.95%, respectively. Furthermore, it was found that the best validation loss function (mean squared error) of 0.004 was obtained after 275 iterations. Additionally, the lowest mean squared error of 1.8 10−8 was obtained during the training process. Most importantly, it was shown that the neural network perfectly learnt the finite element data in just 12 s, which was more than 800 faster than the finite-element-method-based solver. Therefore, the neural network fitting approach is more efficient in predicting the performance of any thermoelectric generator given some predefined input, thus, facilitating the fast production of high-performing thermoelectric devices;
- Many interesting findings were uncovered in this study; however, there is always room for future studies in every good research endeavor. The next study will seek to model a fully modified thermoelectric device made of several thermoelectric cells to find the optimum number of couples that produces the highest performance in the modified device design. After that, a neural network fitting approach will be introduced to quickly facilitate the ease and speed at which optimization information can be drawn to model very efficient, high-performing thermoelectric devices. Thereafter, the operational lifetime of a circular leg thermoelectric generator and the proposed trapezoidal leg thermoelectric generator will be compared when operated under the same solar flux boundary conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anaadumba, R.; Liu, Q.; Marah, B.D.; Nakoty, F.M.; Liu, X.; Zhang, Y. A Renewable Energy Forecasting and Control Approach to Secured Edge-Level Efficiency in a Distributed Micro-Grid. Cybersecurity 2021, 4, 1. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. The Solar Energy Assessment Methods for Nigeria: The Current Status, the Future Directions and a Neural Time Series Method. Renew. Sustain. Energy Rev. 2020, 92, 146–159. [Google Scholar] [CrossRef]
- Li, M.; Xu, S.; Chen, Q.; Zheng, L.-R. Thermoelectric-Generator-Based DC–DC Conversion Networks for Automotive Applications. J. Electron. Mater. 2011, 40, 1136–1143. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, Y.-C.; Xiao, L. Conceptual Design and Performance Analysis of Concentrated Solar-Driven TIC/AMTEC/TEG Hybrid System. Int. J. Energy Res. 2018, 42, 4674–4686. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A. Optimization of a Cooling System Based on Peltier Effect for Photovoltaic Cells. Sol. Energy 2013, 91, 152–160. [Google Scholar] [CrossRef]
- Rowe, D.M. Thermoelectrics, an Environmentally-Friendly Source of Electrical Power. Renew. Energy 1999, 16, 1251–1256. [Google Scholar] [CrossRef]
- Lee, H. Thermoelectrics, 1st ed.; John Wiley & Sons Ltd.: West Sussex, UK, 2017; ISBN 9781118848951. [Google Scholar]
- Shi, Y.; Wang, Y.; Mei, D.; Feng, B.; Chen, Z. Design and Fabrication of Wearable Thermoelectric Generator Device for Heat Harvesting. IEEE Robot. Autom. Lett. 2018, 3, 373–378. [Google Scholar] [CrossRef]
- Zheng, X.F.; Liu, C.X.; Yan, Y.Y.; Wang, Q. A Review of Thermoelectrics Research—Recent Developments and Potentials for Sustainable and Renewable Energy Applications. Renew. Sustain. Energy Rev. 2014, 32, 486–503. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Lee, M.-Y. Numerical Study on Geometric Parameter Effects of Power Generation Performances for Segmented Thermoelectric Generator. Int. J. Air-Cond. Refrig. 2018, 26, 1850004. [Google Scholar] [CrossRef]
- Hong, M.; Zheng, K.; Lyv, W.; Li, M.; Qu, X.; Sun, Q.; Xu, S.; Zou, J.; Chen, Z.-G. Computer-Aided Design of High-Efficiency GeTe-Based Thermoelectric Devices. Energy Environ. Sci. 2020, 13, 1856–1864. [Google Scholar] [CrossRef]
- Khan, A.U.; Kobayashi, K.; Tang, D.M.; Yamauchi, Y.; Hasegawa, K.; Mitome, M.; Xue, Y.; Jiang, B.; Tsuchiya, K.; Golberg, D.; et al. Nano-Micro-Porous Skutterudites with 100% Enhancement in ZT for High Performance Thermoelectricity. Nano Energy 2017, 31, 152–159. [Google Scholar] [CrossRef]
- Ghomian, T.; Kizilkaya, O.; Domulevicz, L.K.; Hihath, J. Molecular Quantum Interference Effects on Thermopower in Hybrid 2-Dimensional Monolayers. Nanoscale 2022, 14, 6248–6257. [Google Scholar] [CrossRef]
- Ghomian, T.; Mehraeen, S. Survey of Energy Scavenging for Wearable and Implantable Devices. Energy 2019, 178, 33–49. [Google Scholar] [CrossRef]
- Ghomian, T.; Darwish, N.; Hihath, J. Thickness-Dependent Seebeck Coefficient in Hybrid 2-Dimensional Layers. In Proceedings of the 2021 IEEE 16th Nanotechnology Materials and Devices Conference (NMDC), Vancouver, BC, Canada, 12–15 December 2021; pp. 1–4. [Google Scholar] [CrossRef]
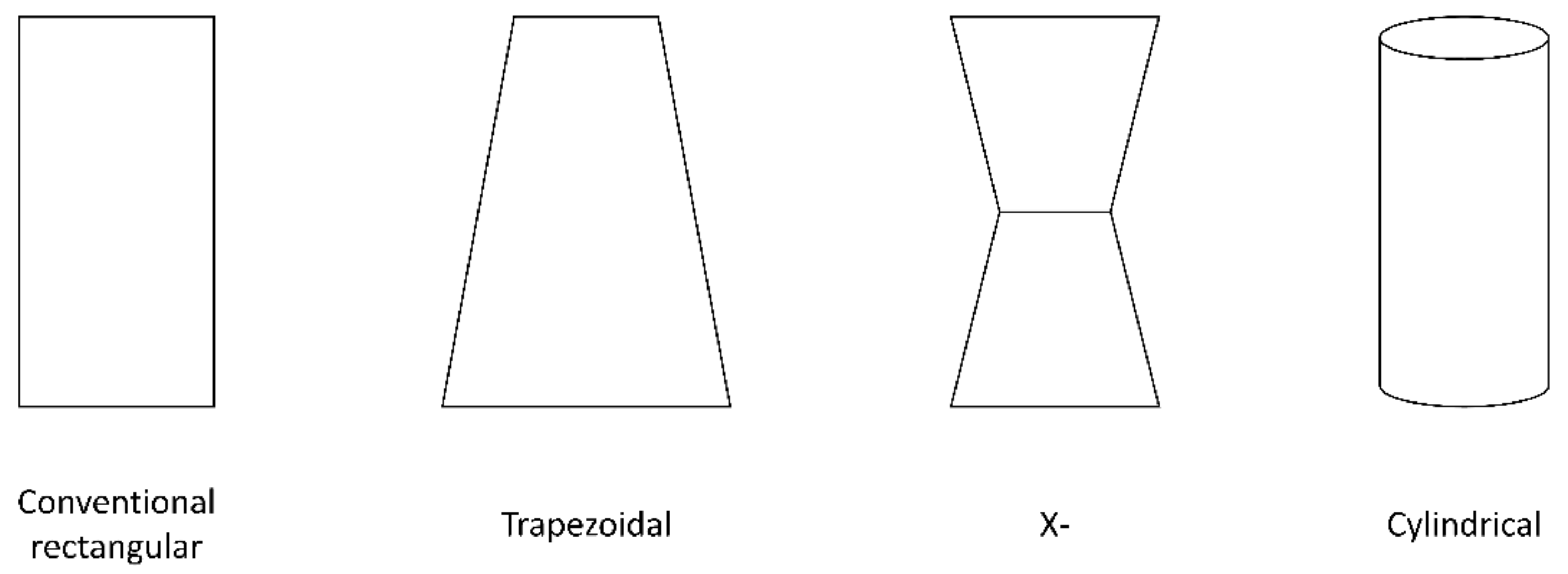
- Şişik, B.; LeBlanc, S. The Influence of Leg Shape on Thermoelectric Performance Under Constant Temperature and Heat Flux Boundary Conditions. Front. Mater. 2020, 7, 595955. [Google Scholar] [CrossRef]
- Pina, A.; Ferrão, P.; Fournier, J.; Lacarrière, B.; Corre, O. Le Optimizing on Thermoelectric Elements Footprint of the for Maximum Power Generation Assessing the Guiqiang Feasibility of Using the Jin Heat Temperature Function District Forecast. Energy Procedia 2017, 142, 730–735. [Google Scholar] [CrossRef]
- Ibeagwu, O.I. Modelling and Comprehensive Analysis of TEGs with Diverse Variable Leg Geometry. Energy 2019, 180, 90–106. [Google Scholar] [CrossRef]
- Olivares-Robles, M.A.; Badillo-Ruiz, C.A.; Ruiz-Ortega, P.E. A Comprehensive Analysis on Nanostructured Materials in a Thermoelectric Micro-System Based on Geometric Shape, Segmentation Structure and Load Resistance. Sci. Rep. 2020, 10, 21659. [Google Scholar] [CrossRef]
- Wang, R.; Meng, Z.; Luo, D.; Yu, W.; Zhou, W. A Comprehensive Study on X-Type Thermoelectric Generator Modules. J. Electron. Mater. 2020, 49, 4343–4354. [Google Scholar] [CrossRef]
- Ranjan, M.; Maiti, T. Device Modeling and Performance Optimization of Thermoelectric Generators under Isothermal and Isoflux Heat Source Condition. J. Power Sources 2020, 480, 228867. [Google Scholar] [CrossRef]
- Ali, H.; Yilbas, B.S.; Al-Sharafi, A. Segmented Thermoelectric Generator: Exponential Area Variation in Leg. Int. J. Energy Res. 2018, 42, 477–489. [Google Scholar] [CrossRef]
- Thimont, Y.; LeBlanc, S. The Impact of Thermoelectric Leg Geometries on Thermal Resistance and Power Output. J. Appl. Phys. 2019, 126, 095101. [Google Scholar] [CrossRef]
- Maduabuchi, C.; Njoku, H.; Eke, M.; Mgbemene, C.; Lamba, R.; Ibrahim, J.S. Overall Performance Optimisation of Tapered Leg Geometry Based Solar Thermoelectric Generators under Isoflux Conditions. J. Power Sources 2021, 500, 229989. [Google Scholar] [CrossRef]
- Maduabuchi, C.; Lamba, R.; Njoku, H.; Eke, M.; Mgbemene, C. Effects of Leg Geometry and Multistaging of Thermoelectric Modules on the Performance of a Photovoltaic-thermoelectric System Using Different Photovoltaic Cells. Int. J. Energy Res. 2021, 45, 17888–17902. [Google Scholar] [CrossRef]
- Yamada, T.; Miyazaki, Y.; Yamane, H. Preparation of Higher Manganese Silicide (HMS) Bulk and Fe-Containing HMS Bulk Using a Na-Si Melt and Their Thermoelectrical Properties. Thin Solid Films 2011, 519, 8524–8527. [Google Scholar] [CrossRef]
- Barber, E. Thermoelectric Materials; Taylor & Francis Group: Boca Raton, FL, USA, 2015; ISBN 9789814463539. [Google Scholar]
- Lee, M.-Y.; Seo, J.; Lee, H.; Garud, K.S. Power Generation, Efficiency and Thermal Stress of Thermoelectric Module with Leg Geometry, Material, Segmentation and Two-Stage Arrangement. Symmetry 2020, 12, 786. [Google Scholar] [CrossRef]
- Su, Q.; Engel, D.T.G. Modeling and Simulation of a Segmented Thermoelectric Generator. Ph.D. Thesis, University of Missouri, Columbia, IN, USA, 2017. [Google Scholar]
- Shittu, S.; Li, G.; Xuan, Q.; Zhao, X.; Ma, X.; Cui, Y. Electrical and Mechanical Analysis of a Segmented Solar Thermoelectric Generator under Non-Uniform Heat Flux. Energy 2020, 199, 117433. [Google Scholar] [CrossRef]
- Cui, Y.J.; Wang, B.L.; Li, J.E.; Wang, K.F. Performance Evaluation and Lifetime Prediction of a Segmented Photovoltaic-Thermoelectric Hybrid System. Energy Convers. Manag. 2020, 211, 112744. [Google Scholar] [CrossRef]
- Liu, H.B.; Meng, J.H.; Wang, X.D.; Chen, W.H. A New Design of Solar Thermoelectric Generator with Combination of Segmented Materials and Asymmetrical Legs. Energy Convers. Manag. 2018, 175, 11–20. [Google Scholar] [CrossRef]
- Fan, S.; Gao, Y. Numerical Analysis on the Segmented Annular Thermoelectric Generator for Waste Heat Recovery. Energy 2019, 183, 35–47. [Google Scholar] [CrossRef]
- Ruiz-Ortega, P.E.; Olivares-Robles, M.A.; Badillo-Ruiz, C.A. Transient Thermal Behavior of a Segmented Thermoelectric Cooler with Variable Cross-Sectional Areas. Int. J. Energy Res. 2021, 45, 19215–19225. [Google Scholar] [CrossRef]
- Kishore, R.; Mahajan, R.; Priya, S. Combinatory Finite Element and Artificial Neural Network Model for Predicting Performance of Thermoelectric Generator. Energies 2018, 11, 2216. [Google Scholar] [CrossRef]
- Lee, Y.; Tay, A.A.O. Stress Analysis of Silicon Wafer-Based Photovoltaic Modules Under IEC 61215 Mechanical Load Test. In Proceedings of the PV Asia Pacific Conference, Marine Bay Sands, Singapore, 29–30 October 2013; Volume 33, pp. 265–271. [Google Scholar]
- Fagehi, H.; Attar, A.; Lee, H. Optimal Design of an Automotive Exhaust Thermoelectric Generator. J. Electron. Mater. 2018, 47, 3983–3995. [Google Scholar] [CrossRef]
- Elarusi, A.H.; Fagehi, H.; Lee, H.; Attar, A. Theoretical Approach to Predict the Performance of Thermoelectric Generator Modules. J. Electron. Mater. 2017, 46, 872–881. [Google Scholar] [CrossRef]
- Lamba, R.; Manikandan, S.; Kaushik, S.C.; Tyagi, S.K. Thermodynamic Modelling and Performance Optimization of Trapezoidal Thermoelectric Cooler Using Genetic Algorithm. Therm. Sci. Eng. Prog. 2018, 6, 236–250. [Google Scholar] [CrossRef]
- Maduabuchi, C. Thermo-Mechanical Optimization of Thermoelectric Generators Using Deep Learning Artificial Intelligence Algorithms Fed with Verified Finite Element Simulation Data. Appl. Energy 2022, 315, 118943. [Google Scholar] [CrossRef]
- Mazzeo, D.; Herdem, M.S.; Matera, N.; Bonini, M.; Wen, J.Z.; Nathwani, J.; Oliveti, G. Artificial Intelligence Application for the Performance Prediction of a Clean Energy Community. Energy 2021, 232, 120999. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Mattei, M.; Poggi, P. Modelling of a Double-Glass Photovoltaic Module Using Finite Differences. Appl. Therm. Eng. 2005, 25, 2854–2877. [Google Scholar] [CrossRef]
- Chen, W.; Chiou, Y. Geometry Design for Maximizing Output Power of Segmented Skutterudite Thermoelectric Generator by Evolutionary Computation. Appl. Energy 2020, 274, 115296. [Google Scholar] [CrossRef]
- He, H.; Liu, W.; Wu, Y.; Rong, M.; Zhao, P.; Tang, X. An Approximate and Efficient Characterization Method for Temperature-Dependent Parameters of Thermoelectric Modules. Energy Convers. Manag. 2019, 180, 584–597. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X.; Golizadeh, Y.; Fan, Y. Comprehensive Study and Optimization of Concentrated Photovoltaic- Thermoelectric Considering All Contact Resistances. Energy Convers. Manag. 2020, 205, 112422. [Google Scholar] [CrossRef]
- Xuan, X.; Ng, K.; Yap, C.; Chua, H. The Maximum Temperature Difference and Polar Characteristic of Two-Stage Thermoelectric Coolers. Cryogenics 2002, 42, 273–278. [Google Scholar] [CrossRef]
- Maduabuchi, C.C.; Mgbemene, C.A. Numerical Study of a Phase Change Material Integrated Solar Thermoelectric Generator. J. Electron. Mater. 2020, 49, 5917–5936. [Google Scholar] [CrossRef]
- Maduabuchi, C.C.; Mgbemene, C.A.; Ibeagwu, O.I. Thermally Induced Delamination of PV-TEG: Implication of Leg’s Joule and Thomson Heating. J. Electron. Mater. 2020, 49, 6417–6427. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X.; Akhlaghi, Y.G.; Ayodele, E. High Performance and Thermal Stress Analysis of a Segmented Annular Thermoelectric Generator. Energy Convers. Manag. 2019, 184, 180–193. [Google Scholar] [CrossRef]
- Kraemer, D.; Jie, Q.; McEnaney, K.; Cao, F.; Liu, W.; Weinstein, L.A.; Loomis, J.; Ren, Z.; Chen, G. Concentrating Solar Thermoelectric Generators with a Peak Efficiency of 7.4%. Nat. Energy 2016, 1, 16153. [Google Scholar] [CrossRef]
- Maduabuchi, C.C.; Eke, M.N.; Mgbemene, C.A. Solar Power Generation Using a Two-stage X-leg Thermoelectric Generator with High-temperature Materials. Int. J. Energy Res. 2021, 45, 13163–13181. [Google Scholar] [CrossRef]
- Lamba, R.; Manikandan, S.; Kaushik, S.C. Performance Analysis and Optimization of Concentrating Solar Thermoelectric Generator. J. Electron. Mater. 2018, 47, 5310–5320. [Google Scholar] [CrossRef]
- Luo, Y.; Kim, C.N. Effects of the Cross-Sectional Area Ratios and Contact Resistance on the Performance of a Cascaded Thermoelectric Generator. Int. J. Energy Res. 2019, 43, 2172–2187. [Google Scholar] [CrossRef]
- Karri, N.K.; Mo, C. Structural Reliability Evaluation of Thermoelectric Generator Modules: Influence of End Conditions, Leg Geometry, Metallization, and Processing Temperatures. J. Electron. Mater. 2018, 47, 6101–6120. [Google Scholar] [CrossRef]
- Li, W.; Paul, M.C.; Montecucco, A.; Knox, A.R.; Siviter, J.; Sellami, N.; Meng, X.; Fernandez, E.F.; Mallick, T.K.; Mullen, P.; et al. Multiphysics Simulations of a Thermoelectric Generator. Energy Procedia 2015, 75, 633–638. [Google Scholar] [CrossRef]
- Erturun, U.; Erermis, K.; Mossi, K. Influence of Leg Sizing and Spacing on Power Generation and Thermal Stresses of Thermoelectric Devices. Appl. Energy 2015, 159, 19–27. [Google Scholar] [CrossRef]
- Wang, X.; Qi, J.; Deng, W.; Li, G.; Gao, X.; He, L.; Zhang, S. An Optimized Design Approach Concerning Thermoelectric Generators with Frustum-Shaped Legs Based on Three-Dimensional Multiphysics Model. Energy 2021, 233, 120810. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Wang, P.; Wang, K.; Xi, L.; Gao, R.; Wang, B. Fast and Accurate Performance Prediction and Optimization of Thermoelectric Generators with Deep Neural Networks. Adv. Mater. Technol. 2021, 6, 2100011. [Google Scholar] [CrossRef]
- Pang, Z.; Niu, F.; O’Neill, Z. Solar Radiation Prediction Using Recurrent Neural Network and Artificial Neural Network: A Case Study with Comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Garud, K.S.; Seo, J.-H.; Cho, C.-P.; Lee, M.-Y. Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery. Symmetry 2020, 12, 259. [Google Scholar] [CrossRef]
- Demeke, W.; Kim, Y.; Jung, J.; Chung, J.; Ryu, B.; Ryu, S. Neural Network-Assisted Optimization of Segmented Thermoelectric Power Generators Using Active Learning Based on a Genetic Optimization Algorithm. Energy Rep. 2022, 8, 6633–6644. [Google Scholar] [CrossRef]
- Zhu, Y.; Newbrook, D.W.; Dai, P.; de Groot, C.H.K.; Huang, R. Artificial Neural Network Enabled Accurate Geometrical Design and Optimisation of Thermoelectric Generator. Appl. Energy 2022, 305, 117800. [Google Scholar] [CrossRef]
- Kim, T.Y. Prediction of System-Level Energy Harvesting Characteristics of a Thermoelectric Generator Operating in a Diesel Engine Using Artificial Neural Networks. Energies 2021, 14, 2426. [Google Scholar] [CrossRef]
- Cai, L.; Li, P.; Luo, Q.; Zhai, P.; Zhang, Q. Geometry Optimization of a Segmented Thermoelectric Generator Based on Multi-Parameter and Nonlinear Optimization Method. J. Electron. Mater. 2017, 46, 1552–1566. [Google Scholar] [CrossRef]
- Yin, T.; Li, W.-T.; Li, K.; He, Z.-Z. Multi-Parameter Optimization and Uncertainty Analysis of Multi-Stage Thermoelectric Generator with Temperature-Dependent Materials. Energy Rep. 2021, 7, 7212–7223. [Google Scholar] [CrossRef]
- Li, G.; Shittu, S.; Ma, X.; Zhao, X. Comparative Analysis of Thermoelectric Elements Optimum Geometry between Photovoltaic-Thermoelectric and Solar Thermoelectric. Energy 2019, 171, 599–610. [Google Scholar] [CrossRef]
- Sun, D.; Shen, L.; Yao, Y.; Chen, H.; Jin, S.; He, H. The Real-Time Study of Solar Thermoelectric Generator. Appl. Therm. Eng. 2017, 119, 347–359. [Google Scholar] [CrossRef]
- Mahmoudinezhad, S.; Rezania, A.; Cotfas, P.A.; Cotfas, D.T.; Rosendahl, L.A. Transient Behavior of Concentrated Solar Oxide Thermoelectric Generator. Energy 2018, 168, 823–832. [Google Scholar] [CrossRef]
- Cheruvu, P.; Kumar, V.P.; Barshilia, H.C. Experimental Analysis and Evaluation of a Vacuum Enclosed Concentrated Solar Thermoelectric Generator Coupled with a Spectrally Selective Absorber Coating. Int. J. Sustain. Energy 2017, 37, 782–798. [Google Scholar] [CrossRef]
- Mahmoudinezhad, S.; Rezaniakolaei, A.; Rosendahl, L.A. Numerical Parametric Study on the Performance of CPV-TEG Hybrid System. Energy Procedia 2019, 158, 453–458. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Zabrocki, K.; Müller, E. TEG Design for Waste Heat Recovery at an Aviation Jet Engine Nozzle. Appl. Sci. 2018, 8, 2637. [Google Scholar] [CrossRef]
- Maduabuchi, C. Improving the Performance of a Solar Thermoelectric Generator Using Nano-Enhanced Variable Area Pins. Appl. Therm. Eng. 2022, 206, 118086. [Google Scholar] [CrossRef]
- Angeline, A.A.; Asirvatham, L.G.; Hemanth, D.J.; Jayakumar, J.; Wongwises, S. Performance Prediction of Hybrid Thermoelectric Generator with High Accuracy Using Artificial Neural Networks. Sustain. Energy Technol. Assess. 2019, 33, 53–60. [Google Scholar] [CrossRef]
- Maduabuchi, C.; Singh, S.; Ozoegwu, C.; Njoku, H.; Eke, M. The Combined Impacts of Leg Geometry Configuration and Multi-Staging on the Exergetic Performance of Thermoelectric Modules in a Solar Thermoelectric Generator. J. Energy Resour. Technol. 2022, 144, 041303. [Google Scholar] [CrossRef]
- Ge, Y.; Lin, Y.; He, Q.; Wang, W.; Chen, J.; Huang, S.M. Geometric Optimization of Segmented Thermoelectric Generators for Waste Heat Recovery Systems Using Genetic Algorithm. Energy 2021, 233, 121220. [Google Scholar] [CrossRef]
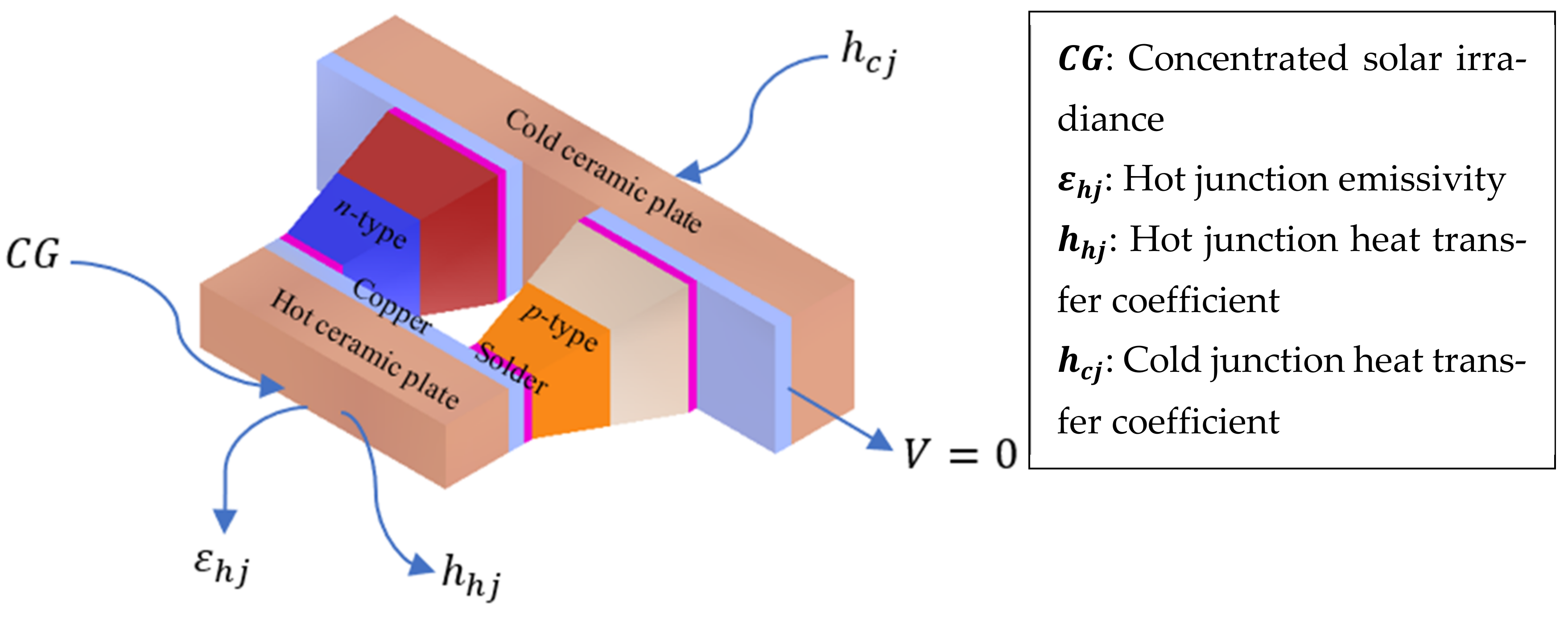
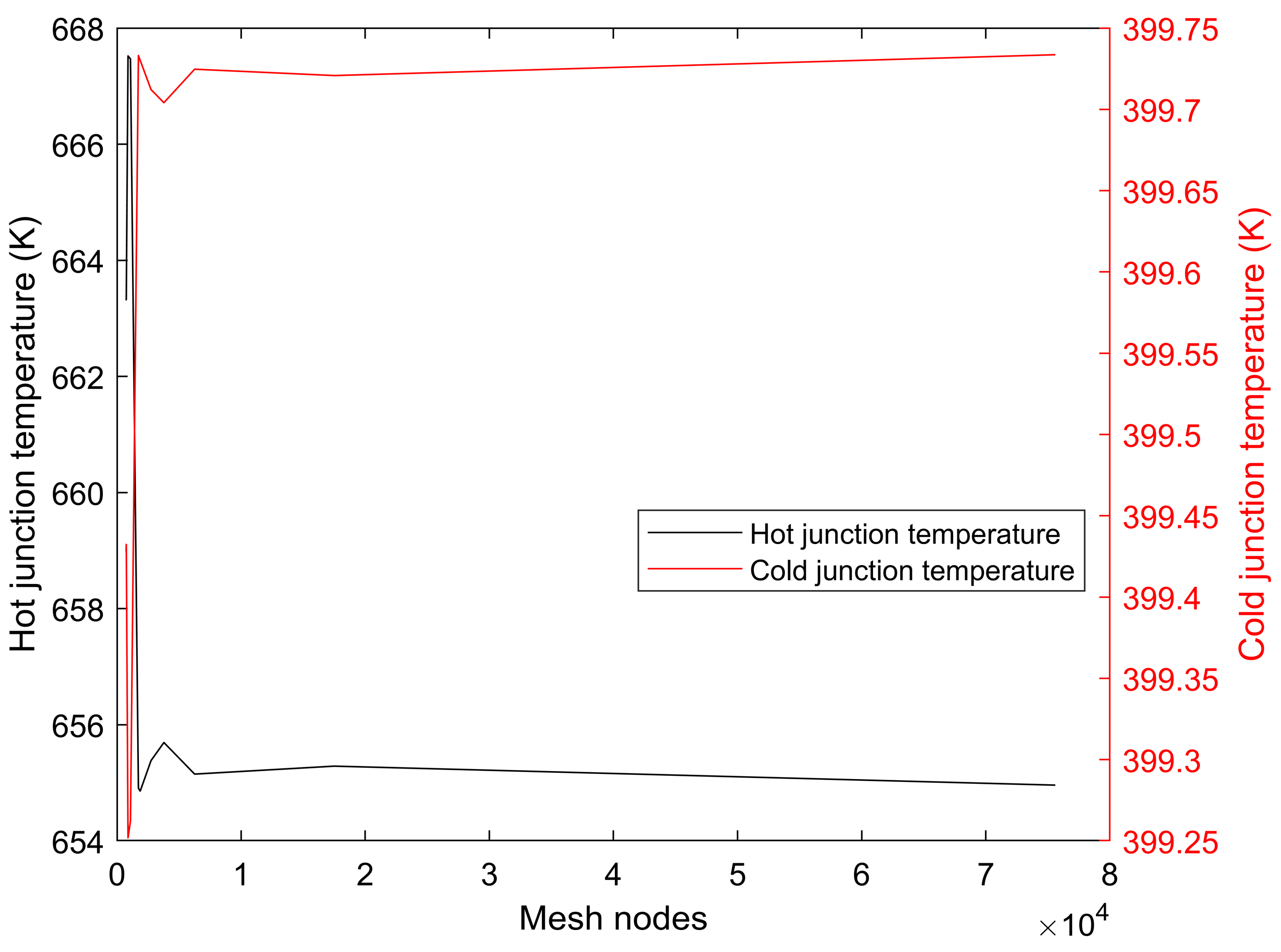
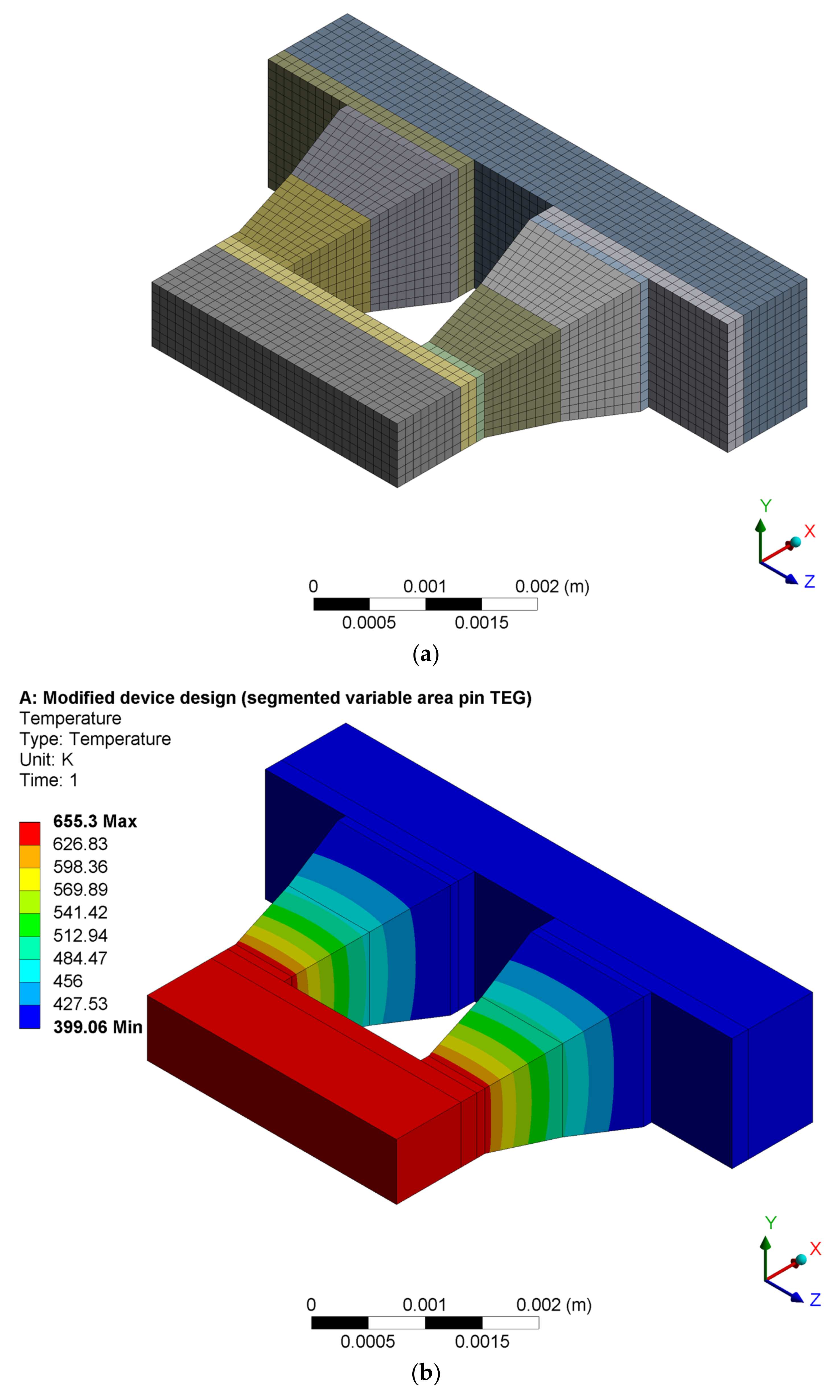
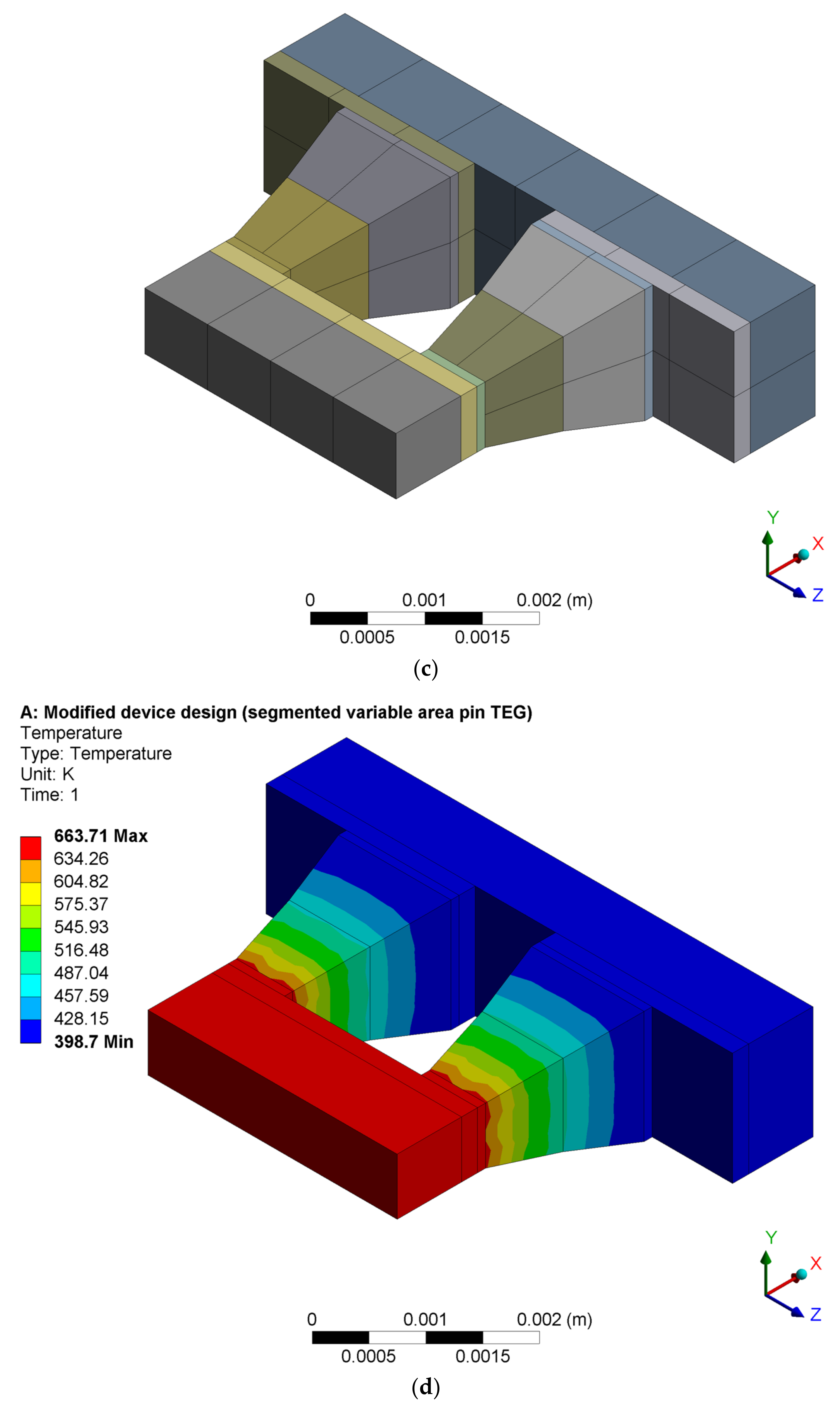



| S/N | Component | Height (mm) | Width (mm) | Depth (mm) |
|---|---|---|---|---|
| 1. | Hot ceramic plate | 0.8 | 3.1 | 0.7 |
| 2. | Cold ceramic plate | 0.8 | 5.8 | 0.7 |
| 3. | Copper | 0.2 | 3.1 | 0.7 |
| 4. | Solder (small) | 0.1 | 0.7 | 0.7 |
| 5. | Solder (big) | 0.1 | 1.4 | 1.4 |
| 6. | n-p-type (small) | 1.62 | 0.7 | 0.7 |
| 7. | n-p-type (big) | 1.62 | 1.4 | 1.4 |
| Property | Expression |
|---|---|
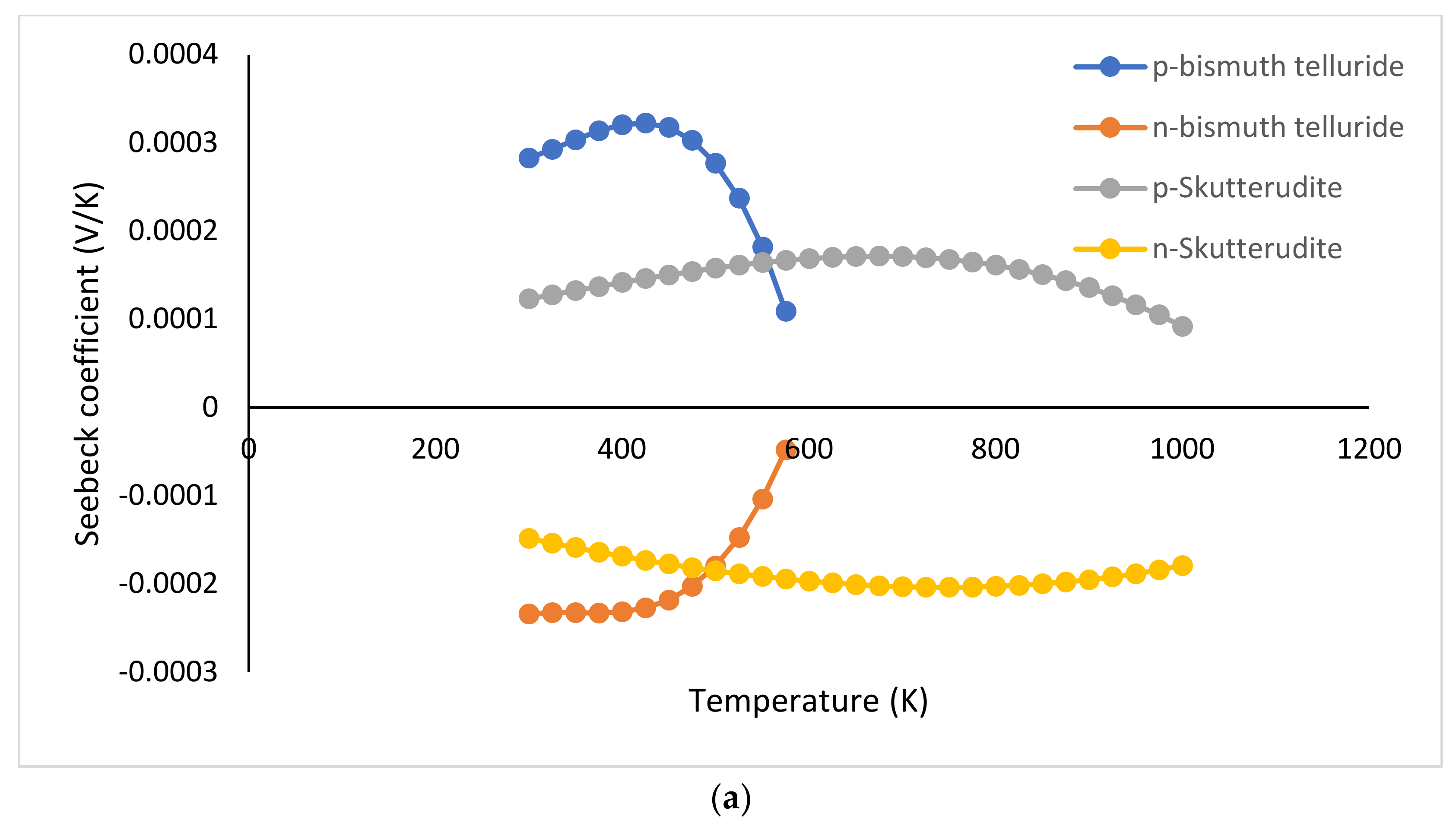
| Seebeck coefficient (V/K) | |
| p-BiTe | −2.24407 × 10−11T3 + 2.22834 × 10−8T2 − 7.301 × 10−6T + 1.023898 × 10−3 |
| n-BiTe | 1.68178 × 10−11T3 − 1.77163 × 10−8T2 + 6.203 × 10−6T − 9.54589 × 10−4 |
| p-SKT | 8.8139 × 10−5 − 3.6827 × 10−10T + 5.5507 × 10−10T2 − 5.0917 × 10−13T3 |
| n-SKT | −7.2398 × 10−5 − 2.7340 × 10−7T + 2.4331 × 10−10T2 + 1.4197 × 10−13T3 |
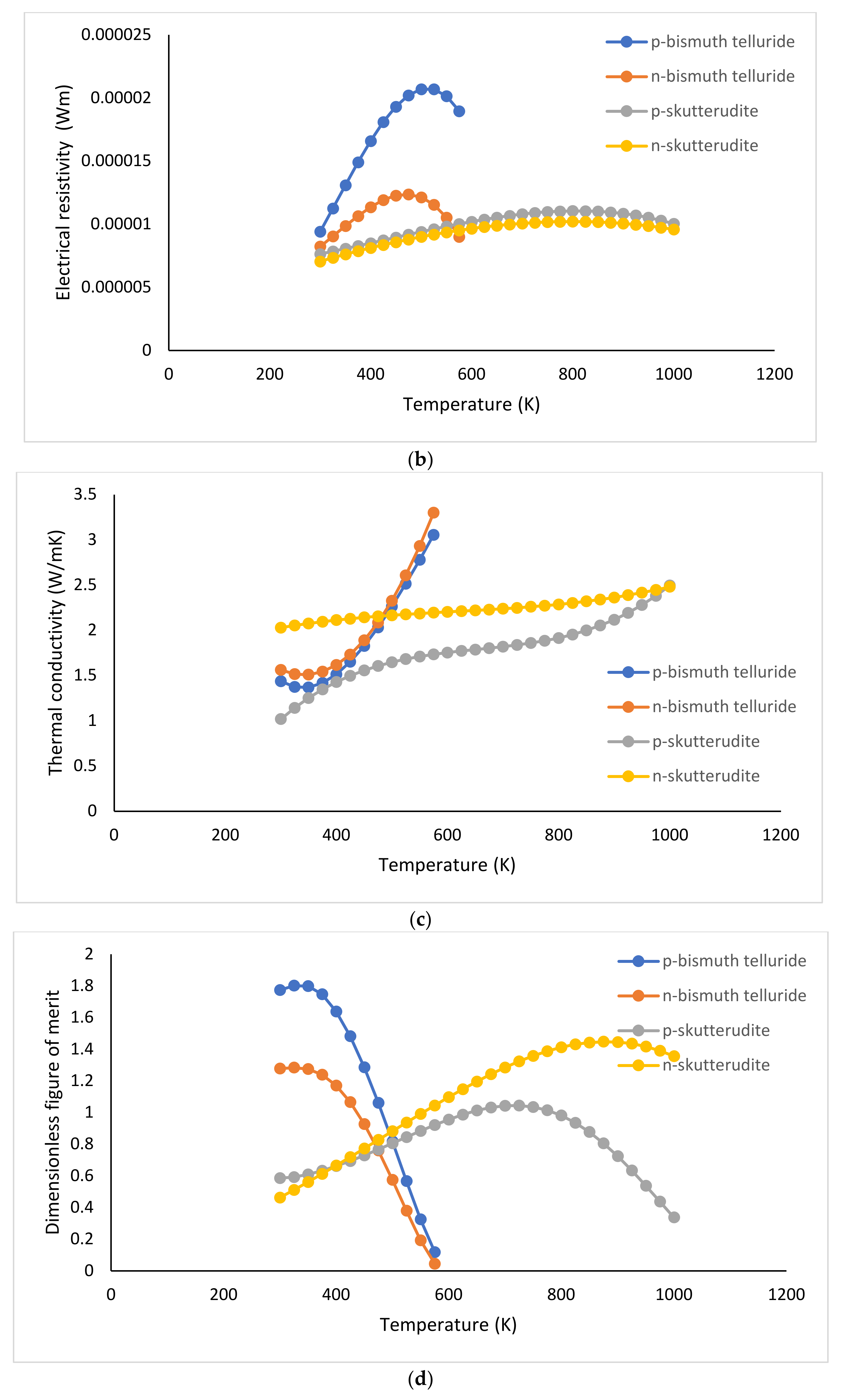
| Electrical resistivity (Wm) | |
| p-BiTe | −7.75456 × 10−13T3 + 7.77051 × 10−10T2 − 0.01853 × 10−5T + 1.60117 × 10−5 |
| n-BiTe | −6.04782 × 10−13T3 + 6.09155 × 10−10T2 − 1.715 × 10−7T + 2.11951 × 10−5 |
| p-SKT | 6.5155 × 10−6 − 2.3672 × 10−9T + 2.6624 × 10−11T2 − 2.0732 × 10−14T3 |
| n-SKT | 2.9221 × 10−6 + 1.5542 × 10−8T − 4.7078 × 10−12T2 − 4.1703 × 10−15T3 |
| Thermal conductivity (W/mK) | |
| p-BiTe | −5.82609 × 10−8T3 + 1.03491 × 10−4T2 − 0.05011T + 8.726 |
| n-BiTe | 3.76869 × 10−9T3 + 2.81722 × 10−5T2 − 0.02057T + 5.09531 |
| p-SKT | −2.0660 + 1.6390 × 10−2T − 2.4031 × 10−5T2 + 1.2202 × 10−8T3 |
| n-SKT | 1.4464 + 3.0553 × 10−3T − 4.4576 × 10−6T2 + 2.4360 × 10−9T3 |
| Dimensionless figure of merit | |
| p-BiTe | |
| n-BiTe | |
| p-SKT | |
| n-SKT |
| Material | Specific Heat Capacity (Jkg−1 K−1) | Density (kgm−3) | Thermal Conductivity (Wm−1 K−1) | Seebeck Coefficient (VK−1) | References | |
|---|---|---|---|---|---|---|
| Alumina | 900 | 3900 | 25 | - | - | [18] |
| Solder | 210 | 7240 | 37.8 | 5 × 10−8 | - | [30] |
| Copper | 800 | 3970 | 401 | 1.72 × 10−8 | - | [45] |
| BiTe | 154.4 | 7740 | [46] | |||
| SKT | 225 | 6800 | f(T) | f(T) | f(T) | [30] |
| S/N | Parameter | Unit | Original Values | Optimum Value |
|---|---|---|---|---|
| 1. | Percentage content of skutterudite | % | 50 | 37 |
| 2. | Height of thermoelectric leg | mm | 1.62 | 3.2 |
| 3. | Cross-sectional area of thermoelectric leg | mm2 | 1.96 | 0.36 |
| 4. | Concentrated solar irradiance | Suns | 250 | 279 |
| 5. | Convective cooling coefficient | kW/m2K | 0.5 | 3 |
| 6. | Wind speed | m/s | 1 | 0.5 |
| 7. | Ambient temperature | K | 295.15 | 273.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maduabuchi, C.; Fagehi, H.; Alatawi, I.; Alkhedher, M. Predicting the Optimal Performance of a Concentrated Solar Segmented Variable Leg Thermoelectric Generator Using Neural Networks. Energies 2022, 15, 6024. https://doi.org/10.3390/en15166024
Maduabuchi C, Fagehi H, Alatawi I, Alkhedher M. Predicting the Optimal Performance of a Concentrated Solar Segmented Variable Leg Thermoelectric Generator Using Neural Networks. Energies. 2022; 15(16):6024. https://doi.org/10.3390/en15166024
Chicago/Turabian StyleMaduabuchi, Chika, Hassan Fagehi, Ibrahim Alatawi, and Mohammad Alkhedher. 2022. "Predicting the Optimal Performance of a Concentrated Solar Segmented Variable Leg Thermoelectric Generator Using Neural Networks" Energies 15, no. 16: 6024. https://doi.org/10.3390/en15166024







