Digitalizing Structure–Symmetry Relations at the Formation of Endofullerenes in Terms of Information Entropy Formalism
Abstract
:1. Introduction
2. Preliminary Remarks
2.1. Mathematical Description of Fullerene Molecules
2.2. Information Entropy Formalism Applied to (Endo)Fullerenes
2.3. Topological Stability of the Fullerene Cages in Endofullerenes
3. Computational Details
3.1. Information Entropy Indices for the Analysis of Chemical Processes
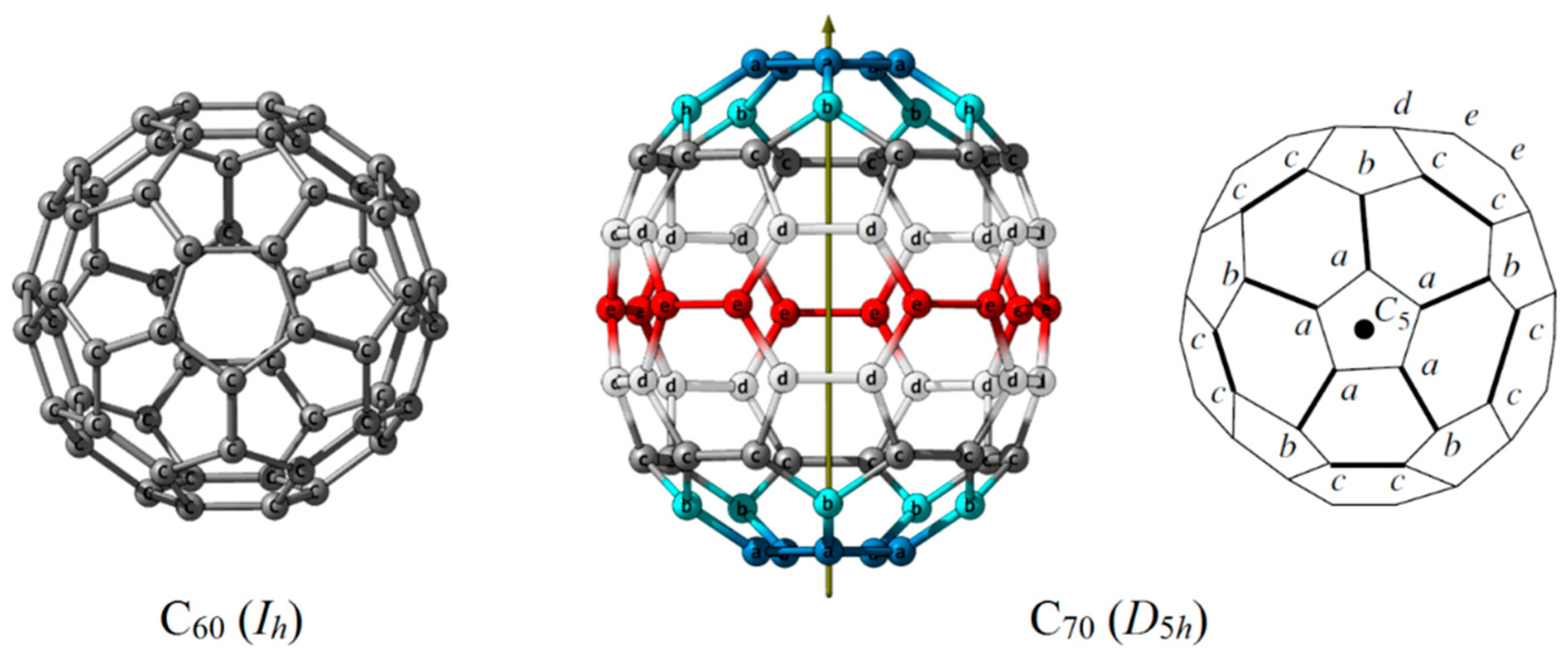
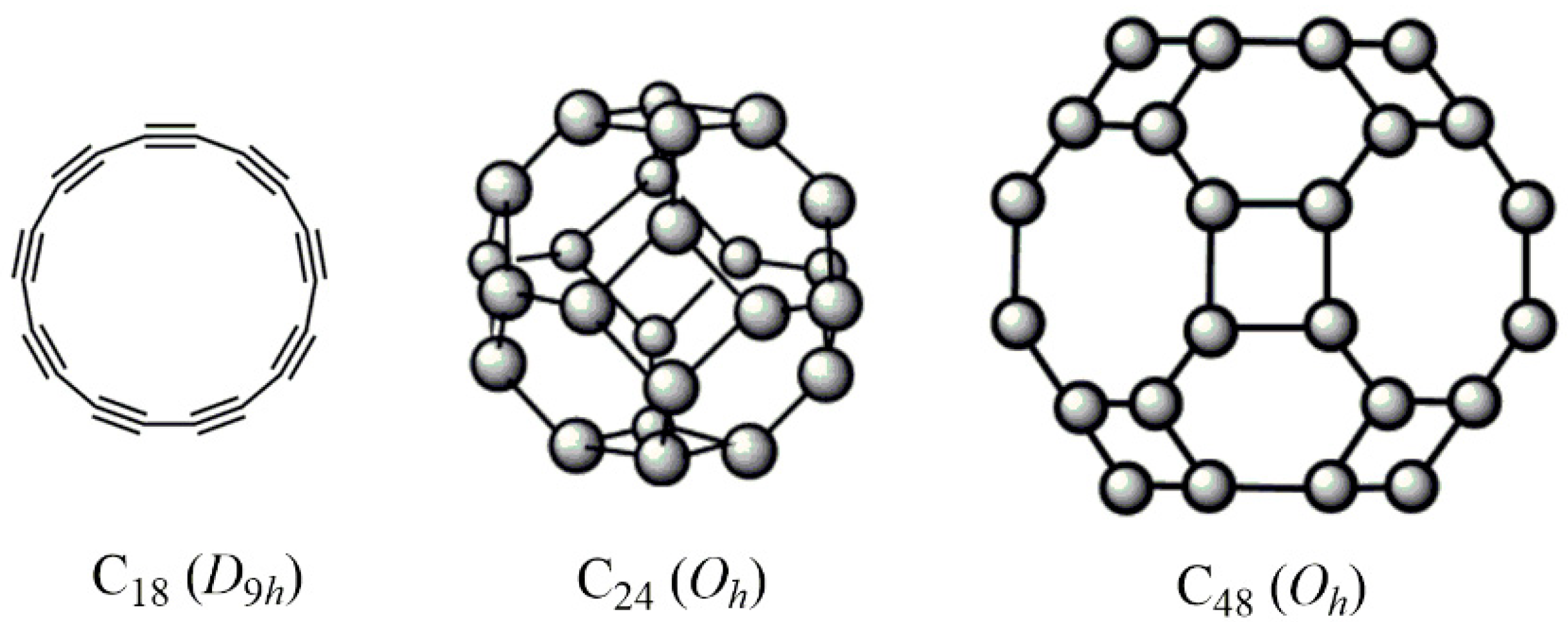
3.2. Structures of (Endo)Fullerenes for Analysis and Symmetry Determination
4. Results
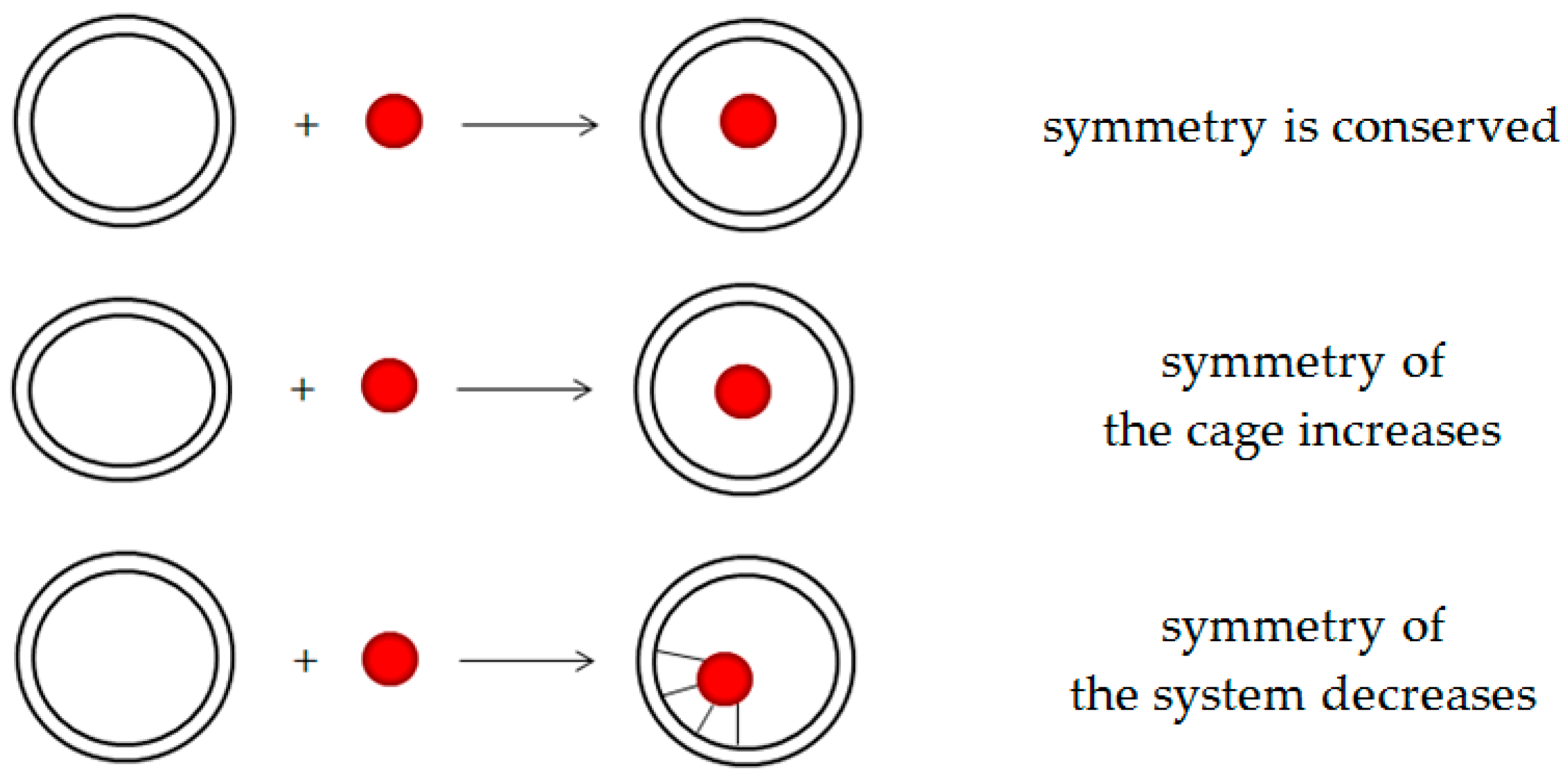
4.1. Introducing X into the Fullerene Cage: Ommon Analytical Expressions
4.2. Introducing X into a Zero-h Fullerene Cage While Serving Initial Symmetry
4.3. Introducing X into Maximum-h Fullerene Cage
4.4. Introducing X into the Fullerene Cage with Initially Reduced Symmetry
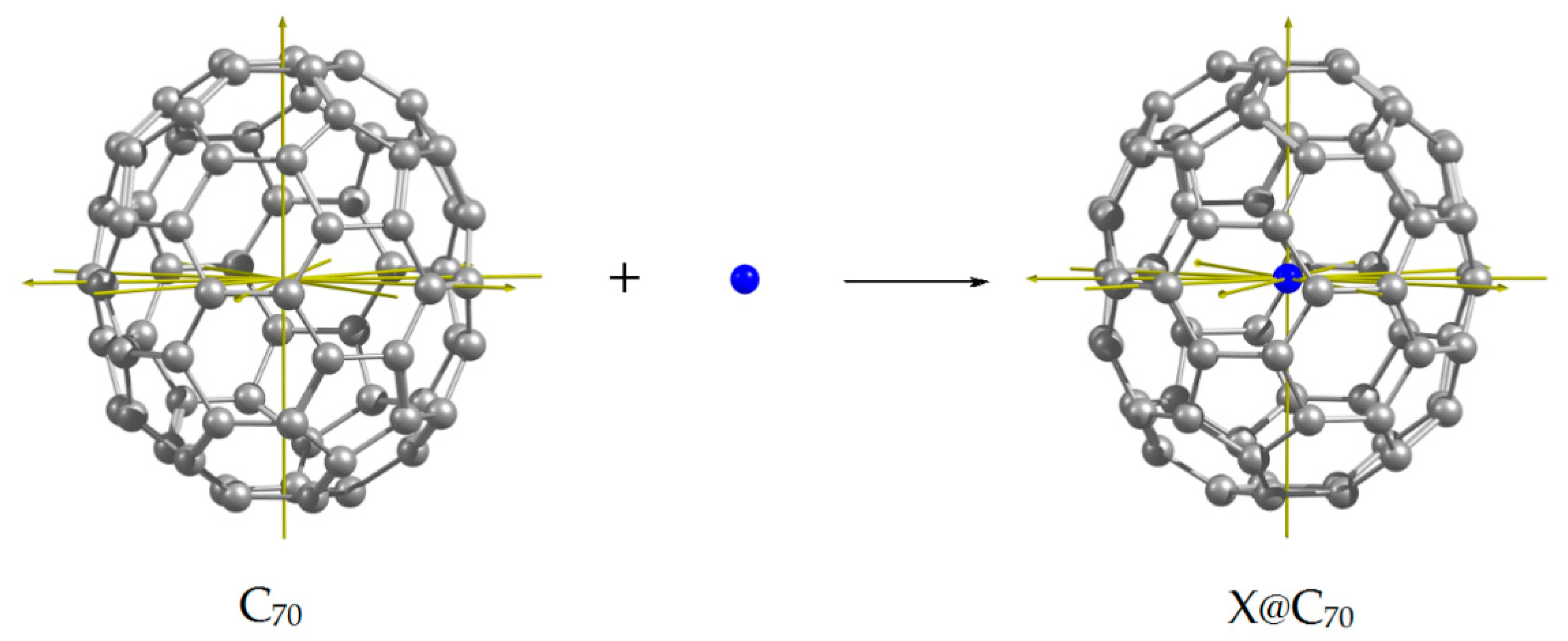
4.5. Introducing X into the Fullerene Cage with X Coordination Relative to the Cage
4.6. Information Entropy Indices of Processes X + CN → X@CN within Series of Isomeric Fullerenes
5. Discussion
5.1. General Remarks
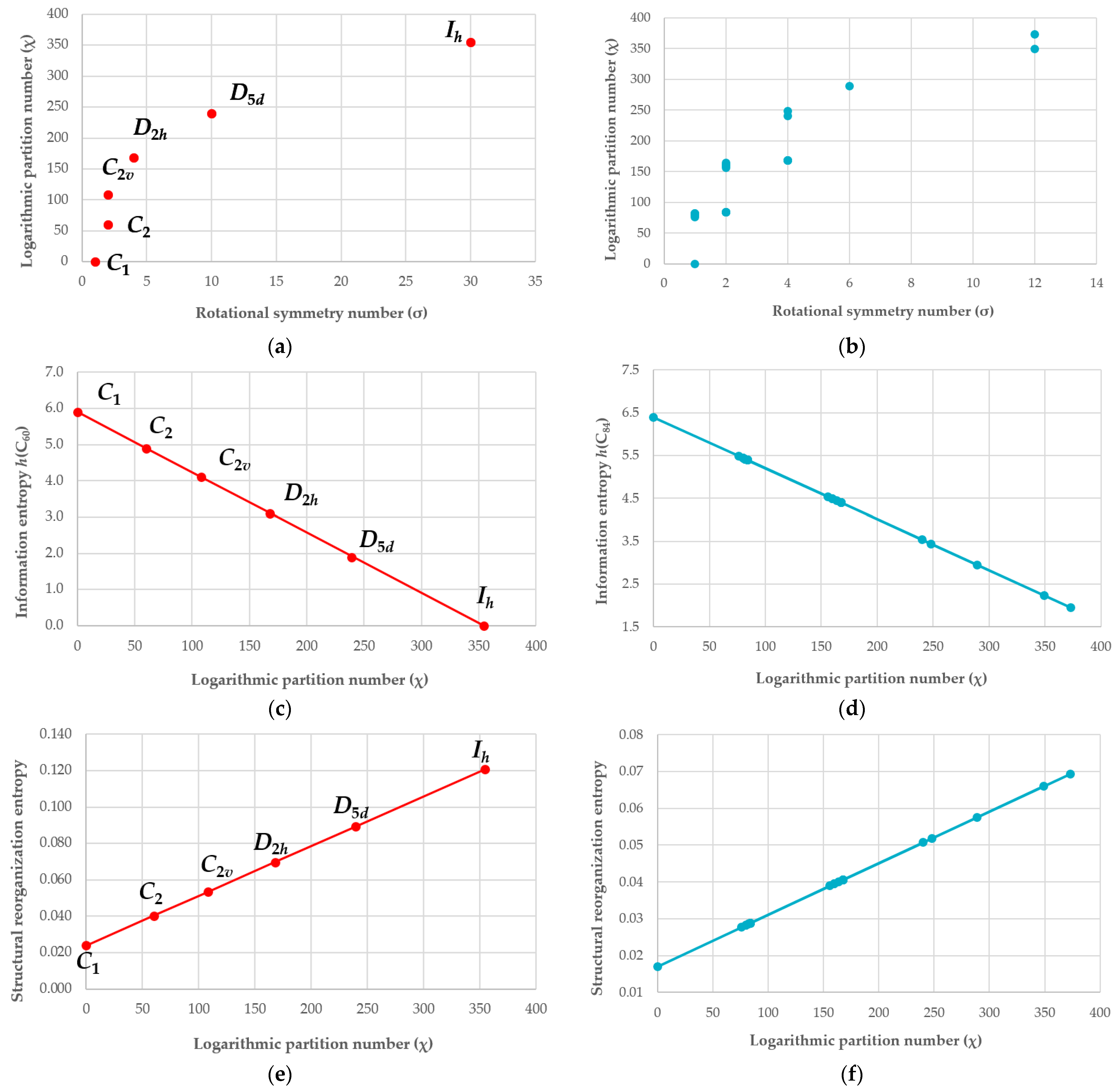
5.2. Dependence of the Strucutral Reorganization Entropy of Encapsulation on the Symmetry and Size of Fullerenes
5.3. Prospectives
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stankevich, M.I.; Stankevich, I.V.; Zefirov, N.S. Topological indices in organic chemistry. Russ. Chem. Rev. 1988, 57, 191–208. [Google Scholar] [CrossRef]
- Bonchev, D. Kolmogorov’s information, Shannon’s entropy, and topological complexity of molecules. Bulg. Chem. Commun. 1995, 28, 567–582. [Google Scholar]
- Barigye, S.J.; Marrero-Ponce, Y.; Pérez-Giménez, F.; Bonchev, D. Trends in information theory-based chemical structure codification. Mol. Divers. 2014, 18, 673–686. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.C.; Harriss, D.K.; Magnuson, V.R. Comparative study of lipophilicity versus topological molecular descriptors in biological correlations. J. Pharm. Sci. 1984, 73, 429–437. [Google Scholar] [CrossRef]
- Basak, S.C.; Gute, B.D.; Grunwald, G.D. Use of topostructural, topochemical, and geometric parameters in the prediction of vapor pressure: A Hierarchical QSAR approach. J. Chem. Inf. Comput. Sci. 1997, 37, 651–655. [Google Scholar] [CrossRef]
- Böttcher, T. An additive definition of molecular complexity. J. Chem. Inf. Model. 2016, 56, 462–470. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information entropy in chemistry: An overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K. Three perspectives on complexity: Entropy, compression, subsymmetry. Eur. Phys. J. Spec. Top. 2017, 226, 3251–3272. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Structural complexity of minerals: Information storage and processing in the mineral world. Mineral. Mag. 2013, 77, 275–326. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Structure description, interpretation and classification in mineralogical crystallography. Crystallogr. Rev. 2017, 23, 2–71. [Google Scholar] [CrossRef]
- Krivovichev, S.V.; Krivovichev, V.; Hazen, R.M.; Aksenov, S.M.; Avdontceva, M.S.; Banaru, A.M.; Gorelova, L.A.; Ismagilova, R.M.; Kornyakov, I.V.; Kuporev, I.V.; et al. Structural and chemical complexity of minerals: An update. Mineral. Mag. 2022, 86, 183–204. [Google Scholar] [CrossRef]
- Banaru, A.M.; Aksenov, S.M. Complexity of molecular nets: Topological approach and descriptive statistics. Symmetry 2022, 14, 220. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of interstellar and circumstellar carbon-containing molecules: Molecular size against structural complexity. Comput. Theor. Chem. 2016, 1097, 83–91. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy changes in chemical reactions. Comput. Theor. Chem. 2018, 1123, 169–179. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; László, I. Isomers of the C84 fullerene: A theoretical consideration within energetic, structural, and topological approaches. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 100–110. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Osawa, E. Information entropy of fullerenes. J. Chem. Inf. Model. 2015, 55, 1576–1584. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Sokolov, V.I. Activation energies and information entropies of helium penetration through fullerene walls. Insights into the formation of endofullerenes nX@C60/70 (n = 1 and 2) from the information entropy approach. RSC Adv. 2016, 6, 72230–72237. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; Tukhbatullina, A.A.; Shepelevich, I.S. Covalently bonded fullerene nano-aggregates (C60)n: Digitalizing their energy-topology-symmetry. Symmetry 2021, 13, 1899. [Google Scholar] [CrossRef]
- Banaru, A.; Aksenov, S.; Krivovichev, S. Complexity parameters for molecular solids. Symmetry 2021, 13, 1399. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; Tukhbatullina, A.A.; Shepelevich, I.S. Structural descriptors of benzenoid hydrocarbons: A mismatch between the estimates and parity effects in helicenes. C 2022, 8, 42. [Google Scholar] [CrossRef]
- Aleskovskii, V.B. Chemical and Information Synthesis. The Beginnings of the Theory. Methods; Publishing House of St. Petersburg University: St. Petersburg, Russia, 1997; 72p. [Google Scholar]
- Talanov, V.M.; Ivanov, V.V. Structure as the source of information on the chemical organization of substance. Russ. J. Gen. Chem. 2013, 83, 2225–2236. [Google Scholar] [CrossRef]
- Bal’makov, M.D. Information basis of nanochemistry. Russ. J. Gen. Chem. 2002, 72, 1023–1030. [Google Scholar] [CrossRef]
- Kadomtsev, B.B. Dynamics and information. Phys. Uspekhi 1994, 37, 425–499. [Google Scholar] [CrossRef]
- Castellano, G.; González-Santander, J.L.; Lara, A.; Torrens, F. Classification of flavonoid compounds by using entropy of information theory. Phytochemistry 2013, 93, 182–191. [Google Scholar] [CrossRef]
- Feng, B.; Zhuang, X. Carbon-enriched meso-entropy materials: From theory to cases. Acta Chim. Sin. 2020, 78, 833–847. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Structural complexity and configurational entropy of crystals. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 274–276. [Google Scholar] [CrossRef]
- Jiménez-Ángeles, F.; Odriozola, G.; Lozada-Cassou, M. Entropy effects in self-assembling mechanisms: Also a view from the information theory. J. Mol. Liq. 2011, 164, 87–100. [Google Scholar] [CrossRef]
- Champion, Y.; Thurieau, N. The sample size effect in metallic glass deformation. Sci. Rep. 2020, 10, 10801. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Liu, S.; Sun, S. Recent progress in the studies of endohedral metallofullerenes. J. Organomet. Chem. 2000, 599, 74–86. [Google Scholar] [CrossRef]
- Akhanova, N.Y.; Shchur, D.V.; Pomytkin, A.P.; Zolotarenko, A.D.; Zolotarenko, A.D.; Gavrylyuk, N.A.; Ualkhanova, M.; Bo, W.; Ang, D. Methods for the synthesis of endohedral fullerenes. J. Nanosci. Nanotechnol. 2021, 21, 2446–2459. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Cross, R.J.; Poreda, R.J. Stable compounds of helium and neon: He@C60 and Ne@C60. Science 1993, 259, 1428–1430. [Google Scholar] [CrossRef] [PubMed]
- Guha, S.; Nakamoto, K. Electronic structures and spectral properties of endohedral fullerenes. Coord. Chem. Rev. 2005, 249, 1111–1132. [Google Scholar] [CrossRef]
- Levin, A.A.; Breslavskaya, N.N. Energy of compressed endoatoms and the energy capacity of small endohedral rare-gas fullerenes. Russ. Chem. Bull. 2005, 54, 1999–2002. [Google Scholar] [CrossRef]
- Yan, H.; Yu, S.; Wang, X.; He, Y.; Huang, W.; Yang, M. Dipole polarizabilities of noble gas endohedral fullerenes. Chem. Phys. Lett. 2008, 456, 223–226. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Bulgakov, R.G. Polarizability exaltation of endofullerenes X@Cn (n = 20, 24, 28, 36, 50, and 60; X is a noble gas atom). JETP Lett. 2010, 92, 662–665. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Tukhbatullina, A.A.; Bulgakov, R.G. Compression of methane endofullerene CH4@C60 as a potential route to endohedral covalent fullerene derivatives: A DFT study. Fuller. Nanotub. Carbon Nanostruct. 2015, 23, 835–842. [Google Scholar] [CrossRef]
- Zakirova, A.D.; Sabirov, D.S. Volume of the fullerene cages of endofullerenes and hydrogenated endofullerenes with encapsulated atoms of noble gases and nonadditivity of their polarizability. Russ. J. Phys. Chem. A 2020, 94, 963–971. [Google Scholar] [CrossRef]
- Osuna, S.; Swart, M.; Sola, M. The reactivity of endohedral fullerenes. What can be learnt from computational studies? Phys. Chem. Chem. Phys. 2011, 13, 3585–3603. [Google Scholar] [CrossRef]
- Ma, F.; Li, Z.-R.; Zhou, Z.-J.; Wu, D.; Li, Y.; Wang, Y.-F.; Li, Z.-S. Modulated nonlinear optical responses and charge transfer transition in endohedral fullerene dimers Na@C60C60@F with n-fold covalent bond (n = 1, 2, 5, and 6) and long range ion bond. J. Phys. Chem. C 2010, 114, 11242–11247. [Google Scholar] [CrossRef]
- Cioslowski, J.; Fleischmann, E.D. Endohedral complexes: Atoms and ions inside the C60 cage. J. Chem. Phys. 1991, 94, 3730. [Google Scholar] [CrossRef]
- Tukhbatullina, A.A.; Zakirova, A.D.; Sabirov, D.S. The volume of the cage of endohedral complexes of the C60 fullerene and halogenide-ions. Vestn. Bashkir. Univ. 2021, 26, 602–604. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Tukhbatullina, A.A.; Shepelevich, I.S. Molecular size and molecular structure: Discriminating their changes upon chemical reactions in terms of information entropy. J. Mol. Graph. Model. 2022, 110, 108052. [Google Scholar] [CrossRef] [PubMed]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995; p. 392. [Google Scholar]
- Schwerdtfeger, P.; Wirz, L.N.; Avery, J. The topology of fullerenes. WIREs Comput. Mol. Sci. 2015, 5, 96–145. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Z. Curved pi-conjugation, aromaticity, and the related chemistry of small fullerenes (<C60) and single-walled carbon nanotubes. Chem. Rev. 2005, 105, 3643–3696. [Google Scholar] [CrossRef]
- Sabirov, D.S. From endohedral complexes to endohedral fullerene covalent derivatives: A density functional theory prognosis of chemical transformation of water endofullerene H2O@C60 upon its compression. J. Phys. Chem. C 2013, 117, 1178–1182. [Google Scholar] [CrossRef]
- Pizzagalli, L. First principles molecular dynamics calculations of the mechanical properties of endofullerenes containing noble gas atoms or small molecules. Phys. Chem. Chem. Phys. 2022, 24, 9449–9458. [Google Scholar] [CrossRef]
- Zhang, J.; Bowles, F.L.; Bearden, D.W.; Keith Ray, W.; Fuhrer, T.; Ye, Y.; Dixon, C.; Harich, K.; Helm, R.F.; Olmstead, M.M.; et al. A missing link in the transformation from asymmetric to symmetric metallofullerene cages implies a top-down fullerene formation mechanism. Nat. Chem. 2013, 5, 880–885. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Murata, Y. Water-mediated thermal rearrangement of a cage-opened C60 derivative. ChemPlusChem 2021, 86, 1559–1562. [Google Scholar] [CrossRef]
- Ugi, I.; Gillespie, P. Representation of chemical systems and interconversions bybe matrices and their transformation properties. Angew. Chem. 1971, 10, 914–915. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of mixing molecules and its application to molecular ensembles and chemical reactions. Comput. Theor. Chem. 2020, 1187, 112933. [Google Scholar] [CrossRef]
- Chemcraft. Available online: http://www.chemcraftprog.com (accessed on 28 July 2021).
- Silant’ev, A.V. Energy spectrum and optical absorption spectrum of fullerene C24 within the Hubbard model. Phys. Solid State 2020, 62, 542–554. [Google Scholar] [CrossRef]
- Kaiser, K.; Scriven, L.M.; Schulz, F.; Gawel, P.; Gross, L.; Anderson, H.L. An sp-hybridized molecular carbon allotrope, cyclo[18]carbon. Science 2019, 365, 1299–1301. [Google Scholar] [CrossRef] [PubMed]
- Osawa, E. Formation mechanism of C60 under nonequilibrium and irreversible conditions—An annotation. Fuller. Nanotub. Carbon Nanostruct. 2012, 20, 299–309. [Google Scholar] [CrossRef]
- Yang, H.; Mercado, B.Q.; Jin, H.; Wang, Z.; Jiang, A.; Liu, Z.; Beavers, C.M.; Olmstead, M.M.; Balch, A.L. Fullerenes without symmetry: Crystallographic characterization of C1(30)-C90 and C1(32)-C90. Chem. Commun. 2011, 47, 2068–2070. [Google Scholar] [CrossRef]
- Tamm, N.B.; Guan, R.; Yang, S.; Troyanov, S.I. New isolated-pentagon-rule isomers of fullerene C96 captured as chloro derivatives. Eur. J. Inorg. Chem. 2020, 2020, 2092–2095. [Google Scholar] [CrossRef]
- Yang, S.; Wang, S.; Troyanov, S.I. The most stable isomers of giant fullerenes C102 and C104 captured as chlorides, C102(603)Cl18/20 and C104(234)Cl16/18/20/22. Chem.–Eur. J. 2014, 20, 6875–6878. [Google Scholar] [CrossRef]
- Tamm, N.B.; Yang, S.; Wei, T.; Troyanov, S.I. Five isolated pentagon rule isomers of higher fullerene C94 captured as chlorides and CF3 derivatives: C94(34)Cl14, C94(61)Cl20, C94(133)Cl22, C94(42)(CF3)16, and C94(43)(CF3)18. Inorg. Chem. 2015, 54, 2494–2496. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Khursan, S.L.; Bulgakov, R.G. 1,3-Dipolar addition reactions to fullerenes: The role of the local curvature of carbon surface. Russ. Chem. Bull. 2008, 57, 2520–2525. [Google Scholar] [CrossRef]
- Manna, D.; Ghanty, T.K. Theoretical prediction of icosahedral U@C20 and analogous systems with high HOMO–LUMO gap. J. Phys. Chem. C 2012, 11, 16716–16725. [Google Scholar] [CrossRef]
- Matsuo, Y.; Okada, H.; Ueno, H. History of Li@C60. In Endohedral Lithium-Containing Fullerenes; Springer: Singapore, 2017; pp. 15–23. [Google Scholar] [CrossRef]
- Chandler, H.J.; Stefanou, M.; Campbell, E.E.B.; Schaub, R. Li@C60 as a multi-state molecular switch. Nat. Commun. 2019, 10, 2283. [Google Scholar] [CrossRef] [PubMed]
- García-Hernández, D.A.; Manchado, A.; Cataldo, F. Hydrogenation of [Li@C60]PF6: A comparison with fulleranes derived from C60. Fuller. Nanotub. Carbon Nanostruct. 2022. [Google Scholar] [CrossRef]
- Sokolov, V.I. Fullerene C60 as a ligand with variable hapticity. Dokl. Akad. Nauk 1992, 326, 647. [Google Scholar]
- Soto, D.; Salcedo, R. Coordination modes and different hapticities for fullerene organometallic complexes. Molecules 2012, 17, 7151–7168. [Google Scholar] [CrossRef] [PubMed]
- Sure, R.; Hansen, A.; Schwerdtfeger, P.; Grimme, S. Comprehensive theoretical study of all 1812 C60 isomers. Phys. Chem. Chem. Phys. 2017, 19, 14296–14305. [Google Scholar] [CrossRef] [PubMed]
- Sabirov, D.; Koledina, K. Classification of isentropic molecules in terms of Shannon entropy. EPJ Web Conf. 2020, 244, 01016. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Aharen, T.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Synthesis of a distinct water dimer inside fullerene C70. Nat. Chem. 2016, 8, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Khong, A.; Jiménez-Vázquez, H.A.; Saunders, M.; Cross, R.J.; Laskin, J.; Peres, T.; Lifshitz, C.; Strongin, R.; Smith, A.B. An NMR Study of He2 Inside C70. J. Am. Chem. Soc. 1998, 120, 6380–6383. [Google Scholar] [CrossRef]
- Morinaka, Y.; Sato, S.; Wakamiya, A.; Nikawa, H.; Mizorogi, N.; Tanabe, F.; Murata, M.; Komatsu, K.; Furukawa, K.; Kato, T.; et al. X-ray observation of a helium atom and placing a nitrogen atom inside He@C60 and He@C70. Nat. Commun. 2015, 4, 1554. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Tukhbatullina, A.A.; Bulgakov, R.G. Dependence of static polarizabilities of C60Xn fullerene cycloadducts on the number of added groups X = CH2 and NH (n = 1–30). Comput. Theor. Chem. 2021, 993, 113–117. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Bulgakov, R.G. Counting the isomers and estimation of anisotropy of polarizability of the selected C60 and C70 bisadducts promising for organic solar cells. J. Phys. Chem. A 2015, 119, 10697–10705. [Google Scholar] [CrossRef]
- Bertz, S.H. Complexity of synthetic reactions. The use of complexity indices to evaluate reactions, transforms and. New J. Chem. 2003, 27, 860–869. [Google Scholar] [CrossRef]
- Parrondo, J.; Horowitz, J.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Minimal energy cost for thermodynamic information processing: Measurement and information erasure. Phys. Rev. Lett. 2011, 102, 250602. [Google Scholar] [CrossRef] [PubMed]
- Davis, S.; González, D. Hamiltonian formalism and path entropy maximization. J. Phys. A Math. Theor. 2015, 48, 425003. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C. Fullerene stability by geometrical thermodynamics. ChemistrySelect 2020, 5, 5–14. [Google Scholar] [CrossRef]
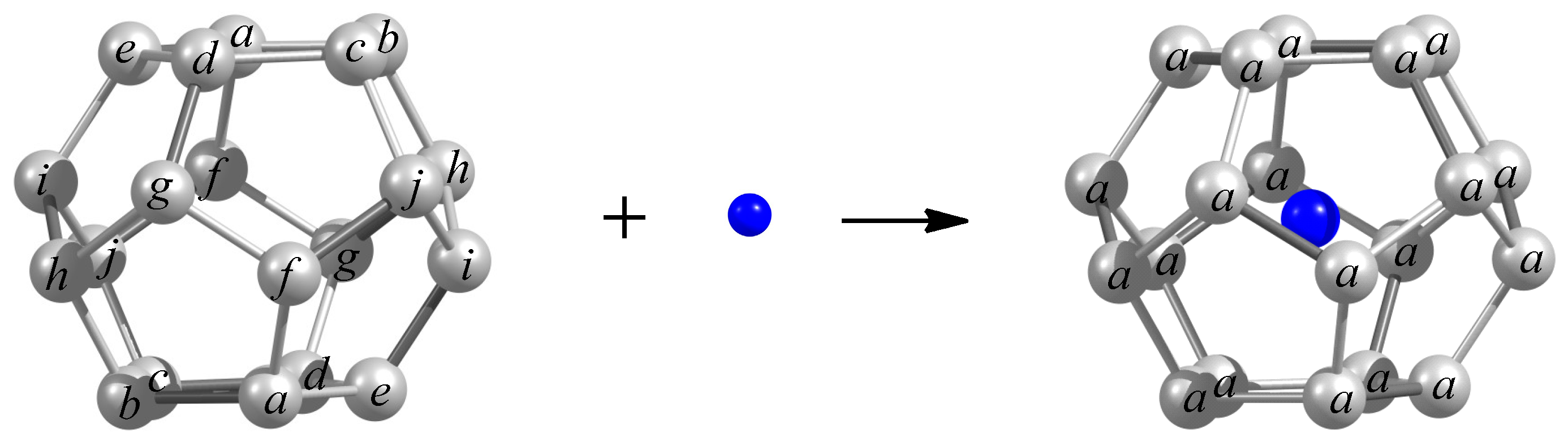
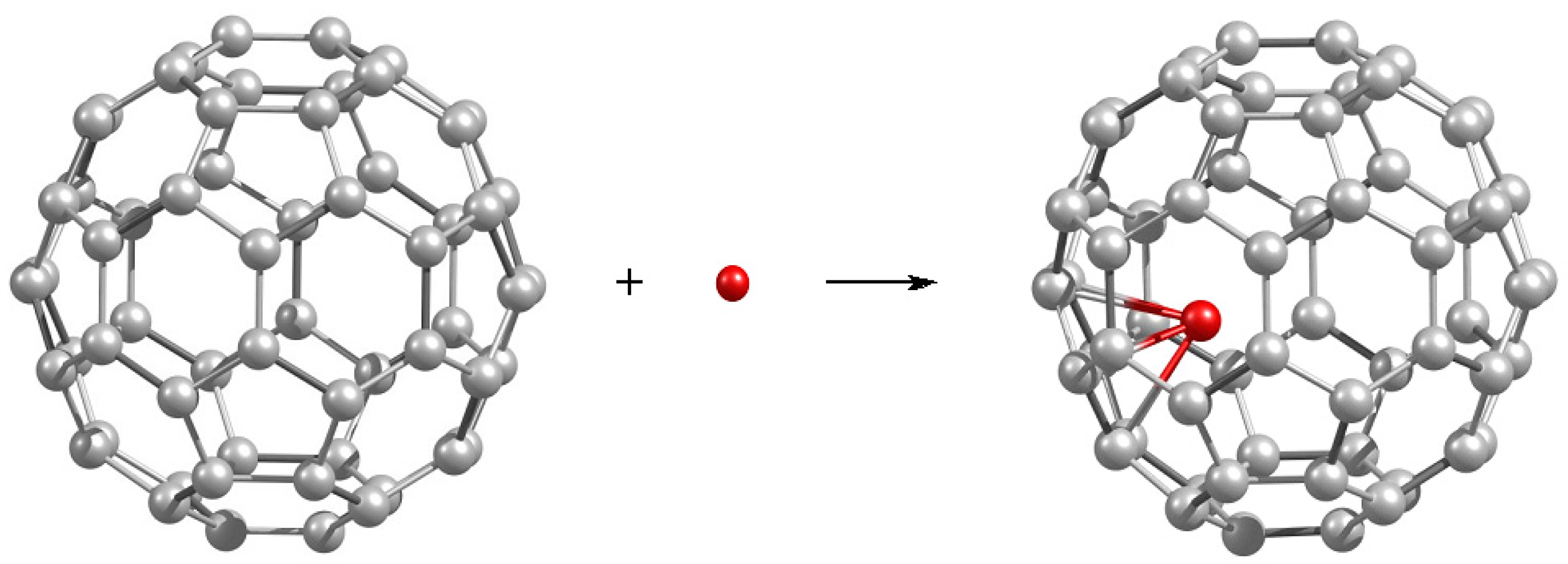
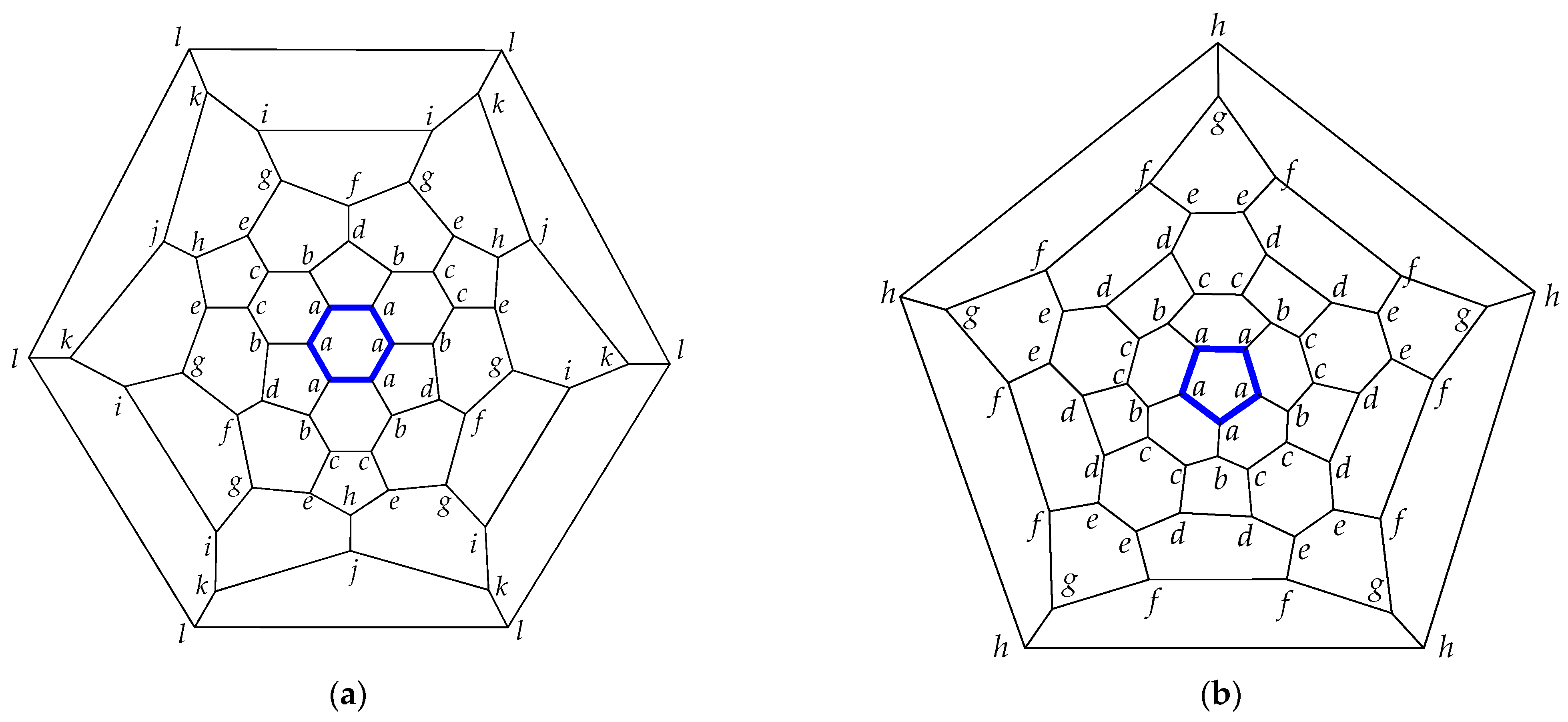
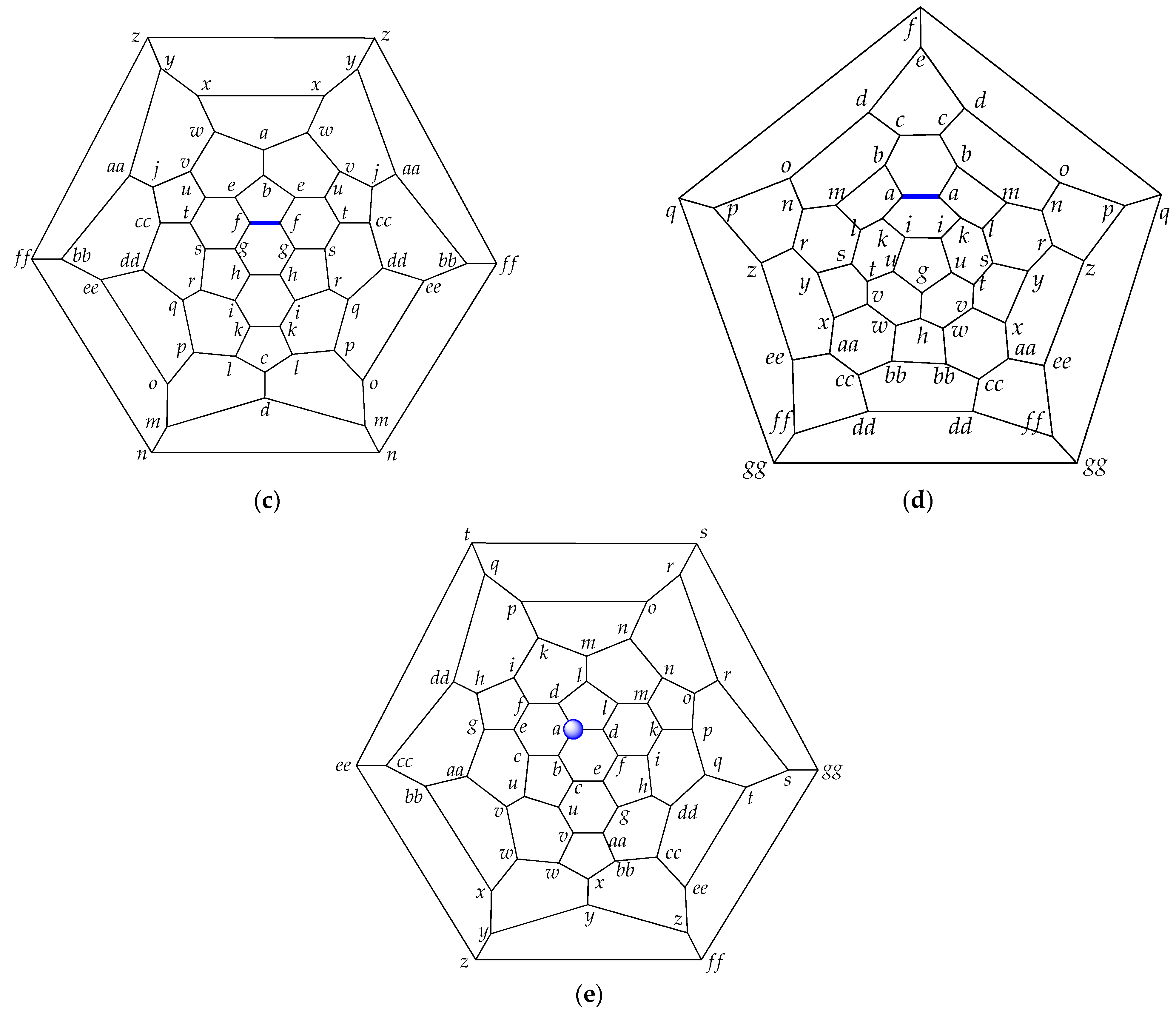

| Fullerene CN (Partition) a | |||||||
|---|---|---|---|---|---|---|---|
| C20 (Ci) b (10 × 2) | 3.3219 | 3.4399 | 0.1180 | 0.1582 | 0.2762 | −0.2762 | 0 |
| C36-15 (D6h) (3 × 12) | 1.5850 | 1.7214 | 0.1364 | 0.0428 | 0.1793 | −0.1793 | 0 |
| C50-271 (D5h) (3 × 10 + 1 × 20) | 1.9219 | 2.0235 | 0.1015 | 0.0377 | 0.1392 | −0.1392 | 0 |
| C70-1 (D5h) (2 × 20 + 3 × 10) | 2.2359 | 2.3112 | 0.0753 | 0.0315 | 0.1068 | −0.1068 | 0 |
| C84-20 (Td) (1 × 12 + 3 × 24) | 1.9502 | 2.0195 | 0.0693 | 0.0229 | 0.0923 | −0.0923 | 0 |
| C84-24 (D6h) (3 × 12 + 2 × 24) | 2.2359 | 2.3019 | 0.0660 | 0.0263 | 0.0923 | −0.0923 | 0 |
| Carbon Molecule | |||||||
|---|---|---|---|---|---|---|---|
| Fullerene C60 (Ih) | 0 | 0.1207 | 0.1207 | 0 | 0.1207 | −0.1207 | 0 |
| Fulleroid C24 (Oh) | 0 | 0.2423 | 0.2423 | 0 | 0.2423 | −0.2423 | 0 |
| Fulleroid C48 (Oh) | 0 | 0.1437 | 0.1437 | 0 | 0.1437 | −0.1437 | 0 |
| Cyclocarbon C18 (D9h) | 0 | 0.2975 | 0.2975 | 0 | 0.2975 | −0.2975 | 0 |
| Fullerene CN | |||||||
|---|---|---|---|---|---|---|---|
| C60 | 5.9069 | 5.9307 | 0.0239 | 0.0968 | 0.1207 | −0.1207 | 0 |
| C70 | 6.1293 | 6.1497 | 0.0205 | 0.0863 | 0.1068 | −0.1068 | 0 |
| C80 | 6.3219 | 6.3399 | 0.0179 | 0.0780 | 0.0960 | −0.0960 | 0 |
| C90 | 6.4919 | 6.5078 | 0.0159 | 0.0713 | 0.0873 | −0.0873 | 0 |
| Fullerene CN | Idealized Symmetry | Actual Symmetry | |||
|---|---|---|---|---|---|
| C20-1 | Ih (1 × 20) | Ci (10 × 2) | 0.0000 | 0.2762 | 3.3219 |
| C24-1 | D6d (2 × 12) | C2 (12 × 2) | 1.0000 | 1.2023 | 3.5850 |
| C26-1 | D3h (1 × 2 + 2 × 6 + 1 × 12) | C1 (26 × 1) | 1.7759 | 1.9386 | 4.7004 |
| C40-1 | D5d (4 × 10) | Ci (20 × 2) | 2.0000 | 2.1166 | 4.3219 |
| C76-2 | Td (1 × 4 + 2 × 12 + 2 × 24) | S4 (3 × 4 + 4 × 8 + 2 × 16) | 2.1148 | 2.1873 | 2.9848 |
| C80-7 | Ih (1 × 20 + 1 × 60) | C3v (1 × 2 + 1 × 6 + 6 × 12) | 0.8113 | 0.8972 | 2.8766 |
| Fullerene CN | |||||
|---|---|---|---|---|---|
| C20-1 (Ci → Ih) | −3.0457 | 0.1582 | −2.8875 | −0.2762 | −3.1637 |
| C24-1 (C2 → D6d) | −2.3827 | 0.1434 | −2.2393 | −0.2423 | −2.4816 |
| C26-1 (C1 → D3h) | −2.7618 | 0.1741 | −2.5877 | −0.2285 | −2.8163 |
| C40-1 (Ci → D5d) | −2.2053 | 0.1054 | −2.0999 | −0.1654 | −2.2653 |
| C76-2 (S4 → Td) | −0.7974 | 0.0388 | −0.7587 | −0.1000 | −0.8587 |
| C80-7 (C3v → Ih) | −1.9794 | 0.0355 | −1.9438 | −0.0960 | −2.0398 |
| Coordination of X Atom inside C60 | Symmetry of X@C60 and Partition | |||
|---|---|---|---|---|
| Pentagon | C5v (4 × 5 + 4 × 10 + 1 × 1) | 2.991 | −0.1207 | +2.870 |
| Hexagon | C3v (8 × 6 + 4 × 3 + 1 × 1) | 3.585 | −0.1207 | +3.464 |
| 5.6-bond | CS (5 × 1 + 28 × 2) | 5.013 | −0.1207 | +4.892 |
| 6.6-bond | C2v (5 × 1 + 28 × 2) | 5.013 | −0.1207 | +4.892 |
| Atom | CS (5 × 1 + 28 × 2) | 5.013 | −0.1207 | +4.892 |
| Isomer | Partition | σ | χ | |||
|---|---|---|---|---|---|---|
| C60 (Ih) | 1 × 60 | 30 | 354.4 | 0.000 | 0.121 | 0.121 |
| C60 (D5d) | 2 × 20 + 2 × 10 | 10 | 239.3 | 1.918 | 2.008 | 0.089 |
| C60 (D2h) | 3 × 4 + 6 × 8 | 4 | 168 | 3.107 | 3.177 | 0.070 |
| C60 (C2v) | 6 × 2 + 12 × 4 | 2 | 108 | 4.107 | 4.160 | 0.053 |
| C60 (C2) | 30 × 2 | 2 | 60 | 4.907 | 4.947 | 0.040 |
| C60 (C1) | 60 × 1 | 1 | 0 | 5.907 | 5.931 | 0.024 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabirov, D.S.; Tukhbatullina, A.A.; Shepelevich, I.S. Digitalizing Structure–Symmetry Relations at the Formation of Endofullerenes in Terms of Information Entropy Formalism. Symmetry 2022, 14, 1800. https://doi.org/10.3390/sym14091800
Sabirov DS, Tukhbatullina AA, Shepelevich IS. Digitalizing Structure–Symmetry Relations at the Formation of Endofullerenes in Terms of Information Entropy Formalism. Symmetry. 2022; 14(9):1800. https://doi.org/10.3390/sym14091800
Chicago/Turabian StyleSabirov, Denis Sh., Alina A. Tukhbatullina, and Igor S. Shepelevich. 2022. "Digitalizing Structure–Symmetry Relations at the Formation of Endofullerenes in Terms of Information Entropy Formalism" Symmetry 14, no. 9: 1800. https://doi.org/10.3390/sym14091800
APA StyleSabirov, D. S., Tukhbatullina, A. A., & Shepelevich, I. S. (2022). Digitalizing Structure–Symmetry Relations at the Formation of Endofullerenes in Terms of Information Entropy Formalism. Symmetry, 14(9), 1800. https://doi.org/10.3390/sym14091800






