Between ℙ and ℚ: The ℙ^ℚ Measure for Pricing in Asset Liability Management

Abstract

Insurance companies issue guarantees that need to be valued according to the market expectations. By calibrating option pricing models to the available implied volatility surfaces, one deals with the so-called risk-neutral measure $\mathbb{Q}$, which can be used to generate market consistent values for these guarantees. For asset liability management, insurers also need future values of these guarantees. Next to that, new regulations require insurance companies to value their positions on a one-year horizon. As the option prices at $t=1$ are unknown, it is common practice to assume that the parameters of these option pricing models are constant, i.e., the calibrated parameters from time $t=0$ are also used to value the guarantees at $t=1$. However, it is well-known that the parameters are not constant and may depend on the state of the market which evolves under the real-world measure $\mathbb{P}$. In this paper, we propose improved regression models that, given a set of market variables such as the VIX index and risk-free interest rates, estimate the calibrated parameters. When the market variables are included in a real-world simulation, one is able to assess the calibrated parameters (and consequently the implied volatility surface) in line with the simulated state of the market. By performing a regression, we are able to predict out-of-sample implied volatility surfaces accurately. Moreover, the impact on the Solvency Capital Requirement has been evaluated for different points in time. The impact depends on the initial state of the market and may vary between −46% and +52%.

1. Introduction

Liabilities of insurance companies depend on the fair value of the outstanding claims that typically involve guarantees (that are also called embedded options). The market consistent value of these guarantees is defined under the risk-neutral measure $\mathbb{Q}$, i.e., they are then computed with pricing formulas that agree on the current implied volatility surfaces. To hedge against the risks involved in these claims, insurers often acquire (complex) option portfolios that also require market consistent risk-neutral valuation themselves. Furthermore, on 1 January 2016 the so-called Solvency II directive came into effect which introduced the Solvency Capital Requirement (SCR). The SCR is defined as the minimum amount of capital which should be held by an insurer, such that the insurer is able to pay its claims over a one-year horizon with a 99.5% probability. The regulator demands that the insurer’s available capital should be greater than, or equal to, the SCR. Because the claims typically depend on future market consistent valuation, computing the SCR, and, more generally performing proper Asset Liability Management (ALM), is a challenging task.

To compute these future market consistent values of the embedded options, insurers require the probability distribution of the values of these embedded options. Typically, this is done by simulating a large number of random future states of the market and, after that, the different states are valued under the market consistent risk-neutral measure. From the simulated embedded option values, the desired statistics can then be extracted. The future states of the market can be computed by means of risk-neutral models ($\mathbb{Q}$ in $\mathbb{Q}$), or real-world models ($\mathbb{Q}$ in $\mathbb{P}$). Risk-neutral simulations are, for example, used to calculate the Credit Value Adjustment (CVA) (see, e.g., Pykhtin (2012)), which is a traded quantity and should therefore be computed using no-arbitrage arguments. For quantities that are not traded (or hedged), the $\mathbb{Q}$ in $\mathbb{Q}$ approach appears to be incorrect (see, e.g., Stein (2016)) and the future state of the market should be modelled using the real-world measure ($\mathbb{Q}$ in $\mathbb{P}$). Real-world models are calibrated to the observed historical time-series and are typically used to compute non-traded quantities such as Value-at-Risk (VaR).

The risk-neutral measure at $t=0$ is connected to the observed implied volatility surface and is therefore well-defined. However, the definition of the risk-neutral measure at future time $t=1$ is debatable. Despite some relevant research on predicting the implied volatility surfaces (see, e.g., Cont et al. (2002), Mixon (2002) and Audrino and Colangelo (2010)), it is common practice to use option pricing models that are only calibrated at time $t=0$, thereby assuming that the risk-neutral measure is independent of the state of the market (see, for example, Bauer et al. (2010) and Devineau and Loisel (2009)). This is however not in line with historical observations, where we see that the implied volatility surface does depend on the state of the market. Another drawback of this approach is that the resulting SCR is pro-cyclical, i.e., the SCR is relatively high when the market is in crisis and relatively low when the market is stable. The undesired effect of pro-cyclicality is that it can aggravate a downturn Bikker and Hu (2015).

In this paper, we investigate the impact of relaxing the assumption that the risk-neutral measure is considered to be independent of the state of the market and develop the so-called VIX Heston model, which depends on the current and also on simulated implied volatilities. This approach, which we have named here the ${\mathbb{P}}^{\mathbb{Q}}$ approach, takes into account the $\mathbb{Q}$ measure information at time $t=0$ and simulates risk-neutral model parameters (thus, future implied volatility surfaces are obtained by means of simulation) based on historically observed relations with some relevant market variables such as the VIX index.

As is well-known, the VIX index is a volatility measure for the S&P-500 index, which is calculated by the Chicago Board Options Exchange (CBOE) (see CBOE (2015)), and it is therefore directly linked to the implied volatility surface. Consequently, extracting information from the VIX index is frequently studied (see, e.g., Duan and Yeh (2012)) and our approach in this paper is based on the methodology presented in Singor et al. (2017), where the development of the Heston model parameters for the S&P-500 index options and the VIX index have been analysed.

The contribution of our present research is two-fold. First, we discuss the justification of using a risk-neutral model with time-dependent parameters. By means of a hedge test, we show that hedging strategies that take into account the changes in the implied volatility surface significantly outperform those strategies that do not, both in simulation and with empirical tests. This leads to the conclusion that the time-dependent risk-neutral measure can be used for the evaluation of future embedded option prices. Secondly, we show the impact of our new approach. For that, we use real data from 2007 to 2016 and compute the SCR on a monthly basis with a constant $\mathbb{Q}$ measure and also with the VIX Heston model where this assumption is relaxed. We conclude that the VIX Heston model predicts out-of-sample implied volatility surfaces accurately and computes more conservative and stable SCRs. The impact of using the new approach on the SCR depends on the initial state of the market and may vary from $-46\%$ to $+52\%$ in our experiments. Moreover, we see that the SCR that is computed with the VIX Heston model is significantly less pro-cyclical, for example, it is lower in the wake of the 2008 credit crisis, as it incorporates the likely normalisation.

The outline of this paper is as follows. In Section 2, we give the definition of the SCR. In Section 3, we explain the dynamic VIX Heston model. In Section 4, we present the hedge tests with the corresponding results, followed by Section 5 where we present the numerical VIX Heston results and the impact of the using ${\mathbb{P}}^{\mathbb{Q}}$ dynamics on the SCR. Section 6 concludes.

2. Solvency Capital Requirement

Let us denote the policy’s net income in the interval $[0,t]$ by $A_t$, which is defined as the cash flows up to time t that are generated under the real-world market. The mathematical definition is given by

$$A_t={\int }_0^t{e}^{\mu (t-s)}\mathrm{cashflow}(s,\Delta s)\mathrm{d}s,$$

(1)

where $\mu$ is the expected return and “$\mathrm{cashflow}(s,\Delta s)$” denotes the generated cash flow over the interval $[s,s+\Delta s]$. Similarly, we define the policy’s liabilities by $L_t$ and they are given by the discounted expected cash flows under the risk-neutral measure in the interval $[t,T]$:

$$L_t={\mathbb{E}}^{{\mathbb{Q}}_t}\left[\left.{\int }_t^T{e}^{-r(s-t)}\mathrm{cashflow}(s,\Delta s)\mathrm{d}s\right|{\mathcal{F}}_t\right],$$

(2)

with risk-free rate r. Note that a positive/negative cash flow corresponds to an income/liability for the insurer. We define

$$N_t:=A_t-L_t,$$

(3)

which can be thought of as the policy’s net value at time t. The Solvency Capital Requirement is now defined as the 99.5% Value-at-Risk (i.e., the 99.5% quantile) of the one-year loss distribution under the real-world measure, i.e.,

$$\mathrm{SCR}={\mathrm{VaR}}_{0.995}\left(N_0-{\tilde{N}}_1\right):=inf\left\{x\left|\mathbb{P}\left(N_0-{\tilde{N}}_1<x\right)>0.995\right.\right\}.$$

(4)

Here, ${\tilde{N}}_1$ is defined as the discounted value of $N_1$.

Guaranteed Minimum Accumulation Benefit

This section is dedicated to deriving the fund dynamics and the SCR of a frequently used guarantee in the insurance industry, namely the Guaranteed Minimum Accumulation Benefit (GMAB) variable annuity rider.

We assume that the fund only contains stocks, but the derivation is similar when different assets are combined. We denote the stock and fund value by $S_t$ and $F_t$, respectively, and define the initial premium by G. We assume the payout at maturity T is at least equal to the initial premium, in other words,

$${\mathrm{Payout}}_T=max\left(F_T,G\right).$$

(5)

The dynamics of the fund are very similar to the stock dynamics, except for a fee $\alpha$ which is deducted from the fund as a payment to the insurer. This fee can be thought of as a dividend yield. Following Milevsky and Salisbury (2001), we obtain

$$\mathrm{d}{F}_t=\mathrm{d}{S}_t\frac{F_t}{S_t}{e}^{-\alpha t},F_0=G.$$

(6)

The specific dynamics depend on the assumptions regarding stock price $S_t$. Here, we assume the Black–Scholes model (geometric Brownian motion, GBM) under the observed real-world measure $\mathbb{P}$, which yields:

$$\mathrm{d}{F}_t^{\mathbb{P}}=(\mu -\alpha )F_t^{\mathbb{P}}\mathrm{d}t+\sigma F_t^{\mathbb{P}}\mathrm{d}{W}_t^{\mathbb{P}},F_0=G.$$

(7)

Moreover, for the valuation, a risk-neutral Heston model is implemented, leading to

$$\left\{\begin{array}{cc}\mathrm{d}{F}_t=(r-\alpha )F_t\mathrm{d}t+\sqrt{v_t}{F}_t\mathrm{d}{W}_t^F,\hfill & F_0=G,\hfill \\ \mathrm{d}{v}_t=\kappa (\overline{v}-v_t)\mathrm{d}t+\gamma \sqrt{v_t}\mathrm{d}{W}_t^v,\hfill & \\ 〈\mathrm{d}{W}_t^S,\mathrm{d}{W}_t^v〉=\rho \mathrm{d}t.\hfill & \end{array}\right.$$

(8)

The income is generated by the accumulated fees, hence

$$A_t={\int }_0^t\alpha F_s^{\mathbb{P}}{e}^{\mu (t-s)}\mathrm{d}s.$$

(9)

The liabilities, on the other hand, depend on the final value of the fund, as follows,

• If $F_T\ge G$, the policyholder receives $F_T$ and the insurer has no liabilities.
• If $F_T<G$, the policyholder receives G and the liabilities of the insurer are equal to $G-F_T$.

Moreover, the insurer continues to claim future fees, hence, according to Equation (2), we can write the liabilities as

$$\begin{array}{cc}\hfill L_t& ={\mathbb{E}}^{{\mathbb{Q}}_t}\left[\left.e^{-r(T-t)}max\left(G-F_T,0\right)-{\int }_t^T{e}^{-r(s-t)}\alpha F_s\mathrm{d}s\right|{\mathcal{F}}_t\right]\hfill \\ & =\mathrm{Put}(F_t,G)+F_t\left(e^{-\alpha (T-t)}-1\right),\hfill \end{array}$$

(10)

where $\mathrm{Put}(F_t,G)$ denotes the value of a European put option on the fund at time t with strike price G and dividend yield $\alpha$. We can substitute these definitions into Equation (4) to obtain

$$\begin{array}{ccc}\hfill \mathrm{SCR}& =& {\mathrm{VaR}}_{0.995}\left(N_0-e^{-r}{N}_1\right)\hfill \\ & =& {\mathrm{VaR}}_{0.995}\left(A_0-L_0-e^{-r}(A_1-L_1)\right)\hfill \\ & =& e^{-r}{\mathrm{VaR}}_{0.995}\left(\mathrm{Put}(F_1,G)-g(F_1,1)\right)-\mathrm{Put}(F_0,G)+g(F_0,0),\hfill \end{array}$$

(11)

with

$$g(F_t,t)={\int }_0^t\alpha F_s{e}^{\mu (t-s)}\mathrm{d}s+F_t\left(1-e^{-\alpha (T-t)}\right),$$

(12)

which can be thought of as the sum of the realized and expected fees. In this case, the SCR depends on the real-world distribution of $F_1$, which determines $g(F_1,1)$ and also influences the risk-neutral valuation of $\mathrm{Put}(F_1,G)$.

Variable annuity riders require a risk-neutral valuation at (future) time $t=1$, as the liabilities are, by definition, conditional expectations under the risk-neutral measure. In the case of a GMAB rider, there is an analytic expression available, but often there is no such expression for $L_t$. Hence, the evaluation of the conditional expectation typically requires an approximation. In that case, often the Least-Squares Monte Carlo algorithm is used to approximate the conditional expectations at $t=1$. The experiments presented in this paper were also performed for the Guaranteed Minimum Withdrawal Benefit (GMWB) variable annuity rider. As the results and conclusions were very similar as for the GMAB, in this paper, we restrict ourselves to the GMAB variable annuity.

The distributions of $g(F_1,1)$ and $\mathrm{Put}(F_1,G)$ in Equation (12) can be obtained by means of a Monte Carlo simulation,

• First, the net policy value $N_0$ is determined, according to definition Equation (3).
• Thereafter, the fund value $F_t$ along with other explanatory variables is simulated according to the real-world measure up to time $t=1$.
• Subsequently, the values of $\mathrm{Put}(F_1,G)$ and $g(F_1,1)$ are evaluated for each trajectory. The value of $g(F_1,1)$ can be obtained directly from the trajectory of $F_t$, however, $\mathrm{Put}(F_1,G)$ requires a risk-neutral valuation for which the risk-neutral measure at time $t=1$ is required.
• Finally, the simulated values are combined to construct the loss distribution. The SCR corresponds to the 99.5% quantile of this distribution.

Some more detail about the Monte Carlo simulation is provided in Appendix A.

3. Dynamic Stochastic Volatility Model

When valuing options, one typically wishes to calibrate a risk-neutral model according to the market’s expectations, which are quantified by the implied volatility surface. This implied volatility surface can be used to extract European option prices for a wide range of maturities and strikes. The market expectation (and so the volatility surface), is however unknown at $t=1$ and therefore practitioners typically use the implied volatility surface at $t=0$ to calibrate the risk-neutral model parameters. In this standard $\mathbb{Q}$ in $\mathbb{P}$ approach, these parameters are assumed to be constant over time, i.e., the risk-neutral measure is independent of the real-world measure. Note that this approach is also used to compute risk measures from the Basel accords, such as credit value adjustment (CVA), capital valuation adjustment (KVA) and potential future exposure (PFE) (see Kenyon et al. (2015); Jain et al. (2016); Ruiz (2014)). However, regarding the computation of CVA, this quantity is typically hedged, and so using only the market expectation at $t=0$ is sufficient.

In the ${\mathbb{P}}^{\mathbb{Q}}$ approach, we relax the assumption of independence. The calibrated risk-neutral model parameters are related to the simulated real-world scenarios.

3.1. Heston Model

We assume the Heston model as a benchmark. The Heston stochastic volatility model (Heston 1993) assumes the volatility of the stock price process to be driven by a CIR model, i.e., under the $\mathbb{Q}$ measure,

$$\left\{\begin{array}{cc}\mathrm{d}{S}_t=r{S}_t\mathrm{d}t+\sqrt{v_t}{S}_t\mathrm{d}{W}_t^1,\hfill & S\left(0\right)=S_0,\hfill \\ \mathrm{d}{v}_t=\kappa (\overline{v}-v_t)+\gamma \sqrt{v_t}\mathrm{d}{W}_t^2,\hfill & v\left(0\right)=v_0\hfill \\ 〈\mathrm{d}{W}_t^1,\mathrm{d}{W}_t^2〉=\rho \mathrm{d}t.\hfill & \end{array}\right.$$

(13)

where r denotes the risk-free rate, $\kappa$ the speed of mean-reversion, $\overline{v}$ the long-term variance, $\gamma$ the volatility of variance and $\rho$ the correlation between asset price and variance. The risk-free rate is assumed to be constant throughout this research. To calibrate these parameters according to the market’s expectations, one wishes to minimize the distance between the model’s and market’s implied volatilities. For the Heston model, consider the following search space for the parameters

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}^{\mathrm{Search}}& =D_{\kappa }\times D_{v_0}\times D_{\overline{v}}\times D_{\gamma }\times D_{\rho }\hfill \\ & =[0,10]\times [0,1]\times [0,1]\times [0,2]\times [-1,1],\hfill \end{array}$$

(14)

where $D_p$ denotes the search domain for parameter p. Using this search space, one is able to find the calibrated parameters at time t by minimizing the sum of squared errors:

$${\mathsf{\Omega }}_t^{\mathrm{Heston}}=\underset{\mathsf{\Omega }\in {\mathsf{\Omega }}^{\mathrm{Search}}}{arg\; min}\left(\sum _K\sum _T{\left({\sigma }^{\mathrm{Market}}(t,K,T)-{\sigma }^{\mathrm{Heston}}(t,\mathsf{\Omega },K,T)\right)}^2\right).$$

(15)

The set of parameters ${\mathsf{\Omega }}_t^{\mathrm{Heston}}=\{\kappa ,v_0,\overline{v},\gamma ,\rho \}$ minimizing this expression is considered risk-neutral and reflects the market’s expectations.

When the market is subject to changes, its expectations will change accordingly. Hence, the implied volatility surface will evolve dynamically over time. Consequently, the Heston parameters may change over time. Figure 1 shows the monthly evolution of the Heston parameters from January 2006 to February 2017.

During this calibration procedure, we assumed $\kappa$ to be constant; an unrestricted $\kappa$ led to unstable results and did not significantly improve the accuracy. The other parameters, however, do not appear constant over time. This may give rise to issues in risk-management applications, where one simulates many real-world paths to assess the sensitivity to the market of a portfolio, balance sheet, etc. In many cases, a risk-neutral valuation is required, which is nested inside the real-world simulation, for example, when the portfolio or balance sheet contains options. Consequently, the future implied volatility surface for each trajectory needs to be known, such that the Heston parameters can be calibrated accordingly. Modelling the implied volatility surface over time is a challenging task (see, e.g., Cont et al. (2002); Mixon (2002); Audrino and Colangelo (2010)), as it quantifies the market’s expectations that depend on many factors. Moreover, even if the implied volatility surface is modelled, one would still need to perform a costly calibration procedure. Performing this calibration for each of the simulated trajectories would require a significant computational effort. As the Heston model is a parameterization of the implied volatility surface, an attractive alternative is to simulate the Heston parameters directly.

Figure 1 clearly shows that the parameters are time-dependent, which is in contrast with the assumptions of the plain Heston model. In this research we first search for relations between the risk-neutral parameters and observe real-world market indices, such as the VIX index. When a relation is found, the future risk-neutral parameters can be extracted from a real-world simulation. In this way, by performing a real-world simulation, we can directly forecast the set of Heston parameters within each simulated trajectory. The risk-neutral measure is then conditioned on the simulated state of the market, without the need of a simulated implied volatility surface.

3.2. VIX Heston Model

We have already described the difficulties of modelling the implied volatility surface, or equivalently, the option prices. A different approach is therefore required to calibrate the Heston parameters in simulated markets. The simulated parameter sets should accurately reflect the expectations of the simulated market, for example by linking the dynamics of the Heston parameters to the dynamics of the market. In Singor et al. (2017), an approach is considered which is based on the assumptions of a linear relationship between the VIX index and the Heston parameters. After analysis, it was concluded that:

• The initial volatility $\sqrt{v_{0,t}}$ and the volatility of the volatility ${\gamma }_t$ are highly correlated to the VIX index, with correlation coefficients of 0.99 and 0.76, respectively.
• The long term volatility $\sqrt{{\overline{v}}_t}$ appears to be correlated to the VIX index trend line (estimated by a Kalman filter) with a correlation coefficient of 0.74.

To this end, the following restrictions are imposed on the Heston model parameters:

$${\mathsf{\Omega }}_t^{\mathrm{Heston}}\left(X\right)=\left\{\begin{array}{ccc}{\kappa }_t\hfill & =\kappa ,\hfill & \kappa \in {\mathbb{R}}_{+},\hfill \\ v_{0,t}\hfill & ={\left(a_{v_0}·{\mathrm{VIX}}_t+b_{v_0}\right)}^2,\hfill & a_{v_0},b_{v_0}\in \mathbb{R},\hfill \\ {\overline{v}}_t\hfill & ={\left(a_{\overline{v}}·{\mathrm{VIX}}_{{\mathrm{filter}}_t}+b_{\overline{v}}\right)}^2,\hfill & a_{\overline{v}},b_{\overline{v}}\in \mathbb{R},\hfill \\ {\gamma }_t\hfill & =a_{\gamma }·{\mathrm{VIX}}_t+b_{\gamma },\hfill & a_{\gamma },b_{\gamma }\in \mathbb{R},\hfill \\ {\rho }_t\hfill & =\rho ,\hfill & \rho \in [-1,1],\hfill \end{array}\right.$$

(16)

where both the speed of mean reversion ${\kappa }_t$ and the correlation coefficient ${\rho }_t$ are assumed to be constant over time. The constant $\rho$ assumption is justified by the fact that $\rho$ displays a mean reverting pattern and it can therefore be approximated by its long-term mean. The constant $\kappa$ assumption is justified by observations in Gauthier and Rivaille (2009). They argued that the effect on the implied volatility surface of increasing $\kappa$ is similar to decreasing $\gamma$. Thus, allowing $\kappa$ to change over time unnecessarily overcomplicates the model. Moreover, numerical experiments show that an unrestricted $\kappa$ sometimes leads to unstable results.

The purpose of the restrictions is to accurately reflect the market’s expectations. To this end, we wish to minimize the distance between the observed and predicted implied volatility surfaces. Therefore, we calibrate the constraint parameters with a procedure similar to Equation (15). By changing the parameter set from ${\mathsf{\Omega }}_t^{\mathrm{Heston}}$ to $X=\{\kappa ,{\alpha }_{v_0},b_{v_0},a_{\overline{v}},b_{\overline{v}},a_{\gamma },b_{\gamma },\rho \}$ and summing over all points in time one obtains

$$X=\underset{X^{\mathrm{S}}\in X^{\mathrm{Search}}}{arg\; min}\left(\sum _{t,K,T}{\left({\sigma }^{\mathrm{Market}}(t,K,T)-{\sigma }^{\mathrm{Heston}}(t,{\mathsf{\Omega }}_t^{\mathrm{Heston}}\left(X^{\mathrm{S}}\right),K,T)\right)}^2\right),$$

(17)

with,

$$\begin{array}{cc}\hfill X^{\mathrm{Search}}& =D_{\kappa }\times D_{a_{v_0}}\times D_{b_{v_0}}\times D_{a_{\overline{v}}}\times D_{b_{\overline{v}}}\times D_{a_{\gamma }}\times D_{b_{\gamma }}\times D_{\rho }\hfill \\ & =\left\{1\right\}\times {\mathbb{R}}^6\times [-1,1].\hfill \end{array}$$

(18)

By including the VIX-index in the real-world simulation, one is able to efficiently evaluate the set of Heston parameters in line with the simulated state of the market. For more information regarding the derivation and properties of the VIX Heston model, we refer the reader to Singor et al. (2017).

It is, however, important to stress the different assumptions in the real-world and risk-neutral markets. Risk-neutral valuations are performed under the Heston model, which assumes constant parameters. However, in real-world simulations, we assume the Heston parameters to change over time, according to the simulated state of the market, similar to Figure 1. One could argue that this approach is invalid, since we are violating the assumptions of the risk-neutral market. To this end, we discuss a justification of this approach, by means of a hedge test. Moreover, to assess the impact of time-dependent Heston parameters, we implement the VIX Heston model as proposed in Singor et al. (2017) in a risk-management application: the Solvency Capital Requirement.

4. Hedge Test

Before implementing the dynamic risk-neutral measure (the VIX Heston model) in a risk-management application, we first test its applicability from a theoretical point of view. For example, in theory, one should be able to hedge against future positions using today’s implied volatility surface. This no longer applies when one assumes a risk-neutral measure that changes over time. To this end, we perform an experimental hedge test that determines which approach is more accurate in terms of future option prices, a dynamic or constant risk-neutral measure.

The plain Heston model assumes $\overline{v}$ and $\gamma$ to be constant, hence, from a theoretical point of view, it would be redundant to hedge against changes of these parameters. However, due to the dynamic behaviour of the implied volatility surface, $\overline{v}$ and $\gamma$ will change over time (see Figure 1). Thus, from an empirical point of view, the option price dynamics are subject to changes of these parameters. To support this claim, we compare three different hedging strategies. The first strategy is the classical Delta-Vega hedge, which does not take any changes of $\overline{v}$ and $\gamma$ into account. The replicating portfolio aims at hedging an option “A”, with value $C_t$, by holding a certain amount of stocks and a different option with value ${\tilde{C}}_t$ (which is called option “B” from this point onwards), i.e.,

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_t=-C_t+{\Delta }^{\left(1\right)}\left(t\right)S_t+{\Delta }^{\left(2\right)}\left(t\right){\tilde{C}}_t+B_t,\hfill \\ {\mathsf{\Pi }}_0=0,\hfill \end{array}\right.$$

(19)

where $B_t$ denotes the risk-free asset (for example, a bank account or a government bond), which grows with constant risk-free rate r. Note that Option B depends on the same underlying market factors as Option A. Following Bakshi et al. (1997), we impose the so-called minimized variance constraints,

$$\left\{\begin{array}{c}〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{S}_t〉=0,\hfill \\ 〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{W}_t^v〉=0,\hfill \end{array}\right.$$

(20)

where $\langle ·,·\rangle$ refers to the covariation between the two processes and $W_t^v$ is the Brownian motion which is independent from $S_t$, driving random changes in the volatility. By imposing these constraints, one obtains a portfolio that has no covariation with the underlying asset and its volatility. In other words, changes in the asset’s value and changes in the asset’s volatility will have neither direct nor indirect (through correlations) effect on the portfolio. These constraints give us the following hedge ratios,

$$\left\{\begin{array}{c}{\Delta }^{\left(1\right)}\left(t\right)=\frac{\partial C}{\partial S_t}-{\Delta }^{\left(2\right)}\left(t\right)\frac{\partial \tilde{C}}{\partial S_t},\hfill \\ {\Delta }^{\left(2\right)}\left(t\right)=\frac{{\displaystyle \partial C/\partial v_t}}{{\displaystyle \partial \tilde{C}/\partial v_t}}.\hfill \end{array}\right.$$

(21)

Under the assumptions of the Heston model, the portfolio dynamics are given by,

$$\begin{array}{cc}\hfill \mathrm{d}{\mathsf{\Pi }}_t& =\mathrm{d}t\left(-\frac{\partial C}{\partial t}-\frac{1}{2}{v}_t{S}_t^2\frac{{\partial }^{2}C}{\partial S_t^2}-\frac{1}{2}{\gamma }^2{v}_t\frac{{\partial }^{2}C}{\partial v_t^2}-\rho \gamma v_t{S}_t\frac{{\partial }^{2}C}{\partial S_t\partial v_t}+r{B}_t\right.\hfill \\ & +\left.{\Delta }^{\left(2\right)}\left(t\right)\left(\frac{\partial C}{\partial t}+\frac{1}{2}{v}_t{S}_t^2\frac{{\partial }^{2}C}{\partial S_t^2}+\frac{1}{2}{\gamma }^2{v}_t\frac{{\partial }^{2}C}{\partial v_t^2}+\rho \gamma v_t{S}_t\frac{{\partial }^{2}C}{\partial S_t\partial v_t}\right)\right),\hfill \end{array}$$

(22)

Note that the random components have disappeared from the portfolio. Thus, the portfolio should be insensitive to changes in the market, if it respects the assumptions of the Heston model.

Secondly, we assume a model which is similar to the classical Delta-Vega hedge, but with adjusted hedge ratios. We call this strategy the adjusted Delta-Vega hedge. Assuming a dynamic model (see Appendix B for more details), we can apply Ito’s lemma to obtain

$$\mathrm{d}{C}_t^{\mathrm{Dynamic}}=\frac{\partial C}{\partial t}\mathrm{d}t+\sum _{p_t}\frac{\partial C}{\partial p_t}\mathrm{d}{p}_t+\frac{1}{2}\sum _{p_t}\sum _{q_t}\frac{{\partial }^{2}C}{\partial p_t\partial q_t}〈\mathrm{d}{p}_t,\mathrm{d}{q}_t〉,$$

(23)

with $p_t,q_t\in \{S_t,v_t,{\overline{v}}_t,{\gamma }_t\}$. For notational purposes, we rewrite this expression as

$$\mathrm{d}{C}_t^{\mathrm{Dynamic}}=c_1\mathrm{d}t+c_2\mathrm{d}{W}_t^S+c_3\mathrm{d}{W}_t^v+c_4\mathrm{d}{W}_t^{\overline{v}}+c_5\mathrm{d}{W}_t^{\gamma },$$

(24)

where the coefficients are defined as

$$\left\{\begin{array}{cc}\hfill c_1=& \frac{\partial C}{\partial t}+r{S}_t\frac{\partial C}{\partial S_t}+\kappa ({\overline{v}}_t-v_t)\frac{\partial C}{\partial v_t}+{\kappa }_{\overline{v}}({\overline{v}}_{\mathrm{Mean}}-{\overline{v}}_t)\frac{\partial C}{\partial {\overline{v}}_t}\hfill \\ & +{\kappa }_{\gamma }({\gamma }_{\mathrm{Mean}}-{\gamma }_t)\frac{\partial C}{\partial {\gamma }_t}+\frac{1}{2}\sum _{p_t}\sum _{q_t}\frac{{\partial }^{2}C}{\partial p_t\partial q_t}〈\mathrm{d}{p}_t,\mathrm{d}{q}_t〉,\hfill \\ \hfill c_2=& \sqrt{v_t}{S}_t\frac{\partial C}{\partial S_t}+\rho {\gamma }_t\sqrt{v_t}\frac{\partial C}{\partial v_t}+\rho {\rho }_{\overline{v}}{a}_{\overline{v}}{\overline{v}}_t\frac{\partial C}{\partial {\overline{v}}_t}+\rho {\rho }_{\gamma }{a}_{\gamma }{\gamma }_t\frac{\partial C}{\partial {\gamma }_t},\hfill \\ \hfill c_3=& {\gamma }_t\sqrt{v_t(1-{\rho }^2)}\frac{\partial C}{\partial v_t}+{\rho }_{\overline{v}}{a}_{\overline{v}}{\overline{v}}_t\sqrt{1-{\rho }^2}\frac{\partial C}{\partial {\overline{v}}_t}+{\rho }_{\gamma }{a}_{\gamma }{\gamma }_t\sqrt{1-{\rho }^2}\frac{\partial C}{\partial {\gamma }_t},\hfill \\ \hfill c_4=& a_{\overline{v}}{\overline{v}}_t\sqrt{1-{\rho }_{\overline{v}}^2}\frac{\partial C}{\partial {\overline{v}}_t},\hfill \\ \hfill c_5=& a_{\gamma }{\gamma }_t\sqrt{1-{\rho }_{\gamma }^2}\frac{\partial C}{\partial {\gamma }_t}.\hfill \end{array}\right.$$

(25)

The hedge ratios now take the correlated components of $\overline{v}$ and $\gamma$ into account, due to the minimized variance constraints of Equation (20). Using Equation (24), the hedge ratios can be derived, giving

$$\left\{\begin{array}{c}{\Delta }_{\mathrm{Adjusted}}^{\left(1\right)}\left(t\right)=\frac{c_2}{\sqrt{v_t}{S}_t}-\frac{{\tilde{c}}_2{c}_3}{\sqrt{v_t}{S}_t{\tilde{c}}_3},\hfill \\ {\Delta }_{\mathrm{Adjusted}}^{\left(2\right)}\left(t\right)=\frac{c_3}{{\tilde{c}}_3},\hfill \end{array}\right.$$

(26)

where ${\tilde{c}}_2$ and ${\tilde{c}}_3$ are defined as in Equation (25) for Option B. The additional stochastic variables ${\overline{v}}_t$ and ${\gamma }_t$ follow mean reverting processes (see Equation (A1) in Appendix B), such that the portfolio dynamics are found to be,

$$\begin{array}{cc}\hfill \mathrm{d}{\mathsf{\Pi }}_t=& \left(-c_1+\frac{c_3}{{\tilde{c}}_3}{\tilde{c}}_1+\frac{{\tilde{c}}_{2}r}{\sqrt{v_t}}-\frac{{\tilde{c}}_2{c}_{3}r}{\sqrt{v_t}{\tilde{c}}_3}+r{B}_t\right)\mathrm{d}t\hfill \\ & +\left(\frac{c_3}{{\tilde{c}}_3}{\tilde{c}}_4-c_4\right)\mathrm{d}{W}_t^{\overline{v}}+\left(\frac{c_3}{{\tilde{c}}_3}{\tilde{c}}_5-c_5\right)\mathrm{d}{W}_t^{\gamma }.\hfill \end{array}$$

(27)

The portfolio still depends on the randomness associated with $\overline{v}$ and $\gamma$. However, the randomness associated with $S_t$ and $v_t$ have disappeared, including the random components of $\overline{v}$ and $\gamma$ that are correlated to $S_t$ and $v_t$.

We also consider a strategy that aims at completely hedging against any changes of $\overline{v}$ and $\gamma$, by introducing two additional options,

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_t=-C_t+{\Delta }_{\mathrm{Full}}^{\left(1\right)}\left(t\right)S_t+{\Delta }_{\mathrm{Full}}^{\left(2\right)}\left(t\right){\tilde{C}}_t+{\Delta }_{\mathrm{Full}}^{\left(3\right)}\left(t\right){\overline{C}}_t+{\Delta }_{\mathrm{Full}}^{\left(4\right)}\left(t\right){\widehat{C}}_t.\hfill \\ {\mathsf{\Pi }}_0=0.\hfill \end{array}\right.$$

(28)

Again, all options depend on the same underlying market factors, but they have different contract details. In this case, we require to be protected against any changes of $S_t$, $v_t$, ${\overline{v}}_t$ and ${\gamma }_t$, hence we impose

$$\left\{\begin{array}{c}〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{S}_t〉=0,\hfill \\ 〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{W}_t^v〉=0,\hfill \\ 〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{W}_t^{\overline{v}}〉=0,\hfill \\ 〈\mathrm{d}{\mathsf{\Pi }}_t,\mathrm{d}{W}_t^{\gamma }〉=0.\hfill \end{array}\right.$$

(29)

Substituting these constraints leads to a system of equations, which is solved by

$$\left[\begin{array}{c}{\Delta }_{\mathrm{Full}}^{\left(1\right)}\left(t\right)\\ {\Delta }_{\mathrm{Full}}^{\left(2\right)}\left(t\right)\\ {\Delta }_{\mathrm{Full}}^{\left(3\right)}\left(t\right)\\ {\Delta }_{\mathrm{Full}}^{\left(4\right)}\left(t\right)\end{array}\right]={\left[\begin{array}{cccc}\sqrt{v_t}{S}_t& {\tilde{c}}_2& {\overline{c}}_2& {\widehat{c}}_2\\ 0& {\tilde{c}}_3& {\overline{c}}_3& {\widehat{c}}_3\\ 0& {\tilde{c}}_4& {\overline{c}}_4& {\widehat{c}}_4\\ 0& {\tilde{c}}_5& {\overline{c}}_5& {\widehat{c}}_5\end{array}\right]}^{-1}\left[\begin{array}{c}{c}_2\\ c_3\\ c_4\\ c_5\end{array}\right].$$

(30)

By imposing Equation (29), one removes all randomness associated with $S_t$, $v_t$, ${\overline{v}}_t$ and ${\gamma }_t$. Hence, the portfolio dynamics only depend on deterministic changes under the assumed market dynamics. From this point onwards, we refer to this strategy as the full hedge strategy.

4.1. Hedge Test Experiments

In this section, we discuss the results of the hedge test which was explained above. This test experiment indicates which approach is more accurate when evaluating future option prices, a measure which assumes $\overline{v}$ and $\gamma$ to be constant or a measure which assumes $\overline{v}$ and $\gamma$ to change over time. We thus consider the classical approach, with constant $\overline{v}$ and $\gamma$, and two approaches that assume $\overline{v}$ and $\gamma$ to change over time. The different hedging strategies are tested in a simulated market as well as in an empirical market.

The empirical hedge test is based on daily implied volatility surfaces of the S&P-500 European put and call options from January 2006 to February 2014.

4.1.1. Simulated Market

First, we evaluate the hedging strategies in a controlled environment. In this test, we assume $S_t$ and $v_t$ to follow the Heston model, with the key difference that $\overline{v}$ and $\gamma$ are time-dependent mean reverting processes (as in Equation (A1) in Appendix B). This set-up will be informative, as it is in line with historical observations. The processes of $S_t$ and $v_t$ are discretized by the Quadratic Exponential (QE) scheme, as proposed in Andersen (2008). Furthermore, the processes of $\overline{v}$ and $\gamma$ are discretized by the Milstein scheme, while also taking the correlations with $v_t$ into account. The details of this simulation scheme can be found in Appendix B.

The performance of the classical Heston Delta-Vega, the adjusted Heston Delta-Vega and the full hedge is compared under the dynamics of this market. The strategies all aim at hedging a short position in a European call option with maturity $T=1.0$ years and strike $K=50$. Moreover, at the start date of the option, $t=0$, we assume

$$\left\{\begin{array}{cccc}{S}_0=49,& v_0=0.05,& {\overline{v}}_0=0.1,& {\gamma }_0=0.7,\\ \kappa =1.0,& \rho =-0.75,& r=0.01.& \end{array}\right.$$

(31)

The adjusted Delta-Vega and full hedge involve additional options. These options depend on the same stock as Option A, but the contract details are different, i.e.,

$$\left\{\begin{array}{cc}\tilde{K}=50.0,\hfill & \tilde{T}=2.0,\hfill \\ \overline{K}=50.0,\hfill & \overline{T}=3.0,\hfill \\ \widehat{K}=50.0,\hfill & \widehat{T}=4.0.\hfill \end{array}\right.$$

(32)

Moreover, we assume the following parameters in the dynamics of the $\overline{v}$ and $\gamma$ processes,

$$\left\{\begin{array}{cccc}{\kappa }_{\overline{v}}=1.4,\hfill & {\overline{v}}_{\mathrm{Mean}}=0.1,\hfill & a_{\overline{v}}=0.8,\hfill & {\rho }_{\overline{v}}=0.9,\hfill \\ {\kappa }_{\gamma }=2.1,\hfill & {\gamma }_{\mathrm{Mean}}=0.7,\hfill & a_{\gamma }=1.0,\hfill & {\rho }_{\gamma }=0.9.\hfill \end{array}\right.$$

(33)

In reality, these parameters cannot be freely chosen, as they are implied by the market. By analysing the historical behaviour of ${\overline{v}}_t$ and ${\gamma }_t$, one is able to estimate these SDE parameters. In this case, however, we assume to know these parameters and use them when determining the hedge strategy.

Ideally, the portfolio value should be equal to zero for each point in time, because the initial portfolio value is equal to zero. Every deviation from zero is thought of as a hedge error. Over the entire life of the option we desire the mean and standard deviation of this error to be as close as possible to zero. To this end, we introduce the following error measures for simulation j,

$$E_{\mathrm{Mean}}^{\left(j\right)}=\frac{1}{N+1}\sum _{i=0}^N{\mathsf{\Pi }}_{\frac{i}{N}T}^{\left(j\right)},E_{\mathrm{Std}}^{\left(j\right)}=\sqrt{\frac{1}{N}{\sum }_{i=0}^N{\left({\mathsf{\Pi }}_{\frac{i}{N}T}^{\left(j\right)}-E_{\mathrm{Mean}}^{\left(j\right)}\right)}^2}.$$

(34)

The overall hedging performance of the M simulations can be judged by

$$\left\{\begin{array}{c}{\overline{E}}_{\mathrm{Mean}}=\frac{1}{M}\sum _{j=1}^M{E}_{\mathrm{Mean}}^{\left(j\right)},\hfill \\ {\overline{E}}_{\mathrm{Std}}=\frac{1}{M}\sum _{j=1}^M{E}_{\mathrm{Std}}^{\left(j\right)}.\hfill \end{array}\right.$$

(35)

In the current set-up, these error measures are random variables, as they are determined by means of Monte Carlo simulations. To this end, we analyse the stability of the error measures across the simulated trajectories by the standard error,

$$\mathrm{SE}\left(E\right)=\frac{\sqrt{\frac{1}{M-1}\sum _{j=1}^M{\left(\overline{E}-E^{\left(j\right)}\right)}^2}}{\sqrt{M}},$$

(36)

with error measure E, its mean $\overline{E}$ and the simulated trajectories $E^{\left(j\right)}$.

The performance of the strategies under these assumptions based on $M=200$ simulations is given in

Table 1. Hedge errors of the different hedging strategies. The standard errors of the estimates are given in parentheses.

Frequency	${\overline{\mathit{E}}}_{\mathbf{Mean}}$	${\overline{\mathit{E}}}_{\mathbf{Std}}$
classical Delta-Vega:
Once per week	−0.339 (0.0207)	0.228 (0.0084)
Once per day	−0.354 (0.0227)	0.210 (0.0080)
Adjusted Delta-Vega:
Once per week	−0.204 (0.0097)	0.137 (0.0072)
Once per day	−0.220 (0.0071)	0.114 (0.0047)
Full hedge:
Once per week	−0.044 (0.0040)	0.068 (0.0042)
Once per day	−0.051 (0.0030)	0.045 (0.0022)

.

These results show that, in this experiment, it is beneficial to take parameter correlations into account when hedging, in terms of both the mean error and the standard deviation. While still not perfect, the dynamic Heston Delta-Vega hedge is better able to remain risk-neutral on average and it deviates less from this average. The full hedge performs even better with a mean approximately equal to zero and a standard deviation equal to or lower than any of the previous strategies, despite the dynamic behaviour of the market.

The purpose of these hedging strategies is to replicate the value of an option. In the case of the classical Delta-Vega hedge, only $S_t$ and $v_t$ are allowed to change. By respecting the assumptions of the Heston model, we are not fully able to replicate the future option values. On the other hand, when assuming the adjusted Heston model, ${\overline{v}}_t$ and ${\gamma }_t$ are allowed to change as well. Hedging strategies considering this dynamic behaviour, produce more accurate future option price estimates in the current set-up. This indicates the importance of taking dynamic parameters into account when determining future option prices, even when the assumptions of the underlying model are violated. However, note that the comparison is not completely fair, since we specifically assume a Heston market with time-dependent $\overline{v}$ and $\gamma$. It can therefore be expected that a strategy taking these assumptions into account outperforms one that does not. Therefore, to better assess the true performance of these strategies, we also perform an empirical test.

4.1.2. Empirical Market

When hedging in practice, the underlying assumptions are not always respected and the true parameters are, of course, unknown. To quantify the effect of these difficulties, we test the hedging strategies on historical data in this section. All hedging ratios depend on the dynamic risk-neutral parameters, hence $v_t$, $\overline{v}$, $\gamma$ and $\rho$ vary over time, according to the changes in the historically observed implied volatility surfaces. Moreover, the adjusted Heston Delta-Vega hedge depends on the correlation and volatility of $\overline{v}$ and $\gamma$, which we define as follows

$$\left\{\begin{array}{c}{\rho }_{\overline{v}}={\rho }_{\gamma }=0.95,\hfill \\ a_{\overline{v}}=\sqrt{\frac{\frac{1}{N}{\sum }_{i=-N}^{-1}log{\left(\frac{{\displaystyle {\overline{v}}_{t_{i+1}}}}{{\displaystyle {\overline{v}}_{t_i}}}\right)}^2}{{\displaystyle \Delta t}}},\hfill \\ a_{\gamma }=\sqrt{\frac{\frac{1}{N}{\sum }_{i=-N}^{-1}log{\left(\frac{{\displaystyle {\gamma }_{t_{i+1}}}}{{\displaystyle {\gamma }_{t_i}}}\right)}^2}{{\displaystyle \Delta t}}}.\hfill \end{array}\right.$$

(37)

It can be quite challenging to determine the correlation between the Brownian motions driving the parameters, hence we assume it to be equal for each time-interval. Moreover, the volatility estimator only depends on past observations; the sum indices vary from $-N$ to $-1$ with $t_{-N}=-1$ year, where $t_0=0$ indicates the starting date of the option.

In this test, we hedge an at-the-money European call option with one year maturity on the S&P-500 index. All hedging strategies are subjected to daily rebalances that are based on the parameters as seen on that date. The transaction costs are excluded from this test, as we are interested in the performance of the hedging strategies with respect to changes in $\overline{v}$ and $\gamma$. Including transaction costs would increase the costs of the full dynamic Heston hedging strategy, as it involves more financial assets. This would bias the results and it is therefore best to exclude the transaction costs from the present test.

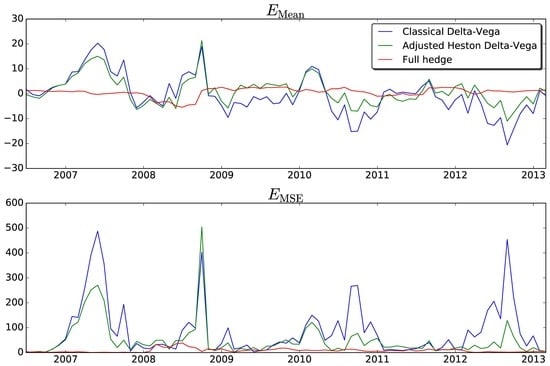
The test is repeated on a monthly basis from July 2006 to February 2013 and the performance is assessed by the mean error and mean squared error during the life of the option,

$$E_{\mathrm{Mean}}^{\left(j\right)}=\frac{1}{N+1}\sum _{i=0}^N{\mathsf{\Pi }}_{\frac{i}{N}T}^{\left(j\right)},E_{\mathrm{MSE}}^{\left(j\right)}=\frac{1}{N+1}\sum _{i=0}^N{\left({\mathsf{\Pi }}_{\frac{i}{N}T}^{\left(j\right)}\right)}^2.$$

(38)

The time intervals of the hedging portfolios overlap in this set-up, since the test is repeated on a monthly basis and the option maturity is one year. However, all strategies depend on different initial conditions and therefore perform differently, despite the overlapping time-intervals. The results of this test are graphically presented in Figure 2.

The hedging performances are similar to the simulation results:

• The classical Delta-Vega hedge does not take changes of the parameters into account and appears to be the most unstable method. This strategy has the most and highest error “peaks” and is therefore most unreliable.
• The adjusted Delta-Vega hedge is still not perfect but appears to be more stable than the classical Delta-Vega hedge, the error “peaks” happen less frequently and are less pronounced. The error can be minimized by optimizing the correlation and volatility of ${\overline{v}}_t$ and ${\gamma }_t$, but the optimization can only be performed afterwards, which is not the objective of this test.
• The full hedge is the most stable out of the three strategies. It does not have any error “peaks” and outperforms the other two strategies in most cases. Moreover, this strategy does not depend on additional parameters which may introduce an error if chosen poorly, such as in the dynamic Heston Delta-Vega hedge.

We can conclude that respecting the assumptions of the underlying model (in this case, the Heston model) does not necessarily lead to more accurate future option prices. By taking changes of the $\overline{v}$ and $\gamma$ parameters into account, we are able to replicate option values more accurately both in a controlled (simulation) and uncontrolled (empirical) environment.

5. VIX Heston Model Results

5.1. Data and Calibration

The dataset contains monthly implied volatility surfaces of the S&P-500 European put and call options from January 2006 to February 2017. Each implied volatility surface contains five different strike levels (80%, 90%, 100%, 110% and 120% of $S_0$) and maturities (0.25, 0.5, 1, 1.5 and 2 years). We split the dataset into a training set and a test set. The training set consists of implied volatility surfaces from January 2006 to February 2014 and is only used to identify the optimal regression components. The test set contains monthly implied volatility surfaces from March 2014 to February 2017 and is used to assess the accuracy of the VIX Heston model.

Furthermore, to assess the robustness of the VIX Heston model, we apply it to monthly implied volatility surfaces of the FTSE-100 (United Kingdom) and STOXX-50 (Europe) as well. The training set includes data from October 2010 to June 2015 and the test set contains data from July 2015 to February 2017.

To assess the accuracy of the VIX Heston model, one must first calibrate the model according to Equation (17). Using the US training set described above, we obtain

$${\mathsf{\Omega }}_t^{\mathrm{Heston}}\left(X\right)=\left\{\begin{array}{cc}{\kappa }_t\hfill & =1.0,\hfill \\ v_{0,t}\hfill & ={\left(0.0140+0.0090·{\mathrm{VIX}}_t\right)}^2,\hfill \\ {\overline{v}}_t\hfill & ={\left(0.0957+0.0087·{\mathrm{VIX}}_{{\mathrm{filter}}_t}\right)}^2,\hfill \\ {\gamma }_t\hfill & =9.6479·{10}^{-5}+0.0270·{\mathrm{VIX}}_t,\hfill \\ {\rho }_t\hfill & =-0.7294.\hfill \end{array}\right.$$

(39)

The calibrated parameters of the UK and Europe datasets can be found in Appendix C. The accuracy is assessed by comparing the predicted to the observed implied volatility surfaces of the test set, according to the following error measures,

$$\left\{\begin{array}{c}\mathrm{SSE}={\displaystyle \sum _{t,K,T}}{\left({\sigma }^{\mathrm{Market}}(t,K,T)-{\sigma }^{\mathrm{Heston}}(t,{\mathsf{\Omega }}_t^{\mathrm{Heston}},K,T)\right)}^2,\hfill \\ \mathrm{MAE}=\frac{1}{N_{\sigma }}{\displaystyle \sum _{t,K,T}}\left|{\sigma }^{\mathrm{Market}}(t,K,T)-{\sigma }^{\mathrm{Heston}}(t,{\mathsf{\Omega }}_t^{\mathrm{Heston}},K,T)\right|,\hfill \\ R^2=1-\frac{\mathrm{SSE}}{{\displaystyle \sum _{t,K,T}}{\left({\sigma }^{\mathrm{Market}}(t,K,T)-{\overline{\sigma }}^{\mathrm{Market}}\right)}^2},\hfill \\ R_{\mathrm{Min}}^2=\underset{t}{min}\left\{R_t^2:t\in [t_{\min },t_{\max }]\right\},\hfill \end{array}\right.$$

(40)

where ${\mathsf{\Omega }}_t^{\mathrm{Heston}}$ is defined as the predicted parameter set, $N_{\sigma }$ as the total number of observed implied volatilities and ${\overline{\sigma }}^{\mathrm{Market}}$ as the average of all observed implied volatilities. The corresponding results are displayed in

Table 2. Out-of-sample accuracy of the regression models according to the error measures defined in Equation (40).

	$\mathbf{SSE}$	$\mathbf{MAE}$	${\mathit{R}}^2$	${\mathit{R}}_{\mathbf{Min}}^2$
US
VIX Heston	0.2286	0.0124	0.8948	0.8159
Unrestricted	0.0185	0.0034	0.9915	0.9798
UK
VIX Heston	0.0577	0.0093	0.9340	0.7401
Unrestricted	0.0126	0.0045	0.9855	0.9690
Europe
VIX Heston	0.0433	0.0078	0.9389	0.7693
Unrestricted	0.0154	0.0051	0.9783	0.9190

. The predicted paths for the Heston parameters of the US dataset can be found in Figure 3. The predicted paths of the Heston parameters of the UK and Europe dataset are graphically presented in Appendix C.

The regression model loses some accuracy compared to the unrestricted model. On average, there is an error of 0.003 between the implied volatility and the unrestricted Heston model in the US dataset, which is approximately equal to an error of 2.2%. The VIX Heston model has an average absolute error of 0.012, which corresponds to a 7.7% error. Thus, by implementing the regression models, we introduce an additional error of 5.5%, on average. The accuracy of the VIX Heston model in the UK and Europe datasets is even higher, where the accuracy loss is equal to 2.9% and 1.2%, respectively.

Finally, we discuss the predictions obtained in dependence of parameter $\gamma$. In the US dataset, the prediction of $\gamma$ is relatively inaccurate (see Figure 3), as the out-of-sample correlation to the VIX index is much lower than the in-sample correlation (0.86 in-sample versus 0.32 out-of-sample). In the UK and Europe datasets, this phenomenon does not seem to be present and consequently the predictions of $\gamma$ are much more accurate (see Figure A1 and Figure A2 in Appendix C). This also explains why the implied volatility surface predictions in the UK and Europe datasets are more accurate than the US predictions, as can be seen in Table 2. Thus, there appears to be another, yet unknown, factor driving $\gamma$ in the US dataset, which is absent in the UK and Europe datasets. Analysis of the cause of this phenomenon might be a topic for future study. However, in this research, we assume that the VIX Heston model is sufficiently accurate to describe the dynamic behaviour of the Heston parameters, as $\gamma$ only has a minor effect on the implied volatility surface.

5.2. SCR Impact Study

In this test, we assess the impact of assuming time-dependent risk-neutral parameters, according to three scenarios. Each scenario corresponds to a different initial market and consequently the initial expected liabilities, $L_0$, will differ. We assume a no-arbitrage fee, i.e., a fee for which $L_0$ is equal to zero. The general contract details of the variable annuity can be found in

Table 3. General contract details of the GMAB rider.

Parameter	Value
$F_0$	1000
G	1000
$T_{\mathrm{GMAB}}$	10
r	0.04

and the initial values of the different scenarios accompanied with the fair premiums are presented in

Table 4. Initial values and fair premiums of the GMAB rider.

Parameter	Scenario 1	Scenario 2	Scenario 3
$v_0$	0.04	0.01	0.27
${\overline{v}}_0$	0.08	0.025	0.24
${\gamma }_0$	0.55	0.05	1.4
${\alpha }_{\mathrm{GMAB}}$	0.0174	0.0057	0.0345

.

We assume the fund value to follow a GBM with initial value $F_0=1000$, so the fund value follows Equation (7). The VIX index is modelled simultaneously, following a mean-reverting path

$$\left\{\begin{array}{cc}\mathrm{d}{\mathrm{vix}}_t\hfill & ={\kappa }_{\mathrm{vix}}({\mathrm{vix}}_{\mathrm{Mean}}-{\mathrm{vix}}_t)+{\gamma }_{\mathrm{vix}}{\mathrm{vix}}_t^{{\lambda }_{\mathrm{vix}}}\left({\rho }_{\mathrm{vix}}\mathrm{d}{W}_t^S+\sqrt{1-{\rho }_{\mathrm{vix}}^2}\mathrm{d}{W}_t^{\mathrm{vix}}\right),\hfill \\ \mathrm{VIX}\hfill & =100·\mathrm{vix}.\hfill \end{array}\right.$$

(41)

The process parameters are estimated with the generalized Method of Moments (see Hansen (1982)),

$$\left\{\begin{array}{c}\sigma =0.21,\mu =0.05,{\kappa }_{\mathrm{vix}}=4.964,{\mathrm{vix}}_{\mathrm{Mean}}=0.207,\hfill \\ {\gamma }_{\mathrm{vix}}=1.859,{\lambda }_{\mathrm{vix}}=1.271.\hfill \end{array}\right.$$

(42)

Moreover, we set ${\rho }_{\mathrm{vix}}=-0.75$, which is in line with observations in the risk-neutral market. The SDEs are discretized by the Milstein scheme.

5.2.1. Guaranteed Minimum Accumulation Benefit

We have simulated 100,000 real-world trajectories and evaluated the loss function as defined in Equation (4) under the two risk-neutral measures (with either constant or time-dependent parameters). This way, we are able to construct and compare the probability density functions under these measures. This process is repeated for the three different scenarios that are presented in Table 3. In Figure 4, we have graphically represented the impact on the probability density function of the loss distribution for the different scenarios. Moreover, the Solvency Capital Requirements associated with these distributions can be found in

Table 5. Solvency Capital Requirement of the scenarios for the original and time-dependent risk-neutral measure.

	Original	Time-Dependent
Scenario 1	170.1	195.5
Scenario 2	166.9	237.5
Scenario 3	178.8	150.8

.

The impact on the probability density functions and the Solvency Capital Requirements is substantial and we wish to highlight a few noteworthy features.

The loss distribution under the original risk-neutral measure appears to be centred around 0, independent of the initial conditions. The one-year loss is defined as the difference between the policy value at the times $t=0$ and $t=1$. On average, the policy value will not change significantly if the risk-neutral parameters stay the same. Therefore, the loss distribution must be centred around 0, as long as the initial risk-neutral parameters do not change. The loss distribution under the time-dependent risk-neutral measure, on the other hand, heavily depends on the risk-neutral parameters at $t=0$. Consider Scenario 2 for example. Initially, the volatility, $\overline{v}$ and $\gamma$ are relatively low, resulting in low initial expected liabilities. However, according to the mean-reverting VIX index, these parameters are more likely to increase over time and with them, the expected liabilities. Consequently, the one-year losses are much higher compared to those under the original risk-neutral measure, which still assumes the relatively low initial parameters at $t=1$. In Figure 4, this effect is clearly visible where the loss function is shifted to the right. Conversely, the one-year losses under the time-dependent risk-neutral measure in Scenario 3 are much lower, as the expected liabilities are more likely to decrease. In conclusion, when the initial volatility is low (high), we can expect a higher (lower) SCR under the time-dependent risk-neutral measure. In the 2008 credit crisis, this resulted in a higher SCR before the crisis and a lower SCR during the crisis.

Besides the shifted mean, the loss distribution under the time-dependent risk-neutral measure also tends to have heavier tails, which is especially visible in Scenario 1. This is caused by the fact that $\overline{v}$ and $\gamma$ depend on the state of the market, which results in more extreme losses (or gains). If, for example, the market crashes, $\overline{v}$ and $\gamma$ are likely to increase. This will generate even higher expected liabilities, resulting in even higher losses. However, if the market flourishes, $\overline{v}$ and $\gamma$ tend to be much lower, leading to lower expected liabilities and lower losses (or higher gains). This feature is present in all scenarios of Figure 4, but is best visible in Scenario 1, where the probability of an extreme loss as well as the probability of an extreme gain is higher under the time-dependent risk-neutral measure. Consequently, the SCRs under the two risk-neutral measures are not necessarily equal, not even when the initial conditions are equal to the average market conditions (such as in Scenario 1).

To give a broad overview of the impact, we determine the SCR of a variable annuity with the GMAB rider for multiple points in time. The contract details presented in Table 3 remain unchanged, but the initial parameters depend on historical data. For computational purposes, the parameter $\alpha$ is assumed to be constant and equal to 0.01. In this test, we compare four different risk-neutral measures:

• A time-dependent risk-neutral measure where all parameters depend on the simulated state of the market.
• A risk-neutral measure where $F_1$ and $v_1$ depend on the simulated market and the risk-neutral parameters are equal to the parameters as observed on $t=0$. This measure is equivalent to the original risk-neutral measure that we have previously defined.
• A risk-neutral measure where $F_1$ and $v_1$ depend on the simulated market and the risk-neutral parameters are equal to the parameters as observed on $t=1$. We refer to this measure as the future risk-neutral measure.
• A risk-neutral measure where $F_1$ and $v_1$ depend on the simulated market and the risk-neutral parameters are equal to the realized regression model predictions at $t=1$ of Figure 3. This measure is different from the time-dependent risk-neutral measure, as it depends on the realized state VIX, instead of the simulated VIX. We refer to this measure as the future VIX risk-neutral measure.

Thus far, we have applied the first two risk-neutral measures in our analysis. The latter two measures can only be applied on historical data (otherwise, the observed parameters at $t=1$ are undefined) and are merely added for explanatory purposes. Ideally, the SCRs under the future and the future VIX risk-neutral measure are equal. The difference between these measures is caused by prediction errors of the regression model. Hence, the difference between the SCRs under these measures be is indication for the accuracy of the regression models.

In Figure 5, the results under the different risk-neutral measures are displayed. The difference between the original and time-dependent risk-neutral measure is also summarized in

Table 6. Difference in SCR between original and time-dependent risk-neutral measure.

	Value	%
Mean absolute difference	41.1	28.7%
Maximum absolute difference	85.3	52.0%

.

5.2.2. Discussion on Impact

The impact on the SCR is significant, with a maximum absolute difference of over 50%. Moreover, the difference appears to be structural over time, with a mean absolute difference of almost 30%. The results in Figure 5 also contain some stylized facts that we have already seen in Figure 4 and we discuss them by distinguishing different time periods:

• 2005–2007: The volatility in these years was relatively low and this translates to a somewhat higher SCR under the original measure and an even higher SCR under the time-dependent measure, which is similar to Scenario 2. The SCR under the future measure is rising, due to higher expected liabilities at $t=1$, indicating that more volatile times are coming.
• Early 2008: The market has not crashed yet, but volatility is starting to increase, resulting in a smaller difference between the time-dependent and original measures, which is comparable to Scenario 1. The future measure, however, takes the fact that the market will crash into account. Hence, the SCR is the highest under the future measure.
• Late 2008–2012: During these years, several spikes occurred in the implied volatility surface, which will increase the initial liabilities and therefore the expected losses will decrease, analogously to Scenario 3. This results in lower SCRs during this period. Moreover, we see that the SCRs under the future risk-neutral measure are lowest during these highly volatile periods, since this measure depends on the realized market at $t=1$, which has returned to its less volatile state. Consequently, the expected liabilities at $t=1$ and the SCR are the lowest under the future risk-neutral measure.
• 2013–2017: This period is comparable to 2005–2007, apart from the fact that the volatility is approximately constant throughout these years. This translates into an almost equal SCR prediction under the original and future risk-neutral measures.

The difference between the future and future VIX measures is small. This means that the expected liabilities at $t=1$ are almost equal under both measures, indicating the accuracy of the regression model, at least for the realized states of the market. Under the assumption that the simulated markets behave similar to historical observations, this means that expected liabilities at $t=1$ under the time-dependent measure will be in line with the simulated states of the market.

Finally, we also mention that we performed a very similar study for the GMWB product. Essentially, the same results were obtained in that case, however, the impact was somewhat less severe.

6. Conclusions

The research in this paper was motivated by the open question of how to value future guarantees that are issued by insurance companies. The future value of these guarantees is essential for regulatory and Asset Liability Management purposes. The complexity of the valuation is found in the fact that, first, these guarantees involve optionalities and thus need to be valued using the risk-neutral measure; and, second, whereas this measure is well-defined at $t=0$, the future risk-neutral measure, at future time $t=1$, is debatable.

For a large part, the liabilities evolve according to real-world models and, therefore, the future values of these guarantees need to be computed conditionally on the real-world scenarios. In this paper, we demonstrate the benefits of option valuation under a new, so-called ${\mathbb{P}}^{\mathbb{Q}}$ measure in Asset Liability Management. This is done by modelling the Heston model parameters, which form the parameterization of the implied volatility surface, conditional on the real-world scenarios.

Basically, we advocate the use of dynamic risk-neutral parameters in the cases in which we need to evaluate asset prices under the $\mathbb{P}$ measure, before an option value is required at a future time point. It means that the development of the real-world asset paths in the future are taken into account in the option valuation.

A hedge test was implemented for an academic test case, where the dynamic strategy outperformed the strategy with static parameters. Importantly, the results from this hedge test case were confirmed by a hedge test based on 12 years of empirical, historical data. Several conclusions have already been given after each of the structured test experiments is presented.

The results obtained by the strategy for the Solvency Capital Requirement of the variable annuities exhibited differences of even 50%, as compared to the conventional risk-neutral pricing of these annuities. Next to that, we saw that the SCR was significantly less pro-cyclical under the new approach, which is a highly desired feature.