Abstract
In this paper, we consider a new corporate bond-pricing model with credit-rating migration risks and a stochastic interest rate. In the new model, the criterion for rating change is based on a predetermined ratio of the corporation’s total asset and debt. Moreover, the rating changes are allowed to happen a finite number of times during the life-span of the bond. The volatility of a corporate bond price may have a jump when a credit rating for the bond is changed. Moreover, the volatility of the bond is also assumed to depend on the interest rate. This new model improves the previous existing bond models in which the rating change is only allowed to occur once with an interest-dependent volatility or multi-ratings with constant interest rate. By using a Feynman-Kac formula, we obtain a free boundary problem. Global existence and uniqueness are established when the interest rate follows a Vasicek’s stochastic process. Calibration of the model parameters and some numerical calculations are shown.
1. Introduction
The study for bond-pricing models is always an attractive topic in financial research fields, as bonds and their derivatives are the largest capital markets in the financial industry Richelson and Richelson (2011). For a for-profit corporation, the price of a bond plays an essential role in determining the valuation of the corporation. This is particularly true for a corporation that requires a large capital such as corporations in mining industry. One of those examples is a corporation conducting crude-oil exploration and production. A corporation’s financial stress very much depends on the bond price of the corporation. It is a challenge in the financial markets to develop a comprehensive and dynamic bond-pricing model when an interest rate is uncertain.
There are two important factors that affect a bond price for a corporation. The first is the credit rating given by various rating agencies, which apply on their own measures. The second is the interest rate. For a long time, credit risks were mainly considered default risks, while credit-rating migration risks were usually neglected. After the financial crisis in 2008 and late the European sovereign debt crisis, researchers and bond traders realized the importance of credit-rating migration. One of the main factors for a dramatic change of a bond price is the credit-rating migration including default (see, for examples, Elton et al. (2001); Bessembinder et al. (2018)). The inflection and the liquidity risks in a corporate bond model are the other important factors (see, for examples, Kariya et al. (2016) and Kang and Pflueger (2015)). We would like to point out that the tax is another important factor in bond modelling (see, for example, Kenneth et al. (2018)). However, we will not consider this factor in this paper.
Traditional bond models with potential defaults have two broad categories: structural and reduced-form (or intensity-based). In a structural model, the default event occurs when the firm’s value falls below some insolvency threshold. A reduced-form approach concerns exogenous reasons rather than the firm’s value itself, where the default time is modelled by introducing a hazard rate (default intensity). The structural model, which will be applied in this paper, was developed first by Merton (1974). He used a predesigned structure to price a corporate bond with a fixed interest rate. The default event may only occur at the maturity of the claim (similar to a European option). The values of such bonds are considered as contingent claims. The value of a corporation, denoted by , follows a geometric Brownian motion:
where the constants and represent, respectively, the drift rate and the volatility. In 1976, Black and Cox (1976) extended Merton’s model by introducing safety covenants. This extended model allows bondholders to recognize the remaining value of a corporation if its assets fall below a certain given threshold (default ratio). In the modified model Black and Cox (1976), the default of a bond is allowed to occur any time up to the bond maturity (similar to a barrier option). Since those fundamental works by Merton and Black-Cox, various extensions have been considered by many researchers, see, for examples, Jarrow and Turnbull (1995) and Longstaff and Schwartz (1995), Leland and Toft (1996), Briys and De Varenne (1997), Lando (1998), Tsiveriotis and Fernandes (1998). The reader may find more references in Monograph by Dixit and Pindyck (1994). Recently, the authors of Li et al. (2018) used a risk-adjusted inside debt metric and corporate conservatism to study the credit risks and found some interesting results which closely matched data from the financial markets. However, those well-known models do not reflect a potential risk of credit-rating change and the interest-rate change. From the real financial market one can clearly observe that either the rating change or the interest-rate change will dramatically affect the bond price for a corporation.
In the study of credit-rating migration, a major tool is to introduce a Markov chain process. Most researchers mainly adopt a transfer intensity matrix. Through this approach, the reduced form framework is naturally developed for the dynamic process of credit rating migrations, see Das and Tufano (1996); Jarrow et al. (1997); Lando (2000); Thomas et al. (2002); Duffie and Singleton (1999); Hurd and Kuznetsov (2007) and so forth. The transfer intensity matrix usually comes from general statistical data, which do not include any particular firm’s assets. However, a firm’s asset value plays a key role in credit rating by rating agencies. In this situation, the Markov chain alone cannot fully capture the credit-rating mitigation for the bond price of a corporation. In 2015, Liang and Zeng (2015) used a structural model for pricing a bond where a credit rating may change. They gave a predetermined migration threshold where a firm’s asset value is divided into high and low rating regions, under the assumption that the value of a firm follows different stochastic processes in different regions. By using the Feynman-Kac theorem, the model can be reduced to a boundary value problem of a partial differential equation. This PDE method is very different from the traditional approaches in the research field for corporate bond modelling. However, a crucial assumption in Liang-Zeng’s model is that the rating migration boundary is predetermined. This assumption is inappropriate in the real financial world. It often depends on the proportion of a firm’s debt to the value of the firm. From this point of view, the migration boundary should be unknown. Under a fixed-interest rate, Hu-Liang-Wu in 2016 (Hu et al. 2015; Liang et al. 2016a, 2016b) proposed a new model to reflect this factor. They obtained a free boundary problem for the bond model. The existence and uniqueness for the free boundary problem are established.
As we stated before, when pricing a corporate bond in the real financial market, the interest rate is a very sensitive factor. On the other hand, the interest rate itself is a stochastic process. However, when a stochastic interest rate is considered in the bond pricing model, the corresponding mathematical model becomes extremely difficult to analyze. In 2017, Liang et al. (2017) used Vasicek’s model for the stochastic interest rate in the bond pricing model with a potential credit migration. This is a considerable improvement in comparison to existing bond models such as Hu et al. (2015); Liang et al. (2016b). They established the well-posedness for the mathematical model in Liang et al. (2017). Some properties of the free boundary such as the monotonicity of free boundary are also derived. However, there are two shortcomings in the model developed in Liang et al. (2017). The first is that the rating change is only allowed to occur one time during the life-span of the bond, which is not practical in the financial market. The second is that the current rating (known information) is not fully reflected in the model.
In the present paper, we extend the model considered in Liang et al. (2017) to overcome those shortcomings. The new bond model will allow the rating change to happen a finite number of times before the maturity of the bond. The rating change is determined solely by the debt-to-asset ratio. Moreover, by taking the current asset of a corporation and its bond rating into consideration, we assume that the assets of a corporation follows a general geometric Brownian motion. For the new model, we apply the Feynman-Kac theory to obtain a partial differential equation with free boundary. Particularly, we employ some PDE techniques used in Liang et al. (2017) to obtain the global existence and uniqueness when the interest rate follows a Vasicek’s process. We would like to mention that in Wu and Liang (2018) recently extended the model in Liang et al. (2017) to the multi-rating case under the assumption of a constant interest rate.
The paper is organized as follows: In Section 2, we propose some basic assumptions for the model with credit-rating migration and stochastic interest rate. In Section 3, by employing the Feynman-Kac theorem, we convert the new model to a free boundary problem. In Section 4, we consider a special case where the interest rate is given by Vasicek’s process. The global existence and uniqueness are established. Some concluding remarks are given in Section 5.
2. The Derivation of the New Model
We begin with some basic assumptions for our bond model.
Let be a complete probability space. We assume that a firm issues only a corporate bond, which is a contingent claim of its value on the space .
There are several models to describe the stochastic interest rate. We use a general model which includes Vasicek’s model as a special case.
2.1. The Interest Rate Model
Suppose that an interest rate follows a general stochastic process:
where is a known function, which is typically bounded by US current interest rate and 30-year treasury bond. is the standard Brownian motion which generates the filtration and is the volatility which can also be determined by historical data.
An important example for (1) is Vasicek’s model where
where , and are given positive functions. We would like to point out that Vasicek’s model is widely accepted in the financial market when parameters and are chosen properly.
2.2. Further Value of a Corporation
Let denote a firm’s value in a risk-neutral world. Suppose that there is a jump for the volatility when the bond rating changes from one rating region to another rating region. The firm’s asset value, denoted by , follows the standard geometric Brownian motion:
where is expected the growth or decay rate of the asset and represents the volatility, is the Brownian motion which generates the filtration , and the correlation between the interest rate and firm’s value is given by
where is a constant.
From the financial market, the expected growth of a corporation with a large debt load strongly depends on . Therefore, a natural assumption is that the expected growth is a function of time, interest rate and the value of the corporation:
where could be negative when the cash flow of a corporation becomes negative.
Moreover, the volatility is a function of time, interest rate and the value of corporation:
We would like to point out that and are assumed to be deterministic functions, which are determined by using the empirical data in the past. They also carry the up-to-date information for the corporation. One of important features for and is that there may have a jump where the rating for a bond changes.
For a rating agency, assume that a rating for a corporate’s bond is purely determined by the proportion, denoted by , of the firm’s debt to the asset .
Suppose that there are at most a finite number of possible rating over the finite time horizon . Let , be denoted the critical values of the debt-to-asset ratio with
Those values can be found from the empirical data for all corporations in every industrial section.
We can also use the empirical data to determine the approximate expected return and volatility in each rating range:
where
Although there is no difference for the order of and in the model, one can observe a fact in the financial market that the volatility is larger and growth of the asset is slower when debt-to-asset is increasing.
Please note that there are n interfaces, denoted by , where
which are unknown.
We assume that the firm issues only one corporate zero-coupon bond with face value F. Denote by the discount value of the bond at time t, which is the same as (debt obligation by Merton’s assumption). Therefore, at the maturity time T, an investor can get . Here we assume that the bondholder has the priority to claim the firm’s asset than the equity holders.
It is now clear that is the conditional expectation of present value of payoff value at the maturity subject to and :
where and satisfy the stochastic processes (1) and (2), respectively.
3. The Mathematical Model
Due to the potential rating change, the firm’s asset may display a jump. However, for a large corporation, we may assume that the bond price is continuous throughout the life-span of the bond. Moreover, we may also assume that is differentiable in each rating interval.
Let
Suppose there exists a risk-neutral measure in the probability space . By using the Feynman-Kac formula, we see that satisfies the following partial differential equation in (see Liang et al. (2017) detailed derivation):
where the functions will take the value in the corresponding ith-rate region.
We would like to point out that the expected rate of return does not occur in the model since we used a risk-neutral measure in the derivation.
At the maturity date T, the bond value is known:
Also, at the boundary , the price of the bond is also equal to 0:
Let
be the interface between two adjacent regions with different bond rating. We also use to be the value of in ith-rating region.
To see the free boundary conditions for on , we note that the value of the bond is continuous when it passes a rating threshold, i.e.,
Also, as derived in Hu et al. (2015); Liang et al. (2016b), another condition on the free boundary ,
Equations (4)–(8) forms a complete mathematical model for a corporate bond under the assumptions given in Section 2. We would like to point out that it is a mathematical challenge to establish the global existence and uniqueness for the problem (4)–(8) due to discontinuous coefficients in Equation (4) and free boundary . However, one can find a numerical solution by using a finite difference method. Due to the scope and page limitation of the paper, we will carry out the numerical simulation for the problem (4)–(8) in a separate paper.
4. Stochastic Interest Rate in Vasicek Model
In this section, we consider a special case where the interest rate is given by Vasicek’s process:
Let be the value of a guaranteed zero-coupon bond with face value 1 at the maturity . From the Feynman-Kac’s formula, we see that satisfies the following PDE Hall (1989):
With the Vasicek’s model, there is an explicit solution for .
Lemma 1.
For the problem (10), there exists a unique solution :
where
The proof can be found in Jiang (2005).
Similar to Liang et al. (2017), we introduce a transform by
where
Then after some elementary calculations, we see that satisfies
where
The interface , which is the credit rating migration boundary, is defined by
For the conditions on free boundary, we use the same assumptions as in Liang et al. (2017): for and ,
By using the standard change of variables and renaming as t, and defining
we obtain the following equation:
where
and is a function of and , i.e.,
The constant is defined in Section 3.
Without loss of generality, we assume that the payoff face value . Now the initial condition is as follows:
The domain will be divided into the different rating region
We shall prove that these exist n subdomains which are separated by free boundary , , and
Hypothesis 1.
Suppose that is differentiable on . Moreover,
Theorem 1.
Under the assumption Hypothesis 1, for the problem (12)–(17) there exists a unique solution . Moreover, there exist n-free boundaries, such that
The mathematical proof for Theorem 1 is rather technical, but can be done by using the same idea as in Liang et al. (2017). We will skip the details here. The interested reader can find a special case when there exists only one free boundary in Liang et al. (2017). We will provide a complete proof in a separate paper.
5. Simulation
5.1. Calibration
For a model implementation, the parameter calibration is important. In this model, the parameters are: .
- The risk free interest rate r can be directly estimated from the market data. In practice, it can be taken by the rate of long term government bonds.
- can be estimated from the credit rating data and the firm’s balance sheet, where the proportion of the debt to the firm’s value is shown in different rating regions.
- The volatility of a firm’s asset value in different rating regions can be calibrated through the market quotes of the firm’s stock prices in different rating respectively. The details are shown as follows:
- Find equity volatilities from stock prices in the marketIf the firm is in ith rating, is defined as the kth day stock price. Then we denote by as the daily volatility, or the standard variance, of the stock price from N observations and an unbiased estimate of the variance rate per day are as follows :Then the volatility per annum is , where is the trading days in ith rating per annum.
- Estimate asset volatility from the equity volatility.Once obtained the equity values and volatilities, we can calibrate the firm’s volatility by using Merton’s model Merton (1974), where the relationship between firm’s volatility and equity one is given by the Black-Scholes formula. Then and can be estimated through the following equations:whereand D is the amount of debt to be paid at time T, and are the firm’s value and equity value at the initial time.
5.2. A Real Example
We choose MTR Corporation Ltd. as an example, which is listed in Hong Kong and the rating is assigned by Moodys (see Wu and Liang (2018)). The firm’s data are quoted in three different ratings. The equity value, credit ratings data, debt, and calculated corresponding volatilities, firm’s value are shown in Table 1 (the prices and values are in billions of Hong Kong dollars, data Source: Wind).

Table 1.
The values, credit ratings, volatilities and debt of MTR.
The migration coefficients of and , are referred from the balance sheet. The risk free rate , which is fixed, is used by the rate of long-term treasury bonds that time, and . By numerical calculation of our model, the bond-value function graph is shown in Figure 1.
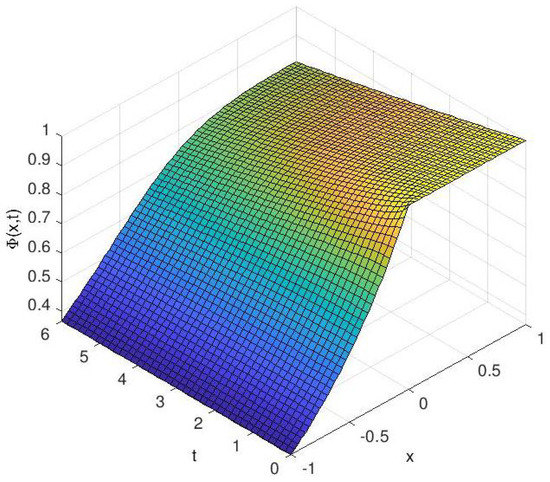
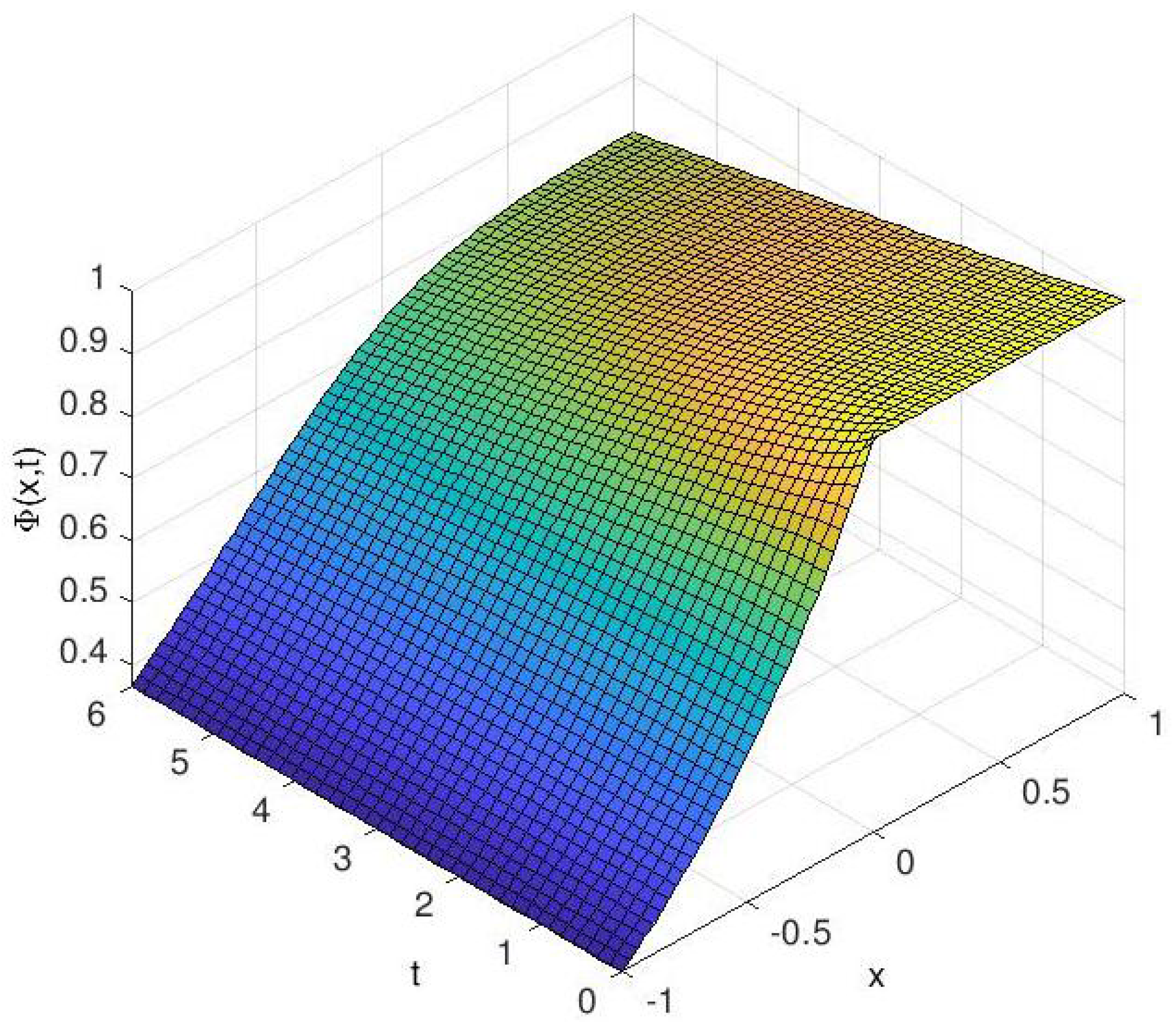
Figure 1.
Bond-Value Function vs. firm’s log value x and time t when fixed interest rate r.
5.3. Migration Free Interfaces
Take interest rate to be stochastic, then the bond value function in a three-dimension region , and the migration interfaces become two-dimension free surfaces. Choose the example which has three rating regions: High, Middle and Low and an interest rate process (9). The free boundaries actually are two free surfaces. Take the parameters with credit rating above are shown:
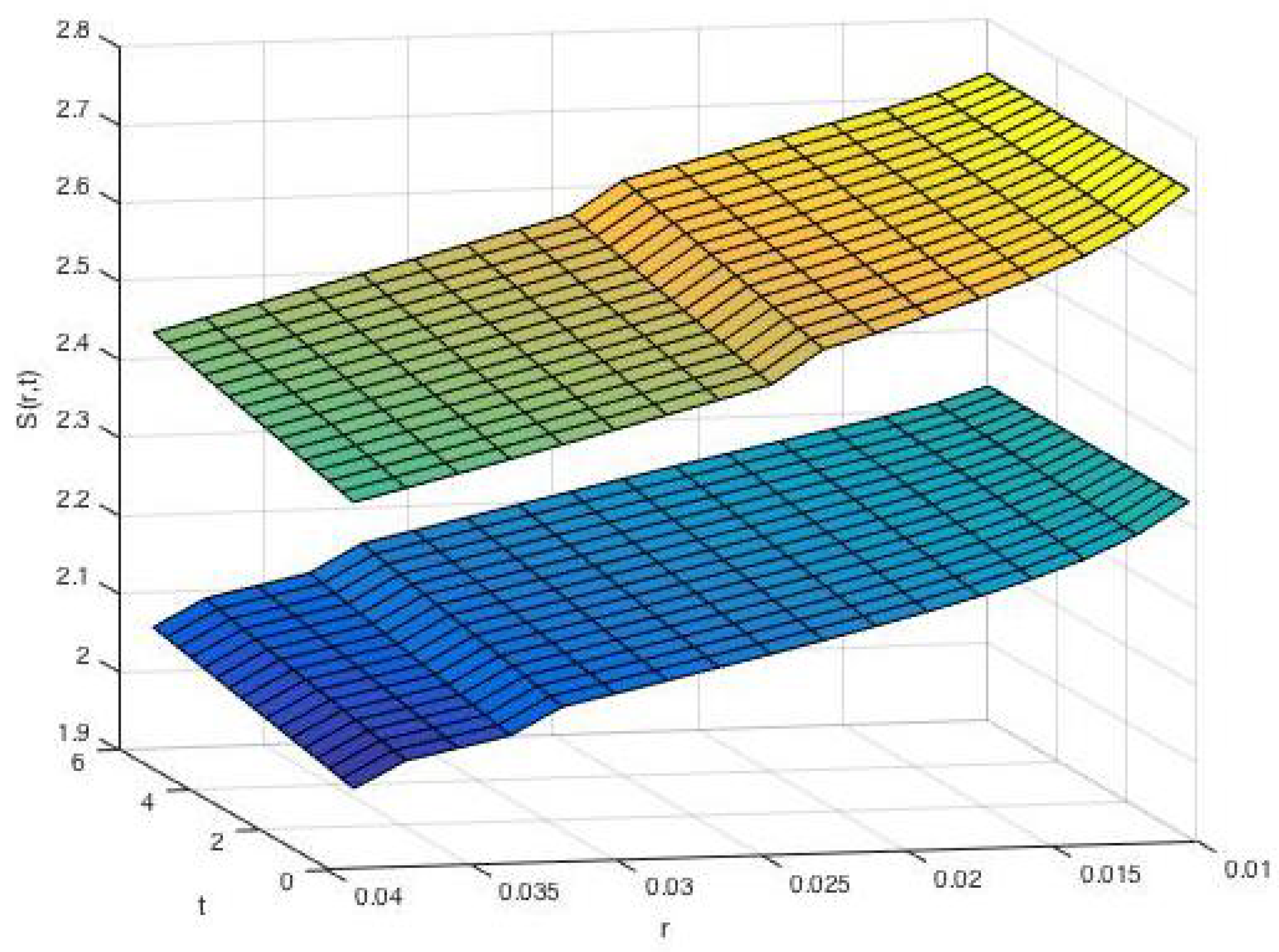
The numerical calculation for our model shows that there are two free surfaces in Figure 2:
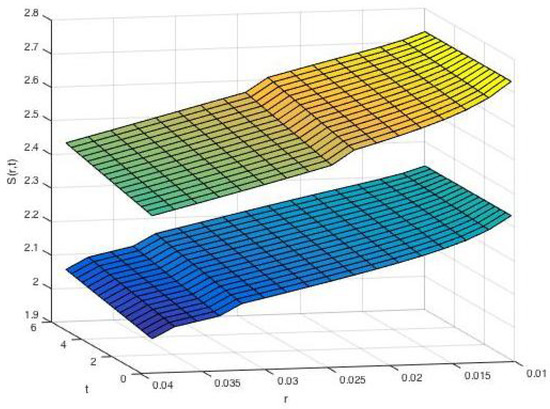
Figure 2.
Multi Migration Free Surfaces.
Figure 1 shows that the value of the bond price function in which the domain of the solution has been divided by free boundary surfaces into three regions: high, middle and low rating regions. From Figure 2, the value changes quite significantly across the free boundary surfaces. Since has an opposite tendency with , where , the free boundary is increasing as expected.
6. Conclusions
In this paper we derived a new model for pricing a corporate bond with potential credit-rating migration risks and a stochastic interest rate. The new model allows a finite number of potential rating changes during the life-span of the bond. The firm’s value is assumed to follow a general geometric Brownian motion with jumps for expected growth (or decay) and volatility. When the interest rate follows a Vasicek’s process, we used a dimension-deduction technique to establish the well-posedness of the free boundary problem for the new model. Calibration to the model parameters is also discussed with an example. The bond-value function’s numerical graph and their migration interfaces are also shown.
This new model extends the previous bond models in two aspects. The first is that a rating change may occur multiple times before the maturity of a bond. The second is that the interest rate itself is uncertain and is assumed to follow a stochastic process. This is particularly important when pricing a long-term corporate bond for corporations due to certain economic cycles. Moreover, our method is based on PDE analysis which is very different from traditional ones in the literature. The new model provides a new insight for evaluating the values of corporations with large debt in different macroeconomic and microeconomic environments. It also provides some additional qualitative information for bond investors when investing in corporate bonds.
Author Contributions
The paper is written by H.-M.Y. J.L. made substantial improvement of the first draft. Y.W. performed certain data analysis.
Funding
Liang thanks the support from National Natural Science Foundation of China 11671301.
Acknowledgments
The authors would like to thank Song-Ping Zhu from University of Wollongon, Australia, for some discussions during the preparation of the paper. They also would like to express their gratitude to Charles Moore and Brian Yin for their proofreading of the paper. Many thanks further go to the anonymous referees for their comments and suggestions which improve a lot the original version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Black, Fischer, and John C. Cox. 1976. Some Effects of Bond Indenture Provisions. Journal of Finance 31: 351–67. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik, Stacey Jacobsen, William Maxwell, and Kumar Venkataraman. 2018. Venkataraman, Capital Commitment and Illiquidity in Corporate Bonds. The Journal of Finance 73: 1665–61. [Google Scholar] [CrossRef]
- Briys, Eric, and François De Varenne. 1997. Valuing Risky Fixed Rate Debt: An Extension. Journal of Financial and Quantitative Analysis 32: 239–49. [Google Scholar] [CrossRef]
- Das, Sanjiv, and Peter Tufano. 1996. Pricing credit-sensitive debt when interest rates, credit ratings, and credit spreads are stochastic. Journal of Financial Engineering 5: 161–98. [Google Scholar]
- Dixit, Avinash K., and Robert S. Pindyck. 1994. Investment under Uncertainty. Princeton: Princeton University Press. [Google Scholar]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling Term Structures of Defaultable Bonds. The Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Elton, Edwin J., Martin J. Gruber, Deepak Agrawal, and Christopher Mann. 2001. Explaining the Rate Spread on Corporate Bonds. The Journal of Finance 56: 247–77. [Google Scholar] [CrossRef]
- Hall, John. 1989. Options, Futures, and Other Derivatives. Upper Saddle River: Prentice-Hall, Inc. [Google Scholar]
- Hu, Bei, Jin Liang, and Yuan Wu. 2015. A Free Boundary Problem for Corporate Bond with Credit Rating Migration. Journal of Mathematical Analysis and Applications 428: 896–909. [Google Scholar] [CrossRef]
- Hurd, Tom, and Alexey Kuznetsov. 2007. Affine Markov chain models of multifirm credit migration. Journal of Credit Risk 3: 3–29. [Google Scholar] [CrossRef]
- Jarrow, Robert, and Stuart Turnbull. 1995. Pricing Derivatives on Financial Securities Subject to Credit Risk. Journal of Finance 50: 53–86. [Google Scholar] [CrossRef]
- Jarrow, Robert A., David Lando, and Stuart M. Turnbull. 1997. A Markov model for the term structure of credit risk spreads. Review of Financial Studies 10: 481–523. [Google Scholar] [CrossRef]
- Jiang, Lishang. 2005. Mathematical Modeling and Methods for Option Pricing. Singapore: World Scientific. [Google Scholar]
- Kang, Johnny, and Carolin E. Pflueger. 2015. Inflation Risk in Corporate Bonds. The Journal of Finance 70: 115–62. [Google Scholar] [CrossRef]
- Kariya, Takeaki, Yoko Tanokura, Hideyuki Takada, and Yoshiro Yamamura. 2016. Measuring Credit Risk of Individual Corporate Bonds in US Energy Sector. Asia-Pacific Finan Markets 23: 229–62. [Google Scholar] [CrossRef]
- Kenneth, J. Kopecky, Zhichuan Li, Timothy F. Sugrue, and Alan L. Tucker. 2018. Revising M&M with Taxes: An alternative equilibriusm process. International Journal of Financial Studies 6: 1–12. [Google Scholar]
- Lando, David. 1998. On Cox Processes and Credit-risky Securities. Review of Derivatives Research 2: 99–120. [Google Scholar] [CrossRef]
- Lando, David. 2000. Some elements of rating based credit risk modeling. In Advanced Fixed-Income Valuation Tools. New York: John Wiley & Sons, Inc., pp. 193–215. [Google Scholar]
- Leland, Hayne, and Klaus Bjerre Toft. 1996. Optimal capital structure, endogenous bankruptcy, and the term strcuture of credit spreads. Journal of Finance 51: 987–1019. [Google Scholar] [CrossRef]
- Li, Zhichuan Frank, Shannon Lin, Shuna Sun, and Alan Tucker. 2018. Risk-adjusted inside debt. Global Finance Journal 35: 12–42. [Google Scholar] [CrossRef]
- Liang, Jin, and Chukun Zeng. 2015. Corporate bonds pricing under credit rating migration and structure framework. A Journal of Chinese University (A) 30: 61–70. [Google Scholar]
- Liang, Jin, Yuejuan Zhao, and Xudan Zhang. 2016a. Utility Indifference Valuation of Corporate Bond with Credit Rating Migration by Structure Approach. Economic Modelling 54: 339–46. [Google Scholar] [CrossRef]
- Liang, Jin, Yuan Wu, and Bei Hu. 2016b. Asymptotic Traveling Wave Solution for a Credit Rating Migration Problem. Journal of Differential Equations 261: 1017–45. [Google Scholar] [CrossRef]
- Liang, Jin, Hong-Ming Yin, Xinfu Chen, and Yuan Wu. 2017. On a corporate bond pricing model with credit rating migration risks and stochastic interest rate. Qualitative Finance and Economics 1: 300–19. [Google Scholar] [CrossRef]
- Longstaff, Francis, and Eduardo Schwartz. 1995. A Simple Approach to Valuing Risky Fixed and Floating Rate Debt. Journal of Finance 50: 789–819. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. Journal of Finance 29: 449–70. [Google Scholar]
- Richelson, Hildy, and Stan Richelson. 2011. Bonds: The Unbeaten Path to Secure Investment Growth, 2nd ed. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Thomas, Lyn, David Allen, and Nigel Morkel-Kingsbury. 2002. A hidden Markov chain model for the term structure of bond credit risk spreads. International Review of Financial Analysis 11: 311–29. [Google Scholar] [CrossRef]
- Tsiveriotis, Kostas, and Chris Fernandes. 1998. Valuing convertible bonds with credit risk. The Journal of Fixed Income 8: 95–102. [Google Scholar] [CrossRef]
- Wu, Yuan, and Jin Liang. 2018. A new model and its numerical method to identify multi credit migration boundaries. International Journal of Computer Mathematics 95: 1688–702. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).