Friendship of Stock Market Indices: A Cluster-Based Investigation of Stock Markets
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methodology
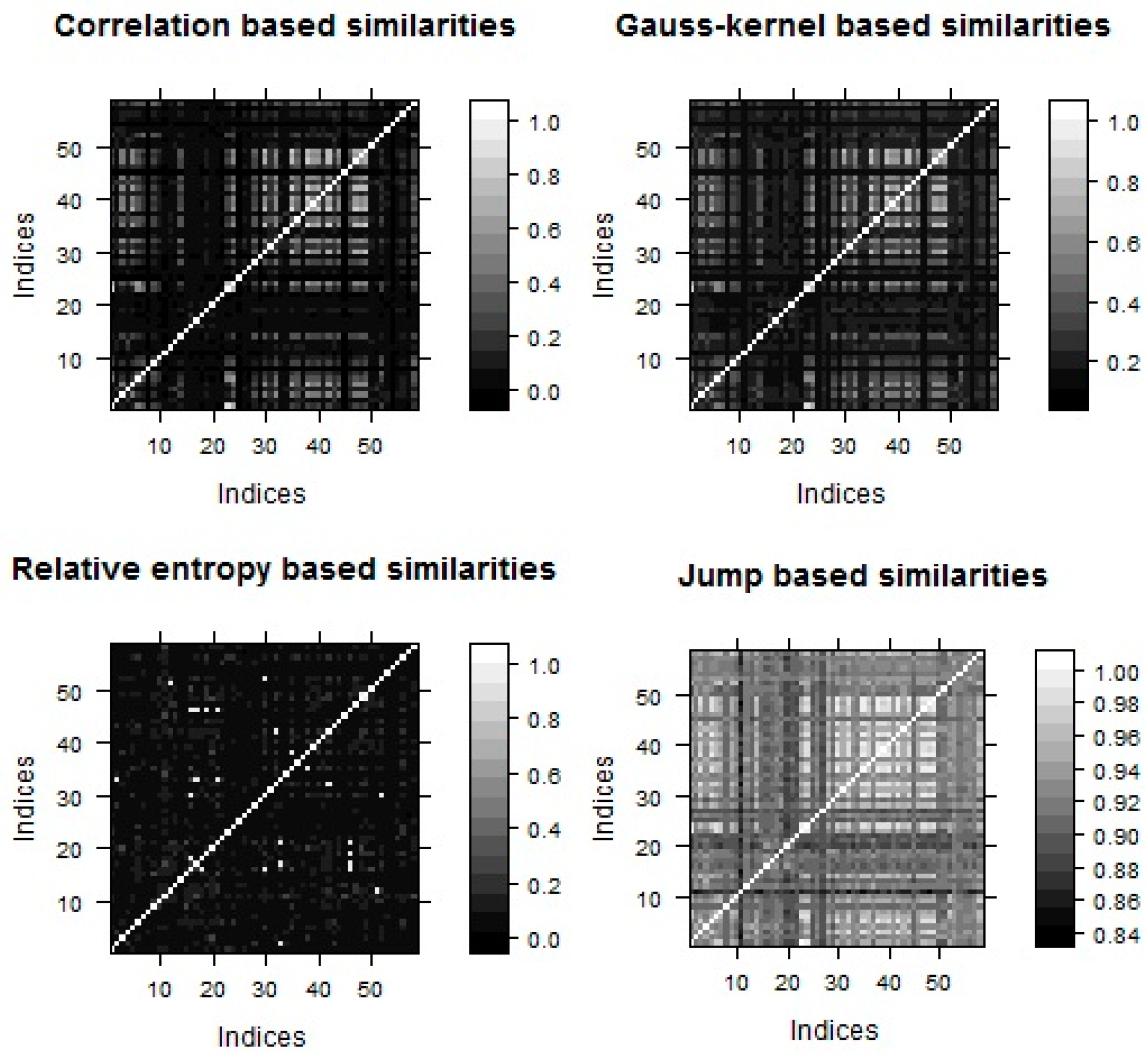
2.2.1. Similarity Matrix
2.2.2. Normalized Modularity
2.2.3. Algorithm
- Constructing the similarity matrix .
- Calculating the normalized modularity matrix .
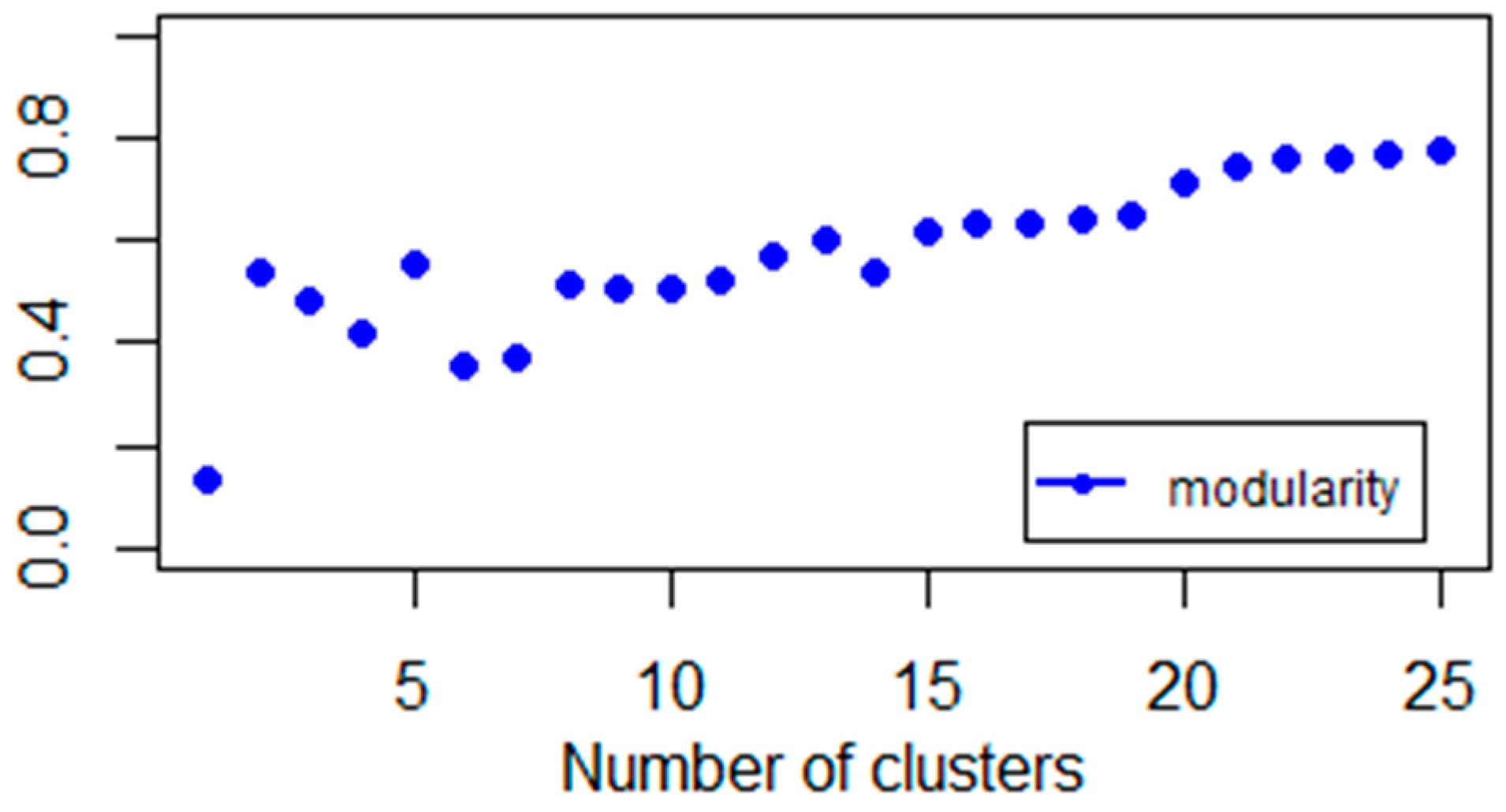
- Based on the spectral gap, determining the number of clusters and optimal k-dimensional representation.
- Appling k-means clustering.
2.2.4. Assessment of Clustering Methods
3. Results
3.1. Similarity Metrics
3.2. Comparing Normalized Modularity and Laplacian
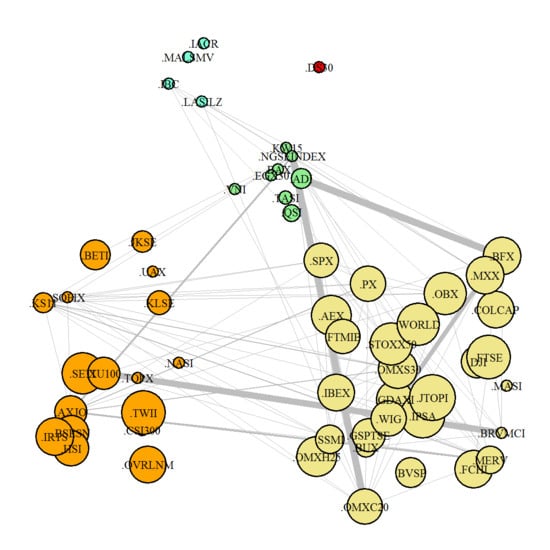
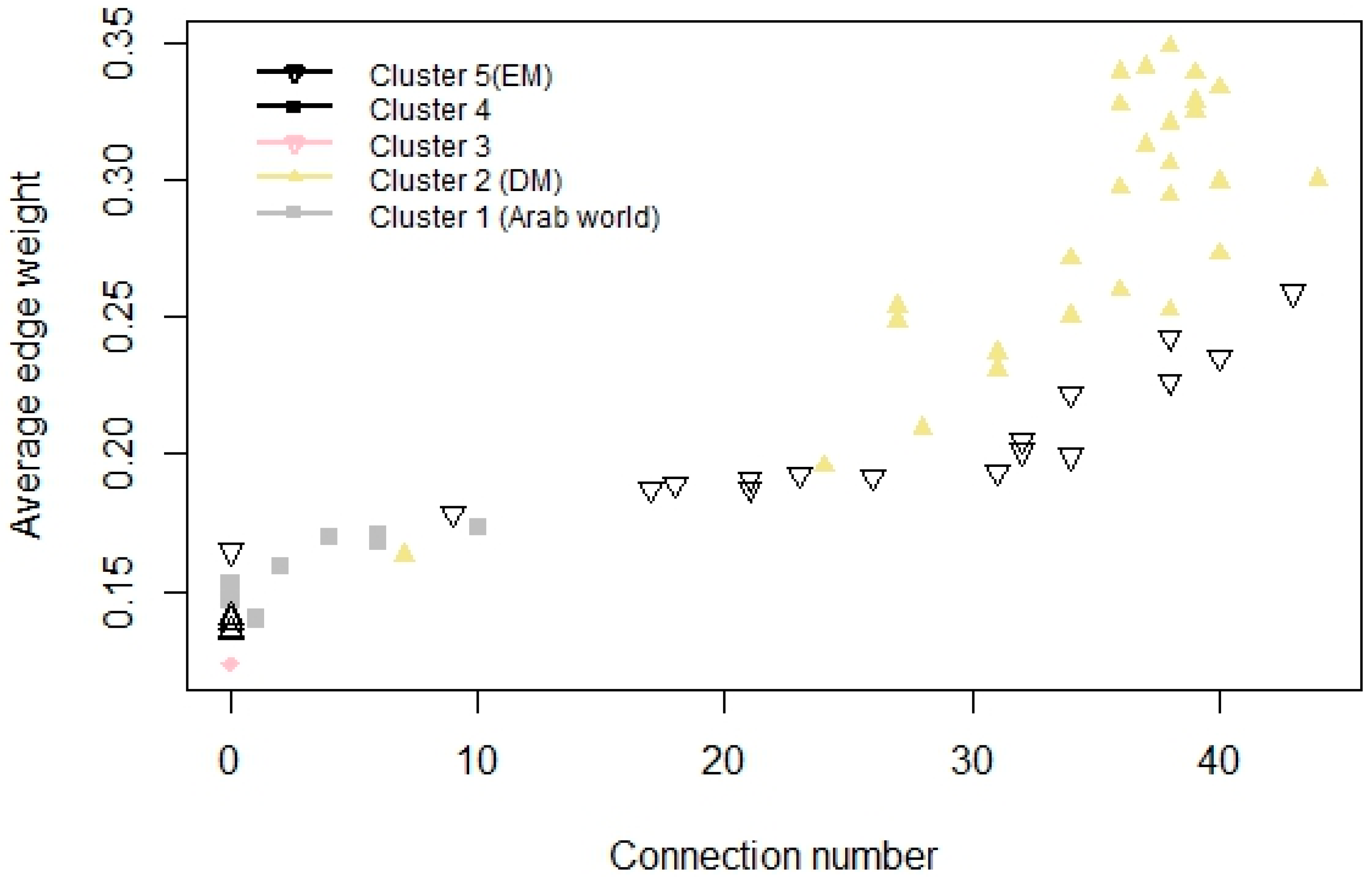
3.3. Equity Index Network Structure
3.4. Equity Index Graph
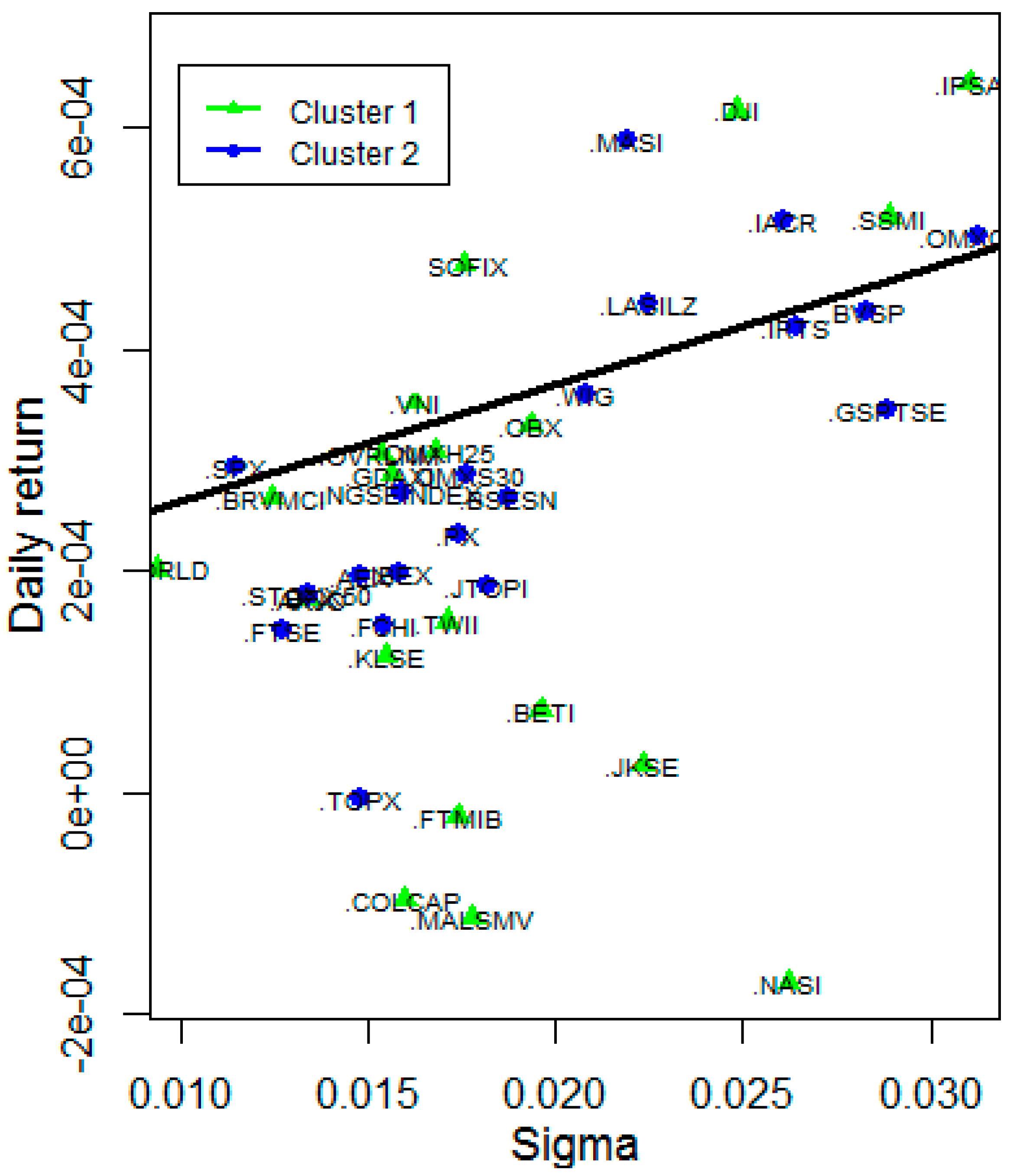
3.5. Risk and Reward
3.6 Time Stability
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Country | Two Clusters | Three Clusters | Five Clusters |
|---|---|---|---|
| United Arab Emirates | 2 | 3 | 1 |
| Saudi Arabia | 2 | 3 | 1 |
| Qatar | 2 | 1 | 1 |
| Kuwait | 2 | 1 | 1 |
| Egypt | 2 | 3 | 1 |
| Bahrain | 2 | 1 | 1 |
| Vietnam | 2 | 1 | 1 |
| Nigeria | 2 | 1 | 1 |
| Dow Jones | 1 | 2 | 2 |
| Denmark | 1 | 1 | 2 |
| Switzerland | 1 | 1 | 2 |
| Canada | 1 | 2 | 2 |
| Mexico | 1 | 2 | 2 |
| Chile | 1 | 2 | 2 |
| Argentina | 1 | 2 | 2 |
| Hungary | 1 | 1 | 2 |
| Morocco | 2 | 1 | 2 |
| S&P 500 | 1 | 2 | 2 |
| MSCI World | 1 | 2 | 2 |
| Czech Republic | 1 | 1 | 2 |
| Togo | 2 | 1 | 2 |
| Spain | 1 | 1 | 2 |
| Norway | 1 | 1 | 2 |
| Luxembourg | 1 | 1 | 2 |
| France | 1 | 1 | 2 |
| South Africa | 1 | 3 | 2 |
| Euro Stocks | 1 | 1 | 2 |
| Sweden | 1 | 1 | 2 |
| UK | 1 | 1 | 2 |
| Netherlands | 1 | 1 | 2 |
| Finland | 1 | 1 | 2 |
| Poland | 1 | 3 | 2 |
| Germany | 1 | 1 | 2 |
| Belgium | 1 | 1 | 2 |
| Italy | 1 | 1 | 2 |
| Brazil | 1 | 2 | 2 |
| Colombia | 1 | 3 | 2 |
| Bangladesh | 2 | 1 | 3 |
| Costa Rica | 2 | 1 | 4 |
| Zambia | 2 | 1 | 4 |
| Malawi | 2 | 1 | 4 |
| Venezuela | 2 | 1 | 4 |
| South Korea | 2 | 3 | 5 |
| Hong Kong | 2 | 3 | 5 |
| Thailand | 2 | 3 | 5 |
| China | 2 | 3 | 5 |
| Kenya | 2 | 3 | 5 |
| India | 2 | 3 | 5 |
| Namibia | 2 | 3 | 5 |
| Turkey | 2 | 3 | 5 |
| Indonesia | 2 | 3 | 5 |
| Malaysia | 2 | 3 | 5 |
| Russia | 2 | 3 | 5 |
| Australia | 2 | 3 | 5 |
| Taiwan | 2 | 3 | 5 |
| Japan | 2 | 3 | 5 |
| Ukraine | 2 | 3 | 5 |
| Bulgaria | 2 | 1 | 5 |
| Romania | 2 | 3 | 5 |
References
- Barabási, Albert L., and Albert Réka. 1999. Emergence of Scaling in Random Networks. Science 26: 509–12. [Google Scholar] [CrossRef]
- Berlinet, Alain, and Thomas-Agnan Christine. 2011. Reproducing Kernel Hilbert Spaces in Probability and Statistics. Berlin: Springer Science & Business Media, pp. 1–108. ISBN 978-1441990969. [Google Scholar]
- Bolla, Marianna. 2011. Penalized version of Newman-Girvan modularity and their relation to normalized cuts and k-means clustering. Physical Review E 84: 016108. [Google Scholar] [CrossRef] [PubMed]
- Chung, Fan R. G. 1997. Spectral Graph Theory. Providence: American Mathematical Society, No. 92. pp. 14–81. ISBN 978-0821803158. [Google Scholar]
- Engelmann, Bernd, Evelyn Hayden, and Dirk Tasche. 2003. Measuring the Discriminative Power of Rating Systems. Banking and Financial Supervision. Frankfurt: Deutsche Bundesbank. [Google Scholar]
- Erdős, Péter, and Rényi Alfréd. 1960. On the Evolution of Random Graphs. Acta Mathematica Hungarica 5: 17–61. [Google Scholar]
- Erdős, Péter, Mihály Ormos, and Dávid Zibriczky. 2011. Non-parametric and semi-parametric asset pricing. Economic Modelling 28: 1150–62. [Google Scholar] [CrossRef]
- Fama, Eugene, and Kenneth R. French. 1996. Multifactor explanations of asset pricing anomalies. The Journal of Finance 51: 55–84. [Google Scholar] [CrossRef]
- Maurizio, Filippone, Francesco Camastra, Francesco Masulli, and Stefano Rovetta. 2007. A survey of kernel and spectral methods for clustering. Pattern Recognition 41: 176–90. [Google Scholar] [CrossRef]
- Heiberger, Raphael H. 2014. Stock network stability in times of crisis. Physica A: Statistical Mechanics and Its Applications 393: 376–81. [Google Scholar] [CrossRef]
- Gregory, Leibon, Scott Pauls, Daniel Rockmore, and Robert Savell. 2008. Topological Structures in the Equities Market Network. PNAS 105: 20589–94. [Google Scholar] [CrossRef]
- Von Luxburg, Ulrike. 2007. Tutorial on Spectral Clustering. Statistics and Computing 17: 395–416. [Google Scholar] [CrossRef]
- Maldonado, Rita, and Saunders Anthony. 1981. International portfolio diversification and the inter-temporal stability of international stock market relationships, 1957–1978. Financial Management 10: 54–63. [Google Scholar] [CrossRef]
- MSCI. 2018. Market Classification. Available online: https://www.msci.com/market-classification (accessed on 3 November 2018).
- Ormos, Mihály, and Dávid Zibriczky. 2014. Entropy-Based Financial Asset Pricing. PLoS ONE 9: E115742. [Google Scholar] [CrossRef] [PubMed]
- Shi, Jianbo, and Jitendra Malik. 2000. Normalized cuts and image segmentation. IEEE Pattern Analysis and Machine Intelligence 22: 888–905. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Song, Dong-Ming, Michele Tumminello, Wei-Xing Zhou, and Rosario N. Mantegna. 2011. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Physical Review E 84: 026108. [Google Scholar] [CrossRef] [PubMed]
- Takumasa, Sakakibara, Tohgoroh Matsuib, Atsuko Mutoha, and Nobuhiro Inuzuka. 2015. Clustering mutual funds based on investment similarity. Procedia Computer Science 60: 881–90. [Google Scholar] [CrossRef]
- Yalamova, Rossitsa. 2009. Correlations in Financial Time Series during Extreme Events-Spectral Clustering and Partition Decoupling Method. Paper presented at World Congress on Engineering, London, UK, July 1–3, Volume 2, pp. 1376–78. [Google Scholar]
- Zhao, Yanchang. 2012. R and Data Mining: Examples and Case Study. Cambridge: Academic Press, pp. 49–59. [Google Scholar]












| Index | Mean | Variance | Skewness |
|---|---|---|---|
| .CSI300 | 0.018 | 0.056 | −0.336 |
| .XU100 | 0 | 0.026 | −0.809 |
| .DJI | 0.012 | 0.009 | −0.819 |
| .UAX | −0.034 | 0.037 | −0.721 |
| .WORLD | 0.004 | 0.002 | −1.889 |
| Method | Coeff. of Cluster | p-Value |
|---|---|---|
| Geographical | −0.000036 | 0.394 |
| MSCI | −0.000041 | 0.293 |
| Spectral | −0.000112 | 0.027 |
| Clusters | p-Value of Intercept | p-Value of s.d. | |
|---|---|---|---|
| Total Sample | 0.62 | 0.12 | 0.05 |
| First cluster | 0.62 | 0.02 | 0.68 |
| Second cluster | 0.29 | 0.00 | 0.59 |
| Fifth cluster | 0.93 | 0.71 | 0.01 |
| ADF t-Value | ADF p-Value |
|---|---|
| −2.67 | 0.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, L.; Ormos, M. Friendship of Stock Market Indices: A Cluster-Based Investigation of Stock Markets. J. Risk Financial Manag. 2018, 11, 88. https://doi.org/10.3390/jrfm11040088
Nagy L, Ormos M. Friendship of Stock Market Indices: A Cluster-Based Investigation of Stock Markets. Journal of Risk and Financial Management. 2018; 11(4):88. https://doi.org/10.3390/jrfm11040088
Chicago/Turabian StyleNagy, László, and Mihály Ormos. 2018. "Friendship of Stock Market Indices: A Cluster-Based Investigation of Stock Markets" Journal of Risk and Financial Management 11, no. 4: 88. https://doi.org/10.3390/jrfm11040088
APA StyleNagy, L., & Ormos, M. (2018). Friendship of Stock Market Indices: A Cluster-Based Investigation of Stock Markets. Journal of Risk and Financial Management, 11(4), 88. https://doi.org/10.3390/jrfm11040088