2. Threshold Stochastic Conditional Duration Model
Let
denote the observed duration at time
t,
, where
T is a positive integer representing the sample size. The duration process of
is characterized by a product of two independent random variables: a lognormal random variable
and a positive random variable
. Then, following
Bauwens and Veredas (
2004), we specify the following set of equations:
where
and
are assumed to be mutually independent shocks with
. For the latent AR(1) process in (
2) to be weakly stationary, it is assumed that
.
Bauwens and Veredas (
2004) assume that
follows either a Gamma distribution or a Weibull distribution with scale parameters equal to 1.
In our proposed model, we allow not only the innovation of the duration process to follow a threshold distribution with two component distributions with positive supports, but also the latent states to follow a threshold AR(1) process which switches between two regimes. These two regimes are determined by the previously observed durations according to a threshold level. In particular, the threshold distribution for the innovations of the measurement equation is given by
where
and
are two generic distributions with positive supports, and
and
are the corresponding parameter vectors.
For the log conditional durations,
, a threshold AR(1) process is defined as:
where
and
are two independent processes with a standard normal distribution. In the threshold specification in (
5), the latent states,
, follow separate AR(1) processes in the two different regimes determined by the previously observed duration
and the threshold level
r. The threshold level
r is treated as a free parameter to be estimated by our proposed MCMC method.
For the components of the threshold distribution of
, following
Bauwens and Veredas (
2004), we use either a Gamma distribution or a Weibull distribution. With this assumption, the probability density functions (pdfs) of
are given respectively by
with the shape parameters
and
, and the scale parameters are all set to 1, and
with the shape parameters
and
and unit scale parameters. Under these assumptions, the distribution of
depends on the shape parameters. At time
t, the observation
affects not only the distribution of
, but also the distribution of
. In other words, the observation,
, contributes to future durations through
and
. The asymmetric property of the marginal distribution of
is influenced by the previously observed duration according to the threshold level
r. Importantly, under the threshold distributional assumption, we no longer need to explicitly specify a correlation structure between the observation and the latent process. In addition, as the variance of
is not equal to 1, the location parameters in the threshold AR(1) processes are no longer required as well.
Under the TSCD model setup, at each time
t, the conditional distribution of
is assumed to depend on the previous observation
and the threshold parameter
r, i.e., the distributions of the observations will switch between the two regimes with the arrivals of the previously observed durations. Similar to the arguments in
De Luca and Gallo (
2004,
2009), who work with Autoregressive Conditional Duration (ACD) models, the two regimes can be interpreted as representing two types of behavior of traders in the market, who are respectively informed and uninformed traders. The informed and uninformed traders are assumed to respond differentially to bad news and good news in the market over the sample period. The proposed TSCD models with two regimes are constructed specifically to characterize these time dependent responses, giving rise to a desirably asymmetric pattern in the marginal distributions of the model.
3. Bayesian Inference
In this section, we develop a suitable MCMC method for parameter estimation of the proposed model. Following the literature, all the latent states,
, are augmented as parameters and simulated or estimated as a by-product of the derived estimators. For each specified TSCD model, the latent states are simulated one at a time by the slice sampler introduced by
Neal (
2003).
In the following MCMC algorithm, we assume that the innovation of the mean equation follows a threshold distribution with two, say Gamma, component distributions with
serving as the parameter vector. Given an observed duration time series of
, the conditional densities of
are given by
Therefore, the posterior density of
can be conveniently split into two parts according to the threshold parameter
r,
where
. Within the Bayesian inference, the posterior distributions of the parameters in
, and the latent states,
, can be readily derived from (
9).
The TSCD model is completed by specifying prior distributions for all the parameters in
. For tractability, we assume that the prior distributions of the parameters in
are mutually independent. The persistence parameters
and
are assumed to have a univariate normal distribution
, truncated in the interval
. Instead of sampling
and
, we sample
and
. The prior distributions of
and
are
, which are inverse Gamma distributions. For the shape parameters
and
we use the half-Cauchy distributions as their prior distributions
The half-Cauchy distribution is also used as the prior distribution for the shape parameters of the Weibull components. For the threshold parameter r, we use a uniform distribution between the first and third quartiles of the observations in . The two quartiles are intended to ensure that there are enough observations in each of the two regimes.
The algorithm of the MCMC estimation procedure for the TSCD model with a threshold Gamma distribution, called TSCD-G model hereafter, is listed in Algorithm 1. The derivation of the full conditionals for the parameters and individual latent state are given explicitly in Step 1 below, where the full conditional of each parameter is defined as the conditional distribution given that other parameters in the model have been sampled.
| Algorithm 1: MCMC algorithm for the TSCD-G model. |
Step 0. Initialize , , , , i=1, 2, and r
Step 1. Sample
Step 2. Sample and
Step 3. Sample r
Step 4. Sample and
Step 5. Go to Step 1. |
Step 0. Initialize , , , and r. To start the MCMC algorithm, the initial values of the parameters of the model are set as , , , , , , and . The initial value of r is set as the mean of the observations, which falls into the interval of the first and third quartiles of the observations. The initial values of are generated from the latent AR(1) process with the above initial parameters.
Step 1. Sample
. Here, we only give the full conditionals of
,
. The full conditionals of
and
are easy to derive and, thus, omitted from this paper. The full conditional of
depends on
and
r. Given that
r has been sampled previously, the full conditional of
can be calculated based on four cases: (i) If
and
, the full conditional of
is given by
where
Here defines as a collection of model parameters except for r. Thus, the full conditional of can be sampled by the slice sampler.
Algorithm of the slice sampler for
- SS1.
Draw
uniformly from the interval
and set
. Let
, then we have
- SS2.
Draw
uniformly from the interval
and set
. Let
then we have
- SS3.
Draw
uniformly from the interval determined by the inequalities in (11) and (12) such as
As a brief remark to the above algorithm, we note that in our approach, each is simulated based on its conditional distribution. So conditionally is known in our situation. Also note that ’s are the only observations available to our model. As we subsequently perform a one-step-ahead prediction for the fitted model, we only need to sample , and do not need to sample .
In each MCMC iteration, when we simulate
, the sampled value of
from the previous MCMC step is set at the initial value. As the full conditionals of
in each MCMC step are similar, this initial value should provide a good starting point. As the slice sampler adapts to the form of the density function of the underlying variable, it is more efficient than many other existing samplers. In addition, under certain conditions,
Roberts and Rosenthal (
1999) also show that the slice algorithm is robust and has geometric periodicity properties. Moreover,
Mira and Tierney (
2002) prove that the slice sampler has a smaller second-largest eigenvalue, which ensures faster convergence to the underlying distribution. Indeed, in our study, we find that even with only five iterations of our slice algorithm, we can feasibly and efficiently estimate the TSCD models by the MCMC.
2The full conditional of
, given (ii)
and
, is
where
The full conditional of is also sampled through the slice sampler. Under the other conditions (iii) and , and (iv) and , the full condition of can be calculated in the same fashion, and the realized full conditionals of can be sampled through the slice sampler.
Step 2. Sample
and
. Given that other parameters and the latent states have been sampled from the previous iteration of the MCMC algorithm, the full conditionals of
,
, are given respectively by
These distributions are not simple distributions that can be simulated directly. Our simple solution to this is to use a random-walk MH method with a univariate normal distribution with mean zero and non-unit variance. The variance can be fined tuned to obtain a reasonable acceptance rate for the MH algorithm. Experience from our study suggests that an acceptance rate between 25% and gives us a more accurate estimate of r in the simulation studies.
Step 3. Sample
r. The full conditional of
r is
The full conditional of r is not a simple distribution either. Therefore, again, we use a random-walk MH method to simulate this posterior distribution with a univariate normal distribution , where is fined tuned for the random-walk MH method to have a reasonable acceptance rate.
Step 4. Sample
,
,
and
. The full conditionals of
are univariate normal distributions truncated in the interval (−1,1), which can be simulated by a slice sampler. The full conditionals of
are inverse Gamma distributions from which the sampling is relatively easy to carry out. The derivation of these full conditionals are not given in this paper, but they can be found for instance in
Men et al. (
2016a) or any in prior studies on SV models such as
Men et al. (
2016b), where MCMC algorithms are used.
To conduct a Bayesian inference in the TSCD model with threshold Weibull component distributions, the estimation algorithm can be derived similarly. As a result, details of these derivations are omitted from the paper.
5. Simulation Studies
In this section, we assess the performance of the TSCD models and the MCMC algorithms by simulation studies. Since the component distributions can be either a Gamma or Weibull distribution, we examine two types of the TSCD models. The values of parameters used to generate artificial duration time series are listed in the second column of
Table 1 in boldface. We generate 12,000 observations from each TSCD model indexed by these parameters, where the first 10,000 observations are fitted by the corresponding TSCD model and the fitted model is then used for the one-step-ahead in-sample and out-of-sample duration forecasting. The estimated parameters as well as the corresponding standard errors and Bayesian highest probability density (HPD) credible intervals, which can be calculated based on the
and
quantiles of the sampled data, are also included in this table. With relatively small standard deviations and narrow credible intervals, we conclude that the estimated parameters are close to their true values.
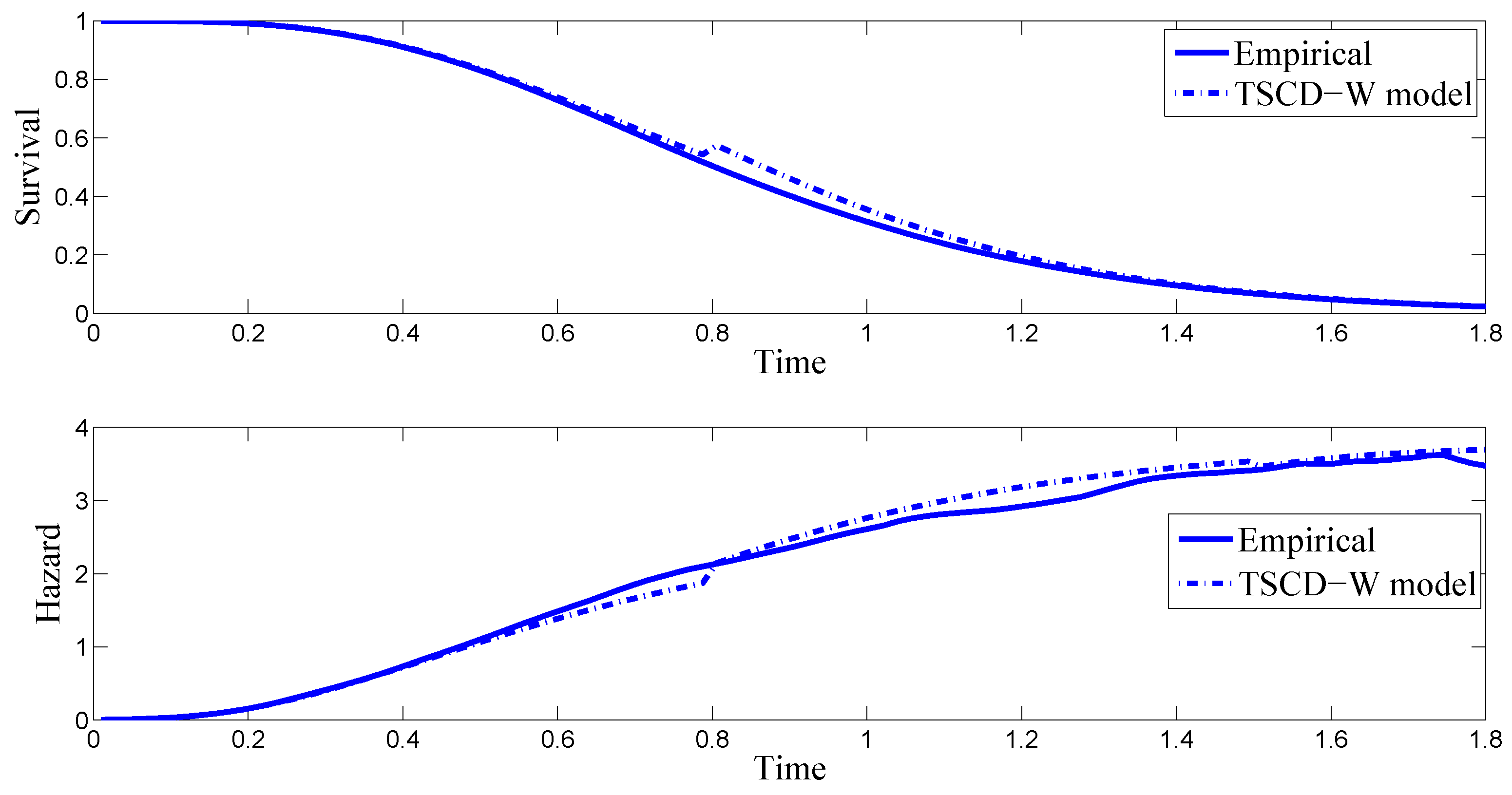
One way to assess the goodness-of-fit of the TSCD models is to compare the empirical survival function and the hazard function with those calculated from the fitted TSCD models visually. Denote by
and
respectively the pdf and cumulative distribution function (cdf) of the observed duration data. Then the survival function and the hazard function of the data are defined as
and
, respectively. As discussed in
Bauwens and Veredas (
2004), both the
and
for a given duration data have to be calculated by using a numerical method such as a kernel density fitting method, which can be found in
Silverman (
1986), pp. 11–13, and
Bowman and Azzalini (
1997). In addition, numerical integration methods such as the Gaussian quadrature method must be used for the calculation of
as well.
Given the highly comparable results reported in
Table 1 for the Gamma and Weibull component cases, for brevity, we focus only on the Weibull component case in the subsequent discussion. The top panel in
Figure 1 compares the empirical survival function of the simulated durations with the conditional survival function based on the TSCD-W model, while the bottom panel plots the corresponding empirical hazard of the simulated data together with the conditional hazard function. It is observed in the presented figures that the empirical survival function and the hazard function implied by the fitted TSCD-W model behave similarly to the empirical counterparts except that there is a very small jump at the threshold value of 0.7983. The reason for this jump is presumably because the threshold level of 0.8 was used in generating the artificial duration time series.
To check the convergence of the MCMC algorithms, we plot the histogram and time series of samples simulated from each posterior distribution of the parameters of the TSCD-W model in
Figure 2 and
Figure 3, respectively. It can be seen visually that the time series drawn from the full conditionals of parameters are convergent. Subsequent statistical tests also confirm this conclusion.
To assess the overall model fit, we consider the PITs calculated from the fitted TSCD-W model.
Figure 4 includes the scatter and histogram plots of the PITs. The two horizontal lines in the histogram plot are the 95% confidence intervals of the uniformity, constructed under the normal approximation of a binomial distribution, the calculation of which is detailed in
Diebold et al. (
1998). It is evident that the PITs originated from the uniform distribution
. The KS test statistic for the PITs is calculated as 0.0136 with the corresponding
p-value of 0.8916. So, we do not reject the null hypothesis at any reasonable level of significance that the fitted TSCD model with the threshold Weibull innovations agrees with the generated duration data.
Figure 5 graphs the cdf of the uniform distribution
together with the empirical cdf of the PITs. The two cdfs appear to be very close with each other, which confirms our earlier conclusion.
Figure 6 compares the simulated durations with the filtered and one-step-ahead in-sample and out-of-sample forecasted durations, where the latter is separated by the vertical dotted line. We observe that the forecasted durations resemble the true durations, indicating that our TSCD-W model is again able to give a reasonably accurate forecast of future durations.
In applications to real data, although the true financial durations are not observable, we are reasonably confident that the fitted TSCD-W model can do a good job for duration forecast. While the above analysis is based on the TSCD-W model, we, unsurprisingly, also reach a very similar conclusion for the TSCD-G model.
Overall, the simulation studies carried out above demonstrate that the TSCD models and MCMC methods can recover the true parameters obtained by using the simulated duration data. In addition, duration forecasting can also be adequately performed using the AFP.
6. Empirical Analysis
In this section, we apply the proposed TSCD model to the classic/benchmark IBM and Boeing transaction data. Both data sets have been used previously in
Knight and Ning (
2008);
Xu et al. (
2011) and
Men et al. (
2015,
2016a). The IBM transaction data cover the period from 1 November 1990 to 31 January 1991 with a total of 24,765 transactions, while the Boeing data covers the period from 1 September 2001, to 31 October 2001 with a total of 90,136 observations. These datasets are admittedly from several decades ago. However, the use of these datasets is intended to facilitate a direct comparison between the results obtained from our models and methods with those in the literature (including our own previous studies), which all have conveniently used these same benchmark datasets. The frequency of the data is tick by tick, which records every single transaction that occurs in the market. Its salient feature is irregularly spaced in time and is primarily caused by financial transactions being clustered over time or occurring in a scattered fashion over time. The main implication of the irregular spacing of these data is that the time between any two consecutive market events, which is the financial duration, is a random variable.
Table 2 and
Table 3 present the estimated parameters of the TSCD models based on the two data sets. The proposed MCMC algorithms were iterated 100,000 times. After the first 50,000 sampled values are discarded as the burn-in to eliminate initial value problems, the parameters and the states were then estimated by sample means. Standard errors and Bayesian HPD intervals are also reported in the two tables. The Bayesian HPD intervals are calculated by the
and
quartiles. The relatively small standard errors of these Bayesian HPD intervals indicate that our estimation process is quite efficient.
We note that for the IBM transaction data, the two persistent parameter estimates (e.g., for the TSCD-W model, and ) and, to a lesser extent, also the two volatility parameter estimates (e.g., for the TSCD-W model, and ) of the latent threshold AR(1) processes are quite different from each other. This indicates that at least two latent dynamic market factors that affect the duration innovation in different scales can be captured by the TSCD model. In other words, the IBM transaction data can be adequately characterized by the two specified threshold processes in the TSCD model. However, for the Boeing transaction data, the parameter estimates between the two regimes are relatively closer to each other (e.g., for the TSCD-W model, and , and and ).
Again, given the highly comparable results for the Gamma and Weibull component cases for both datasets reported in
Table 2 and
Table 3, for brevity and without much loss of generality, we focus our ensuing discussion only for the Weibull component case, i.e., the TSCD-W model. However, the fitted TSCD-G model will later be subjected to a formal model discrimination against the fitted TSCD-W model for both datasets.
To check the convergence of the samples drawn from the full conditionals, we again plot the time series and histograms for each parameter of the TSCD-W models based on the Boeing transaction data in
Figure 7 and
Figure 8. It is visually evident that these time series are convergent. Please note that in our TSCD models, after 50,000 iterations, the generated time series typically converge.
Figure 9 compares the duration time series with the filtered (or, Bayesian estimated) durations, and with the one-step-ahead in-sample and out-of-sample forecasted durations. It is observed that the forecasted durations also resemble the true durations closely.
As we did in the simulation studies, we compare in
Figure 10 the empirical survival function of the Boeing durations with the conditional survival function based on the estimated TSCD-W model. The bottom panel plots the corresponding empirical hazard of the Boeing data together with the conditional hazard function. It is observed that the empirical survival function and the hazard function behave similarly to the counterparts implied by the fitted TSCD model except that there is a very small jump at the threshold value of 1.1775 in the hazard function implied by the fitted model.
To check the goodness-of-fit of the model, we plot the scatter and histogram plots of the PITs originated from the fitted TSCD-W model in
Figure 11, while
Figure 12 plots the empirical cdf of the PITs together with the theoretical cdf of the uniform distribution
. The plots reveal that the PITs do not appear to follow a uniform distribution over the interval (0,1). The results from the KS test confirm this assertion. The reason for these unfavorable results can be understood by inspecting
Figure 11 and
Figure 12 where we see that the right tail of the marginal distribution of the data is well fitted, but the left tail of the marginal distribution is less so. The intensity of small durations is around 0.18.
Bauwens and Veredas (
2004);
Feng et al. (
2004) and
Men et al. (
2015,
2016a) also observed a similar lack of fit for their SCD models to duration data. Fractional latent processes have been proposed to improve the fit of the model. Distributional assumptions for the innovations of the duration equation other than the Gamma and Weibull distributions may also prove to be fruitful in this regard.
3Given the above qualification, we next proceed to select a better TSCD model for each of the two data sets of transactions by calculating the DIC values from the four fitted TSCD models.
Berg et al. (
2004) propose that the DIC be calculated by using the conditional likelihood. It is referred to as the conditional DIC. The conditional DIC is widely used for comparing SV models and is also used in the earlier version of this paper. In this paper, we follow
Celeux et al. (
2006) in computing the DIC by using an observed-data likelihood. This is referred to as an observed-data DIC. This observed-data DIC is not computed in practice due to the difficulty in evaluating the observed-data likelihood. However, despite its popularity, the Monte Carlo study reported by
Chan and Grant (
2016) shows that the conditional DIC tends to pick overfitted models (often with negative values of
, which is difficult to justify), whereas the observed-data DIC is better able to choose the correct model. The challenge associated with the computation of the observed-data DICs for the proposed TSCD models is overcome by suitably modifying importance sampling algorithms proposed by
Chan and Grant (
2016) for estimating the observed-data likelihoods for SV models.
The observed-data DIC measures are listed in
Table 4. First, note that the computed values of
for both models are positive, suggesting a positive penalty for model complexity, which makes sense. Second, for both the IBM and Boeing transaction data, the TSCD-G model is preferred given that the two fitted TSCD-G models have smaller observed-data DIC values compared to the TSCD-W counterparts.
4To undertake a further specification analysis, we pre-set
, and
to arrive at a restricted TSCD (RTSCD) model.
5 Thus, this RTSCD model is obtained by not allowing the latent first-order autoregressive process of the log conditional duration process to switch between the two regimes. However, it still permits the innovations of the duration process to follow a threshold distribution with a positive support. To select a better fitted RTSCD models for the IBM and Boeing transaction data, we compute the observed-data DICs from the models. The values of the observed-data DICs are presented in
Table 5. Among the observed-data DIC values, the smallest ones are from the RTSCD-G model, which means that the RTSCD-G model is better suited than the RTSCD-W model for the analysis of the real transaction data of the IBM and Boeing stocks.
6 In addition, the computed DICs for the unrestricted TSCD models are uniformly smaller than those for the RSTCD models, suggesting that the unrestricted TSCD models are the preferred models for both datasets.
7 Thus, for these datasets, the latent first-order autoregressive process of the log conditional duration process switch between the two regimes.
What is the economic interpretation of the findings in this paper? The findings are consistent with the prediction of the market micro-structure theory (MMT) in finance. The MMT suggests that there are informed and uninformed traders in the financial market. The interaction between the two trader types through information-revealing price formation processes is consistent with the observed financial market behavior. The informed traders will buy if the market price of an asset is below the true value (based on their information set). Conversely, they will sell, if the price is above the value. However, information is not free to the traders, and there are traders who base their trading decisions by observing the asset prices. As this latter trader type is a follower, its actions will be regulated by a distinct innovation process. This difference in behavior is consistent with the introduction of the two regimes for the innovation process in the TSCD model, since the instantaneous rate of transaction can be seen as being different across the two trader types.