The Role of Redenomination Risk in the Price Evolution of Italian Banks’ CDS Spreads

Abstract

The recent financial crisis offered an interesting opportunity to analyze the markets’ behavior in a high-volatility framework. In this paper, we analyzed the price discovery process of the Italian banks’ Credit Default Swap (CDS) spreads through the Merton model, extended with the inclusion of a redenomination risk proxy, as to say, the risk that Italy could leave the eurozone. This paper contributes to the literature by integrating the classic Merton model with a political-sensitive market variable able to explain the greatest variance in the Italian banks’ CDS spreads during the most relevant and commonly recognized periods of socio-political and financial distress. Results show that the redenomination risk is progressively becoming the main driver of the process during crises, in particular for the sovereign debt crisis and in 2018.

1. Introduction

The recent financial crisis offers an interesting opportunity to analyze the markets’ behavior in a high-volatility framework. In particular, the second wave of the crisis, identified as the sovereign debt crisis (2010–2012), driven by the effects of the recession on public finances and of its expected worsening, due to the actual and possible support to the distressed financial sector on public budgets, induced the re-assessment of financial operators portfolios, both for the new values of sovereign bonds risk and for its consequences on banks’ shares values and riskiness. This turmoil affected in some way all financial markets, but banks’ shares, bonds and CDS spreads were directly involved, due to the banks’ exposures to sovereign bonds. These effects, on the one side, determined a significant risk of a vicious circle between banks’ and public finances distress (Galliani and Zedda 2015), and, on the other side, showed a significant impact on banks’ ratings and share values (Lahmann 2012), suggesting that politics can actually affect the banking system risk evaluation by market investors.

In this framework, one of the most successful points of populist parties’ campaigns is the idea that the banking system is the main driver of the economic disaster and that ordinary citizens pay for crimes committed by banks, which are conscious of the pro-establishment governmental support in case of difficulties, thus prone to moral hazard. In technical terms, the explicit message of these political parties is the idea that the banking system risk induces (Granger-causes) the sovereign risk and not vice versa.

The Italian case, from an empirical point of view, offers an interesting opportunity to study these dynamics, so to verify if there is a feedback loop in terms of risk, or if the relationship can be more correctly described as unidirectional, and, in the latter case, which risk drives the other one.

The case of Italy is particularly suited for this analysis as it suffers both weak GDP growth and a high public debt, so it is subject to volatility and speculation during periods of financial stress. On top of this, from March 2018, Italy has experienced a government coalition so-defined anti-establishment or populist (Politi and Ghiglione 2018), explicitly oriented to deficit growth and against the EU Commission austerity, so that the markets considered the possibility of a path of severe financial and economic instability, leading to the “Italexit ”and eventually to the end of the euro. As a consequence, the Italian economy resulted in being highly sensitive to macro events, which overwhelmed the role of economic fundamentals. This paper contributes to the literature by integrating the classic Merton (1974) model with a political-sensitive market variable able to explain the greatest variance in the Italian banks’ CDS spreads during the most relevant and commonly recognized periods of socio-political and financial distress

For analyzing the dynamics which characterized the bank credit risk within the considered time span, we firstly analyzed the lead–lag structure between the banking and sovereign CDS series, then assessed the determinants of bank CDS spreads by means of an extension of the classic Merton (1974) model, including a redenomination risk variable, during the most volatile phases of this decade.

Results show that the inclusion of the redenomination risk variable enhances the explanatory power of the classic Merton (1974) model.

The structure of the paper is the following. Section 2 reports the literature review, Section 3 describes the models and data, Section 4 reports the results of the analysis and Section 5 reports the economic discussion and conclusions.

2. Literature Review

In a recent literature, four main streams analyzed the relationship among sovereign bonds and banks’ values.

The first stream is aimed at analyzing the determinants of sovereign and corporate CDS spreads. Collin-Dufresne et al. (2002) used the structural approach for identifying the theoretical determinants of CDS spreads of corporate bonds, finding that its explicative power is poor. Zhang et al. (2005) analyzed the determinants of CDS spreads relative to CDS written on US entities (sovereign entities excluded) and denominated in US dollars, on monthly values for a panel of 307 issuers from January 2001 to December 2003, specifically focusing on volatility effects at the firm level and jump-to-default risks. They used a regression model, including performance indicators (Return on Equity, ROE, and dividend payout ratio), structure indicators (leverage) and macro variables (slope of the risk-free rate, etc.), showing that 54% of the credit spread is explained by volatility and jump-to-default risk.

The second stream is aimed at analyzing the determinants of banks’ CDS spreads and their linkages with sovereign risk. A reference paper is Acharya et al. (2011), which described a two-way feedback effect between sovereign risk and banking risk, where bank bailouts by governments produce a negative effect on the sovereign’s public finances that, in turn, reduces the implicit value that the government guarantees for bank debt. This process generates a strong co-movement between the CDS spreads of sovereign countries and financial companies. Avino and Cotter (2014) also investigated the interconnectedness of bank and sovereign CDS markets in the period preceding the financial crisis that started in mid-2007. They proved that, especially during crisis periods, sovereign CDS spreads incorporate more timely information on the default probability of European banks than their corresponding bank CDS spreads.

The third stream is aimed at investigating the explanatory power of the Merton (1974) model determinants in the price discovery process of the CDS premia. Among the others, Guazzarotti (2004) verified that the Merton model’s main determinants explain less than 20% of the CDS values variation, while the residual 70% is unexplained by the default risk factors. Ericsson et al. (2009) investigated the relationship between the theoretical determinants of default risk as defined in Merton (1974) and current market premia on corporate CDSs, employing both a cross-section regression model and a panel model, finding that the theoretical determinants explain around 60% of the CDS spreads. Di Cesare and Guazzarotti (2005) did a similar exercise, analyzing, through the Merton model, the CDS spreads determinants of a sample of non-financial European firms, with five-year CDS, from 2001 to 2004. They show that the default risk factors included in the model explain around 40% of spreads variations.

A subsequent paper by the same authors (Di Cesare and Guazzarotti 2010), on a sample of 167 non-financial US firms, both for the pre-crisis period and for the subsequent years, proved that the financial leverage variation modifies the credit risk pricing in the CDS market.

The fourth literature stream is focused on the banks’ CDS premia price discovery process.

Studying banking CDS spreads, Panetta et al. (2009) verified a negative relationship between CDS spreads and the amount of state interventions for rescuing banks. Considering that the capital injections on the total assets (or total loans) ratio is a proxy of the financial leverage variation, they explain that the negative correlation (0.7 at 10% of significance) means that the banks’ CDS spreads decrease as the capital injection goes up, as to say, when the financial leverage goes down.

Chiaramonte and Casu (2010) analyzed the determinants of CDS spreads, verifying if these can be considered a good proxy of bank default risk. They split their analysis time span into three sub-periods, the pre-crisis (January 2005 to end June 2007), the main crisis (July 2007 to March 2009) and the lower crisis (April 2009 to June 2011), and only considered the typical banking balance-sheet ratios. They found that also the pre-crisis period—but mainly the crisis—mainly reflects the risk measured by balance sheet ratios, while Tier1 ratio and financial leverage are non-significant in all three sub-periods, and liquidity indicators are only significant during the crisis.

Samaniego-Medina et al. (2016) empirically analyzed banks’ CDS spreads determinants for a panel of 45 European banks for 2004–2010, using both market values and balance sheet ratios. They found that the market variables had a higher explicative power during the crisis (2008–2010) than during the pre-crisis period (2004–2007).

This paper is mainly related to the last two literature streams, and contributes to them by integrating the classic Merton model with a political-sensitive market variable that explains the significant variance in the Italian banks’ CDS spreads during different periods of socio-political and financial distress.

3. Model and Data Description

The main aim of this paper is to evaluate how a redenomination risk variable impacts on the explanatory power of the classic Merton (1974) model, and to investigate the determinants of the Italian banks’ credit risk during the most volatile phases of this decade: the financial crisis (August 2007–October 2009)1; the sovereign debt crisis (October 2009–July 2012)2; and the anti-establishment government/pre-Italy’s budget update (March 2018–September 2018)3.

The analysis is performed on the Italian banks’ credit risk estimation (Italian banks proxy), proxied by the weighted average of the values of the five years senior (modified-modified restructuring) CDS contracts of the most capitalized Italian banks4. Specifically, it includes the Intesa San Paolo and Unicredit 5y CDS contracts, weighted by the respective market capitalization, for the time interval Q2 2007–Q3 2018, with daily values coming from Bloomberg (2859 observations)5. In this framework, the 5y CDS contracts for both series show the higher liquidity, as it can be observed by the bid–offer spreads. The descriptive statistics of the dataset are shown in

Table 1. Descriptive statistics–April 2007 to September 2018 (2859 Obs.).

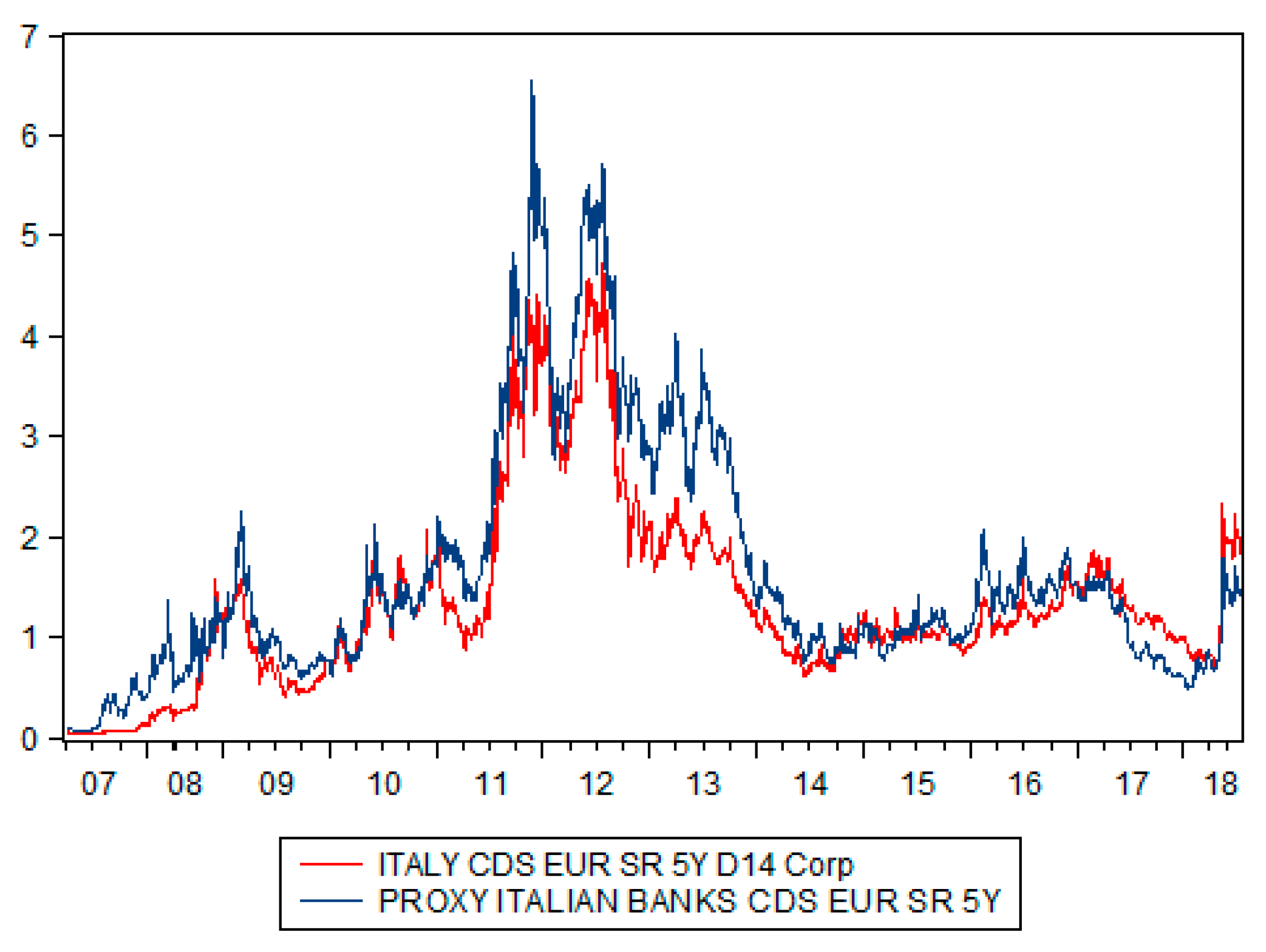
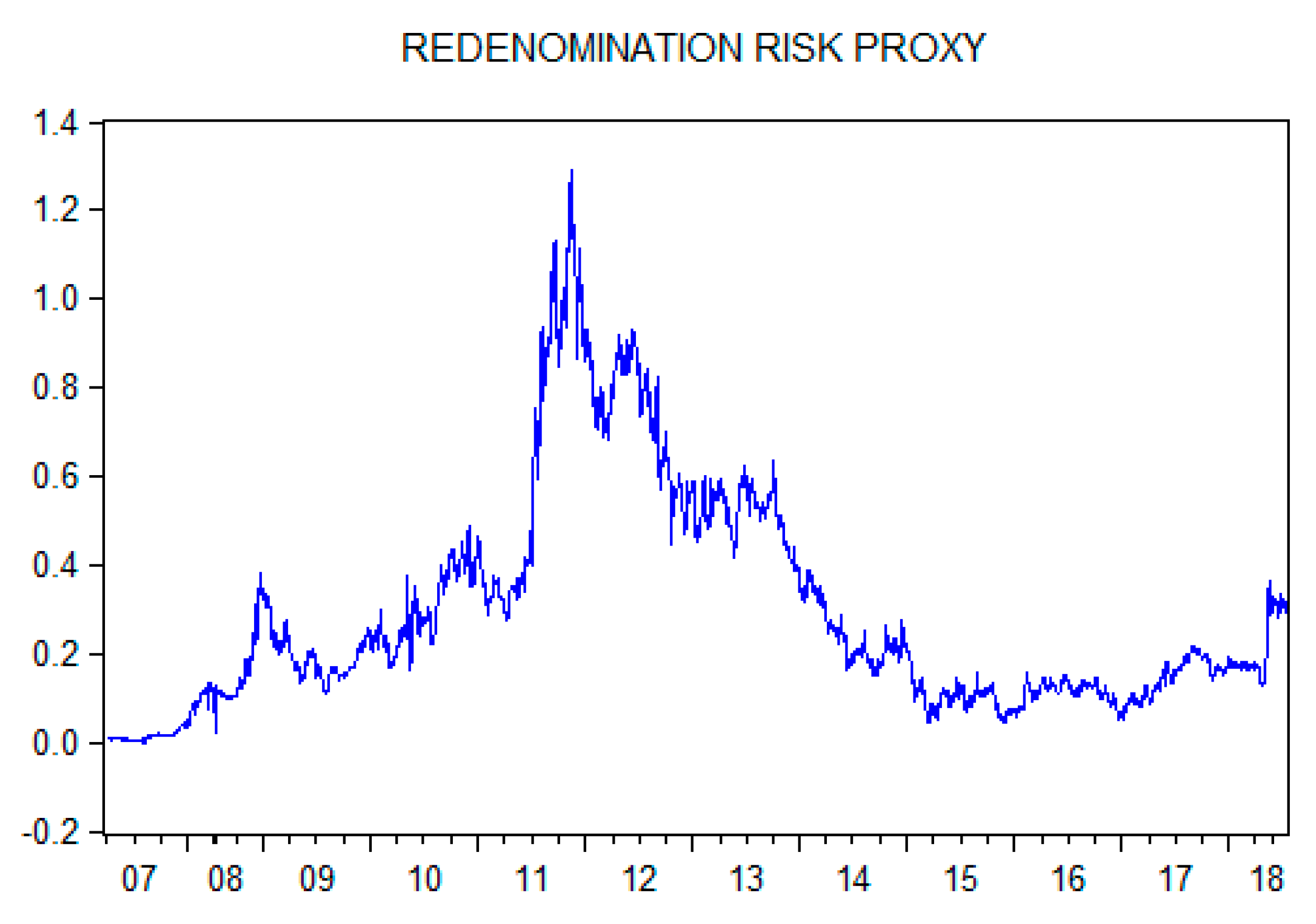
Variable (Basis Points—0.01%)	Mean	SD	Min	Max	Median
Sovereign Italian 5y CDS	134.58	91.48	4.04	472.86	114.90
Italian banks proxy 5y CDS	163.86	120.26	6.70	653.68	128.27

Source: authors’ calculations based on Bloomberg data.

. The overtime movements of the series are shown in Figure 1.

About the modeling, the starting point is the classic Merton model6 which can be represented as follows:

$$ITB{S}_t={\beta }_0+{\beta }_{1}r{f}_t+{\beta }_2{\sigma }_t+{\beta }_3{L}_t$$

(1)

where

• t = 1, 2, …, T is the time horizon;
• $ITB{S}_t$ is the Italian banks’ 5y CDS spread proxy at time t;
• $r{f}_t$ is the risk-free rate at time t;
• ${\sigma }_t$ is the volatility of the assets at time t;
• $L_t$ is the leverage ratio at time t.

For testing the influence of a possible Italexit, we expanded the model for including a proxy of the sovereign debt redenomination risk, as to say, the risk that the considered sovereign debt could be redenominated into new local currencies (which does not automatically imply the break-up of the euro area). The extended model can be represented as follows:

$$ITB{S}_t={\beta }_0+{\beta }_{1}r{f}_t+{\beta }_2{\sigma }_t+{\beta }_3{L}_t+{\beta }_{4}R{R}_t$$

(2)

where $R{R}_t$ is the debt redenomination risk measure at time t, proxied by the quanto CDS spread as in De Santis (2019).

The same model can also be expressed in elasticities terms, through a log–log transformation. This transformation is useful both from a technical point of view, as it solves the non-stationarity problem7 and allows dealing with non-negative variables, and, from the economic evaluation point of view, allows for a straightforward interpretation of the parameters estimates, as the percent change of the dependent variable is directly explained by a percent change of the independent variable.

After the log–log transformation, the model to be estimated can be represented by the following Equation (3):

$$log\left(ITB{S}_t/ITB{S}_{t-1}\right)={\beta }_0+{\beta }_{1}log\left(r{f}_t/r{f}_{t-1}\right)+{\beta }_{2}log\left({\sigma }_t/{\sigma }_{t-1}\right)+{\beta }_{3}log\left(L_t/L_{t-1}\right)+{\beta }_{4}log\left(R{R}_t/R{R}_{t-1}\right)+{\epsilon }_t$$

(3)

where ${\epsilon }_t$ is the error term.

For testing the model, we followed De Santis (2019), which proposed to use the difference between the quanto CDS for Italy and Germany, which is the benchmark for the euro area sovereign debt market, as a proxy of the redenomination risk associated with the break-up of the euro area.

In operational terms, the quanto CDS spread is computed as the difference between the CDS spreads on bonds denominated in US dollar, and the CDS spreads on equivalent bonds denominated in euros.

Formally, the quanto CDS spread at time t, $QC{S}_t$, is computed as follows:

$$QC{S}_t=\left(ITEUCD{S}_t-ITUSDCD{S}_t\right)-\left(DEEUCD{S}_t-DEUSDCD{S}_t\right)$$

(4)

where

• $ITUSDCD{S}_t$ is the sovereign Italian 5y CDS spread in US dollars;
• $ITEUCD{S}_t$ is the sovereign Italian 5y CDS spread in euros;
• $DEEUCD{S}_t$ is the sovereign German 5y CDS spread in US dollars;
• $DEUSDCD{S}_t$ is the sovereign German 5y CDS spread in euros.

In this way, the quanto CDS measures the compensation demanded by market participants for the risk that a euro denominated asset could be redenominated into a different currency. US dollar is the best currency benchmark in order to calculate the quanto CDS spread for three main reasons: it is the classical safe haven asset during high-volatility periods; the most important commodities (i.e., oil, gold, etc.) are exchanged in USD; USA is the more suitable comparison for the euro area from a socio-political perspective. The computed quanto CDS spreads series are reported in Figure 2.

For the estimation of the extended model, the risk-free rate is proxied by the daily 5y euro swap rate8, the volatility9 is proxied by the daily price volatility and the financial leverage is proxied by the daily debt to equity ratio10, with the data coming from Bloomberg. For a more in-depth analysis of the subjacent economic process, we focused our attention on the most significant phases of the Italian sovereign bonds market evolution, as to say, the financial crisis (2007–2009), the sovereign debt crisis (2009–2012), and the pro-deficit government (March 2018–September 2018)11. The descriptive statistics of the dataset, both for the whole sample and for the most significant considered episodes, are shown in

Table 2. Descriptive statistics of data—extended model (EM).

Variable	Mean	SD	Min	Max	Median
Financial crisis (Aug 2007–Oct 2009)—492 Obs.
Δ5y Euro Swap Rate (%)	3.68	0.79	2.63	5.19	3.92
ΔDaily Volatility Stock (%)	2.82	1.26	1.30	4.40	3.05
E/D (%)12	36.50	7.53	18.14	45.03	39.41
ΔQuanto CDS Spread (0.01%)	13.64	8.50	−0.22	38.05	13.47
Sovereign debt crisis (Oct 2009–Jul 2012)—723 Obs.
Δ5y Euro Swap Rate (%)	2.20	0.52	1.01	3.23	2.15
ΔDaily Volatility Stock (%)	3.42	0.66	2.54	4.40	3.49
E/D (%)	31.98	9.21	17.47	42.55	38.63
ΔQuanto CDS Spread (0.01%)	52.41	29.70	16.15	129.25	38.80
Anti-establishment Government (Mar 2018–Sep 2018)—96 Obs.
Δ5y Euro Swap Rate (%)	0.36	0.06	0.22	0.47	0.37
ΔDaily Volatility Stock (%)	1.75	0.95	1.59	1.95	1.69
E/D (%)	33.57	0.95	32.39	34.54	33.51
ΔQuanto CDS Spread (0.01%)	23.74	7.83	12.83	36.62	20.19
Q2 2007–Q3 2018—2859 Obs.
Δ5y Euro Swap Rate (%)	1.61	1.43	−0.18	5.19	1.12
ΔDaily Volatility Stock (%)	2.89	0.91	1.29	4.40	2.77
E/D (%)	33.74	6.59	17.47	45.03	35.13
ΔQuanto CDS Spread (0.01%)	29.28	25.10	−0.22	129.25	19.55

Source: authors’ calculations based on Bloomberg data.

.

About the expected results, the risk-free rate is expected to be negatively correlated with the CDS spreads, as a higher risk-free rate is symptomatic of better macroeconomic conditions. At the micro-level, a higher interest rate has a positive impact on the net interest income, improving banks’ profitability, which, in turn, should reduce the probability of default. The stock volatility is expected to be positively correlated with the CDS spread, as higher volatility means more uncertainty, a smaller distance to default and a higher probability of default.

The leverage ratio is generally expected to be positively correlated with the CDS spread. In Merton’s approach, higher leverage indicates a shorter distance to the default barrier and a higher probability of default (Galil et al. 2013). The debt to equity (DE) ratio is a leverage ratio that shows how much a company’s financing comes from debt or equity. A higher DE ratio means that more of a company’s financing is from debt versus issuing shares of equity. A relatively high DE ratio is commonplace in the banking industry: banks carry higher debt amounts because of the amount of fixed assets that banks own as a result of their branch network (Maverick 2018).

Assuming that the bank is fully respecting Basel principles and central bank capital requirements, the standard measure of the leverage ratio, defined as debt to equity ratio, could be expected to be negatively correlated with the CDS spread. During a period of economic expansion, savers are more willing to spend money and make investments in durable goods. At the same time, it is reasonable to expect that the bank’s management increases the investment weight in riskier assets (high expected yield, but high risk-weighted asset coefficient) and buyback operations. Moreover, market operators are more willing to increase their exposure in bank shares (high-beta), due to a higher trust in the financial system and future economic perspectives. Hence, assuming that market participants move faster and with a decisively larger exposure than retail savers, this would imply that the ratio’s denominator grows faster than the numerator in a stable and non-volatile way, which, in turn, should reduce the leverage ratio. On the contrary, during adverse economic conditions or negative economic outlook, it is reasonable to expect an increase in the leverage ratio and a positive correlation with the CDS spread due to a faster and volatile contraction of the denominator than the numerator of the ratio. In absolute terms, the numerator and the denominator of the leverage ratio tend to move together and in the same direction during different stages of the business cycle (procyclicality), but with a different pace of growth. What could make the difference in the explanation of the leverage ratio impact on the CDS premium, therefore, is the business cycle outlook. As long as savers and investors are confident about the future economic perspectives and trust in the financial system, assuming no capitalization problems by banks, it is reasonable to expect a higher positive and stable variation in the denominator than the numerator of the ratio. In the case of a negative economic outlook or, even worse, during stages of generalized panic about the capacity of the banking system to ensure stability, then it is possible to observe volatile variations in the leverage ratio and a positive relationship with the CDS premium (due to higher credit risk).

4. Results

4.1. Financial Crisis

The augmented Dickey–Fuller test (see the Appendix A

Table A1. Augmented Dickey–Fuller test.

Augmented Dickey-Fuller Test
Residuals
Period	t-Statistic	Prob. *
Financial crisis (492 Obs.)	−19.24291	0.0000
Sovereign debt crisis (723 Obs.)	−21.51060	0.0000
Pro deficit Government (96 Obs.)	−9.863148	0.0000

* MacKinnon (1996) one-sided p-values. Source: author’s own calculations in Eviews 10.

) shows that series are stationary, and the evaluations on the correlation between the regressors (in Appendix A

Table A5. Correlation matrix: period August 2007–October 2009 (492 Obs.).

Variable	Δ(Risk-Free Rate)	Δ(Volatility)	Δ(Leverage)	Δ(Reden. Risk)
Δ(Risk-free Rate)	1	0.16308	0.14920	−0.00185
Δ(Volatility)	0.16308	1	0.18848	0.14343
Δ(Leverage)	0.14920	0.18848	1	0.12399
Δ(Reden. Risk)	−0.00185	0.14343	0.12399	1

Source: author’s own calculations in Eviews 10.

) do not suggest multicollinearity problems.

Table 3. OLS estimates: period August 2007–October 2009 (492 Obs.).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
β0	−0.000309	0.003002	−0.102779	0.9182
Δ(Risk-free Rate)	−0.814622 ***	0.221771	−3.673263	0.0003
Δ(Volatility)	0.131785	0.820409	0.160633	0.8724
Δ(Leverage)	0.017579	0.050774	0.346210	0.7293
Δ(Reden. Risk)	0.080068 ***	0.024640	3.249537	0.0012
R2	0.10
Adj. R2	0.09
Prob(F-statistic)	0.00

Note: *** signals parameter significance at 1%. Source: authors’ calculations in Eviews 10 based on Bloomberg data.

shows the estimated coefficients for the August 2007–October 2009 period (financial crisis).

The obtained R² of just 10% signals that the model is not able to explain a significant part of the change in the Italian banks’ CDS spreads, in particular when considering that the redenomination proxy variable adds around 6% in terms of explanatory power to the classic Merton Model over the selected period (see the Appendix A

Table A2. OLS estimates: period August 2007–October 2009 (492 Obs.).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
β0	6.44 × 10−6	0.003116	0.002066	0.9984
Δ(Risk-free Rate)	−0.861810 ***	0.267762	−3.218569	0.0014
Δ(Volatility)	0.407496	0.960730	0.424152	0.6716
Δ(Leverage)	0.043429	0.068708	0.632086	0.5276
R2	0.05
Adj. R2	0.04
Prob(F-statistic)	0.00

Note: *** signals parameter significance at 1%. Source: author’s own calculations in Eviews 10.

). The risk-free rate and the redenomination risk proxy percentage change sensitivities result to be statistically significant at a 1% threshold.

The relationship between the risk-free variable and the CDS spread is negative as expected, reporting a coefficient of about −0.82. This means that an increase/decrease of 100 basis points of the regressor corresponded to a decrease/increase of approximately 82 basis points of the CDS spread.

The relationship between the redenomination risk variable and the CDS spread is positive, as expected, and reporting a coefficient of about 0.08, which means that an increase of 100 basis points in the quanto CDS spread induced an average increase of around 8 basis point in the CDS spread.

The leverage and daily stock volatility variables result to be not statistically significant. The F-test still confirms the regressors’ appropriateness in the analysis, which is significant with a 95% confidence interval.

4.2. Sovereign Debt Crisis

The augmented Dickey–Fuller test shows that series are stationary, and the evaluations on the correlation between the regressors do not suggest multicollinearity problems (see the Appendix A Table A1 and

Table A6. Correlation matrix: period October 2009–July 2012 (723 Obs.).

Variable	Δ(Risk-Free Rate)	Δ(Volatility)	Δ(Leverage)	Δ(Reden. Risk)
Δ(Risk-free Rate)	1	0.03003	0.01426	−0.18996
Δ(Volatility)	0.03003	1	0.11177	−0.06803
Δ(Leverage)	0.01426	0.11177	1	−0.03480
Δ(Reden. Risk)	−0.18996	−0.06803	−0.03480	1

Source: author’s own calculations in Eviews 10.

for more details).

Table 4. OLS estimates: period October 2009–July 2012 (723 Obs.).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
β0	0.001337	0.001216	1.099076	0.2721
Δ(Risk-free Rate)	−0.340677 ***	0.066582	−5.116620	0.0000
Δ(Volatility)	0.401680	0.278591	1.441824	0.1498
Δ(Leverage)	0.002897	0.009493	0.305228	0.7603
Δ(Reden. Risk)	0.491289 ***	0.029953	16.40215	0.0000
R2	0.40
Adj. R2	0.40
Prob(F-statistic)	0.00

Note: *** signals parameter significance at 1%. Source: Authors’ calculations in Eviews 10 based on Bloomberg data.

shows the estimated coefficients for the October 2009–July 2012 period (sovereign debt crisis).

In this period, the estimated determination coefficient R² goes up to 40%, significantly increasing from the previous period estimation. A significant part of this increase can be attributed to the inclusion of the redenomination risk proxy, which added a benefit of around 32% in terms of the explanatory power of the model over the selected period (see the Appendix A

Table A3. OLS estimates: period October 2009–July 2012 (723 Obs.).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
β0	0.002165	0.001519	1.425300	0.1545
Δ(Risk-free Rate)	−0.552276 ***	0.085677	−6.446025	0.0000
Δ(Volatility)	0.109614	0.733384	0.149464	0.8812
Δ(Leverage)	−0.006041	0.013461	−0.448774	0.6537
R2	0.08
Adj. R2	0.08
Prob(F-statistic)	0.00

Note: *** signals parameter significance at 1%. Source: author’s own calculations in Eviews 10.

).

The risk-free rate and the redenomination risk proxy resulted to be statistically significant at a 1% threshold, respectively reporting a coefficient of −0.34 and 0.49, which confirms, as expected, that the market perception of a redenomination risk had a significant role during this period of financial instability.

As in the previous period, the leverage value and daily stock volatility variables showed no statistical significance.

The F-test still confirms the model significance at a 95% confidence interval.

4.3. Pro Deficit Government

Even in this case, the augmented Dickey–Fuller test shows that series are stationary, and the evaluations on the correlation between the regressors do not suggest multicollinearity problems (see the Appendix A for more details Table A1 and

Table A7. Correlation matrix: period March 2018–September 2018 (96 Obs.).

Variable	Δ(Risk-Free Rate)	Δ(Volatility)	Δ(Leverage)	Δ(Reden. Risk)
Δ(Risk-free Rate)	1	−0.09275	−0.00188	−0.32308
Δ(Volatility)	−0.09275	1	−0.01285	0.11611
Δ(Leverage)	−0.00188	−0.01285	1	−0.01423
Δ(Reden. Risk)	−0.32308	0.11611	−0.01423	1

Source: author’s own calculations in Eviews 10.

).

Table 5. OLS estimates: period March 2018–September 2018 (96 Obs.).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
β0	0.002929	0.004784	0.612316	0.5419
Δ(Risk-free Rate)	−0.288470 ***	0.084666	−3.407152	0.0010
Δ(Volatility)	0.115309	0.322290	0.357779	0.7213
Δ(Leverage)	−0.286173 **	0.118990	−2.405022	0.0182
Δ(Reden. Risk)	0.635197 ***	0.107532	5.907030	0.0000
R2	0.65
Adj. R2	0.64
Prob(F-statistic)	0.00

Note: *** signals parameter significance at 1%, ** is for significance at 5%. Source: authors’ calculations in Eviews 10 based on Bloomberg data.

shows the estimated coefficients for the March 2018–September 2018 period (pro-deficit government).

The R² obtained in this estimation reaches 65%, showing that, during the pro-deficit government period, the model explanatory power is even higher than it was for the sovereign debt crisis. Here also, a significant part of this explanatory power can be attributed to the redenomination risk proxy (around 36%).

Regarding the estimated coefficients, the risk-free rate and the redenomination risk proxy are statistically significant at a 1% threshold. The risk-free rate reported a coefficient of about −0.29, reversing the sign of the previous periods’ estimation, while the redenomination risk coefficient raised to 0.64, which is even higher than it was during the sovereign debt crisis period when the Italian economy was close to a potential default.

Within this period, the leverage variable becomes statistically significant, even if just at a 5% threshold, reporting a coefficient of about −0.29, nearly the same value obtained for the risk-free rate during the same period. This result can be explained by reminding that Italy in 2017 reported some positive GDP growth (differently from the two periods of economic contraction analyzed previously) and that its value can be due to the numerator and denominator’s different adjustment speeds of the ratio. The daily stock volatility variable results to be not statistically significant.

4.4. Granger-Causality Tests

The Granger-causality tests allow further analysis of the results obtained for the pro-deficit government period between the daily banks’ stock price percentage variation and the daily redenomination risk growth rate.

The results, reported in

Table 6. Granger-causality test: period March 2018–September 2018.

Null Hypothesis	Obs	F-Statistic	Prob.
%Δ daily banks’ stock price does not Granger-cause redenomination risk growth rate	96	2.51428	0.1162
redenomination risk growth rate does not Granger-cause %Δ daily banks’ stock price		0.43497	0.5112

Source: authors’ calculations in Eviews 10 based on Bloomberg data.

, suggest the existence of a feedback relationship between the two variables over the considered time span. The correspondent impulse response functions, reported in Figure 3 and Figure 4, allow a more specific evaluation of the daily banks’ stock price percentage change and the redenomination risk growth rate impulse responses following a unit shock of the other variable. Results show that the impulse coming from one variable has a negative response on the other variable, resulting in a progressive smoothed rebounding from negative to positive as in a typical negative AR1 autocorrelated process.

Even if two graphs show a similar shape, the values scale highlights that the response to the redenomination risk growth rate has a higher impact on the process.

5. Economic Discussion and Conclusions

From an economic point of view, the estimations reported above show how the redenomination risk impacted on the Italian banks’ CDS spreads.

The economic evolution reported above explains why the political variable plays a fundamental role in this period. In quantitative terms, the redenomination risk component progressively gained the role of main driver of the sensitivity of the Italian banks’ CDS spreads, in so pricing the risk of an “Italexit” event already in the sovereign debt crisis, but more during the anti-establishment government period.

In fact, during the sovereign debt crisis, the higher sovereign CDS premia had not suffered from a high redenomination risk component, as market operators were expecting the ECB to intervene, which happened on 26 July 2012, when the ECB announced its plan to buy bonds from the euro area’s distressed countries, known as outright monetary transactions. As pointed out by Nelson (2017), this intervention obtained the expected effects, as traders immediately reacted to it, bringing down bond yields across the eurozone.

In the following years, characterized by the quantitative easing (QE) program launched in March 2015 by the ECB, the increased amount of outstanding liquidity injected in financial markets lowered the market volatility. This price stability went on for three years and was broken in March 2018, when Italy experienced an (anti-establishment or populist) pro-deficit government coalition. Populist parties’ rhetoric has been frankly against the technocratic European Union since their origins, completely in line with the political idea that in June 2016 caused the famous “Brexit”. So, after the Brexit event, the market participants’ read-across of what happened in the UK with what could potentially happen in other European governments led by populist parties became almost automatic. The market values reacted by a significant volatility spike, immediately reflected in its sovereign CDS spreads.

As reported by Reed (2018), the high volatility Italian banks had suffered in 2018 was mainly due to political uncertainty, rather than to business outlook. Further, it is exactly in this period that the redenomination risk variable showed the highest coefficient and significance in our estimations.

The political turmoil went evident since Italy’s two populist parties had a significant result in the parliament elections. From April to September (the first six months after the elections), foreign net sales of Italian bank securities were of about EUR 13 billion (USD 14.8 billion), while sovereign bond sales reached EUR 58 billion (Sirletti and Salzano 2018). In this framework, the repeatedly declared intention to leave the euro area by both political parties, during and after the electoral campaign, added further uncertainty about the future of the Italian economy and powered the sell-off of the Italian government bonds over the year (Ainger 2018). As banks typically hold large shares of domestic sovereign bonds13, the widening of the BTP-Bund spread had a significant negative impact on their balance sheets, entailing negative effects in terms of CET1 ratio.

This was due not only to the general pro-deficit attitude declared by the same government coalition, but also as the critique on the excessive costs paid for sustaining the national banking system resulted in being one of the most successful arguments proposed by the anti-establishment parties during the electoral campaign. In other words, the underlying message is that the government’s riskiness (as perceived by the market) is a pure consequence of the excessive risks taken by the banking sector, which induced economic instability, and weakened public finances, which, in turn, determined higher BTP-Bund spreads and expected costs for rescuing distressed banks.

These political factors became so strong in influencing the market behavior, as at the same time the euro area was suffering the influence of populist parties, reducing the attitude of member states’ governments to dialogue and coordination. In such a socio-political framework, economic fundamentals become secondary and raise the entire system vulnerability to financial speculation. From an operative perspective, the evolution of the quanto CDS spreads could be a significant leading indicator on the price discovery process of the banks’ CDS spreads for European countries led by euro-skeptical governments.

In this paper, we analyzed the drivers of Italian bank credit risk during the most volatile phases of this decade, namely the financial crisis (August 2007–October 2009), the sovereign debt crisis (October 2009–July 2012) and the anti-establishment government/pre-Italy’s budget update (March 2018–September 2018) period.

Results show that the inclusion of the redenomination risk variable enhances the explanatory power of the classic Merton (1974) model, already during the sovereign debt crisis, but even more during the anti-establishment government period, showing how the market reacts to specific political interventions, reducing the banks economic fundamentals to a secondary role in a context of economic uncertainty and lack of political coordination.