A Note on the Empirical Relation between Oil Prices and the Value of the Dollar
Abstract
:1. Introduction
2. Previous Work
3. Real Effective Exchange Rates
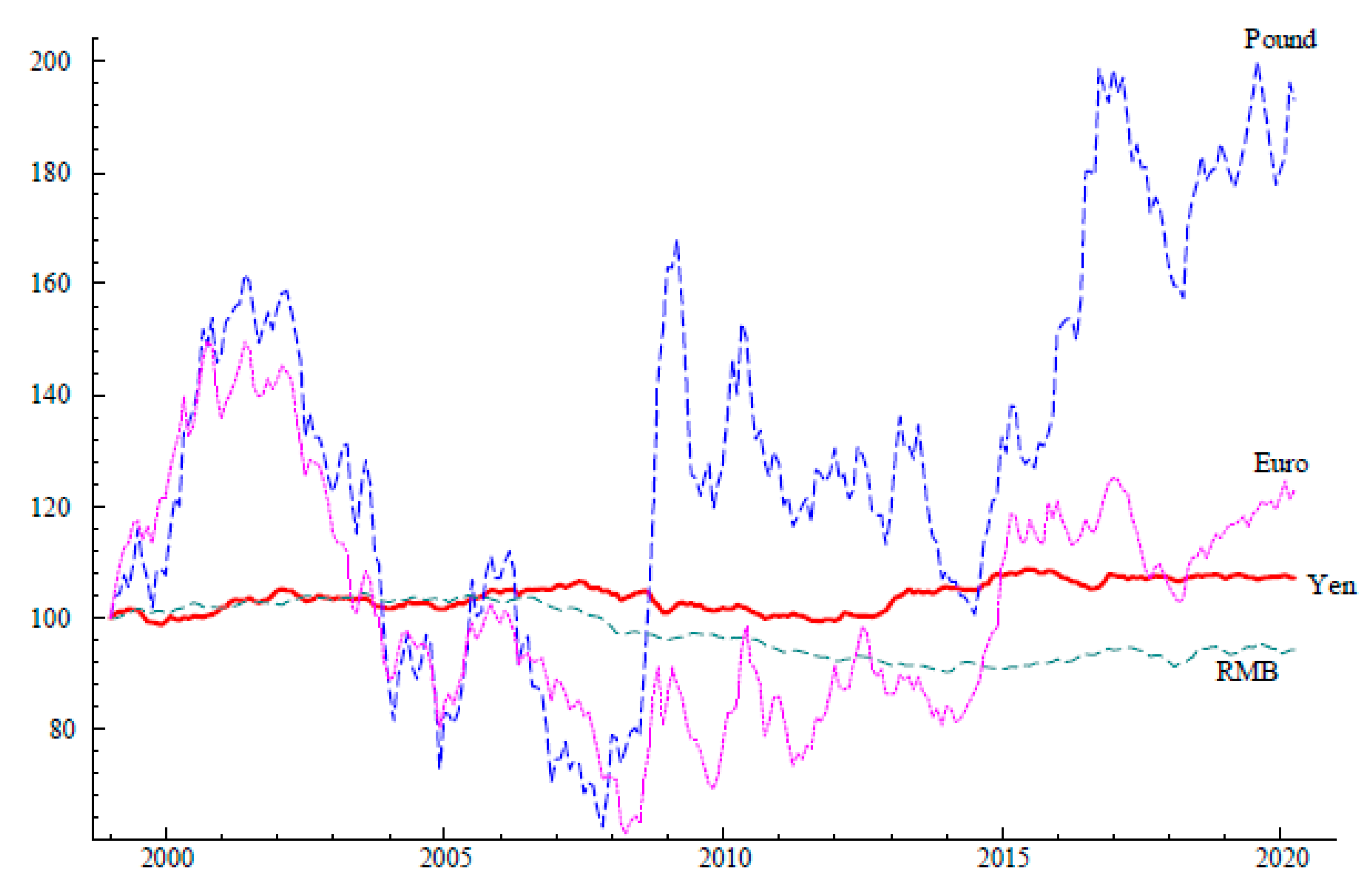
3.1. Measurement
3.2. Limitations
4. Analysis
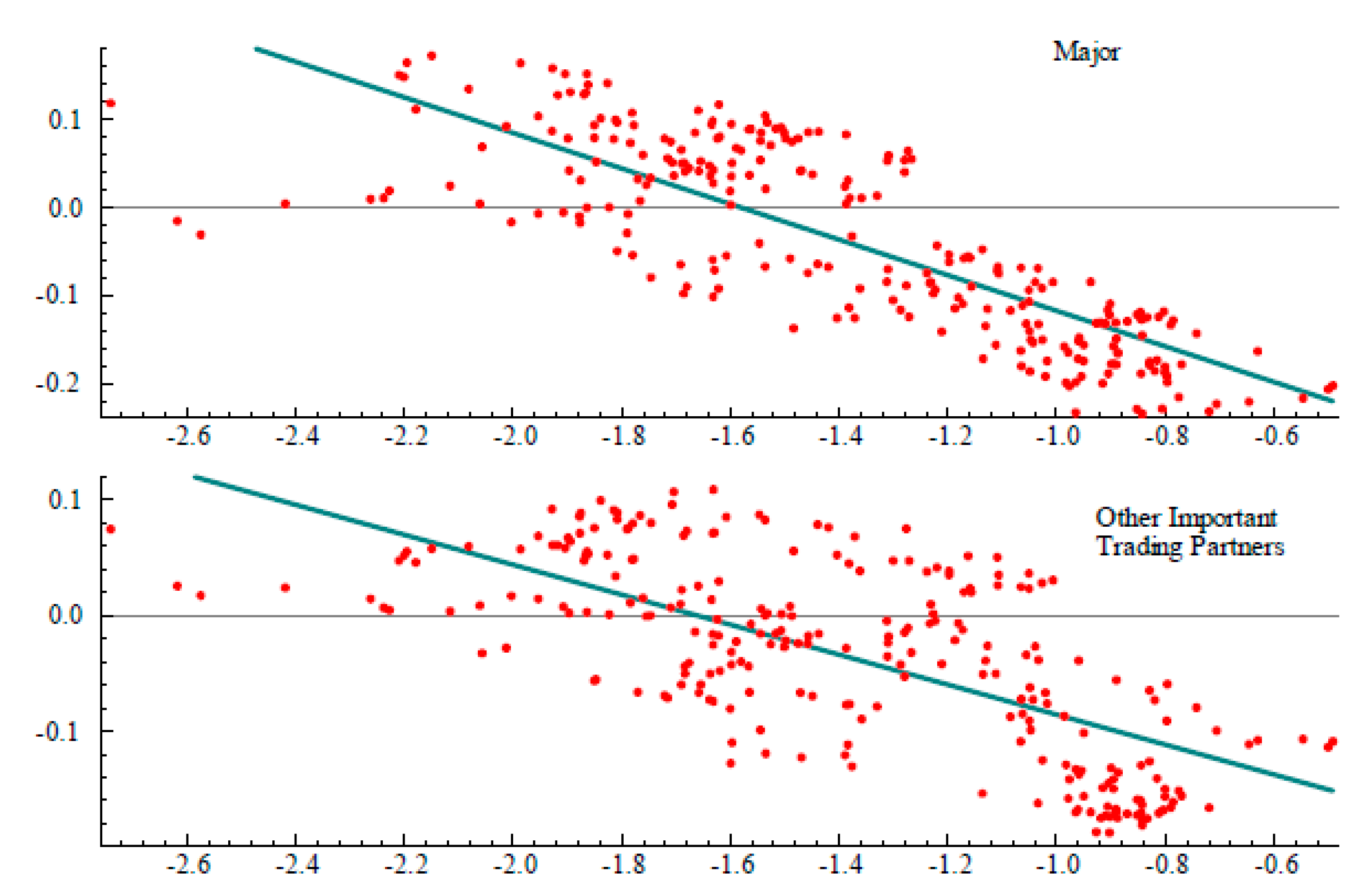
4.1. Unconditional Correlations
4.2. Vector Error Correction Framework
- Model 1:
- Effective Broad yt = (pt dt)’
- Model 2:
- Effective, Major and Other Trading Partners yt = (pt dmt dot)’
- Model 3:
- Bilateral rates yt
- p is the real price of oil
- d is the broad measure of the dollar
- dt is the measure of the dollar for the major currencies
- do is the measure for other important trading partners
- is the price-adjusted price of the dollar in terms of the yen
- is the price-adjusted price of the dollar in terms of the euro
- is the price-adjusted price of the dollar in terms of the pound
- is the price-adjusted price of the dollar in terms of the renminbi.
4.2.1. Time-Series Properties
4.2.2. Cointegration
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Data Sources and Transformations
- d = log(TWEXBPA/99.84)
- dm = log(TWEXMPA/98.189)
- do = log(TWEXOPA/l10.784)
- p = po − pus
- po = log(MCOILWTICO
- pus = log(CPIAUCNS)
- = log(EXJPUS*CPIAUCNS/JPNCPIALLMINMEI
- = log((l/EXUSUK)*CPIAUCNS/CP0000GBM086NEST)
- = log(EXCHUS*CPIAUCNS/CHNCPIALLMINMEI)
- = log((l/EXUSEU)*CPIAUCNS/CP0000EZl9M086NEST)
- Nominal Yen/dollar DEXJPUS
- Nominal China: DEXCHUS
- Nominal Euro: DEXUSEU
- Nominal UK: DEXUSUK
- US CPI: CPIAUCNS
- Japanese CPI: JPNCPIALLMINMEI
- Chinese CPI: CHNCPIALLMINMEI
- euro CPI: CP0000EZ19M086NEST
- UK CPI CP0000GBM086NEST
Appendix A.2. Augmented Dickey-Fuller Test Results
| Levels of Logarithms | |||||||||
| ADF | (T = 249, Constant; 5% = −2.87, 1% = −3.46) | ||||||||
| Lag | £/$ | rmb/$ | €/$ | ¥/$ | D | Dm | Do | p | |
| 6 | −1.48 | −0.71 | −1.71 | −1.31 | −1.35 | −1.38 | −1.16 | −1.42 | |
| 5 | −1.58 | −0.81 | −1.60 | −1.38 | −1.31 | −1.33 | −1.15 | −1.50 | |
| 4 | −1.72 | −0.88 | −1.59 | −1.58 | −1.27 | −1.40 | −1.09 | −1.44 | |
| 3 | −1.67 | −0.91 | −1.50 | −1.71 | −1.15 | −1.15 | −1.11 | −1.51 | |
| 2 | −1.50 | −0.93 | −1.50 | −1.85 | −1.07 | −1.17 | −1.02 | −1.67 | |
| 1 | −1.39 | −0.97 | −1.63 | −1.66 | −1.30 | −1.31 | −1.25 | −1.59 | |
| 0 | −0.91 | −0.71 | −1.23 | −1.23 | −0.70 | −0.76 | −0.72 | −0.77 | |
| Difference of Logarithms | |||||||||
| (T = 248, Constant; 5% = −2.87, 1% = −3.46) | |||||||||
| Lag | ∆£/$ | ∆rmb/$ | ∆€/$ | ∆¥/$ | ∆D | ∆Dm | ∆Do | ∆p | |
| 6 | −6.414 ** | −6.307 ** | −5.771 ** | −6.602 ** | −5.996 ** | −6.050 ** | −5.630 ** | −4.956 ** | |
| 5 | −6.228 ** | −7.664 ** | −5.616 ** | −7.400 ** | −5.221 ** | −5.539 ** | −5.417 ** | −5.282 ** | |
| 4 | −6.472 ** | −7.144 ** | −6.450 ** | −7.944 ** | −5.754 ** | −6.118 ** | −5.886 ** | −5.164 ** | |
| 3 | −6.589 ** | −7.288 ** | −7.156 ** | −7.940 ** | −6.430 ** | −6.437 ** | −6.849 ** | −6.159 ** | |
| 2 | −7.479 ** | −7.816 ** | −8.663 ** | −8.282 ** | −7.920 ** | −8.474 ** | −7.658 ** | −6.614 ** | |
| 1 | −9.327 ** | −8.879 ** | −10.36 ** | −8.875 ** | −10.08 ** | −9.899 ** | −10.29 ** | −6.805 ** | |
| 0 | −12.65 ** | −10.24 ** | −12.19 ** | −12.25 ** | −10.47 ** | −11.28 ** | −10.66 ** | −9.471 ** | |
| Sample Statistics | |||||||||
| ∆£/$ | ∆rmb/$ | ∆€/$ | ∆¥/$ | ∆D | ∆Dm | ∆Do | ∆p | ||
| Monthly Growth Rates 1990:2−2020:4 255 Obs. | |||||||||
| Mean | 0.001 | −0.001 | 0.001 | 0.001 | 0.000 | 0.001 | 0.000 | −0.001 | |
| Std.Devn. | 0.021 | 0.010 | 0.023 | 0.023 | 0.012 | 0.016 | 0.011 | 0.098 | |
| Skewness | 0.400 | 0.086 | −0.080 | −0.030 | 0.438 | −0.113 | 1.329 | −1.799 | |
| Excess Kurtosis | 1.143 | 0.690 | 0.429 | 0.596 | 1.653 | 0.590 | 4.923 | 7.329 | |
| Minimum | −0.057 | −0.033 | −0.068 | −0.073 | −0.034 | −0.048 | −0.032 | −0.561 | |
| Maximum | 0.077 | 0.035 | 0.070 | 0.072 | 0.056 | 0.058 | 0.062 | 0.210 | |
| Median | 0.000 | −0.001 | 0.001 | 0.000 | 0.000 | 0.002 | −0.001 | 0.013 | |
| Normality | test (p-val) | 0.0018 ** | 0.0432 * | 0.211 | 0.082 | 0.0000 ** | 0.082 | 0.0000 ** | 0.0000 ** |
References
- Amano, Robert, and Simon van Norden. 1998. Oil Prices and the Rise and Fall of the US Real Exchange Rate. Journal of International Money and Finance 17: 299–316. [Google Scholar] [CrossRef]
- Beckmann, Joscha, Robert Czudaj, and Vipin Arora. 2017. The Relationship between Oil Prices and Exchange Rates: Theory and Evidence; EIA Working Paper Series; Washington, DC: EIA, June.
- Benassy-Quere, Aganes, Valerie Mignon, and Alexis Penot. 2005. China and the Relationship between the Oil Price and the Dollar. CEPII Working Paper No 2005–16. Paris: CEPII, October. [Google Scholar]
- Breitenfellner, Andreas, and Jesus Crespo Cuaresma. 2008. Crude Oil Prices and the USD/EUR Exchange Rate. In Monetary Policy and the Economy. Wien: Oesterreichische Nationalbank (Austrian Central Bank), Q4/08, OeNB. pp. 102–21. [Google Scholar]
- Cheng, Kevin. 2008. Dollar Depreciation and Commodity Prices. In World Economic Outlook. Washington, DC: IMF, chp. 3. [Google Scholar]
- Doornik, Jurgen, and David Hendry. 2013. Empirical Econometric Modeling Vols. I and II. London: Timberlake Consultants. [Google Scholar]
- Federal Reserve Bank of New York. 2020. Oil Price Dynamics Report. Available online: https://www.newyorkfed.org/research/policy/oil_price_dynamics_report.html (accessed on 23 July 2020).
- Fratzscher, Marcel, Daniel Schneider, and Ine van Robays. 2014. Oil Prices, Exchange Rates and Asset Prices. ECB Working Paper l689. Frankfurt: ECB, July. [Google Scholar]
- Golub, Stephen. 1983. Oil Prices and Exchange Rates. Economic Journal 93: 576–93. [Google Scholar] [CrossRef]
- Grisse, Christian. 2010. What Drives the Oil-Dollar Correlation? New York: Federal Reserve Bank of New York. [Google Scholar]
- Huang, Bwo-Nung, Chi-Chuan Lee, Yu-Fang Chang, and Chien-Chiang Lee. 2020. Dynamic Linkage Between Oil Prices and Exchange Rates: New Global Evidence. Empirical Economics April. [Google Scholar] [CrossRef]
- Johansen, Soren. 1988. Statistical Analysis of Cointegration Vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar]
- Kilian, Lutz. 2009. Not all oil price shocks are alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. American Economic Review 99: 1059–69. [Google Scholar] [CrossRef] [Green Version]
- Krugman, Paul. 1980. Oil and the Dollar. NBER Working Paper No. 554. Cambridge: NBER. [Google Scholar]
- Leahy, Michael P. 1998. New Summary Measures of the Foreign Exchange Value of the Dollar; Washington, DC: Federal Reserve Bulletin, October.
- Reboredo, Juan, Miguel Rivera-Castro, and Gilney Zebende. 2014. Oil and US Dollar Exchange-rate Dependence: A Detrended Cross-correlation Approach. Energy Economics 42: 132–39. [Google Scholar] [CrossRef]
- Truman, Edwin. 2019. Federal Reserve Board Oral History Project: Interview with Edwin Truman. Available online: https://www.federalreserve.gov/aboutthefed/files/edwin-m-truman-interview-20091130.pdf (accessed on 23 July 2020).
- von Beschwitz, Bastian, Christopher Collins, and Deepa Datta. 2019. Revisions to the Federal Reserve Dollar Indexes. Available online: https://www.federalreserve.gov/econres/notes/feds-notes/revisions-to-the-federal-reserve-dollar-indexes-20190115.htm (accessed on 23 July 2020).
- Yousefi, Ayoub, and Tony S. Wirjanto. 2005. A Stylized Exchange Rate Pass-through Model of Crude Oil Price Formation. OPEC Review 29: 177–87. [Google Scholar] [CrossRef]
| 1. | For an early treatment of oil as a financial asset, see Fratzscher et al. (2014). |
| 2. | As noted in the June 2020 Monetary Policy Report of the Federal Reserve, “On April 20, the price of front-month oil futures contracts for West Texas Intermediate (WTI) closed at negative $38 per barrel. These WTI futures contracts are settled by physical delivery; as worries about the lack of available storage space intensified, prices spiraled downward. Few contracts were actually traded at these negative prices, and prices recovered in the following days.” See https://www.federalreserve.gov/monetarypolicy/files/202006l2_mprfullreport.pdf. |
| 3. | For a recent and thorough review of this literature see Beckmann et al. (2017). |
| 4. | More than 90 percent of international foreign exchange reserves are held in assets denominated in these currencies. See the IMF’s Currency Composition of Official Foreign Exchange Reserves. In terms of the global oil market, these five countries account for 55 percent of world oil consumption in 2019. |
| 5. | A switch to daily data would preclude measuring the variables in real terms because there are no official data for daily CPIs. |
| 6. | Breitenfellner and Cuaresma (2008) trace the origins of this relation. |
| 7. | Using PPP exchange rates. See the IMF’s World Economic Outlook. |
| 8. | |
| 9. | |
| 10. | We are using the U.S. official measure of the external value of the dollar which uses weights that are updated every year. The measures of the IMF and the BIS update their weights with less frequency. See Truman (2019, pp. 126–31) for the history of this index. |
| 11. | Appendix A.1 contains all the data sources and transformations used in this paper. |
| 12. | In this sense, D is unlike the CPI in which the weights do not change from year to year. The obvious solution to this limitation is to use an effective exchange rate in which the weights do not vary from year to year as the indexes from the IMF and the BIS. Nevertheless, even if the weights were literally fixed, the reliance on the resulting aggregates still requires us to assume the existence of a market for D and would not remove the identification issues raised above. |
| 13. | Specifically, the 2020 weights for Russia and Saudi Arabia, two large oil producers are 0.53 percent and 0.49 percent, respectively. See https://www.federalreserve.gov/releases/hl0/weights/default.htm. |
| 14. | Note that using fixed weights would address that issue but it would not provide a financial market for the "fixed-weight external value of the dollar.” Further, movements in a fixed-weight index cannot, by construction, identify which currencies are responsible for those movements. |
| 15. | One of the referees noted that one could use the volatility spillover measure. This suggestion reinforces the point of the paper about using bilateral exchange rates. The volatility of the effective exchange rates is not meaningful, given that offsetting changes in exchange rates would induce a seemingly stable average. |
| 16. | Following the suggestion of one of the referees, the intercept c is included in the cointegration vector . |
| 17. | Indeed, the Euro area and China are the largest oil consumers (after the United States) and account for 29 percent of world oil consumption in 2019; if we include both Japan and the United Kingdom, that share increases to 34 percent. Source: International Energy Agency as reported in https://en.wikipedia.org/wiki/List_of_countries_by_oil_consumption. |
| 18. | Again, note that this equation is not determining p in terms of or the other way around. Instead, it is showing the relation among five endogenous variables that is consistent with no-arbitrage relation in these markets. In response to a shock, all the variables in the model respond according to Equation (1). These responses stop as soon as arbitrage opportunities are fully exploited. |
| 19. | For example, based on the IMF’s COFER data, the euro accounts for 20 percent of the world’s official foreign exchange reserves, whereas the renminbi accounts for 2 percent. Using an alternative indicator, the turnover of OTC foreign exchange instruments in 2019 for the euro is $2.l trillion and $285 billion dollars for the renminbi. See https://stats.bis.org/statx/srs/table/dll.3. |
| 20. | These observations benefited greatly from the comments by a referee. |
| 21. | We could not reject dynamic stability based on impulse responses. These results are available on request. |
| 22. | See the Minutes of the Federal Open Market Committee from May 2020 at https://www.federalreserve.gov/monetarypolicy/files/fomcminutes20200429.pdf. Further, the Federal Reserve Bank of New York’s Oil Price Dynamics Report does not rely on effective exchange rates but instead on bilateral rates (Federal Reserve Bank of New York 2020). |
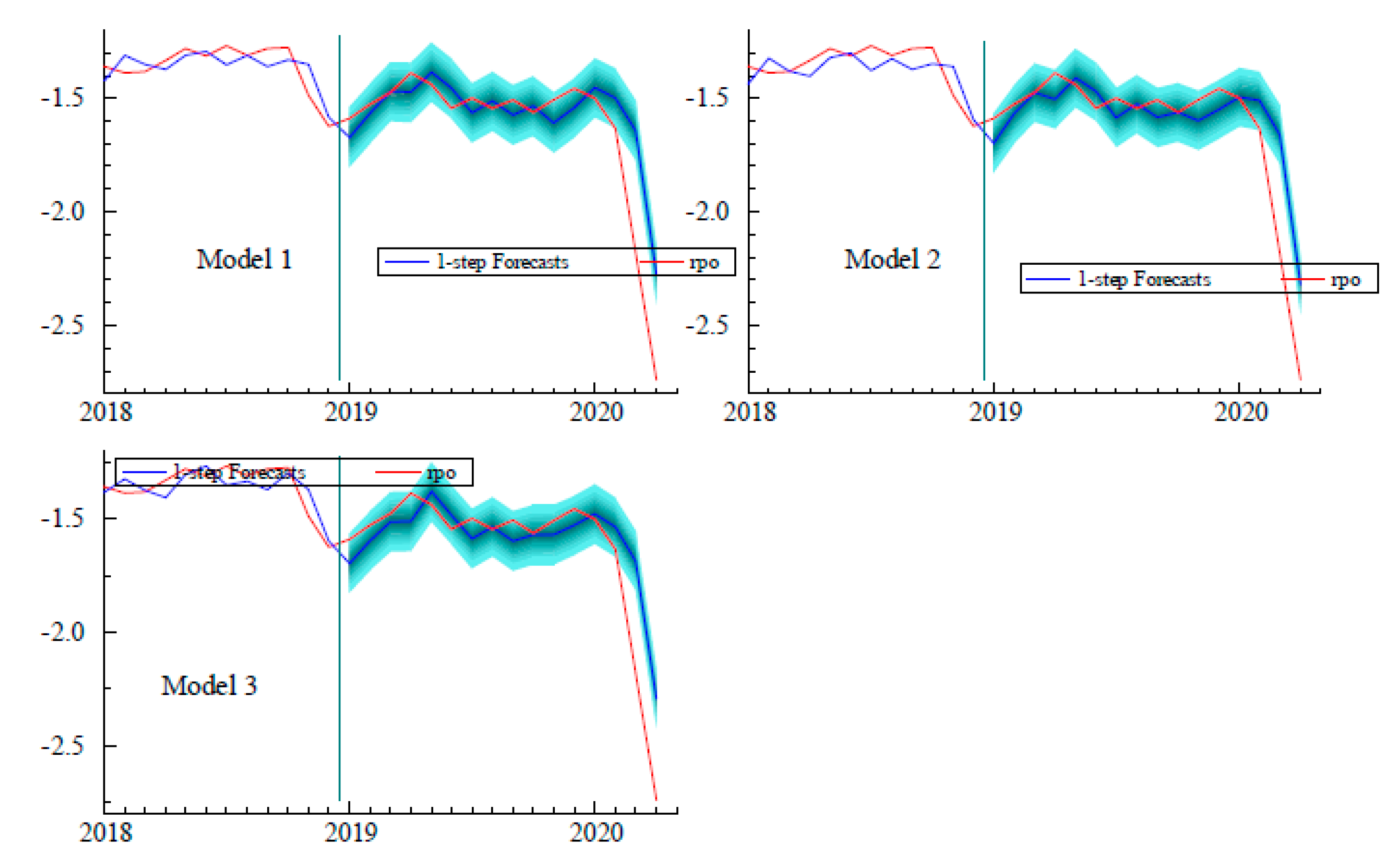
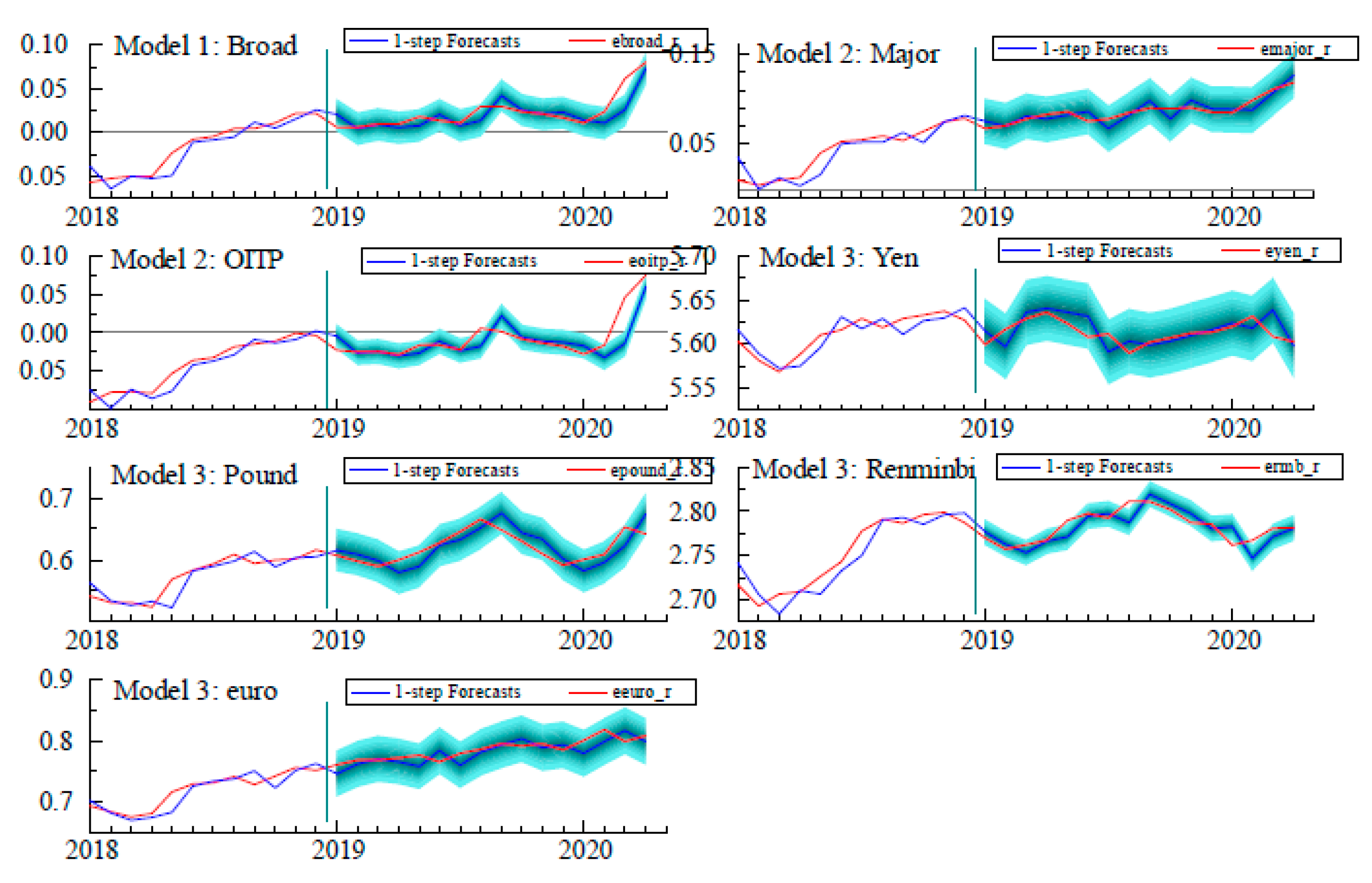
| 23. | The estimation sample ends in December 20l8, meaning that forecasts are based on those estimates without further update. The “one-step-ahead” refers to the practice of financial forecasters of starting their forecasts from the most recent data. As for the length of the horizon, one year is arbitrary but it is the horizon over which analysts focus, such as the Federal Reserve Bank of New York’s Oil-price Dynamics Report. |
| 24. | We appreciate the comments from a referee on the lack of identification associated with our model. |
| 25. | For example, one could combine futures and options contracts. The futures contract would be for a given price of oil; the option contract would have strike prices determined by a long-run relation between the price of oil and the dollar. Moreover, the Federal Reserve Bank of New York releases its weekly analysis of the price of oil and they use bilateral exchange rates. |






| (A) | |||||
| Study | Measure of Dollar | Sample Span | China Included? | ||
| Huang et al. (2020) | Bilateral Rates | 1997–2015-Monthly | yes | ||
| Reboredo et al. (2014) | Bilateral Rates | 2000–2012-Monthly | no | ||
| Fratzscher et al. (2014) | NEER | 2001–2012-Daily | no | ||
| Grisse (2010) | NEER | 2003–2010-Weekly | no | ||
| Breitenfellner and Cuaresma (2008) | 1983–2006-Monthly | no | |||
| Cheng (2008) | NEER & REER | 2000–2007-Monthly | no | ||
| Yousefi and Wirjanto (2005) | REER | 1989–1999-Monthly | no | ||
| Benassy-Quere et al. (2005) | REER & | 1974–2004-Monthly | yes | ||
| Amano and van Norden (1998) | REER | 1972–1993-Monthly | no | ||
| This study | Bilateral Rates | 1999–2020-Monthly | yes | ||
| Memo. REER: real effective exchange rate; NEER: nominal effective exchange rate | |||||
| (B) | |||||
| Study | Parameter Constancy | Residuals’ Properties | Forecasts | Stationarity | Causality |
| Huang et al. (2020) | no | no | no | yes | no |
| Reboredo et al. (2014) | no | no | no | no | yes |
| Fratzscher et al. (2014) | no | no | no | no | yes |
| Grisse (2010) | no | no | no | no | yes |
| Breitenfellner and Cuaresma (2008) | no | no | yes | no | no |
| Cheng (2008) | no | no | no | no | no |
| Yousefi and Wirjanto (2005) | no | no | no | no | no |
| Benassy-Quere et al. (2005) | no | indep. | no | yes | yes |
| Amano and van Norden (1998) | no | no | yes | yes | yes |
| This study | yes | yes | yes | yes | yes |
| H₀ | n | p-Value for χ²(n) | |
|---|---|---|---|
| Model 1 | p↛d | 6 | 0.75 |
| d↛p | 6 | 0.004 | |
| Model 2 | p↛e | 12 | 0.71 |
| e↛p | 12 | 0.002 | |
| Model 3 | p↛r | 24 | 0.03 |
| r↛p | 24 | 0.03 | |
| p: real price of oil | |||
| d: of model 1 | |||
| e: 2 × 1 vector (dm, do) of model 2 | |||
| r: 4 × 1 vector of bilateral real exchange rates of model 3 | |||
| Number of Eigenvalues | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
| Rank of | Trace | Max | Trace | Max | Trace | Max |
| 0 | 0.009 | 0.003 | 0.007 | 0.005 | 0.001 | 0.005 |
| 1 | 0.680 | 0.679 | 0.301 | 0.415 | 0.441 | 0.461 |
| 2 | 0.337 | 0.336 | 0.655 | 0.623 | ||
| 3 | 0.761 | 0.791 | ||||
| 4 | 0.628 | 0.626 | ||||
| Model | Cointegration Coefficients | Adjustment Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | β | c | αp | αd | ||||||
| 3.92 | 1.79 | −0.12 | 0 | |||||||
| se | 0.47 | 0.14 | 0.03 | 0.04 | ||||||
| Model 2 | βm | β₀ | c | αp | αm | αo | ||||
| 2.59 | 1.1 | 1.76 | −0.14 | 0 | 0 | |||||
| se | 0.44 | 0.53 | 0.12 | 0.03 | 0.01 | 0.003 | ||||
| Model 3 | βyen/$ | βeuro/$ | βpound/$ | βrmb/$ | c | αp | αyen/$ | αeuro/$ | αpound/$ | αrmb/$ |
| 0.46 | 1.93 | 0.65 | 1.05 | −5.12 | −0.1 | 0.01 | −0.02 | 0 | 0 | |
| se | 0.27 | 0.4 | 0.57 | 0.34 | 2.04 | 0.03 | 0.01 | 0.01 | 0.01 | 0.003 |
| Variable | H₀:Indep. | H₀:Homosk. | H₀:Normality | |
|---|---|---|---|---|
| Model 1 | p | 0.78 | 0.61 | 0.06 |
| d | 0.06 | 0.72 | 0 | |
| Model 2 | p | 0.39 | 0.58 | 0.09 |
| dm | 0.07 | 0.39 | 0.77 | |
| do | 0.33 | 0.09 | 0 | |
| Model 3 | p | 0.93 | 0.15 | 0 |
| ryen/$ | 0.36 | 0.17 | 0.49 | |
| reuro/$ | 0.14 | 0 | 0.83 | |
| rpound/$ | 0.21 | 0.51 | 0.2 | |
| rrmb/$ | 0.04 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marquez, J.; Merler, S. A Note on the Empirical Relation between Oil Prices and the Value of the Dollar. J. Risk Financial Manag. 2020, 13, 164. https://doi.org/10.3390/jrfm13080164
Marquez J, Merler S. A Note on the Empirical Relation between Oil Prices and the Value of the Dollar. Journal of Risk and Financial Management. 2020; 13(8):164. https://doi.org/10.3390/jrfm13080164
Chicago/Turabian StyleMarquez, Jaime, and Silvia Merler. 2020. "A Note on the Empirical Relation between Oil Prices and the Value of the Dollar" Journal of Risk and Financial Management 13, no. 8: 164. https://doi.org/10.3390/jrfm13080164
APA StyleMarquez, J., & Merler, S. (2020). A Note on the Empirical Relation between Oil Prices and the Value of the Dollar. Journal of Risk and Financial Management, 13(8), 164. https://doi.org/10.3390/jrfm13080164




