How Integrated are Regional Green Equity Markets? Evidence from a Cross-Quantilogram Approach
Abstract
:1. Introduction
2. Related Literature
3. Data and Preliminary Analyses
3.1. Data Sources
3.2. Preliminary Analyses
4. Empirical Methodology
5. Empirical Results
5.1. Cross-Quantile Dependence Among Green Equity Markets
5.1.1. Main Results
5.1.2. Robustness Analyses
5.2. Cross-Quantile Dependence between Regional Green Equity Markets and Energy Commodity Markets
5.3. Cross-Quantile Dependence between Regional Green Equity Markets and the Stock Market
6. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
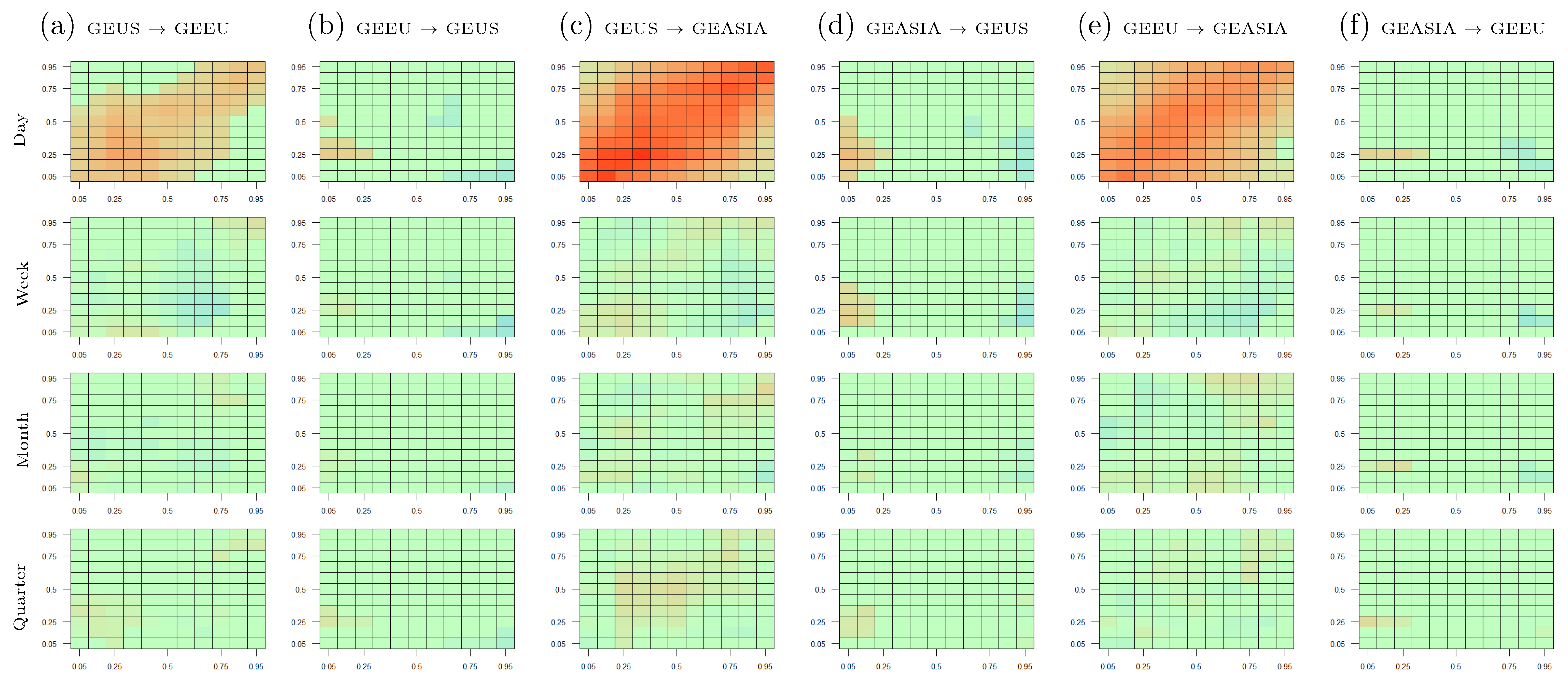
Appendix A. Numerical Cross-Quantilogram Values
| Quantiles | GEUS→GEEU | GEEU→GEUS | GEUS→GEASIA | GEASIA→GEUS | GEEU→GEASIA | GEASIA→GEEU |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | 0.10 [0.01, 0.25] | 0.06 [−0.01, 0.13] | 0.10 [0.01, 0.23] | 0.08 [−0.01, 0.20] | 0.20 [0.10, 0.31] | 0.04 [−0.02, 0.15] |
| 0.1 | 0.11 [0.04, 0.20] | 0.06 [0.00, 0.12] | 0.29 [0.22, 0.36] | 0.08 [0.03, 0.16] | 0.20 [0.12, 0.28] | 0.05 [0.00, 0.12] |
| 0.2 | 0.16 [0.10, 0.22] | 0.07 [0.00, 0.12] | 0.29 [0.23, 0.36] | 0.06 [−0.01, 0.13] | 0.21 [0.15, 0.29] | 0.09 [0.02, 0.13] |
| 0.3 | 0.14 [0.08, 0.20] | 0.02 [−0.04, 0.07] | 0.27 [0.22, 0.33] | 0.02 [−0.04, 0.07] | 0.22 [0.16, 0.28] | 0.02 [−0.04, 0.08] |
| 0.4 | 0.10 [0.04, 0.16] | −0.01 [−0.06, 0.05] | 0.25 [0.19, 0.31] | −0.03 [−0.09, 0.02] | 0.21 [0.15, 0.27] | −0.01 [−0.06, 0.04] |
| 0.5 | 0.10 [0.04, 0.16] | −0.05 [−0.11, 0.00] | 0.24 [0.18, 0.29] | −0.04 [−0.09, 0.02] | 0.20 [0.15, 0.25] | −0.02 [−0.08, 0.03] |
| 0.6 | 0.11 [0.04, 0.17] | −0.05 [−0.11, 0.01] | 0.24 [0.19, 0.29] | −0.03 [−0.08, 0.02] | 0.21 [0.15, 0.27] | −0.03 [−0.08, 0.03] |
| 0.7 | 0.10 [0.04, 0.15] | −0.06 [−0.11, −0.01] | 0.24 [0.18, 0.29] | −0.02 [−0.07, 0.04] | 0.19 [0.13, 0.25] | −0.02 [−0.07, 0.04] |
| 0.8 | 0.10 [0.03, 0.17] | −0.01 [−0.07, 0.04] | 0.27 [0.21, 0.33] | 0.00 [−0.05, 0.06] | 0.19 [0.13, 0.25] | 0.02 [−0.04, 0.07] |
| 0.9 | 0.12 [0.05, 0.18] | 0.01 [−0.04, 0.06] | 0.25 [0.17, 0.33] | 0.02 [−0.04, 0.09] | 0.17 [0.10, 0.25] | 0.01 [−0.04, 0.08] |
| 0.95 | 0.11 [0.02, 0.19] | 0.05 [0.00, 0.13] | 0.27 [0.15, 0.36] | 0.04 [−0.02, 0.10] | 0.17 [0.06, 0.29] | 0.02 [−0.03, 0.09] |
| Quantiles | GEUS→Energy | Energy→GEUS | GEEU→Energy | Energy→GEEU | GEASIA→Energy | Energy→GEASIA |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | 0.04 [−0.03, 0.11] | 0.02 [−0.04, 0.10] | 0.00 [−0.05, 0.06] | 0.01 [−0.04, 0.07] | 0.00 [−0.04, 0.06] | 0.05 [−0.02, 0.15] |
| 0.1 | 0.05 [−0.02, 0.13] | 0.06 [−0.01, 0.14] | 0.01 [−0.04, 0.06] | 0.05 [0.00, 0.12] | 0.02 [−0.03, 0.09] | 0.10 [0.04, 0.17] |
| 0.2 | 0.05 [0.00, 0.12] | 0.03 [−0.03, 0.09] | 0.05 [−0.01, 0.11] | 0.08 [0.02, 0.15] | 0.02 [−0.04, 0.07] | 0.08 [0.03, 0.15] |
| 0.3 | 0.03 [−0.03, 0.09] | 0.03 [−0.02, 0.10] | 0.04 [−0.01, 0.10] | 0.03 [−0.02, 0.09] | 0.00 [−0.05, 0.06] | 0.13 [0.06, 0.18] |
| 0.4 | 0.01 [−0.05, 0.06] | 0.02 [−0.03, 0.08] | 0.02 [−0.05, 0.06] | 0.04 [−0.01, 0.10] | −0.02 [−0.09, 0.04] | 0.10 [0.04, 0.16] |
| 0.5 | −0.01 [−0.06, 0.05] | 0.00 [−0.06, 0.05] | 0.02 [−0.04, 0.08] | 0.04 [−0.02, 0.08] | −0.02 [−0.07, 0.03] | 0.10 [0.05, 0.16] |
| 0.6 | 0.00 [−0.06, 0.05] | −0.02 [−0.07, 0.04] | 0.00 [−0.06, 0.07] | 0.01 [−0.05, 0.07] | 0.00 [−0.06, 0.05] | 0.10 [0.04, 0.16] |
| 0.7 | −0.02 [−0.07, 0.03] | −0.02 [−0.07, 0.03] | −0.03 [−0.08, 0.03] | 0.01 [−0.05, 0.07] | 0.00 [−0.07, 0.05] | 0.08 [0.03, 0.14] |
| 0.8 | 0.00 [−0.06, 0.07] | 0.00 [−0.06, 0.06] | −0.01 [−0.06, 0.04] | 0.01 [−0.04, 0.07] | 0.00 [−0.04, 0.07] | 0.11 [0.04, 0.17] |
| 0.9 | 0.00 [−0.06, 0.07] | 0.02 [−0.04, 0.08] | 0.01 [−0.04, 0.07] | 0.03 [−0.03, 0.10] | 0.04 [−0.02, 0.10] | 0.09 [0.02, 0.16] |
| 0.95 | 0.06 [0.00, 0.16] | 0.02 [−0.03, 0.11] | 0.01 [−0.04, 0.08] | 0.05 [−0.01, 0.12] | 0.05 [−0.02, 0.13] | 0.08 [0.01, 0.18] |
| Quantiles | GEUS→OIL | OIL→GEUS | GEEU→OIL | OIL→GEEU | GEASIA→OIL | OIL→GEASIA |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | 0.01 [−0.03, 0.09] | 0.03 [−0.03, 0.11] | −0.01 [−0.04, 0.05] | 0.02 [−0.03, 0.09] | 0.00 [−0.04, 0.06] | 0.07 [0.00, 0.15] |
| 0.1 | 0.06 [0.01, 0.14] | 0.05 [−0.02, 0.11] | 0.02 [−0.05, 0.07] | 0.06 [−0.01, 0.13] | 0.03 [−0.03, 0.08] | 0.09 [0.01, 0.16] |
| 0.2 | 0.03 [−0.03, 0.09] | 0.04 [−0.01, 0.10] | 0.03 [−0.04, 0.08] | 0.09 [0.02, 0.14] | 0.01 [−0.05, 0.07] | 0.10 [0.05, 0.16] |
| 0.3 | 0.01 [−0.04, 0.07] | 0.03 [−0.02, 0.09] | 0.02 [−0.04, 0.08] | 0.05 [−0.01, 0.11] | 0.00 [−0.05, 0.06] | 0.13 [0.07, 0.19] |
| 0.4 | −0.01 [−0.07, 0.05] | 0.01 [−0.04, 0.07] | 0.01 [−0.05, 0.06] | 0.04 [−0.01, 0.10] | −0.03 [−0.08, 0.03] | 0.10 [0.05, 0.16] |
| 0.5 | −0.03 [−0.09, 0.03] | 0.00 [−0.06, 0.05] | 0.01 [−0.04, 0.07] | 0.04 [−0.02, 0.09] | −0.03 [−0.08, 0.03] | 0.10 [0.06, 0.17] |
| 0.6 | 0.00 [−0.07, 0.05] | −0.02 [−0.07, 0.04] | −0.01 [−0.07, 0.04] | 0.03 [−0.03, 0.08] | 0.00 [−0.05, 0.05] | 0.11 [0.06, 0.17] |
| 0.7 | −0.04 [−0.09, 0.02] | −0.01 [−0.06, 0.04] | −0.04 [−0.09, 0.02] | 0.03 [−0.03, 0.10] | 0.00 [−0.05, 0.07] | 0.11 [0.06, 0.16] |
| 0.8 | 0.01 [−0.05, 0.07] | 0.02 [−0.04, 0.08] | 0.00 [−0.06, 0.05] | 0.04 [−0.02, 0.10] | 0.02 [−0.03, 0.07] | 0.11 [0.05, 0.17] |
| 0.9 | 0.01 [−0.04, 0.08] | 0.03 [−0.02, 0.10] | 0.01 [−0.04, 0.07] | 0.05 [−0.02, 0.11] | 0.04 [−0.01, 0.11] | 0.08 [0.02, 0.15] |
| 0.95 | 0.05 [−0.01, 0.15] | 0.01 [−0.03, 0.09] | 0.01 [−0.04, 0.08] | 0.05 [−0.02, 0.12] | 0.03 [−0.02, 0.12] | 0.07 [0.01, 0.17] |
| Quantiles | GEUS→GAS | GAS→GEUS | GEEU→GAS | GAS→GEEU | GEASIA→GAS | GAS→GEASIA |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | −0.02 [−0.05, 0.05] | 0.04 [−0.02, 0.12] | −0.02 [−0.05, 0.04] | 0.01 [−0.04, 0.08] | −0.01 [−0.05, 0.05] | 0.02 [−0.04, 0.09] |
| 0.1 | 0.04 [−0.02, 0.10] | 0.02 [−0.04, 0.08] | 0.01 [−0.04, 0.07] | 0.02 [−0.04, 0.09] | 0.02 [−0.04, 0.07] | 0.03 [−0.03, 0.09] |
| 0.2 | 0.01 [−0.05, 0.07] | 0.00 [−0.05, 0.06] | 0.02 [−0.03, 0.08] | 0.03 [−0.02, 0.08] | 0.01 [−0.04, 0.07] | 0.02 [−0.03, 0.08] |
| 0.3 | −0.01 [−0.06, 0.04] | 0.02 [−0.04, 0.07] | 0.03 [−0.02, 0.10] | 0.01 [−0.04, 0.07] | −0.01 [−0.06, 0.05] | 0.01 [−0.04, 0.06] |
| 0.4 | −0.03 [−0.08, 0.03] | 0.00 [−0.06, 0.06] | 0.03 [−0.02, 0.09] | −0.03 [−0.08, 0.04] | −0.02 [−0.07, 0.03] | −0.05 [−0.10, 0.01] |
| 0.5 | 0.01 [−0.04, 0.06] | −0.02 [−0.08, 0.03] | 0.03 [−0.03, 0.08] | −0.02 [−0.08, 0.03] | 0.00 [−0.05, 0.05] | −0.01 [−0.06, 0.04] |
| 0.6 | 0.01 [−0.05, 0.06] | −0.03 [−0.09, 0.03] | 0.03 [−0.03, 0.08] | −0.02 [−0.08, 0.04] | 0.00 [−0.05, 0.06] | −0.02 [−0.06, 0.05] |
| 0.7 | 0.01 [−0.05, 0.06] | −0.04 [−0.09, 0.02] | 0.02 [−0.04, 0.08] | −0.02 [−0.08, 0.03] | 0.02 [−0.02, 0.08] | −0.01 [−0.06, 0.05] |
| 0.8 | 0.01 [−0.04, 0.06] | −0.02 [−0.07, 0.04] | 0.00 [−0.06, 0.06] | 0.00 [−0.05, 0.05] | 0.00 [−0.05, 0.07] | 0.01 [−0.04, 0.06] |
| 0.9 | −0.02 [−0.07, 0.03] | 0.00 [−0.05, 0.06] | 0.01 [−0.04, 0.07] | 0.00 [−0.05, 0.06] | 0.04 [−0.02, 0.11] | 0.01 [−0.05, 0.07] |
| 0.95 | 0.00 [−0.05, 0.05] | 0.01 [−0.04, 0.08] | 0.01 [−0.05, 0.07] | 0.02 [−0.03, 0.08] | 0.02 [−0.03, 0.09] | 0.01 [−0.04, 0.07] |
| Quantiles | GEUS→BMI | BMI→GEUS | GEEU→BMI | BMI→GEEU | GEASIA→BMI | BMI→GEASIA |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | 0.10 [0.03, 0.21] | 0.09 [0.01, 0.18] | 0.05 [−0.01, 0.13] | 0.08 [−0.01, 0.21] | 0.06 [−0.01, 0.17] | 0.24 [0.13, 0.37] |
| 0.1 | 0.14 [0.07, 0.20] | 0.09 [0.02, 0.16] | 0.09 [0.01, 0.14] | 0.09 [0.02, 0.16] | 0.07 [0.01, 0.14] | 0.25 [0.17, 0.33] |
| 0.2 | 0.14 [0.08, 0.21] | 0.09 [0.01, 0.14] | 0.11 [0.05, 0.18] | 0.15 [0.08, 0.21] | 0.09 [0.03, 0.16] | 0.26 [0.20, 0.34] |
| 0.3 | 0.14 [0.08, 0.19] | 0.04 [−0.02, 0.10] | 0.10 [0.04, 0.15] | 0.10 [0.04, 0.15] | 0.06 [−0.01, 0.12] | 0.29 [0.21, 0.34] |
| 0.4 | 0.12 [0.07, 0.17] | 0.00 [−0.05, 0.06] | 0.08 [0.02, 0.14] | 0.06 [0.00, 0.12] | 0.00 [−0.05, 0.06] | 0.26 [0.21, 0.32] |
| 0.5 | 0.10 [0.05, 0.17] | −0.04 [−0.10, 0.01] | 0.04 [−0.02, 0.11] | 0.05 [−0.02, 0.11] | 0.00 [−0.06, 0.05] | 0.24 [0.19, 0.30] |
| 0.6 | 0.13 [0.06, 0.17] | −0.05 [−0.10, 0.01] | 0.03 [−0.02, 0.09] | 0.05 [0.00, 0.11] | 0.00 [−0.05, 0.06] | 0.24 [0.18, 0.30] |
| 0.7 | 0.11 [0.07, 0.17] | −0.02 [−0.08, 0.02] | 0.04 [−0.01, 0.09] | 0.07 [0.02, 0.13] | 0.01 [−0.04, 0.07] | 0.24 [0.18, 0.30] |
| 0.8 | 0.13 [0.06, 0.19] | −0.01 [−0.06, 0.04] | 0.07 [0.01, 0.13] | 0.07 [0.01, 0.11] | 0.02 [−0.03, 0.08] | 0.24 [0.18, 0.30] |
| 0.9 | 0.09 [0.03, 0.16] | 0.01 [−0.03, 0.08] | 0.08 [0.01, 0.15] | 0.07 [0.00, 0.13] | 0.02 [−0.04, 0.08] | 0.24 [0.15, 0.33] |
| 0.95 | 0.10 [0.02, 0.20] | 0.03 [−0.02, 0.11] | 0.08 [0.01, 0.16] | 0.04 [−0.01, 0.10] | 0.04 [−0.02, 0.11] | 0.20 [0.10, 0.33] |
| Quantiles | GEUS→PSE | PSE→GEUS | GEEU→PSE | PSE→GEEU | GEASIA→PSE | PSE→GEASIA |
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |
| 0.05 | 0.06 [0.00, 0.15] | 0.09 [0.01, 0.20] | 0.02 [−0.03, 0.09] | 0.08 [0.00, 0.18] | 0.08 [0.00, 0.17] | 0.27 [0.17, 0.38] |
| 0.1 | 0.09 [0.02, 0.15] | 0.07 [0.01, 0.15] | 0.07 [0.01, 0.13] | 0.08 [0.01, 0.17] | 0.07 [0.00, 0.14] | 0.27 [0.21, 0.36] |
| 0.2 | 0.09 [0.01, 0.15] | 0.09 [0.02, 0.14] | 0.08 [0.02, 0.13] | 0.16 [0.10, 0.22] | 0.07 [0.02, 0.14] | 0.28 [0.21, 0.35] |
| 0.3 | 0.03 [−0.02, 0.09] | 0.04 [−0.01, 0.10] | 0.03 [−0.03, 0.08] | 0.16 [0.09, 0.21] | 0.03 [−0.03, 0.09] | 0.30 [0.23, 0.35] |
| 0.4 | −0.01 [−0.08, 0.05] | −0.01 [−0.06, 0.05] | 0.01 [−0.04, 0.06] | 0.12 [0.06, 0.18] | −0.01 [−0.06, 0.05] | 0.25 [0.19, 0.30] |
| 0.5 | −0.04 [−0.09, 0.02] | −0.02 [−0.07, 0.04] | −0.02 [−0.08, 0.04] | 0.10 [0.03, 0.15] | −0.02 [−0.08, 0.03] | 0.23 [0.17, 0.28] |
| 0.6 | −0.04 [−0.10, 0.01] | −0.03 [−0.08, 0.03] | −0.04 [−0.09, 0.02] | 0.08 [0.03, 0.14] | −0.02 [−0.07, 0.04] | 0.22 [0.17, 0.28] |
| 0.7 | 0.00 [−0.06, 0.05] | −0.03 [−0.08, 0.03] | −0.02 [−0.08, 0.03] | 0.10 [0.05, 0.17] | −0.01 [−0.07, 0.05] | 0.25 [0.19, 0.30] |
| 0.8 | 0.01 [−0.04, 0.08] | 0.01 [−0.05, 0.06] | 0.00 [−0.06, 0.05] | 0.11 [0.04, 0.17] | −0.02 [−0.06, 0.05] | 0.24 [0.18, 0.31] |
| 0.9 | 0.02 [−0.03, 0.09] | 0.03 [−0.03, 0.10] | 0.02 [−0.04, 0.07] | 0.08 [0.02, 0.16] | 0.02 [−0.04, 0.08] | 0.23 [0.15, 0.31] |
| 0.95 | 0.08 [0.00, 0.18] | 0.07 [−0.01, 0.16] | 0.05 [−0.01, 0.12] | 0.09 [0.01, 0.17] | 0.02 [−0.03, 0.09] | 0.22 [0.12, 0.33] |
Appendix B. Cross-Quantile Dependence between Regional Green Equity and Other Assets at Alternative Lags




Appendix C. Granger Causality Tests in Quantiles
Appendix D. Robustness Analyses: Cross-Quantile Dependence Among Green Equity Markets
- 1.
- Quantile Granger causality tests: Figure A6. The x-axis indicates the quantiles and the y-axis indicates the test statistics for a specific pair of assets. For example, the top-left graph in Figure A6 is named “GEUS-GEEU”, which captures the quantile Granger causality test of whether the GEUS returns Granger cause the GEEU returns. The red and blue lines in each graph correspond to the critical values at the 95% and 99% confidence levels.
- 2.
- Cross-quantilograms with GARCH-standardized residuals: Figure A7
- 3.
- Cross-quantilograms after controlling for market uncertainties (proxied by the OVX, VIX and EPU indexes): Figure A8, Figure A9 and Figure A10
- 4.
- Cross-quantilograms among regional clean energy markets: Figure A11
- 5.
- Cross-quantilograms before, during and after the 2014–2016 oil price collapse: Figure A12, Figure A13 and Figure A14
- 6.
- Recursive cross-quantilograms: Figure A15










Appendix E. Robustness Analyses: Cross-Quantile Dependence between Regional Green Equity Markets and Energy Commodity Markets
- 1.
- Quantile Granger causality tests: Figure A16.
- 2.
- Cross-quantilograms with GARCH-standardized residuals: Figure A17
- 3.
- Cross-quantilograms after controlling for market uncertainties (proxied by the OVX, VIX and EPU indexes): Figure A18, Figure A19 and Figure A20
- 4.
- Cross-quantilograms among regional clean energy markets: Figure A21
- 5.
- Cross-quantilograms before, during and after the 2014-2016 oil price collapse: Figure A22, Figure A23 and Figure A24
- 6.












Appendix F. Robustness Analyses: Cross-Quantile Dependence between Regional Green Equity Markets and the Stock Market
- 1.
- Quantile Granger causality tests: Figure A28.
- 2.
- Cross-quantilograms with GARCH-standardized residuals: Figure A29
- 3.
- Cross-quantilograms after controlling for market uncertainties (proxied by the OVX, VIX and EPU indexes): Figure A30, Figure A31 and Figure A32
- 4.
- Cross-quantilograms among regional clean stock markets: Figure A33
- 5.
- Cross-quantilograms before, during and after the 2014–2016 oil price collapse: Figure A34, Figure A35 and Figure A36
- 6.
- Recursive cross-quantilograms: Figure A37 and Figure A38











References
- Ahmad, Wasim. 2017. On the dynamic dependence and investment performance of crude oil and clean energy stocks. Research in International Business and Finance 42: 376–89. [Google Scholar] [CrossRef]
- Ahmad, Wasim, Perry Sadorsky, and A. Sharma. 2018. Optimal hedge ratios for clean energy equities. Economic Modelling 72: 278–95. [Google Scholar] [CrossRef]
- Arouri, Mohamed, Sabri Boubaker, and Duc Khuong Nguyen. 2013. Emerging Markets and the Global Economy: A Handbook. Cambridge: Academic Press. [Google Scholar]
- Bloomberg New Energy Finance. 2019. Global Trends in Clean Energy Investment. Available online: https://about.bnef.com/clean-energy-investment/ (accessed on 1 December 2020).
- Bohl, Martin T., Philipp Kaufmann, and Pierre L. Siklos. 2015. What drove the mid-2000s explosiveness in alternative energy stock prices? Evidence from US, European and global indices. International Review of Financial Analysis 40: 194–206. [Google Scholar] [CrossRef]
- Bondia, Ripsy, Sajal Ghosh, and Kakali Kanjilal. 2016. International crude oil prices and the stock prices of clean energy and technology companies: Evidence from non-linear cointegration tests with unknown structural breaks. Energy 101: 558–65. [Google Scholar] [CrossRef]
- Boubaker, Sabri, and Jamel Jouini. 2014. Linkages between emerging and developed equity markets: Empirical evidence in the PMG framework. The North American Journal of Economics and Finance 29: 322–35. [Google Scholar] [CrossRef]
- Bouri, Elie, Jalkh Naji, Apunam Dutta, and Gazi Salah Uddin. 2019. Gold and crude oil as safe-haven assets for clean energy stock indices: Blended copulas approach. Energy 178: 544–53. [Google Scholar]
- Climate Finance Leadership Initiative. 2019. Financing the Low-Carbon Future: A Private Sector View on Mobilizing Climate Finance. Available online: https://data.bloomberglp.com/company/sites/55/2019/09/Financing-the-Low-Carbon-Future_CFLI-Full-Report_September-2019.pdf (accessed on 1 December 2020).
- Dawar, Ishaan, Anupam Dutta, Elie Bouri, and Tareq Saeed. 2020. Crude oil prices and clean energy stock indices: Lagged and asymmetric effects with quantile regression. Renewable Energy 163: 288–99. [Google Scholar] [CrossRef]
- Dutta, Apunam, Elie Bouri, Debojyoti Das, and David Roubaud. 2020. Assessment and optimization of clean energy equity risks and commodity price volatility indexes: Implications for sustainability. Journal of Cleaner Production 243: 118669. [Google Scholar] [CrossRef]
- Ferrer, Roman, Syed Jawad Hussain Shahzad, Raquel López, and Francisco Jareño. 2018. Time and frequency dynamics of connectedness between renewable energy stocks and crude oil prices. Energy Economics 76: 1–20. [Google Scholar] [CrossRef]
- Han, Heejoon, Oliver Linton, Tatsushi Oka, and Yoon-Jae Whang. 2016. The cross-quantilogram: Measuring quantile dependence and testing directional predictability between time series. Journal of Econometrics 193: 251–70. [Google Scholar] [CrossRef] [Green Version]
- Henriques, Irene, and Perry Sadorsky. 2008. Oil prices and the stock prices of alternative energy companies. Energy Economics 30: 998–1010. [Google Scholar] [CrossRef]
- Jeong, Kiho, Wolfgang K. Härdle, and Song Song. 2012. A consistent nonparametric test for causality in quantile. Econometric Theory 28: 861–87. [Google Scholar] [CrossRef] [Green Version]
- Kocaarslan, Baris, and Ugur Soytas. 2019. Dynamic correlations between oil prices and the stock prices of clean energy and technology firms: The role of reserve currency (US dollar). Energy Economics 84: 104502. [Google Scholar] [CrossRef]
- Kumar, Surender, Shunsuke Managi, and Akimi Matsuda. 2012. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Economics 34: 215–26. [Google Scholar] [CrossRef]
- Kyritsis, Evangelos, and Apostolos Serletis. 2019. Oil prices and the renewable energy sector. The Energy Journal 40. [Google Scholar] [CrossRef]
- Lau, Marco Chi Keung, Samuel A. Vigne, Shixuan Wang, and Larisa Yarovaya. 2017. Return spillovers between white precious metal ETFs: The role of oil, gold, and global equity. International Review of Financial Analysis 52: 316–32. [Google Scholar] [CrossRef] [Green Version]
- Managi, Shunsuke, and Tatsuyoshi Okimoto. 2013. Does the price of oil interact with clean energy prices in the stock market? Japan and the World Economy 27: 1–9. [Google Scholar] [CrossRef] [Green Version]
- Nasreen, Samia, Aviral Kumar Tiwari, Juncal Cuñado Eizaguirre, and Mark E. Wohar. 2020. Dynamic connectedness between oil prices and stock returns of clean energy and technology companies. Journal of Cleaner Production 260: 121015. [Google Scholar] [CrossRef]
- Pham, Linh. 2019. Do all clean energy stocks respond homogeneously to oil price? Energy Economics 81: 355–79. [Google Scholar] [CrossRef]
- Reboredo, Juan Carlos. 2015. Is there dependence and systemic risk between oil and renewable energy stock prices? Energy Economics 48: 32–45. [Google Scholar] [CrossRef]
- Reboredo, Juan Carlos, Miguel A. Rivera-Castro, and Andrea Ugolini. 2017. Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Economics 61: 241–52. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2012. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Economics 34: 248–55. [Google Scholar] [CrossRef]
- Slimane, Faten Ben, Sabri Boubaker, and Jamel Jouini. 2020. Does the Euro–Mediterranean partnership contribute to regional integration? Journal of Policy Modeling 42: 328–48. [Google Scholar] [CrossRef]
- Song, Yingjie, Qiang Ji, Ya-Juan Du, and Jiang-Bo Geng. 2019. The dynamic dependence of fossil energy, investor sentiment and renewable energy stock markets. Energy Economics 84: 104564. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Juncal Cunado, Rangan Gupta, and Mark E. Wohar. 2018. Volatility spillovers across global asset classes: Evidence from time and frequency domains. The Quarterly Review of Economics and Finance 70: 194–202. [Google Scholar] [CrossRef]
- Uddin, Gazi Salah, Md Lutfur Rahman, Axel Hedström, and Ali Ahmed. 2019. Cross-quantilogram-based correlation and dependence between renewable energy stock and other asset classes. Energy Economics 80: 743–59. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. 2013. 2012 Brief: Average Wholesale Natural Gas Prices Fell 31% in 2012. Available online: https://www.eia.gov/todayinenergy/detail.php?id=9490 (accessed on 1 December 2020).
- U.S. Energy Information Administration. 2017. Natural Gas Prices in 2016 were the Lowest in Nearly 20 Years. Available online: https://www.eia.gov/todayinenergy/detail.php?id=29552 (accessed on 1 December 2020).
- Xia, Tongshui, Qiang Ji, Dayong Zhang, and Jinhong Han. 2019. Asymmetric and extreme influence of energy price changes on renewable energy stock performance. Journal of Cleaner Production 241: 118338. [Google Scholar] [CrossRef]
- Yahya, Muhammad, Sajal Ghosh, Kakali Kanjilal, Anupam Dutta, and Gazi Salah Uddin. 2020. Evaluation of cross-quantile dependence and causality between non-ferrous metals and clean energy indexes. Energy 202: 117777. [Google Scholar] [CrossRef]
| 1. | |
| 2. | This literature belongs to the broader literature on financial market integration (see, for example, Arouri et al. (2013); Boubaker and Jouini (2014); Slimane et al. (2020)). |
| 3. | These quantiles capture various conditions in each market. Specifically, the lower quantiles capture an extreme downward movement, while the upper quantiles indicate an extreme upward movement. |
| 4. | These lags capture the dependence between the markets across the short-run, medium-run and long-run investment horizons. The choice of these lag lengths is consistent with the previous literature (e.g., Ferrer et al. (2018); Uddin et al. (2019)). |
| 5. | The secondary diagonal refers to the diagonal that runs from the top-right corner to the bottom-left corner of the heat maps. |
| 6. | As seen in Figure 3, the cross-quantilograms are most likely to be significant for lag 1 when the markets’ returns are in the same quantiles. The cross-quantilogram values for other combinations of quantiles and lags are available upon request. |
| 7. | |
| 8. | A number of GARCH(1,1) models with various conditional distribution assumptions are employed to select the best GARCH model for each variable. The best-fit GARCH(1,1) model for each variable is selected based on the Bayesian information criteria. Then, the standardized returns are obtained from the standardized residuals of each GARCH model. Details on the results of these GARCH(1,1) processes are available upon request. |
| 9. | The author only presents the cross-quantilograms of the robustness analyses for lag 1 to conserve space. Moreover, as indicated in Section 5.1, the cross-quantilograms are the most significant at lag 1. The cross-quantilograms for other lag lengths are similar to the main results in Figure 3 and are available upon request. |
| 10. | An alternative proxy for the oil market is the WTI crude oil prices, the Brent crude oil prices, and the NYMEX continuos contract crude oil future prices. An alternative proxy for the natural gas market includes the Henry Hub natural gas prices or the NYMEX continuous contract natural gas future prices. The author finds that the correlations between these alternative measures of the oil and natural gas markets are more than 0.90. Thus, this paper relies on the S&P GSCI Crude Oil and Natural Gas indexes, because the global scope of these indexes provides a common benchmark to study the heterogeneous dependence structure between green equity and energy commodity across regions. |
| 11. | Table A2 presents the numerical values of the cross-quantilograms between regional green equity and energy commodity markets for selected pairs of quantiles. |
| 12. | According to Bloomberg New Energy Finance (2019), the U.S. and Europe are the dominant destinations of green investments before 2014, while green investments in Asia only became more popular after 2014. |
| 13. | |
| 14. | As indicated in the main results (Section 5), the interdependence between the markets are the most significant at lag 1 and dissipates at longer lags. |
| 15. | As indicated in the main results (Section 5), the interdependence between the markets are the most significant at lag 1 and dissipates at longer lags. |
| 16. | As indicated in the main results (Section 5), the interdependence between the markets are the most significant at lag 1 and dissipates at longer lags. |




| Mean | Median | Max | Min | Std.Dev. | Skewness | Kurtosis | Jarque-Bera | ADF | Q(30) | Obs. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Green equity: | ||||||||||||
| GEUS | 0.035 | 0.088 | 6.553 | −7.396 | 1.047 | −0.369 * | 7.605 * | 1975.0 * | −14.477 * | 60.0 * | 2025.0 * | 2179 |
| GEEU | 0.013 | 0.059 | 5.647 | −8.884 | 1.175 | −0.470 * | 7.783 * | 2157.4 * | −15.107 * | 68.3 * | 1513.9 * | 2179 |
| GEASIA | −0.001 | 0.036 | 4.728 | −10.058 | 0.988 | −0.811 * | 10.331 * | 5117.6 * | −12.672 * | 41.84 | 78.5 * | 2179 |
| Energy commodity: | ||||||||||||
| Energy | −0.017 | 0.060 | 8.850 | −9.347 | 1.717 | −0.122 * | 5.966 * | 804.1 * | −13.557 * | 42.96 | 814.1 * | 2179 |
| OIL | −0.019 | 0.067 | 10.150 | −10.796 | 2.034 | −0.0745 | 5.775 * | 701.1 * | −13.545 * | 50.6 * | 955.1 * | 2179 |
| GAS | −0.026 | −0.025 | 16.643 | −19.183 | 2.574 | −0.07454 | 6.447 * | 1080.7 * | −14.501 * | 61.3 * | 798.6 * | 2179 |
| Stock market: | ||||||||||||
| PSE | 0.054 | 0.091 | 7.415 | −6.686 | 1.087 | −0.389 * | 7.353 * | 1775.6 * | −14.723 * | 46.2 * | 978.1 * | 2179 |
| BMI | 0.023 | 0.058 | 4.041 | −5.433 | 0.795 | −0.644 * | 7.823 * | 2262.4 * | −14.781 * | 117.3 * | 1536.9 * | 2179 |
| Uncertainty variables: | ||||||||||||
| VIX | −0.013 | −0.490 | 76.825 | −31.414 | 7.744 | 1.140 * | 10.331 * | 5351.5 * | −16.736 * | 53.8 * | 131.5 * | 2179 |
| OVX | 0.005 | −0.356 | 42.497 | −43.991 | 4.914 | 0.951 * | 13.236 * | 9840.8 * | −14.829 * | 50.5 * | 222.1 * | 2179 |
| EPU | −0.014 | −1.292 | 321.562 | −314.833 | 50.983 | 0.08598 | 5.580 * | 606.9 * | −20.740 * | 424.8 * | 254.1 * | 2179 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, L. How Integrated are Regional Green Equity Markets? Evidence from a Cross-Quantilogram Approach. J. Risk Financial Manag. 2021, 14, 39. https://doi.org/10.3390/jrfm14010039
Pham L. How Integrated are Regional Green Equity Markets? Evidence from a Cross-Quantilogram Approach. Journal of Risk and Financial Management. 2021; 14(1):39. https://doi.org/10.3390/jrfm14010039
Chicago/Turabian StylePham, Linh. 2021. "How Integrated are Regional Green Equity Markets? Evidence from a Cross-Quantilogram Approach" Journal of Risk and Financial Management 14, no. 1: 39. https://doi.org/10.3390/jrfm14010039
APA StylePham, L. (2021). How Integrated are Regional Green Equity Markets? Evidence from a Cross-Quantilogram Approach. Journal of Risk and Financial Management, 14(1), 39. https://doi.org/10.3390/jrfm14010039




