Simultaneous Analysis of Insurance Participation and Acreage Response from Subsidized Crop Insurance for Cotton
Abstract
:1. Introduction
2. Evolution of US Crop Insurance
3. Data and Methods
4. Results
4.1. Parameter Estimates and Marginal Effects
4.1.1. Insurance Participation Response
4.1.2. Percent of Cropland Planted with Cotton (PCOTACRES) Response
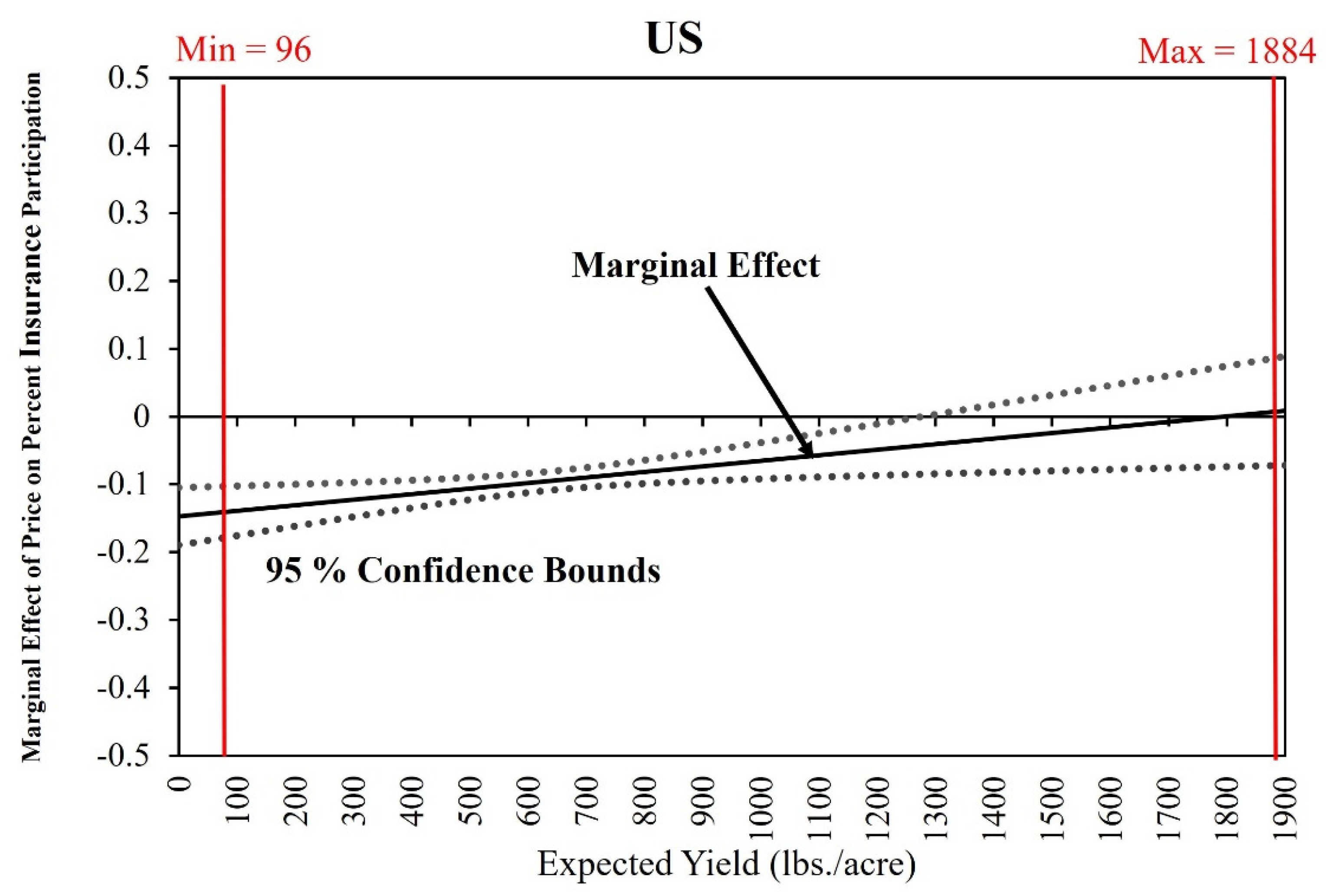
4.2. Marginal Effect of Expected Price on PINSUR Given Yield
4.3. Marginal Effects of Expected Price on PCOTACRES Given Yield
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | This study does not include the relatively very small acreage and production of extra long staple or pima cotton, and upland cotton is subsequently referred to as cotton. |
| 2 | Monthly prices from the National Cotton Council of America (http://www.cotton.org/econ/prices/monthly.cfm) (Accessed on 5 July 2018). |
| 3 | Southeast region includes Alabama, Florida, Georgia, North Carolina, South Carolina, and Virginia; Delta region includes Arkansas, Louisiana, Mississippi, Missouri, and Tennessee; southwest region includes Kansas, Oklahoma, and Texas; west region includes Arizona, California, and New Mexico. |
References
- Ali, Williams, Awudu Abdulai, and Ashok K. Mishra. 2020. Recent advances in the analyses of demand for agricultural insurance in developing and emerging countries. Annual Review of Resource Economics 12: 411–30. [Google Scholar] [CrossRef]
- Azzam, Azzeddine, Cory Walters, and Taylor Kaus. 2021. Does subsidized crop insurance affect farm industry structure? Lessons from the US. Journal of Policy Modeling. [Google Scholar] [CrossRef]
- Babcock, Bruce. 2011. Time to Revisit Crop Insurance Premium Subsidies? CARD Policy Briefs. p. 2. Available online: https://lib.dr.iastate.edu/card_policybriefs/2 (accessed on 7 March 2020).
- Baltagi, Badi H., and Young-Jae Chang. 2000. Simultaneous Equations with Incomplete Panels. Econometric Theory 16: 269–79. [Google Scholar] [CrossRef]
- Baltagi, Badi Hani. 2005. Econometric Analysis of Panel Data, 3rd ed. Hoboken: Wiley. [Google Scholar]
- Barnett, Barry, Keith Coble, Thomas Knight, Leslie Meyer, Robert Dismukes, and Jerry Skees. 2002. Impact of the Cotton Crop Insurance Program on Cotton Planted Acreage; Technical Report, Report Prepared for the Board of Directors, Federal Crop Insurance Corporation, Risk Management Agency. Washington, DC: U.S. Department of Agriculture. Available online: https://legacy.rma.usda.gov/fcic/2002/717CottonReport_RMAFCIC.pdf (accessed on 7 March 2020).
- Bekkerman, Anton, Eric J. Belasco, and Vincent H. Smith. 2019. Does Farm Size Matter? Distribution of Crop Insurance Subsidies and Government Program Payments across U.S. Farms. Applied Economic Perspectives and Policy 41: 498–518. [Google Scholar] [CrossRef]
- Coble, Keith H., Thomas O. Knight, Rulon D. Pope, and Jeffery R. Williams. 1996. Modeling Farm-Level Crop Insurance Demand with Panel Data. American Journal of Agricultural Economics 78: 439–47. [Google Scholar] [CrossRef]
- Cole, Shawn A., and Wentao Xiong. 2017. Agricultural insurance and economic development. Annual Review of Economics 9: 235–62. [Google Scholar] [CrossRef]
- Cornwell, Christopher, Peter Schmidt, and Donald Wyhowski. 1992. Simultaneous Equations and Panel Data. Journal of Econometrics 51: 151–81. [Google Scholar] [CrossRef]
- Dahal, Bhishma R., Sudip Adhikari, and Aditya R. Khanal. 2021. Willingness to pay for crop insurance: A case from citrus farmers in Nepal. Journal of Agribusiness in Developing and Emerging Economies. [Google Scholar] [CrossRef]
- Deal, John L. 2004. The Empirical Relationship Between Federally-Subsidized Crop Insurance and Soil Erosion. Ph.D. dissertation, North Carolina State University, Raleigh, NC, USA. [Google Scholar]
- Deryugina, Tatyana, and Megan Konar. 2017. Impacts of Crop Insurance on Water Withdrawals for Irrigation. Advances in Water Resources 110: 437–44. [Google Scholar] [CrossRef]
- Duffy, Patricia A., James W. Richardson, and Michael K. Wohlgenant. 1987. Regional Cotton Acreage Response. Southern Journal of Agricultural Economics 19: 99–110. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Cornejo, Jorge, and William D. McBride. 2002. Adoption of Bioengineered Crops. In Agricultural Economic Report. Number 810. Washington, DC: Economic Research Service/USDA. [Google Scholar] [CrossRef]
- Frisvold, George B., Russell Tronstad, and Jorgen Mortensen. 2000. Adoption of Bt Cotton: Regional Differences in Producer Costs and Returns. Proceedings of the Beltwide Cotton Conference 1: 337–40. [Google Scholar]
- Glauber, Joseph. W. 2007. Double Indemnity: Crop Insurance and the Failure of U.S. Agricultural Disaster Policy. Paper Prepared for American Enterprise Institute Project, Agricultural Policy for the 2007 Farm Bill and Beyond; Available online: https://www.aei.org/wp-content/uploads/2017/07/The-2007-Farm-Bill-and-Beyond.pdf?x91208 (accessed on 21 August 2021).
- Glauber, Joseph W. 2004. Crop Insurance Reconsidered. American Journal of Agricultural Economics 86: 1179–95. [Google Scholar] [CrossRef]
- Glauber, Joseph W., Keith J. Collins, and Peter J. Barry. 2002. Crop Insurance, Disaster Assistance, and the Role of the Federal Government in Providing Catastrophic Risk Protection. Agricultural Finance Review 62: 81–101. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, Barry K. 1993. An Empirical Analysis of the Demand for Multiple Peril Crop Insurance. American Journal of Agricultural Economics 75: 425–34. [Google Scholar] [CrossRef]
- Goodwin, Barry K., and Vincent H. Smith. 2013. What Harm Is Done By Subsidizing Crop Insurance? American Journal of Agricultural Economics 95: 489–97. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, Barry K., Monte L. Vandeveer, and John L. Deal. 2004. An Empirical Analysis of Acreage Effects of Participation in the Federal Crop Insurance Program. American Journal of Agricultural Economics 86: 1058–77. [Google Scholar] [CrossRef]
- Hazell, Peter B. 1992. The appropriate role of agricultural insurance in developing countries. Journal of International Development 4: 567–81. [Google Scholar] [CrossRef]
- Hazell, Peter, and Panos Varangis. 2020. Best practices for subsidizing agricultural insurance. Global Food Security 25: 100326. [Google Scholar] [CrossRef]
- Horowitz, John K., and Erik Lichtenberg. 1993. Insurance, Moral Hazard, and Chemical Use in Agriculture. American Journal of Agricultural Economics 75: 926–35. [Google Scholar] [CrossRef]
- Hsiao, Cheng. 2003. Analysis of Panel Data, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Keeton, Kara, and Jerry R. Skees. 1999. The Potential Influence of Risk Management Programs on Cropping Decisions at the Extensive Margin. Master’s thesis, University of Kentucky, Lexington, KY, USA. [Google Scholar]
- Knisley, Shelbi R. 2016. Changes in Southern Cotton and Peanut Producing Regions. No. 333-2016-14818. Available online: https://ageconsearch.umn.edu/record/235431/ (accessed on 21 August 2021).
- Miglietta, Pier Paolo, Donatella Porrini, Giulio Fusco, and Fabian Capitanio. 2021. Crowding out agricultural insurance and the subsidy system in Italy: Empirical evidence of the charity hazard phenomenon. Agricultural Finance Review 81: 237–49. [Google Scholar] [CrossRef]
- Mishra, Ashok K., R. Wesley Nimon, and Hisham S. El-Osta. 2005. Is Moral Hazard Good for the Environment? Revenue Insurance and Chemical Input Use. Journal of Environmental Management 74: 11–20. [Google Scholar] [CrossRef]
- O’Donoghue, Erik. 2014. The Effects of Premium Subsidies on Demand for Crop Insurance. USDA-ERS Economic Research Report, 169. [Google Scholar] [CrossRef]
- Serra, Teresa, Barry K. Goodwin, and Allen M. Featherstone. 2003. Modeling Changes in the U.S. Demand for Crop Insurance during the 1990s. Agricultural Finance Review 63: 109–25. [Google Scholar] [CrossRef] [Green Version]
- Shaik, Saleem, Keith H. Coble, Thomas O. Knight, Alan E. Baquet, and George F. Patrick. 2008. Crop Revenue and Yield Insurance Demand: A Subjective Probability Approach. Journal of Agricultural and Applied Economics 40: 757–66. [Google Scholar] [CrossRef] [Green Version]
- Smith, Vincent H. 2020. The US federal crop insurance program: A case study in rent seeking. Agricultural Finance Review 80: 339–58. [Google Scholar] [CrossRef]
- Smith, Vincent H., and Barry K. Goodwin. 1996. Crop Insurance, Moral Hazard, and Agricultural Chemical Use. American Journal of Agricultural Economics 78: 428–38. [Google Scholar] [CrossRef]
- USDA. 2017a. National Agricultural Statistics Service (NASS), 1985 to 2016. Quick Stats 1.0, State and County Data. Online. Available online: http://www.nass.usda.gov/ (accessed on 15 December 2017).
- USDA. 2017b. Risk Management Agency (RMA), 1995 to 2016. Summary of Business Online and Online Premium Calculator. Online. Available online: http://www.rma.usda.gov/ (accessed on 9 May 2017).
- USDA. 2018. Agricultural Marketing Service (AMS), (Various Issues). Cotton Market News. Online. Available online: http://www.marketnews.usda.gov/portal/cn (accessed on 5 January 2018).
- Vandeveer, Monte L., and C. Edwin Young. 2001. The Effects of the Federal Crop Insurance Program on Wheat Acreage; Economic Research Service. Washington, DC: U.S. Department of Agriculture, pp. 21–30.
- Williams, Michael R. 1995–2016. Cotton Insect Loss Estimates, Proceedings of the Beltwide Cotton Conferences. Online. Available online: http://www.entomology.msstate.edu/resources/tips/cotton-losses/data/ (accessed on 26 December 2018).
- Woodard, Joshua D. 2015. Estimating Demand for Government Subsidized Insurance: Evidence from the U.S. Agricultural Insurance Market. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2826036 (accessed on 21 August 2021).
- Woodard, Joshua D. 2016. Crop Insurance Demand More Elastic than Previously Thought. Choices, 31. Available online: https://www.jstor.org/stable/choices.31.3.15 (accessed on 21 August 2021).
- Wu, Junjie, and Richard M. Adams. 2001. Production Risk, Acreage Decisions and Implications for Revenue Insurance Programs. Canadian Journal of Agricultural Economics/Revue Canadienne d’agroeconomie 49: 19–35. [Google Scholar] [CrossRef]
- Wu, Junjie. 1999. Crop Insurance, Acreage Decisions, and Nonpoint-Source Pollution. American Journal of Agricultural Economics 81: 305–20. [Google Scholar] [CrossRef]
- Young, C. Edwin, Monte L. Vandeveer, and Randall D. Schnepf. 2001. Production and Price Impacts of U.S. Crop Insurance Programs. American Journal of Agricultural Economics 83: 1196–203. [Google Scholar] [CrossRef]
- Yu, Jisang, Aaron Smith, and Daniel A. Sumner. 2018. Effects of Crop Insurance Premium Subsidies on Crop Acreage. American Journal of Agricultural Economics 100: 91–114. [Google Scholar] [CrossRef] [Green Version]
- Zahid, Zobia, Muhammad Kashif Riaz Khan, Amjad Hameed, Muhammad Akhtar, Allah Ditta, Hafiz Mumtaz Hassan, and Ghulam Farid. 2021. Dissection of Drought Tolerance in Upland Cotton through Morpho-Physiological and Biochemical Traits at Seedling Stage. Frontiers in Plant Science 12: 260. [Google Scholar] [CrossRef] [PubMed]






| Region # of Observations | Delta | Southeast | Southwest | West | US |
|---|---|---|---|---|---|
| 1647 | 4036 | 3310 | 479 | 9472 | |
| Dependent variables | |||||
| PINSURit | 0.432 * | 0.569 | 0.540 | 0.378 | 0.525 |
| (0.203) | (0.221) | (0.236) | (0.192) | (0.230) | |
| PCOTACRESit | 0.146 | 0.194 | 0.175 | 0.102 | 0.174 |
| (0.123) | (0.150) | (0.204) | (0.106) | (0.167) | |
| Independent variables | |||||
| SUBSIDYPERLBit | 0.024 | 0.042 | 0.054 | 0.016 | 0.042 |
| (0.016) | (0.024) | (0.036) | (0.018) | (0.030) | |
| PRORit−1 | 2.587 | 2.572 | 2.821 | 2.489 | 2.657 |
| (8.47) | (8.708) | (5.733) | (5.405) | (7.599) | |
| E[Picot,it] | 0.739 | 0.746 | 0.699 | 0.797 | 0.731 |
| (0.187) | (0.191) | (0.171) | (0.195) | (0.186) | |
| YLDit−5 | 803 | 690 | 583 | 1146 | 695 |
| (162) | (141.56) | (238) | (293) | (232.20) | |
| E[Picot,it] YLDit−5 | 591.3 | 515.9 | 409.3 | 925 | 512.4 |
| (177.8) | (166.9) | (195.7) | (356) | (224.7) | |
| YLDVARit | 0.184 | 0.238 | 0.274 | 0.163 | 0.237 |
| (0.066) | (0.075) | (0.107) | (0.074) | (0.093) | |
| PBTit | 0.793 | 0.757 | 0.511 | 0.392 | 0.659 |
| (0.249) | (0.249) | (0.357) | (0.366) | (0.327) | |
| RREVINDEXit | 0.931 | 0.882 | 0.879 | 0.588 | 0.874 |
| (0.532) | (0.655) | (0.614) | (0.753) | (0.630) | |
| DCPSTAX | 0.125 | 0.114 | 0.132 | 0.061 | 0.120 |
| (0.331) | (0.318) | (0.339) | (0.239) | (0.324) | |
| Other descriptors | |||||
| Cotton planted acres | 28,109 | 13,924 | 39,258 | 24,108 | 25,793 |
| (35,373) | (14,103) | (64,098) | (38,909) | (44,0043) | |
| Total cropland acres | 176,107 | 69,096 | 205,664 | 298,672 | 147,406 |
| (107,082) | (39,400) | (117,083) | (286,862) | (129,758) | |
| Cotton insured acres | 24,926 | 13,116 | 37,627 | 20,236 | 24,124 |
| (31,507) | (13,485) | (62,903) | (33,790) | (42,511) | |
| Dependent Variable | Delta N = 1647 | Southeast N = 4036 | Southwest N = 3310 | West N = 479 | US N = 9472 |
| (a) | |||||
| Intercept | −0.01149 *** (0.00393) | −0.00691 *** (0.00260) | −0.01238 *** (0.00257) | 0.05273 (0.16149) | −0.00934 *** (0.00148) |
| E[Pcot,it] | 0.15539 (0.10641) | −0.13886 ** (0.06594) | −0.08703 ** (0.03448) | 0.58585 (2.50084) | −0.12282 *** (0.02244) |
| YLDit | 0.00011 (0.00013) | −0.00005 (0.00008) | −0.00011 ** (0.00006) | −0.00141 (0.00397) | −0.00011 *** (0.00003) |
| E[Pcot,it] YLDit | −0.00011 (0.00015) | 0.00003 (0.00010) | 0.00002 (0.00006) | −0.00083 (0.00292) | 0.00001 (0.00004) |
| YLDVARit | 0.28717 *** (0.10550) | −0.01962 (0.04601) | 0.04862 (0.03303) | −0.78313 (2.02821) | −0.00262 (0.02377) |
| PBTit | 0.44285 *** (0.03964) | 0.17829 *** (0.03109) | 0.12766 *** (0.01092) | −0.00705 (0.25789) | 0.17402 *** (0.00794) |
| SUBSIDYPERLBit | 7.00171 *** (0.50352) | 4.84789 *** (0.13402) | 4.46006 *** (0.15390) | 5.31541 (4.08394) | 4.64178 *** (0.07636) |
| PRORit−1 | 0.00110 ** (0.00046) | 0.00019 (0.00023) | 0.00174 *** (0.00041) | 0.00109 (0.01892) | 0.00056 *** (0.00018) |
| PCOTACRESit | 1.33629 *** (0.46835) | −1.47798 ** (0.43738) | −0.72529 *** (0.26162) | −0.16851 (0.45524) | −0.86598 *** (0.14083) |
| DCPSTAX | 0.23648 *** (0.02355) | 0.16246 *** (0.01849) | 0.16775 *** (0.01289) | −0.22387 (0.95475) | 0.16242 *** (0.00785) |
| Dependent Variable | Delta N = 1647 | Southeast N = 4036 | Southwest N = 3310 | West N = 479 | US N = 9472 |
| (b) | |||||
| Intercept | 0.00046 (0.00170) | 0.00330 *** (0.00097) | 0.00521 *** (0.00098) | 0.00338 * (0.00205) | 0.00459 *** (0.00065) |
| E[Pcot,it] | −0.00031 (0.04544) | −0.05774 ** (0.02538) | 0.03337 ** (0.01380) | 0.04546 (0.04609) | 0.03567 *** (0.01045) |
| YLDit | −0.00010 ** (0.00005) | −0.00003 (0.00003) | 0.00010 *** (0.00002) | −0.00009 ** (0.00004) | 0.00004 *** (0.00001) |
| E[Pcot,it] YLDit | −0.00016 ** (0.00006) | 0.00007 * (0.00004) | −0.00009 *** (0.00002) | −0.00006 (0.00004) | −0.00009 *** (0.00002) |
| YLDVARit | −0.13778 *** (0.03577) | −0.00592 (0.01933) | −0.02849 ** (0.01294) | −0.04260 (0.05027) | −0.02827 *** (0.01088) |
| PBTit | −0.02148 * (0.01231) | −0.07045 *** (0.00691) | −0.03280 *** (0.00467) | −0.00128 (0.01213) | −0.04505 *** (0.00379) |
| RREVINDEXit | −0.02136 *** (0.00362) | −0.00882 *** (0.00161) | −0.01737 *** (0.00168) | 0.00122 (0.00370) | −0.01734 *** (0.00110) |
| PINSURit | −0.12811 *** (0.02148) | 0.01896 (0.01204) | 0.09890 *** (0.00959) | −0.01256 (0.03013) | 0.04981 *** (0.00744) |
| DCPSTAX | −0.01922 *** (0.00829) | −0.04298 *** (0.00512) | −0.05513 *** (0.00444) | −0.01928 (0.01397) | −0.05271 *** (0.00315) |
| Dependent Variable | Delta N = 1647 | Southeast N = 4036 | Southwest N = 3310 | West N = 479 | US N = 9472 |
| (a) | |||||
| YLDVARit | 0.08800 (0.06370) | −0.01057 (0.03989) | 0.06465 (0.03204) | −0.08285 (0.23871) | 0.02096 (0.02290) |
| PBTit | 0.35361 *** (0.0166) | 0.27472 *** (0.00994) | 0.14131 *** (0.00979) | 0.01850 (0.05152) | 0.20422 *** (0.00618) |
| REVINDEXit | −0.02437 *** (0.00658) | 0.01268 ** (0.00326) | 0.01176 *** (0.00417) | −0.02611 * (0.01367) | 0.01440 *** (0.00228) |
| SUBSIDYPERLBit | 5.97826 *** (0.22813) | 4.71577 *** (0.11708) | 4.16154 *** (0.09933) | 6.74184 *** (1.93728) | 4.44985 *** (0.06970) |
| PRORit−1 | 0.00094 ** (0.00037) | 0.00018 (0.00022) | 0.00162 *** (0.00039) | 0.00138 (0.02310) | 0.00054 *** (0.00017) |
| PCOTACRESit | 1.33629 *** (0.46835) | −1.47798 *** (0.43738) | −0.72529 *** (0.26162) | −16.85069 (45.52391) | −0.86598 *** (0.14083) |
| Dependent Variable | Delta N = 1647 | Southeast N = 4036 | Southwest N = 3310 | West N = 479 | US N = 9472 |
| (b) | |||||
| YLDVARit | −0.14905 *** (0.03554) | −0.00612 (0.01922) | −0.02210 * (0.01235) | −0.04156 (0.04974) | −0.02723 *** (0.01067) |
| PBTit | −6.67858 *** (0.92518) | −0.06524 *** (0.00479) | −0.01882 *** (0.00377) | −0.00152 (0.01166) | −0.03487 *** (0.00288) |
| REVINDEXit | −0.01824 *** (0.00367) | −0.00858 *** (0.00157) | −0.01621 *** (0.00160) | 0.00155 (0.00360) | −0.01662 *** (0.00106) |
| SUBSIDYPERLBit | −0.76589 *** (0.12744) | 0.08939 (0.05643) | 0.41159 *** (0.03790) | −0.08465 (0.19900) | 0.22163 *** (0.03245) |
| PRORit−1 | −0.00012 ** (0.00005) | 0.000003 (0.000005) | 0.00016 *** (0.00004) | −0.00002 (0.00030) | 0.00003 *** (0.00001) |
| PINSURit | −0.12811 *** (0.02148) | 0.01896 (0.01204) | 0.09890 *** (0.00959) | −0.01256 (0.03013) | 0.04981 *** (0.00744) |
| Delta | Southeast | Southwest | West | US | |
|---|---|---|---|---|---|
| YLDVARit | −26,249 *** (6259) | −423 (1328) | −4545 * (2540) | −12,716 (15,219) | −4013 *** (1573) |
| PBTit | −11,761 *** (1629) | −4508 *** (331) | −3872 *** (776) | −464 (3569) | −5141 *** (425) |
| RREVINDEXit | −3212 *** (646) | −593 *** (108) | −3333 *** (329) | 474 (1102) | −2451 *** (157) |
| SUBSIDYPERLBit($/lb) | −134,878 *** (22,442) | 6177 (3899) | 84,649 *** (7795) | −25,902 (60,890) | 32,669 *** (4783) |
| PRORit−1 | −21.25 ** (9.19) | 0.24 (0.33) | 33.00 *** (8.48) | −5.31 (91.35) | 3.94 *** (1.38) |
| Delta | Southeast | Southwest | West | US | |
|---|---|---|---|---|---|
| EPCOTACRES/PINSUR | −0.39021 (1.02424) | 3.29876 (3.74565) | −0.68339 (0.42661) | −0.78285 (1.12306) | −0.57759 *** (0.21159) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sall, I.; Tronstad, R. Simultaneous Analysis of Insurance Participation and Acreage Response from Subsidized Crop Insurance for Cotton. J. Risk Financial Manag. 2021, 14, 562. https://doi.org/10.3390/jrfm14110562
Sall I, Tronstad R. Simultaneous Analysis of Insurance Participation and Acreage Response from Subsidized Crop Insurance for Cotton. Journal of Risk and Financial Management. 2021; 14(11):562. https://doi.org/10.3390/jrfm14110562
Chicago/Turabian StyleSall, Ibrahima, and Russell Tronstad. 2021. "Simultaneous Analysis of Insurance Participation and Acreage Response from Subsidized Crop Insurance for Cotton" Journal of Risk and Financial Management 14, no. 11: 562. https://doi.org/10.3390/jrfm14110562
APA StyleSall, I., & Tronstad, R. (2021). Simultaneous Analysis of Insurance Participation and Acreage Response from Subsidized Crop Insurance for Cotton. Journal of Risk and Financial Management, 14(11), 562. https://doi.org/10.3390/jrfm14110562






