Housing Market in the Time of Pandemic: A Price Gradient Analysis from the COVID-19 Epicentre in China
Abstract
:1. Introduction
2. Literature Review
2.1. The Impacts of COVID-19 on the Housing Market
2.2. Systematic Risk, Idiosyncratic Risk, and Local Risk
2.3. Price Gradient Analysis on the Property Market
3. Empirical Model
3.1. House Price Gradient Models
3.1.1. Price Gradient among Districts (District Gradient Model)
3.1.2. Price Gradient from the Epicentre (Distance Gradient Model)
3.2. Data
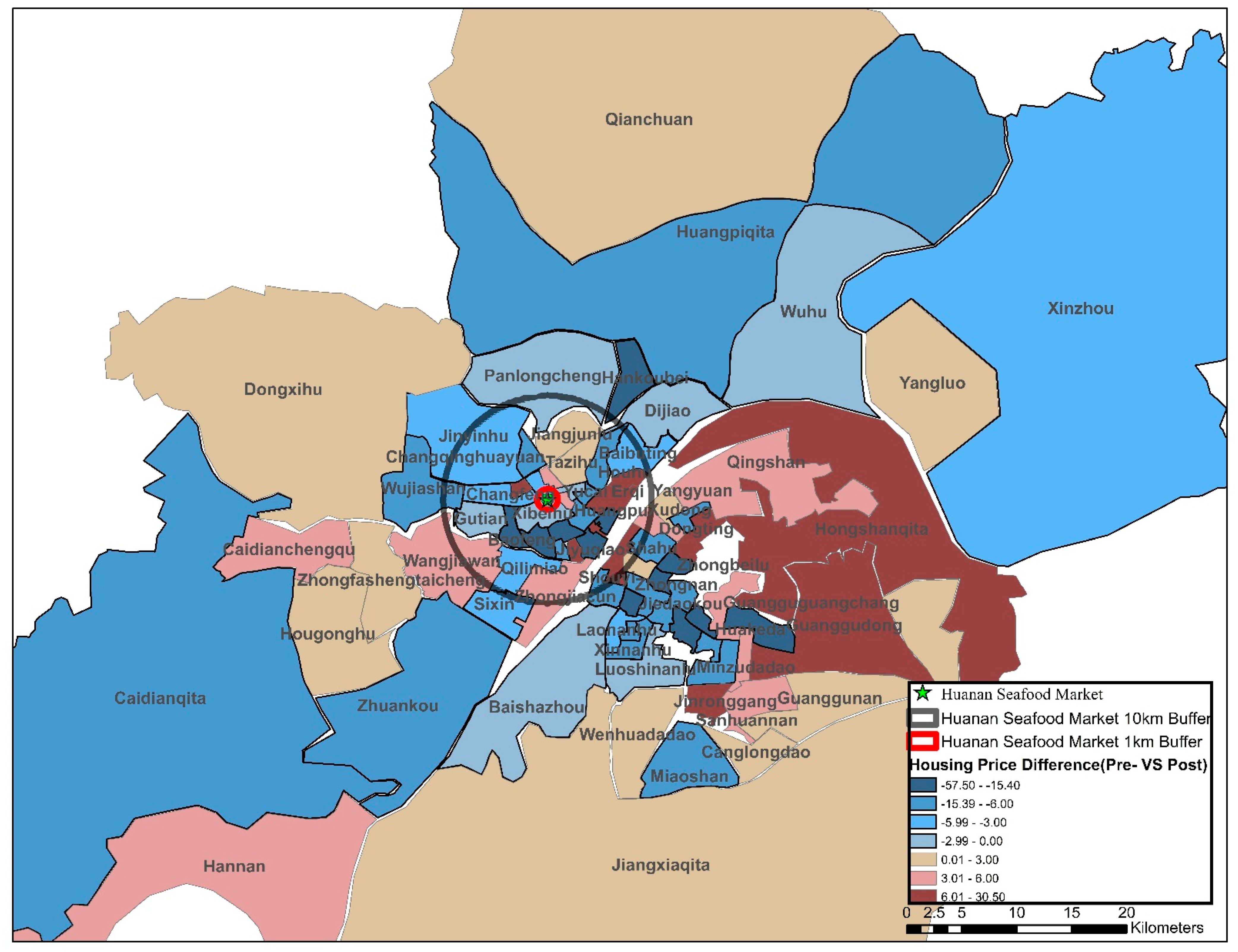
4. Empirical Results and Discussion
5. When Risks Are Everywhere, Do People Internalise Them? A Test on Living Density
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. A Toy Model That Motivates Price Gradient Analysis
References
- Alexander, Diane, and Ezra Karger. 2020. Do Stay-at-Home Orders Cause People to Stay at Home? Effects of Stay-at-Home Orders on Consumer Behavior (22 June 2020). FRB of Chicago Working Paper No. 2020-12. Available online: https://ssrn.com/abstract=3583625 (accessed on 4 March 2021).
- Alonso, William. 1964. Location and Land Use: Toward a General Theory of Land Rent. Cambridge: Harvard University Press. [Google Scholar]
- Anas, Alex, and David Pines. 2008. Anti-sprawl policies in a system of congested cities. Regional Science and Urban Economics 38: 408–23. [Google Scholar] [CrossRef]
- Anas, Alex, and Hyok-Joo Rhee. 2006. Curbing excess sprawl with congestion tolls and urban boundaries. Regional Science and Urban Economics 36: 510–41. [Google Scholar] [CrossRef] [Green Version]
- Apergis, Nicholas. 2021. The role of housing market in the effectiveness of monetary policy over the Covid-19 era. Economics Letters 2020: 109749. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, Steven J. Davis, Kyle J. Kost, Marco C. Sammon, and Tasaneeya Viratyosin. 2020. The Unprecedented Stock Market Impact of COVID-19 (No. w26945). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Bank for International Settlements. 2020. BIS Residential Property Price Statistics, Q2 2020. Available online: https://www.bis.org/statistics/pp_residential_2011.htm (accessed on 4 March 2021).
- Beja, Avraham. 1972. On systematic and unsystematic components of financial risk. The Journal of Finance 27: 37–45. [Google Scholar] [CrossRef]
- Brodeur, Abel, David M. Gray, Anik Islam, and Suraiya Bhuiyan. 2020. A Literature Review of the Economics of COVID-19. IZA Discussion Paper No. 13411. Available online: https://ssrn.com/abstract=3636640 (accessed on 4 March 2021).
- Brueckner, Jan K. 1987. The structure of urban equilibria: A unified treatment of the Muth-Mills model. Handbook of Regional and Urban Economics 2: 821–45. [Google Scholar]
- Brueckner, Jan K., and Robert W. Helsley. 2011. Sprawl and blight. Journal of Urban Economics 69: 205–13. [Google Scholar] [CrossRef]
- Chen, Kaiji, and Yi Wen. 2017. The great housing boom of China. American Economic Journal: Macroeconomics 9: 73–114. [Google Scholar] [CrossRef] [Green Version]
- Couch, Chris, and Jay Karecha. 2006. Controlling urban sprawl: Some experiences from Liverpool. Cities 23: 353–63. [Google Scholar] [CrossRef]
- D’Lima, Walter, Luis A. Lopez, and Archana Pradhan. 2020. COVID-19 and Housing Market Effects: Evidence from U.S. Shutdown Orders. Available online: https://ssrn.com/abstract=3647252 (accessed on 4 March 2021).
- Del Giudice, Vincenzo, Pierfrancesco De Paola, and Francesco Paolo Del Giudice. 2020. COVID-19 infects real estate markets: Short and mid-run effects on housing prices in Campania region (Italy). Social Sciences 9: 114. [Google Scholar] [CrossRef]
- Del Rio-Chanona, R. Maria, Penny Mealy, Anton Pichler, Francois Lafond, and J. Doyne Farmer. 2020. Supply and demand shocks in the COVID-19 pandemic: An industry and occupation perspective. arXiv arXiv:2004.06759. [Google Scholar]
- Fang, Hanming, Long Wang, and Yang Yang. 2020. Human mobility restrictions and the spread of the novel coronavirus (2019-ncov) in china. Journal of Public Economics 191: 104272. [Google Scholar] [CrossRef]
- Ferguson, Neil, Daniel Laydon, Gemma Nedjati Gilani, Natsuko Imai, Kylie Ainslie, Marc Baguelin, Sangeeta Bhatia, Boonyasiri Adhiratha, Cucunubá Zulma, Cuomo-Dannenburg Gina, and et al. 2020. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID19 Mortality and Healthcare Demand. London. Available online: https://spiral.imperial.ac.uk/bitstream/10044/1/77482/14/2020-03-16-COVID19-Report-9.pdf (accessed on 4 March 2021).
- Francke, Marc, and Matthijs Korevaar. 2020. Housing Markets in a Pandemic: Evidence from Historical Outbreaks. Available online: https://ssrn.com/abstract=3566909 (accessed on 4 March 2021).
- Glaeser, Edward L., and Matthew E. Kahn. 2004. Sprawl and urban growth. In Handbook of Regional and Urban Economics. Amsterdam: Elsevier, vol. 4, pp. 2481–527. [Google Scholar]
- Gong, Yifan, and Charles Ka Yui Leung. 2020. When education policy and housing policy interact: Can they correct for the externalities? Journal of Housing Economics 50: 101732. [Google Scholar] [CrossRef]
- Gopinath, Gita. 2020. Limiting the economic fallout of the coronavirus with large targeted policies. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever It Takes. London: CEPR Press, pp. 41–48. [Google Scholar]
- Hanushek, Eric, and Kuzey Yilmaz. 2007. The complementarity of Tiebout and Alonso. Journal of Housing Economics 16: 243–61. [Google Scholar] [CrossRef]
- Huang, Chaolin, Yeming Wang, Xingwang Li, Llili Ren, Jianpinng Zhao, Yi Hu, Li Zhang, Guohui Fan, Jiuyang Xu, Xiaoying Gu, and et al. 2020a. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 395: 497–506. [Google Scholar] [CrossRef] [Green Version]
- Huang, Naqun, Jindong Pang, and Yanmin Yang. 2020b. The Impact of the COVID-19 Epidemic on the Housing Market in China. Available online: https://ssrn.com/abstract=3642444 (accessed on 4 March 2021).
- Jaeger, Jochen AG, and Christian Schwick. 2014. Improving the measurement of urban sprawl: Weighted Urban Proliferation (WUP) and its application to Switzerland. Ecological Indicators 38: 294–308. [Google Scholar] [CrossRef]
- Knight Frank. 2020. Global House Price Index, Research, Q2 2020. Available online: https://www.bayleys.co.nz/media/bdf9502b-cb96-4015-af53-6a5bcf548416 (accessed on 4 March 2021).
- Koren, Miklós, and Rita Pető. 2020. Business Disruptions from Social Distancing. Available online: https://arxiv.org/pdf/2003.13983.pdf (accessed on 4 March 2021).
- Leung, Charles Ka Yui, Siu Kei Wong, and Patrick Wai Yin Cheung. 2007. On the stability of the implicit prices of housing attributes: A dynamic theory and some evidence. International Real Estate Review 10: 65–91. [Google Scholar]
- Leung, Charles Ka Yui, Patrick Wai Yin Cheung, and Edward C.H. Tang. 2011. Financial Crisis and the Comovements of Housing Sub-Markets: Do Relationships Change after a Crisis? Available online: https://mpra.ub.uni-muenchen.de/id/eprint/31627 (accessed on 4 March 2021).
- Ling, David C., Chongyu Wang, and Tingyu Zhou. 2020. A first look at the impact of COVID-19 on commercial real estate prices: Asset-level evidence. The Review of Asset Pricing Studies 10: 669–704. [Google Scholar] [CrossRef]
- Liu, Ding, Weihong Sun, and Xuan Zhang. 2020. Is the Chinese economy well positioned to fight the COVID-19 pandemic? The financial cycle perspective. Emerging Markets Finance and Trade 56: 2259–76. [Google Scholar] [CrossRef]
- Malpezzi, Stephen. 2002. Hedonic pricing models: A selective and applied review. In Housing Economics and Public Policy. Boston: Blackwell Science Ltd., pp. 67–89. [Google Scholar]
- Manzoli, Elisabetta, and Sauro Mocetti. 2019. The House Price Gradient: Evidence from Italian Cities. Italian Economic Journal 5: 281–305. [Google Scholar] [CrossRef]
- Marona, Bartłomiej, and Mateusz Tomal. 2020. The COVID-19 pandemic impact upon housing brokers’ workflow and their clients’ attitude: Real estate market in Krakow. Entrepreneurial Business and Economics Review 8: 221–32. [Google Scholar] [CrossRef]
- Mazur, Mieszko, Man Dang, and Miguel Vega. 2021. COVID-19 and the march 2020 stock market crash. Evidence from S&P1500. Finance Research Letters 38: 101690. [Google Scholar]
- McKibbin, Warwick, and Roshen Fernando. 2020. The economic impact of COVID-19. In Economics in the Time of COVID-19. London: CEPR Press, p. 45. [Google Scholar]
- Mieszkowski, Peter, and Edwin S. Mills. 1993. The causes of metropolitan suburbanisation. Journal of Economic Perspectives 7: 135–47. [Google Scholar] [CrossRef] [Green Version]
- Mills, Edwin S. 1967. An aggregative model of resource allocation in a metropolitan area. The American Economic Review 57: 197–210. [Google Scholar]
- Muth, Richard F. 1969. Cities and Housing: The Spatial Pattern of Urban Residential Land Use. Chicago: University of Chicago Press. [Google Scholar]
- Nicola, Maria, Zaid Alsafi, Catrin Sohrabi, Ahmed Kerwan, Ahmed Al-Jabir, Christos Iosifidis, Maliha Agha, and Riaz Agha. 2020. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. International Journal of Surgery 78: 185–93. [Google Scholar] [CrossRef]
- O’Sullivan, Arthur. 2007. Urban Economics, 6th ed. New York: McGraw Hill. [Google Scholar]
- Ozili, Peterson K., and Thankom Arun. 2020. Spillover of COVID-19: Impact on the Global Economy (27 March 2020). Available online: https://ssrn.com/abstract=3562570 (accessed on 4 March 2021).
- Qian, Xianhang, Shanyun Qiu, and Guangli Zhang. 2021. The Impact of COVID-19 on Housing Price: Evidence from China. Finance Research Letters, 101944, in press. [Google Scholar] [CrossRef]
- Sina. 2020. 2019 Wuhan property market illustration: residential volume and price rise, office building competition intensifies, the “first-store economy” promotes the recovery of retail properties (2019年武漢樓市圖鑑:住宅量價齊升辦公樓競爭加劇 首店經濟促零售物業回暖). January 17. Available online: https://news.sina.com.tw/article/20200117/34019206.html (accessed on 4 March 2021).
- So, Mike KP, Amanda MY Chu, and Thomas WC Chan. 2021. Impacts of the COVID-19 pandemic on financial market connectedness. Finance Research Letter 38: 101864. [Google Scholar] [CrossRef]
- Stulz, René M. 1996. Rethinking risk management. Journal of Applied Corporate Finance 9: 8–25. [Google Scholar] [CrossRef]
- Susskind, Daniel, and David Vines. 2020. The economics of the COVID-19 pandemic: An assessment. Oxford Review of Economic Policy 36: S1–S13. [Google Scholar] [CrossRef]
- Tanrıvermiş, Harun. 2020. Possible impacts of COVID-19 outbreak on real estate sector and possible changes to adopt: A situation analysis and general assessment on Turkish perspective. Journal of Urban Management 9: 263–69. [Google Scholar] [CrossRef]
- Tuzel, Selale, and Miao Ben Zhang. 2017. Local risk, local factors, and asset prices. The Journal of Finance 72: 325–70. [Google Scholar] [CrossRef] [Green Version]
- Uchehara, Ikechukwu, Mansur Hamma-Adama, Kwadwo Ayeh Obiri, Naeimeh Jafarifar, and David Moore. 2020. Impacts and risk management of COVID-19 pandemic on real estate supply chain. International Journal of Real Estate Studies 14: 41–53. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNODRR). 2020. Review of COVID-19 Disaster Risk Governance in Asia-Pacific: Towards Multi-Hazard and Multi-Sectoral Disaster Risk Reduction. Geneva: World Health Organization, Available online: https://www.undrr.org/publication/review-covid-19-disaster-risk-governance-asia-pacific-towards-multi-hazard-and-multi (accessed on 4 March 2021).
- Viscusi, W. Kip. 2020. Pricing the global health risks of the COVID-19 pandemic. Journal of Risk and Uncertainty 61: 101–28. [Google Scholar] [CrossRef]
- Von Thünen, Johann. 1826. Isolated State. Translated by Carla M. Wartenberg. Oxford: Pergamon Press. [Google Scholar]
- Wang, Bingbing. 2021. How Does COVID-19 Affect House Prices? A Cross-City Analysis. Journal of Risk and Financial Management 14: 47. [Google Scholar] [CrossRef]
- Wheaton, William C. 1977. A bid rent approach to housing demand. Journal of Urban Economics 4.2: 200–217. [Google Scholar] [CrossRef] [Green Version]
- World Health Organization. 2020. Origin of SARS-CoV-2. In WHO/2019-nCoV/FAQ/Virus_origin/2020.1. Geneva: World Health Organization, Available online: https://www.who.int/publications/i/item/origin-of-sars-cov-2 (accessed on 4 March 2021).
- Wong, Grace. 2008. Has SARS Infected the Property Market?Evidence from Hong Kong. Journal of Urban Economics 63: 74–95. [Google Scholar] [PubMed]
- Wuhan Municipal Health Commission. 2020. Wuhan COVID-19 Infected Numbers Report (1 August 2020). Available online: http://wjw.wuhan.gov.cn/ztzl_28/fk/tzgg/202008/t20200802_1414093.shtml (accessed on 4 March 2021).
- Yang, Minhua, and Junni Zhou. 2021. The impact of COVID-19 on the housing market: Evidence from the Yangtze river delta region in China. Applied Economics Letters, 1–4. [Google Scholar] [CrossRef]
- Yiu, Chung Yim, and Siu Kei Wong. 2005. The Effects of Expected Transport Improvements on Housing Prices. Urban Studies 42: 113–25. [Google Scholar] [CrossRef]
- Yoruk, Baris. 2020. Early Effects of the COVID-19 Pandemic on Housing Market in the United States (21 May 2020). Available online: https://ssrn.com/abstract=3607265 (accessed on 4 March 2021).
- Zhang, Dayong, Min Hu, and Qiang Ji. 2020. Financial markets under the global pandemic of COVID-19. Finance Research Letters 36: 101528. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Yunhui. 2020. US Housing Market During COVID-19: Aggregate and Distributional Evidence (September 1. 2020). IMF Working Paper No. 2020/212. Available online: https://ssrn.com/abstract=3744679 (accessed on 4 March 2021).


| Description | Variable | Mean | S.D. | Min | Max |
|---|---|---|---|---|---|
| Sales Price (RMB × 10,000) | Pit | 166.93 | 94.79 | 11.50 | 2200.00 |
| Size (sq m) | SIZEi | 90.85 | 32.89 | 7.35 | 679.06 |
| Living room (No.) | LRMi | 1.60 | 0.53 | 0.00 | 5.00 |
| Bedroom (No.) | BRMi | 2.38 | 0.80 | 1.00 | 8.00 |
| Bathroom (No.) | BARMi | 1.25 | 0.47 | 0.00 | 8.00 |
| Kitchen (No.) | KITi | 1.00 | 0.09 | 0.00 | 4.00 |
| Building age (year) | AGEi | 10.72 | 6.88 | 0.00 | 80.00 |
| Subway (1 = yes; 0 = no) | SWi | 0.64 | 0.48 | 0.00 | 1.00 |
| Tax wavier (1 = yes; 0 = no) | TWi | 0.26 | 0.44 | 0.00 | 1.00 |
| Building direction | DIRi | 8 Directions N, NE, E, SE, S, SW, W, NW | |||
| Area and District | Da and Dd | 62 areas A1, …, A81 in 9 districts D1, …, D9 | |||
| Distance from the epicentre (km) | 10.38 | 6.95 | 0.07 | 35.84 | |
| Size of Area (sq km) | Aa | 102.06 | 303.96 | 0.89 | 1820.95 |
| Population in area | POPa | 103,762 | 84,668.03 | 2461.00 | 314,096.00 |
| Household density (per sq km) | Ha/Aa | 7546.51 | 6662.27 | 16.39 | 26,586.27 |
| Building density (per sq km) | Ba/Aa | 77.38 | 25.46 | 25.93 | 180.10 |
| Di | [0, 5) | [5, 10) | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | Total |
|---|---|---|---|---|---|---|---|---|
| D1 | 2334 | 2446 | 97 | 0 | 0 | 0 | 0 | 4877 |
| D2 | 2276 | 135 | 0 | 0 | 0 | 0 | 0 | 2411 |
| D3 | 0 | 0 | 0 | 0 | 464 | 1357 | 252 | 2073 |
| D4 | 777 | 446 | 0 | 0 | 0 | 0 | 0 | 1223 |
| D5 | 0 | 0 | 0 | 0 | 0 | 238 | 122 | 363 |
| D6 | 750 | 1736 | 166 | 0 | 0 | 0 | 0 | 2652 |
| D7 | 0 | 313 | 2966 | 2747 | 192 | 0 | 0 | 6218 |
| D8 | 0 | 1787 | 2050 | 0 | 0 | 0 | 0 | 3837 |
| D9 | 0 | 2376 | 873 | 0 | 0 | 0 | 0 | 3249 |
| Total | 6137 | 9239 | 6152 | 2747 | 656 | 1595 | 374 | 26,903 |
| (1a) | (1b) | (2a) | (2b) | (3a) | (3b) | |
|---|---|---|---|---|---|---|
| Variable | Hedonic | District Gradient | Distance Gradient | |||
| −0.020 (−27.17) *** | −0.023 (−23.17) *** | |||||
| 0.0002 (0.39) | −0.0001 (−0.30) | |||||
| D1 | 0.340 (50.77) *** | 0.341 (37.23) *** | −0.078 (−4.77) *** | |||
| D2 | 0.334 (44.12) *** | 0.357 (34.46) *** | −0.145 (−7.76) *** | |||
| D3 | omitted | omitted | omitted | |||
| D4 | 0.244 (27.66) *** | 0.262 (21.78) *** | −0.191 (−10.76) *** | |||
| D5 | −0.720 (−51.61) *** | −0.697 (−38.24) *** | −0.664 (−47.70) *** | |||
| D6 | 0.099 (13.90) *** | 0.096 (9.87) *** | −0.304 (−19.04) *** | |||
| D7 | 0.369 (59.46) *** | 0.370 (42.36) *** | 0.125 (11.76) *** | |||
| D8 | 0.562 (80.79) *** | 0.571 (59.49) *** | 0.239 (17.91) *** | |||
| D9 | 0.221 (31.80) *** | 0.213 (22.38) *** | −0.129 (−9.10) *** | |||
| A6 | 0.677 (37.42) *** | 0.662 (26.00) *** | 0.104 (3.44) *** | |||
| A7 | 0.494 (30.05) *** | 0.596 (26.58) *** | −0.063 (2.18) ** | |||
| A17 | 0.573 (37.00) *** | 0.626 (29.93) *** | −0.076 (−2.40) ** | |||
| A21 | 0.426 (21.77) *** | 0.481 (17.59) *** | −0.225 (6.66) *** | |||
| A20 | −0.730 (−47.28) *** | −0.670 (−32.00) *** | −0.718 (−46.93) *** | |||
| A47 | omitted | omitted | omitted | |||
| D1 × p2 | 0.009 (0.74) | |||||
| D2 × p2 | −0.036 (−2.49) ** | |||||
| D3 × p2 | 0.003 (0.27) | |||||
| D4 × p2 | −0.030 (−1.72) * | |||||
| D5 × p2 | −0.050 (−1.76) * | |||||
| D6 × p2 | 0.009 (0.67) | |||||
| D7 × p2 | 0.008 (0.69) | |||||
| D8 × p2 | −0.006 (0.43) | |||||
| D9 × p2 | 0.028 (2.02) ** | |||||
| A6 × p2 | 0.118 (3.39) *** | |||||
| A7 × p2 | −0.129 (4.07) *** | |||||
| A17 × p2 | −0.029 (−0.96) | |||||
| A21 × p2 | −0.024 (−0.63) | |||||
| A20 × p2 | −0.068 (−2.22) ** | |||||
| A47 × p2 | 0.001 (0.04) | |||||
| Structure F.E. | Yes | Yes | Yes | |||
| Time F.E. | Yes (Monthly) | Yes (Quarterly) | Yes (Monthly) | |||
| District F.E. | Yes | Yes | Yes | |||
| Adj. R-Sq | 0.751 | 0.821 | 0.751 | 0.8095 | 0.758 | 0.825 |
| No. of Obs. | 25,860 | 25,860 | 25,860 | 25,860 | 25,860 | 25,860 |
| (1c) | (2c) | (3c) | ||||
|---|---|---|---|---|---|---|
| Hedonic Density | District Gradient | Distance Gradient | ||||
| Variable | Coeff. | t-Stat | Coeff. | t-Stat | Coeff. | t-Stat |
| 9.14 × 10−6 | (21.25) *** | 8.65 × 10−6 | (18.28) *** | 6.88 × 10−6 | (14.84) *** | |
| −9.35 × 10−7 | (−1.78) * | 1.51 × 10−7 | (0.23) | −9.97 × 10−7 | (−1.65) * | |
| −0.016 | (−20.68) *** | |||||
| −0.0002 | (−0.41) | |||||
| D1 | 0.278 | (39.36) *** | 0.275 | (28.31) *** | −0.042 | (−2.59) *** |
| D2 | 0.246 | (29.80) *** | 0.265 | (23.36) *** | −0.116 | (−6.27) *** |
| D3 | omitted | omitted | omitted | |||
| D4 | 0.160 | (17.20) *** | 0.177 | (13.83) *** | −0.168 | (−9.51) *** |
| D5 | −0.714 | (−51.73) *** | −0.694 | (−38.66) *** | −0.670 | (−48.44) *** |
| D6 | 0.081 | (11.48) *** | 0.078 | (8.05) *** | −0.239 | (−14.67) *** |
| D7 | 0.322 | (50.18) *** | 0.320 | (35.92) *** | 0.138 | (13.00) *** |
| D8 | 0.500 | (68.47) *** | 0.505 | (50.00) *** | 0.256 | (19.24) *** |
| D9 | 0.188 | (26.87) *** | 0.178 | (18.68) *** | −0.086 | (−5.98) *** |
| D1 × p2 | 0.008 | (0.55) | ||||
| D2 × p2 | −0.040 | (−2.46) ** | ||||
| D3 × p2 | 0.003 | (0.21) | ||||
| D4 × p2 | −0.035 | (−1.89) * | ||||
| D5 × p2 | −0.053 | (−1.87) * | ||||
| D6 × p2 | 0.008 | (0.56) | ||||
| D7 × p2 | 0.005 | (0.36) | ||||
| D8 × p2 | −0.008 | (−0.58) | ||||
| D9 × p2 | 0.022 | (1.58) | ||||
| Structural F.E. | Yes | Yes | Yes | |||
| Time F.E. | Yes (Monthly) | Yes (Quarterly) | Yes (Monthly) | |||
| Location F.E. | Yes (District) | Yes | Yes (District) | |||
| Adj. R-Sq | 0.757 | 0.756 | 0.761 | |||
| No. of Obs. | 25,860 | 25,860 | 25,860 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheung, K.S.; Yiu, C.Y.; Xiong, C. Housing Market in the Time of Pandemic: A Price Gradient Analysis from the COVID-19 Epicentre in China. J. Risk Financial Manag. 2021, 14, 108. https://doi.org/10.3390/jrfm14030108
Cheung KS, Yiu CY, Xiong C. Housing Market in the Time of Pandemic: A Price Gradient Analysis from the COVID-19 Epicentre in China. Journal of Risk and Financial Management. 2021; 14(3):108. https://doi.org/10.3390/jrfm14030108
Chicago/Turabian StyleCheung, Ka Shing, Chung Yim Yiu, and Chuyi Xiong. 2021. "Housing Market in the Time of Pandemic: A Price Gradient Analysis from the COVID-19 Epicentre in China" Journal of Risk and Financial Management 14, no. 3: 108. https://doi.org/10.3390/jrfm14030108
APA StyleCheung, K. S., Yiu, C. Y., & Xiong, C. (2021). Housing Market in the Time of Pandemic: A Price Gradient Analysis from the COVID-19 Epicentre in China. Journal of Risk and Financial Management, 14(3), 108. https://doi.org/10.3390/jrfm14030108



_Cheung.jpeg)




