Policy and Business Cycle Shocks: A Structural Factor Model Representation of the US Economy †
Abstract
:1. Introduction
2. Theory
2.1. The Factor Model
2.2. Identification
2.3. Estimation
2.4. Discussion
3. Identifying the Structural Shocks
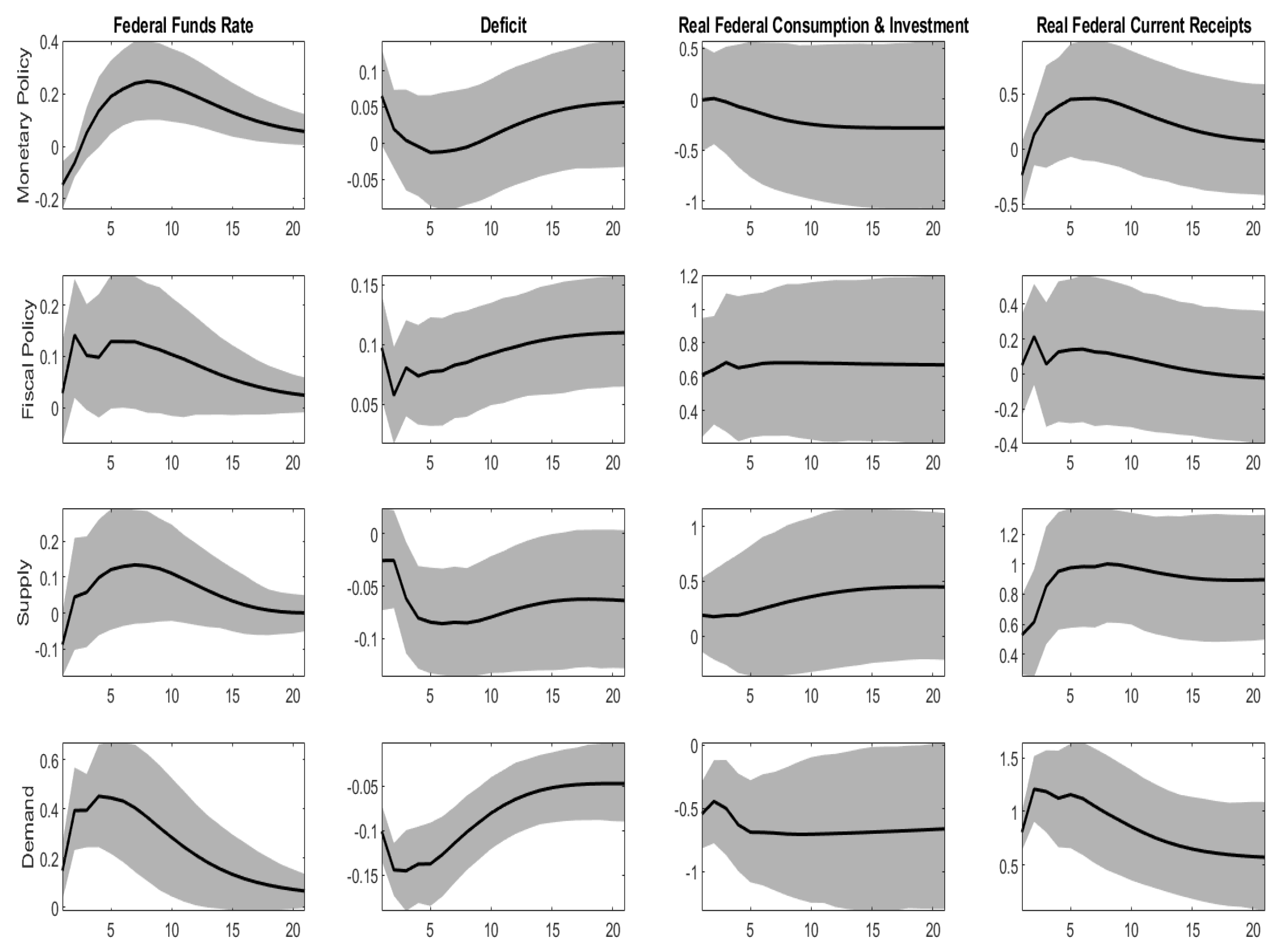
3.1. Data, Data Treatment and Specification of the Number of Factors
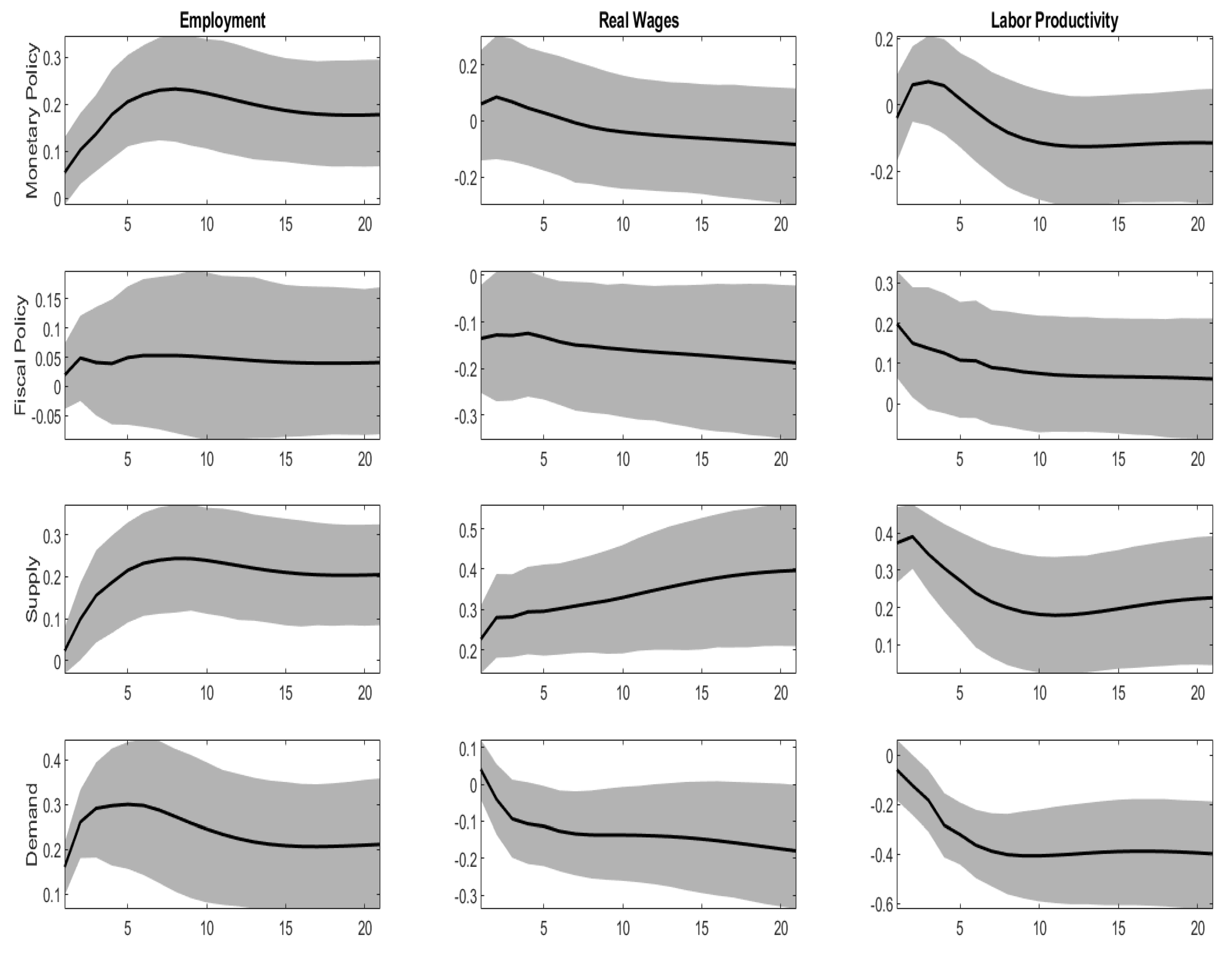
3.2. How Many Macroeconomic Shocks?
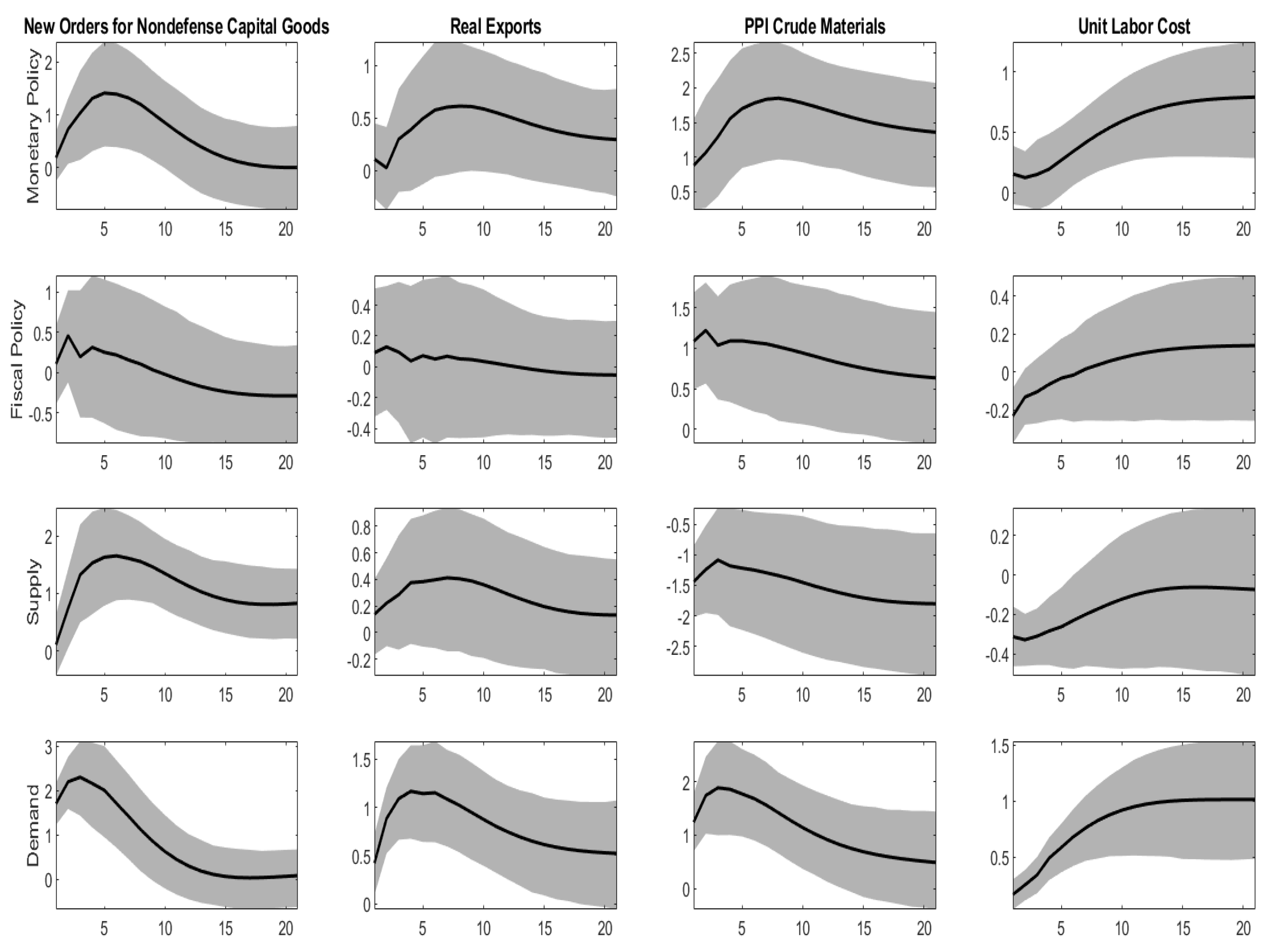
3.3. Identifying Restrictions
4. Results
4.1. Validating the Identification of Structural Shocks
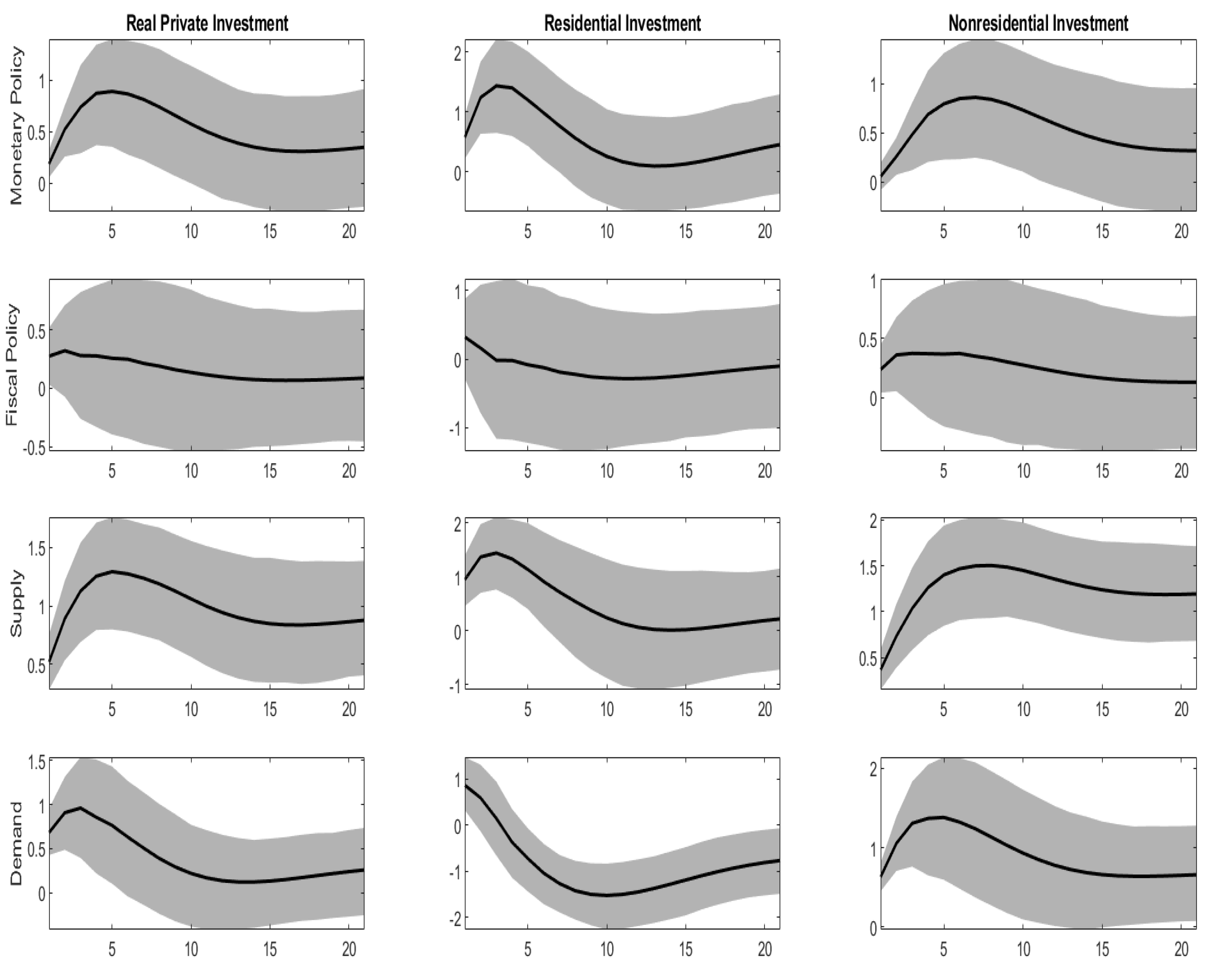
4.2. The Relative Importance of Demand and Supply Shocks
4.3. The Role of Monetary and Fiscal Policy
4.4. Demand Shocks, Employment and Labor Productivity
4.5. Policy Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Data
| No. Series | Transf. | Mnemonic | Long Label |
| 1 | 5 | GDPC1 | Real Gross Domestic Product, 1 Decimal |
| 2 | 5 | GNPC96 | Real Gross National Product |
| 3 | 5 | NICUR/GDPDEF | National Income/GDPDEF |
| 4 | 5 | DPIC96 | Real Disposable Personal Income |
| 5 | 5 | OUTNFB | Nonfarm Business Sector: Output |
| 6 | 5 | FINSLC1 | Real Final Sales of Domestic Product, 1 Decimal |
| 7 | 5 | FPIC1 | Real Private Fixed Investment, 1 Decimal |
| 8 | 5 | PRFIC1 | Real Private Residential Fixed Investment, 1 Decimal |
| 9 | 5 | PNFIC1 | Real Private Nonresidential Fixed Investment, 1 Decimal |
| 10 | 5 | GPDIC1 | Real Gross Private Domestic Investment, 1 Decimal |
| 11 | 5 | PCECC96 | Real Personal Consumption Expenditures |
| 12 | 5 | PCNDGC96 | Real Personal Consumption Expenditures: Nondurable Goods |
| 13 | 5 | PCDGCC96 | Real Personal Consumption Expenditures: Durable Goods |
| 14 | 5 | PCESVC96 | Real Personal Consumption Expenditures: Services |
| 15 | 5 | GPSAVE/GDPDEF | Gross Private Saving/GDP Deflator |
| 16 | 5 | FGCEC1 | Real Federal Consumption Expenditures & Gross Investment, 1 Decimal |
| 17 | 5 | FGEXPND/GDPDEF | Federal Government: Current Expenditures/GDP deflator |
| 18 | 5 | FGRECPT/GDPDEF | Federal Government Current Receipts/GDP deflator |
| 19 | 2 | FGDEF | Federal Real Expend-Real Receipts |
| 20 | 1 | CBIC1 | Real Change in Private Inventories, 1 Decimal |
| 21 | 5 | EXPGSC1 | Real Exports of Goods & Services, 1 Decimal |
| 22 | 5 | IMPGSC1 | Real Imports of Goods & Services, 1 Decimal |
| 23 | 5 | CP/GDPDEF | Corporate Profits After Tax/GDP deflator |
| 24 | 5 | NFCPATAX/GDPDEF | Nonfinancial Corporate Business: Profits After Tax/GDP deflator |
| 25 | 5 | CNCF/GDPDEF | Corporate Net Cash Flow/GDP deflator |
| 26 | 5 | DIVIDEND/GDPDEF | Net Corporate Dividends/GDP deflator |
| 27 | 5 | HOANBS | Nonfarm Business Sector: Hours of All Persons |
| 28 | 5 | OPHNFB | Nonfarm Business Sector: Output Per Hour of All Persons |
| 29 | 5 | UNLPNBS | Nonfarm Business Sector: Unit Nonlabor Payments |
| 30 | 5 | ULCNFB | Nonfarm Business Sector: Unit Labor Cost |
| 31 | 5 | WASCUR/CPI | Compensation of Employees: Wages & Salary Accruals/CPI |
| 32 | 5 | COMPNFB | Nonfarm Business Sector: Compensation Per Hour |
| 33 | 5 | COMPRNFB | Nonfarm Business Sector: Real Compensation Per Hour |
| 34 | 5 | GDPCTPI | Gross Domestic Product: Chain-type Price Index |
| 35 | 5 | GNPCTPI | Gross National Product: Chain-type Price Index |
| 36 | 5 | GDPDEF | Gross Domestic Product: Implicit Price Deflator |
| 37 | 5 | GNPDEF | Gross National Product: Implicit Price Deflator |
| 38 | 5 | INDPRO | Industrial Production Index |
| 39 | 5 | IPBUSEQ | Industrial Production: Business Equipment |
| 40 | 5 | IPCONGD | Industrial Production: Consumer Goods |
| 41 | 5 | IPDCONGD | Industrial Production: Durable Consumer Goods |
| 42 | 5 | IPFINAL | Industrial Production: Final Products (Market Group) |
| 43 | 5 | IPMAT | Industrial Production: Materials |
| 44 | 5 | IPNCONGD | Industrial Production: Nondurable Consumer Goods |
| 45 | 1 | AWHMAN | Average Weekly Hours: Manufacturing |
| 46 | 2 | AWOTMAN | Average Weekly Hours: Overtime: Manufacturing |
| 47 | 2 | CIVPART | Civilian Participation Rate |
| 48 | 5 | CLF16OV | Civilian Labor Force |
| 49 | 5 | CE16OV | Civilian Employment |
| 50 | 5 | USPRIV | All Employees: Total Private Industries |
| 51 | 5 | USGOOD | All Employees: Goods-Producing Industries |
| 52 | 5 | SRVPRD | All Employees: Service-Providing Industries |
| 53 | 5 | UNEMPLOY | Unemployed |
| 54 | 5 | UEMPMEAN | Average (Mean) Duration of Unemployment |
| 55 | 1 | UNRATE | Civilian Unemployment Rate |
| 56 | 5 | HOUST | Housing Starts: Total: New Privately Owned Housing Units Started |
| 57 | 1 | FEDFUNDS | Effective Federal Funds Rate |
| 58 | 1 | TB3MS | 3-Month Treasury Bill: Secondary Market Rate |
| 59 | 1 | GS1 | 1-Year Treasury Constant Maturity Rate |
| 60 | 1 | GS10 | 10-Year Treasury Constant Maturity Rate |
| 61 | 1 | AAA | Moody’s Seasoned Aaa Corporate Bond Yield |
| 62 | 1 | BAA | Moody’s Seasoned Baa Corporate Bond Yield |
| 63 | 1 | MPRIME | Bank Prime Loan Rate |
| 64 | 5 | BOGNONBR | Non-Borrowed Reserves of Depository Institutions |
| 65 | 5 | TRARR | Board of Governors Total Reserves, Adjusted for Changes in Reserve |
| 66 | 5 | BOGAMBSL | Board of Governors Monetary Base, Adjusted for Changes in Reserve |
| 67 | 5 | M1SL | M1 Money Stock |
| 68 | 5 | M2MSL | M2 Minus |
| 69 | 5 | M2SL | M2 Money Stock |
| 70 | 5 | BUSLOANS | Commercial and Industrial Loans at All Commercial Banks |
| 71 | 5 | CONSUMER | Consumer (Individual) Loans at All Commercial Banks |
| 72 | 5 | LOANINV | Total Loans and Investments at All Commercial Banks |
| 73 | 5 | REALLN | Real Estate Loans at All Commercial Banks |
| 74 | 5 | TOTALSL | Total Consumer Credit Outstanding |
| 75 | 5 | CPIAUCSL | Consumer Price Index For All Urban Consumers: All Items |
| 76 | 5 | CPIULFSL | Consumer Price Index for All Urban Consumers: All Items Less Food |
| 77 | 5 | CPILEGSL | Consumer Price Index for All Urban Consumers: All Items Less Energy |
| 78 | 5 | CPILFESL | Consumer Price Index for All Urban Consumers: All Items Less Food & Energy |
| 79 | 5 | CPIENGSL | Consumer Price Index for All Urban Consumers: Energy |
| 80 | 5 | CPIUFDSL | Consumer Price Index for All Urban Consumers: Food |
| 81 | 5 | PPICPE | Producer Price Index Finished Goods: Capital Equipment |
| 82 | 5 | PPICRM | Producer Price Index: Crude Materials for Further Processing |
| 83 | 5 | PPIFCG | Producer Price Index: Finished Consumer Goods |
| 84 | 5 | PPIFGS | Producer Price Index: Finished Goods |
| 85 | 5 | OILPRICE | Spot Oil Price: West Texas Intermediate |
| 86 | 5 | USSHRPRCF | US Dow Jones Industrials Share Price Index (EP) NADJ |
| 87 | 5 | US500STK | US Standard & Poor’s Index if 500 Common Stocks |
| 88 | 5 | USI62...F | US Share Price Index NADJ |
| 89 | 5 | USNOIDN.D | US Manufacturers New Orders for Non Defense Capital Goods (BCI 27) |
| 90 | 5 | USCNORCGD | US New Orders of Consumer Goods & Materials (BCI 8) CONA |
| 91 | 1 | USNAPMNO | US ISM Manufacturers Survey: New Orders Index SADJ |
| 92 | 5 | USVACTOTO | US Index of Help Wanted Advertising VOLA |
| 93 | 5 | USCYLEAD | US The Conference Board Leading Economic Indicators Index SADJ |
| 94 | 5 | USECRIWLH | US Economic Cycle Research Institute Weekly Leading Index |
| 95 | 5 | GS10-FEDFUNDS | |
| 96 | 5 | GS1-FEDFUNDS | |
| 97 | 5 | BAA-FEDFUNDS | |
| 98 | 5 | GEXPND/GDPDEF | Government Current Expenditures/GDP deflator |
| 99 | 5 | GRECPT/GDPDEF | Government Current Receipts/GDP deflator |
| 100 | 1 | GDEF | Governnent Real Expend-Real Receipts |
| 101 | 5 | GCEC1 | Real Government Consumption Expenditures & Gross Investment, 1 Decimal |
| 102 | 1 | GS5 | 5-Year Treasury Constant Maturity Rate |
| 1 | An alternative approach is represented by Banbura et al. (2010), which develops a Bayesian VAR model that can handle many economic time series. |
| 2 | Observe that, if , the residuals of the above VAR relation have a singular variance covariance matrix. Equations (1) to (3) need further qualification to ensure that all of the factors are loaded, so to speak, by enough variables with large enough loadings (see FGLR, Assumption 4); this “pervasiveness” condition is necessary to have uniqueness of the common and the idiosyncratic components, as well as the number of static factors r and dynamic factors q. |
| 3 | Unlike the dynamic factors, the static factors do not have a structural economic interpretation; rather, they are a statistical tool which is useful to model the dynamics of the system. Loosely speaking, given the number of primitive shocks q, the number of “static factors” r governs the “degree of heterogeneity” of the impulse–response functions. For instance, in the simple case , if all the impulse–response functions are proportional. On the other hand, if r is larger, different variables can load the shock with different delays, so that we may have leading, coincident and lagging variables. If r is large enough, any (finite order) MA dynamics can be written in the form (1)–(3) (FGLR, Section 2). |
| 4 | Note that has to be large enough to retain relevant lagged auto- and cross-covariances. |
| 5 | We impose an upper bound to the number of impulse–response functions to retain for each step of the bootstrap procedure in order to avoid that a single bootstrap provide a disproportionately large number of functions. |
| 6 | Outliers were detected as values differing from the median more than 6 times the interquartile difference and replaced with the median of the five previous observations. |
| 7 | The test has two parameters identifying the lower and the upper bound of the frequencies of interest. Since we are mainly interested in business cycle fluctuations, we set such parameters in such a way to include waves of periodicity between 2 and 12 years. |
| 8 | The Bai and Ng criteria have two parameters. We set for all criteria and , , , . Such values produced good results in our simulations (not shown here). |
| 9 | The real federal deficit is constructed as the difference between current federal expenditures and current federal receipts, divided by the GDP deflator. |
| 10 | For the monetary policy shock a similar picture emerges but the effect on labor productivity is not significant. |
| 11 | According to the above explanations, productivity is related to the business cycle, rather than demand per se). This is consistent with our estimated response of productivity to supply shocks, which reaches its maximum after about one year and then declines sharply, dissipating about one half of the impact effect in the following six quarters (see Figure 6). |
References
- Aghion, Philippe, and Gilles Saint-Paul. 1998. Virtues of Bad Times: Interaction between Productivity Growth and Economic Fluctuations. Macroeconomic Dynamics 2: 322–44. [Google Scholar] [CrossRef]
- Altissimo, Filippo, Riccardo Cristadoro, Mario Forni, Marco Lippi, and Giovanni Veronese. 2010. New EuroCOIN: Tracking Economic Growth in Real Time. The Review of Economics and Statistics 92: 1024–34. [Google Scholar] [CrossRef]
- Alessi, Lucia, and Mark Kerssenfischer. 2019. The response of asset prices to monetary policy shocks: Stronger than thought. Journal of Applied Econometrics 34: 661–72. [Google Scholar] [CrossRef]
- Altug, Sumru. 1989. Time-to-Build and Aggregate Fluctuations: Some New Evidence. International Economic Review 30: 889–920. [Google Scholar] [CrossRef] [Green Version]
- Amengual, Dante, and Mark W. Watson. 2007. Consistent Estimation of the Number of Dynamic Factors in a Large N and T Panel. Journal of Business and Economic Statistics 25: 91–96. [Google Scholar] [CrossRef]
- Bai, Jushan. 2003. Inferential Theory for Factor Models of Large Dimensions. Econometrica 71: 135–71. [Google Scholar] [CrossRef]
- Bai, Jushan, and Serena Ng. 2002. Determining the number of factors in approximate factor models. Econometrica 70: 191–221. [Google Scholar] [CrossRef] [Green Version]
- Bai, Jushan, and Serena Ng. 2007. Determining the Number of Primitive Shocks in Factor Models. Journal of Business and Economic Statistics 25: 52–60. [Google Scholar] [CrossRef] [Green Version]
- Banbura, Marta, Domenico Giannone, and Lucrezia Reichlin. 2010. Large Bayesian vector auto regressions. Journal of Applied Econometrics 25: 71–92. [Google Scholar] [CrossRef]
- Bean, Charles R. 1990. Endogenous growth and the pro-cyclical behaviour of productivity. European Economic Review 34: 355–63. [Google Scholar] [CrossRef]
- Bernanke, Ben, and Jean Boivin. 2003. Monetary policy in a data-rich environment. Journal of Monetary Economics 50: 525–46. [Google Scholar] [CrossRef] [Green Version]
- Bernanke, Ben S., Jean Boivin, and Piotr Eliasz. 2005. Measuring Monetary Policy: A Factor Augmented Autoregressive (FAVAR) Approach. Quarterly Journal of Economics 120: 387–422. [Google Scholar]
- Blanchard, Olivier Jean, and Danny Quah. 1989. The Dynamic Effects of Aggregate Demand and Supply Disturbances. American Economic Review 79: 655–73. [Google Scholar]
- Blanchard, Olivier Jean, and Roberto Perotti. 2002. An Empirical Characterization of the Dynamic Effects of Changes in Government Spending and Taxes on Output. Quarterly Journal of Economics 117: 1329–68. [Google Scholar] [CrossRef] [Green Version]
- Caballero, Ricardo, and Mohamad L. Hammour. 1994. The Cleansing Effect of Recessions. American Economic Review 84: 1350–68. [Google Scholar]
- Chamberlain, Gary. 1983. Funds, factors, and diversification in arbitrage pricing models. Econometrica 51: 1281–304. [Google Scholar] [CrossRef] [Green Version]
- Chamberlain, Gary, and Michael Rothschild. 1983. Arbitrage, factor structure and mean variance analysis in large asset markets. Econometrica 51: 1305–24. [Google Scholar] [CrossRef]
- Christiano, Lawrence J., Martin Eichenbaum, and Charles L. Evans. 1999. Monetary policy shocks: What have we learned and to what end? In Handbook of Macroeconomics. Amsterdam: Elsevier, vol. 1, pp. 65–148. [Google Scholar]
- Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson. 2004. The Response of Hours to a Technology Shock: Evidence Based on Direct Measures of Technology. Journal of the European Economic Association 2: 381–95. [Google Scholar] [CrossRef] [Green Version]
- Connor, Gregory, and Robert A. Korajczyk. 1988. Risk and return in an equilibrium APT. Application of a new test methodology. Journal of Financial Economics 21: 255–89. [Google Scholar] [CrossRef]
- Davis, Steven, and John Haltiwanger. 1992. Gross Job Creation, Gross Job Destruction, and Employment Reallocation. The Quarterly Journal of Economics 107: 819–63. [Google Scholar] [CrossRef]
- Forni, Mario, and Luca Gambetti. 2010. The Dynamic Effects of Monetary Policy: A Structural Factor Model Approach. Journal of Monetary Economics 57: 203–13. [Google Scholar] [CrossRef]
- Forni, Mario, Domenico Giannone, Marco Lippi, and Lucrezia Reichlin. 2009. Opening the black box: Structural factor models with large cross-sections. Econometric Theory 25: 1319–47. [Google Scholar] [CrossRef] [Green Version]
- Forni, Mario, Marc Hallin, Marco Lippi, and Lucrezia Reichlin. 2000. The generalized dynamic factor model: Identification and estimation. The Review of Economics and Statistics 82: 540–54. [Google Scholar] [CrossRef]
- Forni, Mario, Marc Hallin, Marco Lippi, and Lucrezia Reichlin. 2005. The generalized factor model: One-sided estimation and forecasting. Journal of the American Statistical Association 100: 830–40. [Google Scholar] [CrossRef] [Green Version]
- Forni, Mario, and Marco Lippi. 2001. The generalized dynamic factor model: Representation theory. Econometric Theory 17: 1113–41. [Google Scholar] [CrossRef] [Green Version]
- Galí, Jordi. 1999. Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations? American Economic Review 89: 249–71. [Google Scholar] [CrossRef] [Green Version]
- Galí, Jordi, and Mohamad Hammour. 1992. Long-Run Effects of Business Cycles Papers 92–26. Columbia: Graduate School of Business. [Google Scholar]
- Geweke, John. 1977. The dynamic factor analysis of economic time series. In Latent Variables in Socio-Economic Models. Amsterdam: North Holland. [Google Scholar]
- King, Robert, Charles Plosser, James Stock, and Mark Watson. 1991. Stochastic Trends and Economic Fluctuations. American Economic Review 81: 819–40. [Google Scholar]
- Hall, Robert E. 1991. Recessions as reorganizations. In NBER Macroeconomics Annual. Cambridge: NBER. [Google Scholar]
- Hallin, Marc, and Roman Liška. 2007. Determining the number of factors in the general dynamic factor model. Journal of the American Statistical Association 102: 603–17. [Google Scholar] [CrossRef]
- Ireland, Peter N. 2004. A method for taking models to the data. Journal of Economic Dynamics and Control 28: 1205–26. [Google Scholar] [CrossRef] [Green Version]
- Leeper, Eric, Todd Walker, and Shu-Chun Yang. 2013. Fiscal Foresight and Information Flows. Econometrica 81: 1115–45. [Google Scholar]
- Lippi, Marco, and Lucrezia Reichlin. 1994. VAR analysis, non fundamental representation, Blaschke matrices. Journal of Econometrics 63: 307–25. [Google Scholar] [CrossRef]
- Quah, Danny. 1990. Permanent and Transitory Movements in Labor Income: An Explanation for “Excess Smoothness” in Consumption. Journal of Political Economy 98: 449–75. [Google Scholar] [CrossRef] [Green Version]
- Ramey, Valery A. 2011. Identifying Government Spending Shocks: It’s All in the Timing. Quarterly Journal of Economics 126: 1–50. [Google Scholar] [CrossRef]
- Ramey, Valery A., and Matthew D. Shapiro. 1998. Costly Capital Reallocation and the Effects of Government Spending. Carnegie Rochester Conference on Public Policy 48: 145–94. [Google Scholar] [CrossRef] [Green Version]
- Saint-Paul, Gilles. 1993. Productivity growth and the structure of the business cycle. European Economic Review 37: 861–83. [Google Scholar] [CrossRef]
- Sargent, Thomas J. 1989. Two Models of Measurements and the Investment Accelerator. The Journal of Political Economy 97: 251–87. [Google Scholar] [CrossRef]
- Sargent, Thomas J., and Christopher A. Sims. 1977. Business cycle modeling without pretending to have too much a priori economic theory. In New Methods in Business Research. Minneapolis: Federal Reserve Bank of Minneapolis. [Google Scholar]
- Sims, Christopher A. 1980. Macroeconomics and Reality. Econometrica 48: 1–48. [Google Scholar] [CrossRef] [Green Version]
- Sims, Christopher A. 1992. Interpreting the Macroeconomic Time Series Facts, The Effects of Monetary Policy. European Economic Review 36: 975–1011. [Google Scholar] [CrossRef]
- Smets, Frank, and Rafael Wouters. 2007. Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach. American Economic Review 97: 586–606. [Google Scholar] [CrossRef] [Green Version]
- Stock, James H., and Mark W. Watson. 2002a. Macroeconomic Forecasting Using Diffusion Indexes. Journal of Business and Economic Statistics 20: 147–62. [Google Scholar] [CrossRef] [Green Version]
- Stock, James H., and Mark W. Watson. 2002b. Forecasting Using Principal Components from a Large Number of Predictors. Journal of the American Statistical Association 97: 1167–79. [Google Scholar] [CrossRef] [Green Version]
- Stock, James H., and Mark W. Watson. 2005. Implications of Dynamic Factor Models for VAR Analysis. NBER Working Papers No. 11467. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Uhlig, Harald. 2005. What are the effects of monetary policy on output? Results from an agnostic identification procedure. Journal of Monetary Economics 52: 381–419. [Google Scholar] [CrossRef] [Green Version]


| Variable | MP | FP | S | D | MP+FP |
|---|---|---|---|---|---|
| GDP | 14.74 | 20.44 | 46.27 | 18.55 | 35.18 |
| Investment | 18.15 | 13.12 | 32.33 | 36.39 | 31.28 |
| Consumption | 14.91 | 12.15 | 54.10 | 18.84 | 27.06 |
| Gov. Exp.&Inv | 19.60 | 35.22 | 13.69 | 31.48 | 54.83 |
| Deficit | 24.74 | 30.13 | 13.21 | 31.92 | 54.87 |
| Industrial production | 12.12 | 14.86 | 27.82 | 45.20 | 26.98 |
| Employment | 20.22 | 10.41 | 21.23 | 48.15 | 30.62 |
| Unemployment | 24.16 | 14.68 | 26.38 | 34.78 | 38.84 |
| Real wage | 23.38 | 23.20 | 38.46 | 14.96 | 46.58 |
| Labor productivity | 14.28 | 21.23 | 49.56 | 14.92 | 35.52 |
| GDP deflator | 30.55 | 12.98 | 20.23 | 36.24 | 43.53 |
| CPI | 23.09 | 16.43 | 27.22 | 33.27 | 39.51 |
| PPI | 18.24 | 21.28 | 32.16 | 28.32 | 39.52 |
| Federal funds rate | 22.74 | 12.71 | 14.90 | 49.65 | 35.45 |
| 10-Year Bond Rate | 24.34 | 17.54 | 12.11 | 46.01 | 41.88 |
| AAA bond yeld | 23.58 | 17.61 | 14.44 | 44.36 | 41.19 |
| S&P500 | 24.70 | 19.22 | 42.62 | 13.46 | 43.92 |
| New orders | 17.56 | 11.79 | 19.26 | 51.39 | 29.36 |
| Variable | MP | FP | S | D | MP+FP |
|---|---|---|---|---|---|
| GDP | 4.64 | 24.61 | 57.14 | 13.61 | 29.25 |
| Investment | 6.39 | 13.04 | 31.71 | 48.86 | 19.44 |
| Consumption | 11.29 | 10.37 | 60.47 | 17.88 | 21.65 |
| Employment | 19.69 | 8.51 | 8.50 | 63.31 | 28.20 |
| GDP deflator | 18.21 | 11.88 | 35.68 | 34.23 | 30.09 |
| GDP | 9.90 | 15.09 | 60.33 | 14.68 | 24.99 |
| Investment | 19.65 | 10.54 | 40.98 | 28.82 | 30.19 |
| Consumption | 14.74 | 9.31 | 66.94 | 9.01 | 24.06 |
| Employment | 20.00 | 7.56 | 21.19 | 51.24 | 27.57 |
| GDP deflator | 24.20 | 10.59 | 27.37 | 37.84 | 34.78 |
| GDP | 9.18 | 13.94 | 65.89 | 11.00 | 23.11 |
| Investment | 21.14 | 13.84 | 45.51 | 19.51 | 34.98 |
| Consumption | 10.36 | 10.59 | 68.20 | 10.85 | 20.95 |
| Employment | 25.26 | 8.84 | 27.89 | 38.01 | 34.10 |
| GDP deflator | 34.29 | 12.68 | 13.99 | 39.04 | 46.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forni, M.; Gambetti, L. Policy and Business Cycle Shocks: A Structural Factor Model Representation of the US Economy. J. Risk Financial Manag. 2021, 14, 371. https://doi.org/10.3390/jrfm14080371
Forni M, Gambetti L. Policy and Business Cycle Shocks: A Structural Factor Model Representation of the US Economy. Journal of Risk and Financial Management. 2021; 14(8):371. https://doi.org/10.3390/jrfm14080371
Chicago/Turabian StyleForni, Mario, and Luca Gambetti. 2021. "Policy and Business Cycle Shocks: A Structural Factor Model Representation of the US Economy" Journal of Risk and Financial Management 14, no. 8: 371. https://doi.org/10.3390/jrfm14080371
APA StyleForni, M., & Gambetti, L. (2021). Policy and Business Cycle Shocks: A Structural Factor Model Representation of the US Economy. Journal of Risk and Financial Management, 14(8), 371. https://doi.org/10.3390/jrfm14080371





