Accuracy of European Stock Target Prices †
Abstract
:1. Introduction
2. Literature Overview
3. Data and Methodology
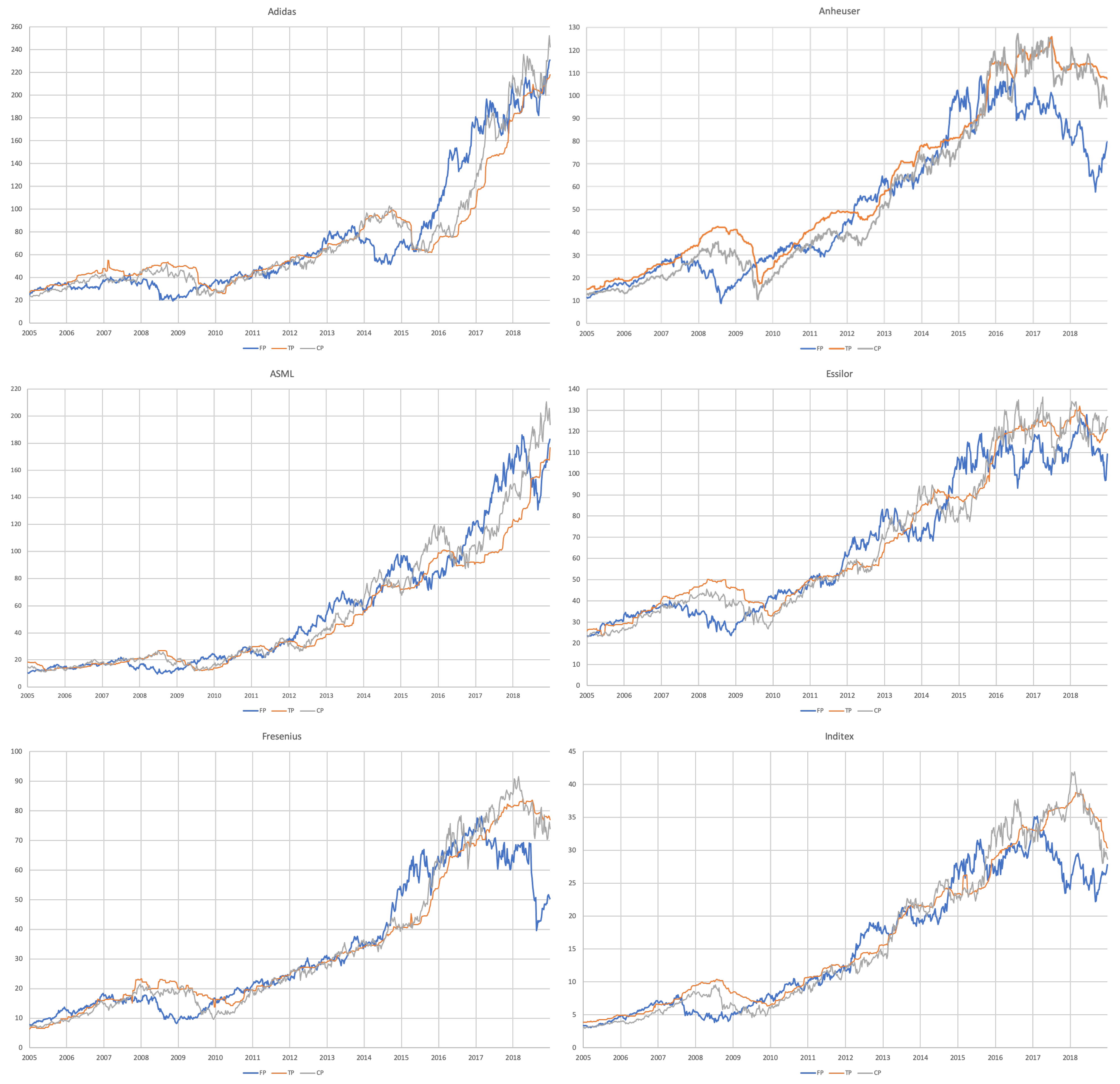
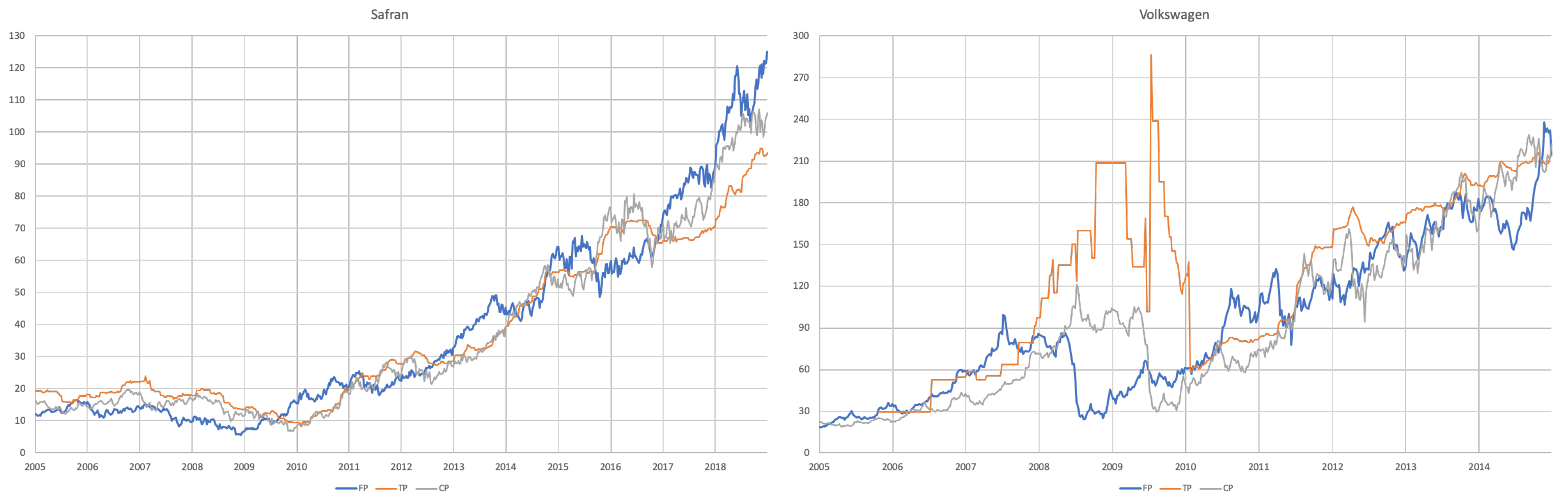
3.1. Data
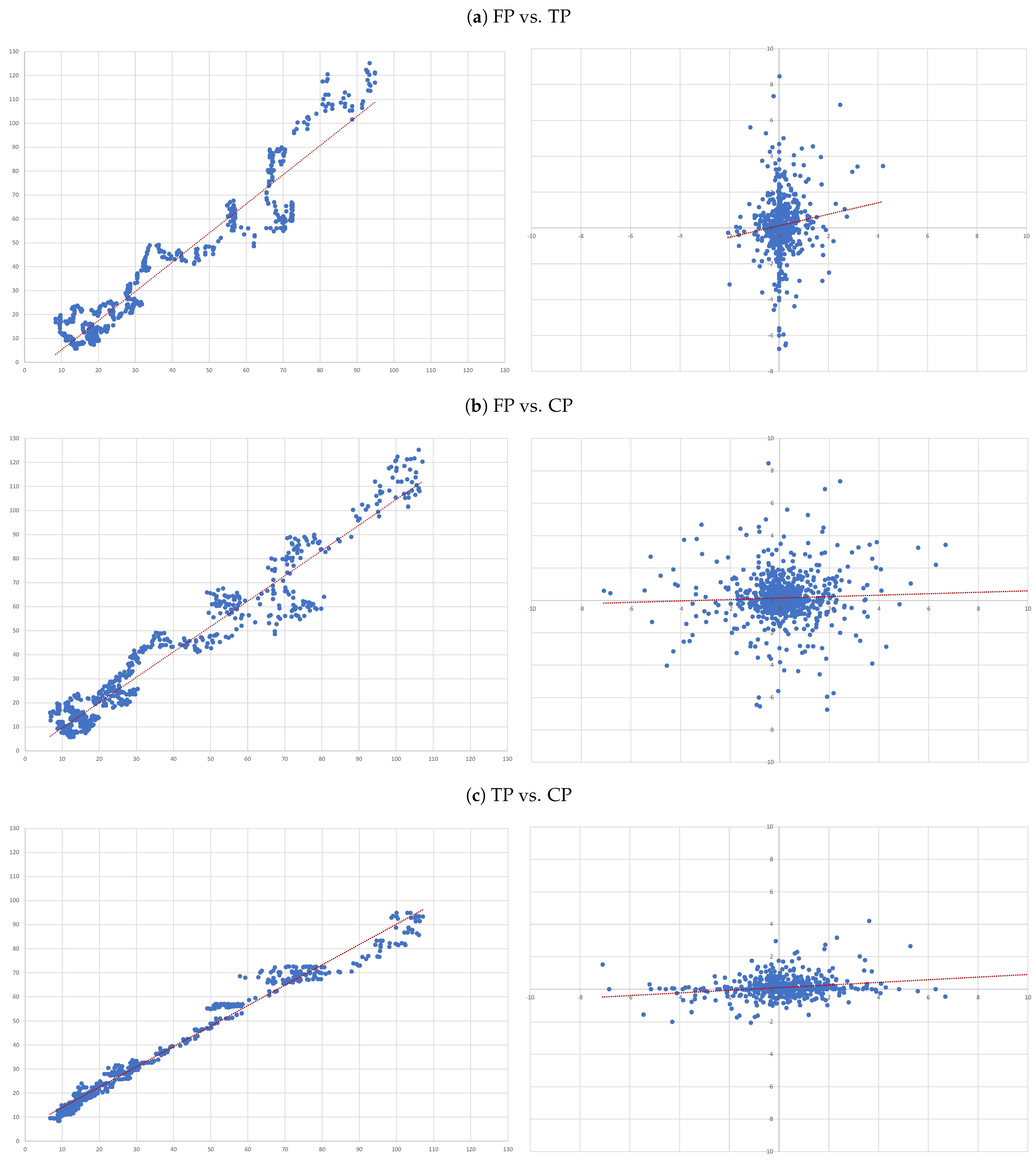
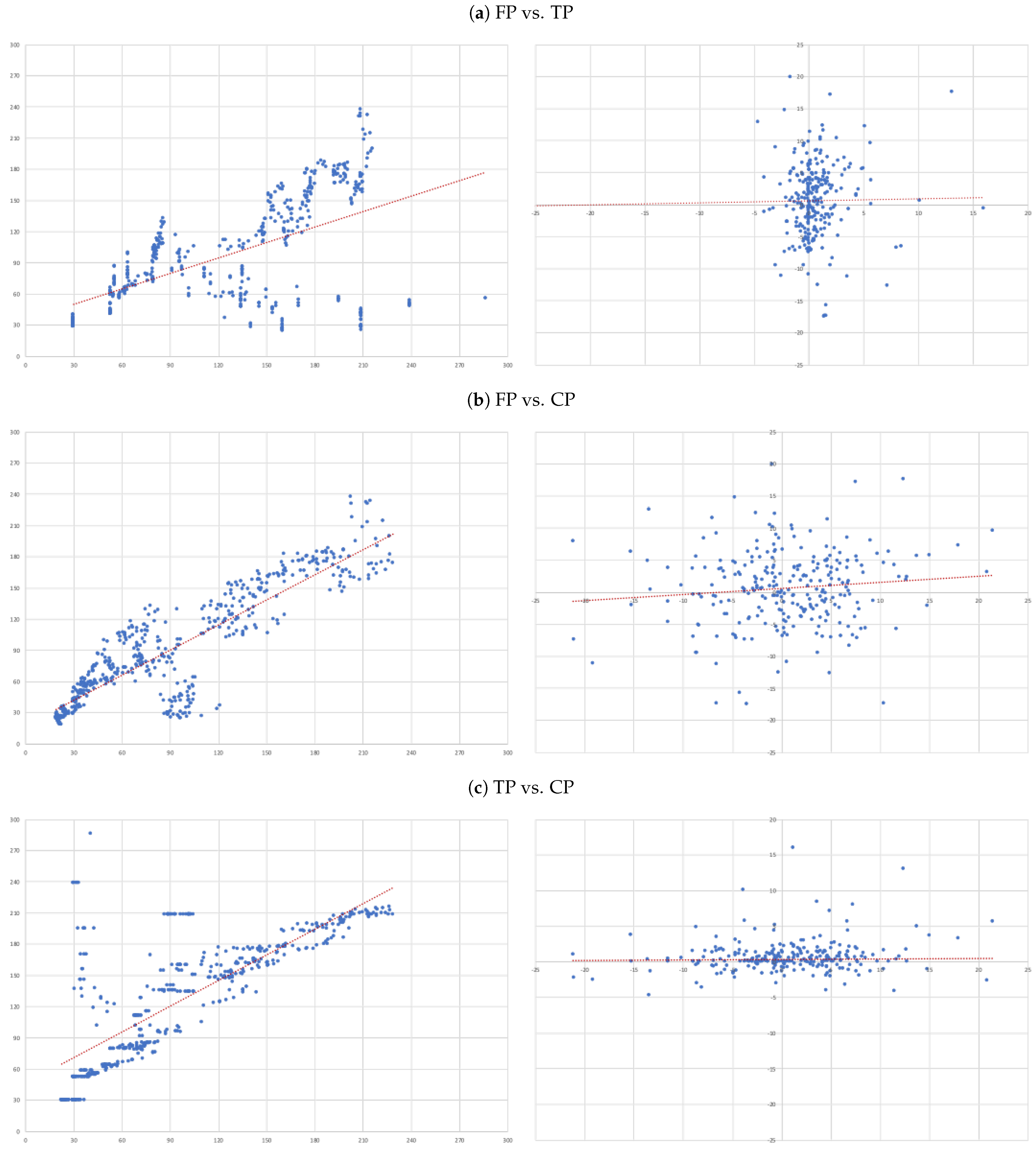
3.2. Research Design
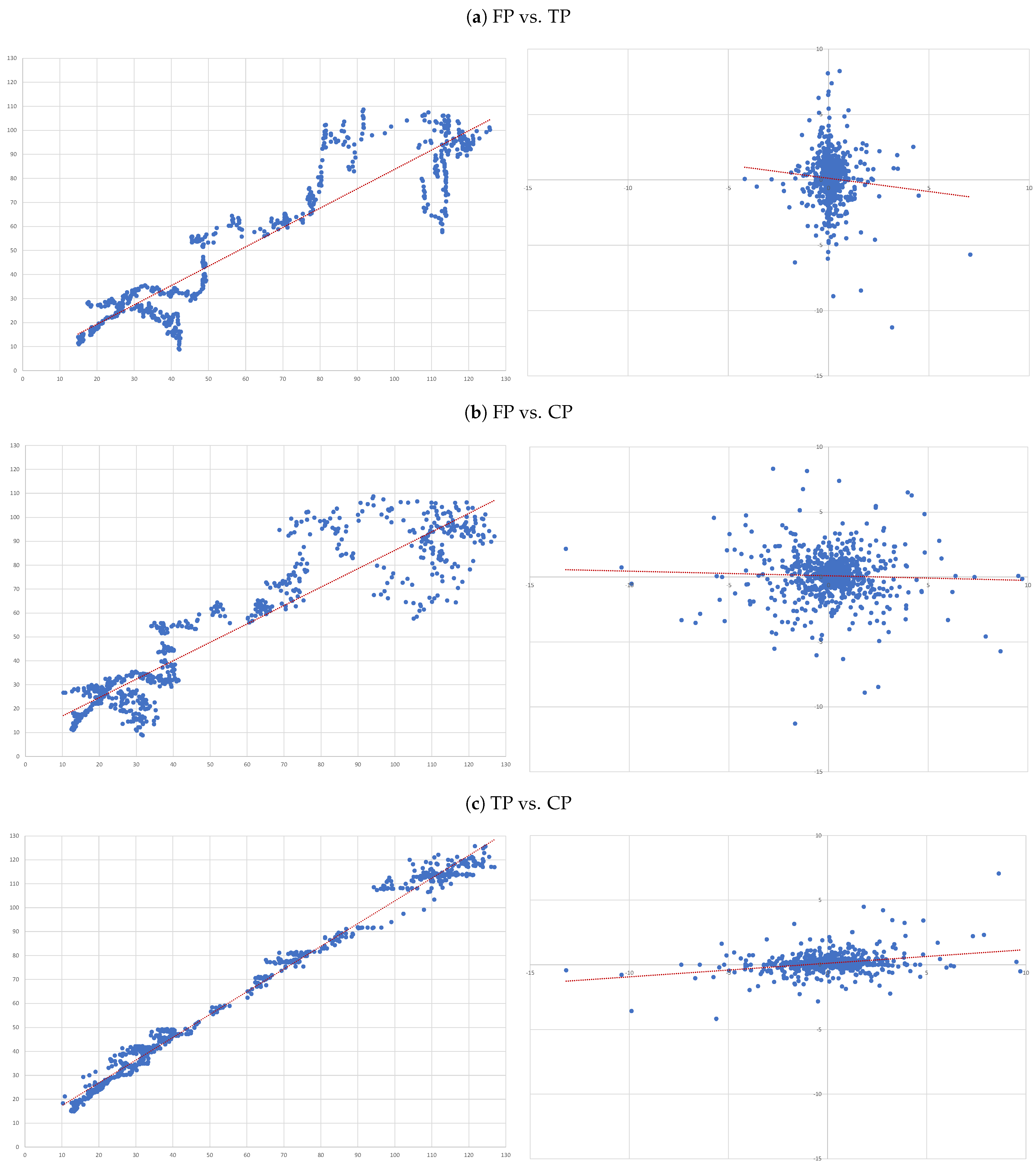
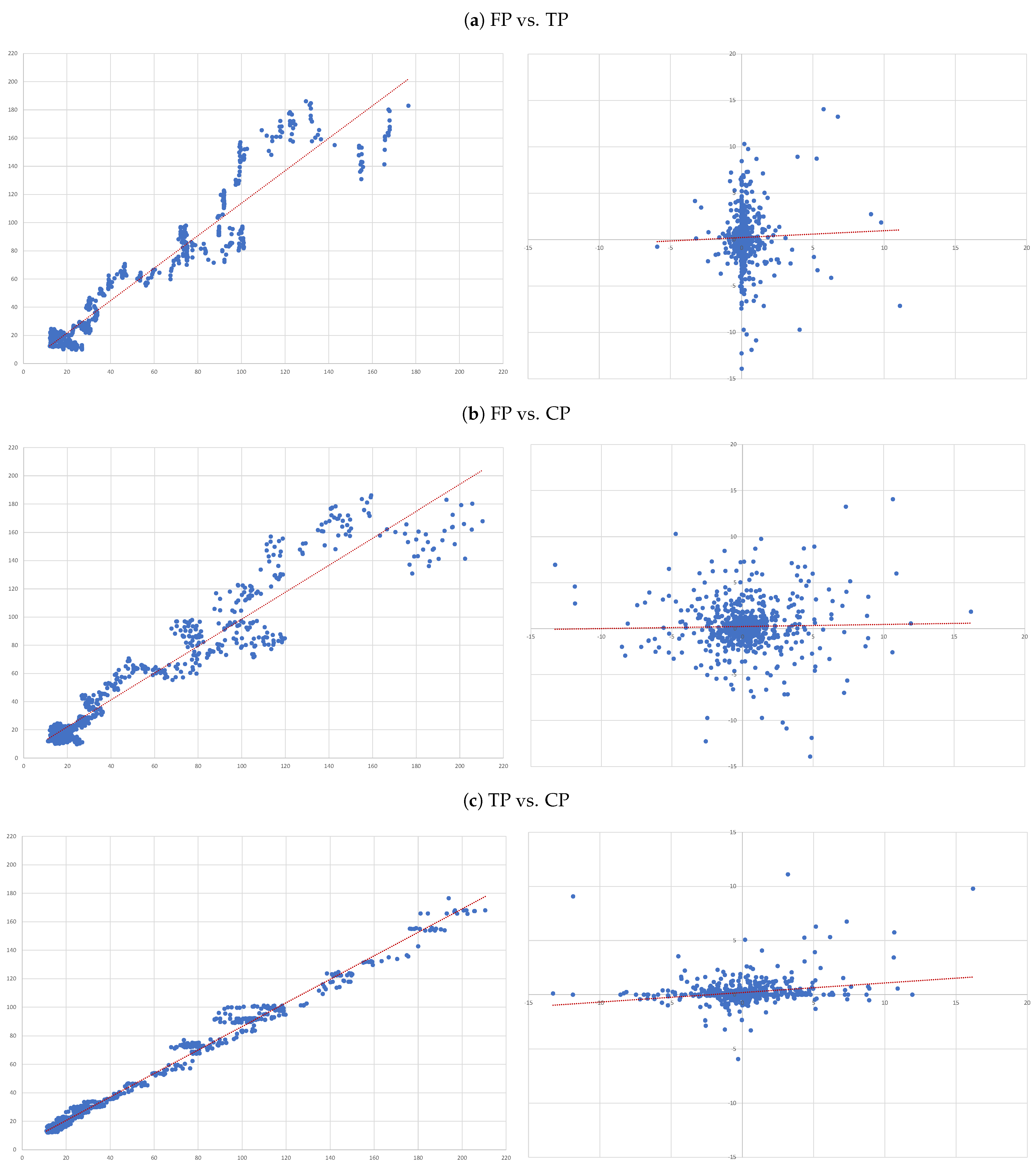
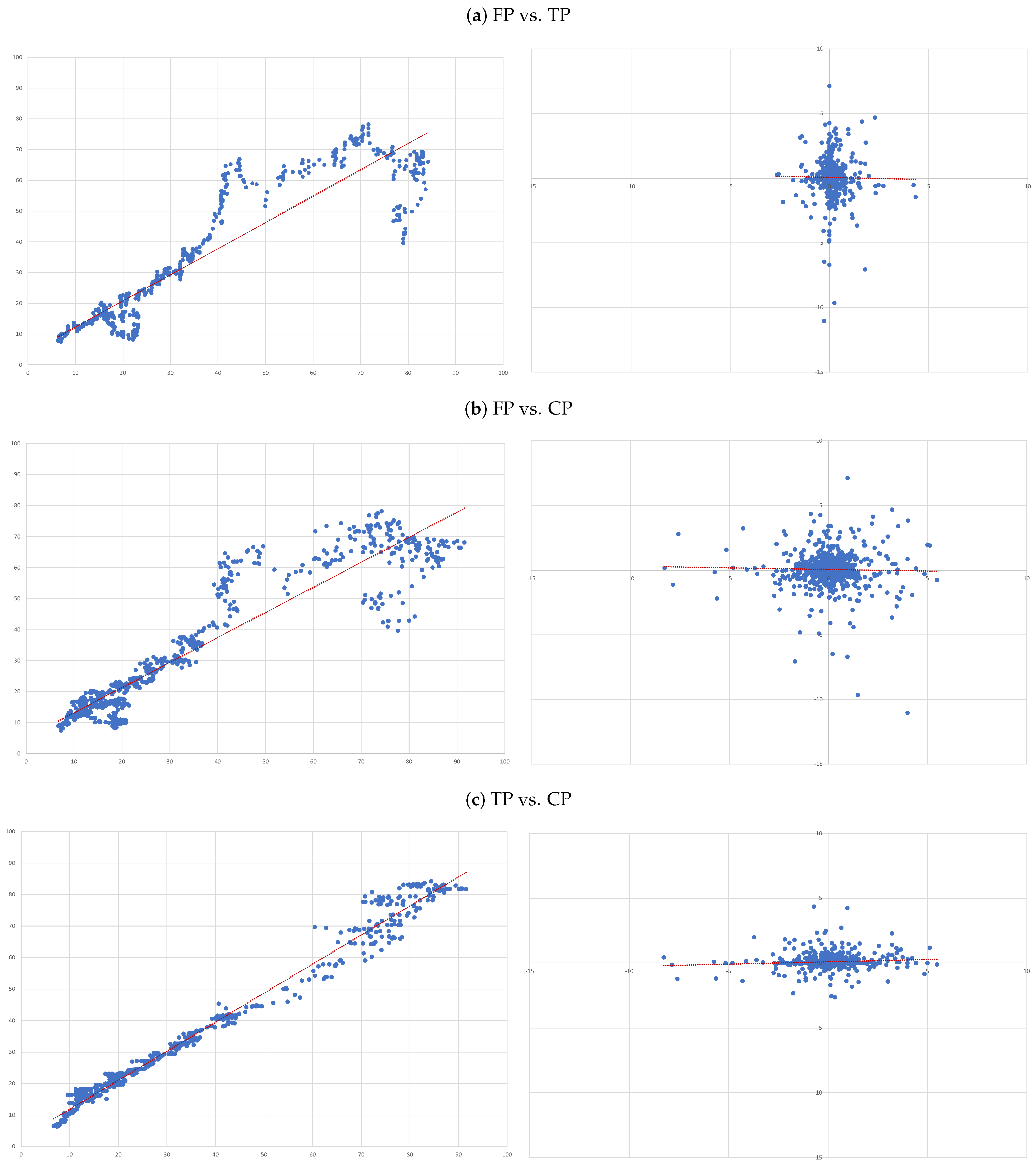
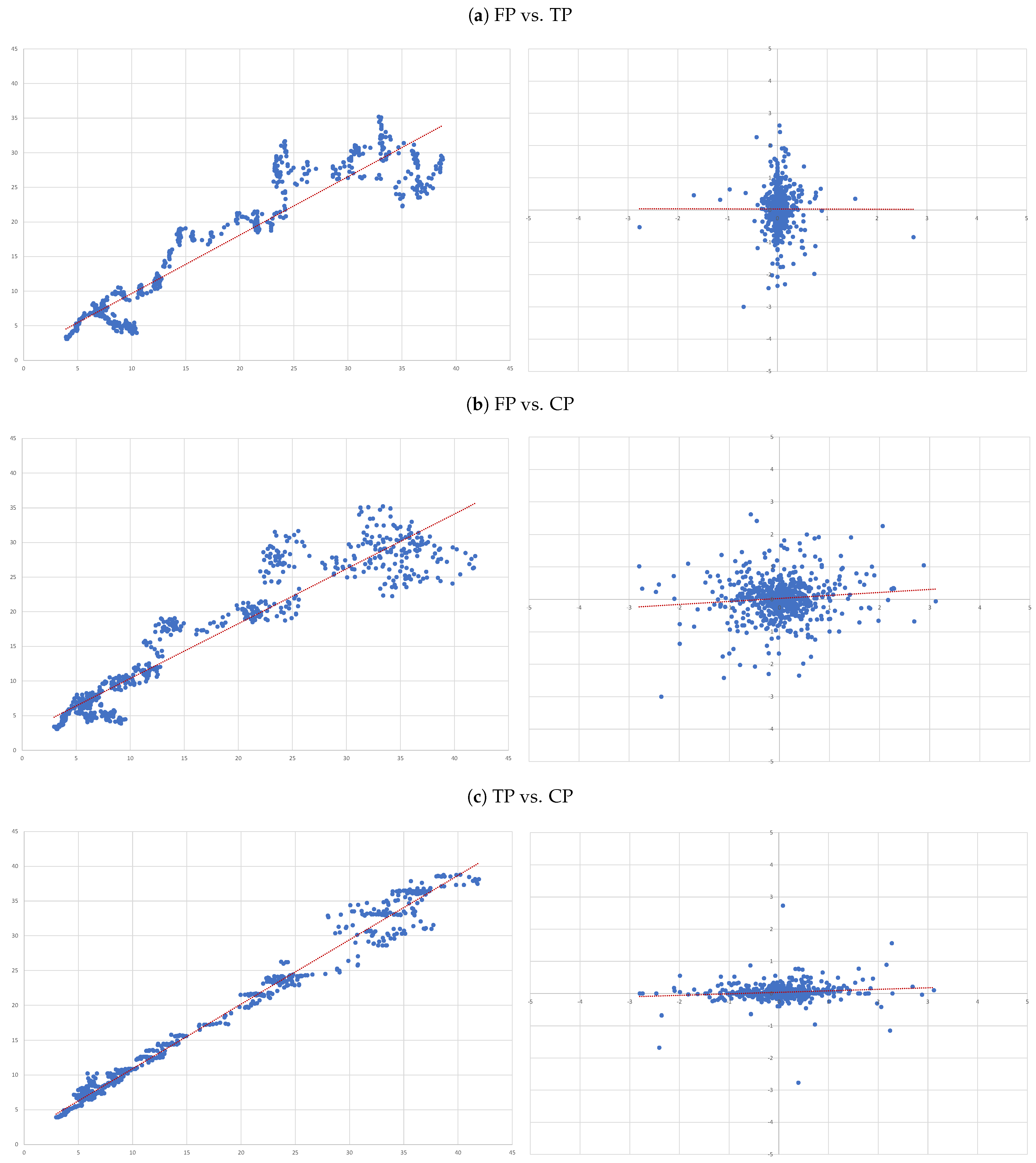
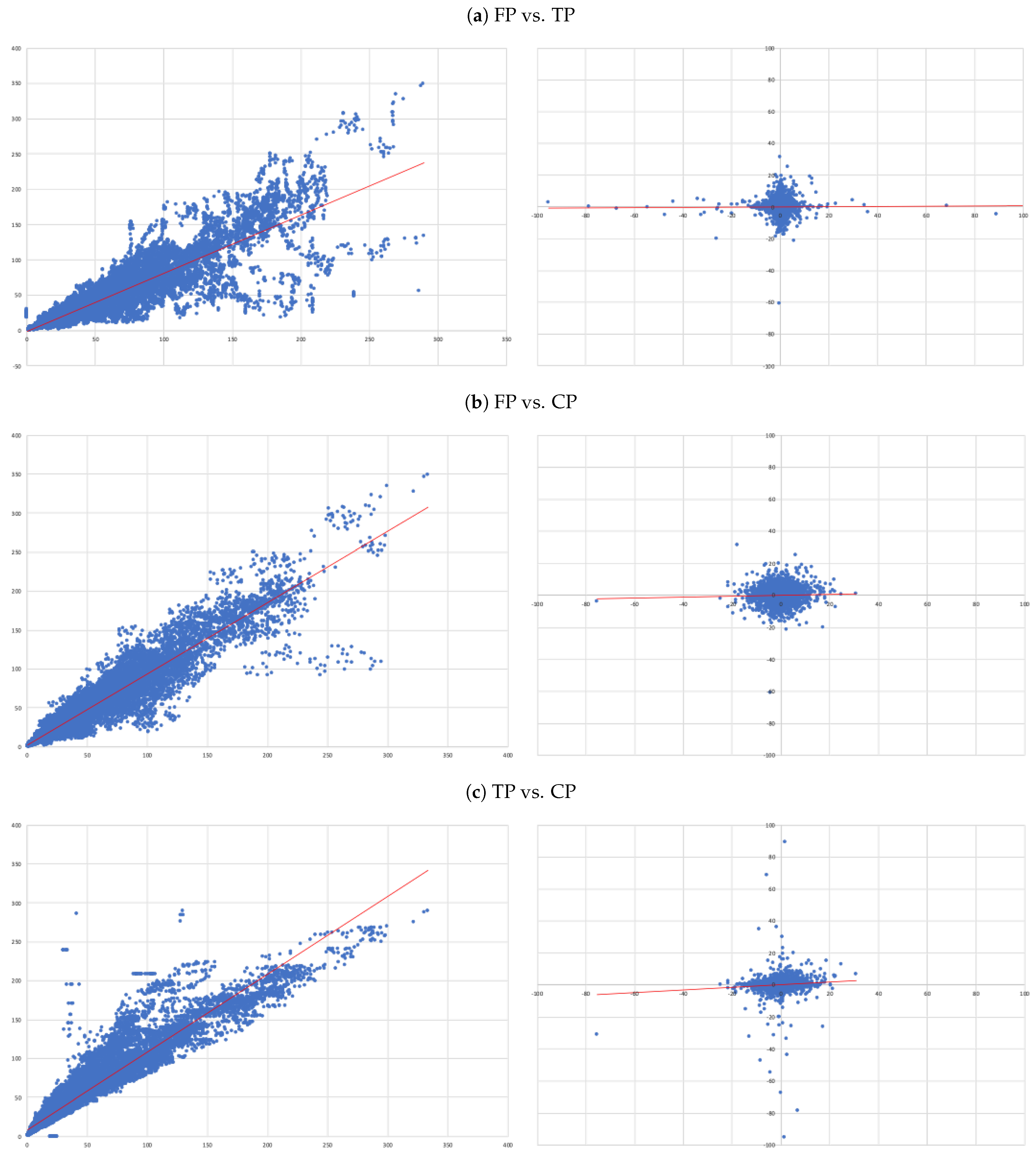
- (A)
- FP vs. TP: we evaluate the accuracy of TP forecasts made by analysts.
- (B)
- FP vs. CP: to compare the accuracy of a forecast as naive as CP to analysts’ TP forecast.
- (C)
- TP vs. CP: to evaluate to what extent TP can be determined by CP.
3.2.1. Overall Panel Regressions
3.2.2. Panel Robustness
- The pre-crisis period, until the end of August 2008;
- The crisis period, from September 2008 until the end of 2012;
- The pots crisis period, from 2013 onwards.
3.2.3. Individual Regressions
4. Results
4.1. Overall Panel Regressions
- In our overall sample and on average, target prices overestimate future prices (positive and statistically significant negative );
- While capitalised prices tend to under estimate them (positive and statistically significant positive ).
- Overall, there is no evidence that target prices can forecast future prices—the second column of results in Table 3. In fact, the regression not only shows and of 0.000, but also the coefficient associated with the independent variable is also not statistically different from zero (as attested by its t-statistics);
- The ability capitalised prices have to explain analysts’ forecasts is very limited—sixth column of results in Table 3. In fact, we only get an . Nonetheless, in relative terms this regression is the “best”, as attested by the all model selection statistics.
4.2. Panel Robustness
- The reason why, overall, our forecast variables (both TP and CP ) have no predicting power over future prices cannot be explained by firm-specific components.
- Firm-specific variables may explain optimism/pessimism in target prices forecasts, as we obtained a wide range of values.
- Analysts became particularly pessimistic during the crisis-period (positive and significant crisis period level intercept) and optimistic in the post-crisis period (negative and significant for the equivalent post-crisis intercept);
- Absence of accuracy, of both target prices and capitalised prices, became even more severe during the crisis period (lowest adjusted ).
4.3. Individual Regressions
- For each of the eight companies presented, the accuracy is not as bad as in the overall sample; the levels of the “FP vs TP” regressions range from 0.0012 (Inditex) to 0.1157 (Safran), suggesting that the accuracy of target prices is less than 12%, and varies considerably from firm to firm.
- Similarly, levels of the “FP vs CP” regressions range from 0.0021 (Essilor) to 0.1214 (Volkswagen), suggesting similar levels of accuracy of the two forecasts with target prices working better for some firms and capitalised prices for others.
- It is interesting that the highest levels are found for the “TP vs CP” regressions, where the levels range from 0.0904 (Fresenius) to as high as 0.3685 (Adidas), suggesting that at least between 10% and 35% of target prices can be explained by simple capitalisation rules.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| FP vs. TP | FP vs. CP | TP vs. CP | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Variable | ||||||
| Mean dependent var | 38.516 | 0.070 | 38.516 | 0.070 | 48.456 | 0.057 |
| S.D. Dependent var | 39.241 | 1.839 | 39.241 | 1.839 | 42.886 | 1.758 |
| Intercept | ||||||
| Coefficient | −0. 811 | 0.069406 | 4.186 | 0.068 | 14.029 | 0.051 |
| Std. Error | 0.179 | 0.010 | 0.108 | 0.010 | 0.090 | 0.009 |
| t-Statistic | −4.532 | 7.212 | 38.883 | 7.033 | 153.288 | 5.542 |
| Prob. | 0.000 | 0. 0000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Independent Variable | ||||||
| Coefficient | 0.812 | 0.004 | 0.857 | 0.026 | 0.859 | 0.080 |
| Std. Error | 0.003 | 0.005 | 0.002 | 0.005 | 0.002 | 0.005 |
| t-Statistic | 246.739 | 0.757 | 382.297 | 5.401 | 450.965 | 1.706 |
| Prob. | 0.000 | 0.449 | 0.000 | 0.000 | 0.000 | 0.000 |
| Regression Statistics | ||||||
| R-squared | 0.843 | 0.003 | 0.916 | 0.004 | 0.949 | 0.010 |
| Adjusted R-squared | 0.843 | 0.001 | 0.916 | 0.002 | 0.949 | 0.009 |
| S.E. Of regression | 15.544 | 1.838 | 11.350 | 1.837 | 9.649 | 1.750 |
| Sum square resid | 8,819,023 | 123,084 | 4,701,829 | 122,988 | 3,398,162 | 111,608 |
| Log Likelihood | −152,118 | −73,975 | −140,624 | −73,960 | −134,690 | −72,188 |
| F-statistic | 3928.6 | 2.014 | 8007.9 | 2.588 | 13,710 | 7.608 |
| Prob (F-statistic) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Model Statistics | ||||||
| AIC | 8.327 | 4.056 | 7.698 | 4.055 | 7.373 | 3.958 |
| BIC | 8.339 | 4.068 | 7.710 | 4.067 | 7.385 | 3.970 |
| HQC | 8.330 | 4.060 | 7.701 | 4.059 | 7.377 | 3.962 |
| Residuals Autocorr. | ||||||
| Durbi–Watson stat | 0.022 | 2.061 | 0.047 | 2.061 | 0.058 | 2.081 |
| FP vs. TP | FP vs. CP | TP vs. CP | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Variable | ||||||
| Mean dependent var | 28.077 | 0.035 | 28.077 | 0.035 | 41.649 | 0.135 |
| S.D. Dependent var | 23.214 | 1.196 | 23.214 | 1.196 | 35.118 | 1.750 |
| Intercept | ||||||
| Coefficient | 3.157 | 0.037 | 2.220 | 0.027 | 0.992 | 0.124 |
| Std. Error | 0.164 | 0.013 | 0.143 | 0.013 | 0.152 | 0.019 |
| t-Statistic | 19.289 | 2.873 | 15.503 | 2.135 | 6.527 | 6.590 |
| Prob. | 0.000 | 0.004 | 0.000 | 0.033 | 0.000 | 0.000 |
| Independent Variable | ||||||
| Coefficient | 0.598 | 0.017 | 0.931 | 0.089 | 1.464 | 0.132 |
| Std. Error | 0.003 | 0.007 | 0.004 | 0.013 | 0.004 | 0.020 |
| t-Statistic | 199.172 | −2.285 | 235.154 | 6.678 | 348.352 | 6.775 |
| Prob. | 0.000 | 0.022 | 0.000 | 0.000 | 0.000 | 0.000 |
| Regression Statistics | ||||||
| R-squared | 0.819 | 0.001 | 0.863 | 0.005 | 0.933 | 0.005 |
| Adjusted R-squared | 0.819 | 0.000 | 0.863 | 0.005 | 0.933 | 0.005 |
| S.E. of regression | 9.868 | 1.195 | 8.580 | 1.193 | 9.107 | 1.746 |
| Sum square resid | 851,841 | 12,426 | 643,983 | 12,370 | 725,530 | 26,514 |
| Log Likelihood | −32,446 | −13,895 | −31,222 | −13,876 | −31,744 | −17,192 |
| F-statistic | 39,670 | 5.220 | 55,297 | 4.460 | 121,349 | 45.898 |
| Prob (F-statistic) | 0.000 | 0.022 | 0.000 | 0.000 | 0.000 | 0.000 |
| Model Statistics | ||||||
| AAIC | 7.417 | 3.195 | 7.137 | 3.190 | 7.256 | 3.953 |
| SIC | 7.418 | 3.196 | 7.139 | 3.192 | 7.258 | 3.954 |
| HQC | 7.417 | 3.195 | 7.138 | 3.191 | 7.257 | 3.953 |
| Residuals Autocorr. | ||||||
| Durbi–Watson stat | 0.027 | 2.072 | 0.028 | 2.067 | 0.056 | 1.944 |
| FP vs. TP | FP vs. CP | TP vs. CP | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Variable | ||||||
| Mean dependent var | 26.324 | 0.038 | 26.324 | 0.038 | 41.647 | 0.073 |
| S.D. Dependent var | 22.156 | 1.582 | 22.156 | 1.582 | 33.856 | 2.539 |
| Intercept | ||||||
| Coefficient | 5.468 | 0.038 | 2.480 | 0.038 | 3.087 | 0.072 |
| Std. Error | 0.213 | 0.015 | 0.158 | 0.015 | 0.187 | 0.024 |
| t-Statistic | 25.705 | 2.557 | 15.672 | 2 557854 | 16.495 | −3.008 |
| Prob. | 0.000 | 0.011 | 0.000 | 0.011 | 0.000 | 0.003 |
| Independent Variable | ||||||
| Coefficient | 0.501 | 0.000 | 0.816 | 0.001 | 1.320 | 0.026 |
| Std. Error | 0.004 | 0.006 | 0.004 | 0.008 | 0.005 | 0.013 |
| t-Statistic | 126.367 | 0.057 | 194.373 | 0.117 | 265.826 | 1.947 |
| Prob. | 0.000 | 0.954 | 0.000 | 0.907 | 0.000 | 0.052 |
| Regression Statistics | ||||||
| R-squared | 0.586 | 0.000 | 0.770 | 0.000 | 0.862 | 0.000 |
| Adjusted R-squared | 0.586 | 0.000 | 0.770 | 0.000 | 0.862 | 0.000 |
| S.E. of regression | 14.262 | 1.582 | 10.631 | 1.582 | 12.570 | 2.539 |
| Sum square resid | 2,298,141 | 28,138 | 1,276,771 | 28,138 | 1,785,249 | 72,490 |
| Log Likelihood | −46,064 | −21,120 | −42,743 | −21,120 | −44,637 | −26,443 |
| F-statistic | 15,969 | 0.003 | 37,781 | 0.014 | 70,664 | 3.791 |
| Prob (F-statistic) | 0.000 | 0.954 | 0.000 | 0.907 | 0.000 | 0.052 |
| Model Statistics | ||||||
| AIC | 8.153 | 3.755 | 7.566 | 3.755 | 7.901 | 4.701 |
| SIC | 8.155 | 3.756 | 7.567 | 3.756 | 7.902 | 4.703 |
| HQC | 8.154 | 3.755 | 7.566 | 3.755 | 7.901 | 4.702 |
| Residuals Autocorr. | ||||||
| Durbi–Watson stat | 0.0203 | 2.2066 | 0.0417 | 2.2067 | 0.0761 | 2.2790 |
| FP vs. TP | FP vs. CP | TP vs. CP | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Variable | ||||||
| Mean dependent var | 52.401 | 0.107 | 52.401 | 0.107 | 56.730 | 0.106 |
| S.D. Dependent var | 49.365 | 2.242 | 49.365 | 2.242 | 50.105 | 0.895 |
| Intercept | ||||||
| Coefficient | −1.026 | 0.098 | 2.701 | 0.103 | 5.021 | 0.093 |
| Std. Error | 0.170 | 0.018 | 0.150 | 0.017 | 0.090 | 0.007 |
| t-Statistic | −6.016 | 5.562 | 18.063 | 5.862 | 55.952 | 13.744 |
| Prob. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Independent Variable | ||||||
| Coefficient | 0.942 | 0.086 | 0.919 | 0.033 | 0.957 | 0.097 |
| Std. Error | 0.002 | 0.020 | 0.002 | 0.007 | 0.001 | 0.003 |
| t-Statisti | 418.079 | 4.406 | 459.943 | 4.518 | 797.498 | 34.875 |
| Prob. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Regression Statistics | ||||||
| R-squared | 0.914 | 0.001 | 0.928 | 0.001 | 0.975 | 0.069 |
| Adjusted R-squared | 0.914 | 0.001 | 0.928 | 0.001 | 0.975 | 0.069 |
| S.E. of regression | 14.498 | 2.241 | 13.278 | 2.241 | 7.967 | 0.864 |
| Sum square resid | 3,467,636 | 82,572 | 2,908,700 | 82,567 | 1,047,283 | 12,266 |
| Log Likelihood | −67,532 | −36,611 | −66,082 | −36,611 | −57,655 | −20,927 |
| F-statistic | 174,790 | 1.941 | 211,548 | 2.041 | 636,003 | 1216 |
| Prob (F-statistic) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Model Statistics | ||||||
| AIC | 8.186 | 4.451 | 8.010 | 4.451 | 6.989 | 2.545 |
| SIC | 8.187 | 4.452 | 8.011 | 4.452 | 6.990 | 2.546 |
| HQC | 8.186 | 4.452 | 8.011 | 4.452 | 6.989 | 2.545 |
| Residuals Autocorr. | ||||||
| Durbi–Watson stat | 0.027 | 2.009 | 0.054 | 2.005 | 0.079 | 1.306 |


| 1 | “Order of integration” is a summary statistic used to describe a unit root process in time series analysis. Specifically, it tells you the minimum number of differences needed to obtain a stationary series (Engle and Granger 1991). |
| 2 | Our crisis period includes both the global financial crisis and the European sovereign debt crisis. |
| 3 | According to Granger and Newbold (2001), we should suspect that a regression is spurious if , where d is the Durbin–Watson statistic, which is the case for all level regressions and not the case for the regressions in differences. |
References
- Abdel-Khalik, A. Rashad, and Bipin B. Ajinkya. 1982. Returns to informational advantages: The case of analysts’ forecast revisions. Accounting Review 57: 661–80. [Google Scholar]
- Admati, Anat R., and Paul Pfleiderer. 1997. Does it all add up? benchmarks and the compensation of active portfolio managers. The Journal of Business 70: 323–50. [Google Scholar] [CrossRef] [Green Version]
- Akaike, Hirotogu. 1973. Information theory as an extension of the maximum likelihood. In IEEE International Symposium on Information Theory. Budapest: Akadémiai Kiadó. [Google Scholar]
- Asquith, Paul, Michael B. Mikhail, and Andrea S. Au. 2005. Information content of equity analyst reports. Journal of Financial Economics 75: 245–82. [Google Scholar] [CrossRef] [Green Version]
- Barber, Brad, Reuven Lehavy, Maureen McNichols, and Brett Trueman. 2001. Can investors profit from the prophets? security analyst recommendations and stock returns. The Journal of Finance 56: 531–63. [Google Scholar] [CrossRef]
- Barr Rosenberg, Kenneth Reid, and Ronald Lanstein. 1984. Persuasive evidence of market inefficiency. Journal of Portfolio Management 11: 9–17. [Google Scholar] [CrossRef]
- Bhargava, Alok, Luisa Franzini, and Wiji Narendranathan. 1982. Serial correlation and the fixed effects model. The Review of Economic Studies 49: 533–49. [Google Scholar] [CrossRef]
- Bilinski, Pawel, Danielle Lyssimachou, and Martin Walker. 2013. Target price accuracy: International evidence. The Accounting Review 88: 825–51. [Google Scholar] [CrossRef]
- Bjerring, James H, Josef Lakonishok, and Theo Vermaelen. 1983. Stock prices and financial analysts’ recommendations. The Journal of Finance 38: 187–204. [Google Scholar] [CrossRef]
- Bonini, Stefano, Laura Zanetti, Roberto Bianchini, and Antonio Salvi. 2010. Target price accuracy in equity research. Journal of Business Finance & Accounting 37: 1177–217. [Google Scholar]
- Bradshaw, Mark, Alan Huang, and Hongping Tan. 2014. Analyst Target Price Optimism around the World. Working Paper. Chestnut Hill: Boston College. [Google Scholar]
- Bradshaw, Mark T., Lawrence D. Brown, and Kelly Huang. 2013. Do sell-side analysts exhibit differential target price forecasting ability? Review of Accounting Studies 18: 930–55. [Google Scholar] [CrossRef]
- Bradshaw, Mark T., Alan G. Huang, and Hongping Tan. 2019. The effects of analyst-country institutions on biased research: Evidence from target prices. Journal of Accounting Research 57: 85–120. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, Mark T., Lian Fen Lee, and Kyle Peterson. 2016. The interactive role of difficulty and incentives in explaining the annual earnings forecast walkdown. The Accounting Review 91: 995–1021. [Google Scholar] [CrossRef] [Green Version]
- Brav, Alon, and Reuven Lehavy. 2003. An empirical analysis of analysts’ target prices: Short-term informativeness and long-term dynamics. The Journal of Finance 58: 1933–67. [Google Scholar] [CrossRef]
- Calomiris, Charles W., and Joseph R. Mason. 1997. Contagion and bank failures during the great depression: The june 1932 chicago banking panic. The American Economic Review 87: 863–883. [Google Scholar]
- Cao, Charles, Bing Liang, Andrew W. Lo, and Lubomir Petrasek. 2017. Hedge fund holdings and stock market efficiency. The Review of Asset Pricing Studies 8: 77–116. [Google Scholar] [CrossRef]
- Cheng, Lee-Young, Yi-Chen Su, Zhipeng Yan, and Yan Zhao. 2019. Corporate governance and target price accuracy. International Review of Financial Analysis 64: 93–101. [Google Scholar] [CrossRef]
- Choi, In. 2001. Unit root tests for panel data. Journal of International Money and Finance 20: 249–72. [Google Scholar] [CrossRef]
- Da, Zhi, Keejae P. Hong, and Sangwoo Lee. 2016. What drives target price forecasts and their investment value? Journal of Business Finance & Accounting 43: 487–510. [Google Scholar]
- Da, Zhi, and Ernst Schaumburg. 2011. Relative valuation and analyst target price forecasts. Journal of Financial Markets 14: 161–92. [Google Scholar] [CrossRef]
- Desai, Hemang, Bing Liang, and Ajai K. Singh. 2000. Do all-stars shine? evaluation of analyst recommendations. Financial Analysts Journal 56: 20–29. [Google Scholar] [CrossRef]
- Dimson, Elroy, and Massoud Mussavian. 1998. A brief history of market efficiency. European Financial Management 4: 91–103. [Google Scholar] [CrossRef] [Green Version]
- Durbin, James, and Geoffrey S. Watson. 1950. Testing for serial correlation in least squares regression: I. Biometrika 37: 409–28. [Google Scholar] [PubMed]
- Elton, Edwin J., Martin J. Gruber, and Andre de Souza. 2019. Are passive funds really superior investments? an investor perspective. Financial Analysts Journal 73: 7–19. [Google Scholar] [CrossRef] [Green Version]
- Engelberg, Joseph, R. David McLean, and Jeffrey Pontiff. 2020. Analysts and anomalies. Journal of Accounting and Economics 69: 101249. [Google Scholar] [CrossRef]
- Engle, Robert, and Clive Granger. 1991. Long-Run Economic Relationships: Readings in Cointegration. Oxford: Oxford University Press. [Google Scholar]
- Falkenstein, Eric G. 1996. Preferences for stock characteristics as revealed by mutual fund portfolio holdings. The Journal of Finance 51: 111–35. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1965. The behavior of stock-market prices. The Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Fama, Eugene F., Lawrence Fisher, Michael C. Jensen, and Richard Roll. 1969. The adjustment of stock prices to new information. International Economic Review 10: 1–21. [Google Scholar] [CrossRef]
- Farmer, Roger E. A. 1999. Macroeconomics of Self-Fulfilling Prophecies. Cambridge: MIT Press. [Google Scholar]
- French, Kenneth R. 2008. Presidential address: The cost of active investing. The Journal of Finance 63: 1537–73. [Google Scholar] [CrossRef]
- Garber, Peter M. 1989. Tulipmania. Journal of Political Economy 97: 535–60. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Paul Newbold. 2001. Spurious regressions in econometrics. In Essays in Econometrics: Collected Papers of Clive WJ Granger vol.32. Cambridge: Cambridge University Press, pp. 109–18. [Google Scholar]
- Hannan, Edward J., and Barry G. Quinn. 1979. The determination of the order of an autoregression. Journal of the Royal Statistical Society: Series B (Methodological) 41: 190–95. [Google Scholar] [CrossRef]
- Im, Kyung So, M. Hashem Pesaran, and Yongcheol Shin. 2003. Testing for unit roots in heterogeneous panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Jordan, Steven J. 2014. Is momentum a self-fulfilling prophecy? Quantitative Finance 14: 737–48. [Google Scholar] [CrossRef]
- Krishna, Daya. 1971. “The self-fulfilling prophecy” and the nature of society. American Sociological Review 36: 1104–7. [Google Scholar] [CrossRef]
- Levin, Andrew, Chien-Fu Lin, and Chia-Shang James Chu. 2002. Unit root tests in panel data: Asymptotic and finite-sample properties. Journal of Econometrics 108: 1–24. [Google Scholar] [CrossRef]
- Lys, Thomas, and Sungkyu Sohn. 1990. The association between revisions of financial analysts’ earnings forecasts and security-price changes. Journal of Accounting and Economics 13: 341–63. [Google Scholar] [CrossRef]
- Malkiel, Burton G. 2003. Passive investment strategies and efficient markets. European Financial Management 9: 1–10. [Google Scholar] [CrossRef]
- Menkhoff, Lukas. 1997. Examining the use of technical currency analysis. International Journal of Finance & Economics 2: 307–18. [Google Scholar]
- Oberlechner, Thomas. 2001. Importance of technical and fundamental analysis in the european foreign exchange market. International Journal of Finance & Economics 6: 81–93. [Google Scholar]
- Okui, Ryo, and Wendun Wang. 2021. Heterogeneous structural breaks in panel data models. Journal of Econometrics 220: 447–73. [Google Scholar] [CrossRef]
- Ottaviani, Marco, and Peter Norman Sørensen. 2006. Reputational cheap talk. The Rand Journal of Economics 37: 155–75. [Google Scholar] [CrossRef]
- Palley, Asa, Thomas D. Steffen, and Frank Zhang. 2019. Consensus Analyst Target Prices: Information Content and Implications for Investors. Working Paper. Available online: https://ssrn.com/abstract=3467800 (accessed on 23 May 2021).
- Reitz, Stefan. 2006. On the predictive content of technical analysis. The North American Journal of Economics and Finance 17: 121–37. [Google Scholar] [CrossRef]
- Schwarz, Gideon. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar] [CrossRef]
- Sharpe, William F. 1991. The arithmetic of active management. Financial Analysts Journal 47: 7–9. [Google Scholar] [CrossRef] [Green Version]
- Shukla, Ravi. 2004. The value of active portfolio management. Journal of Economics and Business 56: 331–46. [Google Scholar] [CrossRef]
- Sorensen, Eric H., Keith L. Miller, and Vele Samak. 1998. Allocating between active and passive management. Financial Analysts Journal 54: 18–31. [Google Scholar] [CrossRef]
- Stickel, Scott E. 1991. Common stock returns surrounding earnings forecast revisions: More puzzling evidence. Accounting Review 66: 402–16. [Google Scholar]
- Tiberius, Victor, and Laura Lisiecki. 2019. Stock price forecast accuracy and recommendation profitability of financial magazines. International Journal of Financial Studies 7: 58. [Google Scholar] [CrossRef] [Green Version]
- Vermorken, Maximilian, Marc Gendebien, Alphons Vermorken, and Thomas Schröder. 2013. Skilled monkey or unlucky manager? Journal of Asset Management 14: 267–77. [Google Scholar] [CrossRef]
- Zulaika, Joseba. 2019. Self-fulfilling prophecy. In The Blackwell Encyclopedia of Sociology. Edited by George Ritzer and C. Rojek. New York: John Wiley & Sons, Ltd., pp. 1–3. [Google Scholar]

| Adidas | BASF | E.ON | L’Oreal | Schneider Electric SE |
| Air Liquide | Bayer | ENEL | LVMH | Siemens |
| Airbus | BNP Paribas | ENI | Mucich RE | Societe Generale |
| Allianz | BMW | Essilor | Nokia | Telefonica |
| Anheuser | Danone | Fresenius | Orange | Total |
| ASML | Carrefour | Iberdrola | Repsol | Unicredit |
| Assicurazioni | Daimler | Inditex | Safran | Unilever |
| AXA Deutsche | Bank | ING | Saint-Gobain | Vinci |
| Banco Bilbao | Deutsche Post | Intesa Sanpaolo | Sanofi | Vivendi |
| Banco Santander | Deutsche Telekom | Philips | SAP | Volkswagen |
| Future Prices (FP) | Target Prices (TP) | Capitalised Prices (CP) | ||||
|---|---|---|---|---|---|---|
| Method | Statistic | Prob | Statistic | Prob | Statistic | Prob |
| LLC | 6.755 | 1.000 | 7.966 | 1.000 | 7.074 | 1.000 |
| IPS | 6.156 | 1.000 | 8.492 | 1.000 | 6.635 | 1.000 |
| ADF– Fisher | 60.653 | 0.999 | 39.983 | 0.999 | 53.817 | 1.000 |
| PP–Fisher | 57.242 | 1.000 | 40.002 | 1.000 | 49.630 | 1.000 |
| FP vs. TP | FP vs. CP | TP vs. CP | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Variable | ||||||
| Mean dependent var | 38.516 | 0.070 | 38.516 | 0.070 | 48.456 | 0.057 |
| S.D. Dependent var | 39.241 | 1.839 | 39.241 | 1.839 | 42.886 | 1.758 |
| Intercept | ||||||
| Coefficient | −1.424 | 0.069 | 1.789 | 0.068 | 8.433 | 0.051 |
| Std. Error | 0.134 | 0.010 | 0.085 | 0.010 | 0.096 | 0.009 |
| t-Statistic | −10.590 | 7.192 | 20.922 | 7.012 | 87.712 | 5.525 |
| Prob. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Independent Variable | ||||||
| Coefficient | 0.824 | 0.007 | 0.916 | 0.029 | 0.999 | 0.081 |
| Std. Error | 0.002 | 0.005 | 0.001 | 0.005 | 0.002 | 0.004 |
| t-Statistic | 396.586 | 1.215 | 613.740 | 5.851 | 594.747 | 17.470 |
| Prob. | 0.000 | 0.224 | 0.000 | 0.000 | 0.000 | 0.000 |
| Regression Statistics | ||||||
| R-squared | 0.811 | 0.000 | 0.912 | 0.001 | 0.906 | 0.008 |
| Adjusted R-squared | 0.811 | 0.000 | 0.912 | 0.001 | 0.906 | 0.008 |
| S.E. of regression | 17.040 | 1.839 | 11.670 | 1.838 | 13.124 | 1.750 |
| Sum square resid | 106.123 | 123,419.8 | 4,977,847 | 123,309 | 6,295,006 | 111,838 |
| Log Likelihood | −155,501 | −740,255 | −141,667 | −74,009 | −145,957 | −72,226 |
| F-statistic | 157,281 | 1.476 | 376,676 | 34.241 | 353,724 | 305.203 |
| Prob (F-statistic) | 0.000 | 0.224 | 0.000 | 0.000 | 0.000 | 0.000 |
| Model Statistics | ||||||
| AIC | 8.509 | 4.056 | 7.752 | 4.055 | 7.987 | 3.958 |
| SIC | 8.509 | 4.057 | 7.753 | 4.056 | 7.987 | 3.958 |
| HQC | 8.509 | 4.056 | 7.752 | 4.056 | 7.987 | 3.958 |
| Residuals Autocorr. | ||||||
| Durbi–Watson stat | 0.019 | 2.055 | 0.047 | 2.055 | 0.037 | 2.007 |
| Panel A: FP vs. TP | |||
| Pre-crisis | Crisis | Post-crisis | |
| In level (1) | |||
| Intercept | 3.15669 *** | 5.467543 *** | −1.025766 *** |
| In Differences (2) | |||
| Intercept | 0.036918 *** | 0.038144 ** | 0.097836 *** |
| Independent Variable | 0.016726 ** | 0.000336 | 0.086016 *** |
| Adjusted R-squared | 0.000485 | 0.000089 | 0.001118 |
| Hannan-Quinn criter. | 3.19534 | 3.755410 | 4.451777 |
| Panel B: FP vs. CP | |||
| Pre-crisis | Crisis | Post-crisis | |
| In level (3) | |||
| Intercept | 2.219831 *** | 2.480338 *** | 2.701088 *** |
| In Differences (4) | |||
| Intercept | 0.027395 ** | 0.038147 ** | 0.102555 *** |
| Independent Variable | 0.089025 *** | 0.000953 | 0.032768 *** |
| Adjusted R-squared | 0.004987 | 0.000088 | 0.001179 |
| Hannan-Quinn criter. | 3.190830 | 3.755 | 4.451717 |
| (a) In levels | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.9132 | 0.9245 | 0.9566 | 0.9489 | 0.9143 | 0.9391 | 0.9584 | 0.5404 |
| R Square | 0.8339 | 0.8547 | 0.9151 | 0.9004 | 0.8359 | 0.8818 | 0.9185 | 0.2921 |
| Adjusted R Square | 0.8336 | 0.8545 | 0.9150 | 0.9003 | 0.8357 | 0.8817 | 0.9184 | 0.2910 |
| Standard Error | 23.0141 | 11.6967 | 14.1228 | 10.2800 | 8.7074 | 3.3725 | 8.6591 | 41.2734 |
| Observations | 731 | 731 | 731 | 731 | 731 | 731 | 731 | 679 |
| Intercept | ||||||||
| Coefficient | −6.5788 | 3.2317 | −1.3111 | 2.7221 | 3.6783 | 1.2282 | −7.0116 | 46.9403 |
| Standard Error | 1.5922 | 0.8641 | 0.8400 | 0.8709 | 0.5775 | 0.2310 | 0.5916 | 4.2281 |
| t Stat | −4.1318 | 3.7398 | −1.5608 | 3.1255 | 6.3691 | 5.3175 | −11.8514 | 11.1019 |
| P-value | 0.0000 | 0.0002 | 0.1190 | 0.0018 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lower 95% | −9.7048 | 1.5352 | −2.9602 | 1.0123 | 2.5445 | 0.7748 | −8.1731 | 38.6385 |
| Upper 95% | −3.4529 | 4.9283 | 0.3381 | 4.4319 | 4.8121 | 1.6817 | −5.8501 | 55.2421 |
| TP Variable | ||||||||
| Coefficient | 1.1167 | 0.8049 | 1.1506 | 0.9225 | 0.8532 | 0.8437 | 1.2215 | 0.4511 |
| Standard Error | 0.0185 | 0.0123 | 0.0130 | 0.0114 | 0.0140 | 0.0114 | 0.0135 | 0.0270 |
| t Stat | 60.4917 | 65.4910 | 88.6353 | 81.1974 | 60.9478 | 73.7592 | 90.6476 | 16.7120 |
| P-value | 0.0000 | 0.0001 | 0.0002 | 0.0003 | 0.0004 | 0.0005 | 0.0006 | 0.0007 |
| Lower 95% | 1.0805 | 0.7808 | 1.1251 | 0.9002 | 0.8257 | 0.8212 | 1.1950 | 0.3981 |
| Upper 95% | 1.1530 | 0.8290 | 1.1761 | 0.9448 | 0.8807 | 0.8661 | 1.2480 | 0.5041 |
| ANOVA | ||||||||
| SS | 1,938,122 | 586,797 | 1,566,947 | 696,737 | 281,640 | 61,878 | 616,104 | 475,771 |
| MS | 1,938,122 | 586,797 | 1,566,947 | 696,737 | 281,640 | 61,878 | 616,104 | 475,771 |
| F | 3659 | 4289 | 7856 | 6593 | 3715 | 5440 | 8217 | 279 |
| Significance F | 0.0000 | 0.0001 | 0.0002 | 0.0003 | 0.0004 | 0.0005 | 0.0006 | 0.0007 |
| (b) In differences | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.0124 | 0.0812 | 0.0297 | 0.0345 | 0.0137 | 0.0012 | 0.1157 | 0.0488 |
| R Square | 0.0002 | 0.0066 | 0.0009 | 0.0012 | 0.0002 | 0,0000 | 0.0134 | 0.0024 |
| Adjusted R Square | −0.0012 | 0.0052 | −0.0005 | −0.0002 | −0.0012 | −0.0014 | 0.0120 | 0.0002 |
| Standard Error | 3.1255 | 0.7287 | 2.6244 | 2.1335 | 1.3584 | 0.5834 | 1.5236 | 6.4974 |
| Observations | 730 | 730 | 730 | 730 | 730 | 730 | 730 | 470 |
| Intercept | ||||||||
| Coefficient | 0.2757 | 0.1192 | 0.2204 | 0.1055 | 0.0616 | 0.0336 | 0.1223 | 0.1998 |
| Standard Error | 0.1174 | 0.0682 | 0.0992 | 0.0800 | 0.0511 | 0.0218 | 0.0573 | 0.2999 |
| t Stat | 2.3488 | 1.7493 | 2.2227 | 1.3178 | 1.2048 | 1.5381 | 2.1327 | 0.6662 |
| P-value | 0.0191 | 0.0807 | 0.0265 | 0.1880 | 0.2287 | 0.1245 | 0.0333 | 0.5056 |
| Lower 95% | 0.0452 | −0.0146 | 0.0257 | −0.0517 | −0.0388 | −0.0093 | 0.0097 | −0.3895 |
| Upper 95% | 0.5061 | 0.253 | 0.415 | 0.2626 | 0.1619 | 0.0765 | 0.2348 | 0.7890 |
| DTP Variable | ||||||||
| Coefficient | 0.0255 | −0.2023 | 0.0737 | 0.0931 | −0.0352 | −0.003 | 0.3207 | 0.0622 |
| Standard Error | 0.0760 | 0.0920 | 0.0918 | 0.0999 | 0.0955 | 0.0914 | 0.1020 | 0.0589 |
| t Stat | 0.3356 | −2.1989 | 0.8029 | 0.9317 | −0.369 | −0.0328 | 3.1430 | 1.0563 |
| P-value | 0.7373 | 0.0282 | 0.4223 | 0.3518 | 0.7122 | 0.9738 | 0.0017 | 0.2914 |
| Lower 95% | −0.1237 | −0.3828 | −0.1066 | −0.1031 | −0.2226 | −0.1825 | 0.1204 | −0.0535 |
| Upper 95% | 0.1746 | −0.0217 | 0.2540 | 0.2894 | 0.1522 | 0.1765 | 0.5211 | 0.1780 |
| ANOVA | ||||||||
| SS | 1.1000 | 15.9185 | 4.4402 | 3.9518 | 0.2513 | 0.0004 | 22.9319 | 47.1055 |
| MS | 1.1000 | 15.9185 | 4.4402 | 3.9518 | 0.2513 | 0.0004 | 22.9319 | 47.1055 |
| F | 0.1126 | 4.835 | 0.6447 | 0.8682 | 0.1362 | 0.0011 | 9.8782 | 1.1158 |
| Significance F | 0.7373 | 0.0282 | 0.4223 | 0.3518 | 0.7122 | 0.9738 | 0.0017 | 0.2914 |
| (a) In levels | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.9404 | 0.9262 | 0.9566 | 0.9487 | 0.9328 | 0.9448 | 0.9697 | 0.7627 |
| R Square | 0.8843 | 0.8579 | 0.9150 | 0.900 | 0.8702 | 0.8927 | 0.9402 | 0.5818 |
| Adjusted R Square | 0.8841 | 0.8577 | 0.9149 | 0.8999 | 0.8700 | 0.8925 | 0.9402 | 0.5811 |
| Standard Error | 19.206 | 11.567 | 14.1260 | 10.3022 | 7.7464 | 3.214 | 7.4152 | 31.724 |
| Observations | 731 | 731 | 731 | 731 | 731 | 731 | 731 | 679 |
| Intercept | ||||||||
| Coefficient | 2.183 | 9.2317 | 3.0541 | 7.5376 | 5.1339 | 2.4446 | −1.0466 | 39.3794 |
| Standard Error | 1.2048 | 0.7764 | 0.8022 | 0.8199 | 0.4897 | 0.2062 | 0.4568 | 2.6745 |
| t Stat | 1.8119 | 11.8897 | 3.8071 | 9.1934 | 10.4831 | 11.8543 | −2.2909 | 14.7239 |
| P-value | 0.0704 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | 0.0000 | 0.0223 | 0.0000 |
| Lower 95% | −0.1823 | 7.7074 | 1.4792 | 5.928 | 4.1725 | 2.0397 | −1.9434 | 34.1281 |
| Upper 95% | 4.5483 | 10.7560 | 4.6291 | 9.1473 | 6.0954 | 2.8494 | −0.1497 | 44.6308 |
| CP Variable | ||||||||
| Coefficient | 0.9747 | 0.7703 | 0.9547 | 0.8697 | 0.8087 | 0.7918 | 1.0556 | 0.5835 |
| Standard Error | 0.0131 | 0.0116 | 0.0108 | 0.0107 | 0.0116 | 0.0102 | 0.0099 | 0.0190 |
| t Stat | 74.6454 | 66.3494 | 88.6132 | 81.0032 | 69.897 | 77.8717 | 107.0977 | 30.6864 |
| P-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lower 95% | 0.9490 | 0.7475 | 0.9335 | 0.8487 | 0.786 | 0.7718 | 1.0363 | 0.5461 |
| Upper 95% | 1.0003 | 0.7931 | 0.9758 | 0.8908 | 0.8315 | 0.8118 | 1.075 | 0.6208 |
| ANOVA | ||||||||
| SS | 2,055,329 | 588,997 | 1,566,881 | 696,404 | 293,167 | 62,639 | 630,679 | 947,694 |
| MS | 2,055,329 | 588,997 | 1,566,881 | 696,404 | 293,167 | 62,639 | 630,679 | 947,694 |
| F | 5572 | 4402 | 7852 | 6562 | 4886 | 6064 | 11,470 | 942 |
| Significance F | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (b) In differences | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.0387 | 0.0390 | 0.0223 | 0.0021 | 0.0246 | 0.1010 | 0.0432 | 0.1214 |
| R Square | 0.0015 | 0.0015 | 0.0005 | 0.0000 | 0.0006 | 0.0102 | 0.0019 | 0.0147 |
| Adjusted R Square | 0.0001 | 0.0002 | −0.0009 | −0.0014 | −0.0008 | 0.0088 | 0.0005 | 0.0126 |
| Standard Error | 3.1234 | 1.8191 | 2.6249 | 2.1348 | 1.3581 | 0.5805 | 1.5325 | 6.4570 |
| Observations | 730 | 730 | 730 | 730 | 730 | 730 | 730 | 470 |
| Intercept | ||||||||
| Coefficient | 0.2714 | 0.0976 | 0.2309 | 0.1173 | 0.0605 | 0.0303 | 0.1493 | 0.1773 |
| Standard Error | 0.1161 | 0.0674 | 0.0976 | 0.0792 | 0.0504 | 0.0215 | 0.0569 | 0.2981 |
| t Stat | 2.3382 | 1.4480 | 2.3659 | 1.4817 | 1.1999 | 1.4061 | 2.6235 | 0.5948 |
| P-value | 0.0196 | 0.1480 | 0.0182 | 0.1389 | 0.2306 | 0.1601 | 0.0089 | 0.5523 |
| Lower 95% | 0.0435 | −0.0347 | 0.0393 | −0.0381 | −0.0385 | −0.0120 | 0.0376 | −0.4085 |
| Upper 95% | 0.4993 | 0.2300 | 0.4224 | 0.2727 | 0.1594 | 0.0725 | 0.2611 | 0.7631 |
| DCP Variable | ||||||||
| Coefficient | 0.0365 | −0.0356 | 0.0224 | 0.0020 | −0.0249 | 0.0924 | 0.0446 | 0.1026 |
| Standard Error | 0.0349 | 0.0337 | 0.0373 | 0.0350 | 0.0376 | 0.0337 | 0.0382 | 0.0388 |
| t Stat | 1.0460 | −1.0539 | 0.6015 | 0.0571 | −0.6629 | 2.7390 | 1.1676 | 2.6450 |
| P-value | 0.2959 | 0.2923 | 0.5477 | 0.9545 | 0.5076 | 0.0063 | 0.2434 | 0.0084 |
| Lower 95% | −0.0320 | −0.1018 | −0.0508 | −0.0668 | −0.0988 | 0.0262 | −0.0304 | 0.0264 |
| Upper 95% | 0.1051 | 0.0307 | 0.0957 | 0.0708 | 0.0489 | 0.1586 | 0.1196 | 0.1788 |
| ANOVA | ||||||||
| SS | 10.6731 | 3.6758 | 2.4931 | 0.0149 | 0.8105 | 2.5277 | 3.2016 | 291.6781 |
| MS | 10.6731 | 3.6758 | 2.4931 | 0.0149 | 0.8105 | 2.5277 | 3.2016 | 291.6781 |
| F | 1.0941 | 1.1108 | 0.3618 | 0.0033 | 0.4394 | 7.5019 | 1.3632 | 6.9958 |
| Significance F | 0.2959 | 0.2923 | 0.5477 | 0.9545 | 0.5076 | 0.0063 | 0.2434 | 0.0084 |
| (a) In levels | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.9907 | 0.9947 | 0.9944 | 0.9910 | 0.9927 | 0.9926 | 0.9909 | 0.8291 |
| R Square | 0.9816 | 0.9895 | 0.9889 | 0.9820 | 0.9855 | 0.9852 | 0.9819 | 0.6875 |
| Adjusted R Square | 0.9815 | 0.9895 | 0.9889 | 0.9820 | 0.9855 | 0.9852 | 0.9819 | 0.6870 |
| Standard Error | 6.2686 | 3.6153 | 4.2426 | 4.4920 | 2.7701 | 1.3281 | 3.2030 | 32.8506 |
| Observations | 731 | 731 | 731 | 731 | 731 | 731 | 731 | 679 |
| Intercept | ||||||||
| Coefficient | 10.3126 | 7.8353 | 4.0534 | 5.7802 | 2.5836 | 1.6513 | 5.5437 | 50.0617 |
| Standard Error | 0.3932 | 0.2427 | 0.2409 | 0.3575 | 0.1751 | 0.0852 | 0.1973 | 2.7695 |
| t Stat | 26.2256 | 32.2865 | 16.8234 | 16.1686 | 14.7528 | 19.3773 | 28.0942 | 18.0760 |
| P-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lower 95% | 9.5406 | 7.3589 | 3.5804 | 5.0784 | 2.2398 | 1.484 | 5.1563 | 44.6238 |
| Upper 95% | 11.0845 | 8.3118 | 4.5264 | 6.4821 | 2.9274 | 1.8186 | 5.9311 | 55.4995 |
| CP Variable | ||||||||
| Coefficient | 0.8397 | 0.9501 | 0.8251 | 0.9345 | 0.9223 | 0.9259 | 0.8464 | 0.7598 |
| Standard Error | 0.0043 | 0.0036 | 0.0032 | 0.0047 | 0.0041 | 0.0042 | 0.0043 | 0.0197 |
| t Stat | 197.029 | 261.8558 | 255.0016 | 199.6117 | 222.9159 | 220.3481 | 198.7974 | 38.5915 |
| P-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lower 95% | 0.8313 | 0.9430 | 0.8188 | 0.9253 | 0.9142 | 0.9176 | 0.8380 | 0.7212 |
| Upper 95% | 0.8480 | 0.9573 | 0.8315 | 0.9437 | 0.9305 | 0.9341 | 0.8548 | 0.7985 |
| ANOVA | ||||||||
| SS | 1,525,453 | 896,221 | 1,170,423 | 804,003 | 381,300 | 85,646 | 405,440 | 1,607,205 |
| MS | 1,525,453 | 896,221 | 1,170,423 | 804,003 | 381,300 | 85,646 | 405,440 | 1,607,205 |
| F | 38,820 | 68,568 | 65,026 | 39,845 | 49,691 | 48,553 | 39,520 | 1489 |
| Significance F | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (b) In differences | ||||||||
| Adidas | Anheuser | ASML | Essilor | Fresenius | Inditex | Safran | Volkswagen | |
| Regression Statistics | ||||||||
| Multiple R | 0.3695 | 0.2876 | 0.2176 | 0.1779 | 0.0904 | 0.1263 | 0.2184 | 0.2012 |
| R Square | 0.1366 | 0.0827 | 0.0473 | 0.0316 | 0.0082 | 0.0159 | 0.0477 | 0.0405 |
| Adjusted R Square | 0.1354 | 0.0815 | 0.0460 | 0.0303 | 0.0068 | 0.0146 | 0.0464 | 0.0384 |
| Standard Error | 1.4169 | 0.7002 | 1.0338 | 0.7785 | 0.5253 | 0.2346 | 0.5400 | 4.9930 |
| Observations | 730 | 730 | 730 | 730 | 730 | 730 | 730 | 470 |
| Intercept | ||||||||
| Coefficient | 0.2103 | 0.1147 | 0.1950 | 0.1214 | 0.0936 | 0.0346 | 0.0914 | 0.1243 |
| Standard Error | 0.0527 | 0.0260 | 0.0384 | 0.0289 | 0.0195 | 0.0087 | 0.0201 | 0.2305 |
| t Stat | 3.9943 | 4.4181 | 5.0737 | 4.2036 | 4.8017 | 3.9763 | 4.5579 | 0.5392 |
| P-value | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0,0000 | 0.5900 |
| Lower 95% | 0.1069 | 0.0637 | 0.1195 | 0.0647 | 0.0553 | 0.0175 | 0.0520 | −0.3287 |
| Upper 95% | 0.3137 | 0.1656 | 0.2704 | 0.1780 | 0.1318 | 0.0517 | 0.1308 | 0.5773 |
| DCP Variable | ||||||||
| Coefficient | 0.1700 | 0.1052 | 0.0884 | 0.0623 | 0.0356 | 0.0468 | 0.0813 | 0.1332 |
| Standard Error | 0.0158 | 0.0130 | 0.0147 | 0.0128 | 0.0146 | 0.0136 | 0.0135 | 0.0300 |
| t Stat | 10.7300 | 8.1030 | 6.0144 | 4.8774 | 2.4487 | 3.4341 | 6.0379 | 4.4432 |
| P-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0146 | 0.0006 | 0.0000 | 0.0000 |
| Lower 95% | 0.1389 | 0.0797 | 0.0595 | 0.0372 | 0.0071 | 0.0201 | 0.0548 | 0.0743 |
| Upper 95% | 0.2011 | 0.1307 | 0.1172 | 0.0874 | 0.0642 | 0.0736 | 0.1077 | 0.1921 |
| ANOVA | ||||||||
| SS | 231.1325 | 32.1946 | 38.6599 | 14.4182 | 1.6545 | 0.6491 | 10.6316 | 492.1667 |
| MS | 231.1325 | 32.1946 | 38.6599 | 14.4182 | 1.6545 | 0.6491 | 10.6316 | 492.1667 |
| F | 115.1337 | 65.6589 | 36.1726 | 23.7889 | 5.9962 | 11.7931 | 36.456 | 19.7418 |
| Significance F | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0146 | 0.0000 | 0.0000 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, J.; Gaspar, R.M. Accuracy of European Stock Target Prices. J. Risk Financial Manag. 2021, 14, 443. https://doi.org/10.3390/jrfm14090443
Almeida J, Gaspar RM. Accuracy of European Stock Target Prices. Journal of Risk and Financial Management. 2021; 14(9):443. https://doi.org/10.3390/jrfm14090443
Chicago/Turabian StyleAlmeida, Joana, and Raquel M. Gaspar. 2021. "Accuracy of European Stock Target Prices" Journal of Risk and Financial Management 14, no. 9: 443. https://doi.org/10.3390/jrfm14090443
APA StyleAlmeida, J., & Gaspar, R. M. (2021). Accuracy of European Stock Target Prices. Journal of Risk and Financial Management, 14(9), 443. https://doi.org/10.3390/jrfm14090443







