High-Frequency Trading (HFT) and Market Quality Research: An Evaluation of the Alternative HFT Proxies
Abstract
:1. Introduction
2. Market Microstructure Setting
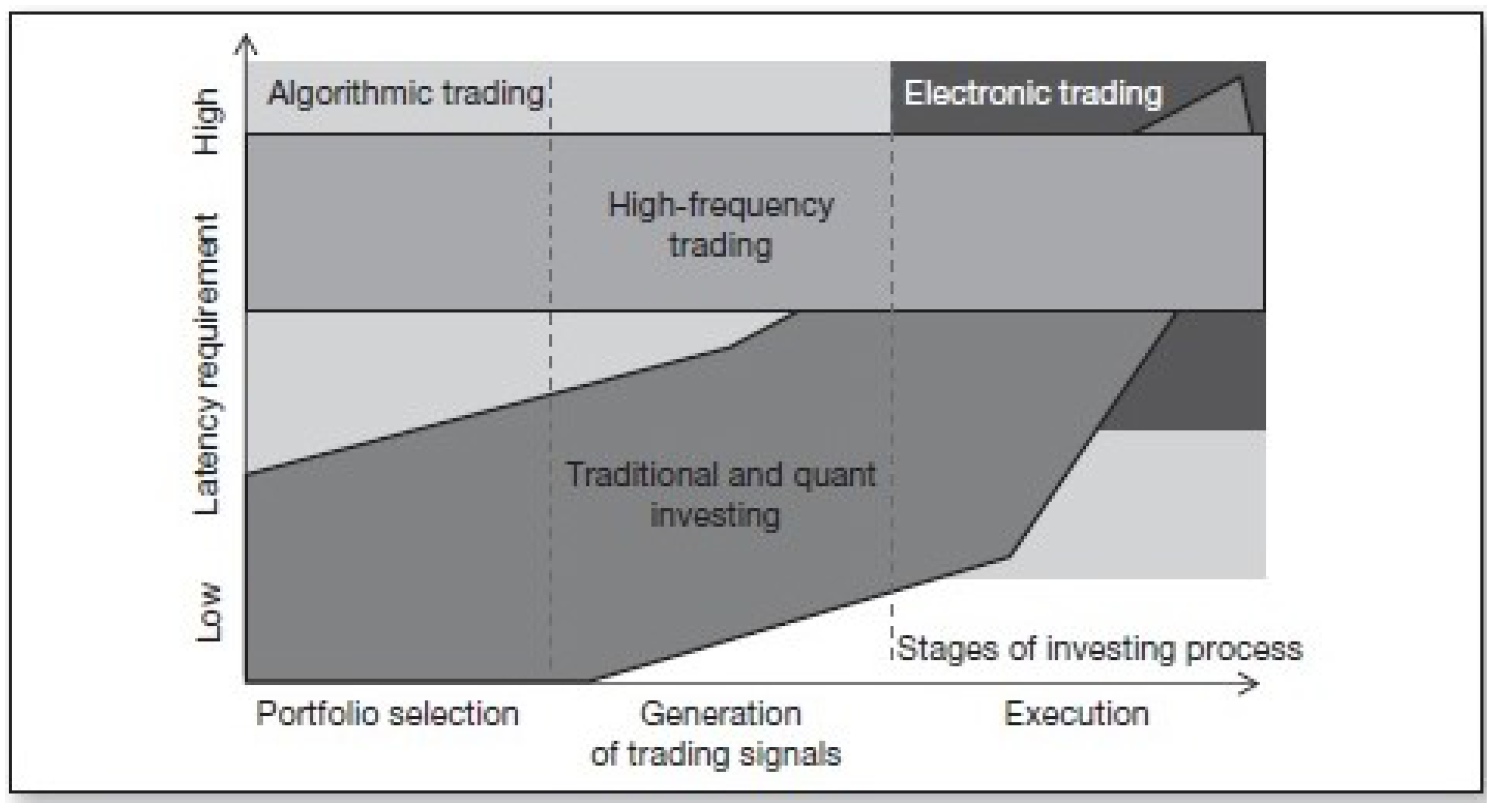
2.1. High-Frequency Trading
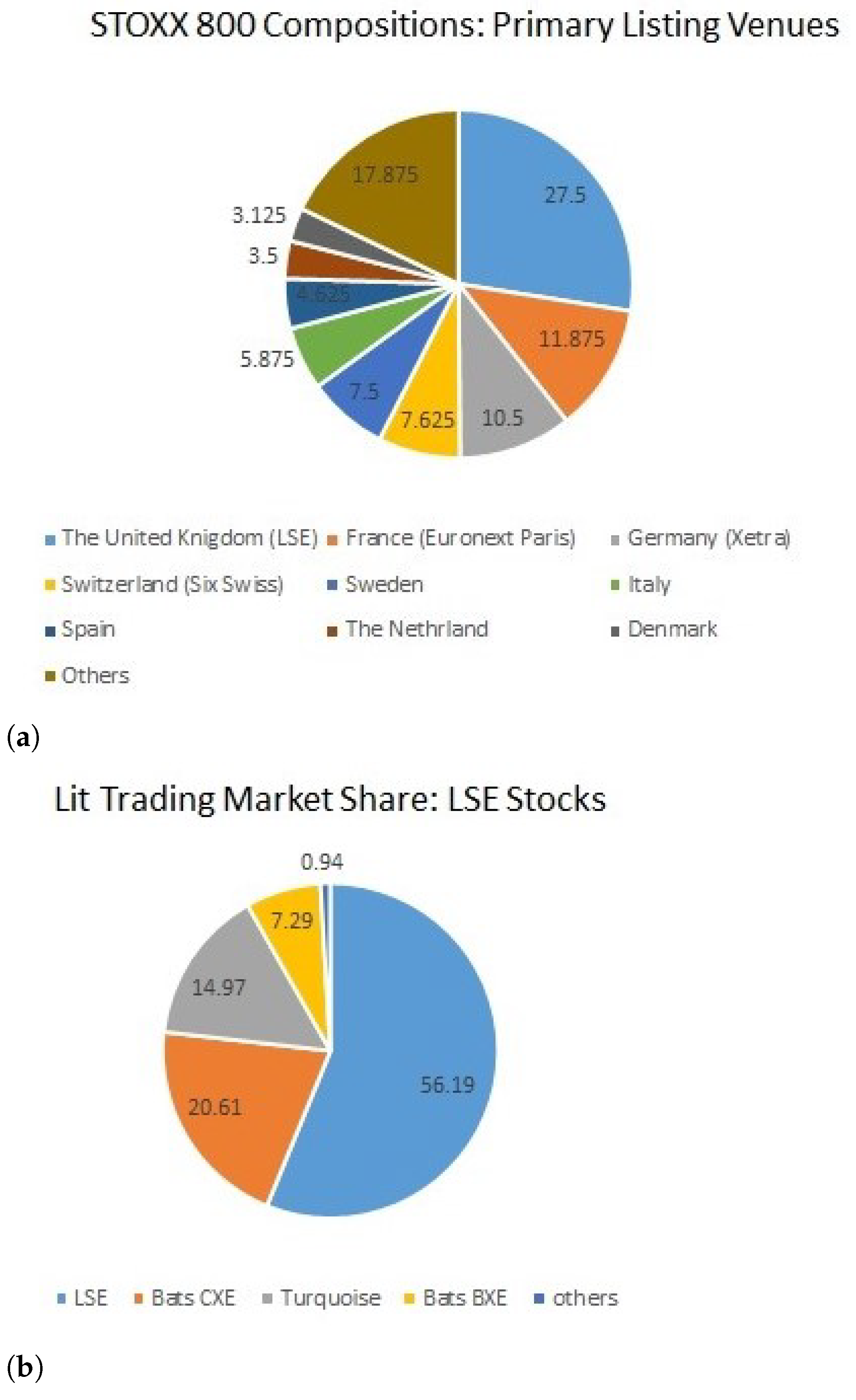
2.2. European Market Structure
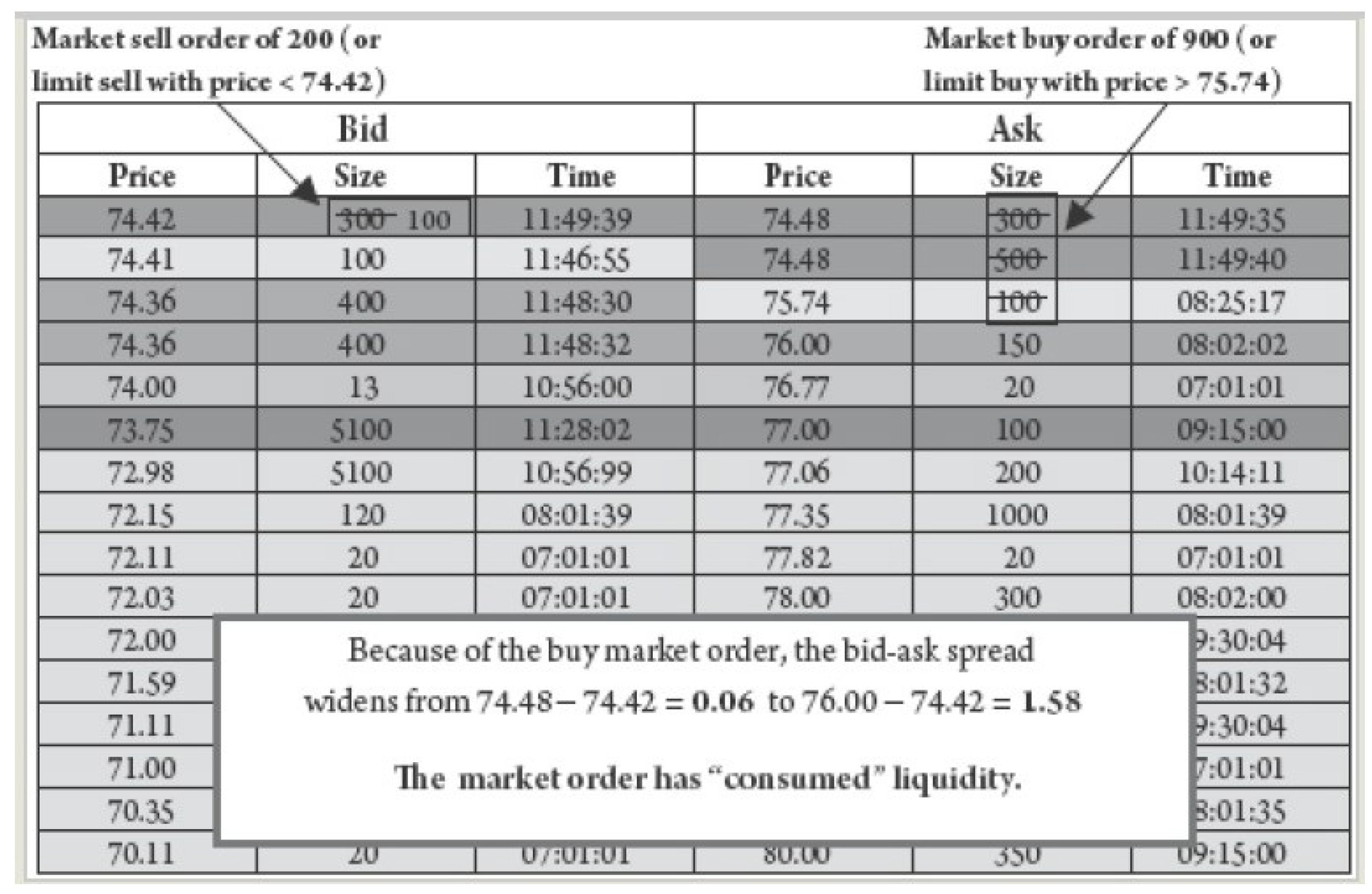
2.3. Limit Order Book (LOB)
2.4. High-Frequency Data
3. Relevant Literature
3.1. HFT Studies Using Direct Method
3.2. HFT Studies Using Indirect Method
4. Data, Variables and Measures, and Methods
4.1. Data
4.2. Variables and Measures
4.2.1. High-Frequency Trading
4.2.2. Market Fragmentation
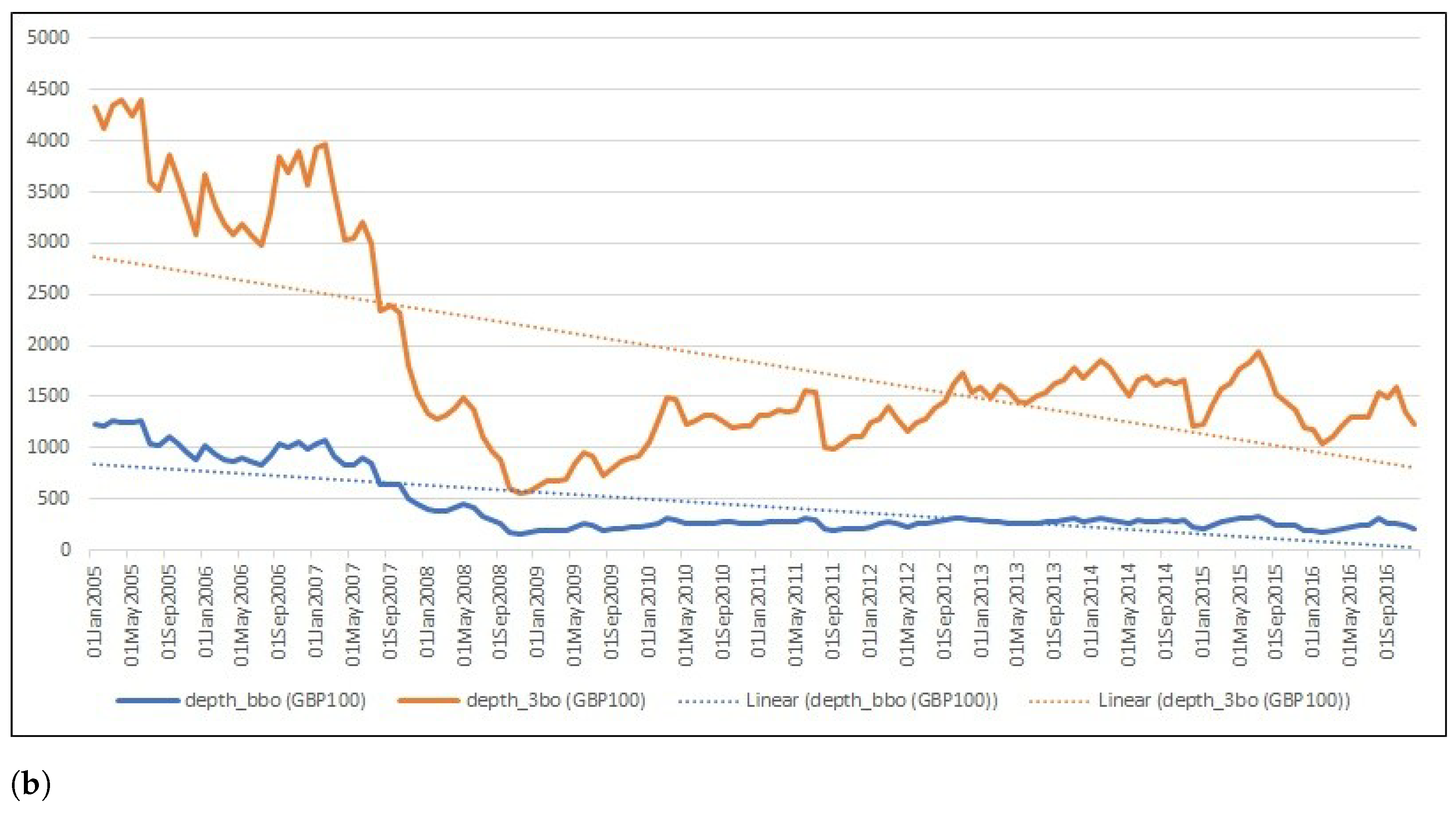
4.2.3. Liquidity Measures
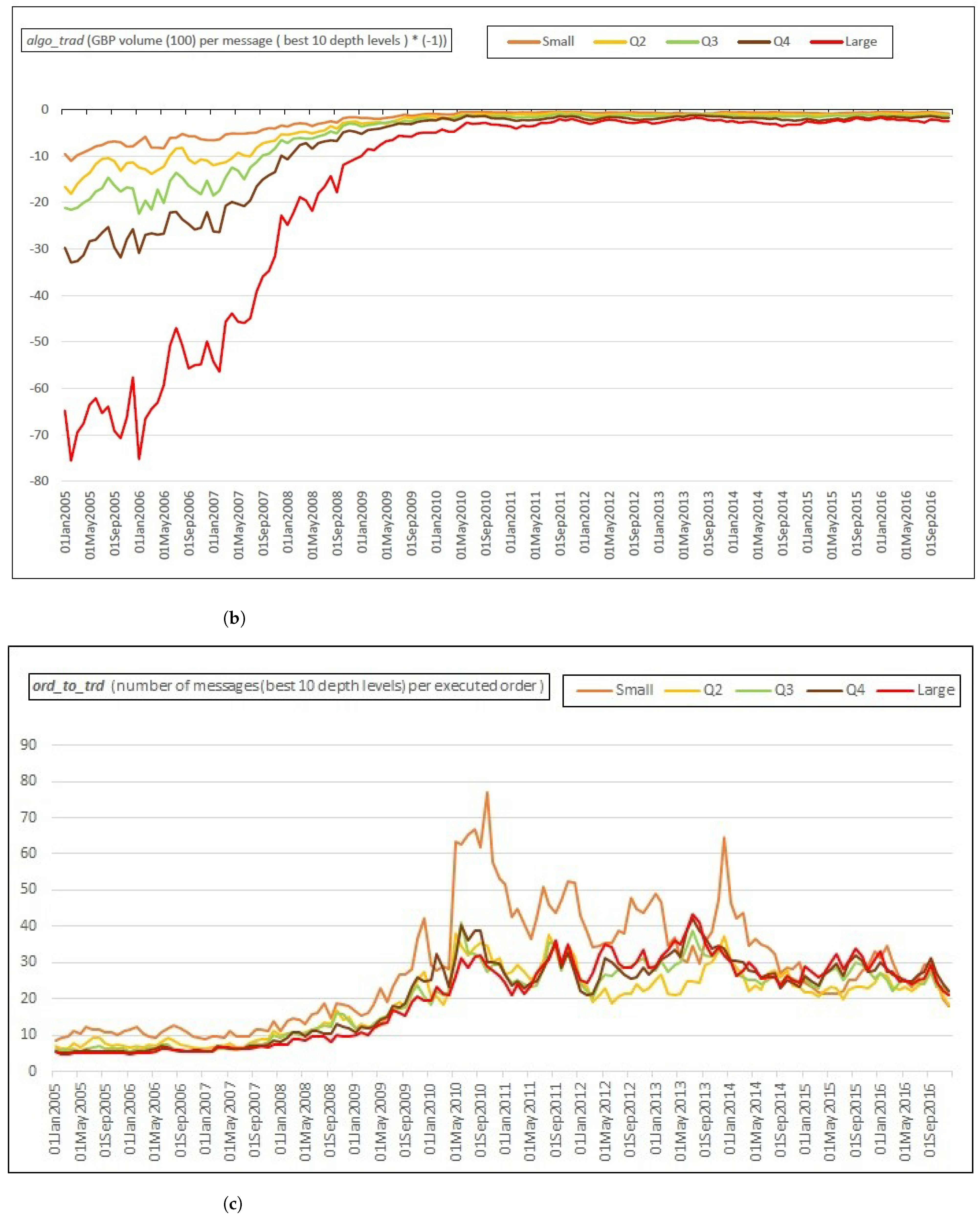
4.2.4. Alternative HFT Proxies: Do They All Fit?
4.3. Methods
5. Results and Discussions
5.1. HFT Proxy: The 10 Best Prices of the LOB
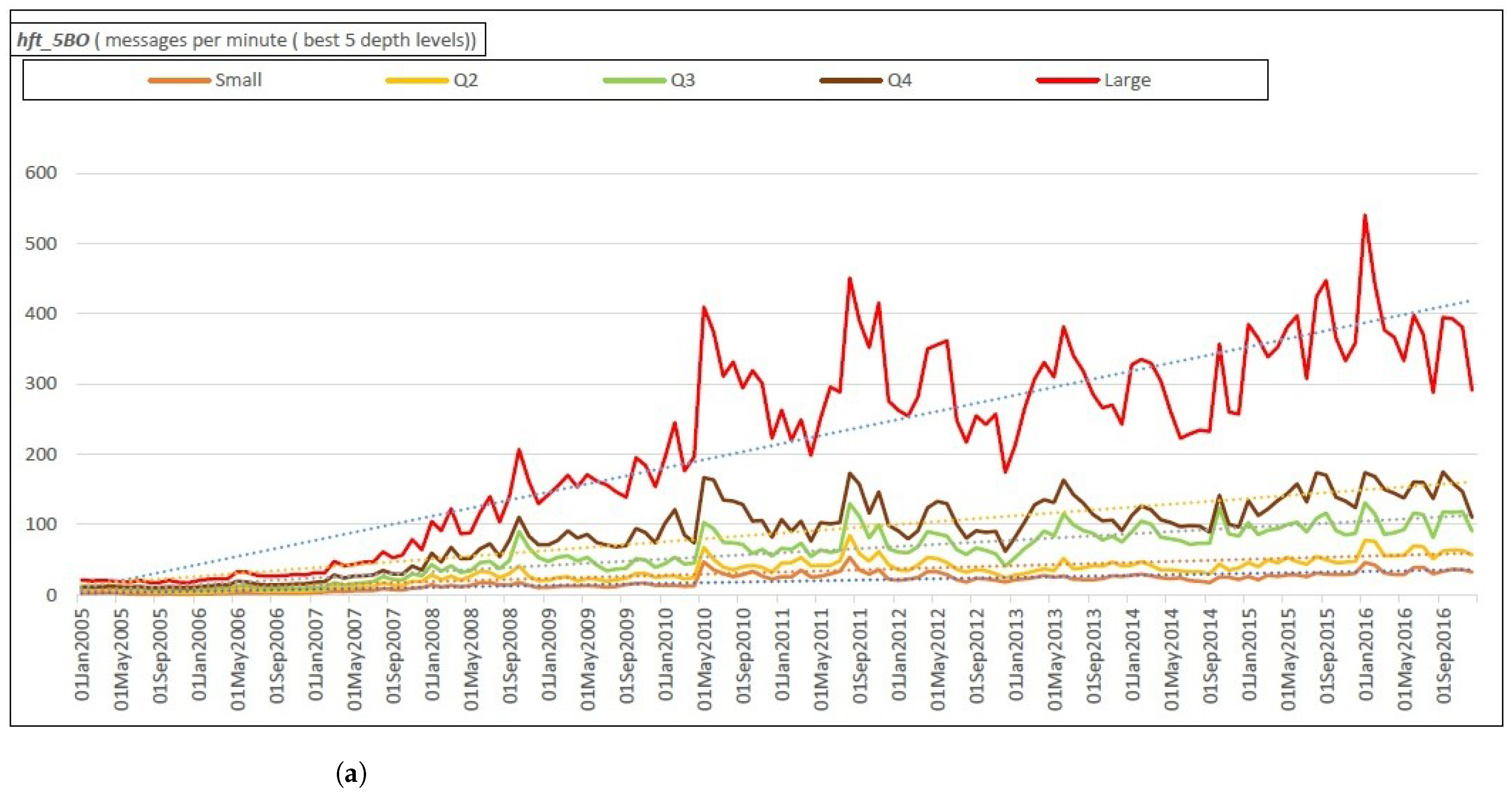
5.2. HFT Proxy: The 5 Best Prices of the LOB
5.3. HFT Proxy: The First Best Price (BBO) of the LOB
5.4. Which Depth Levels of LOB Should We Rely on?
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| #RIC | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L | BATS.L |
|---|---|---|---|---|---|---|---|---|---|---|
| Date[L] | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 | 29-Sep-16 |
| Time[L] | 4:11:45 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM | 4:11:46 PM |
| Type | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth | Market Depth |
| L1-BidPrice | 4941 | 4941 | 4941 | 4941 | 4941 | 4941 | 4941 | 4941 | 4941 | 4941 |
| L1-BidSize | 1044 | 1044 | 897 | 897 | 897 | 697 | 697 | 697 | 697 | 547 |
| L1-BuyNo | 6 | 6 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 3 |
| L1-AskPrice | 4942 | 4942 | 4942 | 4941.5 | 4941.5 | 4941.5 | 4941.5 | 4941.5 | 4941.5 | 4941.5 |
| L1-AskSize | 1083 | 1083 | 1083 | 200 | 200 | 200 | 200 | 299 | 434 | 434 |
| L1-SellNo | 7 | 7 | 7 | 1 | 1 | 1 | 1 | 2 | 3 | 3 |
| L2-BidPrice | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 | 4940.5 |
| L2-BidSize | 2098 | 2098 | 2098 | 2098 | 2098 | 2098 | 2098 | 2098 | 2098 | 2098 |
| L2-BuyNo | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| L2-AskPrice | 4942.5 | 4942.5 | 4942.5 | 4942 | 4942 | 4942 | 4942 | 4942 | 4942 | 4942 |
| L2-AskSize | 1769 | 1769 | 1769 | 1083 | 1083 | 1083 | 1103 | 1103 | 1103 | 1103 |
| L2-SellNo | 13 | 13 | 13 | 7 | 7 | 7 | 8 | 8 | 8 | 8 |
| L3-BidPrice | 4940 | 4940 | 4940 | 4940 | 4940 | 4940 | 4940 | 4940 | 4940 | 4940 |
| L3-BidSize | 1938 | 1938 | 1938 | 1938 | 1938 | 1938 | 1938 | 1938 | 1938 | 1938 |
| L3-BuyNo | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| L3-AskPrice | 4943 | 4943 | 4943 | 4942.5 | 4942.5 | 4942.5 | 4942.5 | 4942.5 | 4942.5 | 4942.5 |
| L3-AskSize | 2048 | 2048 | 2048 | 1769 | 1769 | 1769 | 1769 | 1769 | 1769 | 1769 |
| L3-SellNo | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| L4-BidPrice | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 | 4939.5 |
| L4-BidSize | 2415 | 2415 | 2415 | 2415 | 2415 | 2415 | 2415 | 2415 | 2415 | 2415 |
| L4-BuyNo | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| L4-AskPrice | 4943.5 | 4943.5 | 4943.5 | 4943 | 4943 | 4943 | 4943 | 4943 | 4943 | 4943 |
| L4-AskSize | 2007 | 2007 | 2007 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 |
| L4-SellNo | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| L5-BidPrice | 4939 | 4939 | 4939 | 4939 | 4939 | 4939 | 4939 | 4939 | 4939 | 4939 |
| L5-BidSize | 2310 | 2310 | 2310 | 2310 | 2310 | 2310 | 2310 | 2310 | 2310 | 2310 |
| L5-BuyNo | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| L5-AskPrice | 4944 | 4944 | 4944 | 4943.5 | 4943.5 | 4943.5 | 4943.5 | 4943.5 | 4943.5 | 4943.5 |
| L5-AskSize | 2192 | 2692 | 2692 | 2007 | 2007 | 2007 | 2007 | 2007 | 2007 | 2007 |
| L5-SellNo | 13 | 14 | 14 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| L6-BidPrice | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 | 4938.5 |
| L6-BidSize | 2140 | 2140 | 2140 | 2140 | 2140 | 2140 | 2140 | 2140 | 2140 | 2140 |
| L6-BuyNo | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| L6-AskPrice | 4944.5 | 4944.5 | 4944.5 | 4944 | 4944 | 4944 | 4944 | 4944 | 4944 | 4944 |
| L6-AskSize | 1681 | 1681 | 1681 | 2692 | 2692 | 2692 | 2692 | 2692 | 2692 | 2692 |
| L6-SellNo | 11 | 11 | 11 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| L7-BidPrice | 4938 | 4938 | 4938 | 4938 | 4938 | 4938 | 4938 | 4938 | 4938 | 4938 |
| L7-BidSize | 3044 | 3044 | 3044 | 3044 | 3044 | 3044 | 3044 | 3044 | 3044 | 3044 |
| L7-BuyNo | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| L7-AskPrice | 4945 | 4945 | 4945 | 4944.5 | 4944.5 | 4944.5 | 4944.5 | 4944.5 | 4944.5 | 4944.5 |
| L7-AskSize | 3363 | 3363 | 3363 | 1681 | 1681 | 1681 | 1681 | 1681 | 1681 | 1681 |
| L7-SellNo | 13 | 13 | 13 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| L8-BidPrice | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 | 4937.5 |
| L8-BidSize | 923 | 923 | 923 | 923 | 923 | 923 | 923 | 923 | 923 | 923 |
| L8-BuyNo | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| L8-AskPrice | 4945.5 | 4945.5 | 4945.5 | 4945 | 4945 | 4945 | 4945 | 4945 | 4945 | 4945 |
| L8-AskSize | 1881 | 1881 | 1881 | 3363 | 3363 | 3363 | 3363 | 3363 | 3363 | 3363 |
| L8-SellNo | 11 | 11 | 11 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| L9-BidPrice | 4937 | 4937 | 4937 | 4937 | 4937 | 4937 | 4937 | 4937 | 4937 | 4937 |
| L9-BidSize | 1109 | 1109 | 1109 | 1109 | 1109 | 1109 | 1109 | 1109 | 1109 | 1109 |
| L9-BuyNo | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| L9-AskPrice | 4946 | 4946 | 4946 | 4945.5 | 4945.5 | 4945.5 | 4945.5 | 4945.5 | 4945.5 | 4945.5 |
| L9-AskSize | 1071 | 1071 | 1071 | 1881 | 1681 | 1681 | 1681 | 1681 | 1681 | 1681 |
| L9-SellNo | 6 | 6 | 6 | 11 | 10 | 10 | 10 | 10 | 10 | 10 |
| L10-BidPrice | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 | 4936.5 |
| L10-BidSize | 370 | 370 | 370 | 370 | 370 | 370 | 370 | 370 | 370 | 370 |
| L10-BuyNo | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| L10-AskPrice | 4946.5 | 4946.5 | 4946.5 | 4946 | 4946 | 4946 | 4946 | 4946 | 4946 | 4946 |
| L10-AskSize | 1178 | 1178 | 1178 | 1071 | 1071 | 1071 | 1071 | 1071 | 1071 | 1071 |
| L10-SellNo | 7 | 7 | 7 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 1 | One of the main reason is that the proxy is adjusted for the rising trade volumes associated with the period on which the study is made. On the contrary, the period 2005–2016 which is used to construct our sample is not associated with any rising phenomenon of trade volume. Conversely, the LSE has lost market share to the competing alternative trading venues during the same period. See Section 4.2.4 for the detail arguments. |
| 2 | In order to capture ‘dark pool’ operators and other similar trading systems, a new category of trading venue called Organised Trading Facility (OTF) is introduced for non-equity instruments in MIFID II, which came into effect on 3 January 2018. |
| 3 | The turnaround time between a message from a trader and its receipt at exchange platform. |
| 4 | Foucault et al. (2013) define liquidity as the degree to which an order can be executed within a short time frame at a price closer to the security’s consensus value. Conversely, if a price deviates substantially from the consensus value, there is illiquidity. |
| 5 | The trade signing methodology adopted in this study goes as follows. In a first phase, algorithms filter all trades not sourcing from the automatic session and then accumulate trades executed on the same milliseconds with the same price. The problem arising from accumulating all trades indiscriminately executed in the same millisecond is carefully avoided. Generally, trade records delivered with the same time-stamp include both buy and sell trades. Therefore, it is important to distinguish them as buyer or seller initiated trades before accumulating them. The second phase is bit more complex and time-consuming where algorithms match trade price with the relevant quotes, both bid and ask, considering several “if and then” conditions. The algorithms attempt to match a trade price with the immediately available prior quotes (either bid or sell), if they find a match with bid then provide a seller-initiated trade flag or a buyer-initiated flag when they find a match with ask. If the algorithms do not find a match with the immediate quotes, then they look for a match to the one before the immediate one, and so on. In contrast, a traditional trade signing approach compares changes in trade price with the changes in mid price to ascertain whether an executed trade is buyer- or seller-initiated, and does not seem to fit a dynamic low-latency environment where quote update speed is very high and the time synchronization between trades and quotes updates is not quite orderly. The algorithms used in this study can assign a trade sign with accuracies reaching over . |
| 6 | The general expressions for the partial effect are evaluated at the sample means of HFT (96) and market fragmentation (), as reported in Table 4. |
| 7 | (, see Table 11. |
References
- Ahn, Hee Joon, Jun Cai, and Cheol Won Yang. 2018. Which liquidity proxy measures liquidity best in emerging markets? Economies 6: 67. [Google Scholar] [CrossRef] [Green Version]
- Aitken, Michael, Haoming Chen, and Sean Foley. 2017. The impact of fragmentation, exchange fees and liquidity provision on market quality. Journal of Empirical Finance 41: 140–60. [Google Scholar] [CrossRef]
- Aldridge, Irene. 2013. High Frequency Trading: A Practical Guide to Algorithmic Strategies and Trading System, 2nd ed. Hoboken: Wiley. [Google Scholar]
- AMF. 2017. Study of the Behaviour of High-Frequency Traders on Euronext Paris. Technical Report. Available online: https://www.amf-france.org/en/news-publications/publications/reports-research-and-analysis/study-behaviour-high-frequency-traders-euronext-paris (accessed on 15 December 2021).
- Baldauf, Markus, and Joshua Mollner. 2021. Trading in Fragmented Markets. Journal of Financial and Quantitative Analysis 56: 93–121. [Google Scholar] [CrossRef] [Green Version]
- Ben Ammar, Imen, and Slaheddine Hellara. 2021. Intraday interactions between high-frequency trading and price efficiency. Finance Research Letters 41: 101862. [Google Scholar] [CrossRef]
- Biais, Bruno, and Thierry Foucault. 2014. HFT and market quality. Bankers, Markets and Investors 128: 5–19. [Google Scholar]
- Boehmer, Ekkehart, Kingsley Fong, and Juan Wu. 2021. Algorithmic Trading and Market Quality: International Evidence. Journal of Financial and Quantitative Analysis 56: 2659–88. [Google Scholar] [CrossRef]
- Boehmer, Ekkehart, Dan Li, and Gideon Saar. 2018. The Competitive Landscape of High-Frequency Trading Firms. The Review of Financial Studies 31: 2227–76. [Google Scholar] [CrossRef]
- Bouveret, Antoine, Cyrille Guillaumie, Carlos Aparicio Roqueiro, Christian Winkler, and Steffen Nauhaus. 2014. High-frequency trading activity in EU equity markets. European Securities and Markets Authority, Economic Report 1: 1–31. [Google Scholar]
- Brogaard, Jonathan, and Corey Garriott. 2018. High-Frequency Trading Competition. Journal of Financial and Quantitative Analysis 54: 1469–97. [Google Scholar] [CrossRef] [Green Version]
- Brogaard, Jonathan, Terrence Hendershott, Stefan Hunt, and Carla Ysusi. 2014. High-frequency trading and the execution costs of institutional investors. Financial Review 49: 345–69. [Google Scholar] [CrossRef]
- Brogaard, Jonathan, Terrence Hendershott, and Ryan Riordan. 2014. Market Integration and High Frequency Intermediation. Available online: https://docs.iiroc.ca/DisplayDocument.aspx?DocumentID=89E7649BE79B49A0BAC4B2BE1685EDA0&Language=en (accessed on 15 December 2021).
- Carrion, Allen. 2013. Very fast money: High-frequency trading on the NASDAQ. Journal of Financial Markets 16: 680–711. [Google Scholar] [CrossRef]
- CFA Institute. 2011. The Structure, Regulation, and Transparency of European Equity Markets under MiFID. Technical Report. Available online: https://www.cfainstitute.org/en/advocacy/policy-positions/structure-regulation-and-transparency-of-european-equity-markets-under-mifid (accessed on 15 December 2021).
- Conrad, Jennifer, Kevin M. Johnson, and Sunil Wahal. 2003. Institutional trading and alternative trading systems. Journal of Financial Economics 70: 99–134. [Google Scholar] [CrossRef]
- Conrad, Jennifer, Sunil Wahal, and Jin Xiang. 2015. High-frequency quoting, trading, and the efficiency of prices. Journal of Financial Economics 116: 271–91. [Google Scholar] [CrossRef] [Green Version]
- Degryse, Hans, Frank De Jong, and Vincent Van Kervel. 2015. The impact of dark trading and visible fragmentation on market quality. Review of Finance 19: 1587–622. [Google Scholar] [CrossRef] [Green Version]
- Foucault, Thierry, Marco Pagano, and Alisa Roell. 2013. Market Liquidity: Theory, Evidence, and Policy. Oxford: Oxford University Press. [Google Scholar]
- Friederich, Sylvain, and Richard Payne. 2015. Order-to-trade ratios and market liquidity. Journal of Banking & Finance 50: 214–23. [Google Scholar] [CrossRef] [Green Version]
- Frino, Alex, Vito Mollica, Eleonora Monaco, and Riccardo Palumbo. 2017. The effect of algorithmic trading on market liquidity: Evidence around earnings announcements on Borsa Italiana. Pacific Basin Finance Journal 45: 82–90. [Google Scholar] [CrossRef]
- Gomber, Peter, B. Arndt, M. Lutat, and T. Uhle. 2011. High-Frequency Trading. Available online: https://www.deutsche-boerse.com/resource/blob/69642/6bbb6205e6651101288c2a0bfc668c45/data/high-frequency-trading_en.pdf (accessed on 15 December 2021).
- Gresse, Carole. 2017. Effects of lit and dark market fragmentation on liquidity. Journal of Financial Markets 35: 1–20. [Google Scholar] [CrossRef]
- Hagströmer, Björn. 2021. Bias in the effective bid-ask spread. Journal of Financial Economics 142: 314–37. [Google Scholar] [CrossRef]
- Hagströmer, Björn, and Lars Nordén. 2013. The diversity of high-frequency traders. Journal of Financial Markets 16: 741–70. [Google Scholar] [CrossRef]
- Hasbrouck, Joel, and Gideon Saar. 2013. Low-latency trading. Journal of Financial Markets 6: 646–79. [Google Scholar] [CrossRef]
- Hendershott, Terrence, Charles M. Jones, and Albert J. Menkveld. 2011. Does algorithmic trading improve liquidity? The Journal of Finance 66: 1–34. [Google Scholar] [CrossRef] [Green Version]
- Hendershott, Terrence, and Ryan Riordan. 2013. Algorithmic trading and the market for liquidity. Journal of Financial and Quantitative Analysis 48: 1001–24. [Google Scholar] [CrossRef] [Green Version]
- Jovanovic, Boyan, and Albert J. Menkveld. 2015. Middlemen in Limit order Markets. Available online: https://ideas.repec.org/p/red/sed010/955.html (accessed on 15 December 2021).
- Kirilenko, Andrei, Albert S. Kyle, Mehrdad Samadi, and Tugkan Tuzun. 2017. The flash crash: High-frequency trading in an electronic market. Journal of Finance 72: 967–98. [Google Scholar] [CrossRef] [Green Version]
- Kollias, Christos, Stephanos Papadamou, and Costas Siriopoulos. 2013. European markets’ reactions to exogenous shocks: A high frequency data analysis of the 2005 london bombings. International Journal of Financial Studies 1: 154–67. [Google Scholar] [CrossRef] [Green Version]
- Lee, Charles M. C., and Mark J. Ready. 1991. Inferring trade direction from intraday data. Journal of Finance 46: 733–46. [Google Scholar] [CrossRef]
- Leone, Vitor, and Frank Kwabi. 2019. High frequency trading, price discovery and market efficiency in the FTSE100. Economics Letters 181: 174–77. [Google Scholar] [CrossRef]
- Linton, Oliver, and Soheil Mahmoodzadeh. 2018. Implications of High-Frequency Trading for Security Markets. Annual Review of Economics 10: 237–59. [Google Scholar] [CrossRef] [Green Version]
- Markellos, Raphael N., Terence Mills, and Costas Siriopoulos. 2003. Intradaily behavior of listed and unlisted security basket indices in the emerging greek stock market. Managerial Finance 29: 29–54. [Google Scholar] [CrossRef]
- Menkveld, Albert J. 2016. The economics of high-frequency trading: Taking stock. Annual Review of Financial Economics 8: 1–24. [Google Scholar] [CrossRef] [Green Version]
- Mishra, Suchismita, and Le Zhao. 2021. Order Routing Decisions for a Fragmented Market: A Review. Journal of Risk and Financial Management 14: 556. [Google Scholar] [CrossRef]
- O’Hara, Maureen. 2015. High frequency market microstructure. Journal of Financial Economics 116: 257–70. [Google Scholar] [CrossRef]
- O’Hara, Maureen, Chen Yao, and Mao Ye. 2014. What’s Not There: Odd Lots and Market Data. The Journal of Finance 69: 2199–36. [Google Scholar] [CrossRef]
- O’Hara, Maureen, and Mao Ye. 2011. Is market fragmentation harming market quality? Journal of Financial Economics 100: 459–74. [Google Scholar] [CrossRef]
- Petersen, Mitchell A., and David Fialkowski. 1994. Posted versus effective spreads. Good prices or bad quotes? Journal of Financial Economics 35: 269–92. [Google Scholar] [CrossRef]
- The Netherlands Authority for the Financial Markets. 2010. High Frequency Trading: The Application of Advanced Trading Technology in the European Marketplace. AFM Report on High Frequency Trading (HFT). Available online: https://www.afm.nl/~/profmedia/files/rapporten/2010/hft-report-engels.ashx (accessed on 20 November 2021).
- The Netherlands Authority for the Financial Markets. 2016. A Case Analysis of Critiques on High Frequency Trading. Technical Report. Available online: https://www.afm.nl/~/profmedia/files/rapporten/2016/case-analysis-critiques-high-frequency-trading.ashx (accessed on 20 November 2021).
- Upson, James, and Robert A. Van Ness. 2017. Multiple markets, algorithmic trading, and market liquidity. Journal of Financial Markets 32: 49–68. [Google Scholar] [CrossRef]
- Zaharudin, Khairul Zharif, Martin R. Young, and Wei-Huei Hsu. 2021. High-frequency trading: Definition, implications, and controversies. Journal of Economic Surveys 36: 75–107. [Google Scholar] [CrossRef]


| RIC | Days | RIC | Days | RIC | Days | RIC | Days | RIC | Days | RIC | Days |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAL | 3028 | BYG | 2892 | GOG | 2991 | LAND | 3028 | RB | 3029 | SPX | 2973 |
| ABF | 3027 | CCL | 3028 | GPOR | 2989 | LGEN | 3028 | RBS | 3028 | SRP | 3017 |
| ADN | 2898 | CLLN | 2989 | GRG | 2977 | LLOY | 3029 | REL | 3028 | SSE | 3028 |
| AHT | 2898 | CNA | 3028 | GRI | 2972 | LSE | 3022 | 2900 | STAN | 3028 | |
| ANTO | 3024 | CNE | 3029 | GSK | 3028 | MCRO | 2855 | RIO | 3028 | SVS | 2968 |
| 2944 | COB | 3024 | HIK | 2816 | MGGT | 3010 | 2722 | SVT | 3028 | ||
| 2572 | CPG | 3028 | HLMA | 2993 | MKS | 3028 | ROR | 2973 | SXS | 2977 | |
| AV | 3027 | CPI | 3026 | HMSO | 3022 | 2399 | RR | 3028 | TATE | 3028 | |
| AVV | 2814 | CRDA | 2934 | HSBA | 3027 | 2382 | RRS | 2968 | 2408 | ||
| AZN | 3028 | 2691 | HSV | 2975 | 2861 | RSA | 3027 | TLW | 3026 | ||
| BAB | 2917 | DGE | 3028 | HSX | 2972 | MRW | 3028 | RTO | 3028 | TPK | 3004 |
| BARC | 3028 | 2503 | ICP | 2980 | MTO | 2987 | 2966 | TSCO | 3028 | ||
| BATS | 3028 | DOM | 2764 | IGG | 2942 | NEX | 3021 | SBRY | 3028 | 2397 | |
| BBA | 3020 | DRX | 2786 | IHG | 3028 | NG | 2886 | SDR | 3023 | UBM | 3027 |
| BDEV | 3028 | DTY | 2874 | III | 3028 | NXT | 3028 | SGC | 3016 | ULE | 2980 |
| BLND | 3027 | ECM | 3021 | IMI | 3024 | OML | 3023 | SGE | 3028 | ULVR | 3027 |
| BLT | 3027 | ELM | 2882 | INCH | 3021 | PFC | 2838 | 2427 | UTG | 2956 | |
| BNZL | 3027 | EMG | 3028 | INF | 2869 | PFG | 3023 | SHB | 2971 | UU | 3028 |
| BOY | 2986 | 2581 | INVP | 2991 | PNN | 3009 | SHP | 3028 | VOD | 3029 | |
| BP | 3029 | EZJ | 3025 | ITRK | 3008 | PRU | 3027 | 2646 | WEIR | 2992 | |
| BRBY | 3011 | 2429 | ITV | 3028 | PSN | 3026 | SMDS | 2997 | WG | 2999 | |
| BT | 3028 | FGP | 3025 | JLT | 2994 | PSON | 3028 | SMIN | 3028 | WMH | 3027 |
| BVIC | 2789 | GFS | 3022 | JMAT | 3027 | PZC | 2956 | SMWH | 3007 | WPP | 3021 |
| BVS | 3005 | GKN | 3028 | KGF | 3029 | 2748 | SN | 3028 | WTB | 3017 | |
| BWY | 3019 | GNK | 2992 | KIE | 2915 | RAT | 2958 | SNR | 2858 | Total days | 439,583 |
| HFT Proxy | Description | Statistics | All | Small | Q2 | Q3 | Q4 | Large |
|---|---|---|---|---|---|---|---|---|
| messages per minute (best 10 depth levels) | Mean | 100.36 | 23.77 | 38.97 | 72.39 | 103.80 | 266.31 | |
| Median | 47.62 | 17.95 | 30.57 | 56.44 | 90.99 | 171.75 | ||
| StdDev | 157.77 | 23.22 | 38.25 | 67.59 | 84.81 | 271.25 | ||
| messages per minute (best 5 depth levels) | Mean | 83.72 | 19.35 | 32.61 | 60.80 | 89.36 | 219.40 | |
| Median | 41.10 | 14.42 | 26.09 | 49.34 | 80.49 | 149.97 | ||
| StdDev | 126.10 | 19.37 | 30.18 | 52.20 | 68.56 | 213.53 | ||
| messages per minute (BBO) | Mean | 39.32 | 9.57 | 15.67 | 28.33 | 43.50 | 100.91 | |
| Median | 20.38 | 7.48 | 12.87 | 23.91 | 40.04 | 76.56 | ||
| StdDev | 54.32 | 8.98 | 13.09 | 21.76 | 30.81 | 88.30 | ||
| number of messages for the 10 best levels per executed order (order-to-trade ratio) | Mean | 22.02 | 28.05 | 19.51 | 20.45 | 21.18 | 20.73 | |
| Median | 19.06 | 19.97 | 17.28 | 18.46 | 20.40 | 19.83 | ||
| StdDev | 21.25 | 36.67 | 15.59 | 14.76 | 13.57 | 13.84 | ||
| GBP volume (100) per message (best 10 depth levels) time (−1) | Mean | −6.93 | −2.24 | −3.73 | −5.14 | −7.51 | −16.21 | |
| Median | −1.96 | −0.88 | −1.37 | −1.77 | −2.38 | −3.60 | ||
| StdDev | 15.51 | 4.19 | 5.87 | 8.42 | 10.93 | 29.12 | ||
| GBP volume (100) per message (best 5 depth levels) time (−1) | Mean | −7.54 | −2.80 | −4.17 | −5.53 | −8.04 | −17.37 | |
| Median | −2.33 | −1.10 | −1.64 | −2.05 | −2.72 | −4.19 | ||
| StdDev | 16.22 | 5.30 | 6.32 | 8.78 | 11.36 | 30.28 | ||
| observations (stock * day) | 439,583 | 90,046 | 88,374 | 87,239 | 86,786 | 87,138 | ||
| Variables | log(hft_10bo) | log(hft_5bo) | log(hft_bbo) | HHItrd | log(spread_bps) | log(espread) | log(depth_bbo) | log(depth_3bo) | Log(mktcap) | log(voltintra) | invprice |
|---|---|---|---|---|---|---|---|---|---|---|---|
| log(hft_10bo) | 1 | ||||||||||
| log(hft_5bo) | 0.996 | ||||||||||
| log(hft_bbo) | 0.981 | 0.988 | |||||||||
| HHItrd | 0.561 | 0.546 | 0.503 | ||||||||
| log(spread_bps) | −0.762 | −0.776 | −0.772 | −0.402 | |||||||
| Log(espread) | −0.757 | −0.766 | −0.754 | −0.451 | 0.955 | ||||||
| log(depth_bbo) | 0.346 | 0.381 | 0.432 | −0.095 | −0.523 | −0.408 | |||||
| log(depth_3bo) | 0.444 | 0.473 | 0.513 | 0.078 | −0.593 | −0.488 | 0.969 | ||||
| Log(mktcap) | 0.740 | 0.754 | 0.772 | 0.271 | −0.829 | −0.773 | 0.722 | 0.768 | |||
| log(voltintra) | −0.020 | −0.027 | −0.012 | −0.241 | 0.360 | 0.372 | −0.215 | −0.276 | −0.234 | ||
| invprice | −0.103 | −0.108 | −0.114 | −0.086 | 0.235 | 0.257 | −0.158 | −0.185 | −0.156 | 0.214 | 1.000 |
| all coefficients are significant at 1% level. | |||||||||||
| Variables | Description | Mean | Median | Std. Dev. | N |
|---|---|---|---|---|---|
| spread_bps | quoted half-spreads | 18.37 | 13.14 | 19.83 | 346,368 |
| espread | effective half-spread | 6.41 | 4.87 | 6.92 | 346,368 |
| depth_bbo | average depth (at BBO/GBP100) | 358.15 | 180.23 | 869.90 | 346,368 |
| depth_3bbo | average cumulative depth (best three levels/GBP100) | 1636.19 | 803.05 | 3613.90 | 346,368 |
| hft_10bo | electronic message rate per minute (the best 10 depth levels) | 114.88 | 58.75 | 169.13 | 346,368 |
| hft_5bo | electronic message rate per minute (the best 5 depth levels) | 95.91 | 51.22 | 135.38 | 346,368 |
| hft_bbo | electronic message rate per minute (at BBO) | 44.88 | 25.34 | 58.11 | 346,368 |
| HHItrd | Herfindhal Index (proxy for trade fragmenatation) | 2.17 | 2.38 | 0.74 | 346,368 |
| mktcap | market capitalization (million GBP) | 9666.37 | 3018.93 | 17,853.14 | 346,368 |
| voltintra | Intraday volatility | 286.23 | 216.32 | 542.32 | 346,368 |
| price | daily average price (GBX) | 934.35 | 598.07 | 973.37 | 346,368 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| −0.278 *** | −0.279 *** | −0.275 *** | −0.32 *** | −0.321 *** | −0.279 *** | |
| (−89.68) | (−90.04) | (−50.21) | (−98.95) | (−99.46) | (−48.42) | |
| HHItrd | 0.049 *** | 0.057 *** | 0.061 *** | 0.139 *** | ||
| (15.9) | (7.21) | (18.99) | (16.6) | |||
| −0.002 | −0.019 *** | |||||
| (−1.15) | (−10.19) | |||||
| log(mktcap) | −0.214 *** | −0.217 *** | −0.218 *** | −0.141 *** | −0.145 *** | −0.153 *** |
| (−52.76) | (−53.5) | (−53.34) | (−32.87) | (−33.83) | (−35.53) | |
| log(voltintra) | 0.165 *** | 0.167 *** | 0.167 *** | 0.211 *** | 0.213 *** | 0.21 *** |
| (56.69) | (58.17) | (57.84) | (62.68) | (64.4) | (62.98) | |
| invprice | 17.751 *** | 17.802 *** | 17.883 *** | 20.303 *** | 20.367 *** | 21.119 *** |
| (23.43) | (23.41) | (23.38) | (22.68) | (22.69) | (23.35) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| Observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.87 | 0.87 | 0.87 | 0.84 | 0.84 | 0.84 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| ) | −0.284 *** | −0.282 *** | −0.183 *** | −0.295 *** | −0.295 *** | −0.285 *** |
| (−45.35) | (−45.25) | (−16.13) | (−43.27) | (−43.22) | (−22.7) | |
| −0.107 *** | 0.078 *** | 0.001 | 0.019 | |||
| (−19.94) | (4.76) | (0.21) | (1.05) | |||
| −0.045 *** | −0.004 | |||||
| (−10.99) | (−0.98) | |||||
| 0.816 *** | 0.823 *** | 0.804 *** | 0.864 *** | 0.864 *** | 0.862 *** | |
| (87.13) | (87.53) | (87.28) | (83.64) | (83.4) | (84.29) | |
| 0.041 *** | 0.037 *** | 0.029 *** | 0.003 | 0.003 | 0.002 | |
| (10.77) | (9.52) | (7.39) | (0.73) | (0.74) | (0.55) | |
| 1.067 | 0.957 | 2.739 | −0.144 | −0.143 | 0.032 | |
| (0.56) | (0.51) | (1.46) | (−0.08) | (−0.08) | (0.02) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.82 | 0.82 | 0.83 | 0.81 | 0.81 | 0.81 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| −0.288 *** | −0.289 *** | −0.283 *** | −0.322 *** | −0.324 *** | −0.282 *** | |
| (−92.96) | (−93.21) | (−54.74) | (−99.98) | (−100.38) | (−51.56) | |
| 0.052 *** | 0.065 *** | 0.065 *** | 0.144 *** | |||
| (17.72) | (9.09) | (20.72) | (18.81) | |||
| −0.003 * | −0.02 *** | |||||
| (−1.96) | (−11.24) | |||||
| −0.198 *** | −0.201 *** | −0.202 *** | −0.127 *** | −0.131 *** | −0.139 *** | |
| (−49.14) | (−49.93) | (−49.97) | (−29.43) | (−30.41) | (−32.17) | |
| 0.167 *** | 0.169 *** | 0.168 *** | 0.21 *** | 0.213 *** | 0.209 *** | |
| (58.38) | (59.99) | (59.69) | (63.96) | (65.83) | (64.35) | |
| 17.159 *** | 17.205 *** | 17.335 *** | 19.847 *** | 19.904 *** | 20.694 *** | |
| (22.65) | (22.68) | (22.7) | (21.99) | (22.04) | (22.83) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| Observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.87 | 0.87 | 0.87 | 0.84 | 0.84 | 0.84 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| −0.25 *** | −0.247 *** | −0.155 *** | −0.268 *** | −0.268 *** | −0.264 *** | |
| (−40.36) | (−40.14) | (−14.76) | (−39.84) | (−39.78) | (−22.66) | |
| −0.105 *** | 0.068 *** | 0.003 | 0.01 | |||
| (−19.51) | (4.5) | (0.52) | (0.62) | |||
| −0.044 *** | −0.002 | |||||
| (−11.27) | (−0.43) | |||||
| 0.811 *** | 0.818 *** | 0.801 *** | 0.863 *** | 0.863 *** | 0.862 *** | |
| (85.82) | (86.18) | (86.22) | (82.97) | (82.75) | (83.75) | |
| 0.029 *** | 0.025 *** | 0.018 *** | −0.007 * | −0.007 * | −0.007 * | |
| (7.69) | (6.42) | (4.59) | (−1.71) | (−1.68) | (−1.75) | |
| 1.584 | 1.492 | 3.227 * | 0.173 | 0.176 | 0.249 | |
| (0.82) | (0.77) | (1.69) | (0.09) | (0.09) | (0.13) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| Observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.82 | 0.82 | 0.82 | 0.81 | 0.81 | 0.81 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| −0.269 *** | −0.269 *** | −0.265 *** | −0.291 *** | −0.292 *** | −0.254 *** | |
| (−81.77) | (−81.87) | (−48.72) | (−84.2) | (−84.41) | (−42.99) | |
| 0.047 *** | 0.054 *** | 0.059 *** | 0.118 *** | |||
| (15.35) | (8.35) | (17.78) | (17.05) | |||
| −0.002 | −0.018 *** | |||||
| (−1.08) | (−9.68) | |||||
| −0.203 *** | −0.207 *** | −0.207 *** | −0.138 *** | −0.142 *** | −0.148 *** | |
| (−47.98) | (−48.64) | (−48.46) | (−29.98) | (−30.81) | (−32.15) | |
| 0.162 *** | 0.164 *** | 0.164 *** | 0.202 *** | 0.204 *** | 0.202 *** | |
| (55.6) | (57) | (56.79) | (60.4) | (62.03) | (60.66 | |
| 17.29 *** | 17.338 *** | 17.406 *** | 20.246 *** | 20.306 *** | 20.963 *** | |
| (20.89) | (20.87) | (20.85) | (20.3) | (20.3) | (20.93) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| Observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.87 | 0.87 | 0.87 | 0.83 | 0.83 | 0.83 |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Log(depth_bbo) | Log(depth_3bo) | |||||
| Explanatory Variables | Model-1 | Model-2 | Model-3 | Model-1 | Model-2 | Model-3 |
| −0.148 *** | −0.146 *** | −0.07 *** | −0.184 *** | −0.184 *** | −0.188 *** | |
| (−24.55) | (−24.45) | (−6.76) | (−27.66) | (−27.63) | (−16.19) | |
| −0.112 *** | 0.007 | −0.004 | −0.01 | |||
| (−20.37) | (0.52) | (−0.57) | (−0.74) | |||
| −0.037 *** | 0.002 | |||||
| (−9.4) | −0.5 | |||||
| 0.764 *** | 0.771 *** | 0.758 *** | 0.825 *** | 0.825 *** | 0.826 *** | |
| (79.74) | (80.22) | (80.13) | −78.28 | −78.11 | −78.92 | |
| −0.002 | −0.007 * | −0.012 *** | −0.032 *** | −0.032 *** | −0.032 *** | |
| (−0.46) | (−1.72) | (−3.05) | (−7.89) | (−7.93) | (−7.85) | |
| 3.97 * | 3.856 * | 5.173 ** | 2.066 | 2.063 | 1.986 | |
| (1.92) | (1.88) | (2.53) | −1.02 | −1.02 | −0.97 | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES |
| Observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.82 | 0.82 | 0.82 | 0.81 | 0.81 | 0.81 |
| LOB Depth Level | ||||||||||||
| −0.265 *** | −0.283 *** | −0.275 *** | −0.254 *** | −0.282 *** | −0.279 *** | −0.07 *** | −0.155 *** | −0.183 *** | −0.188 *** | − 0.264*** | −0.285 *** | |
| (−48.72) | (−54.74) | (−50.21) | (−42.99) | (−51.56) | (−48.42) | (−6.76) | (−14.76) | (−16.13) | (−16.19) | (−22.66) | (−22.7) | |
| 0.054 *** | 0.065 *** | 0.057 *** | 0.118 *** | 0.144 *** | 0.139 *** | 0.007 | 0.068 *** | 0.078 *** | −0.01 | 0.01 | 0.019 | |
| (8.35) | (9.09) | (7.21) | (17.05) | (18.81) | (16.6) | (0.52) | (4.5) | (4.76) | (−0.74) | (0.62) | (1.05) | |
| * HHItrd | −0.002 | −0.003 * | −0.002 | −0.018 *** | −0.02 *** | −0.019 *** | −0.037 *** | −0.044 *** | −0.045 *** | 0.002 | −0.002 | −0.004 |
| (−1.08) | (−1.96) | (−1.15) | (−9.68) | (−11.24) | (−10.19) | (−9.4) | (−11.27) | (−10.99) | −0.5 | (−0.43) | (−0.98) | |
| −0.207 *** | −0.202 *** | −0.218 *** | −0.148 *** | −0.139 *** | −0.153 *** | 0.758 *** | 0.801 *** | 0.804 *** | 0.826 *** | 0.862 *** | 0.862 *** | |
| (−48.46) | (−49.97) | (−53.34) | (−32.15) | (−32.17) | (−35.53) | (80.13) | (86.22) | (87.28) | −78.92 | (83.75) | (84.29) | |
| 0.164 *** | 0.168 *** | 0.167 *** | 0.202 *** | 0.209 *** | 0.21 *** | −0.012 *** | 0.018 *** | 0.029 *** | −0.032 *** | −0.007 * | 0.002 | |
| (56.79) | (59.69) | (57.84) | (60.66) | (64.35) | (62.98) | (−3.05) | (4.59) | (7.39) | (−7.85) | (−1.75) | (0.55) | |
| 17.406 *** | 17.335 *** | 17.883 *** | 20.963 *** | 20.694 *** | 21.119 *** | 5.173 ** | 3.227 * | 2.739 | 1.986 | 0.249 | 0.032 | |
| (20.85) | (22.7) | (23.38) | (20.93) | (22.83) | (23.35) | (2.53) | (1.69) | (1.46) | −0.97 | (0.13) | (0.02) | |
| stock/firm fixed effect | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| time fixed effect | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| observations | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 | 346,368 |
| R-Square | 0.87 | 0.87 | 0.87 | 0.83 | 0.84 | 0.84 | 0.82 | 0.82 | 0.83 | 0.81 | 0.81 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, S. High-Frequency Trading (HFT) and Market Quality Research: An Evaluation of the Alternative HFT Proxies. J. Risk Financial Manag. 2022, 15, 54. https://doi.org/10.3390/jrfm15020054
Hossain S. High-Frequency Trading (HFT) and Market Quality Research: An Evaluation of the Alternative HFT Proxies. Journal of Risk and Financial Management. 2022; 15(2):54. https://doi.org/10.3390/jrfm15020054
Chicago/Turabian StyleHossain, Shahadat. 2022. "High-Frequency Trading (HFT) and Market Quality Research: An Evaluation of the Alternative HFT Proxies" Journal of Risk and Financial Management 15, no. 2: 54. https://doi.org/10.3390/jrfm15020054
APA StyleHossain, S. (2022). High-Frequency Trading (HFT) and Market Quality Research: An Evaluation of the Alternative HFT Proxies. Journal of Risk and Financial Management, 15(2), 54. https://doi.org/10.3390/jrfm15020054






