Risk Management and Agency Theory: Role of the Put Option in Corporate Bonds

Abstract

This study sets out a new methodology to exemplify, through a set of risk metrics called the Greeks, impact of a bond’s structured provisions (e.g., call, put, and conversion options) on its risk characteristics and its propensity for agency conflicts. The methodology is assessed by applying it to a sample of 159 non-convertible bonds, with time-scheduled call and put provisions issued between 1977 and 2005. A structural contingent-claims valuation model is used to value the bonds and estimate the Greeks. The methodology is used to assess the impact of the call and put provisions on the bond’s credit risk and interest-rate risk, as well as the provisions’ ability to mitigate the agency conflict associated with over-investment, under-investment, asset-substitution, and information asymmetry about the firm’s true risk among stakeholders. The main findings of this study are that the put option plays a key role in reducing credit risk, mitigating agency conflict, and protecting against volatility shocks; conversely, the call option plays a key role in reducing interest-rate risk. The methodology is sufficiently general to apply to bonds and preferred stock with any set of structured provisions.

1. Introduction

This study proposes a new methodology to assess the impact of a bond’s structured provisions (e.g., the call, put, and conversion terms) on its credit risk, interest-rate risk, and propensity to mitigate agency conflict due to asset-substitution, over-investment, under-investment, and information asymmetry about the firm’s risk via a set of risk metrics called the Greeks (Delta, Gamma, Vega, and Rho). The Greeks are a standardized set of risk measures associated with financial derivatives. The proposition is that the Greeks are a reduced-form representation of the structured provisions that can be used to assess the bond’s risk and agency characteristics. Quite simply, the bond’s structured provisions are encapsulated in the Greeks, and the Greeks can be used to assess the bond’s susceptibility to credit risk, interest-rate risk, and agency conflict. The proposition is simple, yet general, because the Greeks are a standardized set of risk metrics with a standardized interpretation that can be used to assess the bond’s credit risk, interest-rate risk, and its propensity for agency conflict without reference to the original structured provisions. Thus, the methodology can be applied to any structured financial security.

The proposition is applied to a sample of 159 non-convertible bonds, with call and put provisions issued between 1977 and 2005. Merton (1974) model is used to value the bonds and estimate the Greeks. The boundary conditions on Merton’s model, for the optimal exercise of the call and put provisions, follow from the perfect-markets policies articulated in Ingersoll (1977). The numerical algorithm to solve Merton’s model is adopted from Brennan and Schwartz (1977). The proposition does not rely on implementing the most accurate pricing model for callable and putable bonds, and there are many. For example, Brennan and Schwartz (1980) extends Merton’s model, permitting the firm’s value and the interest rate to be stochastic, and Wang and Chou (2005) show how callable and putable bonds may be priced using Duffie and Singleton’s (1999) reduced-form approach, where the default-adjusted interest rate and the hazard rate follow stochastic processes. It is not the objective of this study to evaluate alternative pricing models, but rather to propose a new methodology independent of the pricing model to assess the risk and agency characteristics of structured (i.e., callable, putable, and/or convertible) bonds.

1.1. The Greeks

Denoting the bond’s valuation function by $f\left(V;r,\sigma \right)$, where $V$ represents the firm’s value, $r$ represents the riskless interest-rate, and σ represents the standard deviation of the firm’s instantaneous return $dV/V$, four standardized risk measures can be calculated:

$$Delta=\left(\frac{V}{f}\right)\frac{df}{dV}$$

(1)

$$Gamma=\frac{d^{2}f}{d{V}^2}$$

(2)

$$Vega=\left(\frac{\sigma }{f}\right)\frac{df}{d\sigma },$$

(3)

$$Rho=\left(\frac{-1}{f}\right)\frac{df}{dr}$$

(4)

The expressions in Equations (1), (3) and (4) are modified from the original Greeks to include the terms in parenthesis see (Hull 2008, Chp. 17). Each measure captures a different characteristic of the bond’s valuation function. Delta measures the percentage change in the bond’s value $\left(\Delta f/f\right)$ relative to a percentage change in the firm’s value $\left(\Delta V/V\right)$; equivalently, Delta is the elasticity of the bond’s value, with respect to the firm’s value. Gamma is the convexity of the valuation function. Vega measures the percentage change in the bond’s value $\left(\Delta f/f\right)$ relative to a percentage change in the firm’s risk $\left(\Delta \sigma /\sigma \right)$; equivalently, Vega is the elasticity of the bond’s value, with respect to the firm’s risk. Rho measures the percentage change in the bond’s value $\left(\Delta f/f\right)$ for a given change in the riskless interest rate $\Delta r$ and is a generalized measure of duration for parallel shifts in the riskless zero-curve.

When generalizing the pricing model to account for stochastic interest rates, the bond’s valuation function will depend on additional parameters associated with the interest rate process. In particular, this includes parameters associated with the mean-reversion and the volatility of the interest rate. Accordingly, the set of Greeks can be expanded to include sensitivity of the bond’s value to these additional parameters.

1.2. Relation between the Greeks and Risk/Agency Issues

Delta is positive and measures the risk of the bond relative to the risk of the firm. In particular, plotting the percentage change of the bond’s value ($\Delta f/f$ against the percentage change of the firm’s value $\left(\Delta V/V\right)$, the slope of the resulting line is Delta. Thus, Delta can be interpreted as the “Beta” of the bond’s return, relative to the firm’s return. In a factor model, accordingly, Delta is a proxy for credit risk. Thus, structured provisions that reduce Delta also mitigate the bond’s credit risk.

Gamma is the second derivative of the bond’s value, with respect to the firm’s value, and measures the convexity of the bond’s valuation function. Nonconvertible bonds have negative convexity, implying they incur greater downside losses (when the firm’s value falls) relative to limited upside gains (when the firm’s value rises). This asymmetry incentivizes asset-substitution, by the firm, from safe to risky assets, which expropriates wealth from bondholders for the benefit of stockholders. More negative values of Gamma imply greater susceptibility to asset-substitution. Thus, structured provisions that make Gamma less negative, zero, or positive mitigate the agency conflict between bondholders and stockholders due to asset-substitution (later, in Section 2, based on the literature review, it is argued that choosing structured provisions, such as Gamma $~0$, also mitigates over-investment, under-investment, and agency conflict due to information asymmetry).

Vega measures the sensitivity of the bond’s value to uncertainty in the firm’s risk, as well as to volatility shocks. It also measures the susceptibility of the bond’s value to the asymmetry, between bondholders and stockholders, against the true risk of the firm. Thus, structured provisions that reduce Vega also mitigate the agency conflict between bondholders and stockholders, arising from information asymmetry, about the firm’s risk.

Rho is a generalized measure of duration, so it is a proxy for the bond’s interest rate risk. Since the riskless interest rate is influenced by macroeconomic factors, it is unlikely to be the source of agency conflict between bondholders and stockholders. However, it plays an important role from a risk management perspective. For example, if the interest rate is high, firms would prefer to choose structured provisions and cap the bond’s value as the interest rate declines.

1.3. Hypotheses

The Greeks are evaluated for each case corresponding to the inclusion/exclusion of the call and/or put provisions, permitting assessment of the marginal impact of each provision on the Greeks and, in turn, on credit risk, interest-rate risk, and agency conflict.

The put provision forces the firm to redeem the bond at the direction of the investor, usually at par. This implies that the put provision protects the bondholder against downside losses when the bond’s value falls below par. Additionally, the bond’s value declines if there is a corresponding decline in the firm’s value. Thus, the put provision protects the bondholder against a decline in the firm’s value. Therefore, the put provision lowers the bond’s Delta. The call provision permits the firm to redeem the bond, usually at par or a premium above par, up to one year’s coupon payment. This implies that the call provision limits the bondholder’s upside gain. The bond’s value rises if there is a corresponding rise in the firm’s value. Thus, the call provision limits the bondholder’s upside gain as the firm’s value rises. Therefore, the call provision also lowers the bond’s Delta. To assess the relative impact of these provisions on Delta, it is necessary to evaluate second-order effects of changes in the firm’s value. Straight (non-callable and non-putable) bonds have negative convexity with respect to changes in the firm’s value. Thus, bonds disproportionately suffer greater downside losses when the firm’s value falls than benefit, from upside gains, when the firm’s value rises. Thus, it is hypothesized that the put, relative to the call, is more effective in lowering Delta and mitigating the bond’s credit risk.

The call provision caps the bondholder’s upside gains when the interest rate falls. Thus, the call provision lowers the bond’s Rho. Conversely, the put provision limits the bondholder’s downside losses when the interest-rate rises. Thus, the put provision also lowers the bond’s Rho. To assess the relative impact of these provisions on Rho, it is necessary to evaluate second-order effects of changes in the interest rate. It is well-known that straight (non-callable and non-putable) bonds have positive convexity with respect to changing interest rates. Thus, bonds disproportionately experience greater upside gains, as the interest rate falls, than downside losses as the interest rate rises. Thus, it is hypothesized that the call, relative to the put, is more effective in lowering Rho and mitigating the bond’s interest-rate risk.

As noted previously, straight (non-callable and non-putable) bonds have negative convexity with respect to changes in the firm’s value, i.e., the bond incurs proportionately larger downside losses when the firm’s value falls than upside gains when the firm’s value rises. The put provision mitigates downside losses, thus lowering the bond’s convexity (i.e., making it less negative) for declining firm values in the limit when the put is exercised. Thus, it is hypothesized that the put option lowers the magnitude of Gamma and, accordingly, mitigates agency conflict due to asset substitution. The call provision limits upside gains, but its impact on convexity is mixed and will depend on higher order derivatives of the bond’s valuation function. In particular, as the firm’s value increases, the convexity is likely to increase before it decreases in the limit when the call is exercised. Thus, the impact of the call option on Gamma, and its potential to mitigate asset substitution, is mixed.

The impact of the call and put provisions on Vega and the potential to mitigate the agency conflict between bondholders and stockholders, arising from information asymmetry about the firm’s risk, is more straightforward. The call and put have the effect of constraining the bond’s value with bounds, so it is hypothesized that both provisions will lower Vega. However, the relative impact of the call and put is an empirical issue.

1.4. Results

The time-scheduled call provision has received remarkable attention in the literature in relation to risk management and agency theory issues. In contrast, the time-scheduled put provision has received far less attention. The results of this study show the important role of the put relative to the call that has been largely overlooked in the literature.

A sample of 159 non-convertible time-scheduled callable and putable bonds, issued from 1977 to 2005, is analyzed. Delta, Gamma, and Vega are reduced, on average, 7–13% by the call provision and a further 68–74% by the put provision; Rho, in contrast, is reduced, on average, about 35% by the call provision and a further 12% by the put provision. The percentage reductions in Delta, Gamma, and Vega, for individual securities averaged across the sample, are about 30% due to the call provision and a further 50% due to the put provision; the corresponding percentage reductions in Rho, in contrast, are about 34% due to the call provision and a further 11% due to the put provision. These results show that agency issues related to asset-substitution and information asymmetry, about the firm’s risk, are more effectively controlled by the put provision relative to the call provision. Furthermore, protection against downside risk is better addressed by the put provision, whereas interest rate risk is better addressed by the call provision.

The model overestimates issuance prices by about 5%; this is not surprising, given the model does not endogenize risk-management and agency-theory issues. The Greeks explain about 25% of the model’s pricing errors in a cross-sectional analysis, and an additional 14% is explained by the structured provisions whose effects are not fully captured by the Greeks. These results suggest the model plus a linearized correction, based on the Greeks and these other provisions, provides a more accurate prediction of prices.

2. Literature Survey

This section surveys theoretical models and conceptual arguments in the literature that delineate relations between the Greeks, on the one hand, and risk-management and agency-theory issues, on the other, that support the proposed hypotheses. The purpose of the survey is to show that the literature supports the proposition that the Greeks, as a standardized set of risk metrics, can be used as a reduced-form representation of any set of structured provisions in assessing the bond’s credit risk, interest-rate risk, and its propensity for mitigating agency conflict without reference to the original structured provisions. The survey also supports the proposed hypotheses in relation to the choice of Greeks that mitigate risk and agency conflict.

2.1. Agency Issues and the Choice for Gamma and Vega

Jensen and Meckling (1976) argue that agency conflict between stockholders and bondholders encourages asset-substitution from safe to risky, which is costly, to prevent via restrictive covenants. Green (1984) shows how equity maximization with debt financing, given agency conflict, also incentivizes asset-substitution. The incentive may be sufficiently egregious to incentivize over-investment and, namely, safe, positive-NPV projects are replaced by risky negative-NPV projects motivated by the wealth transfer from bondholders to stockholders. Both studies suggest mitigating the problem by adding a conversion provision to straight debt, thereby altering the payoff function from concave to convex for larger firm values. In other words, these studies suggest that asset-substitution and over-investment can be mitigated if Gamma > 0.

Myers (1977) examines agency conflict and under-investment. Future equity investments that capitalize on growth options may be foregone if benefits from the investments accrue disproportionately to bondholders owing to either reduction in the firm’s risk or improvement in the firm’s prospects. (Bodie and Taggart [1978] 1980) argue that a call provision mitigates the under-investment problem. Specifically, if benefits from future equity investments accrue disproportionately to bondholders, the call feature may be used to garnish these benefits and thereby mitigate the under-investment problem. In other words, these studies suggest that underinvestment can be mitigated if Gamma < 0.

Combining these strategies, asset-substitution, over-investment, and under-investment may be simultaneously mitigated by selecting structured provisions such that |Gamma| ≅ 0.

Furthermore, Brennan and Schwartz (1988) evaluate agency issues due to uncertainty between stockholders and bondholders about the firm’s risk. They show that a convertible provision can lower the sensitivity of the bond’s price to the firm’s risk. Accordingly, they conclude that younger firms with higher market and earnings variability, i.e., higher risk uncertainty, should issue convertibles consistent with the findings of Mikkelson (1981). Generalizing Brennan and Schwartz’s proposition, agency issues, due to risk uncertainty, may be addressed by selecting structured provisions such that |Vega| ≅ 0.

2.2. Information Asymmetry and the Choice for Gamma and Vega

Myers and Majluf (1984) illustrate how asymmetric information between managers and investors result in under-investment. Brennan and Kraus (1987, Theorem 4) demonstrate how prudent financing choices overcome this problem. In particular, if the financing instrument is convex at issuance, its value is lowest for the firm with the smallest variance; thus, investors will assume the issuing firm has the lowest variance, and no firm with higher variance will issue the security. Conversely, if the financing instrument is concave at issuance, its value is lowest for the firm with the largest variance; thus, investors will assume the issuing firm has the largest variance and no firm with lower variance will issue the security. Thus, at issuance, Brennan and Kraus find that neither convex nor concave payoffs sustain in a signaling equilibrium with risk uncertainty and so firms would prefer to issue securities such that |Gamma| ≅ 0.

Constantinides and Grundy (1989, Proposition 3 and Figure 1) provide further support that, under-investment, may be mitigated by prudent financing choices in a signaling equilibrium. They propose convertible bond financing coupled with a stock repurchase. Specifically, if the issue size is sufficiently large to cover the investment expenditure, with excess capital utilized for stock repurchase, it could be an incentive compatible signaling equilibrium holds, in which old investors maximize the value of their holdings and new investors pay fair value for their claim. The equilibrium requires the issued claim to be locally convex at the issue price and concave at lower values. Thus, to mitigate under-investment under asymmetric information, Constantinides and Grundy propose issuing securities with Gamma > 0 at issuance and Gamma < 0 at lower firm values.

2.3. Credit Risk and the Choice for Delta

Delta captures the credit risk of a security, which is characterized as debt-like if Delta is small and equity-like if Delta is large. Chatfield and Moyer (1986) argue that a put provision mitigates bond default, and Tewari and Ramanlal (2010) find that putable-bond default is rare, notwithstanding steep declines in equity. These studies suggest that the put provision lowers Delta and correspondingly the risk of default. Thus, capital market imperfections, such as agency issues and information asymmetry, which encumber firms to credibly appease investors concerned about downside risk, can obtain financing by issuing securities with structured provisions such that Delta approaches zero (investors seeking equity participation in growth firms may prefer larger Delta facilitated by a conversion provision).

2.4. Interest-Rate Risk and the Choice for Rho

Rho is a generalized measure for interest rate risk similar to duration. A variety of structured provisions have been proposed to mitigate interest rate risk. Byrd et al. (2004) show that a conversion provision reduces interest rate risk. Kish and Livingston (1992) argue that a call provision, used when interest rates are high, enables refinancing as the interest rates fall. This is affirmed by Guntay et al. (2004) and Tewari et al. (2015). Furthermore, Chatfield and Moyer (1986) argue that volatile interest rates accelerate issuance of putable bonds. These studies show that both the call provision and the put provision can be used to mitigate interest rate risk. This study furthers this inquiry by assessing the relative impact of the call and put provisions to mitigate interest rate risk.

3. Data

The sample data includes all fixed-coupon nonconvertible bonds with explicitly specified time-scheduled call and put dates, issued between 1977 and 2005, listed in the Securities Data Corporation (SDC) platinum database. Issues with poison puts and super point puts are excluded since they are putable contingent on a reorganization event or ratings downgrade, as opposed to a deterministic time schedule. Calculating the firm’s value requires the market value for each firm’s common stock, preferred stock, and debt. The market value of common stock are estimated using daily stock price data and the number of common shares outstanding that are available on the Center for Research in Security Prices (CRSP) database for 60 trading days prior to issuance (roughly the preceding quarter). The market value of preferred stock and debt are unavailable; however, their book value, as of the issue date, are available on Compustat. These are used to calculate the firm’s value. Furthermore, the market value of common stock and the book values of preferred stock and debt are shown to be sufficient to calculate an upper bound and lower bound on the firm’s true volatility, as of the issuance date. The final sample, for which data are available to estimate the model’s parameters, is 159 issues. Average maturity is 19 years (stdev. = 8.7 years), and the average coupon rate is 8.53% (stdev. = 2.9%).

3.1. Firm and Issue Characteristics

The median firm value, calculated as the market value of equity plus the book value of debt and preferreds, is $3.43 billion (lower/upper quartile = $0.22/$8.58 billion), suggesting callable-putable bonds are issued by firms across the size spectrum. The average debt-to-equity ratio is 1.21 (stdev. = 0.98), indicating that firms with larger proportions of debt in their capital structure issue putable securities. The average issue size, as a percentage of firm value, following Huckins (1999) is 7.70% (stdev. = 5.91%), signifying that the issues constitute a material part of capital structure. The majority of issues (152) are set for over-the-counter (OTC) trading, while the remaining (7) were listed on organized exchanges (NYSE and NASDAQ). The majority of issues are senior notes (154); the remaining (5) were subordinated. OTC status notwithstanding, seniority coupled with put protection enabled the majority (122) to be designated investment-grade by S&P and Moody’s, and the remaining (37) were rated high-yield.

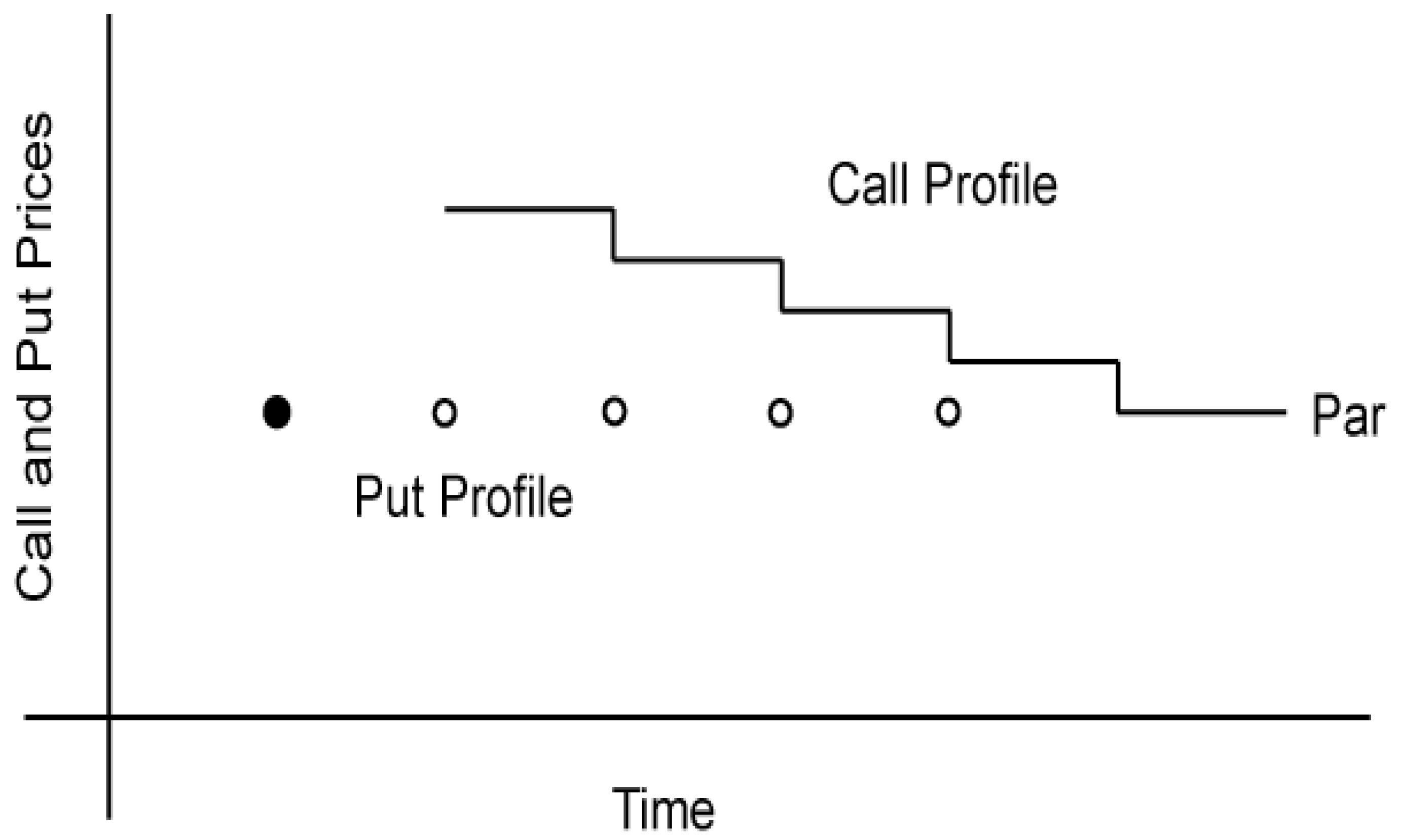
3.2. Call and Put Profiles

Figure 1 is a schematic representation of the typical call and put profiles for the sample issues. The firm’s option to call and the investor’s option to put are deferred for all issues. The average call-deferred period is 5.4 years (stdev. = 2.9 years), and the average put-deferred period is 4.2 years (stdev. = 3.0 years). The first-put date precedes, or is equal to, the first-call date for 146 issues. For some issues (67), the call profile is stepwise and continuous with the initial call price set above par and reduced by fixed amounts annually until the call price equals par, which remains as such until maturity. For other issues (92), the initial call price is set at par and remains at par until maturity. The call profile is continuous, i.e., issues are callable anytime (subject to a call-notice period) once the call-deferred period has passed. The put profile, in contrast, is neither stepwise nor continuous. Once the put-deferred period has passed, the issue is putable at par for one day only. For the majority of issues in the sample (134), the put option is never reactivated, and these issues remain non-putable for the remaining time to maturity. The remaining (25) issues have the put option reactivated until maturity at periodic intervals of one (23), two (1), and three (1) years. The reactivation is for one day only in each additional instance.

3.3. Issuances in 1998

The year 1998 saw an uncharacteristically large number of issues (69), encompassing 43% of the sample.

Table 1. Industry classification of issuing firms.

Industry	Number of Issues (Full Sample)	Number of Issues (In 1998)
Agriculture	1	0
Communication	3	3
Finance	27	10
Insurance	6	2
Manufacturing	21	15
Mineral	6	2
Real Estate	7	7
Retail	11	10
Transportation	3	2
Utilities	63	16
Total	159	69

This table lists the industry classification of the full sample of issuing firms, corresponding to the 159 sample issues of callable-putable fixed-coupon bonds in the period 1977–2005, as well as the subsample of firms corresponding to the 69 issues in 1998.

provides the industry classification of issuing firms for the full sample and the subsample of 1998 issues. The large number of 1998 issues cannot be relegated to an industry phenomenon.

One explanation is currency devaluations in Asia that escalated into a global financial crisis in 1998. Turmoil in financial markets accompanied deterioration in the U.S. trade imbalance. Slowdown in manufacturing activity accompanied a decline in consumer confidence. Revised GDP forecasts were 1.9% for 1999 and 2.4% for 2000, down from 4.2% in 1998. The large number of callable-putable bonds issued in 1998 may reflect investors seeking protection in a deteriorating global environment. This possibility is assessed by evaluating the firm’s risk. The mean value of annualized standard deviations of daily percentage changes in the firm’s value in the quarter, prior to the 69 issuance dates in 1998, is 0.26, and the corresponding mean value for the remaining 90 issuance dates is 0.30 (t-stat for the difference of means = 1.61). The evidence does not support higher firm risk in 1998.

Crabbe and Nikoulis (1997) provide an alternative explanation. Putable debt enables hedging the negative convexity of callable bonds. Putable debt issuances likely accompany a flatter yield curve when expected future interest rate volatility is low. A confluence of both effects occurred in 1998. Using Federal Reserve data, the mean spread between 30-year and 3-month Treasury rates, for the 69 issuance dates in 1998, is 0.27% and the corresponding mean spread for the remaining 90 issuance dates is 1.01% (t-stat for difference of means = 3.03). Additionally, 41/69 issues in 1998 became putable in 2001–2003 when $46.6 billion of corporate debt became callable. The evidence supports Crabbe and Nikoulis (1997).

4. Methodology

The methodology is set out in six parts. The first part describes the bond’s valuation model. Merton (1974) model is used to value the bonds. The boundary conditions on Merton’s model follow from the optimal exercise of the call and put provisions, based on the perfect-markets policies articulated in Ingersoll (1977).

The second part discusses the impact of indenture provisions and bankruptcy reorganization that can result in deviations from the perfect-markets policies for the optimal exercise of the call and put provisions, which, in turn, can impact the boundary conditions.

The third part explains how the boundary conditions are implemented. The call provision usually has a call-protection period when the bond is not callable, and when the bond does become callable, the call price is usually above the par value and decreases, with time, to equal the par value as the maturity approaches. Once callable, the bond can be called anytime on short notice. In contrast, the put provision can only be exercised on specific contractually specified dates, and the put price is fixed at the par value. The location of the lower boundary, where the put is exercised, and the upper boundary, where the call is exercised cannot be exogenously specified but must be determined endogenously, when solving for the bond’s valuation function, and the process is delineated.

The fourth part details the numerical algorithm to solve Merton’s model. The numerical algorithm adopts the implicit finite-difference method described in Brennan and Schwartz (1977). In addition to the complexities arising from the implementation of the boundary conditions, discrete coupon payments on the bond and discrete dividend payments on the stock can incentivize early exercise of the call and put provisions immediately prior to these payments. These are explained and accommodated in the algorithm.

The fifth part estimates the model’s parameters. Three sets of parameters are required to value the bond: the riskless rate, the standard deviation of the firm’s value, and cashflows to equityholders and debtholders. Riskless rates are estimated based on the constant-maturity Treasury rates posted daily by the Federal Reserve. The standard deviation of the firm’s value is estimated based on the market value of equity and the book value of debt and preferred stock. Dividends to stockholders are estimated based on the number of shares outstanding at issuance and the dividend history immediately prior to issuance. Dividend payments are assumed to occur at the same rate and frequency in the future. Payments to bondholders are calculated using the coupon rate and issue size.

The sixth part provides estimators for the Greeks. The Greeks correspond to first-order and second-order derivatives of the bond’s valuation function on the issue date; hence, their estimates are prone to numerical errors. As such, several steps are delineated to control numerical errors and ensure convergence of the Greeks.

4.1. Model

Merton (1974) model is adopted. The firm’s value V follows the lognormal process:

$$\frac{dV}{V}=\left[\alpha \left(t\right)-\delta \left(t\right)\right]dt+\sigma dz$$

(5)

where $\alpha \left(t\right)$ is the instantaneous expected rate of return on the firm per unit time; δ(t) = C(t)/V is the total dollar payout by the firm per unit time to all claims C(t) as a proportion of the firm’s value V; σ is the (annualized) standard deviation of the instantaneous return ($dV/V$); $dz$ is the standard Gauss–Wiener process.

The bond’s value, denoted by $f\left(V,\tau \right)$, depends on the firm’s value $V$, the time-to-maturity τ, and satisfies the differential equation:

$$\frac{1}{2}{\sigma }^2{V}^2{f}_{vv}+\left[r\left(\tau \right)V-C\left(\tau \right)\right]f_v-r\left(\tau \right)f+c\left(\tau \right)-f_{\tau }=0$$

(6)

A remarkable property of Equation (6) is that it does not depend on the expected rate of return on the firm $\alpha \left(t\right)$ nor on the risk-preferences of investors. In Equation (6), r(τ) is the riskless short rate, C(τ) is the total dollar payout by the firm per unit time to all claims, c(τ) the total dollar payout by the firm per unit time to the bond, and $\tau =T-t$ is the time-to-maturity in years (where T is the maturity time). The terms $f_{vv}$ and $f_v$ are the first and second derivatives of the bond’s value ($f$) with respect to the firm’s value (V), and $f_{\tau }$ is the first derivative of the bond’s value ($f$) with respect to the time-to-maturity (τ). The bond’s value $f\left(V,\tau \right)$ is the total value of debt outstanding, i.e., the price of one bond multiplied by the number of bonds outstanding. The firm’s value $V$, is the total value of debt, preferred, and common shares outstanding.

The time-varying short rate r(τ) is set to its expected path implied by the Treasury par curve on the valuation date posted at the Federal Reserve website, thereby precluding riskless arbitrage. The time-varying cashflows C(τ) and c(τ) are set to account for the discrete nature of these cashflows, as well as the projected increase in dividends, based on the current estimated dividend growth rate. Issue priority, bankruptcy reorganization, contractually stipulated calls and puts, and endogenous early exercise of these provisions are also accounted for in the model.

The model, together with the perfect-markets policies, in relation to the optimal exercise of call and conversion provisions discussed in Ingersoll (1977), has been successfully applied to price callable and convertible bonds by numerical methods in Brennan and Schwartz (1977). Furthermore, the theoretically predicted perfect-markets policies, in relation to the optimal exercise of call and conversion provisions, are shown to hold in practice in Asquith (1995), Byrd et al. (1998), Butler (2002), Michael (2003), Sarkar (2003), and Altintig and Butler (2005). The theoretically predicted perfect-markets policies are also shown to hold in variations of the valuation model, as illustrated by Jones et al. (1984), King (1986), Carayannopoulos (1996), and Ramanlal et al. (1996, 1998).

The model does not accommodate stochastic interest rates; Brennan and Schwartz (1980) find that errors from assuming non-stochastic rates are slight. David (2001) successfully employs default risk only to assess poison put provisions, while Elkamhi et al. (2012) employ default risk and interest-rate risk, using an explicit finite-difference bivariate lattice model. The current model employs an implicit finite-difference method to ensure convergence and stability of the numerical solution for credibility when calculating the Greeks, which require numerical evaluation of higher-order derivatives. To endogenize agency costs, the reader is referred to Duffie (2001, Chapter 11).

4.2. Indenture Provisions and Bankruptcy Reorganization

An indenture-provision violation can force the firm into bankruptcy prior to maturity resulting in capital-structure reorganization. Black and Cox (1976) propose such reorganization will occur at some lower boundary specified either exogenously (according to contract stipulation) or endogenously (determined by an optimal decision-making process by firms and/or investors). If the bond is putable at par, the putable boundary is reached well before the firm reaches a distress level commensurate with bankruptcy. For the current sample of 159 issues with an average put-deferred period of 4.2 years, only one issue faced bankruptcy prior to the initial put date (Solutia Inc. issued debt on 16 October 1997 that was putable on 15 October 2004, but the firm filed for bankruptcy on 17 December 2003). The average implied cumulative default rate for the sample is comparable to Moody’s Aaa rated bonds for the period 1970–2006 (See Hull 2008, Table 22.1). While the put is deferred and activated for one day only, the impending provision appears sufficient to deter bankruptcy. Accordingly, the lower boundary, corresponding to the (deferred) put, supplants the competing lower boundary due to bankruptcy.

Black and Cox (1976) also address debt subordination. In particular, they describe how bonds with different priorities may be valued. However, strict priority, though contractually stated, is often violated in liquidation and/or reorganization proceedings. Thus, how priority is treated in practice, notwithstanding contractual stipulations, must be incorporated in the valuation model. Virtually all bonds in the sample have senior priority; furthermore, it can be argued that the (deferred) put provision de facto serves to assign senior-most priority to putable bonds, as well as to enforce strict priority by virtue of the option to exercise. Black and Cox (1976) show that, when strict priority is enforceable, the senior-most bond in a firm, which may have multiple bonds with lower priorities outstanding, has a value that is the same as the corresponding bond of an identical firm that has issued a single bond. The intuition is as follows: how the remainder of the firm is distributed among subordinate claimants is irrelevant to the senior-most claimant under strict priority. This equivalence is invoked in the current valuation of callable-putable bonds.

4.3. Optimal Exercise of Call and Put Provisions

Figure 2 is a schematic representation, illustrating impact of the optimal exercise of the call and put provisions on the bond’s valuation function under the perfect-markets policy. The valuation function $f\left(V,\tau \right)$, depends on the initial condition $f\left(V,\tau =0\right)$, and the boundary conditions $f\left(V_{min},\tau \right)$ and $f\left(V_{max},\tau \right)$, where [$V_{min}$, $V_{max}$] is the domain of f. The boundary conditions, as well as the domain, will vary from issuance until maturity and will depend on the specific call and put profiles. The initial condition is the payoff at maturity $f\left(V,\tau =0\right)$ = Min(V, B), depicted by the (closely) dotted line in Figure 2, which indicates that investors collect the face value of debt (B) if less than the firm’s value (V) default occurs and bondholders claim the firm.

When the call and put provisions are inactive during the call-deferred and put-deferred periods, the domain of $f\left(V,\tau \right)$) is [0,$\infty$), the boundary conditions are $f\left(0,\tau \right)=0$ and $f_v\left(\infty ,\tau \right)=0$, and the corresponding valuation function is depicted by Line 1. The bond’s value approaches zero as the firm’s value approaches zero at the lower boundary and at the upper boundary, as the firm’s value approaches infinity, the slope of the valuation function approaches zero.1 When the call and put provisions are active, following passage of the call-deferred and put-deferred periods, the call profile κ(τ) yields the upper-boundary condition $f\left(V_{max},\tau \right)=\kappa \left(\tau \right)$ and the put profile p(τ) yields the lower-boundary condition $f\left(V_{min},\tau \right)=p\left(\tau \right)$. The domain is [$V_{min},V_{max}$], and the corresponding valuation function is depicted by Line 2. Two cases are represented corresponding to low interest-rates/volatility (the upper line) and high interest-rates/volatility (the lower line). Under the perfect-markets policy, firms call when the bond’s value rises to equal the call price and investors’ put when the bond’s value falls to equal the put price. When the interest-rate/volatility is low, the valuation function $f\left(V,\tau \right)$ may rise above the call price κ(τ) for $V>V_{max}$, in which case the firm calls when $V=V_{max}$. Conversely, when the interest-rate/volatility is high, the valuation function $f\left(V,\tau \right)$ may drop below the put price p(τ) prematurely for some $V>p\left(\tau \right)$ (i.e., even before the firm’s value $V$ reaches the default boundary $V=p\left(\tau \right)$) because rising interest rates or rising firm volatility can prematurely depress the bond’s value below the put price. Thus, in the region $p\left(\tau \right)<V<V_{min}$, the put option is exercised because the market value of the bond has declined below the put price due to rising interest rates or rising firm volatility, and not because the firm’s value is barely sufficient to redeem the bond. In this case, investors exercise the put early when $V=V_{min}$ even before the firm defaults. The domain [$p\left(\tau \right)\le V_{min},V_{max}\le \infty$] is determined endogenously while solving for the valuation function.

4.4. Numerical Method

The numerical solution to Equation (6) is obtained following Brennan and Schwartz (1977). The cashflows C(τ) and c(τ) in Equation (6) are zero, except at discrete points in time, corresponding to coupon dates and dividend dates. Hence, Equation (6) can be simplified as follows see (Brennan and Schwartz 1977, Equation 7’, on page 1707).

$$\frac{1}{2}{\sigma }^2{V}^2{f}_{vv}+r\left(\tau \right)V{f}_v-r\left(\tau \right)f-f_{\tau }=0$$

(7)

Accretions to the bond’s value occur on the coupon date and dilutions to the firm’s value occur on coupon dates and dividend dates. These are accounted for in the numerical algorithm when the events occur (discussed below). Writing the partial derivatives as finite differences, Equation (7) can be written as the following difference equation (see Brennan and Schwartz 1977, Equation (19)):

$$a_{i,j}{f}_{i-1,j}+b_{i,j}{f}_{i,j}+c_{i,j}{f}_{i+1,j}=f_{i,j-1}i=1,\dots ,\left(n-1\right) \mathrm{and} j=1,\dots ,m$$

(8)

where,

$$a_{i,j}=\frac{1}{2}{r}_{j}ki-\frac{1}{2}{\sigma }^{2}k{i}^2$$

$$b_{i,j}=1+r_{j}k+{\sigma }^{2}k{i}^2$$

$$c_{i,j}=\frac{-1}{2}{r}_{j}ki-\frac{1}{2}{\sigma }^{2}k{i}^2$$

and,

$$f_{i,j}=f\left(ih,jk\right)=f\left(V,\tau \right)$$

In Equation (8), the symbols $i\in \left\{0,1,2\dots n\right\}$ and $j\in \left\{0,1,2\dots m\right\}$ index the grid for the firm’s value and the time-to-maturity, respectively. The symbols h and k are discrete increments in the firm’s value ($h=\Delta V$ and the time-to-maturity ($k=\Delta \tau$. The interest rate $r_j$ is the forward riskless rate, calculated on the issuance date for the time period ($j-1$) to $j$.

Denoting the firm’s value at issuance by $V_o$, the domain for the bond’s valuation function is set to $\left[0,5V_o\right]$ so that, when the put and call provisions are inactive, the boundary conditions are imposed at the extremities of this domain. The grid size for the firm’s value is set to $h=\Delta V=5V_o/\mathrm{10,000}$. The grid size for time-to-maturity is set at $k=\Delta \tau =1/360$, where $\tau$ is measured in years, and the grid size it set to one day in the 30/360 convention, which assumes 30 days in a month and 360 days in a year. The average maturity for the sample is 19 years. Thus, the average number of time steps in the numerical algorithm is 6840, and the grid size on which the difference equation is defined is on average 10,000 × 6840.

The initial condition for the difference equation is the bond’s payoff at maturity:

$$f_{i,0}=Min\left(ih,B\right) \mathrm{for} i\in \left\{0,1,2\dots n\right\}$$

where, $B$ is the face value of debt. The boundary conditions for the difference equation are specified as follows.

If, at any time $j$, neither the call nor the put is active:

$$f_{0,j}=0 \left(lower boundary condition\right)$$

$$\frac{f_{n,j}-f_{n-1,j}}{h}=0 \left(upper boundary condition\right)$$

If, at any time $j$, the call is active and the call price is denoted by ${\kappa }_j$, or the put is active and the put price is denoted by $p_j$, then the domain for $f_{i,j}$, denoted by $\left[i_{min},i_{max}\right]$, must be solved endogenously, such that:

$$f_{i,j}\ge p_j for all i\ge i_{min} \left(modified lower boundary condition\right)$$

$$f_{i,j}\ge {\kappa }_j for all i\ge i_{max} \left(modified upper boundary condition\right)$$

For any time $j$, Equation (8) is a set of (n − 1) linear equations, corresponding to i = 1, 2… (n − 1), for the (n + 1) unknowns, corresponding to $f_{i,j}$ for i = 0, 1, 2… n, where the remaining two equations come from the lower and upper boundary conditions. When the modified boundary conditions hold, there are $\left(i_{max}-i_{min}-1\right)$ equations for $\left(i_{max}-i_{min}+1\right)$ unknowns, where the remaining two equations from the modified lower and upper boundary conditions are:

$$f_{i,j}=p_j when i=i_{min}$$

$$f_{i,j}={\kappa }_j when i=i_{max}$$

At any time $j$, Equation (8) can be solved for $f_{i,j}$ given $f_{i,j-1}$ that was solved for at the previous time $j-1$. Thus, starting with the initial condition $\left(f_{i,0}\right)$, the numerical process can be iterated through m time steps to yield the valuation function at issuance $\left(f_{i,m}\right)$.

As the iterative process is conducted, the numerical solution for $f_{i,j}$ at any time $j$ must be adjusted on dividend payment dates (denoted by $jd$ when the dividend D is paid to stockholders, and on coupon payment dates (denoted by $jc$ when the coupon I is paid to bondholders. The dividend payment D results in a dilution of the firm’s value from $i$ to $\left(i-d\right)$, where $d=D/h$, resulting in a corresponding decrease in the bond’s value. Thus, it may be optimal for bondholders to exercise the put option immediately prior to the dividend date. The coupon payment I results in a dilution of the firm’s value from $i$ to $\left(i-c\right)$, where $c=I/h$, but more importantly, the coupon payment also results in a dilution of the bond’s value given the payout to bondholders. Thus, it may be optional for the firm to exercise the call option immediately prior to the coupon date.

On a coupon payment date $\left(jc\right)$, if the bond is non-callable, its pre-coupon value at time $j{c}^{+}$ (denoting the instant immediately before the coupon payment in real-time) must equal its post-coupon value at time $j{c}^{-}$ (denoting the instant immediately after the coupon payment in real-time) plus the coupon payment. The firm’s value at time $j{c}^{-}$ immediately after the coupon payment is also diluted from $i$ to $\left(i-c\right)$ because of the coupon payment. Combining these effects, the bond’s value at time $j{c}^{+}$ immediately before the coupon payment can be written as:

$$f_{i,j{c}^{+}=f_{i-c,j{c}^{-}+ I}}$$

If the bond is callable on the coupon payment date $\left(jc\right)$ with the call price (immediately before the coupon payment in real-time) denoted by ${\kappa }_{j{c}^{+}}$, the firm will exercise the call option immediately before making the coupon payment if ${\kappa }_{j{c}^{+}<f_{i-c,j{c}^{-}}+I}$. Thus, the bond’s value at time $j{c}^{+}$, immediately before the coupon payment, can be written as:

$$f_{i,j{c}^{+}=min[f_{i-c,j{c}^{-}+I}, {\kappa }_{j{c}^{+}}]}$$

These correspond to Brennan and Schwartz (1977, Equations (16) and (17), respectively).

On a dividend payment date ($jd$), if the bond is non-putable, its pre-dividend value at time $j{d}^{+}$ (denoting the instant immediately before the dividend payment in real-time) must equal its post-dividend value at time $j{d}^{-}$ (denoting the instant immediately after the dividend payment in real-time). The firm’s value at time $j{d}^{-}$, immediately after the dividend payment, is also diluted from $i$ to $\left(i-d\right)$ because of the dividend payment. Combining these effects, the bond’s value at time $j{d}^{+}$, immediately before the dividend payment, can be written as:

$$f_{i,j{d}^{+}=f_{i-d,j{d}^{-}}}$$

If the bond is putable on the dividend payment date $\left(jd\right)$, with the put price (immediately before the dividend payment in real-time) denoted by $p_{j{d}^{+}}$, the bondholder will exercise the put immediately before the dilutive effect of the dividend payment if $p_{j{c}^{+}>f_{i-d,j{d}^{-}}}$. Thus, the bond’s value at time $j{d}^{+}$, immediately before the dividend payment, can be written as:

$$f_{i,j{d}^{+}=max[f_{i-d,j{d}^{-}}, p_{j{c}^{+}}]}$$

This corresponds to Brennan and Schwartz (1977, Equation (15)) except that the put option (rather than the conversion option) protects the bondholder against the dilutive effect of the dividend payment.

4.5. Model Parameters

Three sets of parameters are required to value the bond: the riskless rate (r), standard deviation of the firm’s value (σ), cashflows to equityholders (D), and debtholders (I).

For the riskless rate, the starting point is the constant-maturity (par) Treasury rates posted daily by the Federal Reserve for the following maturities: 1-month, 3-month, 6-month, 1-year, 2-year, 3-year, 5-year, 7-year, 10-year, 20-year, and 30-year. The par-curve is interpolated using a cubic-spline methodology, and par rates are extracted at 6-month intervals, which are then used to evaluate continuously-compounded zero rates at 6-month intervals following Hull (2008, Chp. 4, Sct. 4.5). The zero rates are then interpolated using the same cubic-spline methodology to obtain a smooth zero-curve. The zero-curve is then used to calculate the forward-rates $r_j$, corresponding to the time interval from $\left(j-1\right)$ to $j$ in Equation (8). The methodology to obtain the forward-rates is provided in Hull (2008, Chp. 4, Equation (4.5)). Under the pure-expectations theory for the term structure of interest-rates, the forward-rates $r_j$ equal the expected future spot rates.

The standard deviation (σ) is the annualized standard deviation of the instantaneous return dV/V. Market prices for all components of capital structure are not readily available. In particular, the market value of equity is available. However, only debt and preferred book values are available. Hence, the upper and lower bounds on the firm value’s standard deviation are calculated.

• For the lower bound, denoted by ${\sigma }_l$, V is calculated using the market-value of equity plus the book-value of debt and the book-value of preferreds. The book values are assumed to be constant. This assumption presumes debt and preferred price movements are inconsequential, relative to equity price movements, when estimating the firm’s volatility.2
• For the upper bound, denoted by ${\sigma }_u$, V is defined, simply, as the market value of equity. This assumption presumes debt and preferred price movements are perfectly positively correlated with equity.3

The instantaneous return dV/V is estimated using daily stock prices and the number of common shares outstanding that day, as well as the face value of debt and preferreds, as such: $\ln \left(V_t/V_{t-1}\right)$. It is evaluated for 60 trading days prior to issuance, and the variance of these daily returns is annualized based on (252) trading days a year. The square-root of the (annualized) variance yields the (annualized) standard deviation. Mean values for the sample are ${\sigma }_l=0.16$ (stdev. = 0.10) and ${\sigma }_u=0.28$ (stdev. = 0.15). For comparison, Jones et al. (1984), in their study of callable bonds, estimate firm-value standard deviations for a sample of 27 firms over a 5-year period; the mean value for their sample is σ = 0.27 (stdev. = 0.12).

Discrete cashflows to equityholders (D) are calculated based on the number of shares outstanding at issuance and the recent dividend history prior to issuance available on CRSP. Dividend payments are assumed to occur at the same rate and frequency in the future. Discrete payments to debtholders (I) are calculated using the coupon rate and issue size stipulated in the SDC database, which is obtained from the issue prospectus filed with the Securities and Exchange Commission. Semiannual coupon payments are assumed to persist until maturity.

4.6. Estimators for the Greeks

To develop estimators for the Greeks, denote the numerical solution for the bond’s valuation function on the issue date as $f\left(V;r,\sigma \right)$ to emphasize the dependence of the bond’s value on the firm’s value (V), the continuously-compounded Treasury zero-curve (r), and the firm’s volatility (σ). The Treasury zero-curve on the issue date is denoted by $\left(r_o\right)$, and the firm’s volatility on the issue date is denoted by ${\sigma }_o\in \left\{{\sigma }_l,{\sigma }_u\right\}$. Denote the firm’s value on the issue date by $V_o$ (calculated as the sum of the market value of equity and the book value of bonds and preferred); the bond’s value on the issue date by $f_o$ (calculated as the office price). The four standardized risk measures depicted in Equations (1)–(4) (i.e., the Greeks) can be estimated by the following Equations (9)–(12):

$$Delta=\left(\frac{V_o}{f_o}\right)\frac{f\left(V_o+\Delta V\right)-f\left(V_o-\Delta V\right)}{2\Delta V} \mathrm{evaluated} \mathrm{at} r_o \mathrm{and} {\sigma }_o$$

(9)

$$Gamma=\frac{f\left(V_o+\Delta V\right)-2f\left(V_0\right)+f\left(V_o-\Delta V\right)}{{\left(\Delta V\right)}^2} \mathrm{evaluated} \mathrm{at} r_o \mathrm{and} {\sigma }_o$$

(10)

$$Vega=\left(\frac{{\sigma }_0}{f_o}\right)\frac{f\left({\sigma }_o+\Delta \sigma \right)-f\left({\sigma }_o-\Delta \sigma \right)}{2\Delta \sigma } \mathrm{evaluated} \mathrm{at} V_o \mathrm{and} r_o$$

(11)

$$Rho=\left(\frac{-1}{f_o}\right)\frac{f\left(r_o+\Delta r\right)-f\left(r_o-\Delta r\right)}{2\Delta r} \mathrm{evaluated} \mathrm{at} V_o \mathrm{and} {\sigma }_o$$

(12)

In the preceding estimators for the Greeks, $\Delta V$ corresponds to a small change around the firm’s value $V_o$ on the issue date; $\Delta \sigma$ corresponds to a small change around the firm’s risk ${\sigma }_o$ on the issue date; $+\Delta r$ ($-\Delta r$) is a scalar quantity equal to the parallel up-shift (down-shift) in the continuously-compounded Treasury zero-curve $r_o$ on the issue date.

As noted previously, the domain for the bond’s valuation function is set to $\left[0,5V_o\right]$ The grid size for the firm value is set at $\Delta V=5V_o/\mathrm{10,000}$. For $\Delta \sigma$, one-percent of ${\sigma }_o$ is chosen, and for $\Delta r$, 5 basis points are chosen.

The Greeks correspond to first-order and second-order derivatives of the bond’s valuation function on the issue date; hence, their estimates are prone to numerical errors, which can propagate over the large number of iterative calculations to solve for the bond’s valuation function and estimate the Greeks. As such, in addition to the fine grid on which Equation (8) is solved, several additional steps are undertaken to control numerical errors and ensure convergence. As a first step, all intermediate calculations leading to the bond’s valuation function, and all estimates for the Greeks, are calculated to 16 significant figures. As a second step, the difference equation in Equation (8) is solved by an implicit finite-difference method, as opposed to an explicit finite-difference method. The implicit method is more accurate but also more complex (see Brennan and Schwartz 1978). In particular, at each time step, the implicit finite-difference method requires the inversion of an ($n\times n$ tri-diagonal matrix, where n = 10,000, corresponding to the number of points on the grid spanning the domain $\left[0,5V_o\right]$. As a third step, the second-order derivative of the valuation function, with respect to $V$, is examined over the entire domain $\left[0,5V_o\right]$ to ensure it is continuous and smooth. Numerical errors are random and tend to add noise in the valuation function that can be seen early, in large erratic variations, in higher order derivatives.

5. Results

In this study, we present three sets of results. First, for the sample of 159 non-convertible callable and putable bonds, offer prices are compared to calculated model prices and the pricing errors are assessed at the upper and lower bounds of the firm’s volatility. Second, the Greeks are calculated and evaluated to assess the role of the call provision, relative to the put provision, in mitigating credit risk, interest-rate risk, and agency risks associated with asset-substitution, over-investment, under-investment, and information asymmetry about the firm’s risk. Third, a cross-sectional analysis of the pricing errors is conducted to investigate if the Greeks, as explanatory variables, can explain the pricing errors.

5.1. Relative Pricing Errors (RPE)

The pricing error at issuance is a joint statement on market efficiency and model specification. The complexity of real-world securities versus the simplicity of analytically tractable models make specification issues a valid criticism of any contingent-claims model. Mispricing at issuance may arise due to idiosyncratic risks of new issues. Furthermore, risk-management and agency-theory issues not incorporated in the model may also impact mispricing at issuance. Thus, pricing errors likely reflect model deficiencies as opposed to market inefficiency. A cross-sectional analysis of pricing errors may identify these deficiencies, latent factors that impact pricing in particular, and this is conducted later in the paper. Conforming to the literature, the following measure for the pricing error at issuance is calculated, referred to as the Relative Pricing Error (RPE):

$$RPE=\frac{OfferPrice-ModelPrice}{ModelPrice}$$

(13)

In Equation (13), Model Price is determined by Equation (8), and Offer Price is as indicated in the issue’s prospectus. A negative RPE indicates that the model price overstates the offer price, or, as is often alluded to in the literature, the security is underpriced at issuance.

Relative pricing error (RPE) is calculated at issuance for each of the 159 issues in the sample for the lower $\left({\sigma }_l\right)$ and upper $\left({\sigma }_u\right)$ bounds of the firm’s estimated risk. The mean value of RPE is −4.97% (stdev. = 3.77%) at the upper bound and −5.56% (stdev. = 3.59%) at the lower bound. The mean values for the two bounds are close despite volatility differences owing to the put provision, which reduces price sensitivity to the firm’s volatility. Histograms of individual-security RPE, for the lower-bound and upper-bound firm volatilities, are displayed in Figure 3. The RPE for the majority of the sample is negative for both the cases, suggesting systematic overpricing by the model and/or underpricing at issuance.

To assess whether prices are more reliably estimated at the upper versus lower bound of the firm’s risk, it is examined how financial institutions that underwrite new-issue derivatives set bid and ask quotes as market makers in after-market OTC trading (based on discussions with traders at Goldman Sachs). Markets makers first set a risk-spread corresponding to the uncertainty in risk of the underlying asset (${\sigma }^{-}$, ${\sigma }^{+}$), which is then used to calculate the bid and ask prices using an option-pricing model. In the immediately preceding new-issue market, offer price is fair if the implied risk (${\sigma }^{implied}$) lies within the risk spread (${\sigma }^{-}$, ${\sigma }^{+}$), and the risk spread in turn within the risk bounds (${\sigma }_l,{\sigma }_u$). Thus, fair offer implies: ${\sigma }_l<{\sigma }^{-}\le {\sigma }^{implied}\le {\sigma }^{+}<{\sigma }_u$. The histograms of RPE in Figure 3, corresponding to the lower and upper bounds, indicate the majority of pricing errors are negative. Thus, the implied risk (${\sigma }_{implied}$) must necessarily be larger than the upper bound (${\sigma }_u$) for the model price to equal the market price assuming Vega < 0 (which holds for callable-putable debt, shown later). The conclusion is that model prices are more reliably calculated at the upper bound of the firm’s risk (which are comparable to those of Jones et al. (1984), provided earlier). Still, where possible, results are presented for both bounds.

5.2. Estimates for the Greeks

The Greeks are estimated at the upper (${\sigma }_u$) and lower (${\sigma }_l$) bounds of the firm’s risk, and a sensitivity analysis of the Greeks to the call and put provisions is conducted. Results are presented in

Table 2. Greeks (Delta, Gamma, Vega, and Rho) evaluated at the Upper Bound of the firm’s volatility.

Contract Provision	Index	Estimate	Delta	Gamma	Vega	Rho
Panel A:
Straight	(0, 0)	Mean	0.070851	−0.000245	−0.150381	8.781216
			(9.75) ***	(−2.02) **	(−8.41) ***	(42.58) ***
Callable	(1, 0)	Mean	0.062580	−0.000227	−0.131519	5.676433
			(9.41) ***	(−1.96) **	(−7.69) ***	(27.60) ***
Putable	(0, 1)	Mean	0.021306	−0.000081	−0.047370	8.053633
			(7.88) ***	(−2.91) ***	(−6.97) ***	(34.68) ***
Callable and Putable	(1, 1)	Mean	0.010445	−0.000060	−0.024703	4.645235
			(5.37) ***	(−2.95) ***	(−4.11) ***	(29.76) ***
Panel B:
Marginal Impact of Call	(1, 0)–(0, 0)	Mean	−0.008271	0.000018	0.018861	−3.104787
			(−6.54) ***	(1.90) **	(7.50) ***	(−16.06) ***
		% Change	−11.67%	−7.35%	−12.54%	−35.36%
Marginal Impact of Put	(0, 1)–(0, 0)	Mean	−0.049545	0.000164	0.103011	−0.727584
			(−8.32) ***	(1.68) **	(7.51) ***	(−5.76) ***
		% Change	−69.93%	−66.94%	−68.50%	−8.29%
Impact of Call and Put	(1, 1)–(0, 0)	Mean	−0.060406	0.000185	0.125678	−4.135981
			(−8.91) ***	(1.75) **	(8.63) ***	(−20.18) ***
		% Change	−85.26%	−75.51%	−83.57%	−47.10%
Panel C:
Put relative to Call	(0, 1)–(1, 0)	Mean	−0.041274	0.000147	0.084149
			(−7.35) ***	(1.58) *	(6.33) ***
		% Change	−65.95%	−64.76%	−63.98%
Call Relative to Put	(1, 0)–(0, 1)	Mean				−2.377199
						(−8.87) ***
		% Change				−29.52%

This table lists the mean values of the Greeks (Delta, Gamma, Vega, and Rho) evaluated for four versions of the model (Straight, Callable, Putable, and Callable and Putable) at the upper bound of the firm’s risk. The table summarizes the marginal impact of the call and put provisions, their combined impact, and their relative impact on these mean values (***, **, and * indicate significance at 1%, 5%, and 10% levels for the one-tailed test).

and

Table 3. Greeks (Delta, Gamma, Vega, and Rho) evaluated at the Lower Bound of the firm’s volatility.

Contract Provision	Index	Estimate	Delta	Gamma	Vega	Rho
Panel A:
Straight	(0, 0)	Mean	0.032502	−0.000211	−0.045297	9.435541
			(5.71) ***	(−1.73) **	(−5.41) ***	(43.89) ***
Callable	(1, 0)	Mean	0.025772	−0.000192	−0.036631	5.785801
			(5.49) ***	(−1.67) **	(−4.87) ***	(25.68) ***
Putable	(0, 1)	Mean	0.012044	−0.000061	−0.014993	8.805308
			(4.16) ***	(−1.98) **	(−5.22) ***	(36.91) ***
Callable and Putable	(1, 1)	Mean	0.002882	−0.000040	−0.003548	4.806963
			(2.61) ***	(−1.98) **	(−3.10) ***	(30.46) ***
Panel B:
Marginal Impact of Call	(1, 0)–(0, 0)	Mean	−0.006730	0.000019	0.008666	−3.649740
			(−4.15) ***	(2.04) **	(4.76) ***	(−17.26) ***
		% Change	−20.71%	−9.00%	−19.13%	−38.68%
Marginal Impact of Put	(0, 1)–(0, 0)	Mean	−0.020457	0.000150	0.030304	−0.630233
			(−5.03) ***	(1.53) *	(4.47) ***	(−4.77) ***
		% Change	−62.94%	−71.09%	−66.90%	−6.68%
Impact of Call and Put	(1, 1)–(0, 0)	Mean	−0.029620	0.000171	0.041749	−4.628578
			(−5.64) ***	(1.62) *	(5.34) ***	(−21.55) ***
		% Change	−91.13%	−81.04%	−92.17%	−49.05%
Panel C:
Put relative to Call	(0, 1)–(1, 0)	Mean	−0.013727	0.000131	0.021638
			(−3.53) ***	(1.41) *	(3.36) ***
		% Change	−53.26%	−68.23%	−59.07%
Call Relative to Put	(1, 0)–(0, 1)	Mean				−3.019507
						(−10.31) ***
		% Change				−34.29%

This table lists the mean values of the Greeks (Delta, Gamma, Vega, and Rho) evaluated for four versions of the model (Straight, Callable, Putable, and Callable and Putable) at the upper bound of the firm’s risk. The marginal impact of the call and put provisions are also evaluated, as is their combined impact and their relative impact on these mean values (***, **, and * indicate significance at 1%, 5%, and 10% levels for the one-tailed test).

. The analysis sheds light on the marginal impact of each provision on the Greeks and, therefore, on the potential for that provision, to address risk-management and agency-theory issues. For callable-putable bonds, Delta ≥ 0, Gamma ≤ 0, Vega ≤ 0, and Rho ≥ 0 at issuance; hence, the focus is on how effectively the call and put provisions drive the Greeks toward these limits.

For each Greek (Delta, Gamma, Vega, and Rho), four models are evaluated and indexed by (0,0), (1,0), (0,1), and (1,1) as follows:

• (0,0) indicates neither the call nor the put is incorporated in the valuation model, i.e., the issue is Straight;
• (1,0) indicates the call is incorporated but not the put, i.e., the issue is Callable only;
• (0,1) indicates the put is incorporated but not the call, i.e., the issue is Putable only;
• (1,1) indicates that both provisions are incorporated in the valuation model, i.e., the issue is Callable and Putable.

Using this notation, a specific Greek $\in$ {Delta, Gamma, Vega, Rho} calculated for a specific model (a, b) $\in$ {(0, 0), (1, 0), (0, 1), (1,1)} and for a specific firm i $\in$ {1, 2, … 159} is denoted by:

$$Gree{k}_{\left(a,b\right)}^i$$

The mean value of a specific Greek $\in$ {Delta, Gamma, Vega, Rho} calculated for a specific model (a, b) $\in$ {(0, 0), (1, 0), (0, 1), (1, 1)} averaged across all firms i $\in$ {1, 2, … 159} is denoted by:

$$Gree{k}_{\{a,b)}$$

5.2.1. Greeks at the Upper Bound

Table 2, Panel A, lists the mean values of the Greeks (Delta, Gamma, Vega, and Rho) for the four versions of the model (Straight, Callable, Putable, and Callable and Putable) averaged across all firms i $\in$ {1, 2, … 159} and evaluated at the upper bound of the firm’s risk as follows:

• $Delt{a}_{\left(0,0\right)}$ = 0.070851   (Straight)
• $Delt{a}_{\left(1,0\right)}$ = 0.062580   (Callable)
• $Delt{a}_{\left(0,1\right)}=$ 0.021306    (Putable)
• $Delt{a}_{\left(1,1\right)}=$ 0.010445    (Callable and Putable)

These results show that the put is more effective than the call in pressing Delta towards zero, although the put and call together are most effective. Similar results hold for Gamma and Vega as follows:

• $Gamm{a}_{\left(0,0\right)}$ = −0.000245   $Veg{a}_{\left(0,0\right)}$ = −0.150381   (Straight)
• $Gamm{a}_{\left(1,0\right)}$ = −0.000227   $Veg{a}_{\left(1,0\right)}$ = −0.131519     (Callable)
• $Gamm{a}_{\left(0,1\right)}=$ −0.000081   $Veg{a}_{\left(0,1\right)}=$ −0.047370  (Putable)
• $Gamm{a}_{\left(1,1\right)}=$ −0.000060  $Veg{a}_{\left(1,1\right)}=$ −0.024703   (Callable and Putable)

Conversely, the call is more effective than the put in pressing Rho towards zero, although the call and put together are most effective:

• $Rh{o}_{\left(0,0\right)}$ = 8.781216   (Straight)
• $Rh{o}_{\left(1,0\right)}$ = 5.676433   (Callable)
• $Rh{o}_{\left(0,1\right)}=$ 8.053633    (Putable)
• $Rh{o}_{\left(1,1\right)}=$ 4.645235    (Callable and Putable)

The t-stats listed in Table 2, Panel A, are for the null hypothesis that the mean value for each Greek (Delta, Gamma, Vega, and Rho), for each of the four versions of the model (Straight, Callable, Putable, and Callable and Putable), is zero. The null is rejected at the 1% or 5% level.

Table 2, Panel B, lists the marginal impact of the call and put provisions and their combined impact in driving the Greeks to their limiting values. For Delta, the marginal impact of Callable relative to Straight is $\left[Delt{a}_{\left(1,0\right)}-Delt{a}_{\left(0,0\right)}\right]=$ −0.008271. The t-stat = 6.54 for the hypothesis that the mean of the paired difference $\left[Delt{a}_{\left(1,0\right)}^i-Delt{a}_{\left(0,0\right)}^i\right]$ is less than zero. The percentage change in the mean value of Delta for Callable relative to Straight is [$Delt{a}_{\left(1,0\right)}-Delt{a}_{\left(0,0\right)}/Delt{a}_{\left(0,0\right)}=$−11.67%. Thus, the call significantly lowers Delta by about 11.67%. Correspondingly, the put significantly lowers Delta by about 69.93%; call and put, together, significantly lower Delta by about 85.26%. These results are represented by the 3-tuple (−11.67%, −69,93%, −85.26%) with the characteristics pattern that the call’s impact is small relative to the put’s impact, whereas their combined impact is substantial in lowering Delta. The 3-tuple for Gamma (−7.35%, −66.94%, −75.51%) and Vega (−12.54%, −68.50%, −83.57%) are characteristically similar. Conversely, the 3-tuple for Rho (−35.36%, −8.29%, −47.10%) is different. Namely, the marginal impact of the call is now large (−35.36%) relative to the marginal impact of the put (−8.29%), whereas the combined impact of the call and put is still substantial (−47.10%). Summarizing these results:

• % Reduction in Delta by (call, put, call and put) = (−11.67%, −69,93%, −85.26%)
• % Reduction in Gamma by (call, put, call and put) = (−7.35%, −66.94%, −75.51%)
• % Reduction in Vega by (call, put, call and put) = (−12.54%, −68.50%, −83.57%)
• % Reduction in Rho by (call, put, call and put) = (−35.36%, −8.29%, −47.10%)

Table 2, Panel C, lists the impact of the put relative to the call. The difference in the mean value of Delta for Putable relative to Callable is $\left[Delt{a}_{\left(0,1\right)}-Delt{a}_{\left(1,0\right)}\right]=$ −0.041274. The mean value of the paired difference $\left[Delt{a}_{\left(0,1\right)}^i-Delt{a}_{\left(1,0\right)}^i\right]$ is significantly less than zero (t-stat = −7.35). The percentage difference [$Delt{a}_{\left(0,1\right)}-Delt{a}_{\left(1,0\right)}/Delt{a}_{\left(1,0\right)}$ is −65.95%. Thus, the impact of the put, relative to call, in lowering Delta is substantial and significant. Similar results hold for Gamma (−64.76%) and Vega (−63.98%). Conversely, the difference in the mean value of Rho for Callable, relative to Putable, is $\left[Rh{o}_{\left(1,0\right)}-Rh{o}_{\left(0,1\right)}\right]=$ −2.3772 (t-stat = −8.77) and the percentage difference [$Rh{o}_{\left(1,0\right)}-Rh{o}_{\left(0,1\right)}/Rh{o}_{\left(0,1\right)}=$ −29.52%. Thus, the impact of the call, relative to the put, in lowering Rho is substantial and significant. Summarizing these results:

• % Reduction in Delta (by put relative to call) = −65.95%
• % Reduction in Gamma (by put relative to call) = −64.76%
• % Reduction in Vega (by put relative to call) = −63.98%
• % Reduction in Rho (by call relative to put) = −29.52%

5.2.2. Greeks at the Lower Bound

Table 3, Panel A, lists the mean values of the Greeks (Delta, Gamma, Vega, and Rho) for the four versions of the model (Straight, Callable, Putable, and Callable and Putable), evaluated at the lower bound of the firm’s risk. Panel B lists the marginal impact of the call and put provisions, as well as their combined impact in driving the Greeks to their limiting values. Panel C evaluates impact of the put relative to the call. The results are largely similar to those presented at the upper bound of the firm’s risk. Thus, the prior conclusions on the role of the call versus put, in relation to the Greeks, are robust to errors in the firm’s risk estimates.

5.2.3. Individual-Security Sensitivity Analysis of the Greeks

This section provides more discriminating evidence of the impact of the call and put provisions on the Greeks. It calculates the percentage reductions in the Greeks due to the call and put provisions for individual issues and then evaluates their sample means. Due to computational limitations that impact the integrity of the numerical calculations, only results for the marginal impact of the call, the marginal impact of the put, and total impact of the call and put on the Greeks at the upper bound of the firm’s risk can be calculated with integrity. Results are summarized in

Table 4. Individual-security sensitivity of the Greeks to the call and/or put provisions.

Impact of Contract Provision *	Estimate	Delta	Gamma	Vega	Rho
Marginal Impact of Call:
$\frac{Gree{k}_{\left(1,0\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i}$	Mean	−32.43%	−27.32%	−33.26%	−34.07%
		−11.88 ***	−10.36 ***	−12.18 ***	−17.70 ***
Marginal Impact of Put:
$\frac{Gree{k}_{\left(0.1\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i}$	Mean	−45.38%	−49.24%	−45.48%	−8.86%
		−15.25 ***	−15.04 ***	−15.33 ***	−5.73 ***
Total Impact of Call and Put:
$\frac{Gree{k}_{\left(1,0\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i}$	Mean	−81.18%	−79.00%	−82.67%	−45.12%
		−35.47 ***	−28.70 ***	−37.16 ***	−25.09 ***

This table lists the sensitivity of the Greeks (Delta, Gamma, Vega, and Rho) to the call and/or put provisions for individual securities, evaluated at the upper bound of the firm’s risk, and averaged across the sample of 159 issues. *$Gree{k}^iϵ\left(Delta,Gamma,Vega,Rho\right)$ for issue i (***, **, and * indicate significance at 1%, 5%, and 10% levels for the one-tailed test).

.

To assess the marginal impact of the call, the marginal impact of the put, and the total impact of the call and put, the following are calculated for each issue i and for each of the four Greeks $\in$ {Delta, Gamma, Vega, Rho}:

$$\frac{Gree{k}_{\left(1,0\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i} \mathrm{Marginal} \mathrm{impact} \mathrm{of} \mathrm{the} \mathrm{call} \mathrm{for} \mathrm{issue} i$$

$$\frac{Gree{k}_{\left(0.1\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i} \mathrm{Marginal} \mathrm{impact} \mathrm{of} \mathrm{the} \mathrm{put} \mathrm{for} \mathrm{issue} i$$

$$\frac{Gree{k}_{\left(1,0\right)}^i-Gree{k}_{\left(0,0\right)}^i}{Gree{k}_{\left(0,0\right)}^i} \mathrm{Total} \mathrm{impact} \mathrm{of} \mathrm{the} \mathrm{call} \mathrm{and} \mathrm{put} \mathrm{for} \mathrm{issue} i$$

The mean values for these measures are listed in Table 4. The mean percentage reduction in Delta (for Callable relative to Straight) is −32.43%, and it is significantly less than zero (t-stat = −11.88). For the marginal impact of the put (i.e., for Putable relative to Straight), the corresponding estimates are −45.38% (t-stat = −15.25); for the call and put combined (i.e., for Callable and Putable relative to Straight), the estimates are −81.18% (t-stat = −35.47). These results reaffirm our prior findings, with a more discriminating analysis, that the marginal impact of the call is less (−32.43%) than the marginal impact of the put (−45.38%), whereas the combined impact of the call and put is substantial (−81.18%). Similar results hold for Gamma and Vega. Conversely, for Rho, the marginal impact of the call is greater (−34.07%) than the marginal impact of the put (−8.86%), whereas the combined impact is once again substantial (−45.12%). The t-stats are all very significant.

5.2.4. Results on the Greeks

The preceding analysis of the Greeks by multiple methods yields a robust conclusion that the put provision is more determinative than the call provision in moving Delta, Gamma, and Vega towards zero, whereas the call provision is more determinative than the put provision in lowering Rho. The conclusion it that the put provision is better suited to control (a) credit risk; (b) agency risks due to asset-substitution, over-investment, and under-investment; (c) uncertainty about the firm’s risk due to information asymmetry and/or future volatility shocks. The call provision, in contrast, is better suited to control interest-rate risk.

5.3. Cross-Sectional Analysis of RPE

Pricing models usually have pricing errors due to the inability of the model to adequately capture the bond’s risk profile encapsulated in the bond’s structured provisions. Thus, a cross-sectional regression of the pricing errors on the bond’s structured provisions can be expected to explain these errors. Is it sufficient to include the structured provisions as explanatory variables to explain the pricing errors, or do the Greeks also contribute towards explaining these errors, recognizing that the Greeks are intended to be a reduced-form representation of the structured provisions? The approach taken is to list potential explanatory variables, investigate multicollinearity between the structured provisions and the Greeks to identify redundant variables, and then conduct the cross-sectional analysis to identify the role of the Greeks. The analysis is conducted at the upper bound of the firm’s risk since pricing is more accurate at this bound

5.3.1. Explanatory Variables

Explanatory variables based on the following risk factors are considered: credit risk, interest-rate risk, reinvestment risk, and agency risks.

Credit risk is proxied by the bond’s credit rating (Issue Rating). Ordinal rankings for ratings are used. Highly speculative issues (B- for S&P and B3 for Moody’s) are assigned the ordinal ranking = 1, and each increment in the S&P and Moody’s ratings is assigned a unit increase in the ordinal ranking until prime issues (AAA for S&P and Aaa for Moody’s), which are assigned the ordinal ranking = 16. Among the 159 sample issues, 122 received specific ratings, while the remaining 37 were rated either investment grade (12 issues) or high yield (25 issues), and these were assigned the average ordinal measure for their respective groups (IG = 11.5 and HY = 3.5). Credit risk is also proxied by beta of the underlying equity (Equity β) for which the Fama and French methodology is used. Credit risk of the security is also proxied by Delta. Furthermore, issues that are putable at periodic intervals, as opposed to just once, mitigate credit risk to a greater extent. Hence, the indicator variable (Put-Idx) set equal to zero (one), if the issue is putable once (more than once), is also a proxy for credit risk. Summarizing, the proxies for credit risk are Issue Rating, Equity β, Delta, and Put-Idx.

Interest rate risk is captured by the generalized measure for duration calculated for parallel shifts in the Treasury curve (Rho). Alternate proxies for interest-rate risk include time-to-maturity (Maturity), the call-deferred period, which is the number of years to when the issue is first callable (Call-Def), and the put-deferred period, which is the number of years to when the issue is first putable (Put-Def). All four variables are measured in years and are key factors associated with the security’s expected lifespan. Summarizing, the proxies for interest-rate risk are Rho, Maturity, Call-Def, and Put-Def.

Reinvestment risk arises when high coupon bonds are called after interest rates fall and is proxied by the coupon rate (Coupon). However, higher coupon rates for larger issues (Issue Size) also increase the firm’s financial risk. Reinvestment risk may be mitigated by a call premium, the provision that the bond is callable above par following passage of the call-deferred period. Hence, the indicator variable (Call-Idx) is set equal to zero (one) if the initial call price is par (above par). Summarizing, the proxies for reinvestment risk are Coupon, Issue Size, and Call-Idx.

Agency risks arise due to asset-substitution, over-investment, and under-investment. Prospect for the associated wealth transfer from bondholders to stockholders is proxied by the convexity of the valuation function (Gamma). The impact of information asymmetry and/or uncertainty about the firm’s risk, or the impact of future volatility shocks on the security’s value, is proxied by (Vega). Summarizing, the proxies for agency risks are Gamma and Vega.

The explanatory variables fall into three categories: Exogenous (Equity β, Issue Size, and Issue Rating), Greeks (Delta, Gamma, Vega, and Rho), and Structured Provisions (Call-Def, Put-Def, Maturity, Coupon, Call-Idx, and Put-Idx).

5.3.2. Multicollinearity

Table 5. Correlation matrix and reduced set of explanatory variables.

Panel A: Correlation matrix
Groups:	Delta	Gamma	Vega	Rho	Call-Def	Put-Def	Maturity	Coupon	Call-Idx	Put-Idx
Group 1: Delta	1.000
Gamma	−0.628	1.000
Vega	−0.863	0.337	1.000
Group 2: Rho	−0.019	0.071	0.069	1.000
Call-Def	0.097	0.048	−0.115	0.771	1.000
Put-Def	−0.089	0.184	0.043	0.585	0.774	1.000
Maturity	−0.058	0.116	0.076	0.490	0.499	0.504	1.000
Group 3: Coupon	0.207	−0.180	−0.125	0.063	0.064	−0.272	−0.259	1.000
Call-Idx	0.277	−0.266	−0.141	0.145	−0.041	−0.410	−0.125	0.730	1.000
Put-Idx	0.216	−0.154	−0.168	0.114	−0.098	−0.265	0.024	0.117	0.436	1.000
Panel B: Regression estimates for variables in Groups 1, 2 and 3
Group 1	Constant		Delta		Gamma		Vega		Adj R2
Regression	−0.0502		−0.9505		1.0326		−0.4204		0.181
	(−16.09) ***		(−2.71) ***		(−0.07)		(−6.38) ***
Reduced	−0.0501		−0.9649				−0.4233		0.186
	(−17.07) ***		(−4.43) ***				(−6.00) ***
Group 2	Constant		Rho		Call-Def		Put-Def	Maturity	Adj R2
Regression	−0.0258		−0.0081		−0.0005		0.0023	0.0004	0.099
	(−3.20) ***		(−3.48) ***		(−0.27)		(1.50)	(0.90)
Reduced	−0.0226		−0.0059						0.088
	(−3.08) ***		(−4.03) ***
Group 3	Constant		Coupon		Call-Idx		Put-Idx		Adj R2
Regression	−0.0243		−0.0019		−0.0170		−0.0150		0.156
	(−2.26) **		(−1.26)		(−1.79) *		(−1.70) *
Reduced	−0.0128		−0.0039				−0.0233		0.144
	(−1.47)		(−4.00) ***				(−3.04) ***

Panel A displays the correlation matrix of 4 Greeks (Delta, Gamma, Vega, and Rho) and 6 structured provisions (Call-Def, Put-Def, Maturity, Coupon, Call-Idx, and Put-Idx) for the sample of 159 issues. The set of 10 variables is partitioned into 3 groups (Group 1, Group 2, and Group 3) based on common risk factors. High correlation coefficients (about 0.5 or greater) are highlighted with solid-lined boxes. Panel B displays cross-sectional regression estimates obtained by regressing the Relative Pricing Error (RPE) against variables in each group to identify and mitigate multicollinearity. Group 1 (Reduced), Group 2 (Reduced), and Group 3 (Reduced) corresponds to the reduced set of explanatory variables in these groups. ***, **, and * indicate significance at 1%, 5%, and 10% levels (2-tailed test). All t-stats are calculated using White’s method (White 1980).

, Panel A, displays multicollinearity effects. Multicollinearity arises largely between the Greeks (Delta, Gamma, Vega, and Rho) and the Structured Provisions (Call-Def, Put-Def, Maturity, Coupon, Call-Idx, and Put-Idx). While the Greeks are a reduced-form representation of the Structured Provisions, they do not fully capture the bond’s risk profile; the Structured Provisions (and indenture covenants) remain the complete descriptor. Thus, both sets of variables, the Greeks and the Structured Provisions, are included in the cross-sectional analysis, however, and multicollinearity among these two sets of variables may be attributed to poor experimental design.

To address this problem, the Greeks (Delta, Gamma, Vega, and Rho) and the Structured Provisions (Call-Def, Put-Def, Maturity, Coupon, Call-Idx, and Put-Idx) are divided into three groups:

Group 1:

(Delta, Gamma, and Vega)

Group 2:

(Rho, Call-Def, Put-Def, and Maturity)

Group 3:

(Coupon, Call-Idx, and Put-Idx)

These choices follow from the preceding discussion on proxies for specific risk types. Group 1 includes proxies for credit risk (Delta) and agency risk (Gamma and Vega); Group 2 includes proxies for interest rate risk (Rho, Call-Def, Put-Def, and Maturity); Group 3 includes proxies for reinvestment risk (Coupon and Call-Idx) and long-term default risk (Put-Idx). Table 5, Panel A, lists the correlation matrix for these three groups. Correlation coefficients approximately 0.5 or greater, deemed high, are emphasized with solid-lined boxes. As expected, the correlation among variables within each group is high but low across groups. Multicollinearity may arise because co-movements of variables are driven by common underlying risk factors or spurious idiosyncratic sample issues. Variables that are not germane are excluded to yield a reduced set of explanatory variables.

5.3.3. Reduced Set of Explanatory Variables

Table 5, Panel B, details the analysis for excluding non-germane variables in each of Group 1, Group 2, and Group 3.

Group 1 displays high multicollinearity between Delta, on the one hand, and Gamma and Vega on the other. Delta captures credit risk whereas Gamma and Vega capture agency risks, thus co-movements cannot be attributed solely to a common risk factor. For nonconvertible debt, a steeper valuation function (i.e., a more positive Delta) accompanies (a) greater curvature (i.e., more negative Gamma), thus the higher negative correlation between Delta and Gamma (−0.628), and (b) greater sensitivity to volatility shocks (i.e., more negative Vega), thus the higher negative correlation between Delta and Vega (−0.863). Regression results for RPE against Group 1 variables is listed in Panel B (see “Regression” under “Group 1”). Delta and Vega are significant; Gamma is insignificant. Multicollinearity may be addressed, in part, by dropping Gamma since the remaining variables, Delta and Vega, capture the representative risk classes in this group. The revised regression of RPE against Delta and Vega is listed in Panel B (see “Reduced” under “Group 1”). Delta and Vega remain significant, while the adjusted $R^2$ is essentially unchanged at 0.18.

Group 2 displays high multicollinearity among all four variables (Rho, Call-Def, Put-Def, and Maturity). The co-movements arise because all four variables are proxies for interest-rate risk. Regression results for RPE against Group 2 variables are listed in Panel B (see “Regression” under “Group 2”). While Rho is significant, the remaining three variables, Call-Def, Put-Def, and Maturity, are insignificant. Rho subsumes the impact of Call-Def, Put-Def, and Maturity; hence, the latter variables are dropped. The revised regression of RPE against Rho is also listed in Panel B (see “Reduced” under Group 2”). Rho remains significant, while the adjusted $R^2$ reduces marginally from 0.099 to 0.088.

Group 3 displays high collinearity between Coupon and Call-Idx. The co-movement holds because both variables are proxies for reinvestment risk. Regression results for RPE against Group 3 variables are listed in Panel B (see “Regression” under “Group 3”). Coupon is insignificant while Call-Idx and Put-Idx are marginally significant. Call-Idx is dropped because it is proxied by Coupon, and Put-Idx is retained because it captures elements of default risk. The revised regression of RPE against Coupon and Put-Idx is also listed in Panel B (see “Reduced” under “Group 3”). Both explanatory variables become very significant while the adjusted $R^2$ reduces marginally from 0.156 to 0.144.

In summary, the choice for the reduced set of Greeks is (Delta, Vega, and Rho) and for the reduced set of Structured Provisions is (Coupon and Put-Idx). The set Exogenous (Equity β, Issue Size, and Issue Rating) remains unchanged.

5.3.4. Cross-Sectional Analysis

Table 6. Cross-sectional analysis of relative pricing error (RPE).

Variables	Exogenous	Greeks	Provisions	Combined
	1	2	3	4
Intercept	−0.0666	−0.0264	−0.0128	−0.0239
	(−5.32) ***	(−3.87) ***	(−1.47)	(−1.81) *
Equity β	0.0061			0.0024
	(1.57)			(0.75)
Issue Size	−0.1163			−0.0722
	(−2.22) **			(−1.40) *
Issue Rating	0.0023			0.0024
	(2.19) **			(2.73) ***
Delta		−0.9018		−0.3705
		(−4.30) ***		(−1.76) **
Vega		−0.3967		−0.3005
		(−5.83) ***		(−4.79) ***
Rho		−0.0052		−0.0051
		(−3.79) ***		(−4.30) ***
Coupon			−0.0039	−0.0023
			(−4.00) ***	(−2.60) ***
Put−Idx			−0.0233	−0.0193
			(−3.04) ***	(−2.94) ***
Adjusted R2	0.1303	0.2506	0.1436	0.4325

This table provides cross-sectional estimates from regressing Relative Pricing Error (RPE) on three sets of explanatory variables for the sample of 159 issues: (1) Exogenous variables (Equity$\beta$, Issue Size, and Issue Rating); (2) the reduced set of Greeks $\left(Delta,Vega,\mathrm{and}Rho\right)$; (3) the reduced set of structured provisions (Coupon and Put-Idx); (4) a comprehensive regression, including all three sets, are variables. ***, **, and * indicate significance at 1%, 5%, and 10% levels (2-tailed test for the intercept; 1-tailed for others). All t-stats are calculated using White’s method (White 1980).

summarizes the cross-sectional analysis of RPE against the listed explanatory variables. Negative values of RPE correspond to underpricing at issuance, while positive values of RPE correspond to overpricing at issuance.

In regression 1, RPE is regressed on Exogenous (Equity β, Issue Size, and Issue Rating) where (−, −, +) are the corresponding hypothesized signs. Higher Equity β implies greater equity risk and larger Issue Size implies greater financial risk, both are likely to result in greater underpricing. Higher Issue Rating implies smaller credit risk and, therefore, lesser underpricing.

In regression 2, RPE is regressed on the reduced-set of Greeks (Delta, Vega, and Rho) where (−, +, −) are the corresponding hypothesized signs. Delta is positive and therefore larger values imply greater credit risk, and hence greater underpricing. Vega is negative and, therefore, smaller (i.e., more negative) values imply greater sensitivity to volatility, larger potential for mispricing due to uncertainty in the firm’s risk, and hence, greater underpricing. Rho is positive and large values imply greater interest-rate risk and therefore greater underpricing.

In regression 3, RPE is regressed on the reduced-set of structured provisions (Coupon and Put-Idx) where (−, −) are the corresponding hypothesized signs. Larger Coupon implies greater reinvestment risk and therefore greater underpricing. For Put-Idx = 1, multiple put dates signal greater downside risk and implies greater underpricing.

Regression 4 is comprehensive and includes all three sets of variables. The hypothesized signs for all three sets of variables are listed in Table 6.

The cross-sectional analysis can be summarized as follows: in regression 1, Equity β is insignificant, Issue Size is negative and significant, and Issue Rating is positive and significant. In regression 2, Delta is negative and significant, Vega is negative and significant (but contrary to the hypothesized sign), and Rho is negative and significant. In regression 3, Coupon and Put-Idx are both negative and significant. These results also hold in the combined regression 4.4

The confounding sign of the Vega coefficient may be traced to the Greeks, evaluated at the upper bound of the firm’s risk. For the sample, Vega < 0, an upward-bias in the firm’s risk results in a downward-bias in the Model Price, manifested as smaller underpricing at issuance and consistent with the observed sign of the Vega coefficient. Thus, Vega controls for the upward bias in the firm’s volatility.

The conclusion is that the Greeks, in addition to the structured provisions, can explain pricing errors in a cross-sectional analysis.

6. Conclusions

This study sets out a new methodology to assess the impact of a bond’s structured provisions (e.g., the call, put, and conversion options) on its credit risk, interest rate risk, and propensity to mitigate agency conflict arising from asset-substitution, over-investment, under-investment, and agency conflict due to information asymmetry via a set of risk metrics called the Greeks (Delta, Gamma, Vega, and Rho). The Greeks are a standardized set of risk metrics associated with financial derivatives. The proposition is that the Greeks are a reduced-form representation of the structured provisions that can be used to assess the bond’s risk and agency characteristics.

The proposition is applied to a sample of 159 non-convertible callable and putable bonds, issued between 1977 and 2005, with insightful results, namely, that the put option plays a key role in reducing credit risk, mitigating agency conflict, and protecting against volatility shocks; conversely, the call option plays a key role in reducing interest-rate risk. The role of the put option in mitigating agency conflict and protecting against volatility shocks is a surprising result that has received scant attention in the literature.

One remarkable property of the proposed methodology is its generality. It can be applied to bonds and preferred stocks with any set of structured provisions to assess the marginal impact of those provisions on the risk and agency characteristics of the security. For example, the conversion provision, the call-deferred period, the put-deferred period, and the period between put dates.

Another remarkable property of the proposed methodology is its simplicity. It requires the estimation of a standardized set of risk metrics. Furthermore, the methodology is specified independent of the underlying security or the valuation model for the security.

One interesting topic for future research is the assessment of tradeoffs between the call-deferred period and the conversion ratio for convertible bonds and convertible preferred stocks. A longer call-deferred period benefits investors, which firms may be willing to offer, but coupled with a lower conversion ratio, it benefits the firm. What is an optimal tradeoff of these provisions from an agency standpoint? This can be investigated by assessing the Greeks for different contracts, characterized by pair-wise choices, for the call-deferred period and the conversion ratio that raise the same amount of funds, but mitigate agency issues in different ways.

The proposed methodology is not without criticism. One criticism is that, while the Greeks are a reduced-form representation of the structured provisions, they do not fully capture the bond’s risk profile; the structured provisions and the indenture covenants remain the complete descriptor. However, reduced-form representations have their advantages, and it remains to show how well the Greeks capture the bond’s risk profile and how the set corresponding to the Greeks may be expanded. It is immediately evident that interest-rate volatility may be included in an expanded set of the Greeks.

Another criticism pertains to the valuation model used for the underlying security whose risk profile is being investigated. No valuation model is without criticism. In relation to the current study, Brennan and Schwartz’s (1980) extension of Merton (1974) model permitting the firm’s value and the interest rate to be stochastic, and Wang and Chou’s (2005) model for pricing callable and putable bonds, using Duffie and Singleton’s (1999) reduced-form approach, are proposals for future research. It is not the objective of the current study to evaluate alternative pricing models but rather to propose a new methodology independent of the pricing model to assess the risk and agency characteristics of structured securities.

Pricing models invariably have pricing errors, which can reasonably be related to the bond’s risk profile encapsulated by the bond’s structured provisions and indenture covenants. Thus, a cross-sectional regression of the pricing errors on the bond’s risk profile can be expected to explain these errors. The question, then, is whether it is sufficient to include the structured provisions as explanatory variables to explain the pricing errors, or do the Greeks further contribute towards explaining these errors, recognizing that the Greeks are intended to be a reduced-form representation of the structured provisions and, therefore, multicollinearity between the Greeks and the structured provisions is likely to pose a problem for model specification. This studies finds it is prudent to include a reduced-set of Greeks and structured provisions to explain pricing errors.

Finally, a key proposition of this study, that the Greeks are a reduced-form representation of the structured provisions and can be used to assess the bond’s risk and agency characteristics, is grounded in the literature. Jensen and Meckling (1976) show how agency issues can result in under-investment and asset-substitution, Myers (1977) shows how agency issues related to growth options can result in under-investment, and Myers and Majluf (1984) show how asymmetric information can result in under-investment. (Bodie and Taggart [1978] 1980) show how callable bonds can mitigate under-investment and asset-substitution. Green (1984) shows how convertibles bonds can mitigate over-investment. Brennan and Kraus (1987) and Constantinides and Grundy (1989) show how convertible bonds mitigate under-investment. Brennan and Schwartz (1988) show how convertible bonds address agency issues arising from uncertainty about the firm’s risk. These studies are used to delineate the relation between the Greeks, on the one hand, and risk-management and agency-theory issues on the other.