Predictors of Excess Return in a Green Energy Equity Portfolio: Market Risk, Market Return, Value-at-Risk and or Expected Shortfall?
Abstract
:1. Introduction
2. Review of Selected Literature and Hypotheses Development
2.1. The Capital Asset Pricing Model
- Rj = the expected return on a security,
- Rf = the risk-free rate,
- bj = beta coefficient, and
- Rm = market return.
2.2. The Fama–French Multifactor Models
2.3. Extreme Value Theory
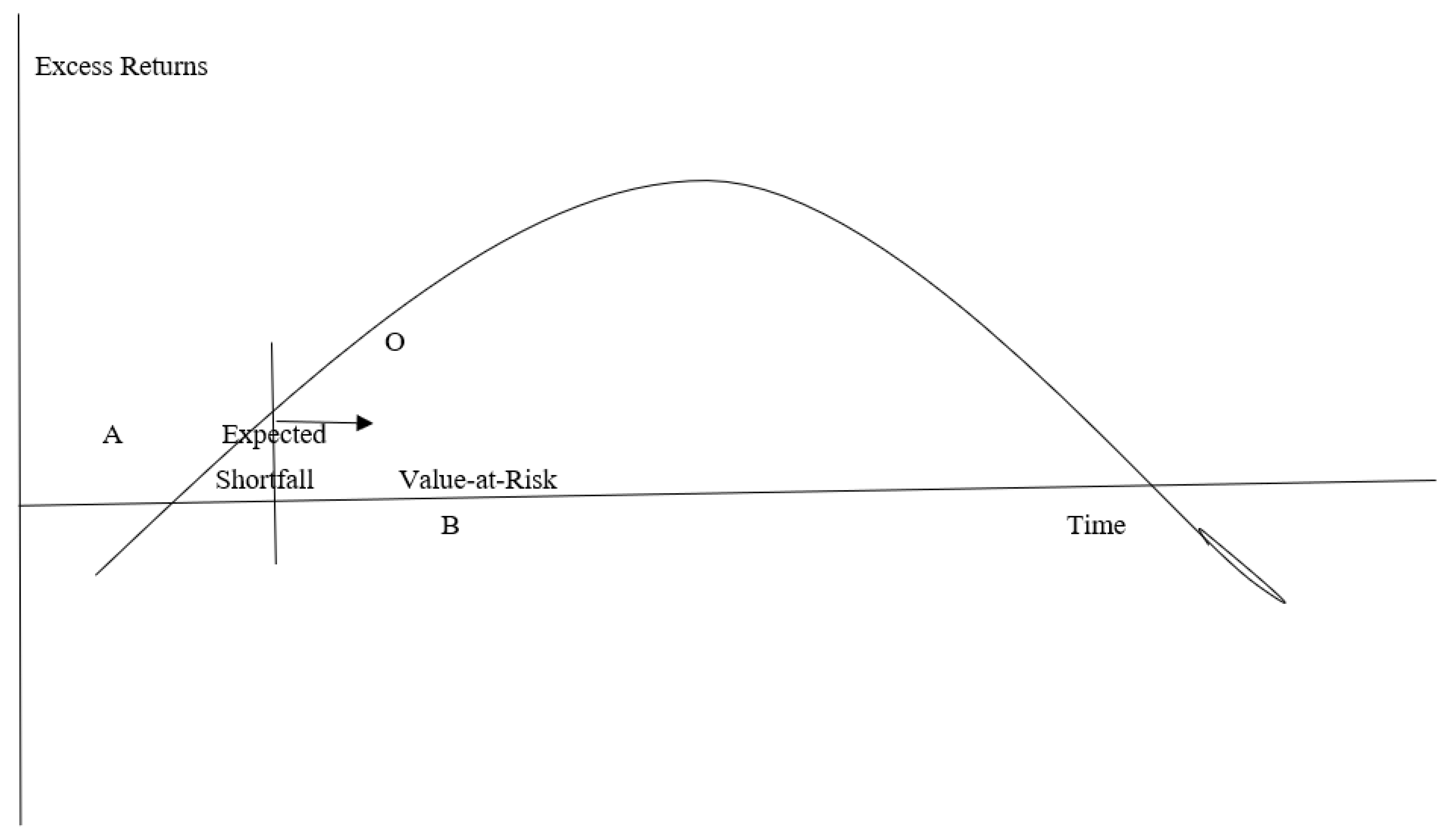
2.3.1. Value-at-Risk
- α = 95 or 99, the VAR percentile,
- Z = Z score of the VAR percentile, and
- σ = standard deviation of security returns.
2.3.2. Expected Shortfall
- c = Value-at-Risk breakpoint of the distribution, and
- p(x) = probability density function of obtaining returns with value x.
3. Materials and Methods
3.1. Sample and Data Characteristics
3.2. Methodology
- Excret = daily excess security returns,
- β = the stock’s beta coefficient,
- Rm = return on the market portfolio, proxied by the S & P 500, and
- Rf = daily Treasury bill rates.
- SMBt = size coefficient,
- LNMEt = log of market capitalization, and
- HMLt = book-to-market coefficient.
- SMBt = size coefficient,
- LNMEt = log of market capitalization,
- HMLt = book-to-market coefficient,
- INVESTMENTt = total assets, and
- OPERATING INCOMEt = Earnings before interest and taxes.
4. Results
4.1. Results Pertaining to the Market Model
4.2. Results Pertaining to the Conditional Extreme Value Distribution
4.2.1. Value-at-Risk Results
4.2.2. Expected Shortfall Results
5. Conclusions
5.1. Discussion of Results
5.2. Limitations of This Study and Scope for Future Research
5.3. Implications for Investors
5.4. Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Atlantic Yield Plc
- Advanced Disposal Services
- American Electric Power
- Airgain, inc
- Air Products & Chemicals
- Ampliphi Biosciences Corp.
- Armata Pharmaceuticals Inc.
- Atlantic Power Corp.
- Avalon Holdings Corp.
- Atlantic yield Plc.
- Brookfield Renewable Partners
- Benchmark Electronics
- Constellium NV
- Clean Harbors, Inc.
- Covanta holdings Corp.
- US Ecology
- Fidelity Merrimack Street Trust
- NRC Group Holdings Corp.
- Pattern Energy Group, Inc.
- Perma Fix Environmental Services, Inc.
- Servicemaster Global Holdings
- Sky Solar Holdings Ltd.
- Sharps Compliance Corp.
- Stericycle Inc
- Tecogen Inc
- York Water Co.
- Aim Immunotech Inc.
- Cincinnati Bell Inc.
- Mr Cooper Group
- DTE Energy
- Estaline Technologies
- Forum Energies Technologies
- Fluor Corp New
- Hemispherx Biopharma
- Johnson Controls International Plc
- Nextera Energy
- Ormat Technologies
- Plug Power
- Renewable Energy Group
- Suncor Energy Inc New
- Waste Management
- Advanced Energy
- Bloom Energy
- Canadian Solar
- Cheniere Energy
- Clearway Energy
- Daqo New Energy
- Enphase Energy
- Fuelcell Energy
- Enviva Partners LP
- Hannon Armstrong
- Jinkosolar
- Nexterra
- Ocean Power Technologies
- Renesola
- Renewable Energy Group
- Sunpower Corp.
- Sunrun
- TPI Composites
- BWX Technologies
- General Electric Inc.
- Solaredge Technologies Inc.
- Azure Power Global Limited
- General America Investors, Inc.
- Sunnova Energy International
- Standex International Corp.
- Neonode, Inc.
- American Super Conductor Corp.
- India Fund, Inc.
- Ballard Power Systems
- Arca Biopharma
- Asbury Automotive Group
- Proshares Trust
- First Trust Global
- Ishares Trust
- Tesla Inc.
- Ameresco Inc
- Gevo Inc.
- Atlantic yield Plc.
- avangrid, Inc.
- Covanta Holding Corp.
- Green Plains, Inc.
- PG&E Corp.
- Alphabet Inc
- Consol Coal Resources LP
- Edison International
- Mosaic Acquisition Corp De
- Southern Co.
- Exelon Corp.
- Idacorp Inc.
- ppl Corp.
- Firstenergy Corp.
- CM Energy Corp.
- WEC Energy Group Inc.
- XCEL Energy Inc.
- Entergy Corp New
- EQT Corp.
- Avista Corp.
- Ameren Corp.
- Duke Energy Corp, New.
- Eversource Energy
- Invacare Corp.
- Otter Tail Corp.
- Dominion Energy
- Rex American Resources Corp.
- American States Water Corp.
- Brookfield Asset Management
- Gladstone Commercial Corp.
- Portland GE
- Halcon Resources Corp.
- Torchlight Energy Resources
- Vivint Solar
- Tantech Holdings
- SPT Energy Co.
- Vivopower International
- Trinity Industries
- Dreyfus Strategic Municipal Bond Fund A
- BNY Mellon Strategic Municipal Bond Fund
- Fueltech
- Companhia Paranaense de Energia
- Clean Energy Funds Corp.
- Companhia Energetica De Minas GE
References
- Atsalakis, George S., Elie Bouri, and Fatois Pasiouras. 2021. Natural disasters and economic growth: A quantile on quantile approach. Annals of Operations Research 306: 83–109. [Google Scholar] [CrossRef]
- Aziz, Tariq, and Valeed Ahmad Ansari. 2017. Idiosyncratic volatility and stock returns: Indian evidence. Cogent Economics and Finance 5: 1–20. [Google Scholar] [CrossRef]
- Benz, R. 1981. The relationship between returns and market value common stocks. Journal of Financial Economics 9: 3–18. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Jalkh Naji, Anupam Dutta, and Gazi Salah Uddin. 2017. Gold and crude oil as safe-haven assets for clean energy stock indices: Blended copula approach. Energy 178: 544–53. [Google Scholar] [CrossRef]
- Bouslah, K., L. Kryzanowski, and B. MZali. 2013. The impact of the dimensions of social performance on firm risk. Journal of Banking and Finance 70: 223–60. [Google Scholar] [CrossRef]
- Brzeszczynski, J., and G. McIntosh. 2014. Performance of portfolios composed of British SRI stocks. Journal of Business Ethics 120: 335–62. [Google Scholar] [CrossRef] [Green Version]
- Cai, L., and C. He. 2014. Corporate environmental responsibility and security prices. Journal of Business Ethics 125: 617–35. [Google Scholar] [CrossRef]
- Chen, James Ming. 2021. The Capital Asset Pricing Model. Encyclopedia 1: 915–33. [Google Scholar] [CrossRef]
- Chen, Q., and D. Giles. 2014. Risk analysis for three precious metals: An application of Extreme Value Theory. Econometrics Working Papers No. 1704. Victoria: University of Victoria. [Google Scholar]
- Clarkson, Peter M., Yue Li, Gordon D. Richardson, and Florin P. Vasvari. 2011. Does it really pay to be green? Determinants and consequences of proactive environmental strategies. Journal of Accounting and Public Policy 30: 122–24. [Google Scholar] [CrossRef]
- Diether, Karl B., Christopher J. Malloy, and Anna Scherbina. 2002. Differences of opinion and the cross-section of stock returns. Journal of Finance 57: 2113–41. [Google Scholar] [CrossRef]
- Dolinar, D., S. Loncarevic, and Z. Orlovic. 2020. Test of the Fama-French Five-Factor Model on the Croatian stock market. Paper presented at the FEB Zagreb International Odyssey Conference on Economics and Business, Zagreb, Croatia, June 16–20; vol. 2, pp. 286–97. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 1996. Multifactor explanations of asset pricing Anomalies. Journal of Finance 51: 55–84. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2012. Size, value and momentum in international stock Returns. Journal of Financial Economics 105: 457–72. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2014. Dissecting anomalies with a five-factor model. Fama-Miller Working Paper 46. [Google Scholar] [CrossRef]
- Goss, Allen, and Gordon S. Roberts. 2011. The impact of corporate social responsibility on the cost of bank loans. Journal of Banking and Finance 35: 1794–810. [Google Scholar] [CrossRef]
- Griffin, John M. 2002. Are the Fama and French factors global or country specific? Review of Financial Studies 1593: 283–803. [Google Scholar] [CrossRef]
- Hamilton, James T. 1995. Pollution as news media and stock market reactions to the toxins release inventory data. Journal of Environmental Economics and Management 28: 98–113. [Google Scholar] [CrossRef]
- Haque, Samiul, and Michael S. Delgado. 2017. Finite sample performance of specification tests for correlated random effects quantile panel regressions. Applied Economics Letters 24: 515–19. [Google Scholar] [CrossRef]
- Hart, Stuart L., and Gautam Ahuja. 1996. Does it pay to be green? An empirical examination of the relationship between emission reduction and firm performance. Business Strategy and the Environment 5: 30–37. [Google Scholar] [CrossRef]
- Huang, L., Ghon Rhee, and L. Wu. 2012. Extreme downside risk and expected stock Returns. Journal of Banking and Finance 36: 1492–502. [Google Scholar] [CrossRef]
- Ibikunle, G., and T. Steffen. 2017. European green mutual fund performance. Journal of Business Ethics 145: 337–55. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, J., and S. Azher. 2014. Value-at-Risk and expected stock returns: Evidence from Pakistan. Lahore Journal of Economics 2: 1–100. [Google Scholar] [CrossRef]
- Jammazi, Rania, and Duc Khuong Nguyen. 2017. Estimating and forecasting portfolio’s Value-at-Risk with wavelet-based extreme value theory: Evidence from crude oil prices and US exchange Rates. Journal of the Operational Research Society 68: 1352–62. [Google Scholar] [CrossRef]
- Konrad, T. 2010. Buying Green Stocks Pays, But Finding Green in Brown Pays More. Available online: http://seekingalpha.com/article/231918-buying-green-stocks-paysbut-finding-green-in-brown-paysmore (accessed on 13 April 2011).
- Lesser, K., S. Lobe, and C. Walkshausl. 2014. Green and socially responsible investing in international markets. Journal of Asset Management 15: 317–31. [Google Scholar] [CrossRef]
- Levi, M., and D. Newton. 2016. Flash of green: Are environmentally driven stock returns sustainable? Managerial Finance 42: 1091–109. [Google Scholar] [CrossRef]
- Lintner, J. 1965. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Liu, X., E. Bouri, and N. Jalkh. 2021. Dynamics and determinants of market integration of green, clean, dirty energy investments and conventional stock indices. Frontiers in Environmental Science 9: 1–8. [Google Scholar] [CrossRef]
- Markowitz, H. 1952. Portfolio selection. Journal of Finance 9: 77–91. [Google Scholar]
- Miller, Edward M. 1977. Risk, uncertainty, and divergence of opinion. Journal of Finance 32: 1151–68. [Google Scholar] [CrossRef]
- Mitchell, M., T. Pulvino, and E. Stafford. 2004. Price pressure around mergers. Journal of Finance 59: 31–63. [Google Scholar] [CrossRef]
- Roll, R. 1977. A critique of the Asset Pricing Theory’s tests: Part I, On past and present instability of the theory. Journal of Financial Economics 4: 129–76. [Google Scholar] [CrossRef]
- Saeed, T., E. Bouri, and H. Alsulami. 2021. Extreme return connectedness and its determinants between clean/green and dirty energy investments. Energy Economics 96: 1–14. [Google Scholar] [CrossRef]
- Saltari, E., and G. Travaglini. 2011. The effects of environmental policies on the abatement investment decisions of a green firm. Resource and Energy Economics 33: 666–85. [Google Scholar] [CrossRef]
- Sarykalin, S., G. Serriano, and S. Uryasev. 2008. Value-at-Risk vs. Conditional Value-at-Risk in risk management and optimization. Tutorials in Operations Research 2: 270–94. [Google Scholar]
- Sasodia, G. Singh, I. Soares, and P. Ferreira. 2016. The effect of sample size on European Union’s renewable energy investment drivers. Applied Economics 48: 5129–37. [Google Scholar] [CrossRef]
- Shalit, H., and S. Yitzakhi. 2003. An asset allocation puzzle: Comment. American Economic Review 91: 1170–79. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Tobin, J. 1958. Liquidity preference as behavior towards risk. Review of Economic Studies 25: 65–86. [Google Scholar] [CrossRef]
| Panel A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| Excess Return | −0.03 (0.07) | 0.03 (4.9) | −0.008 (1.1) | −0.003 (0.41) | 0.01 (0.002) | 0.06 (5.16) | −0.007 (0.59) | 0.003 (0.55) | 0.007 (1.6) | 0.009 (0.73) |
| Market Return | 3 × 103 (9 × 10−5) | 1 × 10−4 (0.01) | 5 × 10−4 (7 × 103) | 8.1 × 10−3 (0.002) | 4 × 10—4 (1.9) | 1.8 × 10−5 (0.007) | 3.9 × 10−4 (0.01) | 7 × 10−4 (.01) | −0.001 (0.01) | 9.8 × 10—4 (0.007) |
| Beta | 0.72 (0.67) | 1.27 (1.0) | 1.28 (1.0) | 1.15 (1.05) | 1.16 (1.0) | 1.11 (1.06) | 1.27 (1.01) | 1.26 (0.97) | 1.24 (0.97) | 1.26 (1.0) |
| Market Capitalization (Log) | 5.53 (4.23) | 19 (5.29) | 18.5 (5.9) | 19 (6.0) | 20 (4.5) | 3.8 (3.02) | 19.7 (5.2) | 19.7 (4.8) | 20.5 (3.3) | 4.1 (2.9) |
| Book-to-Market | 3.5 × 10−4 (0.001) | 1071 (4283) | 1045 (413) | 5360 (648) | 2723 (44) | 4.03 × 10−4 (0.002) | 463 (911) | 902 (257) | 1077 (90) | 4.2 × 10−4 (0.001) |
| EBIT (millions) | 167.7 (278) | 308.7 (1102) | 289 (10) | 308 (911 | 292.1 (51) | 73.88 (212.8) | 258 (197) | 223 (195) | 243 (51) | 33.41 (568) |
| Assets (millions) | 24,797 (1100) | 2534 (11) | 1124 (18) | 6917 (30) | 10,968 (222) | 2199 (438) | 2550 (70) | 250.3 (4.09) | ||
| Panel B | ||||||||||
| Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| Excess Return | 42.27 −2.05 | 587 −2.11 | 127 −2.08 | 0.04 −0.03 | 202 −2.11 | 0.04 −0.03 | 55.65 −2.15 | 63.5 −2.07 | 210.21 −2.14 | 62.57 −2.06 |
| Market Return | −0.04 −0.03 | 0.04 −0.06 | 0.02 −0.02 | 33.4 −2.1 | 0.04 −0.06 | 595 −2.1 | 0.02 −0.03 | 0.07 −0.05 | 0.11 −0.09 | 0.03 −0.02 |
| Beta | 1.84 0 | 5.33 −0.27 | 5.33 −0.27 | 5.33 −0.27 | 5.33 −0.27 | 5.33 −1.19 | 5.33 −1.19 | 5.33 −1.19 | 5.33 −1.19 | 5.33 −0.83 |
| Market Cap | 14.56 0 | 26 0 | 26 0 | 26.36 0 | 26.29 0 | 8.49 0 | 25 0 | 26.27 −0.85 | 25.49 2.10 | 8.07 0 |
| Book-to-Market | 5.2 × 10−3 −4.7 × 10−3 | 28,590 0 | 27,134 −318 | 79,147 0 | 24.91 −15.5 | 0.21 0 | 3636 0 | 14,681 −64.5 | 20,156 0.44 | 0.03 0 |
| EBIT (millions) | 762 0 | 7492 −85 | 7796 −579 | 6229 −136 | 4066 −102 | 1067 0 | 24,118 −761 | 3326 −1764 | 2628 −516 | 1607 0 |
| Assets (millions) | 73,913 4.12 | 70,771 3 | 16,570 0 | 655 8.6 | 655 8.6 | 89,993 3 | 37,803 8.6 | 48,779 6.8 | 36,168 0 | |
| Maxima are listed first in each cell | ||||||||||
| Panel C | ||||||||||
| Variable | Excess Return | Market Return | Beta | Market Capitalization | Book to Market | EBIT | Assets | |||
| Excess Return | 1 | |||||||||
| Market Return | −0.02 | 1 | ||||||||
| Beta | 0.01 | 0.001 | 1 | |||||||
| Market Capitalization | 0.07 | 0.004 | 0.58 | 1 | ||||||
| Book to Market | 0 | 1 × 10−5 | 0.33 | 0.002 | 1 | |||||
| EBIT | 0.3 | 0.04 | 0.03 | 0.31 | 0.05 | 1 | ||||
| Assets | 0.002 | 0.15 | 0.04 | 0.30 | 0.04 | 0.93 | 1 | |||
| Independent Variables (CAPM Predictors of Excess Return) | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|---|---|
| Market Return | 3.57 *** | 5.15 | 3.32 * | 0.93 | −4.93 | −0.91 | −1.05 | 3.86 *** | 2.74 | −1.41 * |
| Beta | 2.28 × 10−3 | −0.45 *** | 7 × 103 | 0.01 * | −2.5 ** | −3.38 × 10−2 | 9 × 10−3 | 0.06 *** | −0.05 | 1.51 × 10−2 |
| N | 16,485 | 12,269 | 15,539 | 12,756 | 13458 | 16,993 | 13,482 | 13,536 | 13,712 | 14,073 |
| R2 | 1.6 × 10−2 | 0.02 | 1.6 × 10−4 | 0.04 | 0.019 | 1.56 × 10−2 | 0.03 | 0.02 | 0.01 | 1.75 × 102 |
| Panel A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 3.06 *** | 6.62 | 4.13 * | 1.54 ** | −8.31 | −3.32 | −0.94 | 3.18 | 3.48 | −2.67 ** |
| Beta | 3.26 × 10−3 * | 6 × 10−2 | 0.09 | 3.88 × 10−3 | −2.36 × 10−3 | −4 × 10−2 | 0.03 | 0.05 | 0.01 | 8.8 × 10−3 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −7.8 × 10−3 | −8.8 × 10−4 | 7.31 × 10−3 | 2.46 × 10−3 | 5.51 × 10−3 | 3.01 × 10−2 | 5.67 × 10−3 | 1.96 × 10−5 | 9.34 × 103 | 4.23 × 10−3 |
| Book-to-Market | −8.44 | 6.3 × 10−5 | 1.16 × 10−5 | 0.00 | −1.69 × 10−5 | 2.11 | 10.41 × 10−5 | 4.61 × 10−5 | 11.25 × 10−6 | 5.74 |
| N | 16,933 | 9010 | 8372 | 7943 | 7601 | 17,811 | 7353 | 6299 | 6987 | 14,316 |
| R2 | 0.05 | 0.04 | 0.03 | 0.08 | 0.03 | 1.52 × 10−2 | 0.05 | 0.17 | 0.02 | 1.77 × 10−2 |
| Panel B | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 1.03 *** | 6.71 | 4.14 * | 1.54 ** | −8.32 | −10.31 | −0.93 | 3.17 | 3.47 | −2.678 |
| Beta | −0.03 *** | 0.05 | 0.09 | 4.34 × 10−3 | 4.08 × 102 | −0.82 | 0.03 | 0.03 | 6.18 × 10−3 | 9.03 × 10−3 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 5.3 × 10−3 *** | −2.9 × 10−3 | 8.04 × 10−3 | 2.59 × 10−3 | −1.35 × 10−3 | −0.06 | 3.62 × 10−3 | 1.38 × 10—3 | 1.32 × 10−2 | 4.18 × 10−3 |
| Book-to-Market | −88.38 *** | −1.05 × 10−5 | 1.99 × 10−5 | 1.02 × 10−5 | 1.97 × 10−3 | −62.79 | 7.43 × 10−4 | 1.3 × 10−4 | 2.22 × 10−4 | 5.75 |
| EBIT | 2.38 × 106 | 1.34 × 10−4 | −1.50 × 10−5 | 7.61 × 10−6 | −6.67 × 10−5 | −3.97 × 10−4 | 3.96 × 10−6 | −5.35 × 10−6 | −3.54 × 10−5 | |
| Assets | 2.90 × 10−6 | 1.16 × 10−6 | 7.03 × 10−7 | −4.90× 10−7 | −8.14 × 10−5 | −2.39 × 10−5 | −3.03 × 10−5 | −5.33 × 10−6 | −9.12 × 10−6 | 2.27 × 10−6 |
| N | 3,534 | 8948 | 8372 | 7943 | 7601 | 5,744 | 7353 | 6299 | 6987 | 14,316 |
| R2 | 0.18 | 0.04 | 0.03 | 0.08 | 0.03 | 0.05 | 0.05 | 0.17 | 0.02 | 1.77 × 102 |
| Panel C | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 1.13 | 43.75 *** | 40.9 *** | −102 | 9.20 | −0.51 | 0.52 | −.12 | −1.13 | 4.39 |
| Beta | 0.09 | −5.91 *** | −4.49 *** | −0.06 | 7.2 × 10−2 * | −2.79 × 10−3 | −7.5 × 10−3 | −.06** | −.03 | −12.51 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 0.05 | −3.9 × 10−3 | −1.4 × 10−2 * | 5.77 × 10−3 | 7.65 × 10−3 * | −1.23 × 10−3 | 8.55 × 10−5 | 2.60 × 10−3 * | 3.11 × 10−3 | 0.33 |
| Book-to-Market | −63.9 | −9.96 × 10−6 | 1 × 10−4 | 2.60 × 10−4 | 6.89 × 103 ** | 0.10 | 6.53 × 10−4 | 2.12 × 10−4 | 4.25 × 10−4 | 46.85 |
| EBIT | 9.01 × 10−4 | 5.60 × 10−4 | 1.96 × 10−3 *** | 5.79 × 10−4 | 1.17 × 103 ** | −2 × 10−6 | −5.24 × 10−4 *** | −6.82 × 10−4 *** | −9.58 × 10−4 *** | |
| Assets | 1.4 × 10−2 | 1.14 × 10−5 | 5.28 × 10−5 *** | −1.0 × 10−5 | −3.1 × 10−4 *** | 4.8 × 10−6 | −2.78 × 10−5 | 1.43 × 10−5 * | −3.3 × 10−6 | −0.67 *** |
| N | 3534 | 8948 | 8372 | 7943 | 7601 | 5744 | 7353 | 6299 | 6987 | 14,316 |
| Panel D | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 3.66 | 45.10 *** | −31 *** | 102 | 20 *** | 0.50 | 0.53 | 0.80 | −2.22 | 5.47 |
| Beta | −1.73*** | −5.24 *** | 0.1 *** | 0.24 | −0.02 | −8.4 × 10−4 | 8.55 × 10−3 | −0.04 ** | −0.05 | −9.36 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −0.07 | 2.28 × 10−2 *** | −9.4 × 10−3 * | 0.07 | 0.06 *** | 2.42 × 10−5 | −4.89 × 10−4 | 8.34 × 10−4 | 1.07 × 10−3 | −0.70 |
| Book-to-Market | 20.03 | −3.40 × 10—4 | 7.4 × 10−4 *** | 1.3 × 10−5 | −5.2 × 10−4 | 0.03 | −2.12 × 10−6 | −3.55 × 10−5 | −7.29 × 10−5 | 12.40 |
| EBIT | −1.2 × 10−3 | 2.4 × 10−4 | −1.4 × 103 *** | 1.35 × 10−3 | 6.68 × 10−4 ** | 4 × 10−6 | −7.87 × 10−5 *** | −1.1 × 10−3 *** | 7.11 × 10−5 | |
| Assets | −0.02*** | 1.31 × 10−5 | 5.6 × 10−7 | −9 × 10−6 | −3.3 × 10−5 | 3.0 × 10−6 | 1.8 × 10−7 | 7.1 × 10−7 | 8.44 × 10−6 | 9.31 *** |
| N | 3534 | 8948 | 8372 | 7943 | 7601 | 5.44 | 7353 | 6299 | 6987 | 14,316 |
| Panel E | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 2.66 | 49.14 *** | −51 *** | 117 | 22 8** | 0.45 | 0.56 | 0.23 | −2.00 | 2.56 |
| Beta | 2.90 *** | −1.92 *** | 0.9 *** | 0.28 | 0.1 ** | 2.30 × 10−3 | 0.01 | −7.35 × 10−3 | −0.03 | −5.50 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −0.02 | 9.66 *** | 2.1 × 10−3 | 0.18 | 0.10 * | 1.11 × 10−3 | 1.37 × 10−3 | −2.34 × 10−3 | −2.06 × 10−3 | −1.38 |
| Book-to-Market | 48.37 | −5.33 × 10−4 ** | 4.53 × 10−4 *** | 3.22 × 10−4 | 4.8 × 105 | 0.43 | −1.42 × 10−4 | −4.42 × 10−5 | −4.69 × 10−4 | 49.13 |
| EBIT | −8.1 × 10−4 | −1.21 × 10—3 ** | 1.4 × 103 *** | −1 × 103 | −8.16 × 10−4 *** | −6.7 × 10−6 | −6.48 × 10−5 *** | −4.61 × 10−6 | −6.06 × 10−4 *** | |
| Assets | −8.04 × 10−3 | 3.8 × 10−5 * | −4.9 × 10−5 *** | 2.6 × 10−5 | −1.61 × 10−5 | 8.2 × 10−6 | 7.08 × 10−6 | 9.42 × 10−6 | 3.48 × 10−5 * | −6.29 *** |
| N | 3534 | 8948 | 8372 | 7943 | 7601 | 5,744 | 7353 | 6299 | 6987 | 14,316 |
| Panel A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 3.3 *** | 7.09 | 3.63 | 1.7 *** | −1.29 | −2.41 | −1.27 | 3.18 | 3.28 | −3.08 |
| Beta | 3.1 × 10−3 * | 6.65 × 10−2 | 0.05 | 0.02 | −1.08 × 10−3 | −0.06 | −0.06 | 0.04 | −0.01 | 0.00 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −4.7 × 103 | 5.06 × 10−3 | 4.7 × 10−3 | 2.9 × 10−3 | 7.1 × 10−3 | −8.24 × 10−3 | 0.02 ** | 9.4 × 10−5 | 8.1 × 10−3 | −6 × 10−3 |
| Book-to-Market | −18.9 | 1.06 × 10−4 | 4.4 × 10−5 | 0.00 | −2.3 × 10−5 | −3.23 | 1.5 × 10−5 | 4.8 × 10−6 | −1.0 × 10−6 | 10.65 |
| Extreme Value Distribution Predictor | ||||||||||
| Value-at-Risk 95 | −1.3 × 10−5 *** | 5.54 × 10−6 *** | −6.7 × 10−6 *** | −0.00 | −6.4 × 10−5 *** | −6.73 × 10−6 *** | −6.7 × 10−6 *** | −5.9 × 10−7 | −3.4 × 10−6 *** | −6.67 × 10−6 *** |
| N | 16,470 | 8285 | 8056 | 6897 | 7326 | 17,944 | 7010 | 6299 | 7025 | 13,659 |
| R2 | 0.09 | 0.05 | 0.07 | 0.12 | 0.06 | 0.04 | 0.08 | 0.17 | 0.04 | 0.04 |
| Panel B | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 1.3 *** | 7.21 | 3.64 | 1.7 *** | −6.05 | −4.42 | −1.25 | 3.18 | 3.2 | −3.08 |
| Beta | −0.07 *** | 0.03 | 0.05 | 0.02 | 5.1 × 10−3 | 0.02 | −0.05 | 0.03 | −0.01 | 0.00 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 3.4 × 10−3 | 3.1 × 10−4 | 7.2 × 10−3 | 4.4 × 10−3 * | 6.5 × 10−3 | −2.45 × 10−3 | 0.02 ** | 1.3 × 10−3 | 9.2 × 10−3 | −6 × 10−3 |
| Book-to-Market | −26.8 | −1.3 × 10−6 | 6.8 × 10−5 | 2.5 × 10−5 | 8.4 × 10−4 | −24.50 | 1.2 × 10−3 | 1.2 × 10−4 | 8.5 × 10−6 | 10.67 |
| EBIT | −3.1 × 10−5 | 2.3 × 10−4 | −8.6 × 10−6 | 1.6 × 10−5 | −1.5 × 10−5 | −2.45 × 10−5 | 1.6 × 10−6 | −4.5 × 10−6 | 3.0 × 10−5 | −6.34 × 10−6 |
| Assets | 1.2 × 10−6 | −2.4 × 10−6 | −1.2 × 106 | −3.5 × 10−5 | −4.8 × 10−5 | −4.9 × 10−6 | −3.6 × 10−6 | 3.75 × 10−6 | ||
| Extreme Value Distribution Predictor | ||||||||||
| Value-at-Risk 95 | −3.3 × 10−6 | 5.5 × 10−6 *** | −6.7 × 10−6 *** | −4.1 × 10−8 | −6.4 × 10−6 *** | −7 × 10−6 *** | −6.7 × 10−6 *** | −5.8 × 10−7 | −3.4 × 10−6 *** | −6.67 × 10−6 *** |
| N | 4767 | 8223 | 8056 | 6897 | 7326 | 12334 | 7010 | 6299 | 7025 | 13,659 |
| R2 | 0.05 | 0.05 | 0.07 | 0.12 | 0.06 | 0.04 | 0.08 | 0.17 | 0.04 | 0.04 |
| Panel C | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.03 | 45.5 *** | −39.4 *** | −100 | 108 ** | 0.49 | 36.4 | 0.46 | −1.05 | 8.4 |
| Beta | −0.01 | 0.24 ** | −4.8 *** | −1.38 | 2.6 *** | −0.01 | −26 *** | −0.07 *** | −1.3 × 10−3 | 4.10 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 6.48 × 10−3 | −0.08 *** | 0.03 *** | −0.15 | −0.49 *** | −6.07 × 10−5 | −0.1 *** | 2.5 × 10−3 * | 1.7 × 10−3 | 1.08 |
| Book-to- Market | 51.2 | −4.2 × 10−5 | −3 × 10−4 * | 7.04 × 10−4 | 0.03 * | −0.90 | 0.09 *** | 1 × 10−4 | 1.2 × 10−3 ** | 15.96 |
| EBIT | 6.7 × 10−4 *** | −2.4 × 10−4 | 3 × 10−3 *** | −8 × 10−6 | 6.5 × 10−3 *** | −6.4 × 10−6 | 1.2 × 10−3 *** | −8 × 104 *** | −2 10 −4 *** | 19.17 *** |
| Assets | 1.4 × 10−5 | 4.1 × 10−5 *** | 7.3 × 10−5 | −1.2 × 10−3 ** | −3.7 × 10−3*** | −1.9 × 10−5 ** | −3.6 × 10—5 * | −13.75 *** | ||
| Extreme Value Distribution | ||||||||||
| Value-at-Risk 95 | 6 × 10 −5 * | −6 × 10−8 | 1.6 × 10−7 | 1 × 10−6 | −4 × 10−7 | −0.00 | −4.1 × 10−5 ** | 1.8 × 10−6 ** | −1.7 × 10−8 | 5.56 × 10−3 *** |
| N | 4767 | 8223 | 8056 | 6897 | 7326 | 12,334 | 7010 | 6299 | 7025 | 13,572 |
| Panel D | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.03 | 52.2 *** | −31 *** | −59.6 | 109 *** | 0.46 | 18.5 | −0.2 | −1.8 | 8.4 |
| Beta | 1.29 *** | 1.5 *** | −1.4 ** | −6.40 | 10 *** | −9.96 × 10−6 | −17 *** | −0.03 ** | −3 × 10−3 | 4.1 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −1 × 10−3 | −0.03 *** | 0.02 *** | −8.3 × 10−3 | −0.31 *** | −9.1 × 10−6 | −0.26 *** | 7.9 × 10−4 | −1 × 10−3 | 1.08 |
| Book-to-Market | −11.74 | −3.6 × 10−5 | −1.3 × 10−4 | −2.7 × 10−5 | −1.2 × 10−3 | 0.08 | 6 × 10−3 | −1.5 × 10−4 | 2.7 × 10−4 | 15.96 |
| EBIT | 6.4 × 10−4*** | 1.1 × 10—4 | −4.6 × 10−4 | 2.3 × 10−3 | 4.9 × 10−3 *** | 7.3 × 10−7 | 2.2 × 10−4 * | −7.4 × 10−4 *** | 7.9 × 10−4 *** | 19.17 *** |
| Assets | 9.2 × 10—6 | −3.7 × 10−5 *** | 2.6 × 10−5 | −1.2 × 10−4 | −4 × 10−4 | 8.4 × 10−6 | −7 × 10—6 | −13.75 *** | ||
| Extreme Value Distribution Predictor | ||||||||||
| Value-at-Risk 95 | 8.66 × 10—6 | 3.2 × 10−7 | 3.2 × 10−7 | −0.00 | −3.2 × 10−6 | 0.00 | −3.4 × 10−5 ** | 3.6 × × 10−8 | 7.9 × 10−8 | 5.56 × 10−3 *** |
| N | 4767 | 8223 | 8056 | 6897 | 7326 | 12,334 | 7010 | 6299 | 7025 | 13,572 |
| Panel E | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 0.09 | 52.5 *** | −43 *** | −5 × 10−3 | 104 ** | 0.44 | 20.9 | 0.18 | −1.8 | 8.11 |
| Beta | 1.27 *** | 2.8 *** | 1.0 ** | −2.8 | 18 *** | 8.59 × 10−2 | −5.2 *** | −0.02 * | 0.05 * | 6.68 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −1 × 10−3 | −0.01 | 0.05 *** | −0.02 | −0.04 * | 1.63 × 10−4 | −0.1*** | −3.2 × 103 ** | −2 × 10−3 | −0.14 |
| Book-to-Market | −43.7 | −3.8 × 10−4 * | 8.6 × 10−4*** | −4.4 × 10−4 | −0.04 *** | .99 | −0.03 ** | −3.1 × 10−4 * | −1.5 × 10−4 | 21.14 |
| EBIT | −6.3 × 10−5 | −9.4 × 10−4 | 2.3 × 10−3 *** | 2.9 × 10−3 | 6.1 × 10−3 | 5.73 × 10−6 | 1 × 10−3 *** | −6.9 × 10−5 *** | 5.2 × 10−4 *** | 10.50 *** |
| Assets | 3.7 × 10−5 * | −2.8 × 10−5 * | 4.2 × 10−5 | 1.7 × 10−3 *** | 1.6 × 10−3 ** | 2.0 × 10−5 *** | 2.2 × 10−5 | −6.70 *** | ||
| Extreme Value Distribution Factor | ||||||||||
| Value-at-Risk 95 | −5.2 × 10−5 * | −4.9 × 10−7 | −7 × 10−7 | 1 × 10−6 | −2.6 × 10−6 | 0.00 | −1.4 × 10−5 | −6.9 × 10−7 | −3.4 × 10−7 | 1 × 10−2 *** |
| N | 4767 | 8223 | 8056 | 6897 | 7326 | 12334 | 7010 | 6299 | 7025 | 13,572 |
| Panel A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 3.3 *** | 6.67 | 3.48 | 1.55 ** | −6.0 | −2.41 | −0.64 | 3.18 | 3.25 | −2.9 *** |
| Beta | 3.1 × 10−3 * | −1.9 × 10−3 | 0.02 | 3.9 × 103 | 3.1 × 10−3 | −0.06 | 0.01 | 0.04 | −2.2 × 10−3 | 7.3 × 10−3 |
| Fama–French Factor | ||||||||||
| Market Capitalization | −4.7 × 10−3 | −2.7 × 10−3 | 5 × 10−3 | 2.4 × 10−3 | 3.5 × 10−3 | −8 × 10−3 | 6.1 × 10−3 | 9.9 × 10−5 | 5.3 × 10−3 | −5 × 10−3 |
| Book-to-Market | −18.7 | 3 × 10−6 | 4.6 × 10−5 | 0.00 | −2 × 10−5 | −3.23 | −6.6 × 10−6 | 4.8 × 10−6 | −1.2 × 10−6 | 9.8 |
| Extreme Value Distribution Factor | ||||||||||
| Value-at-Risk 99 | −1 × 10−5 *** | −7.1 × 10−6 *** | −5.6 × 10−7 *** | 0.00 | −6.4 × 10−6 *** | −5.6 × 10−6 *** | −5.5 × 10−6 *** | −5 × 10−8 | −2.9 × 106 *** | −5.6 × 10−6 *** |
| N | 16,874 | 9013 | 8372 | 8007 | 7601 | 17,945 | 7354 | 6299 | 7025 | 14,319 |
| R2 | 0.09 | 0.07 | 0.07 | 0.08 | 0.06 | 0.04 | 0.07 | 0.17 | 0.04 | 0.04 |
| Panel B | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| Market Return | 1.3 *** | 6.75 | 3.49 | 1.54 8* | −6.04 | −4.42 | −0.64 | 3.18 | 3.2 | −2.9 *** |
| CAPM Predictor | ||||||||||
| Beta | −0.07 *** | −2.7 × 10−3 | 0.02 | 4.3 × 10−3 | 0.02 | −0.02 | 0.01 | 0.03 | 1.1 × 10−3 | 7.4 × 10−3 |
| Market Capitalization | 3 × 10−3 | −3.4 × 10−3 | 7.1 × 10−3 | 2.4 × 10−3 | 1.6 × 10−3 | −2 × 10−3 | 4.4 × 10−3 | 1.3 × 10−3 | 5.9 × 10−3 | −5.1 × 10−3 |
| Book-to-Market | −26.2 | −1.9 × 10−5 | 6.8 × 10−5 | 1.0 × 10−5 | 5.1 × 10−4 | −24.5 | 6.1 × 10−4 | 1.2 × 10−4 | 5.0 × 10−5 | 9.1 |
| EBIT | −3 × 10−5 | 1.7 × 10−4 | −6.8 × 10−6 | 7.5 × 10−6 | −1.8 × 10−5 | −2.4 × 10−4 | 4.2 × 10−5 | −4.5 × 10−6 | 2.3 × 10−5 | 6.2 × 10−6 |
| Assets | 7.6 × 10−7 | −2.3 × 10−5 | −4.8 × 10−7 | −2.1 × 10−5 | −2.5 × 10−5 | −4.9 × 10−6 | −2.1 × 10−6 | 4.5 × 10−7 | ||
| Extreme Vslue Distribution Predictor | ||||||||||
| Value-at-Risk 99 | −2.7 × 10−6 | −7.1 × 10−6 *** | −5.6 × 10−6 *** | 1 × 10−9 | −6.4 × 10−6 *** | −6 × 10−6 *** | −5.5 × 10−6 *** | −4.8 × 10−7 | −2.9 × 10−6 *** | −5.6 × 10−6 *** |
| N | 4850 | 8951 | 8372 | 8007 | 7601 | 12335 | 7354 | 6299 | 7025 | 14,319 |
| R2 | 0.05 | 0.07 | 0.07 | 0.08 | 0.06 | 0.08 | 0.07 | 0.17 | 0.04 | 0.04 |
| Panel C | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.12 | 42 *** | −42.5 *** | −23.4 | 18 *** | 0.49 | 0.92 | −0.12 | −0.5 | 8.08 |
| Beta | −0.20 | −0.4 *** | −2.3 *** | −1.2 | −0.05 | −0.01 | 0.01 | −0.06 *** | −0.05 | 2.15 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 6.7 × 10−4 | −.06*** | −0.04 *** | .21 | 6.6 × 10−3 * | −6 × 10−5 | 2.5 × 10−3 * | 4.8 × 10−3 *** | 9.4 × 10−4 | 1.29 |
| Book-to-Market | 44.2 | 2.5 × 10−4 | 2.3 × 10−4 | −4.1 × 10−4 | 8.2 × 103 *** | −0.9 | 3.3 × 10−4 | 4.2 × 10−5 | 6 × 10−4 | 54.9 |
| EBIT | 3.7 × 10−4 ** | −2.8 × 10−4 | 1.1 × 10−3 ** | 5.8 × 10−3 | −1.0 × 10−3 *** | −6.4 × 10−6 | −5.1 × 10−4 *** | −1 × 10−3 *** | −1.5 × 10−3 *** | 26.1 *** |
| Assets | 1.2 × 10−5 | 5.3 × 10−5 *** | 2.7 × 10−5 | −4 × 10−4 *** | −2.6 × 10−5 | −2.6 × 10−5 *** | 1 × 10−5 | −14.1 *** | ||
| Extreme Value Distribution Predictor | ||||||||||
| Value-at-Risk 99 | 4.2 × 105 * | −2.1 × 10−7 | −9.9 × 10−7 | −6 × 10−6 | 1.4 × 10−7 | 0.00 | −7.4 × 10−8 | 1.8 × 10−6 *** | −2 × 10−9 | 5.8 × 10−3 *** |
| N | 4850 | 8951 | 8372 | 8007 | 7601 | 12,335 | 7354 | 6299 | 7025 | 14,319 |
| Panel D | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.06 | 48 *** | −37.8 *** | 23 | 25 *** | 0.46 | 0.61 | −0.41 | −1.36 | 7.17 |
| Beta | −0.05 ** | 1.7 *** | −1.9 *** | 0.25 | 0.01 | −9.9 × 10—5 | 0.02* | −0.02 * | −0.01 | |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 0.003 | −0.04 *** | −1.4 × 10−2 *** | 0.80 | 0.05 *** | −9.1 × 10−6 | 5 × 10−3 *** | 1.7 × 10−3 | −2.1 × 10−4 | −0.06 |
| Book-to-Market | 3.07 | −8.8 × 10−5 | 4.3 × 10−4 *** | −2.1 × 10−4 | −6.2 × 10−4 | 0.08 | −1.5 × 10−6 | −6.5 × 10−5 | 6.0 × 10−5 | 11.38 |
| EBIT | 9.5 × 10−5 | −2 × 10−4 | −5.2 × 10−5 | −2.9 × 10−3 | 8.4 × 10−4 *** | 7.3 × 10−6 | −3.3 × 10−4 *** | −6.7 × 10−4 *** | −1.3 × 10−3 *** | 16.3 *** |
| Assets | 1.3 × 10−5 | −2.6 × 105*** | −0.5 × 10−5 | −3.6 × 10−4 | 8.9 × 10—6 | 6.0 × 10−6 | 2.7 × 10−5 | −10.2 *** | ||
| Extreme Value Distribution Predictor | ||||||||||
| Value-at-Risk 99 | 6.5 × 106 | −3 × 10−7 | 4 × 10−8 | −3 × 10−6 | −4 × 10−8 | 0.00 | 3.4 × 10−9 | 4.4 × 10−8 | 1.9 × 10−8 | 4.3 × 10−3 *** |
| N | 4850 | 8951 | 8372 | 8007 | 7601 | 12,335 | 7354 | 6299 | 7025 | 14,319 |
| Panel E | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.23 | 50 *** | −45.3 *** | −28 | 25 *** | 0.44 | 1.09 | 0.27 | −1.1 | 1.77 |
| Beta | 0.59 *** | 3.6 *** | 1.0 *** | 0.61 | 0.04 | 8.5 × 10−3 | 0.02 * | −0.01 | 1.3 × 10−3 | −1.2 |
| Fama–French Factor | ||||||||||
| Market Capitalization | −7 × 10−3 | −8.9 × 10−3 | 0.01 ** | 0.74 | 0.11 *** | 1.6 × 10−4 | 4.3 × 10−3 ** | −3 × 10−3 ** | −1.2 × 10−3 | −0.73 |
| Book-to-Market | −1.33 | −2.5 × 10−4 | 5.4 × 10−4 *** | −1.1 × 10−3 | −9.6 × 10−4 | 0.99 | 8.2 × 10−5 | −2.0 × 10−4 | −5.8 × 10−4 | −80 |
| EBIT | 1.7 × 10−4 | −8.3 × 10−4 | 1.1 × 10−3 ** | −0.01 | −1.1 × 103 *** | 5.7 × 10−6 | −1.8 × 10−4 *** | 3.2 × 10−4 *** | 4.8 × 10− 4*** | −3.5 *** |
| Assets | 4.2 × 10−5 ** | −4.1 × 10−5 *** | 6.8 × 10−5 | −2.3 × 10−5 | 5.2 × 10−6 | 1.8 × 10−5 ** | 4.8 × 10−5 ** | 0.42 ** | ||
| Extreme Value Distribution Factor | ||||||||||
| Value-at-Risk 99 | −2.6 × 10−5 | −4 × 10−7 | 4.5 × 10−7 | 1 × 10−6 | −5.2 × 10−7 | 0.00 | 6.8 × 10−8 | −1.1 × 10−6 ** | 3 × 10−9 | 2.6 × 10−3 |
| N | 4850 | 8951 | 8372 | 8007 | 7601 | 12,335 | 7354 | 6299 | 7025 | 14,319 |
| Panel A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 3.0 *** | 6.86 | 4.3 * | 1.54 ** | −8.7 | −3.6 | −0.93 | 3.18 | 5.77 | −4.7 |
| Beta | 3.3 × 10−3 ** | 0.04 | 0.05 | 4.4 × 10−3 | −0.04 | 0.18 | 0.03 | 0.04 | 0.08 | 0.09 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −9.9 × 10—3 * | 1.2 × 10−3 | 2.4 × 10−3 | 2.8 × 10−3 | 7.9 × 10−3 | −.02 | 6.7 × 10−3 | −5.9 × 10−5 | 1.2 × 10−3 | 0.07 * |
| Book-to-Market | −8.0 | 5.4 × 10−5 | −2.3 × 10−5 | 0.00 | −1.9 × 10−5 | −2.4 | −1.2 × 10−5 | 5.1 × 10−6 | 6.6 × 10−7 | 18.7 |
| Extreme Value Distribution Predictor | ||||||||||
| Expected Shortfall | −3.8 × 10−7 | −9 × 10−8 | −2.1 × 10−6 * | 0.00 | 7.4 × 10−8 | −1.8 × 10−6 *** | 7.1 × 10−7 | −4.6 × 10−7 | 4.7 × 10−8 | −1.5 × 10−6 *** |
| N | 16,940 | 8513 | 8055 | 7922 | 7074 | 16261 | 7011 | 6299 | 4779 | 7763 |
| R2 | 0.05 | 0.04 | 0.03 | 0.08 | 0.03 | 0.02 | 0.05 | 0.17 | 0.03 | 0.03 |
| Panel B | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 1.3 *** | 6.96 | 4.3 * | 1.54 ** | −8.7 | −6.7 | −0.92 | 3.17 | 5.75 | −4.7 *** |
| Beta | −0.07 *** | 0.03 | 0.04 | 3.7 × 10−3 | −0.04 | −0.02 | 0.04 | 0.03 | 0.05 | 0.09 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | 3.6 × 10−3 | −1.9 × 10−3 | 5.9 × 10−3 | 4.1 × 10−3 | 6.1 × 10−3 | −0.02 | 4.6 × 10−3 | 1.3 × 10−3 | 0.02 | 0.08 * |
| Book-to-Market | −28 | −4.2 × 10−5 | 1.1 × 10−5 | 2.2 × 10−5 | 2.9 × 10−3 | −28 | 6.3 × 10−4 | 1.3 × 10−4 | 4.7 × 10−4 | 19.1 |
| EBIT | −3.3 × 10−5 | 1.4 × 10−4 | −1.7 × 10−5 | 1.6 × 10−5 | −5.9 × 10−5 | 2.7 × 10−5 | 4.3 × 10−6 | −5.2 × 10−6 | −1.2 × 10−4 | 1 × 10−5 |
| Assets | 5.8 × 10−6 | −3.7 × 10−6 | −1.08 × 10−6 | −1.2 × 10−4 | −2.6 × 10−5 | −5.3 × 10−6 | −1.9 × 10−5 | −1.7 × 10−5 | ||
| Extreme Value Distribution Predictor | ||||||||||
| Expected Shortfall | 1 × 10−8 | 5.9 × 10−8 | −2.3 × 10—6 * | 3.1 × 10−8 | 1.1 × 10−7 | 5 × 10—6 *** | 5.9 × 10−7 | −4.4 × 10−7 | 7.3 × 10−8 | −1.1 × 10−6 *** |
| N | 4855 | 8451 | 8055 | 7922 | 074 | 10,776 | 7011 | 6299 | 4779 | 7763 |
| R2 | 0.05 | 0.04 | 0.03 | 0.08 | 0.03 | 0.03 | 0.05 | 0.17 | 0.03 | 0.03 |
| Panel C | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | 0.05 | 42 *** | −40 *** | −9.2 | 0.73 | 0.46 | −16.9 | 0.67 | −26 | 6.93 |
| Beta | −0.5*** | −0.88 *** | −0.35 *** | −11 *** | −0.07 * | −9 × 10−3 | −28 *** | −0.06 *** | −5.27 | 0.35 |
| Fama–French Predictor | ||||||||||
| Market Capitalization | −4.4 × 10−4 | −0.05 *** | 0.01 ** | −0.1 *** | 1 × 10−3 | −2.4 × 10−4 | −0.05 * | 3.7 × 10−3 ** | 0.91 | 0.07 |
| Book-to-Market | −27 | −1.4 × 10−4 | −7.8 × 10−4*** | 1.9 × 10—4 | 5 × 10−4 | −0.77 | 0.06 *** | −1.2 × 10−4 | −1.8 *** | 14.24 |
| EBIT | 1 × 10−3 *** | 4.3 × 10—4 | 1.5 × 10−3 ** | −1.3 × 10−3 *** | 8 × 10−5 | −5.6 × 10−6 | 4.7 × 10−4 *** | 7.8 × 10−4 *** | −1.8 *** | 5.65 *** |
| Assets | 2.9 × 10−5 | 3.6 × 10−5 *** | 8.1 × 10−6 | −4 × 10−6 | −2.5 × 10−3 *** | −8.2 × 10−7 | 0.06 *** | 6.04 *** | ||
| Extreme Value Distribution Predictor | ||||||||||
| Expected Shortfall | 9 × 10−8 | 2.1 × 10−8 | 1.5 × 10−6 *** | −1.6 × 10−6 *** | 4.3 × 10−7 *** | 0.00 | −3.2 × 10−6 | 6.1 × 10−7 *** | 2.9 × 104 *** | 2.1 × 10−4 |
| N | 4855 | 8451 | 8055 | 7922 | 7074 | 10,776 | 7011 | 6299 | 4779 | 7763 |
| Panel D | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Predictor | ||||||||||
| Market Return | −0.13 | 48 *** | −23 *** | −9.2 | 0.33 | 0.44 | −25 | 0.11 | −8.77 | 8.61 |
| Beta | 2.8 *** | −0.37 *** | 0.85 *** | −3.7 *** | 0.19 *** | −9.3 × 10−5 | −14 *** | −0.02 * | −1.14 | 0.07 |
| Fama–French Factor | ||||||||||
| Market Capitalization | −2.6 × 10−3 | −0.04 *** | 0.04 *** | −0.05 *** | −7.8 × 10−4 | −8.07 × 10−6 | −0.06 ** | 2.2 × 10−3 | 0.26 | −0.45 |
| Book-to-Market | −67 | 2.6 × 10−5 | 3.9 × 10−5 | −2.7 × 10−4 * | 3.6 × 10−6 | 0.07 | 0.03 ** | 2.4 × 10−4 | −2.6 *** | 15.56 |
| EBIT | −3.4 × 10−4 *** | −7.5 × 10−4 | −1.5 × 10−4 | −1 × 10−3 *** | −1.2 × 10−5 | 7.4 × 10−7 | 0.001 *** | 5.4 × 10−4 *** | −0.05 | 0.30 |
| Assets | 7.6 × 10−6 | 4.3 × 10−5 *** | 3 × 10−5 *** | 1.2 × 105 | −1.3 × 10−3 ** | −1.4 × 10−5 ** | 0.11 *** | 11.0 *** | ||
| Extreme Value Distribution Factor | ||||||||||
| Expected Shortfall | 1.9 × 10−7 | −1.4 × 10−8 | 8.5 × 10−7 ** | −1.7 × 10−8 | −1 × 10−8 | 0.00 | −3.5 × 10−5 *** | 6 × 10−8 | 3 × 10−5 | 0.00 |
| N | 4855 | 8451 | 8055 | 7922 | 7074 | 10,776 | 7011 | 6299 | 4779 | 7763 |
| Panel E | ||||||||||
| Independent Variable | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| CAPM Factor | ||||||||||
| Market Return | 0.7 | 56 *** | −40.5 *** | −9.2 | −0.66 | 0.41 | 21 | −0.86 | −0.02 | 6.97 |
| Beta | 3.2 *** | 0.92 *** | 3.5 *** | −0.34 *** | 0.18 *** | 7.3 × 10−3 | −11 *** | −1.4 × 10−3 | 6.84 | 4.79 |
| Fama–French Factor | ||||||||||
| Market Capitalization | −0.01 * | 3.9 × 10−3 *** | 0.05 *** | −0.04 *** | −1.8 × 10−3 | 4.1 × 10−4 | −0.03 | −2 × 10−3 | −0.33 | −2.46 |
| Book-to-Market | 20 | 2.9 × 10—4 | −3.3 × 10−4 ** | −5.7 × 10−4 *** | −4.3 × 10−4 | 0.81 | −3.4 × 10−3 | −3.3 × 10−4 * | −1.72 *** | 67.82 |
| EBIT | −2.7 × 10−4 * | −1.2 × 10−3 ** | 1.1 × 10−3 *** | −1 × 10−3 *** | −6.5 × 10−5 | 5.2 × 10−6 | 1.1 × 10−4 | 4.9 × 10−3 *** | 2.59 *** | 0.18 |
| Assets | −2.4 × 10−5 | −9.8 × 10−5 *** | 4.6 × 10−5 *** | 1.8 × 10−5 | 1.2 × 10−4 | 1.8 × 10−5 | 0.06 *** | 17.6 *** | ||
| Expected Value Distribution Factor | ||||||||||
| Expected Shortfall | −1.5 × 10−7 | −4.6 × 10−8 * | 7.6 × 10−8 | 1.1 × 10−6 ** | −6.5 × 10−8 | 0.00 | −3.2 × 10−6 | 3.9 × 10−7 | −1.3 × 10−5 | −4.4 × 10−4 |
| N | 4855 | 8451 | 8055 | 7922 | 7074 | 10776 | 7011 | 6299 | 4779 | 7763 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, R.; El-Chaarani, H.; Tao, Z. Predictors of Excess Return in a Green Energy Equity Portfolio: Market Risk, Market Return, Value-at-Risk and or Expected Shortfall? J. Risk Financial Manag. 2022, 15, 80. https://doi.org/10.3390/jrfm15020080
Abraham R, El-Chaarani H, Tao Z. Predictors of Excess Return in a Green Energy Equity Portfolio: Market Risk, Market Return, Value-at-Risk and or Expected Shortfall? Journal of Risk and Financial Management. 2022; 15(2):80. https://doi.org/10.3390/jrfm15020080
Chicago/Turabian StyleAbraham, Rebecca, Hani El-Chaarani, and Zhi Tao. 2022. "Predictors of Excess Return in a Green Energy Equity Portfolio: Market Risk, Market Return, Value-at-Risk and or Expected Shortfall?" Journal of Risk and Financial Management 15, no. 2: 80. https://doi.org/10.3390/jrfm15020080







