Dynamic and Static Volatility Interruptions: Evidence from the Korean Stock Markets †
Abstract
:1. Introduction
2. Literature Review
3. Volatility Interruptions in the Korean Stock Markets
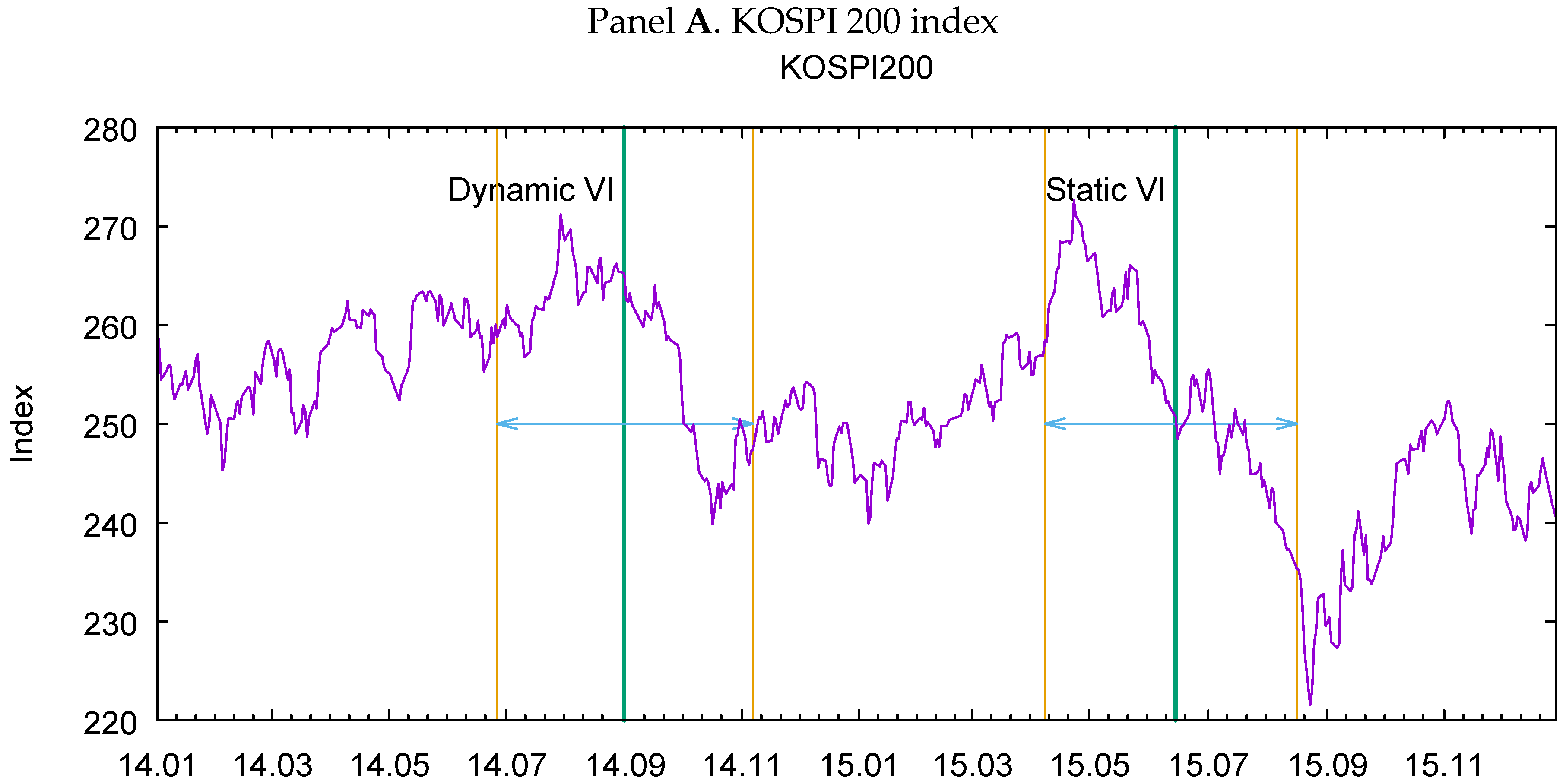
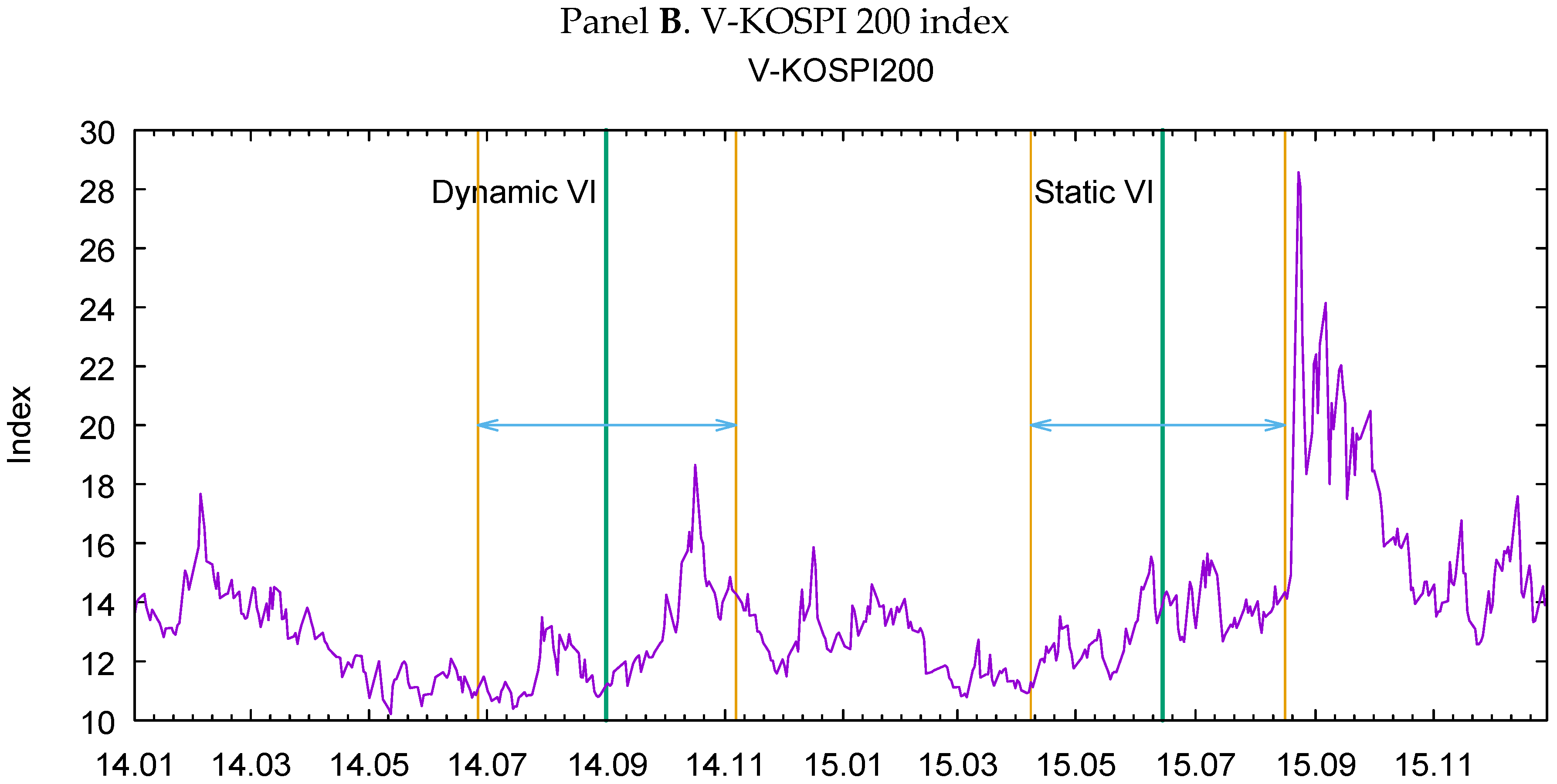
4. Sample Period and Data
5. Descriptive Statistics on VI Occurrences
6. Price-Stabilization Effect
6.1. Comparison of the Intraday Volatility before and after the VI Occurrence
6.2. Binomial Distribution Analysis
6.3. Panel-Data Analysis as a Robustness Check
7. Price-Discovery Effect
8. The Relationship of VIs with Price-Limit System
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | An RE trading mechanism is an integral part of a call auction mechanism. The ending time of the call auction is not fixed, but extended under certain circumstances for a brief randomly-chosen span of time less than or equal to a “maximum duration” such as 30 s or one minute (Eom et al. 2021). Deutsche Börse Cash Market (2020) states that the Deutsche Börse (DB) introduced a RE mechanism to avoid manipulative orders. Eom et al. (2021) show that the KRX RE mechanism helps to discourage spoofing at the open and close. |
| 2 | Vis are considered as implicit dynamic price-limit systems, compared to the explicit price-limit systems. |
| 3 | In other words, reversal in these two price changes is an indication of stabilization; see Section 6.2 and Section 6.3. |
| 4 | The KRX is comprised of two equity markets, KOSPI and KOSDAQ. KOSPI is the main board, while KOSDAQ is the new (or growth) market which provides funding mainly to IT-related, newly incorporated, and/or innovative small- and medium-sized enterprises (SMEs). |
| 5 | The LULD is an extreme form of static VI, specifically focusing on preventing the recurrence of cases similar to the Flash Crash in 2010. It applies a rolling price limit to individual stocks, using price bands (5 or 10%) calculated over the previous five minutes trading (Eom et al. 2021). |
| 6 | The introductions of these KRX rules were very different from the staggered introductions of the single-stock trading pauses (SSTP) or the Tick Size Pilot Program (TSPP) in the U.S. stock markets. These U.S. rules were applied differently to pre-determined groups of firms, so that test groups and a control group can be clearly identified. As a consequence, the SSTP and, especially, the TSSP have sparked research using the difference-in-difference (DID) analysis (e.g., Hautsch and Horvath 2019; Chung et al. 2020; Brogaard and Pan, forthcoming; among many others). In contrast, the KRX introduced the rules sequentially, but applied them to all firms unilaterally, so that we cannot conduct a DID analysis. However, the sequential introductions of the different aspects of VI do allow us to analyze the effects of the individual VI components (see footnote 13 in Section 6.2 for more discussion). |
| 7 | Eom et al. (2021) analyze the (conditional) RE mechanism on the KRX, a built-in component of the VI, and show that its price-discovery effect could be different depending on trading session. |
| 8 | Broadly defined circuit breakers theoretically lead to a reduction in transactional risk (Greenwald and Stein 1991); stabilization of derivatives markets (Chowdhry and Nanda 1998); and the magnet effect whereby price limits become self-fulling (Subrahmanyam 1994). Empirically, market-wide circuit breakers bring about the magnet effect and curtailed trading activity (Goldstein and Kavajecz 2004). Price limits cause delayed price discovery, volatility spillover, delayed trading, and the magnet effect (e.g., Kim and Rhee 1997; Cho et al. 2003; among many others). For a comprehensive survey, please see Sifat and Mohamad (2019). |
| 9 | A limitation of their analysis is that they treat all data equally for the analyses despite the fact that those trading venues are very different in parameters and characteristics. |
| 10 | During the two years, 2014 and 2015, there were two other changes in the KRX; the KRX decreased the transaction unit and adjusted the rules on basket trading on 2 June 2014, and revised the call auction system during the off-hours trading period on 17 November 2014. We avoided these dates in choosing our test periods, and thus precluded any possible confounding. |
| 11 | At the end of 2014, the KRW/USD rate was 1088.50 and the exchange rate did not change dramatically during our sample period. According to the exchange rate at the end of 2014, 1000 KRW was about 0.92 USD. |
| 12 | The variance-ratio test of Lo and MacKinlay (1988) could be another candidate to test the price-stabilizing effect of VIs: testing whether prices follow a random walk before and after each VI occurrence. However, our sample consists of too few observations over 30 (or 10) min to calculate a meaningful variance ratio during a given hour before and after the VI occurrence. Furthermore, the variance-ratio test is not appropriate in the high-frequency data since the intraday volatility is not stable (Andersen et al. 2001). |
| 13 | Since our interest is the effect of invocation of VIs on price stabilization, an event study focused on the VI invocations is the most natural way to address the problem. One might argue that we should use, as a control group, trades that occurred before the KRX implemented VIs. However, it is not possible to study the VIs, especially the potential execution price in our analyses, in the period before either dynamic or static VI was implemented. Within the extensive literature, there are only a handful of papers that use a DID approach (see footnote 6 for references). As mentioned in footnote 6, these papers are able to do this only because of the staggered introductions of the SSTP or the TSPP. Their setting is very unusual in providing natural control and test groups. To alleviate concerns about methodology, we also considered constructing the control group of stocks that experienced a large price change but not large enough to invoke the VI (e.g., 1.9%) before the adoption of each VI. However, we found that the number of observations is too small (e.g., 40 in 2014 and 76 in 2015) to implement a meaningful analysis by the DID approach. |
| 14 | If the last execution (last call auction) price fails to properly reflect the market demand, but the potential price is an accurate one, then the transaction should be completed at the potential price, in which the VIs are not required at all. |
| 15 | In untabulated results, we also test the price-stabilization effect of static VI using the last execution price instead of the last call auction price and find that the results are qualitatively the same. |
| 16 | A trinomial analysis could be considered. In this case, however, an additional assumption would be needed; no new information that might affect the price arrived during the VI session, for which “we cannot disentangle the effects of the [VI] session and the informational arrival, and in particular cannot assign probabilities to the three possibilities (continuation, reversal, no change). However, there is a natural distribution, 50/50, over two possibilities (continuation and reversal), allowing us to use the binomial distribution for the price-stabilization effect of [VI] trading mechanism” (see Eom et al. 2021). |
| 17 | The net price-stabilization effect of dynamic VI during the continuous session is higher in the pre-event period in 2015 than in the post-event period of 2014; since there was no change in the trading rules between those periods, this suggests that the increase reflects some change in market conditions rather than a change in trading rules. |
| 18 | The coefficients of control variables, trade size and firm size, are generally very small and statistically weak. The coefficient signs in dynamic VI are generally intuitive. However, those in static VI seems to be related to the difference of opinion among traders as explained in Section 5. |
| 19 | This methodology is slightly different from that of Corwin and Lipson (2000). They focus on explaining whether “ reflects some information not captured in ”. |
| 20 | Put differently, “ suggests that returns exhibit continuations from before to after [()] and suggests that returns exhibit reversals. Barclay and Hendershott (2003) provide an alternative interpretation of the slope coefficient. They note that if [()] is measured with error, the slope coefficient will be reduced. Thus, for , the magnitude of the coefficient provides an estimate of the signal-to-noise ratio for [()]” (see Chakrabarty et al. 2011). |
| 21 | The coefficients in step 2 should be interpreted in the context of those in step 1. Annex H in Guillaumie et al. (2020) provide a useful graphical explanation for the implications of our two-step regression model. |
| 22 | In a panel logit regression model, the marginal effect of each regressor is , where is the cumulative logistic distribution function. Since the mean of the logit distribution is zero, we set . Hence, , and the marginal effect of each regressor is 0.25. Substitute 0.25 for each coefficient (see Greene 2000, p. 817). |
| 23 | Panel B of Table 1 shows that static VIs were much more frequently invoked than dynamic VIs in the post-event period in 2015; for example, static VIs were invoked five times more than dynamic VIs in terms of the total number of VI occurrences. Taking this into account, we expect that the actual contribution of static VI could be somewhat notable. |
References
- Abad, David, and Roberto Pascual. 2010. Switching to a temporary call auction in times of high uncertainty. Journal of Financial Research 33: 45–75. [Google Scholar] [CrossRef]
- Alderighi, Stefano, Pedro Gurrola-Perez, Kaitao Lin, and Bill Speth. 2021. Circuit Breakers and Other Market Safeguards. London: World Federation of Exchanges. [Google Scholar]
- Andersen, Torben, Tim Bollerslev, and Ashish Das. 2001. Variance-ratio statistics and high-frequency data: Testing for changes in intraday volatility patterns. Journal of Finance 56: 305–27. [Google Scholar] [CrossRef]
- Barclay, Michael J., and Terrence Hendershott. 2003. Price discovery and trading after hours. Review of Financial Studies 16: 1041–73. [Google Scholar] [CrossRef]
- Brady, Nicholas F. 1988. Report of the Presidential Task Force on Market Mechanisms; Washington, DC: Government Printing Office.
- Brogaard, Jonathan, and Jing Pan. Forthcoming. Dark pool trading and information acquisition. Review of Financial Studies.
- Brugler, James, Oliver Linton, Joseph Noss, and Lucas Pedace. 2018. The Cross-Sectional Spillovers of Single Stock Circuit Breakers. London: Bank of England. [Google Scholar]
- Chakrabarty, Bidisha, Shane A. Corwin, and Marios A. Panayides. 2011. When a halt is not a halt: An analysis of off-NYSE trading during NYSE market closures. Journal of Financial Intermediation 20: 361–86. [Google Scholar] [CrossRef]
- Cho, David D., Jeffrey Russell, George C. Tiao, and Ruey Tsay. 2003. The magnet effect of price limits: Evidence from high-frequency data on Taiwan Stock Exchange. Journal of Empirical Finance 10: 133–68. [Google Scholar] [CrossRef] [Green Version]
- Chowdhry, Bhagwan, and Vikram Nanda. 1998. Leverage and market stability: The role of margin rules and price limits. Journal of Business 71: 179–210. [Google Scholar] [CrossRef]
- Chung, Kee H., Albert J. Lee, and Dominik Rösch. 2020. Tick size, liquidity for small and large orders, and price informativeness: Evidence from the tick size pilot program. Journal of Financial Economics 136: 879–99. [Google Scholar] [CrossRef]
- Corwin, Shane A., and Marc L. Lipson. 2000. Order flow and liquidity around NYSE trading halts. Journal of Finance 55: 1771–801. [Google Scholar] [CrossRef]
- Deutsche Börse Cash Market. 2020. Market Model for the Trading Venue Xetra®: T7 Release 8.1. Frankfurt am Main: Deutsche Börse. [Google Scholar]
- Diether, Karl B., Christopher J. Malloy, and Anna Scherbina. 2002. Difference of opinion and the cross section of stock returns. Journal of Finance 57: 2113–41. [Google Scholar] [CrossRef]
- Eom, Kyong Shik, Jangkoo Kang, and Kyung Yoon Kwon. 2017. PIN, adjusted PIN, and PSOS: Difference of opinion in the Korean stock market. Asia-Pacific Journal of Financial Studies 46: 463–90. [Google Scholar] [CrossRef]
- Eom, Kyong Shik, Jinho Ok, and Jong-Ho Park. 2007. Pre-trade transparency and market quality. Journal of Financial Markets 10: 319–41. [Google Scholar] [CrossRef]
- Eom, Kyong Shik, Kyung Yoon Kwon, and Jong-Ho Park. 2021. Effectiveness of the conditional random-end trading mechanism on the Korea Exchange: Normal trade and Option Shock. Journal of Futures Markets 41: 1545–68. [Google Scholar] [CrossRef]
- Foucault, Thierry, Ohad Kadan, and Eugene Kandel. 2005. Limit order book as a market for liquidity. Review of Financial Studies 18: 1171–217. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, Michael A., and Kenneth A. Kavajecz. 2004. Trading strategies during circuit breakers and extreme market movements. Journal of Financial Markets 7: 301–33. [Google Scholar] [CrossRef]
- Greene, William H. 2000. Econometric Analysis, 4th ed. Upper Saddle River: Prentice Hall. [Google Scholar]
- Greenwald, Bruce C., and Jeremy C. Stein. 1991. Transactional risk, market crashes, and the role of circuit breakers. Journal of Business 64: 443–62. [Google Scholar] [CrossRef]
- Guillaumie, Cyrille, Giuseppe Loiacono, Christian Winkler, and Steffen Kern. 2020. Market Impacts of Circuit Breakers: Evidence from EU Trading Venues. Paris: ESMA. [Google Scholar]
- Hautsch, Nikolaus, and Akos Horvath. 2019. How effective are trading pauses? Journal of Financial Economics 131: 378–403. [Google Scholar] [CrossRef] [Green Version]
- Kandel, Eugene, Barbara Rindi, and Luisella Bosetti. 2012. The effect of a closing call auction on market quality and trading strategies. Journal of Financial Intermediation 21: 23–49. [Google Scholar] [CrossRef]
- Kim, In Joon, Tong Suk Kim, and Won Tark Doh. 1999. The relationship between price changes and volume: The impact of market microstructure. Journal of Korean Financial Studies 24: 273–99. (In Korean). [Google Scholar]
- Kim, Kenneth A., and S. Ghon Rhee. 1997. Price limit performance: Evidence from Tokyo Stock Exchange. Journal of Finance 52: 885–901. [Google Scholar] [CrossRef]
- Lei, Adrian C. H., Xiaorong Ma, and Martin H. Y. Yick. 2020. Callable bull/bear contracts, call auction sessions, and price manipulations: Evidence from Hong Kong. Journal of Futures Markets 40: 1731–50. [Google Scholar] [CrossRef]
- Lo, Andrew W., and A. Craig MacKinlay. 1988. Stock market prices do not follow random walks: Evidence from a simple specification test. Review of Financial Studies 1: 41–66. [Google Scholar] [CrossRef]
- Sifat, Imtiaz Mohammad, and Azhar Mohamad. 2019. Circuit breakers as market stability levers: A survey of research, praxis, and challenges. International Journal of Finance & Economics 24: 1130–69. [Google Scholar]
- Subrahmanyam, Avanidhar. 1994. Circuit breakers and market volatility: A theoretical perspective. Journal of Finance 49: 237–54. [Google Scholar] [CrossRef]
- The Government Office for Science. 2012. Foresight: The Future of Computer Trading in Financial Markets; London: The Government Office for Science.
- Zimmermann, Kai. 2013. Price Discovery in European Volatility Interruptions. Frankfurt am Main: Goethe University Frankfurt am Main. [Google Scholar]

| 2014 | 2015 | |||
|---|---|---|---|---|
| Post | Pre | Post | ||
| Dynamic | Dynamic | Dynamic | Static | |
| Panel A. Descriptive statistics of stocks with and without VI occurrences | ||||
| Stocks with VI occurrences | ||||
| Number of stocks | 435 | 525 | 550 | 1119 |
| 375,230.7 | 528,551.2 | 388,946.3 | 740,847.3 | |
| 1473.7 | 3879.7 | 4467.0 | 5893.0 | |
| 243,668.5 | 337,647.3 | 586,870.7 | 450,687.2 | |
| 24,570.5 | 24,569.9 | 38,497.0 | 32,494.7 | |
| 5.0282 | 5.9514 | 6.2306 | 6.2951 | |
| 3.1512 | 3.8717 | 3.9710 | 4.1536 | |
| Stocks without VI occurrences | ||||
| Number of stocks | 1241 | 1160 | 1135 | 566 |
| 421,884.7 | 580,600.0 | 650,133.4 | 216,985.5 | |
| 4641.6 | 7042.2 | 6144.9 | 5012.4 | |
| 933,070.9 | 1,052,214.8 | 923,792.8 | 1,531,739.7 | |
| 31,892.9 | 36,415.6 | 32,190.6 | 37,717.4 | |
| 4.2295 | 4.7429 | 5.0159 | 3.6671 | |
| 2.7551 | 3.0821 | 3.2525 | 2.1692 | |
| Panel B. VI occurrences | ||||
| Number of stocks with at least one VI occurrence | 435 | 525 | 550 | 1119 |
| Total number of VI occurrences | 1068 | 958 | 1113 | 5796 |
| Number of VI occurrences per stock | 0.64 | 0.57 | 0.66 | 3.44 |
| Panel C. Total number of VI occurrences based on the last execution price prior to the occurrence | ||||
| Price (KRW) | ||||
| <1000 | 155 | 53 | 66 | 422 |
| 1000≤ and <5000 | 568 | 452 | 438 | 2043 |
| 5000≤ and <10,000 | 156 | 188 | 214 | 1034 |
| 10,000≤ and <50,000 | 141 | 189 | 234 | 1680 |
| 50,000≤ and <100,000 | 16 | 39 | 58 | 271 |
| 100,000≤ | 32 | 37 | 103 | 346 |
| No. of Observations | Before VI | After VI | Difference (p-Value) | |
|---|---|---|---|---|
| Dynamic VI: Post-event in 2014 | 193 | 0.0756 | 0.0501 | 0.0255 *** (0.0000) |
| Dynamic VI: Pre-event in 2015 | 162 | 0.0833 | 0.0542 | 0.0291 *** (0.0000) |
| Dynamic VI: Post-event in 2015 | 258 | 0.0936 | 0.0588 | 0.0348 *** (0.0000) |
| Static VI: Post-event in 2015 | 2852 | 0.0855 | 0.0725 | 0.0130 *** (0.0000) |
| No. of Unchanged Prices (A) | No. of Reversals of Price Changes (B) | No. of Continuations of Price Changes (C) | Total No. of VI Occurrences (D) | Stabilization Ratio (%) (E) | Price-Stabilization Effect (%) a (F) | Price-Continuation Effect (%) b (G) | Net Price-Stabilization Effect (%) c (H) | |
|---|---|---|---|---|---|---|---|---|
| Panel A. Dynamic VI: Post-event period in 2014 | ||||||||
| Continuous session | 85 | 699 | 136 | 920 | 83.7 *** | 44.42 | 36.35 | 31.26 |
| Closing call auction | 66 | 65 | 17 | 148 | 79.3 *** | 31.97 | 17.96 | 21.62 |
| Total | 151 | 764 | 153 | 1068 | 83.3 *** | 43.36 | 34.31 | 30.40 |
| Panel B. Dynamic VI: Pre-event period in 2015 | ||||||||
| Continuous session | 38 | 715 | 85 | 838 | 89.3 *** | 53.65 | 43.36 | 43.34 |
| Closing call auction | 44 | 67 | 9 | 120 | 88.2 *** | 27.98 | 10.22 | 23.45 |
| Total | 82 | 782 | 94 | 958 | 89.2 *** | 51.54 | 40.19 | 41.62 |
| Panel C. Dynamic VI: Post-event period in 2015 | ||||||||
| Continuous session | 61 | 825 | 110 | 996 | 88.2 *** | 53.18 | 56.54 | 40.27 |
| Closing call auction | 61 | 41 | 15 | 117 | 73.2 *** | 26.25 | 17.73 | 14.47 |
| Total | 122 | 866 | 125 | 1113 | 87.3 *** | 51.91 | 51.88 | 38.82 |
| Panel D. Static VI: Post-event period in 2015 | ||||||||
| Opening call auction | 26 | 86 | 89 | 201 | 49.1 | 30.90 | 15.88 | 7.11 |
| Continuous session | 849 | 2813 | 1842 | 5504 | 60.4 *** | 11.10 | 11.94 | 1.98 |
| Closing call auction | 45 | 26 | 20 | 91 | 56.5 | 16.21 | 7.30 | 5.99 |
| Total | 920 | 2925 | 1951 | 5796 | 60.0 *** | 11.73 | 12.08 | 2.21 |
| Adj | ||||
|---|---|---|---|---|
| Panel A. Post-event period in 2014: Dynamic VI | ||||
| 0.0118 (1.39) | −0.2851 *** (−20.62) | 0.0008 *** (2.94) | −0.0015 ** (−1.97) | 0.28 |
| Panel B. Pre-event period in 2015: Dynamic VI | ||||
| −0.0113 (−1.41) | −0.4182 *** (−30.42) | 0.0003 (1.19) | 0.0001 (0.19) | 0.49 |
| Panel C. Post-event period in 2015: Dynamic VI | ||||
| −0.0083 (−1.16) | −0.3433 *** (−22.28) | 0.0003 (1.17) | −0.0001 (−0.28) | 0.31 |
| Panel D. Post-event period in 2015: Static VI | ||||
| −0.0054 * (−1.77) | −0.0460 *** (−16.18) | −0.0008 *** (−5.71) | 0.0007 *** (3.38) | 0.04 |
| Adj | No. of Observations | Prob. > F | |||
|---|---|---|---|---|---|
| Panel A. Post-event period in 2014: Dynamic VI | |||||
| Step 1 | −0.0059 *** (−3.42) | 0.4392 *** (9.40) | 0.1728 | 419 | <2.2 × 10−16 |
| Step 2 | −0.0068 *** (−4.65) | 1.3508 *** (32.36) | 0.7145 | 419 | <2.2 × 10−16 |
| Panel B. Pre-event period in 2015: Dynamic VI | |||||
| Step 1 | 0.0049 ** (2.91) | 0.4361 *** (12.02) | 0.2433 | 447 | <2.2 × 10−16 |
| Step 2 | −0.0015 (−1.02) | 0.9280 *** (20.79) | 0.4915 | 447 | <2.2 × 10−16 |
| Panel C. Post-event period in 2015: Dynamic VI | |||||
| Step 1 | −0.0044 ** (−3.19) | 0.4128 *** (10.93) | 0.2037 | 464 | <2.2 × 10−16 |
| Step 2 | −0.0062 *** (−5.36) | 1.0627 *** (26.82) | 0.6081 | 464 | <2.2 × 10−16 |
| Panel D. Post-event period in 2015: Static VI | |||||
| Step 1 | 0.0141 *** (26.52) | −0.3087 *** (−39.01) | 0.2548 | 4449 | <2.2 × 10−16 |
| Step 2 | 0.0266 *** (19.65) | 0.8984 *** (23.05) | 0.1065 | 4449 | <2.2 × 10−16 |
| Variable | Upper Price-Limit Hits | Lower Price-Limit Hits | ||
|---|---|---|---|---|
| Coefficient | z | Coefficient | z | |
| Panel A. Pre-event period in 2015 | ||||
| 0.4758 ** | 2.45 | 0.2319 | 0.68 | |
| 0.0425 | 0.25 | 0.0323 | 0.11 | |
| −3.1103 *** | −14.77 | 3.7305 *** | 9.82 | |
| 30.1273 *** | 35.41 | 29.3607 *** | 17.03 | |
| 4.6534 *** | 9.22 | −0.1689 | −0.32 | |
| Panel B. Post-event period in 2015 | ||||
| 1.6965 *** | 3.36 | 0.3484 | 0.08 | |
| −0.0071 | −0.02 | 2.9220 ** | 2.33 | |
| 2.1976 *** | 8.74 | −1.0825 | −1.58 | |
| −1.4126 *** | −6.69 | 1.6889 ** | 2.30 | |
| −2.9877 *** | −3.80 | 4.0696 * | 1.87 | |
| 16.9507 *** | 6.81 | 5.1778 | 0.65 | |
| 2.4923 *** | 3.27 | 3.8874 | 1.62 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eom, K.S.; Kwon, K.Y.; La, S.C.; Park, J.-H. Dynamic and Static Volatility Interruptions: Evidence from the Korean Stock Markets. J. Risk Financial Manag. 2022, 15, 105. https://doi.org/10.3390/jrfm15030105
Eom KS, Kwon KY, La SC, Park J-H. Dynamic and Static Volatility Interruptions: Evidence from the Korean Stock Markets. Journal of Risk and Financial Management. 2022; 15(3):105. https://doi.org/10.3390/jrfm15030105
Chicago/Turabian StyleEom, Kyong Shik, Kyung Yoon Kwon, Sung Chae La, and Jong-Ho Park. 2022. "Dynamic and Static Volatility Interruptions: Evidence from the Korean Stock Markets" Journal of Risk and Financial Management 15, no. 3: 105. https://doi.org/10.3390/jrfm15030105
APA StyleEom, K. S., Kwon, K. Y., La, S. C., & Park, J. -H. (2022). Dynamic and Static Volatility Interruptions: Evidence from the Korean Stock Markets. Journal of Risk and Financial Management, 15(3), 105. https://doi.org/10.3390/jrfm15030105






