An Early Warning System for Currency Crises in Emerging Countries
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Sample Selection
3.2. Variables under Study and Hypotheses Development
3.3. The EWS Model
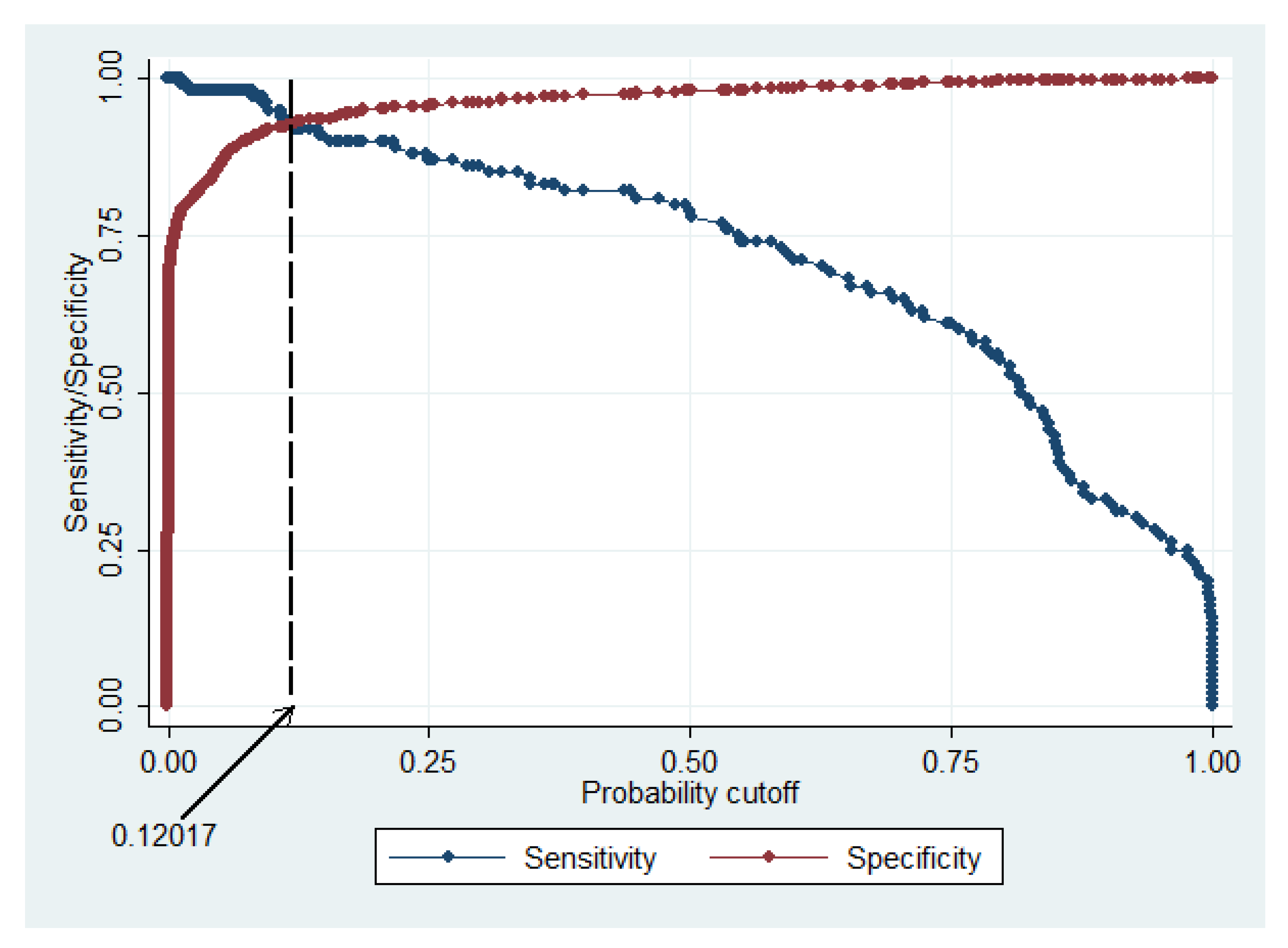
3.4. Determination of the Optimal Cut-Off Threshold
- A is the number of good signals for a correctly signaled crisis,
- B is the number of false alarms, when there is a signal, but no crisis occurs
- C is the number of missing alarms, when there is a signal, and a crisis occurs
- D is the number of no signals and no crisis occurs
4. Results and Discussion
4.1. Empirical Results
Descriptive Statistics
4.2. Regression Results
4.3. Impact of Macroeconomics Variables
4.4. Impact of Institutional Variables
4.5. Selection of the Optimal Cut-Off Threshold and Forecasting Crises
4.5.1. Forecasting the Currency Crisis
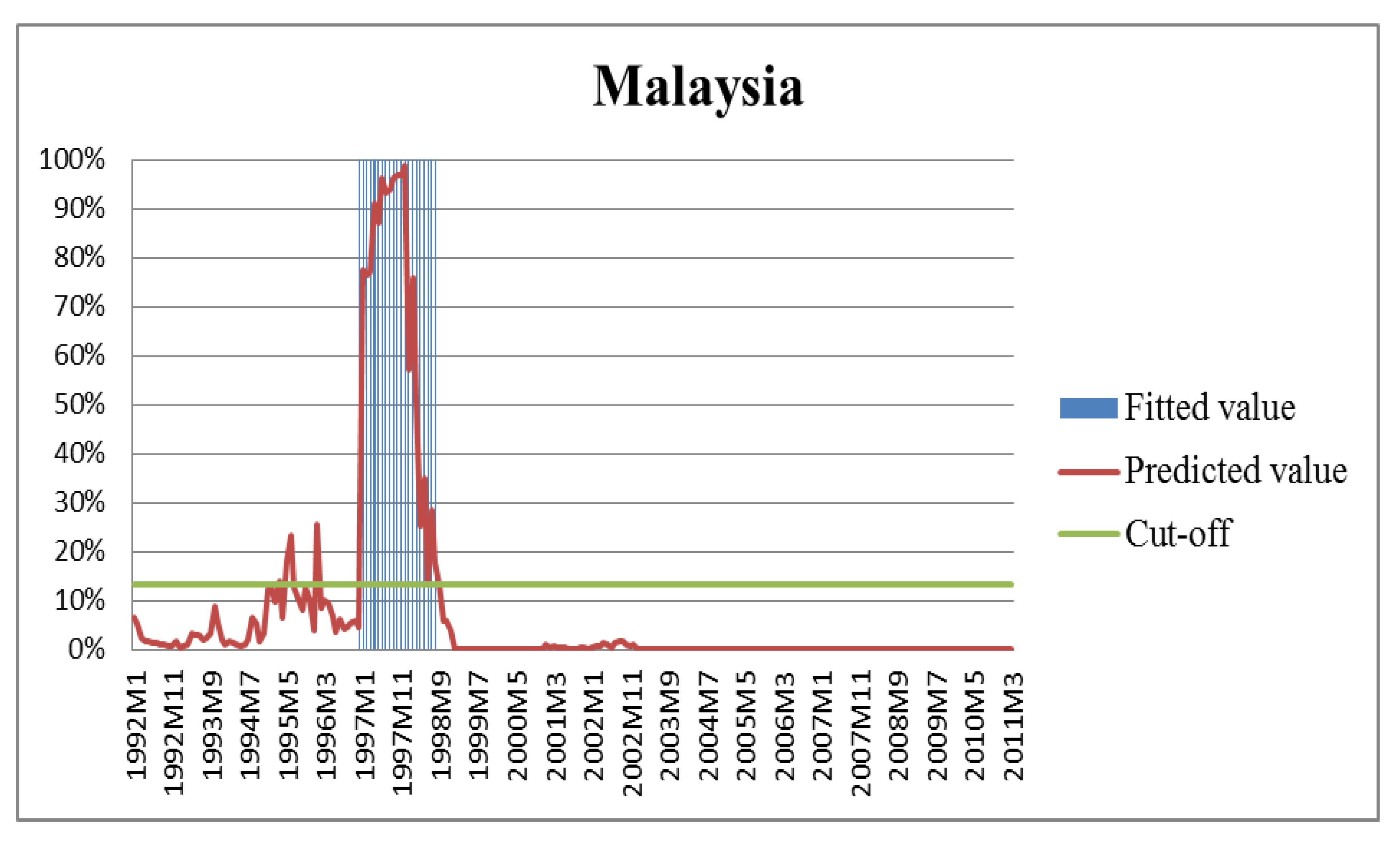
4.5.2. Asian Financial Crisis 1997–1998
4.5.3. Turkey’s Crisis in 1994 and 2001
5. Robustness Checks of the EWS Model
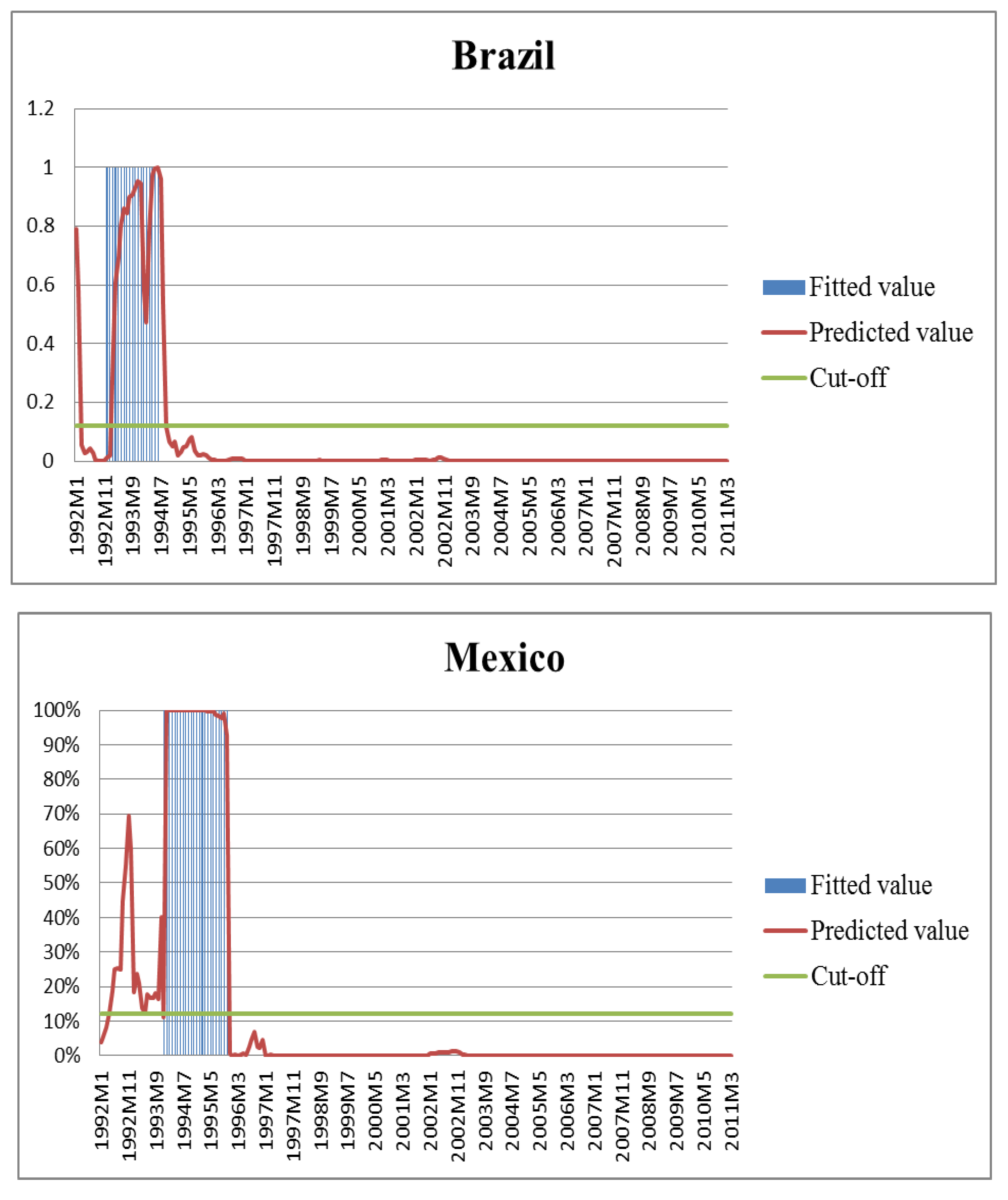
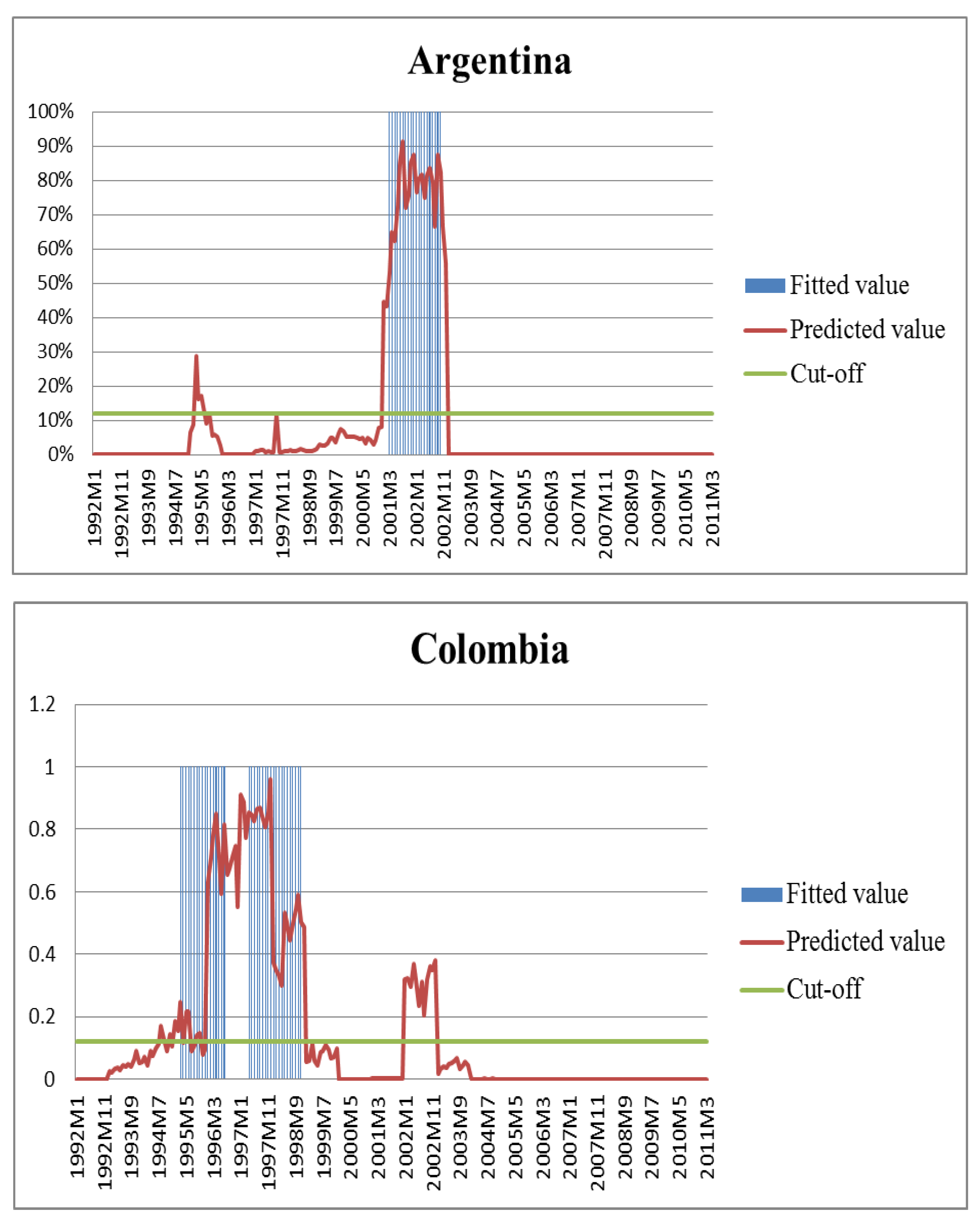
5.1. Out-of-Sample Test on Latin America
5.2. Selection of the Optimal Cut-Off Threshold and Predict Crises in Latin America
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | We thank one anonymous reviewer for raising this point. |
References
- Ahsan, Ahsan. 2011. Financial crisis and central bank independence and governance (CBIG) in the Asia Pacific. Corporate Ownership & Control 8: 313–35. [Google Scholar] [CrossRef]
- Ari, Ali. 2012. Early warning systems for currency crises: The Turkish case. Economic Systems 36: 391–410. [Google Scholar] [CrossRef][Green Version]
- Basel Committee on Banking Supervision. 2005. Compliance and the Compliance Function in Banks. Basel: Bank for International Settlements. [Google Scholar]
- Berg, Andrew, and Catherine Pattillo. 1999a. Predicting currency crises: The indicators approach and an alternative. Journal of International Money and Finance 18: 561–86. [Google Scholar] [CrossRef]
- Berg, Andrew, and Catherine Pattillo. 1999b. What caused the Asian crises: An early warning system approach. Economic Notes 28: 285–334. [Google Scholar] [CrossRef]
- Berg, Andrew, and Catherine Pattillo. 1999c. Are currency crises predictable? A test. IMF Staff Papers 46: 107–38. [Google Scholar] [CrossRef]
- Berg, A., E. Borensztein, and C. Pattillo. 2005. Assessing early warning systems: How have they worked in practice? IMF Staff Papers 52: 462–502. [Google Scholar] [CrossRef]
- Boonman, Tjeerd M., Jan P. A. M. Jacobs, Gerard H. Kuper, and Alberto Romero. 2019. Early warning systems for currency crises with real-time data. Open Economies Review 30: 813–35. [Google Scholar] [CrossRef]
- Burkart, Oliver, and Virginie Couder. 2002. Leading indicators of currency crises for emerging countries. Emerging Markets Review 3: 107–33. [Google Scholar] [CrossRef]
- Bussiere, Matthieu, and Marcel Fratzscher. 2006. Towards a new early warning system of financial crises. Journal of International Money and Finance 25: 953–73. [Google Scholar] [CrossRef]
- Candelon, Bertrand, Elena-Ivona Dumitrescu, and Christophe Hurlin. 2012. How to evaluate an early-warning system: Toward a unified statistical framework for assessing financial crises forecasting methods. IMF Economic Review 60: 75–113. [Google Scholar] [CrossRef]
- Comelli, Fabio. 2014. Comparing parametric and non-parametric early warning systems for currency crises in emerging market economies. Review of International Economics 22: 700–21. [Google Scholar] [CrossRef]
- Demirgüç-Kunt, Asli, and Enrica Detragiache. 1998. The determinants of banking crises in developing and developed countries. IMF Staff Papers 45: 81–109. [Google Scholar] [CrossRef]
- Duca, Marco Lo, and Tuomas A. Peltonenn. 2013. Assessing systemic risks and predicting systemic events. Journal of Banking & Finance 37: 2183–95. [Google Scholar] [CrossRef]
- Edison, Hali J. 2003. Do indicators of financial crises work? An evaluation of an early warning system. International Journal of Finance & Economics 8: 11–53. [Google Scholar] [CrossRef]
- Eichengreen, Barry, Andrew K. Rose, and Charles Wyplosz. 1995. Exchange market mayhem: The antecedents and aftermath of speculative attacks. Economic Policy 10: 249–312. [Google Scholar] [CrossRef]
- Eichengreen, Barry, Andrew K. Rose, and Charles Wyplosz. 1996. Contagious Currency Crises. No. w5681. Cambridge: Massachusetts National Bureau of Economic Research. [Google Scholar]
- Esquivel, Gerardo, and Felipe Larrain. 1998. Explaining Currency Crises. Development Discussion Paper No. 666 November 1998. Cambridge: Cambridge: Harvard Institute for International Development, pp. 1–36. [Google Scholar] [CrossRef]
- Flood, Robert P., and Peter M. Garber. 1984. Collapsing exchange-rate regimes: Some linear examples. Journal of International Economics 17: 1–13. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A., and Andrew K. Rose. 1996. Currency crashes in emerging markets: An empirical treatment. Journal of International Economics 41: 351–66. [Google Scholar] [CrossRef]
- Frankel, Jeffrey, and George Saravelos. 2012. Can leading indicators assess country vulnerability? Evidence from the 2008–09 global financial crisis. Journal of International Economics 87: 216–31. [Google Scholar] [CrossRef]
- Glick, Reuven, and Ramon Moreno. 1999. Money and Credit, Competitiveness, and Currency Crises in Asia and Latin America. San Francisco: Center for Pacific Basin Monetary and Economic Studies, Economic Research Department, Federal Reserve Bank of San Francisco. [Google Scholar]
- Gujarati, Damodar N. 2003. Basic Econometrics, 4th ed. New York: McGraw-Hill. [Google Scholar]
- Holopainen, Markus, and Peter Sarli. 2017. Toward robust early-warning models: A horse race, ensembles and model uncertainty. Quantitative Finance 17: 1933–1963. [Google Scholar] [CrossRef]
- Kamin, Steven B., John W. Schindler, and Shawna L. Samuel. 2001. The Contribution of Domestic and External Factors to Emerging Market Devaluation Crises: An Early Warning Systems Approach. FRB International Finance Discussion Paper. No. 571. Washington: FRB International Finance, pp. 1–49. [Google Scholar]
- Kaminsky, Graciela L., and Carmen M. Reinhart. 1999. The twin crises: The causes of banking and balance-of-payments problems. American Economic Review 89: 473–500. [Google Scholar] [CrossRef]
- Kaminsky, Graciela, Saul Lizondo, and Carmen M. Reinhart. 1998. Leading indicators of currency crises. IMF Staff Papers 45: 1–48. [Google Scholar] [CrossRef]
- Krugman, Paul. 1979. A model of balance-of-payments crises. Journal of Money, Credit and Banking 11: 311–25. [Google Scholar] [CrossRef]
- Kumar, Mohan, Uma Moorthy, and William Perraudin. 2003. Predicting emerging market currency crashes. Journal of Empirical Finance 10: 427–54. [Google Scholar] [CrossRef][Green Version]
- Lambert, Jerome, and Ilya Lipkovich. 2008. A macro for getting more out of your ROC curve. In San Antonio, Texas. In SAS Global Forum, Paper. San Diego: SAS Global, vol. 231. [Google Scholar]
- Leblang, David, and Shanker Satyanath. 2008. Politically generated uncertainty and currency crises: Theory, tests, and forecasts. Journal of International Money and Finance 27: 480–97. [Google Scholar] [CrossRef]
- Li, Wei-Xuan, Clara Chia-Sheng Chen, and Joseph J. French. 2015. Toward an early warning system of financial crises: What can index futures and options tell us? The Quarterly Review of Economics and Finance 55: 87–99. [Google Scholar] [CrossRef]
- Obstfeld, Maurice. 1995. The logic of currency crises. In Monetary and Fiscal Policy in an Integrated Europe. Berlin/Heidelberg: Springer. [Google Scholar]
- Obstfeld, Maurice. 1996. Models of currency crises with self-fulfilling features. European Economic Review 40: 1037–47. [Google Scholar] [CrossRef]
- Peltonen, Tuomas A. 2006. Are Emerging Market Currency Crises Predictable?—A Test. No. 571. Frankfurt am Main: European Central Bank. [Google Scholar]
- Reagle, Derrick, and Dominick Salvatore. 2005. Robustness of forecasting financial crises in emerging market economies with data revisions—A note. Open Economies Review 16: 209–16. [Google Scholar] [CrossRef]
- Sevim, Cuneyt, Asil Oztekin, Ozkan Bali, Serkan Gumus, and Erkam Guresen. 2014. Developing an early warning system to predict currency crises. European Journal of Operational Research 237: 1095–104. [Google Scholar] [CrossRef]
- Shimpalee, Pattama L., and Janice Boucher Breuer. 2006. Currency crises and institutions. Journal of International Money and Finance 25: 125–45. [Google Scholar] [CrossRef]





| Table Panel A: Summary of descriptive statistics of the entire period, 1992–2011 | |||||
| Variables | Obs | Mean | Std. Dev. | Min | Max |
| RESERVE | 1155 | −17.19 | 29.85 | −374.54 | 53.33 |
| EXPORT | 1155 | 13.14 | 22.28 | −68.43 | 371.37 |
| IMPORT | 1155 | 12.59 | 21.41 | −48 | 79.51 |
| RER | 1155 | 32.51 | 86.20 | −44.87 | 837.01 |
| CAGDP | 1155 | 1.33 | 6.24 | −9.73 | 16.85 |
| STDRES | 1155 | 63.36 | 46.70 | 9.05 | 236.20 |
| GDP | 1155 | 4.55 | 4.25 | −13.13 | 10.00 |
| GOVERNMENT | 1155 | 8.24 | 1.60 | 5.08 | 11.00 |
| CORRUPTION | 1155 | 2.52 | 0.80 | 1.00 | 4.00 |
| LAW | 1155 | 3.59 | 0.98 | 2.00 | 5.00 |
| EXTERNAL | 1155 | 3.40 | 1.22 | 1.42 | 5.00 |
| INTERNAL | 1155 | 8.64 | 1.78 | 4.08 | 12.00 |
| Table Panel B: Summary of descriptive statistics for the tranquil period, 1992–2011 | |||||
| Variables | Obs | Mean | Std. Dev. | Min | Max |
| RESERVE | 1033 | −18.89 | 29.47 | −374.54 | 32.96 |
| EXPORT | 1033 | 12.26 | 21.60 | −68.43 | 371.37 |
| IMPORT | 1033 | 12.64 | 21.12 | −46.11 | 79.39 |
| RER | 1033 | 23.05 | 65.79 | −44.87 | 482.29 |
| CAGDP | 1033 | 1.57 | 6.23 | −9.73 | 16.85 |
| STDRES | 1033 | 56.61 | 40.61 | 9.05 | 236.2 |
| GDP | 1033 | 4.95 | 3.63 | −13.13 | 10.00 |
| GOVERNMENT | 1033 | 8.18 | 1.58 | 5.08 | 11.00 |
| CORRUPTION | 1033 | 2.46 | 0.78 | 1.00 | 4.00 |
| LAW | 1033 | 3.52 | 0.98 | 2.00 | 5.00 |
| EXTERNAL | 1033 | 3.35 | 1.21 | 1.42 | 5.00 |
| INTERNAL | 1033 | 8.52 | 1.70 | 4.08 | 12.00 |
| Table Panel C: Summary of descriptive statistics for the crisis period, 1992–2011 | |||||
| Variables | Obs | Mean | Std. Dev. | Min | Max |
| RESERVE | 122 | −2.81 | 29.24 | −95.61 | 53.33 |
| EXPORT | 122 | 20.62 | 26.26 | −15.58 | 105.8 |
| IMPORT | 122 | 12.15 | 23.88 | −48 | 79.51 |
| RER | 122 | 112.63 | 163.44 | −2.82 | 837.01 |
| CAGDP | 122 | −0.77 | 5.91 | −8.07 | 13.20 |
| STDRES | 122 | 120.47 | 55.29 | 32.28 | 236.20 |
| GDP | 122 | 1.12 | 6.83 | −13.13 | 10.00 |
| GOVERNMENT | 122 | 8.76 | 1.66 | 5.08 | 10.75 |
| CORRUPTION | 122 | 3.04 | .79 | 1.25 | 4.00 |
| LAW | 122 | 4.24 | .68 | 2.50 | 5.00 |
| EXTERNAL | 122 | 3.88 | 1.21 | 2.00 | 5.00 |
| INTERNAL | 122 | 9.59 | 2.15 | 5.58 | 12.00 |
| Variables | VIF | SQRT VIF | Tolerance | R-Square |
|---|---|---|---|---|
| RESERVE | 1.24 | 1.11 | 0.8074 | 0.1926 |
| EXPORT | 1.42 | 1.19 | 0.7023 | 0.2977 |
| IMPORT | 1.83 | 1.35 | 0.5471 | 0.4529 |
| RER | 1.70 | 1.30 | 0.5899 | 0.4101 |
| CAGDP | 1.55 | 1.25 | 0.6447 | 0.3553 |
| STDRES | 1.96 | 1.40 | 0.5095 | 0.4905 |
| GDP | 1.76 | 1.33 | 0.5666 | 0.4334 |
| GOVERNMENT | 1.14 | 1.07 | 0.8759 | 0.1241 |
| CORRUPTION | 1.95 | 1.39 | 0.5140 | 0.4860 |
| LAW | 2.44 | 1.56 | 0.4100 | 0.5900 |
| EXTERNAL | 1.42 | 1.19 | 0.7059 | 0.2941 |
| INTERNAL | 3.04 | 1.74 | 0.3288 | 0.6712 |
| RESE- RVE | EXP- ORT | IMPO- RT | RER | CAGDP | STD- RES | GDP | GOVER- NMENT | CORRU- PTION | LAW | EXTE- RNAL | INTE- RNAL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RESERVE | 1.0000 | |||||||||||
| EXPORT | −0.0263 | 1.0000 | ||||||||||
| IMPORT | −0.2389 | 0.4783 | 1.0000 | |||||||||
| RER | 0.0767 | −0.0422 | −0.2024 | 1.0000 | ||||||||
| CAGDP | 0.0957 | −0.1336 | −0.2533 | −0.0546 | 1.0000 | |||||||
| STDRES | −0.0251 | 0.0344 | 0.0740 | 0.3785 | −0.4489 | 1.0000 | ||||||
| GDP | −0.2579 | 0.0961 | 0.4676 | −0.4121 | −0.3082 | −0.0149 | 1.0000 | |||||
| GOVERNMENT | 0.1443 | 0.1118 | 0.0284 | −0.1283 | 0.1311 | −0.1829 | 0.0360 | 1.0000 | ||||
| CORRUPTION | −0.1177 | 0.1716 | 0.0771 | 0.0714 | −0.2737 | 0.2607 | 0.1978 | 0.0065 | 1.0000 | |||
| LAW | 0.0505 | 0.1636 | 0.1094 | 0.0882 | −0.2246 | 0.3886 | 0.0934 | 0.1228 | 0.5478 | 1.0000 | ||
| EXTERNAL | 0.1848 | 0.0647 | −0.0556 | −0.2840 | 0.1514 | −0.1915 | 0.0280 | 0.1655 | 0.1460 | 0.2177 | 1.0000 | |
| INTERNAL | 0.1356 | 0.1818 | 0.1076 | −0.3068 | 0.0855 | −0.1707 | 0.1737 | 0.2641 | 0.4890 | 0.5623 | 0.4843 | 1.0000 |
| Indicators | Coefficient (1) | Std. Err. (2) | p Value (3) | dy/dx (4) |
|---|---|---|---|---|
| RESERVE | 0.0171211 | 0.0106439 | 0.108 | 5.55 × 10−6 |
| EXPORT | −0.0208022 | 0.0093243 | 0.026 | −6.74 × 10−6 |
| IMPORT | −0.0612803 | 0.012334 | 0.000 | 0.0000199 |
| RER | 0.0128762 | 0.0026582 | 0.000 | 4.17 × 10−6 |
| CAGDP | −0.4071764 | 0.0669344 | 0.000 | −0.0001319 |
| STDRES | 0.0689924 | 0.0072239 | 0.000 | 0.0000224 |
| GDP | −0.665357 | 0.0891327 | 0.000 | −0.0002155 |
| GOVERNMENT | 1.695356 | 0.1935787 | 0.000 | 0.0005492 |
| CORRUPTION | 1.116541 | 0.3515389 | 0.001 | 0.0003617 |
| LAW | −2.122407 | 0.4992513 | 0.000 | −0.0006876 |
| EXTERNAL | −0.9823548 | 0.2615287 | 0.000 | −0.0003182 |
| INTERNAL | 2.393928 | 0.2752958 | 0.000 | 0.0007755 |
| CONS | −35.9565 | 3.281402 | 0.000 |
| Coefficient | Std. Err | z | p Value | |
|---|---|---|---|---|
| _hat | 1.019015 | 0.1183753 | 8.61 | 0.000 |
| _hatsq | 0.0094695 | 0.0310432 | 0.31 | 0.760 |
| Cutoff | Sensitivity (Se) | Specificity (Sp) | Missing Alarm (Type I) | False Alarm (Type II) | Type I + Type II |
|---|---|---|---|---|---|
| >=0.05 | 95.90% | 89.45% | 4.10% | 10.55% | 14.65% |
| >=0.10 | 94.26% | 93.13% | 5.74% | 6.87% | 12.61% |
| >=0.1327 | 94.26% | 93.90% | 5.74% | 6.10% | 11.84% |
| >=0.15 | 92.62% | 94.39% | 7.38% | 5.61% | 12.99% |
| >=0.20 | 90.98% | 95.16% | 9.02% | 4.84% | 13.86% |
| >=0.30 | 86.89% | 96.22% | 13.11% | 3.78% | 16.89% |
| >=0.40 | 81.15% | 97.48% | 18.85% | 2.52% | 21.37% |
| >=0.50 | 77.05% | 98.16% | 22.95% | 1.84% | 24.79% |
| >=0.60 | 72.13% | 98.55% | 27.87% | 1.45% | 29.32% |
| >=0.70 | 68.03% | 99.32% | 31.97% | 0.68% | 32.65% |
| >=0.80 | 58.20% | 99.71% | 41.80% | 0.29% | 42.09% |
| >=0.90 | 47.54% | 100.00% | 52.46% | 0.00% | 52.46% |
| >=0.95 | 34.43% | 100.00% | 65.57% | 0.00% | 65.57% |
| Crisis | Non-Crisis | Total | |
|---|---|---|---|
| Crisis signal | 115 | 63 | 178 |
| No crisis signal | 7 | 970 | 977 |
| Total | 122 | 1033 | 1155 |
| Number of crises occurrence | 115 | ||
| % of crises called (sensitivity) | 94.26% | ||
| % of non-crisis called (specificity) | 93.90% | ||
| % of false alarm (Type 2 error) | 6.10% | ||
| % of missing alarm (Type 1 error) | 5.74% | ||
| % of observation correctly called | 93.94% | ||
| Country | Sample in 1994M1 (1) | Crisis in 1994 (2) | Sample in 1997M1 (3) | Crisis in 1997 (4) |
|---|---|---|---|---|
| Indonesia | 0.0086 | No | 0.9539 | 1997M8 |
| Malaysia | 0.0105 | No | 0.7740 | 1997M7 |
| Philippines | 0.0680 | No | 0.9964 | 1997M10 |
| Thailand | 0.0000 | No | 0.9897 | 1997M7 |
| Turkey | 0.4384 | 1994M4 | 0.0007 | No |
| Country | Sample in 2001M1 (5) | Crisis in 2001 (6) | Sample in 2007M1 (7) | Crisis in 2007 (8) |
| Indonesia | 0.0000 | No | 0.0001 | No |
| Malaysia | 0.0114 | No | 0.0000 | No |
| Philippines | 0.0006 | No | 0.0000 | No |
| Thailand | 0.0004 | No | 0.0000 | No |
| Turkey | 0.6188 | 2001M2 | 0.0019 | No |
| Country | Crisis | Non-Crisis | Missing Alarm | False Alarm |
|---|---|---|---|---|
| Indonesia | 21 | 207 | 3 | |
| Malaysia | 20 | 205 | 1 | 5 |
| Philippines | 19 | 195 | 5 | 12 |
| Thailand | 24 | 195 | 12 | |
| Turkey | 31 | 168 | 1 | 31 |
| Variables | Coefficient | Std. Error | p-Value | dy/dx |
|---|---|---|---|---|
| RESERVE | 0.0509148 | 0.0114312 | 0.011 | 0.0000319 |
| EXPORT | 0.0243299 | 0.0147422 | 0.099 | 0.0000152 |
| IMPORT | −0.0097348 | 0.0103742 | 0.307 | −6.10 × 10−6 |
| RER | 0.0000538 | 0.0000132 | 0.012 | 3.37 × 10−8 |
| CAGDP | −0.3175547 | 0.1117279 | 0.000 | −0.000199 |
| STDRES | 0.0569191 | 0.0103949 | 0.000 | 0.0000357 |
| GDP | −0.0962102 | 0.117412 | 0.370 | −0.0000603 |
| GOVERNMENT | −1.692191 | 0.2108984 | 0.000 | −0.0010604 |
| CORRUPTION | 0.8619664 | 0.4716313 | 0.015 | 0.0005402 |
| LAW | 3.380178 | 0.6085447 | 0.000 | 0.0021182 |
| EXTERNAL | −1.416234 | 0.7054774 | 0.002 | −0.0008875 |
| INTERNAL | −2.507323 | 0.3633715 | 0.000 | −0.0015712 |
| _CONS | 19.22054 | 4.336006 | 0.000 |
| Crisis | Non-Crisis | Total | |
|---|---|---|---|
| Signal | 92 | 59 | 151 |
| No signal | 8 | 765 | 773 |
| Total | 100 | 824 | 924 |
| Number of crises that occurred | 92 | ||
| % of crises called (sensitivity) | 92.00% | ||
| % of non-crisis called (specificity) | 92.84% | ||
| % of false alarm (Type 2 error) | 8.00% | ||
| % of missing alarm (Type 1 error) | 7.16% | ||
| % of observation correctly called | 92.75% | ||
| Country | Crisis | Non-Crisis | Missing Alarm | False Alarm |
|---|---|---|---|---|
| Argentina | 20 | 202 | 9 | |
| Brazil | 17 | 208 | 2 | 4 |
| Colombia | 32 | 168 | 5 | 26 |
| Mexico | 23 | 187 | 1 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferdous, L.T.; Kamal, K.M.M.; Ahsan, A.; Hong Thuy Hoang, N.; Samaduzzaman, M. An Early Warning System for Currency Crises in Emerging Countries. J. Risk Financial Manag. 2022, 15, 167. https://doi.org/10.3390/jrfm15040167
Ferdous LT, Kamal KMM, Ahsan A, Hong Thuy Hoang N, Samaduzzaman M. An Early Warning System for Currency Crises in Emerging Countries. Journal of Risk and Financial Management. 2022; 15(4):167. https://doi.org/10.3390/jrfm15040167
Chicago/Turabian StyleFerdous, Lutfa Tilat, Khnd Md Mostafa Kamal, Amirul Ahsan, Nhung Hong Thuy Hoang, and Munshi Samaduzzaman. 2022. "An Early Warning System for Currency Crises in Emerging Countries" Journal of Risk and Financial Management 15, no. 4: 167. https://doi.org/10.3390/jrfm15040167
APA StyleFerdous, L. T., Kamal, K. M. M., Ahsan, A., Hong Thuy Hoang, N., & Samaduzzaman, M. (2022). An Early Warning System for Currency Crises in Emerging Countries. Journal of Risk and Financial Management, 15(4), 167. https://doi.org/10.3390/jrfm15040167







