1. Introduction
Fertility is an endogenous choice variable that shows a procyclical pattern, indicating that it often moves in the same direction as the business cycle (
Sobotka et al. 2011). House prices are also a procyclical variable. During the expansionary phase of a business cycle, higher house prices increase the housing wealth of households, which may have a positive impact on fertility. This backdrop demands some good research to explore the impact of house prices on fertility under a dynamic macroeconomic framework. By using the annual data of 1975–2020 for the U.S., this paper investigates the relationship by using a structural vector autoregression model and the Toda–Yamamoto causality test.
The long-run decline in fertility in the OECD countries since the 1960s has raised the unlikely prospect that children are inferior goods.
Becker and Lewis (
1973) solved this puzzle by modeling the quantity–quality trade-off in children. Their model can explain an initial fall in fertility rate as income rises and subsequent rise in fertility rate at higher levels of income. Hence, the number of children desired depends on the income or wealth of a household.
Barro and Becker (
1989) used the microeconomic foundations of
Becker (
1960) to build a macroeconomic growth model with endogenous fertility, in which there is a low-income or Malthusian steady-state and a high-income steady-state, such as those observed in developed countries.
As fertility is endogenous, an interesting question is whether fertility rates respond to different price signals, such as house prices and interest rates (returns from financial wealth). Considering the heterogeneous nature of wealth, we differentiate between housing wealth and financial wealth in the budget constraint of a representative agent and try to find the impact of higher housing wealth (reflected by higher house prices) on the fertility choice of the agent. In this context, the paper assumes that changes in housing prices are a potentially important determinant of demand for children, thereby influencing fertility, because house prices can reasonably be considered as a store of wealth and house price appreciation can be tapped into while still owning the wealth, particularly in the U.S.
There are three main strands of literature studying the relationship between house prices and the fertility rate, with various authors arriving at mixed conclusions. The first group of studies found that higher house prices increase the fertility rate for homeowners of developed countries—see
Lovenheim and Mumford (
2013),
Dettling and Kearney (
2014),
Aksoy (
2016),
Atalay et al. (
2017),
Daysal et al. (
2020), and
Simo-Kengne and Bonga-Bonga (
2020). The second group of studies found that higher house prices decrease the fertility rate of developing countries such as China or the fertility rate for non-homeowners of developed countries—see
Yi and Zhang (
2010),
Hui et al. (
2012),
Pan and Xu (
2012),
Clark et al. (
2020),
Liu et al. (
2020), and
Liu et al. (
2021). The third group of studies discovered that higher fertility rates or population growth will increase house prices—see
Mankiw and Weil (
1989),
Kohler and Merwe (
2015), and
Choi and Jung (
2016).
Most of the studies in the current literature used cross-sectional or regional data and thus ignored the macroeconomic dynamics that could help explain the relationship between house prices and fertility behavior for the entire economy. For example, house prices (housing wealth) and fertility rates are influenced when other important macroeconomic variables, such as real GDP and interest rates (a return from financial wealth), increase. To find the response of fertility rates originating from a shock in house prices, one needs to isolate the impact of other shocks (for example, a technology shock that changes real GDP or a monetary policy shock that changes interest rates) on the fertility rate. Without a comprehensive macroeconomic framework containing variables that can influence house prices and fertility rates, we are only halfway to explaining the empirical house prices–fertility rate relationship. Unfortunately, the existing literature lacks sufficient research on the fertility rate and macroeconomic dynamics in a more generalized aggregate dimension. Additionally, these papers leave open the question of causality among various important macroeconomic variables and fertility. This gap in the literature motivates us to write this paper.
The scientific goal of this paper is to set up an appropriate structural vector autoregression (VAR) model using the annual data of 1975–2020 of per capita real GDP, fertility rate, house prices, and interest rates for the U.S. and to explore the endogenous behavior of the fertility rate. Specifically, impulse response analysis and the variance decomposition approach of the VAR model are used to investigate the impact of house prices and interest rates on fertility. Another goal of the paper is to set up an appropriate causality model with the same set of variables and test the causality among the variables. Specifically, the causality test investigates whether the direction of causality, from house prices and interest rates to the fertility rate, is significant.
This research is unique in several aspects. First, we incorporate per capita real GDP and an interest rate in the structural VAR model, making the model more realistic. Second, whereas most studies focused their inquiry mostly at the regional level, our study provides a comprehensive macroeconomic dynamic model of the fertility rate and house prices for the entire U.S. economy. Third, we conduct the robust Toda–Yamamoto procedure to test bidirectional causality between the fertility rate and house prices and between the fertility rate and interest rates. To the best of our knowledge, we perform the Toda–Yamamoto causality test between the fertility rate and other wealth indicators for the first time in the literature for the U.S. economy.
The results of the VAR show that U.S. house prices and interest rates have a significant positive effect on the U.S. fertility rate. The robust Toda–Yamamoto causality test finds unidirectional causality, from interest rates and house prices to the fertility rate. We conclude that easy fiscal and monetary policies may be conducive to higher house prices, which may increase the fertility rate in the U.S.
2. Literature Review and Theoretical Considerations
There are some well-established studies that differentiate between housing wealth and financial wealth and consider their impact on the economic decisions of households.
Iacoviello (
2004) showed that housing price is a potential determinant of household consumption.
Lustig and Van Nieuwerburgh (
2005) argued that the housing wealth to human wealth ratio is a potentially significant determinant of consumption growth. Similarly,
Piazzesi et al. (
2007) argued that housing wealth could provide consumption insurance to households; see also
Simo-Kengne and Bonga-Bonga (
2020).
Case et al. (
2005) found a positive and statistically significant relationship between housing wealth and the marginal propensity to consume.
Bostic et al. (
2009) conducted a study using U.S. microdata and found that housing wealth affects private consumption, which, in turn, affects real GDP growth.
As supported by the literature, we separate the total wealth of a representative agent into housing wealth and financial wealth. In this respect, we consider the utility of a dynastic individual in the model of
Barro and Becker (
1989) to be represented as
where the individual gets utility,
Ut, from his/her consumption
u(
ct), the number and utility of children,
ntUt+1, and his/her degree of altruism towards the children,
a(
nt). Utility in the model of
Barro and Becker (
1989) is constrained by the budget
which shows that spending on the individual’s consumption,
ct, the costs of raising children,
ntBt, and bequests to children,
nt(
Kt+1), are limited by the individual’s earnings,
wt, and assets, (1
+ rt)
Kt.
As wealth is heterogeneous, we slightly modify the budget constraint to
where spending on the individual’s consumption,
ct, the costs of raising children,
nt(
Bt), financial wealth bequests to children,
nt(
Ft+1), and housing wealth bequests to children,
nt(
Ht+1), are limited by the individual’s earnings,
wt, financial wealth values, (
1 + rt)
Ft, and housing wealth values, (1
+ pt)
Ht.
It is important to separate housing wealth from financial wealth due to some special characteristics of real housing wealth. When house prices increase, the individual can consume the increased value of real housing wealth via a second mortgage without giving up ownership or having to worry about current tax consequences (certainly, one can borrow against financial wealth too from organizations that offer such loans, such as the TIAA, but loans against housing also have a potential tax advantage). This is not readily true for financial wealth when the financial wealth is in retirement funds that are usually unavailable or only available at a penalty until the individual reaches a certain age. Therefore, higher house prices increase the housing wealth of a consumer, which can affect his economic decisions, including his fertility choice. Hence, we use the house price as a proxy for household wealth.
The budget constraint (1) indicates that when the interest rate (
rt) goes up, the financial wealth of the individual goes up. On the other hand, when the house price (
pt) goes up, the housing wealth of the individual goes up. Thus, consistent with
Barro and Becker’s (
1989) model, the dynastic individual can save more and ensure more wealth for his/her offspring when the interest rates and house prices are high; see also
Manuelli and Seshadri (
2009). Thus, house prices and interest rates are important potential determinants of a household’s fertility.
There is some literature supporting the prediction of
Barro and Becker’s (
1989) model that higher house prices are associated with higher fertility rates.
Lovenheim and Mumford (
2013) used the U.S. data for the period of 1985–2007 and linear probability models to show that a USD 100,000 increase in housing wealth among homeowners causes a 16% to 18% increase in the probability of having a child. Using the OLS and instrumental variable methods with the housing price cycle data of 1997–2006,
Dettling and Kearney (
2014) observed that at the mean U.S. homeownership rate, the net effect of a USD 10,000 increase in house prices was associated with a 0.8% increase in fertility rates. Using the data of English counties for the period of 1995–2013,
Aksoy (
2016) used both OLS and instrumental variable techniques to show that a 10% increase in house prices leads to a 2.8% increase in births for homeowners.
Atalay et al. (
2017) used the Australian survey panel data of 2001–2014 and the linear probability model to show that an AUD 100,000 increase in house prices increases the probability of having a child by 7.5 percent among homeowners. The pooled cross-sectional Logit model of
Clark and Ferrer (
2019) showed that in Canada, a CAD 10,000 increase in lagged real estate board average house prices increases the odds of giving birth by 2%.
Daysal et al. (
2020) used Danish register data for the period of 1992–2011 and the fixed effect model to show that for a DKK 100,000 increase in house prices, the likelihood of giving birth increases by 2.32%. Using the spatial Durbin model,
Simo-Kengne and Bonga-Bonga (
2020) examined the effect of house prices on fertility across South African provinces. Provincial annual data from 1998 to 2015 showed that an increase in regional house prices decreased the local fertility rate. However, the spillover effect increases fertility in other regions. The paper concludes that, besides labor market conditions and female job participation, the housing market plays an important role in fertility decisions.
As discussed in the Introduction section, the existing literature lacks sufficient studies that investigate the relationship between demographic analyses and important macroeconomic variables under a dynamic framework. Our study tries to extend the literature by including per capita real GDP, an interest rate, a fertility rate, and house prices in a macro-econometric model that attempts to determine the dynamic and causality relationships between the fertility rate and other variables, especially house prices.
3. Data
We collected annual data on the total fertility rate, the S&P/Case-Shiller U.S. national home price index, the consumer price index, per capita real GDP, and the federal funds rate from the Federal Reserve Economic Database (FRED). As fertility rate data are available only on an annual basis, it is standard practice to use annual data in demographic research—see, for example,
Case et al. (
2005). We divide the Shiller index by the consumer price index to get house prices in real terms.
The variable
yt indicates the per capita real GDP. We denote
ht as the real house prices and
ft as the total fertility rate. Finally,
it indicates the level of the federal funds rate. The summary statistics of the variables are provided in
Table 1.
Based on the ADF test and the KPSS test (presented in
Appendix A), it is found that the variables in log levels are nonstationary. However, when first-differenced, they become stationary. Following
Wang et al. (
1994), we performed the Engle–Granger two-step process to test for potential cointegration between/among the variables in level form and found no evidence of cointegration. The cointegration results are shown in
Table 2.
As no cointegrating relationships are found between/among the variables, we posit a structural VAR with stationary (first-differenced) variables, focusing on the short-run dynamic effects of the structural disturbances using impulse response and variance decomposition analyses. The unit root, stationarity, and cointegration test results are not reported for brevity but are available upon request.
4. Methodology
A structural VAR (SVAR) model is used to investigate the dynamic impact of house prices and interest rates on the fertility rate under a macroeconomic framework. This current research uses the SVAR model because the impulse response functions from this model provide a graphical approach to show how the fertility rate responds to sudden changes (shocks) in wealth and other important macroeconomic variables over time in a dynamic framework. This analysis is attractive for policymakers because they like to learn how the fertility rate behaves instantaneously and over time following different shocks in order to prepare appropriate short- and long-run policies.
We create a 4 × 1 vector,
zt = (∆
lnyt, ∆
lnht, ∆
lnft,
it)’, and use an
m-th order SVAR to describe the dynamic interrelations among the variables in
zt as follows
where the contemporaneous coefficient matrices,
B and
Γj (
j = 1,…,
m), are 4 × 4 parameter matrices,
Γ0 is a 4 × 1 vector of parameters,
Dt is a dichotomous variable that equals 1 during recession years and 0 otherwise, and
εt is a 4 × 1 vector of Gaussian innovations,
εt = (
εty,
εth,
εtf,
εti)’. The impulse response functions can be represented as
, which indicates how
zi,t responds to a one-unit change in
εj,t.
Following
Bjørnland and Leitemo (
2009) and
Istiak (
2022a,
2022b), stationary variables are used in the SVAR model. We also follow the standard practice in the econometric literature of SVAR of using the federal funds rate in levels and ordering the economic variables to precede the policy variables in the model; see
Bjørnland and Leitemo (
2009),
Istiak and Serletis (
2017),
Istiak (
2019),
Istiak and Serletis (
2020), among others. We also follow
Bjørnland and Leitemo (
2009) and
Istiak and Serletis (
2017) and include real GDP and interest rates as the first and last variables of the SVAR model, respectively (we also use alternative orderings of the variables in the SVAR model, as shown in the robustness section). The SVAR model of Equation (2), with
zt with the ordering (∆
lnyt, ∆
lnht, ∆
lnft,
it), is considered the baseline model. The time series graphs of the variables used in the baseline model are shown in
Figure 1.
The standard recursive identification process is followed for the structural identification of Model (2). As this is a popular method of identifying the VAR, the detailed process of this method is not discussed here. Interested readers can see
Kilian’s (
2013) study to learn about the recursive identification process.
The AIC criterion indicates applying three lags in the SVAR model. With three lags, the SVAR satisfies the stability condition and other diagnostic tests, such as no autocorrelation and normality of residuals. Hence, we decide to focus on the baseline model with three lags.
5. Empirical Results from the SVAR Model
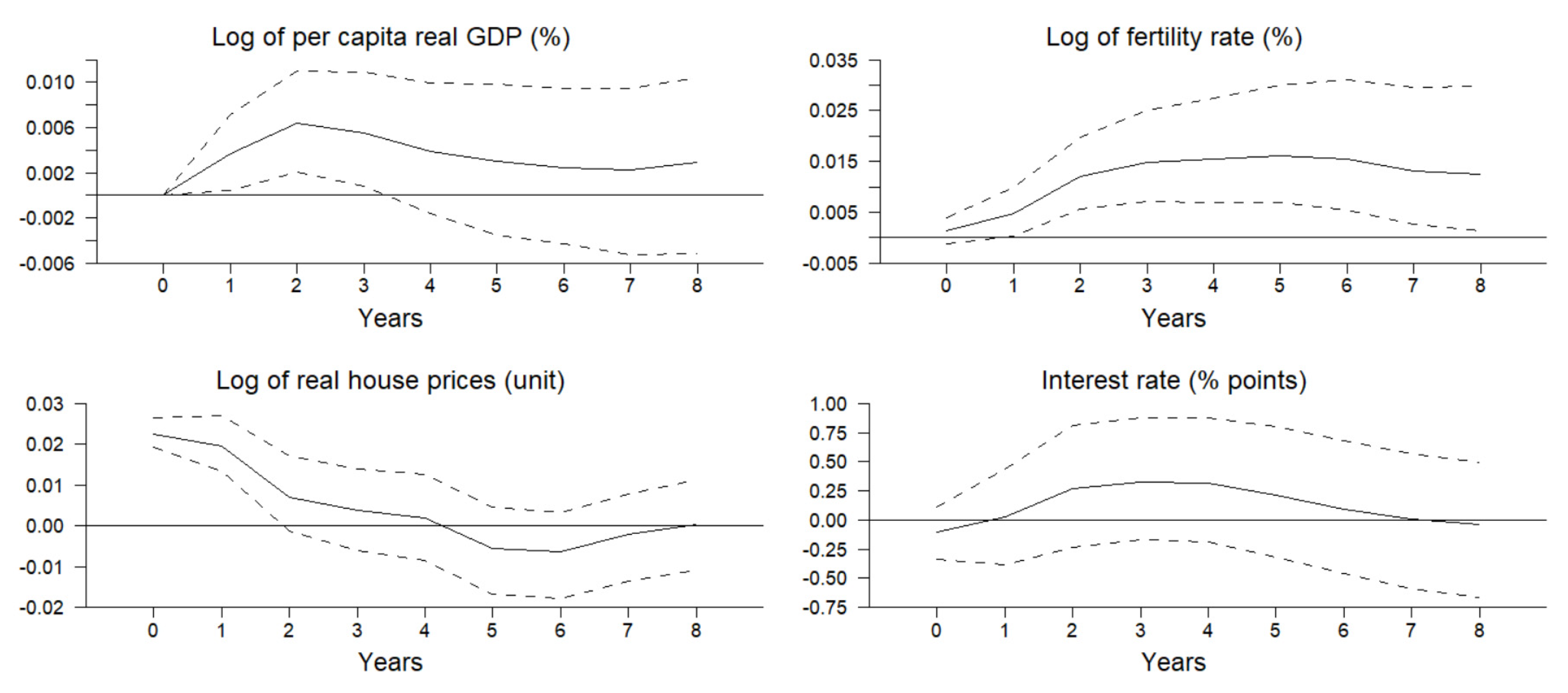
Figure 2 shows that one standard deviation unexpected increase in the log of per capita real GDP or a per capita real GDP shock significantly increases the fertility rate and supports the prediction that fertility and income are positively correlated.
Figure 2 also shows that a per capita real GDP shock significantly increases interest rates for two years. A per capita real GDP shock does not have any significant impact on house prices.
As can be seen in
Figure 3, one standard deviation unexpected increase in the log of real house prices or a house price shock significantly increases the fertility rate. The result is consistent with the prediction of
Barro and Becker’s (
1989) model that housing wealth (proxied by housing prices) and fertility are positively correlated; see also
Dettling and Kearney (
2014).
Figure 3 also shows that a house price shock has no significant impact on the interest rate. However, the shock has a significant positive impact on per capita real GDP.
Figure 4 shows that a fertility rate shock decreases per capita real GDP. This finding is consistent with
Wang et al. (
1994), who argue that a fertility shock retards capital accumulation and decreases labor employment, leading to a decline in output in the short run. This result is also consistent with
Mishra and Smyth (
2010) and
Mishra et al. (
2010), who argue that the female labor force participation rate and total fertility rate are inversely related. According to their empirical findings, we speculate that when fertility goes up, the female labor force participation rate goes down and real GDP goes down as well.
Figure 4 also shows that a fertility rate shock has no significant impact on the interest rate and real house prices.
Figure 5 shows that an interest rate shock significantly increases the fertility rate, which supports our prediction that fertility and interest rates should be positively related according to the dynastic utility mechanism, as shown in
Section 2. Additionally, as the interest rate on savings increases, the retirement benefit rises. Hence, the potentially affected household would like to increase its family size (which leads to higher fertility). Additionally, an interest rate shock has a significant negative impact on house prices. This finding makes sense because a high interest rate (mortgage rate) reduces demand for housing and, thus, reduces house prices.
Table 3 shows the variance decomposition analysis of all the variables used in the baseline SVAR model. We get that house prices and interest rates are important in explaining fertility rate variations. House prices and interest rates explain 18.39% and 24.35% of the variation of fertility, respectively, after the tenth year. On the other hand, the fertility rate does not have a significant impact on the variation of house prices and interest rates. Fertility explains only 15.76% and 10.55% of the variation of house prices and interest rates, respectively, after the tenth year.
Robustness of the Results from the Impulse Response Analysis of the SVAR Model
We check the robustness of our results through different variations of the baseline SVAR model.
First, we re-ran the baseline SVAR model and replaced the Shiller home price index with the all-transactions house price index (collected from the FRED website). The responses from
Figure 6 and
Figure 7 are very similar to those of
Figure 3 and
Figure 5, respectively.
Second, as the fertility rates among homeowners and renters may differ when the house price goes up, we re-ran the baseline SVAR model and included the homeownership rate (collected from the FRED website) as an exogenous variable in the model. The responses from
Figure 8 and
Figure 9 are very similar to those of
Figure 3 and
Figure 5, respectively.
Third, we re-ran the baseline SVAR model and positioned the fertility rate in the last place of the ordering of the SVAR model, thus making the fertility rate “most endogenous” in the system. The responses from
Figure 10 and
Figure 11 are very similar to those of
Figure 3 and
Figure 5, respectively.
Fourth, we re-ran the baseline SVAR model and positioned the fertility rate in the last place of the ordering and also interchanged the ordering of the interest rate and house prices. The responses from
Figure 12 and
Figure 13 are very similar to those of
Figure 3 and
Figure 5, respectively.
Hence, we get robust evidence that a house price shock and an interest rate shock will have significant positive impacts on the fertility rate with different variations of the SVAR model and house price indices.
6. Empirical Results from the Toda–Yamamoto Causality Test
To test for causality, many prior studies have used the standard Granger causality test. The Granger causality test may create spurious results. Additionally, the test results may incur specification bias. To mitigate these problems,
Toda and Yamamoto (
1995) proposed an augmented VAR, including some extra lags of the dependent variables. Like the regular Granger causality test, the construction of Toda and Yamamoto’s causality test does not depend on the orderings of the variables in the causality model. Toda and Yamamoto’s causality test is better than the Granger causality test because the former test can be used for a group of variables in levels with different orders of integration.
The Toda and Yamamoto causality test for variables in levels can be represented as
where
Xt = (
lnyt,
lnht,
lnft,
it)’. This is our baseline causality model, including the log of per capita real GDP, the log of the S&P/Case-Shiller U.S. national home price index, the log of the total fertility rate, and the level of the federal funds rate.
Dt is a dichotomous variable that equals 1 during the recession years and 0 otherwise. We keep
Dt in the causality model (3) to keep it consistent with the SVAR model (2). The SIC criteria suggest two lags for the model, indicating
m = 2. The parameter
dmax indicates the maximum number of integrations of the variables used in the model. In
Section 3, we found that all the variables (in the level form) had a unit root, indicating
dmax = 1. This causality model can be implemented only if
dmax ≤
m, as in our case. The Toda–Yamamoto test checks the null hypothesis of non-causality among the variables. The test results are shown in
Table 3.
The second column of
Table 4 shows the causality results from the baseline causality model. In the baseline model, we find statistically significant evidence of causality, from house prices to the fertility rate (at the 5% significance level), from the interest rate to the fertility rate (at the 1% significance level), and from the fertility rate to real per capita GDP (at the 10% significance level).
Robustness of the Results from the Toda–Yamamoto Causality Test
We investigate the robustness of our results from the baseline causality model (Model (3)) by replacing the total fertility rate with the general fertility rate, the crude birth rate, and the cubic-detrended total fertility rate, respectively. The general fertility rate and crude birth rate data are collected from the website of the Centres for Disease Control and Prevention. These are Models A, B, and C in
Table 4. We used the cubic-detrended total fertility rate, following
Galbraith and Thomas (
1941),
Kirk (
1960),
Lee (
1987), and
Wang et al. (
1994), among others. To check the robustness of the interest rate, we also replaced the federal funds rate of the baseline causality model with the 30-year and 10-year treasury constant maturity rates, respectively. We collected the 30-year and 10-year treasury constant maturity rate data from the FRED website. The data are reported as Models D and E in
Table 4.
For all the models, we found statistically significant evidence of causality, from house prices to the fertility rate (with a 10% significance level), from the interest rate to the fertility rate (with a 10% significance level), and from the fertility rate to real per capita GDP (with a 10% significance level). We do not find any statistically significant evidence of causality among the other variables.
7. Economic Discussions of the Findings
The impulse responses from the SVAR model show that a house price shock significantly increases the fertility rate. The variance decomposition analysis shows that house prices are important in explaining fertility rate variations. Moreover, the Toda–Yamamoto test shows statistically significant evidence of causality from house prices to the fertility rate. All these results show that house prices (as a proxy of housing wealth) influence the fertility choice for the U.S. economy. It can be noted that higher house prices benefit the owners but may impose a cost (in the form of higher rent) on tenants. Hence, it is possible that higher house prices are associated with a higher fertility rate for homeowners and a lower fertility rate for tenants. The U.S. Census Bureau indicated that the U.S. homeownership rate was 67.4% in the third quarter of 2020 (see,
https://www.census.gov/housing/hvs/files/currenthvspress.pdf (accessed on 29 January 2021)). As most families own a house in the U.S., higher house prices will increase the overall fertility rate in the U.S. Hence, the empirical evidence of this paper shows that homeowners treat children as a normal good. Therefore, when house prices increase, the homeowners feel that their wealth has increased, and this positive wealth/income effect induces them to have more children. Our findings are consistent with those of
Lovenheim and Mumford (
2013),
Dettling and Kearney (
2014),
Aksoy (
2016),
Atalay et al. (
2017), and
Daysal et al. (
2020).
The impulse responses from the SVAR model show that an interest rate shock significantly increases the fertility rate. The variance decomposition analysis shows that interest rates are important in explaining fertility rate variations. Moreover, the Toda–Yamamoto test indicates statistically significant evidence of causality, from interest rates to the fertility rate. All these results show that a higher interest rate (as a proxy of financial wealth) increases the fertility rate in the U.S. economy. When the interest rate on savings increases, the retirement benefit rises. Under this circumstance, dynastic individuals are more confident in spending more on their children and/or leaving more wealth for their children. Hence, a higher interest rate induces people to have more children.
The Toda–Yamamoto test indicates statistically significant evidence of unidirectional causality, from house prices (as a proxy of housing wealth) to the fertility rate and from interest rates (as a proxy of financial wealth) to the fertility rate, but not the other way around.
Malthus (
1798) assumed that higher income increases fertility, which reduces income at a later stage. Hence, in a Malthusian economy, one would expect bidirectional causality between wealth and the fertility rate. In Becker’s economy, where children are consumer durable goods, one would expect unidirectional causality, from wealth to fertility rate. The results of the Toda–Yamamoto causality test show that the U.S. economy, throughout the period 1975–2020, has been consistent with the underpinnings of Becker’s economy.
8. Conclusions
The relationship between house prices and human fertility behavior is an ongoing topic in the literature. Most of the studies use cross-sectional or regional data to explain the relationship between the two variables. This may ignore the macroeconomic dynamics of other important variables, for example, real GDP and interest rates, on the relationship between house prices and fertility behavior. We try to fill this gap in the literature by testing the endogenous behavior of fertility in a macroeconomic dynamic framework with heterogeneous wealth. In this respect, we use
Barro and Becker’s (
1989) model and divide the total wealth of a representative consumer into household wealth and financial wealth. We also use house prices and interest rates as proxies of changes in household and financial wealth in
Barro and Becker’s (
1989) model, respectively.
We use a structural VAR model and the U.S. annual time-series data between 1975 and 2020 to investigate the dynamic relationship between house prices and the fertility rate. Further, we use the Toda–Yamamoto-augmented Granger causality test to assess for causality among the macroeconomic variables.
The impulse response functions from the structural VAR model show that changes in house prices and interest rates have a significant positive effect on the fertility rate. The outcome indicates that children are consumer durable goods. The results are robust to different specifications and orderings of the structural VAR model. The variance decomposition analyses indicate that house prices and interest rates are responsible for explaining a significant portion of the variance of the forecast error for the fertility rate. Our findings are consistent with those of
Lovenheim and Mumford (
2013),
Dettling and Kearney (
2014),
Aksoy (
2016),
Atalay et al. (
2017), and
Daysal et al. (
2020), who have found that higher house prices are associated with higher fertility rates in developed countries.
The Toda–Yamamoto causality tests have found statistically significant evidence of unidirectional causality, from house prices to the fertility rate and from the interest rate to the fertility rate. The causality results are robust for different measures of fertility rates and interest rates. Our results from the structural VAR model and the Toda–Yamamoto causality test show evidence that the house price is a vital determinant of the fertility rate in the U.S. This finding supports
Simo-Kengne and Bonga-Bonga (
2020), who have found that along with labor market conditions and female job participation, the housing market plays an important role in fertility decisions in South Africa.
The positive relationship between house prices and the fertility rate, as found in our study, has important fiscal and monetary policy implications that are typically unnoticed by policymakers. For example, tax rebates on new house purchases may increase house prices and fertility rates. Similarly, when the federal government reduces the federal funds rate, the mortgage rate goes down, leading to a rise in housing demand and house prices. Given that house prices and the fertility rate are positively related, an easy monetary policy may increase the fertility rate. Hence, expansionary fiscal and monetary policies may be associated with a higher population in the near future. As a response, the state and local health departments should be ready to provide extra delivery care and other birth-related facilities. The community leaders should also plan accordingly to ensure the basic services, infrastructure, and transport facilities for the future higher population.