Pricing European Options under Stochastic Volatility Models: Case of Five-Parameter Variance-Gamma Process
Abstract
1. Introduction
2. Variance-Gamma Process: Stochastic Volatility Model
2.1. Lévy Framework and Asset Pricing
2.2. Ornstein–Uhlenbeck Proces
2.3. Variance-Gamma Process: Semi-Martingale
2.4. Variance-Gamma Process: Parameter Estimations
3. Variance-Gamma Process: Probability versus Lévy Density
3.1. Lévy Measure and the Structure of the Jumps
3.2. Variance-Gamma Process: Asymptotic Distribution
4. Variance-Gamma Process: Pricing European Options
4.1. Variance-Gamma Process: Risk-Neutral Esscher Measure
4.2. Variance-Gamma Model: Extended Black–Scholes Formula
Equivalent Martingale Measure (EMM) Computation
4.3. Variance-Gamma Model: Generalized Black–Scholes Formula
4.4. European Option Pricing by Fractional Fast Fourier Transform (FRFT)
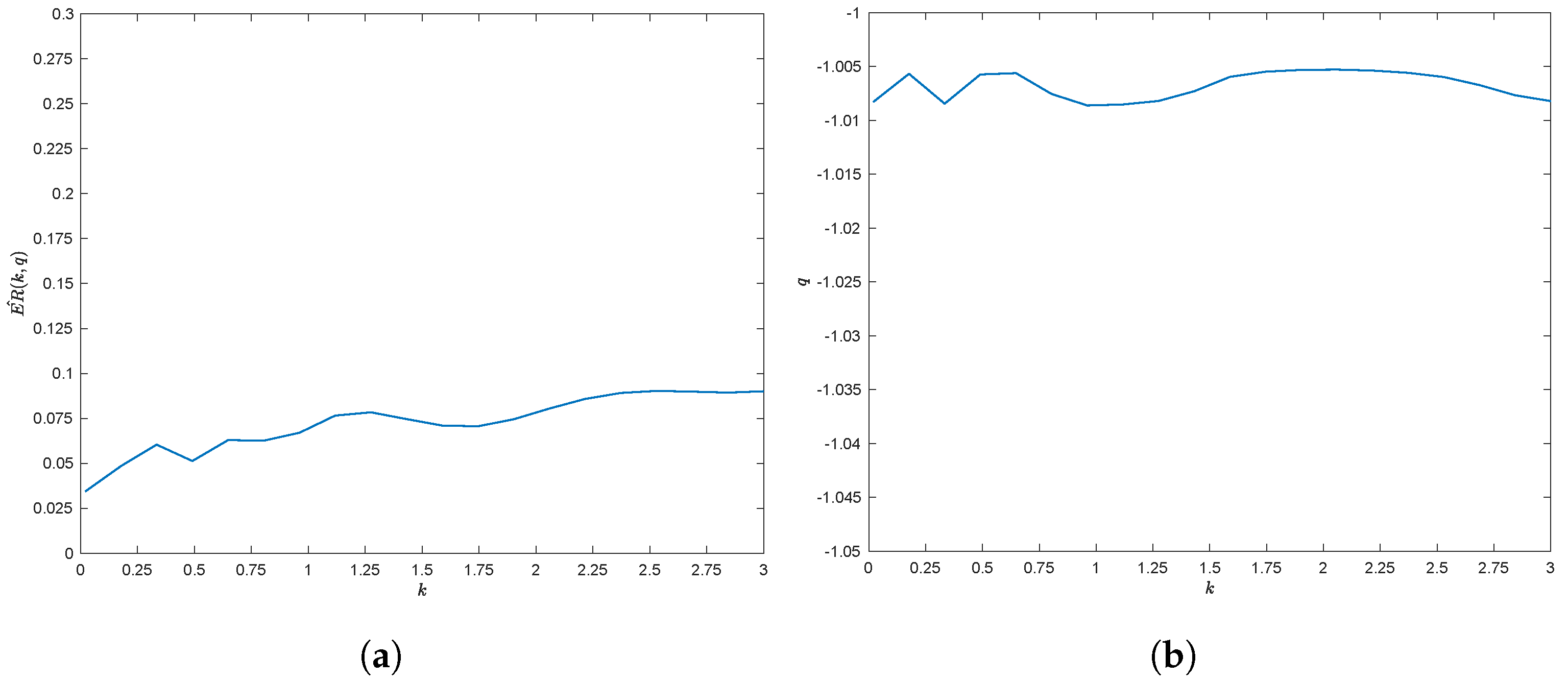
4.4.1. Evaluation of Parameter q
4.4.2. Calculating the Fourier Integral by FRFT
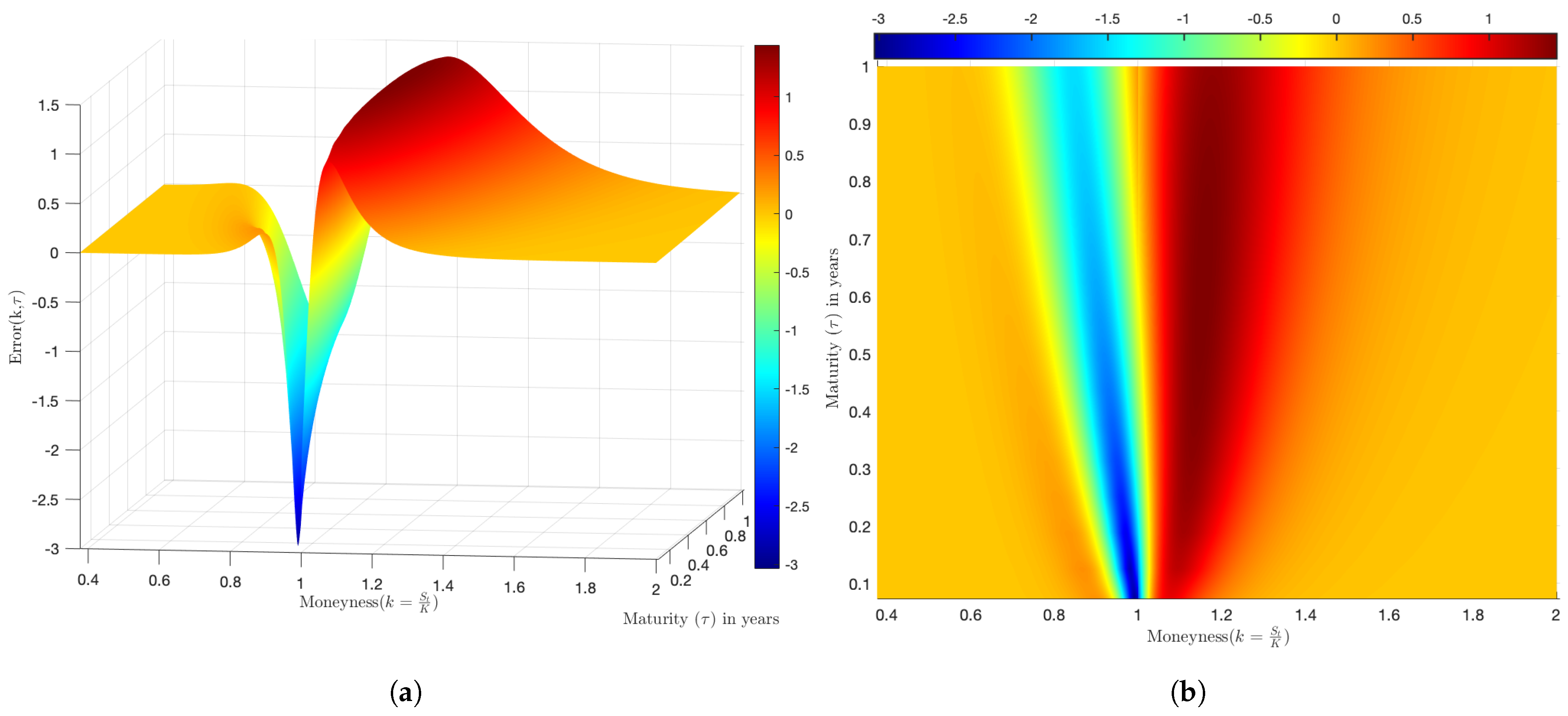
4.5. Empirical Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adeosun, Mabel E., Sunday O. Edeki, and Olabisi O. Ugbebor. 2016. On a variance gamma model (vgm) in option pricing: A difference of two gamma processes. Journal of Informatics and Mathematical Sciences 8: 1–16. [Google Scholar]
- Alhagyan, Mohammed, Masnita Misiran, and Zurni Omar. 2020. Discussions on continuous stochastic volatility models. Global and Stochastic Analysis 7: 55–64. [Google Scholar]
- Andrusiv, Andrii, and Hans-Jürgen Engelbert. 2020. On the minimal entropy martingale measure for lévy processes. Stochastics 92: 1223–43. [Google Scholar] [CrossRef]
- Applebaum, David. 2009. Lévy Processes and Stochastic Calculus. Cambridge: Cambridge University Press. [Google Scholar]
- Arias-de Reyna, Juan. 1990. On the theorem of frullani. Proceedings of the American Mathematical Society 109: 165–75. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2001a. Modelling by lévy processes for financial econometrics. In Lévy Processes. Boston: Birkhäuser, pp. 283–318. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2001b. Non-gaussian Ornstein–uhlenbeck-based models and some of their uses in financial economics. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63: 167–241. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002. Financial Volatility, Lévy Processes and Power Variation. Oxford: Nuffield College, Unpublished book. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2003. Integrated ou processes and non-gaussian ou-based stochastic volatility models. Scandinavian Journal of Statistics 30: 277–95. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Jens Ledet Jensen, and Michael Sørensen. 1998. Some stationary processes in discrete and continuous time. Advances in Applied Probability 30: 989–1007. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Boyarchenko, Svetlana, and Sergei Z. Levendorskii. 2002. Non-Gaussian Merton-Black-Scholes Theory. Singapore: World Scientific, vol. 9. [Google Scholar]
- Carr, Peter, Hélyette Geman, Dilip B. Madan, and Marc Yor. 2003. Stochastic volatility for lévy processes. Mathematical Finance 13: 345–82. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Elias S. W. Shiu. 1993. Option pricing by Esscher Transforms. Paris: HEC Ecole des Hautes Études Commerciales. [Google Scholar]
- Heston, Steven L. 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Hull, John, and Alan White. 1987. The pricing of options on assets with stochastic volatilities. The Journal of Finance 42: 281–300. [Google Scholar] [CrossRef]
- Hull, John C. 2003. Options Futures and Other Derivatives. Toronto: Pearson Education India. [Google Scholar]
- Kendall, Maurice George. 1946. The Advanced Theory of Statistics, 2nd ed. London: Charles Griffin. [Google Scholar]
- Ken-Iti, Sato. 1999. Lévy Processes and Infinitely Divisible Distributions. Cambridge: Cambridge University Press. [Google Scholar]
- Kou, Steven G. 2002. A jump-diffusion model for option pricing. Management Science 48: 1086–101. [Google Scholar] [CrossRef]
- Kyprianou, Andreas E. 2014. Fluctuations of Lévy Processes with Applications: Introductory Lectures. Berlin: Springer Science & Business Media. [Google Scholar]
- Li, Cuixiang, Huili Liu, Mengna Wang, and Wenhan Li. 2020. The pricing of compound option under variance gamma process by FFT. Communications in Statistics-Theory and Methods 50: 6122–36. [Google Scholar] [CrossRef]
- Madan, Dilip B., and Frank Milne. 1991. Option pricing with VG martingale components 1. Mathematical Finance 1: 39–55. [Google Scholar] [CrossRef]
- Madan, Dilip B., Peter P. Carr, and Eric C. Chang. 1998. The variance gamma process and option pricing. Review of Finance 2: 79–105. [Google Scholar] [CrossRef]
- Matsuda, Kazuhisa. 2004. Introduction to Merton Jump Diffusion Model. New York: Department of Economics, The Graduate Center, The City University of New York. [Google Scholar]
- Mozumder, Sharif, Ghulam Sorwar, and Kevin Dowd. 2015. Revisiting variance gamma pricing: An application to s&p500 index options. International Journal of Financial Engineering 2: 1550022. [Google Scholar]
- Nzokem, Aubain H. 2020. Stochastic and Renewal Methods Applied to Epidemic Models. Ph.D. Thesis, York University, YorkSpace Institutional Repository, Toronto, ON, Canada. [Google Scholar]
- Nzokem, Aubain H. 2021a. Fitting infinitely divisible distribution: Case of gamma-variance model. arXiv arXiv:2104.07580. [Google Scholar]
- Nzokem, Aubain H. 2021b. Gamma variance model: Fractional Fourier Transform (FRFT). Journal of Physics: Conference Series 2090: 012094. [Google Scholar] [CrossRef]
- Nzokem, Aubain H. 2021c. Numerical solution of a gamma—Integral equation using a higher order composite newton-cotes formulas. Journal of Physics: Conference Series 2084: 012019. [Google Scholar] [CrossRef]
- Nzokem, Aubain H. 2021d. Sis epidemic model: Birth-and-death Markov chain approach. International Journal of Statistics and Probability 10: 10–20. [Google Scholar] [CrossRef]
- Nzokem, Aubain H., and Montshiwa Volition T. 2022. Fitting generalized tempered stable distribution: Fractional Fourier Transform (FRFT) approach. arXiv arXiv:2205.00586. doi:10.1007/978-981-19-8406-8_34. [Google Scholar] [CrossRef]
- Protter, Philip. 2005. Stochastic Integration and Differential Equations. A New Approach. Berlin: Springer, vol. 21. [Google Scholar] [CrossRef]
- Tankov, Peter. 2003. Financial Modelling with Jump Processes. New York: Chapman and Hall/CRC. [Google Scholar] [CrossRef]
- Uhlenback, George E., and Leonard S. Ornstein. 1930. On the theory of the Brownian motion. Physical Review 36: 823–41. [Google Scholar] [CrossRef]
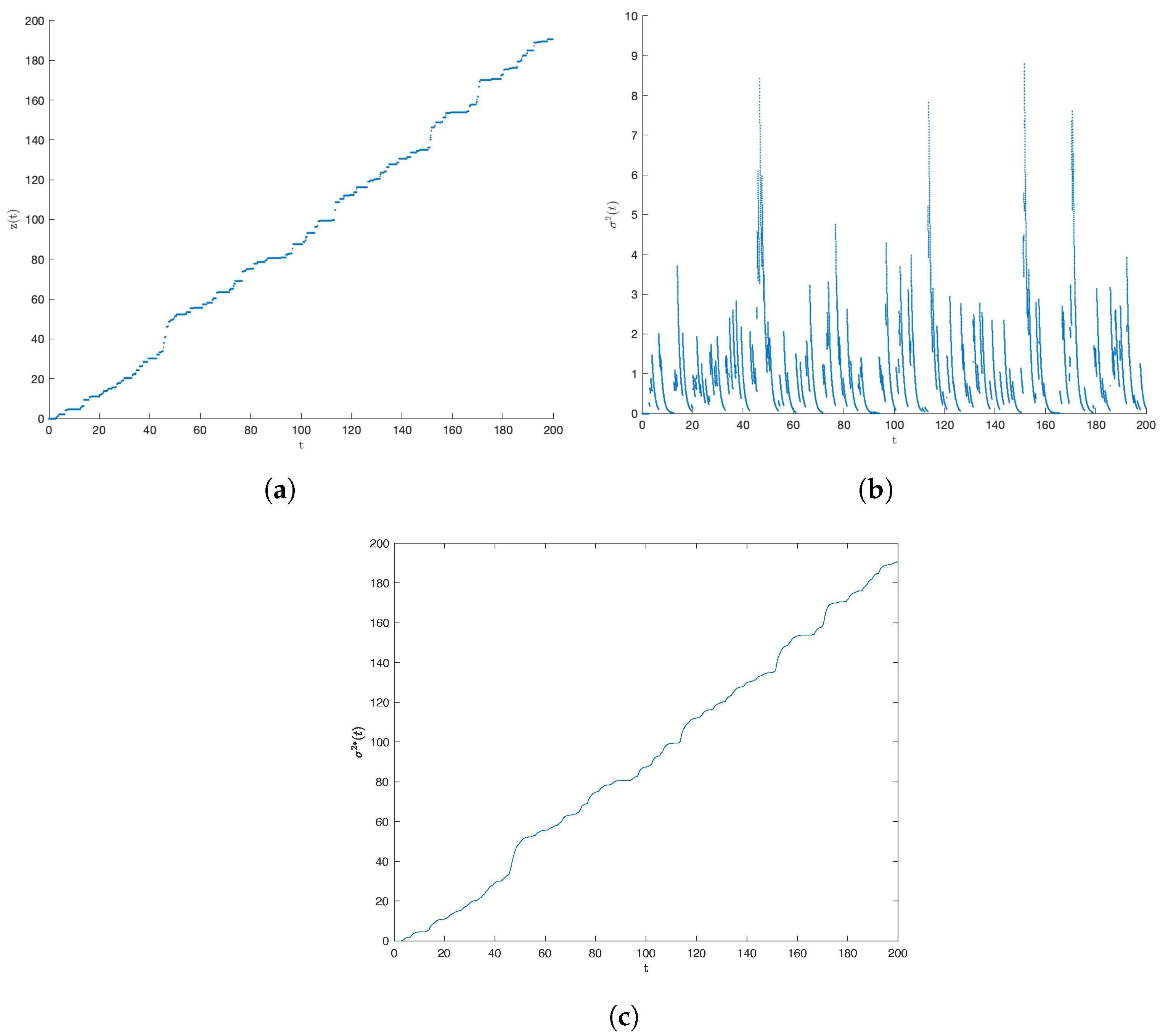
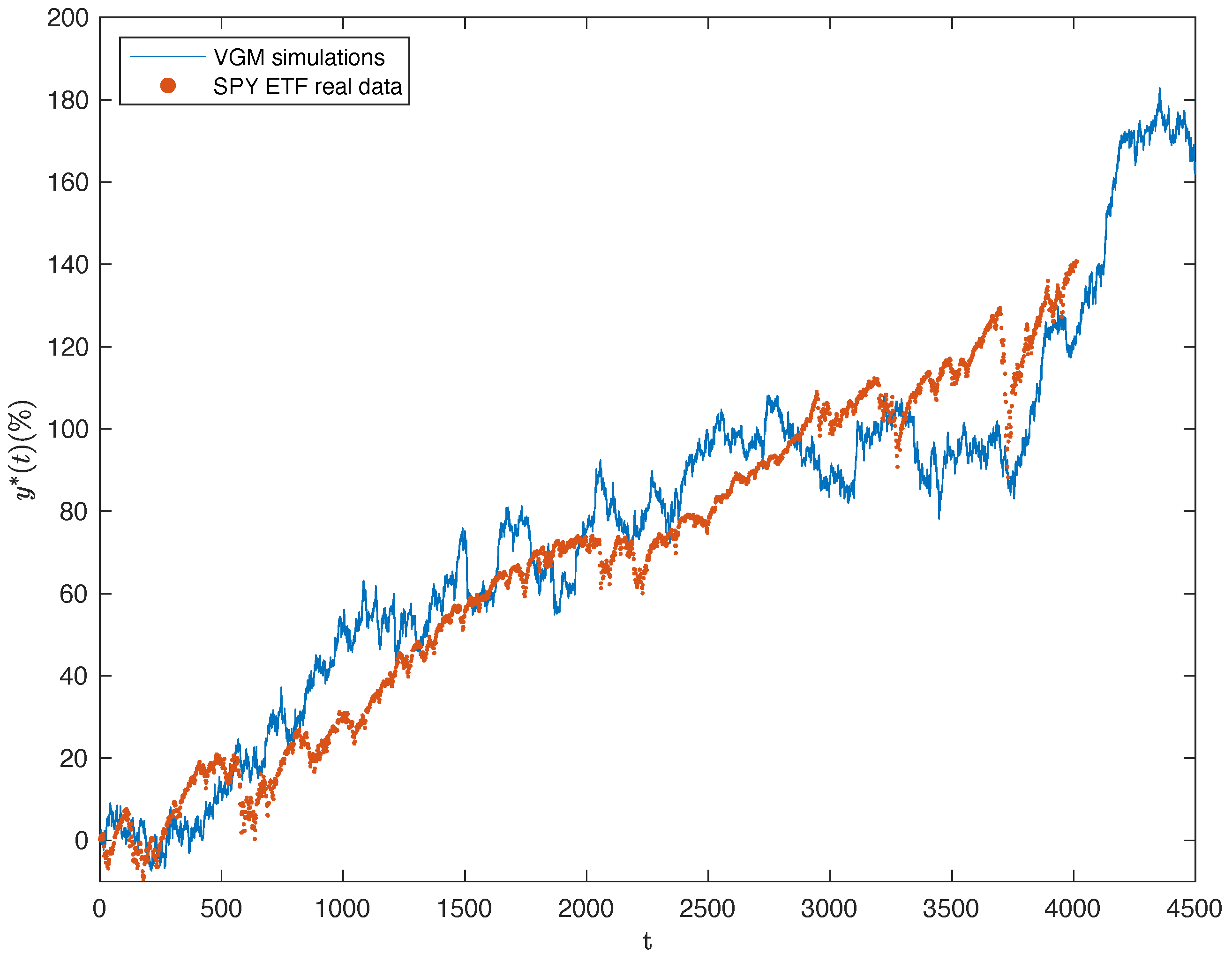
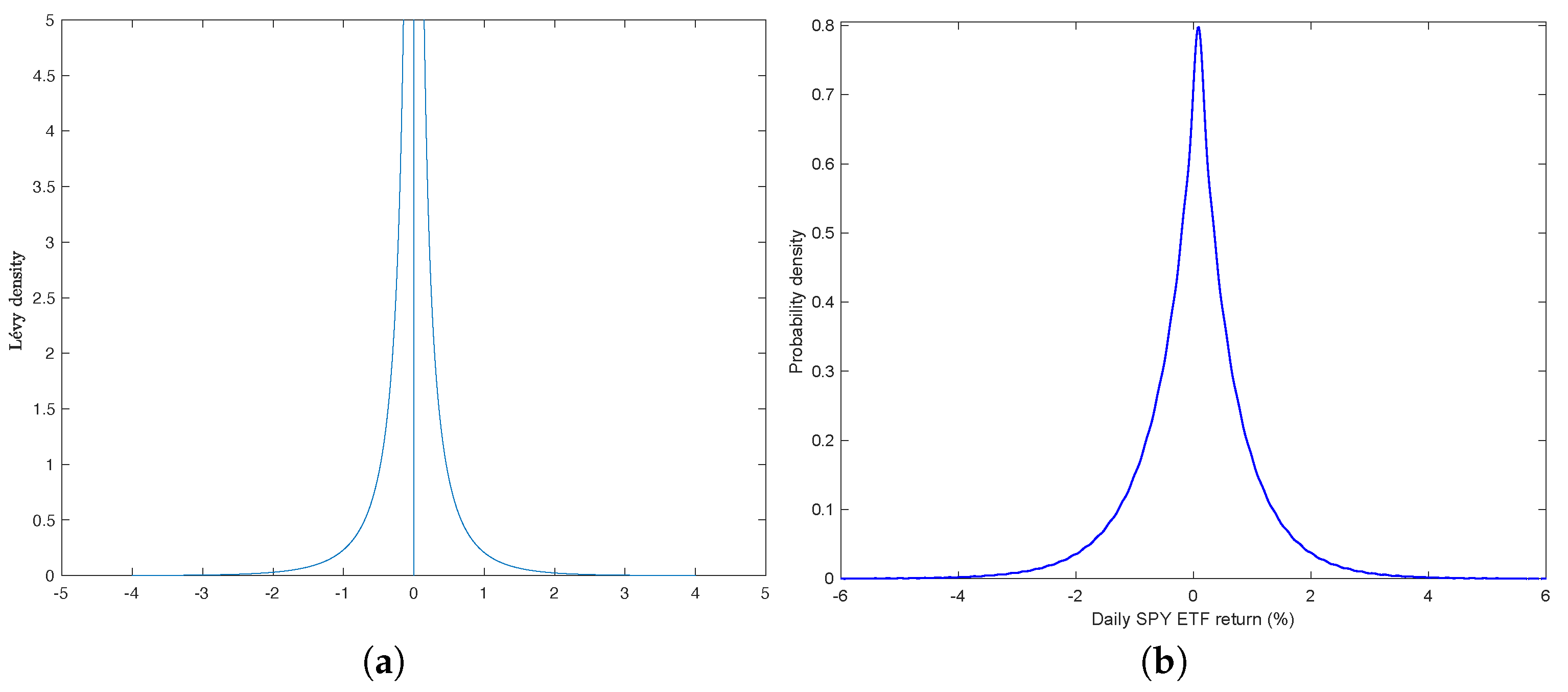
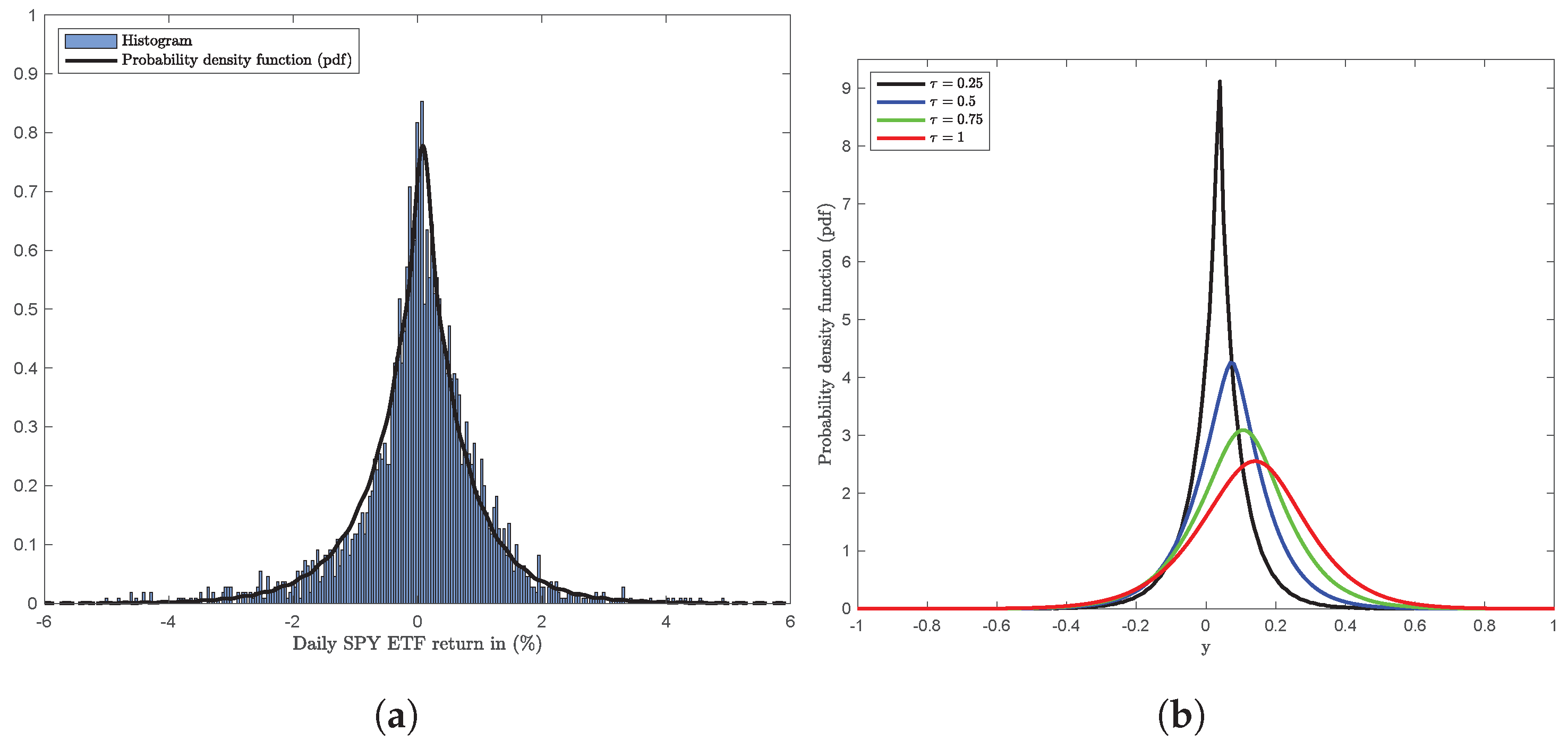
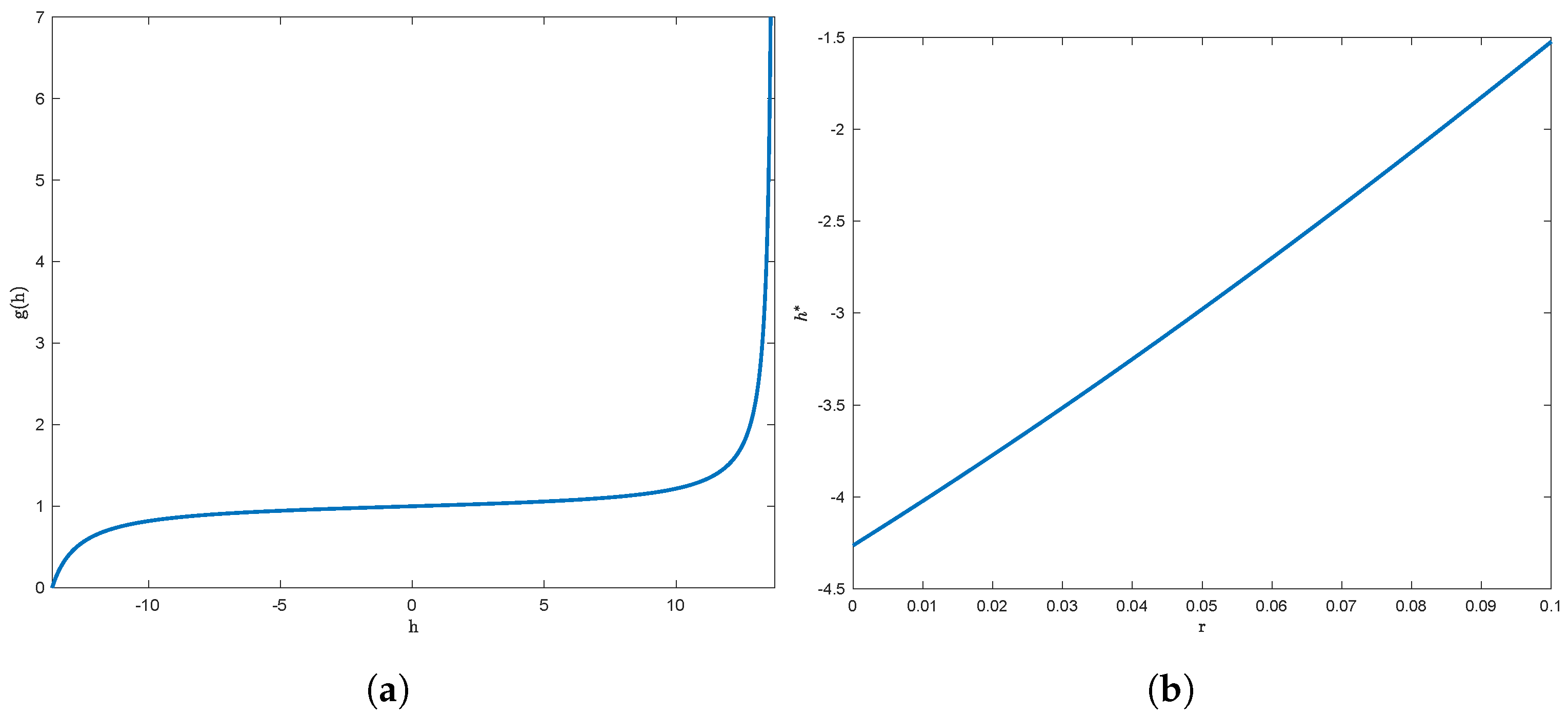
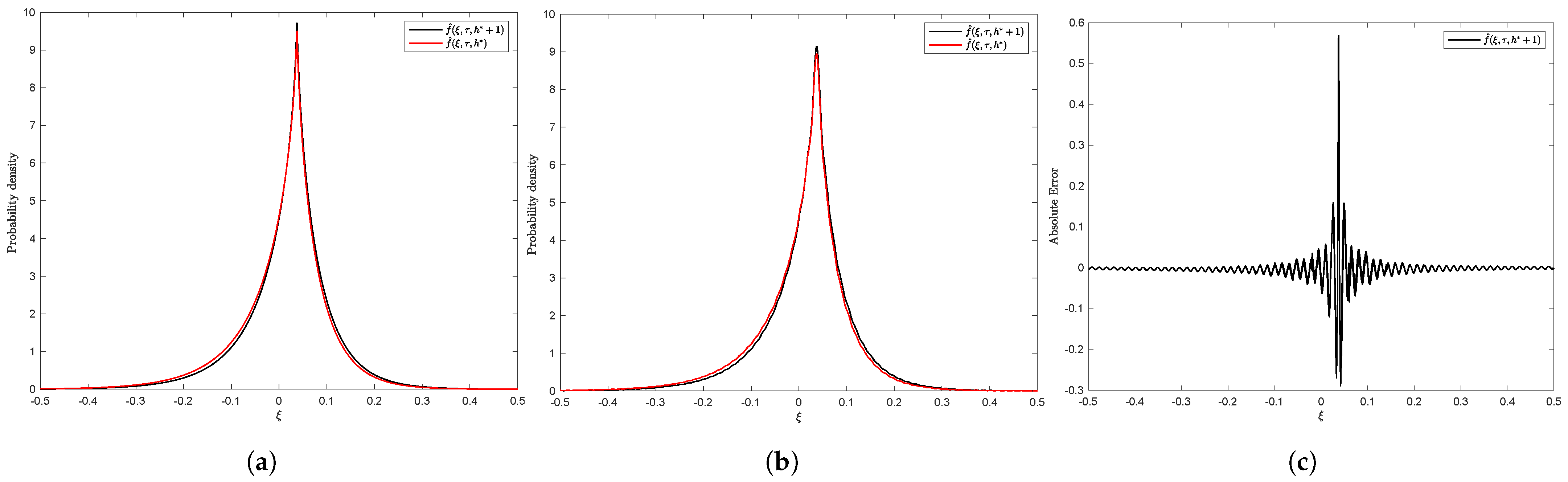
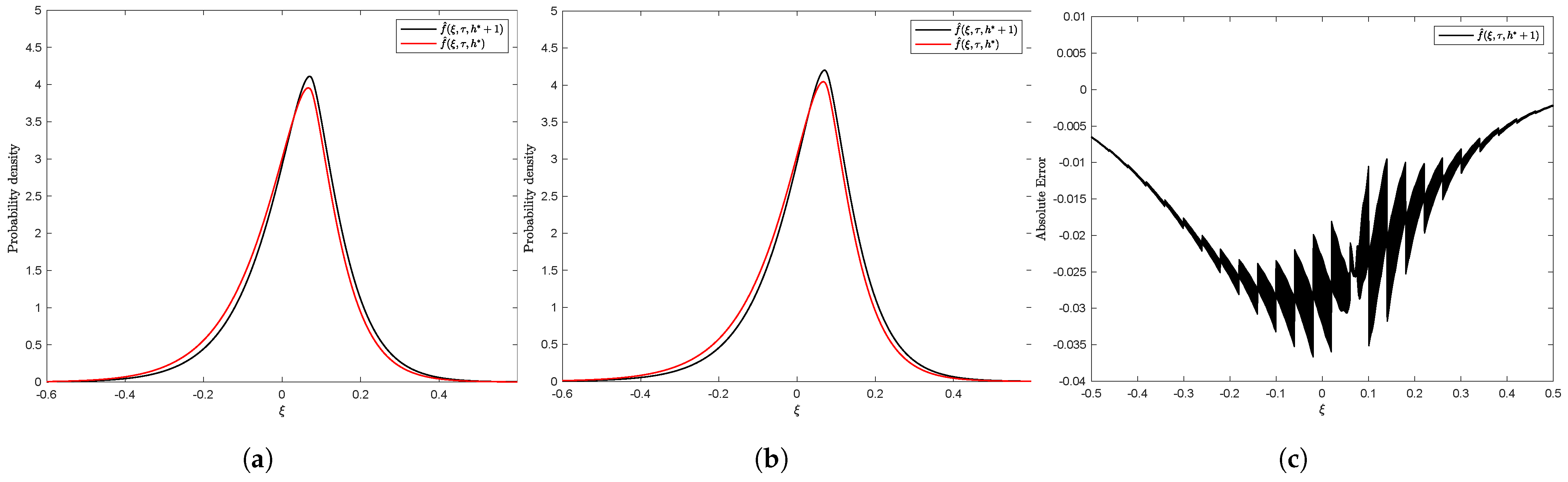
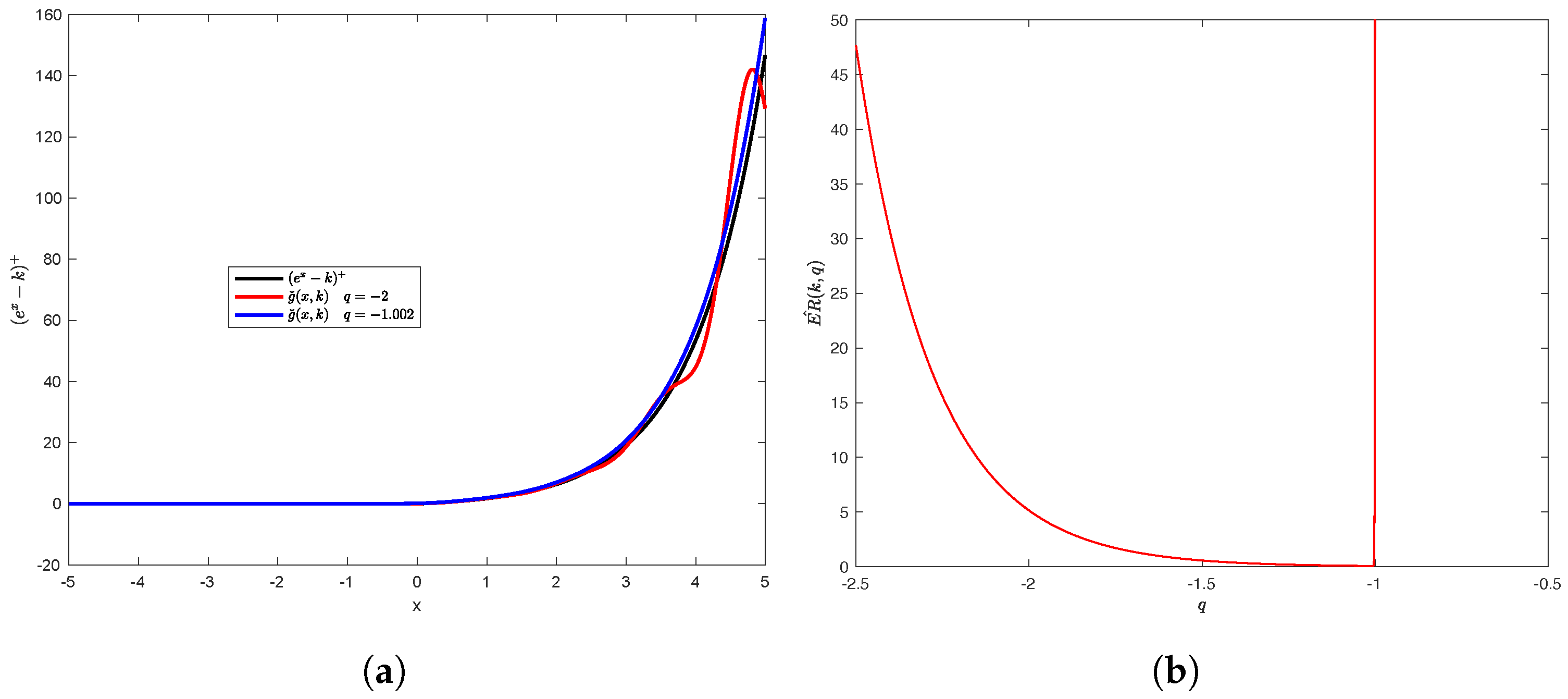
| Model | Parameters | Statistics |
|---|---|---|
| VG | ||
| Iterations | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | −3582.8388 | 598.743231 |
| 2 | 0.05905599 | −0.0009445 | 1.03195903 | 0.9130208 | 1.03208412 | −3561.5099 | 833.530396 |
| 3 | 0.06949925 | 0.00400035 | 1.04101444 | 0.88478895 | 1.05131996 | −3559.5656 | 447.807305 |
| 4 | 0.07514039 | 0.00055771 | 1.17577397 | 0.67326429 | 1.17778666 | −3569.6221 | 211.365781 |
| 5 | 0.08928373 | −0.0263716 | 1.03756321 | 0.83842661 | 0.94304967 | −3554.4434 | 498.289445 |
| 6 | 0.08676498 | −0.0521887 | 1.03337015 | 0.85591875 | 0.95066351 | −3550.6419 | 204.467192 |
| 7 | 0.086995 | −0.0608517 | 1.02788937 | 0.87382621 | 0.95054954 | −3549.8465 | 66.8039738 |
| 8 | 0.08542912 | −0.058547 | 1.02705241 | 0.88258411 | 0.94321299 | −3549.7023 | 15.3209117 |
| 9 | 0.08478622 | −0.0576654 | 1.02995166 | 0.88447791 | 0.93670036 | −3549.6921 | 1.14764198 |
| 10 | 0.08477798 | −0.0577736 | 1.02922308 | 0.88449072 | 0.93831041 | −3549.692 | 0.17287708 |
| 11 | 0.08476475 | −0.0577271 | 1.02960343 | 0.88450434 | 0.93755549 | −3549.692 | 0.07850459 |
| 12 | 0.08477094 | −0.0577488 | 1.02942608 | 0.8844984 | 0.93790784 | −3549.692 | 0.03723941 |
| 13 | 0.08476804 | −0.0577386 | 1.02950937 | 0.88450117 | 0.93774266 | −3549.692 | 0.01732146 |
| 14 | 0.0847694 | −0.0577434 | 1.02947043 | 0.88449987 | 0.93781995 | −3549.692 | 0.00813465 |
| 15 | 0.08476876 | −0.0577411 | 1.02948868 | 0.88450048 | 0.93778375 | −3549.692 | 0.00380345 |
| 16 | 0.08476906 | −0.0577422 | 1.02948014 | 0.88450019 | 0.9378007 | −3549.692 | 0.00178206 |
| 17 | 0.08476892 | −0.0577417 | 1.02948414 | 0.88450033 | 0.93779276 | −3549.692 | 0.00083415 |
| 18 | 0.08476898 | −0.0577419 | 1.02948226 | 0.88450026 | 0.93779648 | −3549.692 | 0.00039063 |
| 19 | 0.08476895 | −0.0577418 | 1.02948314 | 0.88450029 | 0.93779474 | −3549.692 | 0.00018289 |
| 20 | 0.08476897 | −0.0577419 | 1.02948273 | 0.88450028 | 0.93779555 | −3549.692 | |
| 21 | 0.08476896 | −0.0577418 | 1.02948292 | 0.88450029 | 0.93779517 | −3549.692 |
| Strike Price | Moneyness | BSM | VGM (68) | VGM (77) | BSM | VGM (68) | VGM (77) | BSM | VGM (68) | VGM (77) | BSM | VGM (68) | VGM (77) | BSM | VGM (68) | VGM (77) | BSM | VGM (68) | VGM (77) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period (In Year) | 0.0625 | 0.125 | 0.25 | 0.5 | 0.75 | 1 | |||||||||||||
| 219.49 | 2.00 | 220.31 | 220.28 | 219.86 | 221.13 | 221.10 | 220.48 | 222.76 | 222.72 | 221.71 | 225.98 | 225.93 | 224.14 | 229.15 | 229.13 | 226.53 | 232.27 | 232.26 | 228.88 |
| 225.12 | 1.95 | 214.70 | 214.74 | 214.10 | 215.54 | 215.58 | 214.74 | 217.21 | 217.25 | 216.01 | 220.52 | 220.54 | 218.53 | 223.77 | 223.82 | 221.01 | 226.97 | 227.04 | 223.45 |
| 231.04 | 1.90 | 208.80 | 208.83 | 208.18 | 209.66 | 209.69 | 208.84 | 211.38 | 211.41 | 210.16 | 214.77 | 214.80 | 212.77 | 218.10 | 218.16 | 215.34 | 221.39 | 221.47 | 217.88 |
| 237.29 | 1.85 | 202.58 | 202.53 | 202.10 | 203.47 | 203.42 | 202.79 | 205.23 | 205.18 | 204.16 | 208.71 | 208.67 | 206.86 | 212.13 | 212.13 | 209.53 | 215.51 | 215.53 | 212.16 |
| 243.88 | 1.80 | 196.02 | 196.06 | 195.38 | 196.92 | 196.97 | 196.10 | 198.73 | 198.78 | 197.51 | 202.31 | 202.37 | 200.32 | 205.83 | 205.93 | 203.10 | 209.31 | 209.43 | 205.84 |
| 250.85 | 1.75 | 189.07 | 189.16 | 188.47 | 190.01 | 190.10 | 189.21 | 191.87 | 191.96 | 190.68 | 195.55 | 195.66 | 193.61 | 199.17 | 199.33 | 196.50 | 202.75 | 202.94 | 199.36 |
| 258.22 | 1.70 | 181.72 | 181.81 | 181.36 | 182.69 | 182.78 | 182.13 | 184.60 | 184.69 | 183.66 | 188.39 | 188.52 | 186.70 | 192.12 | 192.30 | 189.71 | 195.81 | 196.03 | 192.70 |
| 266.05 | 1.65 | 173.93 | 173.98 | 173.53 | 174.92 | 174.97 | 174.33 | 176.89 | 176.95 | 175.92 | 180.79 | 180.91 | 179.09 | 184.64 | 184.83 | 182.24 | 188.45 | 188.69 | 185.37 |
| 274.36 | 1.60 | 165.64 | 165.64 | 165.45 | 166.67 | 166.66 | 166.28 | 168.70 | 168.70 | 167.94 | 172.73 | 172.82 | 171.26 | 176.70 | 176.87 | 174.56 | 180.63 | 180.88 | 177.84 |
| 283.21 | 1.55 | 156.83 | 156.75 | 156.56 | 157.88 | 157.81 | 157.43 | 159.98 | 159.91 | 159.18 | 164.14 | 164.21 | 162.66 | 168.25 | 168.42 | 166.14 | 172.33 | 172.59 | 169.60 |
| 292.65 | 1.50 | 147.42 | 147.28 | 146.81 | 148.51 | 148.38 | 147.73 | 150.68 | 150.56 | 149.56 | 154.98 | 155.05 | 153.24 | 159.24 | 159.45 | 156.93 | 163.49 | 163.79 | 160.59 |
| 302.75 | 1.45 | 137.37 | 137.50 | 136.72 | 138.50 | 138.63 | 137.69 | 140.74 | 140.89 | 139.62 | 145.20 | 145.61 | 143.53 | 149.64 | 150.21 | 147.45 | 154.08 | 154.76 | 151.34 |
| 313.56 | 1.40 | 126.60 | 126.45 | 126.29 | 127.77 | 127.64 | 127.31 | 130.09 | 129.99 | 129.36 | 134.73 | 135.00 | 133.53 | 139.39 | 139.85 | 137.71 | 144.06 | 144.63 | 141.86 |
| 325.17 | 1.35 | 115.03 | 115.01 | 114.85 | 116.24 | 116.25 | 115.94 | 118.65 | 118.71 | 118.15 | 123.51 | 124.07 | 122.64 | 128.44 | 129.20 | 127.14 | 133.40 | 134.25 | 131.59 |
| 337.68 | 1.30 | 102.57 | 102.48 | 102.35 | 103.83 | 103.80 | 103.53 | 106.34 | 106.39 | 105.94 | 111.50 | 112.20 | 110.84 | 116.79 | 117.68 | 115.72 | 122.10 | 123.05 | 120.53 |
| 351.18 | 1.25 | 89.11 | 89.15 | 88.69 | 90.42 | 90.55 | 90.00 | 93.08 | 93.33 | 92.69 | 98.68 | 99.71 | 98.12 | 104.44 | 105.61 | 103.48 | 110.16 | 111.34 | 108.71 |
| 365.82 | 1.20 | 74.53 | 74.60 | 74.52 | 75.91 | 76.15 | 76.02 | 78.82 | 79.18 | 79.08 | 85.10 | 86.32 | 85.17 | 91.45 | 92.73 | 91.09 | 97.65 | 98.88 | 96.78 |
| 381.72 | 1.15 | 58.69 | 59.15 | 58.38 | 60.22 | 60.94 | 60.20 | 63.67 | 64.34 | 63.82 | 70.94 | 72.47 | 70.85 | 77.99 | 79.48 | 77.46 | 84.70 | 86.09 | 83.68 |
| 399.07 | 1.10 | 41.51 | 42.09 | 41.76 | 43.56 | 44.29 | 44.08 | 48.03 | 48.30 | 48.53 | 56.55 | 57.74 | 56.68 | 64.32 | 65.45 | 64.03 | 71.52 | 72.55 | 70.80 |
| 418.08 | 1.05 | 23.73 | 24.37 | 24.15 | 27.03 | 27.33 | 27.36 | 32.83 | 32.25 | 33.00 | 42.51 | 43.25 | 42.47 | 50.85 | 51.63 | 50.57 | 58.42 | 59.16 | 57.83 |
| 438.98 | 1.00 | 8.92 | 6.45 | 6.76 | 13.11 | 11.13 | 11.40 | 19.53 | 18.35 | 18.43 | 29.61 | 29.17 | 29.01 | 38.11 | 38.01 | 37.61 | 45.79 | 45.79 | 45.20 |
| 462.08 | 0.95 | 1.64 | 1.19 | 1.27 | 4.40 | 2.94 | 3.02 | 9.62 | 7.41 | 7.50 | 18.70 | 17.17 | 17.09 | 26.72 | 25.85 | 25.50 | 34.12 | 33.67 | 33.01 |
| 487.76 | 0.90 | 0.10 | 0.35 | 0.40 | 0.89 | 0.96 | 1.02 | 3.68 | 2.82 | 2.94 | 10.42 | 8.69 | 8.83 | 17.24 | 15.73 | 15.71 | 23.87 | 22.75 | 22.48 |
| 516.45 | 0.85 | 0.00 | 0.10 | 0.13 | 0.09 | 0.31 | 0.34 | 1.02 | 1.03 | 1.11 | 4.96 | 3.92 | 4.09 | 10.02 | 8.48 | 8.63 | 15.46 | 13.90 | 13.93 |
| 548.73 | 0.80 | 0.00 | 0.03 | 0.04 | 0.00 | 0.10 | 0.12 | 0.19 | 0.37 | 0.41 | 1.94 | 1.66 | 1.78 | 5.12 | 4.19 | 4.37 | 9.10 | 7.80 | 7.96 |
| 585.31 | 0.75 | 0.00 | 0.01 | 0.01 | 0.00 | 0.03 | 0.04 | 0.02 | 0.12 | 0.14 | 0.60 | 0.64 | 0.72 | 2.23 | 1.85 | 2.02 | 4.76 | 3.91 | 4.14 |
| 627.11 | 0.70 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.04 | 0.04 | 0.14 | 0.23 | 0.26 | 0.80 | 0.75 | 0.83 | 2.15 | 1.77 | 1.91 |
| 675.35 | 0.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.02 | 0.07 | 0.09 | 0.22 | 0.27 | 0.31 | 0.81 | 0.72 | 0.81 |
| 731.63 | 0.60 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.03 | 0.05 | 0.09 | 0.11 | 0.24 | 0.26 | 0.31 |
| 798.15 | 0.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.03 | 0.06 | 0.08 | 0.10 |
| 877.96 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nzokem, A.H. Pricing European Options under Stochastic Volatility Models: Case of Five-Parameter Variance-Gamma Process. J. Risk Financial Manag. 2023, 16, 55. https://doi.org/10.3390/jrfm16010055
Nzokem AH. Pricing European Options under Stochastic Volatility Models: Case of Five-Parameter Variance-Gamma Process. Journal of Risk and Financial Management. 2023; 16(1):55. https://doi.org/10.3390/jrfm16010055
Chicago/Turabian StyleNzokem, Aubain Hilaire. 2023. "Pricing European Options under Stochastic Volatility Models: Case of Five-Parameter Variance-Gamma Process" Journal of Risk and Financial Management 16, no. 1: 55. https://doi.org/10.3390/jrfm16010055
APA StyleNzokem, A. H. (2023). Pricing European Options under Stochastic Volatility Models: Case of Five-Parameter Variance-Gamma Process. Journal of Risk and Financial Management, 16(1), 55. https://doi.org/10.3390/jrfm16010055






