1. Introduction
Is Main Street the cause of what happens on Wall Street or vice versa? In other words, do business cycles cause financial cycles or vice versa? This is a central question in macroeconomic research, policy analysis and financial practice. It is well known that business cycles are closely linked with financial cycles (e.g.,
Borio 2014;
Claessens et al. 2012). For example, expansions are good for both Main Street and Wall Street. Conversely, recessions are bad for both Main Street and Wall Street. When both the business and the financial cycles are close to their peak, business and financial conditions are especially good. When both the business and the financial cycles are close to their trough, business and financial conditions are especially tough. These stylized facts establish a correlation but not a causal relation between the business and financial cycles. Consequently, the direction of causality remains an important and yet unanswered question in the literature.
1The main objective of this paper is to fill this gap in the literature by evaluating the direction and timing of Granger causality between the business and financial cycles of the G7 countries. This allows us to evaluate the role of the financial sector in the propagation of economic fluctuations and vice versa, which has been at the heart of economic policy since the global financial crisis. Our analysis of Granger causality is based on a vector autoregression (VAR) model with one important innovation: data on business cycles, which are based on monthly industrial production, are at a higher frequency than data on financial cycles, which are based on quarterly aggregate credit. For this reason, we implement the mixed-frequency vector autoregression (MF-VAR) approach of
Ghysels et al. (
2016,
2020), which has several econometric advantages that we discuss in our analysis.
In addition to the mixed-frequency causality tests based on monthly industrial production and quarterly aggregate credit, we also perform same-frequency causality tests based on quarterly GDP and quarterly credit. The same-frequency analysis forms the benchmark against which the mixed-frequency results are assessed. The two approaches employ similar information since industrial production is highly correlated with GDP but are differentiated by data availability: industrial production data are available monthly, whereas GDP data are only available quarterly. Hence, the main advantage of mixed frequency is the use of more data for the same sample period, which, combined with the novel MF-VAR methodology of
Ghysels et al. (
2016,
2020), can lead to higher statistical power (
Ghysels 2016). Specifically, mixed-frequency causality tests avoid data aggregation and hence preserve the dynamics of the monthly variable, thus lowering the risk of detecting spurious causality.
2 In short, evaluating both the mixed-frequency and the same-frequency approach provides a comprehensive view of the causality between the real and financial sectors.
Our empirical investigation focuses on the G7 countries: USA, Canada, UK, Germany, France, Italy and Japan. The sample period ranges from 1962 to 2019. For each country, the mixed-frequency analysis evaluates whether the monthly industrial production index causes quarterly aggregate credit or vice versa. The same-frequency analysis evaluates whether quarterly GDP causes quarterly aggregate credit or vice versa. We also determine the timing of causality by identifying the periods when causality is statistically significant. We then assess the role of the US as a global leader in causing the domestic cycles of the other G7 countries. We do so by examining whether US industrial production (or credit) causes the industrial production (or credit) of each of the remaining G7 countries.
3In addition, we assess whether causality is related to the phase of the cycles, e.g., whether the causal relation between the two cycles is stronger in recessions or expansions. We then evaluate whether causality is related to the nominal interest rate, which is perhaps the most relevant economic fundamental for the two cycles. Finally, we enhance our understanding of financial cycles by exploring whether equity prices and housing prices have a causal relation with industrial production or GDP. Although aggregate credit is widely considered to be the primary determinant of financial cycles, equity and housing prices are also thought of as determinants of the financial cycle.
Our main finding is that, for the full sample period, there is strong causality between the business and financial cycles and it goes in both directions. Bidirectional causality is especially strong for the North American countries (USA and Canada). For the continental European countries (Germany post-1990, France and Italy), it is the business cycle that causes the financial cycle. For countries with strong financial centers (UK and Japan), it is the financial cycle that causes the business cycle. The exact timing of causality varies across countries, but for most countries causality is strong around the 2007-2008 global financial crisis. Moreover, causality tends to be a bit stronger during bad times, i.e., during business cycle recessions.
We also find that the US business cycle strongly causes the business cycles of five out of the six remaining G7 countries, with the exception being Japan. This causal relation is strong at all times but is slightly stronger during good times, i.e., during business cycle expansions. In contrast, there is little evidence that the US financial cycle is causing other countries’ business or financial cycles. Hence, US leadership is primarily based on its business cycle, not its financial cycle.
The strong bidirectional causality between the business and financial cycles is further confirmed when using the equity price index and the housing price index as alternative ways to describe the financial cycle. In particular, the evidence on the bidirectional causality between monthly industrial production and monthly equity prices is especially strong. Finally, for robustness, we separately assess causality for the four European countries for which monthly credit data are available for a shorter sample period beginning in the late 1990s. We find that the monthly credit results are generally consistent with the main analysis but a bit weaker due to the substantially shorter sample.
A general theme that pervades our findings is that mixed-frequency analysis provides stronger results. In some cases, the results are similar, but in many cases the mixed-frequency results are substantially stronger. For example, in assessing the US as a global leader, the US industrial production significantly causes another country’s credit for four out of six countries. In contrast, in evaluating whether quarterly US GDP causes other countries’ credit, there is no evidence of causality for any country. Similar findings are observed when using monthly equity price data, which delivers stronger results than quarterly equity price data. In conclusion, mixed-frequency analysis provides a crucial advantage in uncovering significant causal relations between the business and financial cycles.
The remainder of the paper is organized as follows. In the next section, we provide a literature review.
Section 3 describes the data and defines the business and financial cycles. The empirical framework for the causality tests using both mixed-frequency and same-frequency data is set out in
Section 4. In
Section 5, we report the empirical results. In
Section 6, we investigate the causal relation between housing prices, equity prices and credit. Policy implications are discussed in
Section 7, and, finally, we conclude in
Section 8.
2. Literature Review
Our empirical analysis is closely related to
Claessens et al. (
2012), who analyze the interaction between the business and financial cycles.
Claessens et al. (
2012) provide a methodology for dating financial cycles, which is then used to assess the overlap between the phases of the two cycles. For example, they assess whether financial cycle downturns coincide with business cycle recessions, as well as the extent to which this coincidence makes recessions worse. In contrast, our analysis takes a different approach by focusing on the direction and timing of the causal relation between the two cycles using a mixed-frequency methodology. In other words, our study concentrates on whether one cycle causes the other one for the G7 countries.
This paper is also related to several recent contributions to the literature, which we discuss briefly.
Stockhammer et al. (
2019) use annual data from seven OECD countries to study the interaction between the business and financial cycles based on a standard VAR approach.
Yan and Huang (
2020) use quarterly data from the US to assess the relation between the business and financial cycles both in the frequency domain using wavelet analysis and in the time domain using a standard VAR approach.
Strohsal et al. (
2019) use quarterly data from the US, UK and Germany to analyze financial cycles in the frequency domain using spectral analysis. Finally,
Prabheesh et al. (
2021) use quarterly data from India and Indonesia to study the relation between the business and financial cycles using a DCC-GARCH model and a structural VAR model.
Additionally, a recent strand of the literature examines the relation between credit, asset prices and real economic activity, based on the multivariate unobserved components time series model introduced by
Harvey and Koopman (
1997). For example,
Galati et al. (
2016) use this approach to extract financial cycles from quarterly time series of credit, the credit-to-GDP ratio and house prices for the US and five European countries for the sample period of 1970 to 2014.
Runstler and Vlekke (
2018) use an extended version of this model to estimate trend and cyclical components in real GDP, real credit, and real property prices using quarterly data from 1973 to 2014 for the US and five European economies. Finally, the WGEM Team on Real and Financial Cycles of the
European Central Bank (
2018) uses this approach to provide a comprehensive analysis that estimates financial cycles in 17 European Union countries and assesses their properties and relation to GDP cycles. Note that all these studies are based on quarterly data.
Our empirical focus on causality between the business and financial cycles is motivated by the theoretical framework of
Bernanke and Gertler (
1989) and
Kiyotaki and Moore (
1997). In this work, a productivity shock in the real economy is amplified and propagated due to credit constraints. For example, consider a firm that is highly leveraged with secured loans against collateralized fixed assets (e.g., land). Suppose that this firm experiences a temporary productivity shock that lowers its net worth. Due to credit constraints, the firm will be unable to borrow more and, therefore, will have to cut its future investment expenditure in fixed assets against which it borrows. This will hurt the firm in the next period as it earns less revenue; its net worth falls further; and again, due to credit constraints, it reduces investment. This feedback effect continues so that an initial temporary shock is amplified and propagated over many periods in the future. In short, therefore, credit constraints can reduce real economic activity, thus ensuring that the credit (financial) cycle has a profound effect on the business cycle.
4The
Bernanke and Gertler (
1989) and
Kiyotaki and Moore (
1997) argument relates to the effect of primary financial markets on real economic activity. It is also possible that real economic activity is affected by secondary financial markets in which securities are traded among investors (as in the stock market) without any capital flowing back to firms.
Bond et al. (
2012) discuss three reasons why secondary financial markets not only reflect but can also affect economic fundamentals. First, real decision makers learn new information (e.g., firm value) from secondary market prices and use this information to guide their real decisions, in turn affecting the firm’s cash flow and value. For example, credit rating agencies are known to be influenced by stock prices, and their decisions can determine the availability of credit to firms. Second, managers might care about the firm’s stock price because their compensation is often tied to the stock price, which in turn affects their incentives in taking real actions. Third, managers may even irrationally follow the stock price and use it as an anchor because of their belief that prices are informative. In all these cases, there will be a feedback effect from secondary financial markets to the real economy, thus motivating the causal relation between the business and financial cycles.
In addition,
Danielsson et al. (
2018) investigate the role of low volatility over long periods in causing banking crises, which in turn have an effect on both the financial and the business cycle. Long-lasting periods of low volatility in financial markets breed overoptimism, leading to credit expansions, excessive lending and a reallocation from safer to riskier assets. This eventually leads to future financial crises providing support to
Minsky’s (
1977) instability hypothesis described by the dictum “stability is destabilizing”. In the same spirit,
Lopez-Salido et al. (
2017) argue that during credit booms investors form overoptimistic expectations about the future. When in the future investors receive disappointing economic news relative to optimistic expectations, there is an endogenous reversal of sentiment, leading to a decline in economic activity induced by a contraction in the supply of credit (see also
Bordalo et al. 2018). In short, these arguments provide a theoretical motivation for the causal relation between the business cycle and the financial cycle that we empirically investigate in this paper.
Finally, there is a large literature on international finance, which motivates the direct effect of the US business and financial cycle in causing the domestic business and financial cycles of other countries. This literature assesses the determinants of international portfolio flows by making a distinction between push factors and pull factors. Push factors reflect the global economic forces that push bond and equity flows from the US to other countries, which are driven primarily by US GDP. Pull factors reflect the domestic economic forces that pull bond and equity flows into a country. In short, push factors are external to the economies receiving the flows and are typically the result of the US global leadership in determining bond and equity flows. This provides a direct economic mechanism through which the US business and financial cycle can affect other countries’ business and financial cycles. For a summary of this literature, see
Sarno et al. (
2016).
3. Business and Financial Cycles
We assess the causal relation between the business and financial cycles for the G7 industrialized countries: USA, Canada, UK, Germany, France, Italy and Japan. Our analysis determines the phase of the business cycle in each country in two distinct ways: using the monthly industrial production index or using quarterly GDP. Business cycles are typically determined by GDP, which, however, is only available at the quarterly frequency. In addition to GDP, we also use industrial production because it is available at the monthly frequency and hence more data are available for the same sample period. Other than the data frequency, the two variables provide similar information: industrial production is a standard measure of real economic activity and is near perfectly correlated with GDP. For example, the correlation between quarterly real US industrial production and quarterly real US GDP for our sample period is equal to
.
5The financial cycle is determined by quarterly aggregate credit, which is standard in the literature (e.g.,
Borio 2014;
Claessens et al. 2012). Credit is a natural aggregate for analyzing the financial cycle because it constitutes the most important link between savings and investment. Credit data are only available at the quarterly frequency. In a subsequent section, we also consider equity and housing price indices as determinants of the financial cycle. In the robustness section, we also consider a short sample of European countries for which credit data are available monthly.
3.1. Data
The seasonally adjusted monthly industrial production index (IPI) is obtained from the FRED database of the Federal Reserve Bank of St. Louis. The IPI data are in real terms. The sample period begins in January 1962 and ends in March 2019 for all countries.
The seasonally adjusted quarterly GDP is also obtained from the FRED database of the Federal Reserve Bank of St. Louis. The GDP data are in real terms. The sample period begins in Q1 (first quarter) of 1962 and ends in Q1 of 2019 for all countries.
Quarterly data on aggregate credit are obtained from the Bank for International Settlements. These data are for nominal aggregate credit in domestic currency offered by domestic banks to the private non-financial sector. The credit data begin on the following dates: Q1 of 1962 for the US, Canada and Germany; Q1 of 1964 for the UK; Q1 of 1965 for Japan; Q1 of 1970 for France; and Q1 of 1975 for Italy. For all countries, the credit data sample ends in Q1 of 2019.
We convert the credit data to real terms by dividing nominal credit by the consumer price index (CPI) of each country. The CPI index is obtained from the FRED database of the Federal Reserve Bank of St. Louis. With this conversion, all business and financial cycle variables are expressed in real terms. In order to avoid potential seasonal effects, we follow
Ghysels et al. (
2016) in using the annual growth rate of industrial production (month-by-month), GDP (quarter-by-quarter) and credit (quarter-by-quarter).
Table 1 reports summary statistics on the real annual growth rates of the three variables.
3.2. Defining Business Cycles
We define the business cycle for the US using the peak and trough dates determined by the National Bureau of Economic Research (NBER) business cycle dating committee. For the other six countries, we define the business cycle using the OECD-based recession indicators obtained from the FRED database of the Federal Reserve Bank of St. Louis. In all cases, the recession phase is defined as the period from the peak (exclusive) to the trough (inclusive), and the expansion phase is the period from the trough (exclusive) to the peak (inclusive).
3.3. Defining Financial Cycles
Following
Claessens et al. (
2012), we identify the phases of the financial cycle based on contractions and expansions of real credit. We identify the turning points in the log of real credit using the algorithm introduced by
Harding and Pagan (
2002). This is a well-established and reproducible methodology for dating different phases of a cycle. The algorithm requires a complete cycle to last at least five quarters and each phase to last at least two quarters. Specifically, a peak in the quarterly log-credit series
occurs at time
t if:
Similarly, a trough occurs at time
t if:
Using the terminology of
Claessens et al. (
2012), the recovery phase of the financial cycle (from trough to peak) is called the “upturn”, whereas the contraction phase (from peak to trough) is called the “downturn”.
3.4. Interaction of Business and Financial Cycles
Our analysis accounts for the interaction between the business and financial cycles by reporting results for three phases: (1) severe recessions, which we define as business cycle recessions that coincide with a financial cycle downturn; (2) recessions, which henceforth we define as business cycle recessions that do not coincide with a financial cycle downturn; and (3) business cycle expansions. Note that, by design, there is no overlap between severe recessions and recessions.
6Table 2 reports the growth rates for the monthly industrial production, quarterly GDP and quarterly aggregate credit during the three phases. In almost all cases, there is a monotonic relation of each variable with the three cycle phases: IPI, GDP and credit gradually improve as we move from a severe recession to a recession, and then to an expansion. This finding is consistent with previous literature (e.g.,
Borio 2014;
Claessens et al. 2012) as it indicates that (1) IPI, GDP and credit display strong cyclical behaviour; and (2) there is a strong interaction between the two cycles since they seem to be moving in the same direction. The interaction between the two cycles is indicated by the fact that severe recessions tend to be substantially worse than recessions. Having thus established this cyclical behaviour, the natural question to consider next is whether one cycle causes the other one.
4. Testing for Causality
An important aspect of our analysis is the use of both same-frequency (quarterly) data and mixed-frequency (monthly plus quarterly) data. This is primarily driven by data availability: industrial production data are available monthly, but GDP and aggregate credit are available quarterly. Throughout our analysis, we consider two causality cases: (1) the mixed-frequency case, which investigates the causal relation between monthly industrial production and quarterly credit; and (2) the same-frequency case, which investigates the relation between quarterly GDP and quarterly credit. Considering both cases provides a comprehensive view of the causality between the real and financial sectors. If, for example, both cases provide evidence of a significant causal relation then we take this to be a strong result that holds irrespective of the data frequency.
The use of monthly industrial production, rather than just quarterly GDP, enriches our analysis because industrial production data are available at a higher frequency than GDP data. Industrial production is a natural alternative to GDP because these two variables are almost perfectly correlated. This is the reason why industrial production has become the standard monthly variable to capture fluctuations in the real economy. In contrast, aggregate credit, which is the standard determinant of the financial cycle, is only available quarterly.
The benchmark approach in our empirical analysis is using same-frequency data, i.e., quarterly GDP and quarterly credit. Assessing the causal relation between GDP and credit requires a standard methodology. In contrast, the mixed-frequency approach requires a new methodology that has only recently become available by
Ghysels et al. (
2016,
2020). Since the mixed-frequency approach has not been implemented in the study of business and financial cycles, it constitutes a novel contribution to the literature.
In what follows, we describe the two sets of causality tests. First, we describe the mixed-frequency tests followed by the benchmark tests based on the quarterly frequency. Note that the quarterly frequency causality tests are a simple case of the more general mixed-frequency causality tests.
4.1. Mixed Frequency
We begin by introducing formal notation that distinguishes between three frequencies: monthly, quarterly and mixed frequency. The monthly variable is defined as , where denotes the quarterly time index, denotes the monthly time index, and is the number of months in one quarter. The quarterly variable is simply defined as .
The mixed-frequency process combines both the monthly and the quarterly variable by stacking them as follows:
where
. Therefore, at each quarter
,
contains three monthly observations for
and one quarterly observation for
.
4.2. Definition of Granger Causality
In order to define causality, we first define the mixed-frequency information set in period
as follows:
In other words,
contains all the information in
and
up to quarter
.
Then, according to
Granger (
1969), we assert that
does
not cause
at the quarterly horizon
h given
, a statement denoted as
, if:
Equation (
5) implies that the
h-quarter-ahead prediction of the quarterly variable
is uncorrelated with the past and present values of the monthly variable
.
Similarly,
does
not cause
at horizon
h given
, a statement denoted as
, if:
Equation (
6) implies that the
h-quarter-ahead prediction of the monthly variable
(a vector containing three months) is uncorrelated with the past and present values of the quarterly variable
.
4.3. The MF-VAR Model
We test for the causal relation between the high-frequency variable (monthly industrial production) and the low-frequency variable (quarterly credit) in the context of the mixed-frequency vector autoregression (MF-VAR) model introduced by
Ghysels (
2016).
7 We illustrate the model below for the simple case where
and
follow an AR(1) process:
or
In this MF-VAR specification, the parameters
,
, and
measure the impact of the lagged
on
. Similarly, the parameters
,
and
measure the impact of the lagged
on
. Furthermore, the matrix
N is positive definite, and hence it is invertible. Then, it is straightforward to show that the model is of the form:
where
and
.
8 4.4. Granger Causality Tests
4.4.1. Does Monthly Industrial Production Cause Quarterly Credit?
In the context of the MF-VAR model, we test whether monthly industrial production causes quarterly credit by estimating the following regression with ordinary least squares (OLS):
This regression follows
Ghysels et al. (
2016,
2020). We test whether
causes
by testing the null hypothesis that
using a Wald test statistic. Following
Ghysels et al. (
2016,
2020), the calculation of the Wald test statistic is based on a bootstrap method with a heteroskedasticity-robust covariance matrix.
4.4.2. Does Quarterly Credit Cause Monthly Industrial Production?
We test whether quarterly credit causes monthly industrial production by estimating the following regression with OLS:
This is a two-sided regression, which incorporates both leads and lags for
. This type of regression was originally introduced by
Sims (
1972) and follows
Ghysels et al. (
2020).
The main difference between regression models (
11) and (
12) is the lead variable
. The coefficient of the lead variable
is the focus of the quarterly-to-monthly causality test. From the point of view of
, the coefficient
represents the predictive relation between the lagged
variable and the
variable. Hence,
determines the quarterly-to-monthly causality. We assess whether
causes
by testing the null hypothesis that
using a Wald test statistic. Again, the Wald test statistic is based on a bootstrap method with a heteroskedasticity-robust covariance matrix.
4.4.3. Lag Selection
For both directions of causality, we follow
Ghysels et al. (
2016) in using 4 quarterly lags (
) and 12 monthly lags (
). This implies that for each causality test, we test 12 zero restrictions. This lag selection exhibits good performance with respect to Ljung-Box Q-tests for the serial correlation of residuals. The Ljung-Box Q-tests are based on the double blocks-of-blocks bootstrap method of
Ghysels et al. (
2020) with 10,000 replications.
In general, there is a tradeoff between adding more lag terms and the performance of Ljung-Box Q-tests. Adding more lags reduces the serial correlation of the residuals but augments the effect of parameter proliferation, which may cause a size distortion to the asymptotic properties of the Wald test. Our lag selection is designed to balance this tradeoff and is also effective in dealing with intra-year seasonalities since the lags use a full year of information.
9 4.5. Testing for the US as a Global Leader
The empirical framework we described so far is designed to test whether the industrial production of a country causes the credit of the same country or vice versa. We refer to this approach as the domestic cycle approach because it considers each country in isolation. We now turn to testing for the role of the US as a global leader in causing the business or financial cycle of another country.
Specifically, we test whether US industrial production (or credit) causes the industrial production (or credit) of another country. In order to do this, we estimate a variation of the original MF-VAR specification with two countries: the US and the domestic country denoted by D. This MF-VAR model is specified as follows:
where
and
,
are the monthly US and domestic variables, respectively;
and
are the quarterly US and domestic variables, respectively;
and
are the monthly error terms; and
and
are the quarterly error terms.
The causality tests for the US as a global leader are set up in a similar way to the tests for individual countries. The main difference here is that because the introduction of the US in the MF-VAR model substantially increases the dimension of the parameters to be estimated, the number of lags must be lower to make estimation feasible. We set
quarterly lags and
monthly lags, which is the highest number of lags that avoids estimation problems due to parameter proliferation. In other words, we test for 12 zero restrictions, which is the same number of restrictions estimated for the individual country results: here, we have half the number of lags but double the number of countries, hence the same number of zero restrictions. Again, the Wald test follows
Ghysels et al. (
2016) and is based on a bootstrap method with a heteroskedasticity-robust covariance matrix.
4.6. Testing for Causality at the Quarterly Frequency
The mixed-frequency causality tests are assessed against the benchmark of quarterly frequency causality tests. The two sets of tests (mixed vs. quarterly) are designed to have the same structure so that they are directly comparable. Specifically, we estimate the same regressions as in Equations (
11) and (
12), with the only difference being that monthly industrial production is replaced by quarterly GDP. For consistency, all lags are set at four quarters. Our approach is also similar in testing for the role of the US as a global leader: the VAR structure remains the same, but now all variables are quarterly.
5. Results
5.1. Domestic Business and Financial Cycles
We begin by assessing the direction of Granger causality between the business and the financial cycles of each individual country. We refer to the individual country cases as the domestic business and financial cycles.
Table 3 reports the
p-values of the Wald test over the full sample for two cases: the causal relation of IPI with credit for mixed frequency and the causal relation of GDP with credit for quarterly frequency. As previously shown in
Table 1, the full sample period is slightly different across countries with the longest sample period ranging from January 1963 to March 2019.
10The empirical evidence reported in
Table 3 indicates that there is strong causality between the business and financial cycles and that it often goes in both directions. This finding holds for both quarterly and mixed frequency. Our discussion focuses on the mixed-frequency results due to the inherent benefits of using higher frequency data (i.e., more data), the novelty of this approach and because the results tend to be stronger. Specifically, we find that IPI causes credit for 4 out of 7 countries, whereas credit also causes IPI for 4 out of 7 countries. For the US and Canada, there is strong bidirectional causality. For France and Italy, it is IP that significantly causes credit. For the UK and Japan, it is credit that significantly causes IPI. Finally, for Germany causality is not significant in either direction, but, as we discuss below, this result is reversed for the post-1990 German reunification period.
The quarterly-frequency results are similar to the mixed-frequency results but overall are a bit weaker. Specifically, the quarterly-frequency p-values are significant for the same cases as the mixed-frequency p-values, with two notable exceptions. First, for the US and Canada quarterly p-values fail to capture the fact that financial cycles cause business cycles; they only show that business cycles cause financial cycles. Second, for Italy the results are actually reversed: for mixed frequency it is the business cycle that causes the financial cycle but for quarterly frequency it is the financial cycle that causes the business cycle. All of the other results for individual countries are the same.
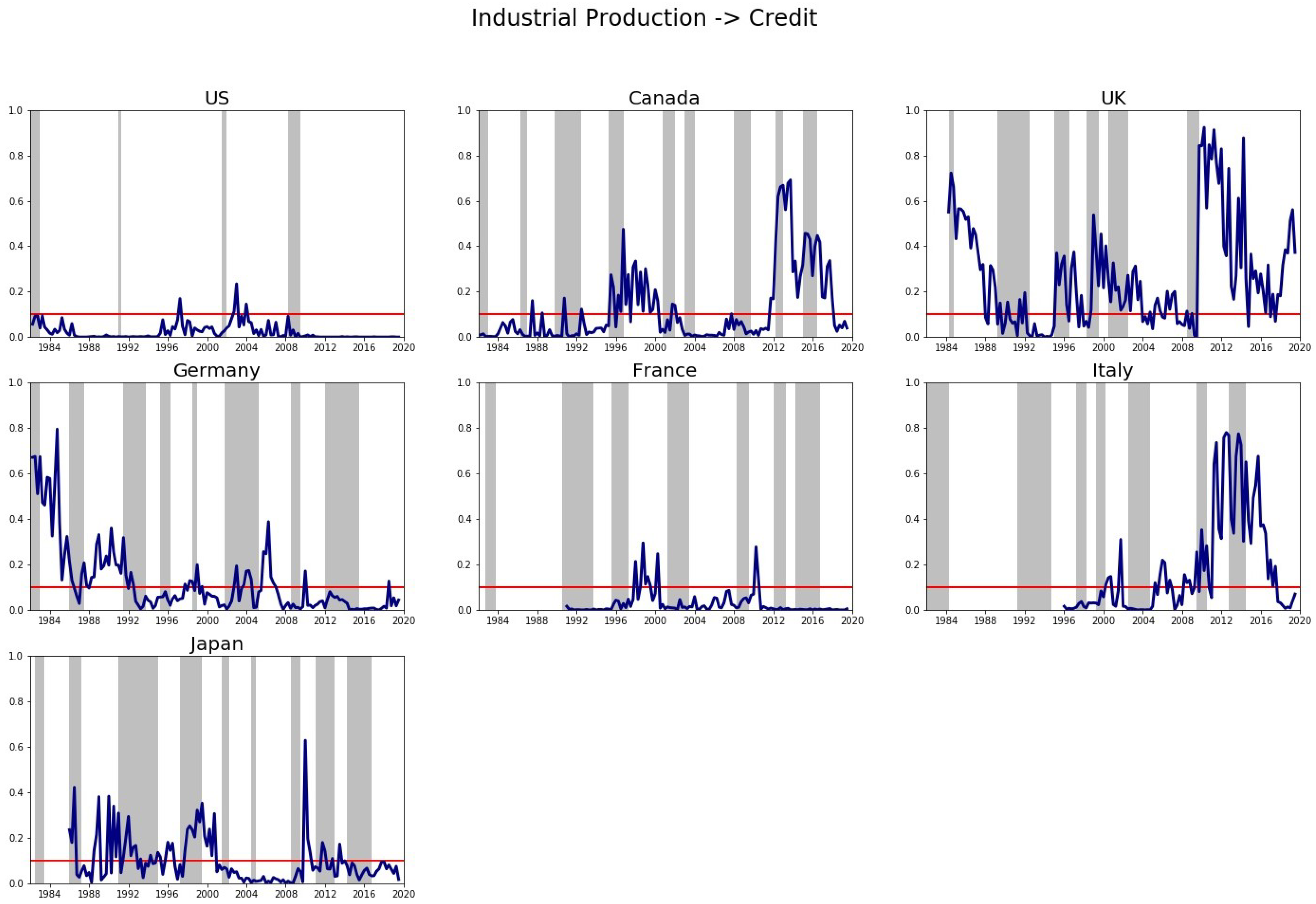
The full sample results in
Table 3 are complemented by
Figure 1 and
Figure 2, which display the
p-values period-by-period using a rolling window of 20 years so that the first
p-value is available for January 1983. The grey areas indicate recessions and severe recessions. Given that the full sample results, with few exceptions, are similar for mixed and quarterly frequency, the figures report results for the mixed-frequency case since this case is more general. The contribution of the figures is that they indicate which time periods are associated with significant causality and which are not. According to the figures, the strongest results (in the sense that causality is significant for long periods of time) relate to IPI-causing credit in the US and France. In addition, in many cases, bidirectional causality is significant around the 2007-2008 global financial crisis. Germany is also an interesting case since we can see that causality of IPI to credit becomes predominantly significant in the post-1990 German reunification period.
In summary, these findings are interesting since for the North American countries (USA and Canada) the business and financial cycles strongly cause one another. For the continental European countries (Germany post-1990, France and Italy), it is the business cycle that causes the financial cycle. Finally, for countries with strong financial centers (UK and Japan), it is the financial cycle that causes the business cycle.
5.2. The US as a Global Leader
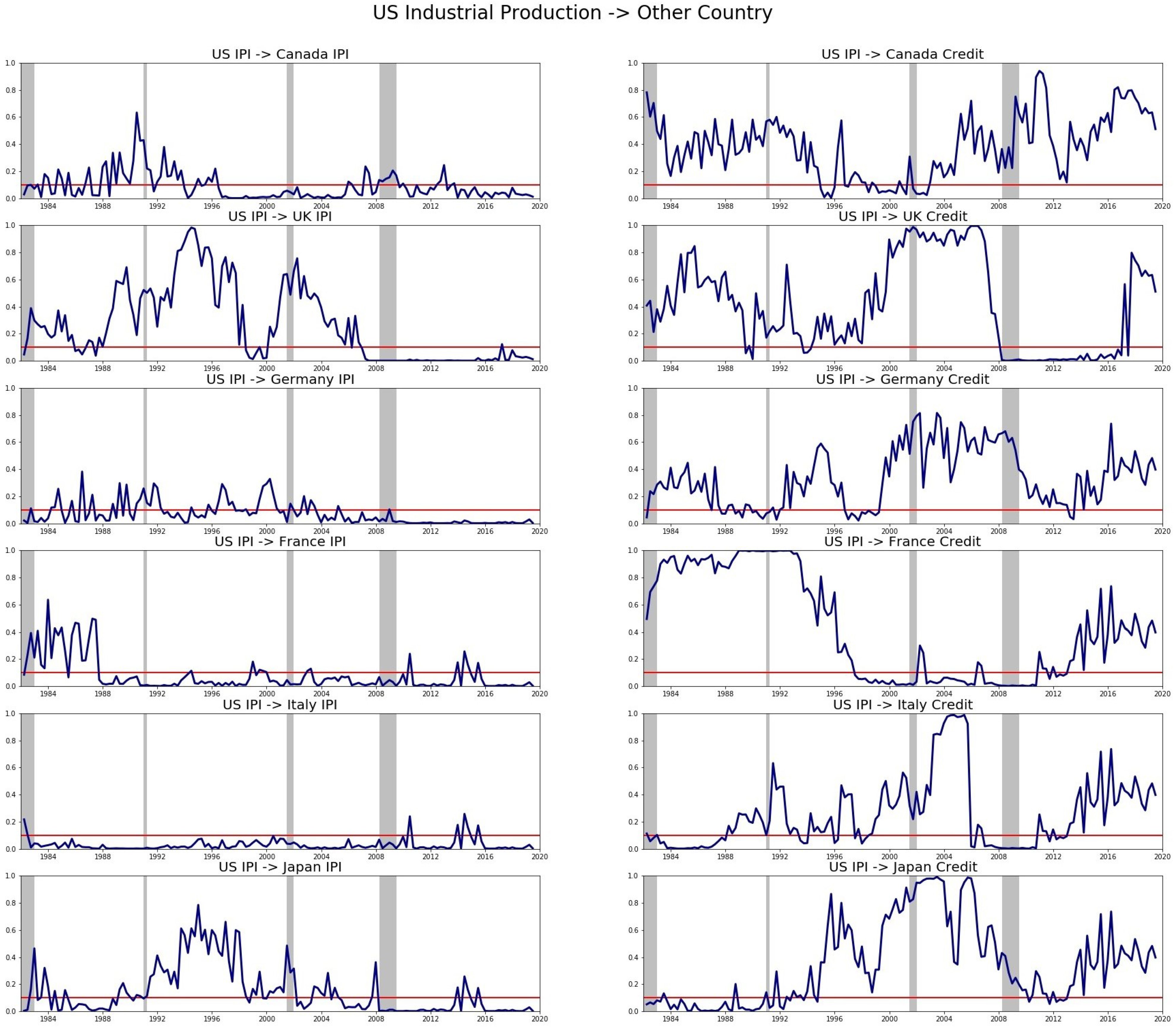
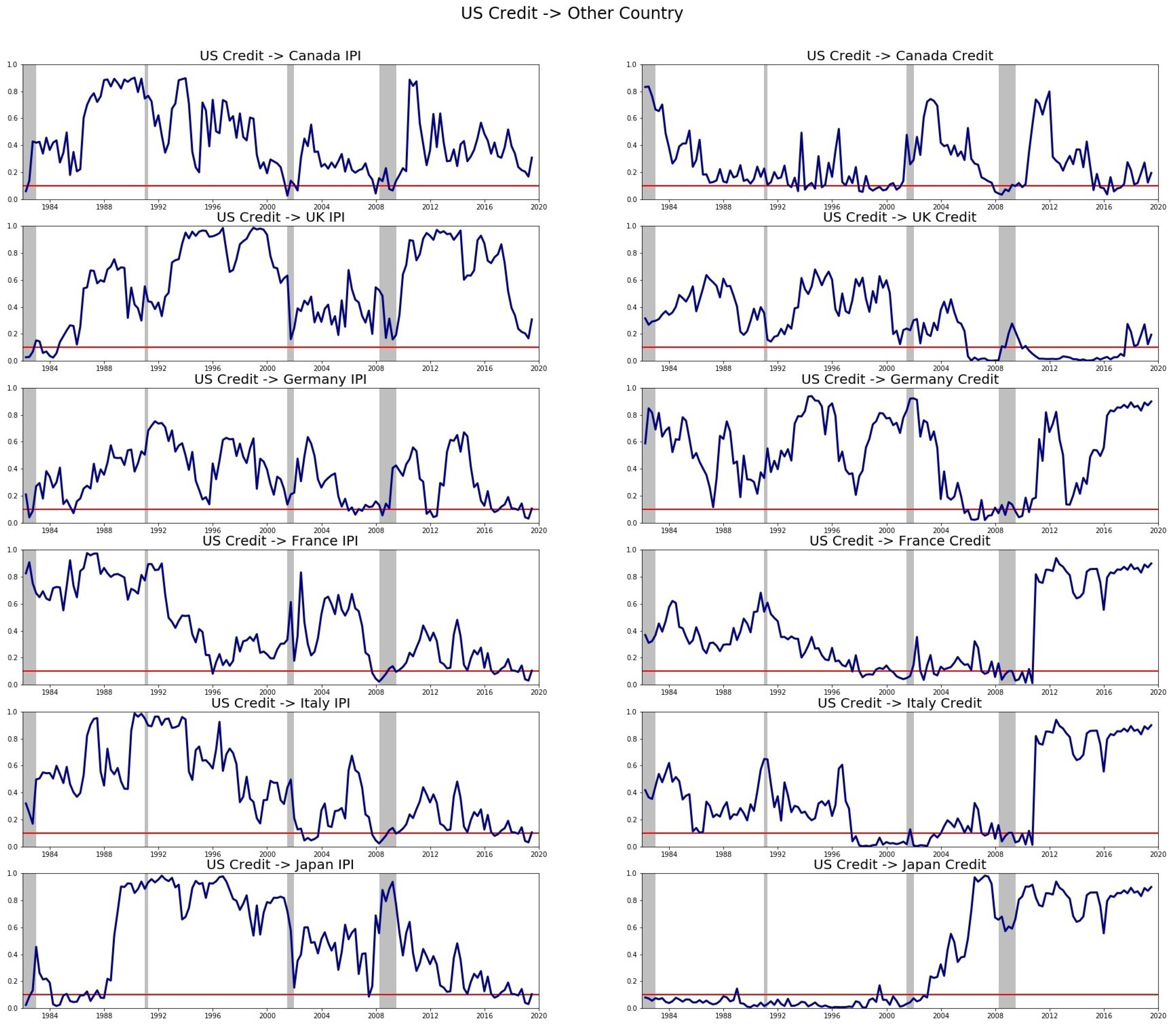
Next, we turn to the role of the US as a global leader, where we examine the following four cross-country causal relations: (1) US IPI causing the IPI of another country, (2) US IPI causing the credit of another country, (3) US credit causing the IPI of another country, and (4) US credit causing the credit of another country. The results are reported in
Table 4 and
Figure 3 and
Figure 4.
Our main finding here is that, for mixed frequency, the US IPI strongly causes the IPI of other countries: the p-value is significant for 5 out of 6 countries (the exception being Japan). The result for quarterly frequency is slightly weaker: the US GDP significantly causes the GDP of 4 out of 6 other countries. Therefore, there is strong evidence that the US business cycle strongly causes the business cycle of other countries.
In terms of the US business cycle causing other countries’ financial cycle, the evidence is strong only for mixed-frequency data (4 out of 6 countries) but is weak for quarterly data (no significance for any country). This is the one case where the mixed-frequency results deviate substantially from the quarterly-frequency results. Given the more general nature of mixed-frequency tests, we take these results as evidence that the US business cycle is transmitted to the financial cycle of other countries.
In terms of the US financial cycle causing other countries’ business or financial cycles, the evidence is generally weak, regardless of data frequency and real activity measure. These results are confirmed by
Figure 3 and
Figure 4, which plot the period-by-period
p-value of the causality tests.
We conclude that the US business cycle strongly causes the business cycle of most other countries. This is an interesting result as it indicates that only the business cycle of the US, and not its financial cycle, has an effect on other countries’ real economic activity. In short, we find strong evidence that real economic activity in the US is transmitted to other countries’ real economic activity, thus supporting the view that the US is a global leader.
5.3. Is Causality Cyclical?
Having established the bidirectional causality of domestic business and financial cycles as well as the leading effect of US business cycles on other countries’ business cycles, we now turn to relating causality to the phase of the cycles. In other words, we ask the following question: when is causality the strongest? Is it during severe recessions, during recessions or during expansions? To answer this question, we compute how often (as a percentage of all time periods) the
p-value is less than or equal to 0.1 during a particular phase. In other words, we assess how often causality is significant during one of the phases.
Table 5 has the results for individual countries, whereas
Table 6 has the results for the US as a global leader.
First, we assess the extent to which causality is cyclical for the domestic cycles. Our discussion again focuses on the mixed-frequency results that seem to be the strongest. We find that for the majority of countries, business cycles cause financial cycles more often in severe recessions and less often in expansions. In simple words, the worse the economic conditions the more likely that IPI causes credit. For the US, for example, in severe recessions the causal relation of IPI to credit is always significant (i.e., 100% of the time). This confirms our main result that the business cycle tends to cause the financial cycle in most countries but also adds to this finding that causality is more likely in severe recessions, where these are defined as business cycle recessions occurring at a time of a financial cycle downturn.
Next, we assess the role of the US as a global leader by computing the proportion of times that causality is significant in terms of the US business/financial cycle’s effect on another country’s business/financial cycle. In this case, we define the three phases (severe recession, recession and expansion) using as references both the US cycle and the domestic cycle. In other words, each phase is shown both from the point of view of the US and that of the other country. Given our previous evidence that the US credit has little or no effect on the domestic cycles,
Table 6 displays the results only for the US business cycle causing the domestic business cycles with both mixed and quarterly frequency data.
Our main result again involves the mixed-frequency data: for most countries, we find that the US IPI causes the domestic IPI more often during expansions. In other words, the transmission of the US business cycle to other countries’ business cycles is more likely when the economy is at its best. This is primarily true when we look at cycle phases from the point of view of the US. Overall, this is an important finding because it indicates that the US is a global leader in exporting its expansions to other countries—more so than its (severe) recessions. To be precise, the US also exports its (severe) recessions to other countries, but the transmission effect is stronger in expansions than in recessions.
In conclusion, the domestic business cycle is more likely to cause the domestic financial cycle when the economic conditions are bad. In contrast, the US business cycle is more likely to cause the domestic business cycles when the economic conditions are good. In short, the domestic business cycle transmission is more likely in recessions, but the US business cycle transmission is more likely in expansions.
5.4. Causality and the Interest Rate
The interest rate is perhaps the most relevant economic variable in terms of affecting both the business and the financial cycle. We relate causality to the interest rate by forming a dummy variable that takes the value of 1 if the p-value for causality at a given time period is less than 0.1, and 0 otherwise. Hence, the dummy variable indicates when causality is significant. The p-value is taken from the rolling-window regressions. Then, for individual country analysis, we estimate a probit regression of the dummy variable on the domestic nominal interest rate. In other words, we assess whether interest rates are related to significant p-values for causality. In this analysis, a positive coefficient on the interest rate implies that a higher interest rate makes causality more likely and vice versa.
For the cross-country analysis (i.e., assessing the leading role of the US), we estimate a probit regression of the dummy variable on the
difference between the domestic and the US nominal interest rate. Using the difference in interest rates is standard practice in international finance when two countries are involved, for example, in interest parity conditions (e.g.,
Della Corte et al. 2009;
Li et al. 2015). Note that interest rates are the 3-month Treasury Bill rates obtained from the FRED database of the Federal Reserve Bank of St. Louis. The results are reported in
Table 7.
We find that for individual countries, causality consistently displays a significant relation to the nominal interest rate, but the sign of the relation differs across countries. In most cases, the sign tends to be positive. For example, when focusing on the mixed-frequency results, the sign of the probit regression coefficient on interest rates is positive for six cases and negative for two. This finding indicates that the interest rate is significantly related to causality in most cases and, when it is, the relation tends to be positive. In short, the higher the interest rate the more likely for one domestic cycle to be causing another domestic cycle.
For the US leadership analysis, causality is also significantly related to the interest rate differential for the majority of cases. When it is, however, the relation tends to be negative. For example, when focusing on the mixed-frequency results, the sign of the probit regression coefficient on the interest rate differential is positive for 5 cases and negative for 12. A negative sign implies that causality is high when the interest rate differential is low, i.e., when either the domestic interest rate is low or the US interest rate is high, or both. In other words, the US tends to export its cycles to other countries when the US interest rate is higher than the domestic interest rate.
6. Equity Prices, Housing Prices and Credit
In this section, we add two further variables to our analysis of the financial cycle: equity prices and housing prices. Aggregate credit is typically the primary variable used in the literature for the study of financial cycles. However, equity and housing prices have also been used, in addition to credit, to provide a comprehensive view of financial cycles (see, e.g.,
Claessens et al. 2012).
6.1. Equity and Housing Price Data
The financial cycle data on equity prices are available both at the monthly and the quarterly frequency. We use the MSCI stock price index to represent the equity price index (EPI) of each country, which is obtained from the Refinitiv Eikon database. The monthly and quarterly EPI data are converted to real terms by dividing by the CPI of each country. The EPI sample period for all seven countries ranges from January (Q1) 1971 to March (Q1) 2019.
The financial cycle data on housing prices are available only at the quarterly frequency. The quarterly housing price index (HPI) is obtained from the OECD Main Economic Indicators for all countries except for the UK. For the UK, we use the Halifax Housing Price Index obtained from the Refinitiv Eikon database because it is not available from the OECD. The HPI data are converted to real terms in the same way as the EPI data above. The sample period for HPI begins on Q1 of 1971 for all countries except for Q1 of 1969 for the UK and Q1 of 1962 for Japan. The sample period ends in Q1 of 2019 for all countries.
Similar to our main analysis, the analysis of HPI and EPI is based on annual growth rates.
Table 8 reports summary statistics for the real annual growth rates of the monthly and quarterly equity price indexes as well as the quarterly housing price indexes.
6.2. Causality Tests Using Housing and Equity Prices
We take a deeper look into the workings of the financial cycle by providing a comprehensive assessment of the following causal relations between a business cycle variable and a new financial cycle variable: (1) monthly IPI causing monthly EPI or vice versa; (2) quarterly GDP causing monthly EPI or vice versa; (3) quarterly GDP causing quarterly EPI or vice versa; (4) monthly IPI causing quarterly HPI or vice versa; and (5) quarterly GDP causing quarterly HPI or vice versa. Some of these relations are same frequency (monthly or quarterly) and some are mixed frequency. The full sample results are reported in
Table 9. Note that the sample periods reflect the sample periods reported in
Table 8.
The results confirm our main finding that there is bidirectional causality between the business and financial cycles: business cycles cause financial cycles and vice versa. For example, monthly IPI significantly causes monthly EPI for four out of the seven countries, whereas monthly EPI significantly causes monthly IPI for six countries. Hence, the causal relation between IPI and EPI is strong and bidirectional.
More importantly, we find that monthly and mixed frequency results are much stronger than quarterly results. For example, monthly IPI significantly causes monthly EPI for four countries, but quarterly GDP causes quarterly EPI for only one country. Similarly, monthly EPI significantly causes monthly IPI for six countries, but quarterly EPI causes quarterly GDP for four countries. In addition, monthly IPI significantly causes quarterly HPI for four countries, but quarterly GDP significantly causes quarterly HPI for only two countries.
In summary, there is a clear pattern in the results: the monthly and mixed frequency results are similar, but the quarterly results are weaker. This indicates the importance of using monthly data over quarterly data where possible. It also justifies the use a mixed-frequency approach when monthly data are not available for both variables. To conclude, using EPI and HPI as additional variables to describe financial cycles confirms our main finding of bidirectional causality between the two cycles and provides strong evidence that a mixed frequency approach performs better than just using quarterly data.
7. Robustness: Using Monthly European Credit Data
Our main analysis is based on quarterly credit data because monthly credit data are not available for the G7 countries. However, the European Central Bank makes monthly credit data available for the subset of the four European G7 countries (UK, Germany, France and Italy) over a short sample period. For robustness, this section uses the European monthly credit data in assessing the causality between the business and financial cycles. Specifically, the monthly credit data are obtained from the Statistical Data Warehouse of the European Central Bank.
11Table 10 reports summary statistics on the European data. The sample period begins in September 1998 for three countries (Germany, France and Italy) and in January 2000 for the UK. For all four countries, the sample period ends in March 2019, which is the end date for all data used in our analysis. As previously, we use annual growth rates expressed in real terms.
The availability of monthly data allows us to implement monthly same-frequency causality tests rather than having to rely on mixed frequency tests. We assess Granger causality between the monthly IPI and monthly credit, and we report the results in
Table 11. Our main finding is that there is significant bidirectional causality for two of the four countries: the UK and France. For the other two countries, Germany and Italy, causality is not significant. Of the eight cases considered in
Table 11, five of them match the result of the main analysis: significant causality of IPI to credit for France, lack of significant causality of IPI to credit for Germany, significant causality of credit to IPI for the UK, and lack of significant causality of credit to IPI for Germany and Italy. For the remaining three cases, there is no match with the results of the main analysis.
Overall, these monthly results appear to be a bit weaker than the main analysis based on mixed frequency results. We conjecture that the weaker results are due to the much shorter sample period: whereas in the main analysis the sample period begins in the early 1960s, in this section it begins in the late 1990s, a difference of over 35 years of data. In other words, our main analysis is based on a sample period that is almost three times longer than the European data. We conclude, therefore, that for the four European countries the results are stronger when we use mixed-frequency analysis for a longer sample period than monthly same-frequency analysis for a much shorter sample period.
8. Discussion and Policy Implications
Understanding the nature of aggregate credit risk (as exemplified by the financial cycle) has important implications for macroeconomic and financial stability. For example,
Schularick and Taylor (
2012) argue that, in the postwar era, credit aggregates are crucial for understanding macroeconomic fluctuations. This is known as the “credit view”. In contrast,
Baker et al. (
2018) provide new evidence in favour of the “money view” of
Friedman and Schwartz (
1963), where broad money aggregates outperform credit aggregates in predicting economic downturns. In either case, credit is essential for determining the financial cycle, and this in turn has important implications for real economic activity. Therefore, it is a priority for central banks to pay attention to the systemic implications of credit aggregates in addition to following inflation targeting rules.
Previous research has identified two important features of the financial cycle (see, e.g.,
Borio et al. 2018). First, financial cycle peaks tend to coincide with banking crises. During expansions, rapid increases in credit drive up property and asset prices, which in turn increase collateral values and thus the amount of credit the private sector can obtain. In recessions, this process is reversed and can lead to a “balance sheet recession” (termed by
Koo 2003) based on the mutually reinforcing interaction between financing constraints and perceptions of value and risk. Balance sheet recessions tend to be deeper, followed by a weaker recovery and can result in permanent output loss.
Second, the financial cycle can be much longer than the business cycle. While the business cycle typically lasts up to eight years, the average length of the financial cycle is about 16 years (see, e.g.,
Borio 2014). The difference in length means that a financial cycle can span more than a business cycle. As a result, while the financial cycle peaks tend to usher in recessions, not all recessions will be preceded by financial cycle peaks.
12Borio (
2014) provides a thorough discussion of the policy implications of dealing with severe recessions due to the interaction of business and financial cycles. This discussion is also relevant in our context. Our main contribution is to determine the direction and timing of causality between the business and financial cycles. Therefore, our analysis allows us to pinpoint when a country’s cycle causes the same country’s other cycle. We also establish the role of the US as global leader in affecting the business and financial cycle of other countries. By design, our analysis identifies causality but does not provide a prescription of appropriate policy responses for alleviating the effects of cycles. For this reason, the discussion in this section is based on
Borio (
2014), who provides detailed information on appropriate policy responses that would be relevant given our findings.
We first focus on dealing with the boom. In the case of prudential policy,
Borio (
2014) proposes the strengthening of the macroprudential/systemic arrangements in place. This implies building buffers in good times, as financial vulnerabilities grow, in order to draw them down in bad times as financial stress materializes. In the case of monetary policy, central banks must adopt a strategy against the build up of financial imbalances even if near-term inflation remains low. One way to achieve this is to extend the policy horizon beyond the standard of two years, which is typical of inflation targeting regimes.
In dealing with the bust,
Borio (
2014) argues that it is critical to distinguish between two different phases: crisis management and crisis resolution. Crisis management is about preventing the implosion of the financial system and reducing the threat of a self-reinforcing downward spiral for economic activity. Crisis resolution focuses on balance sheet repair in an effort to lay the foundations of economic recovery. In summary, these are the main policy responses advocated by
Borio (
2014) that are relevant in an economy where business and financial cycles cause each other.
9. Conclusions
An emerging literature in financial economics has established the presence of financial cycles, which are primarily based on the cyclical behaviour of aggregate real credit issued by banks. Financial cycles are distinct from but correlated with business cycles. When both cycles are approaching their peak, the economic and financial conditions are extraordinarily good. Similarly, when both cycles are approaching their trough, the economic and financial conditions are extraordinarily bad. An open question in this literature that remains is whether business cycles cause financial cycles or vice versa. This is a question with fundamental implications for research, policy and financial practice.
Our paper bridges this gap in the literature by investigating the direction and timing of Granger causality between the two cycles. Our methodology is primarily based on a mixed-frequency vector autoregression that exploits the fact that real economic activity measured by industrial production is observed at a higher frequency than aggregate credit. We complement the mixed-frequency approach with a standard same-frequency approach based on quarterly GDP and quarterly aggregate credit. In short, implementing both approaches provides a comprehensive view of the causality between the real and financial sectors.
The empirical evidence establishes four main findings for the G7 countries: (1) there is a statistically significant causal relation between the business and financial cycles for the G7 countries; (2) the causal relation is often bidirectional: business cycles cause financial cycles and vice versa; (3) the direction of causality depends on the country: it is bidirectional for the US and Canada; the business cycle causes the financial cycle for Germany, France and Italy; and the financial cycle causes the business cycle for the UK and Japan; and finally (4) the US is a global leader in that the US business cycle causes the business cycles of other countries. Overall, these findings indicate that Main Street and Wall Street are not only correlated but actually affect each other, with the US Main Street playing a leading role among the G7 countries.