Does Geopolitical Risk Matter for Sovereign Credit Risk? Fresh Evidence from Nonlinear Analysis
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
4. Data Description and Preliminary Tests
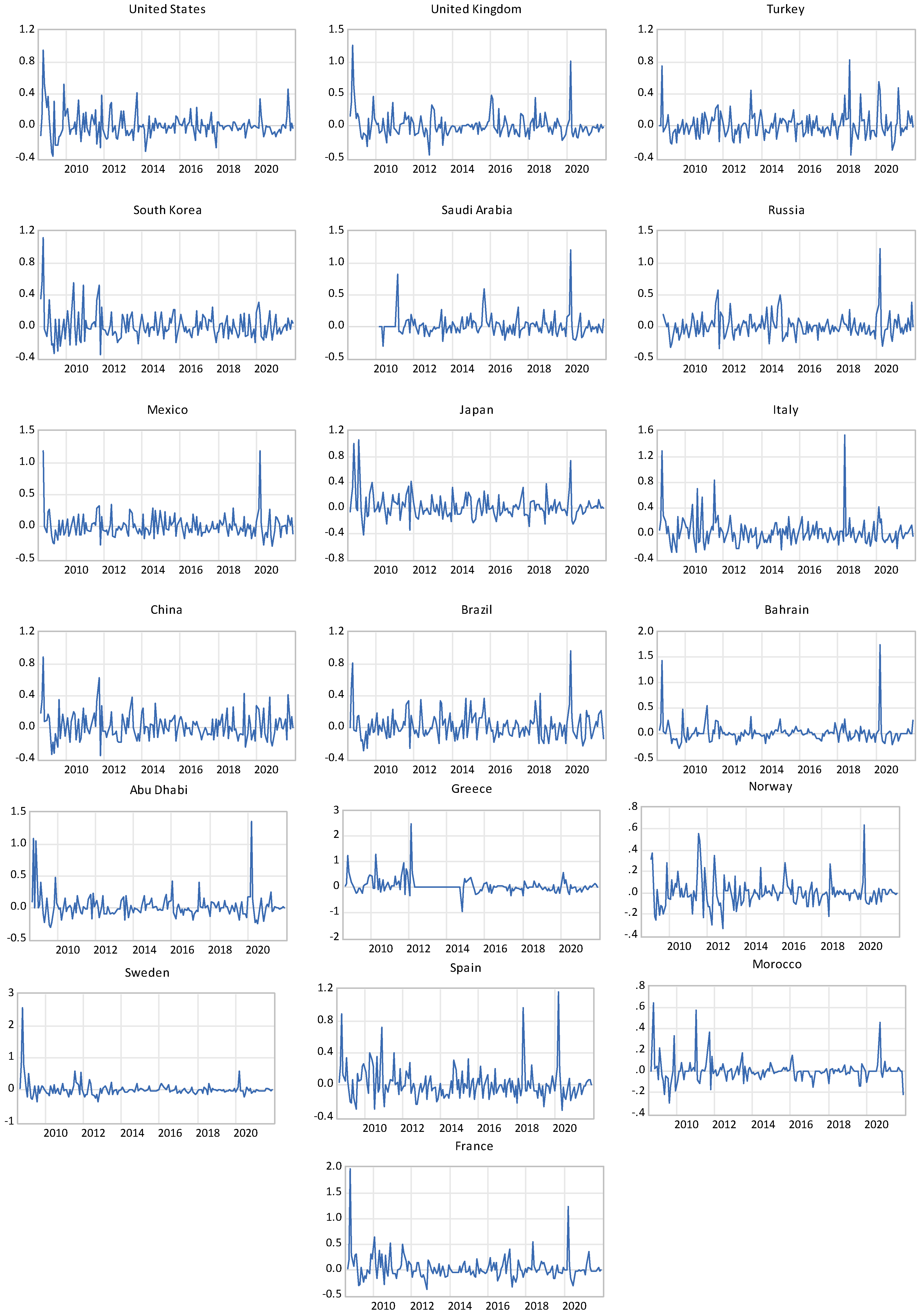
4.1. Data Description
4.2. Preliminary Statistics
5. Empirical Results and Discussion
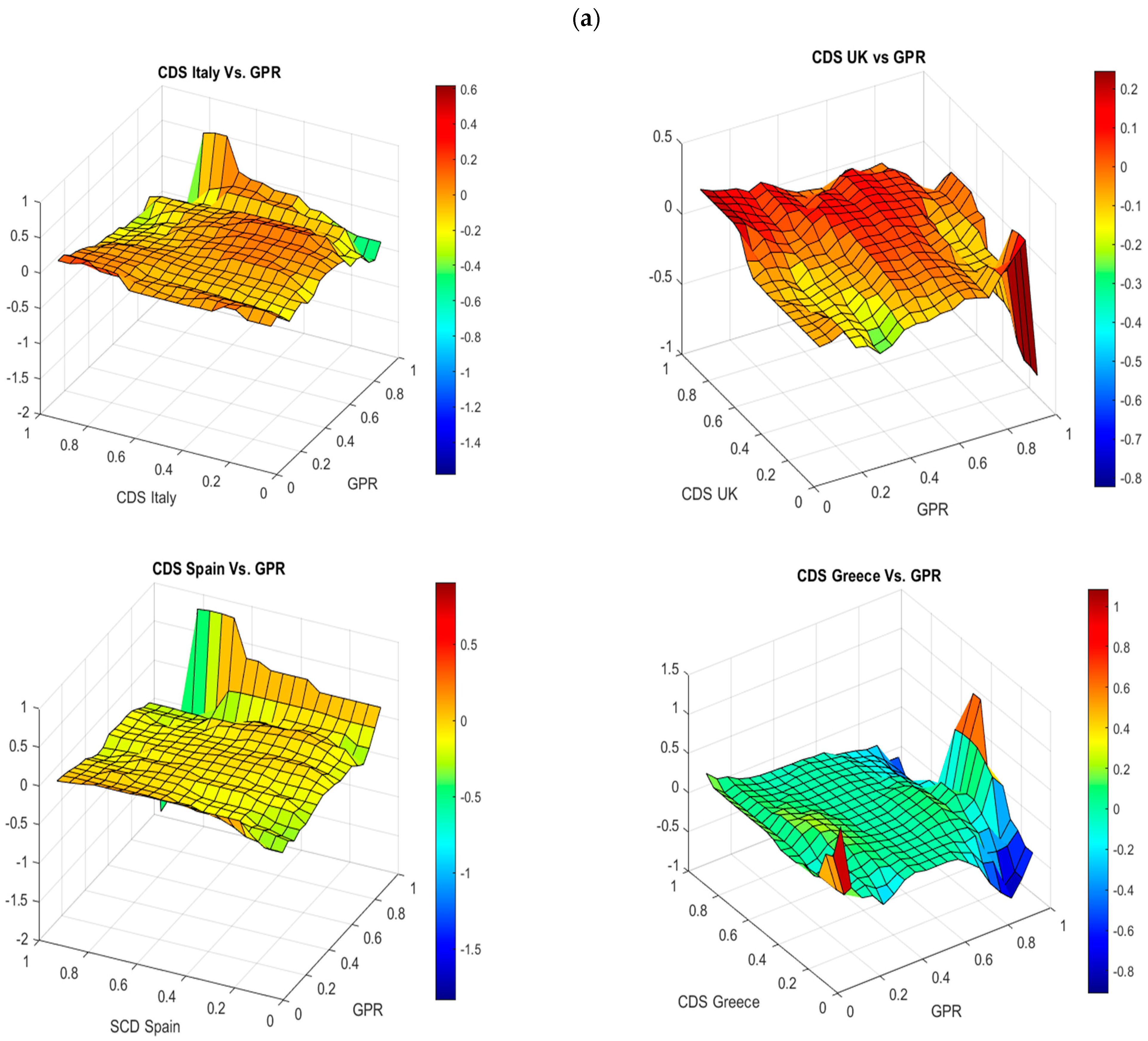
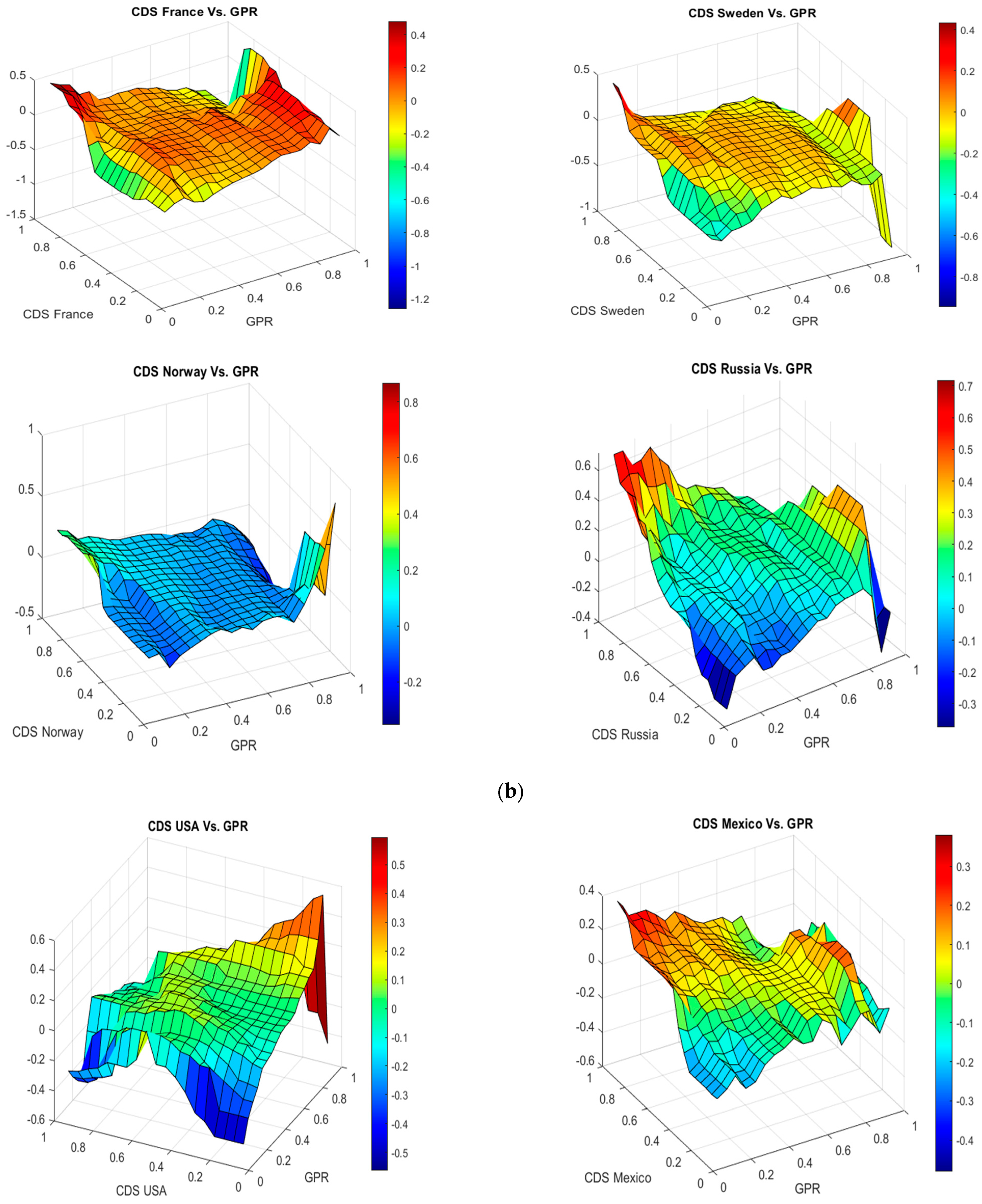
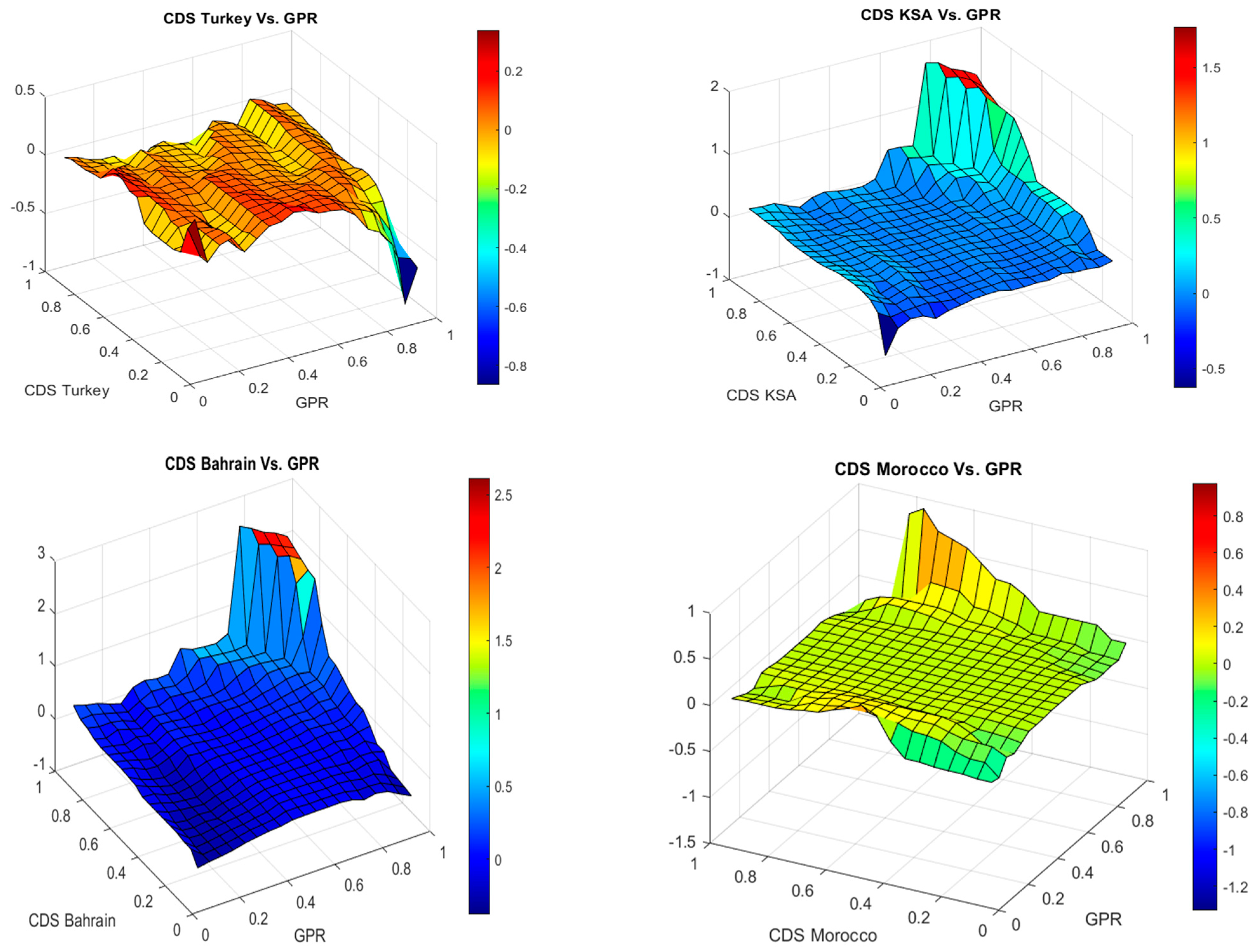
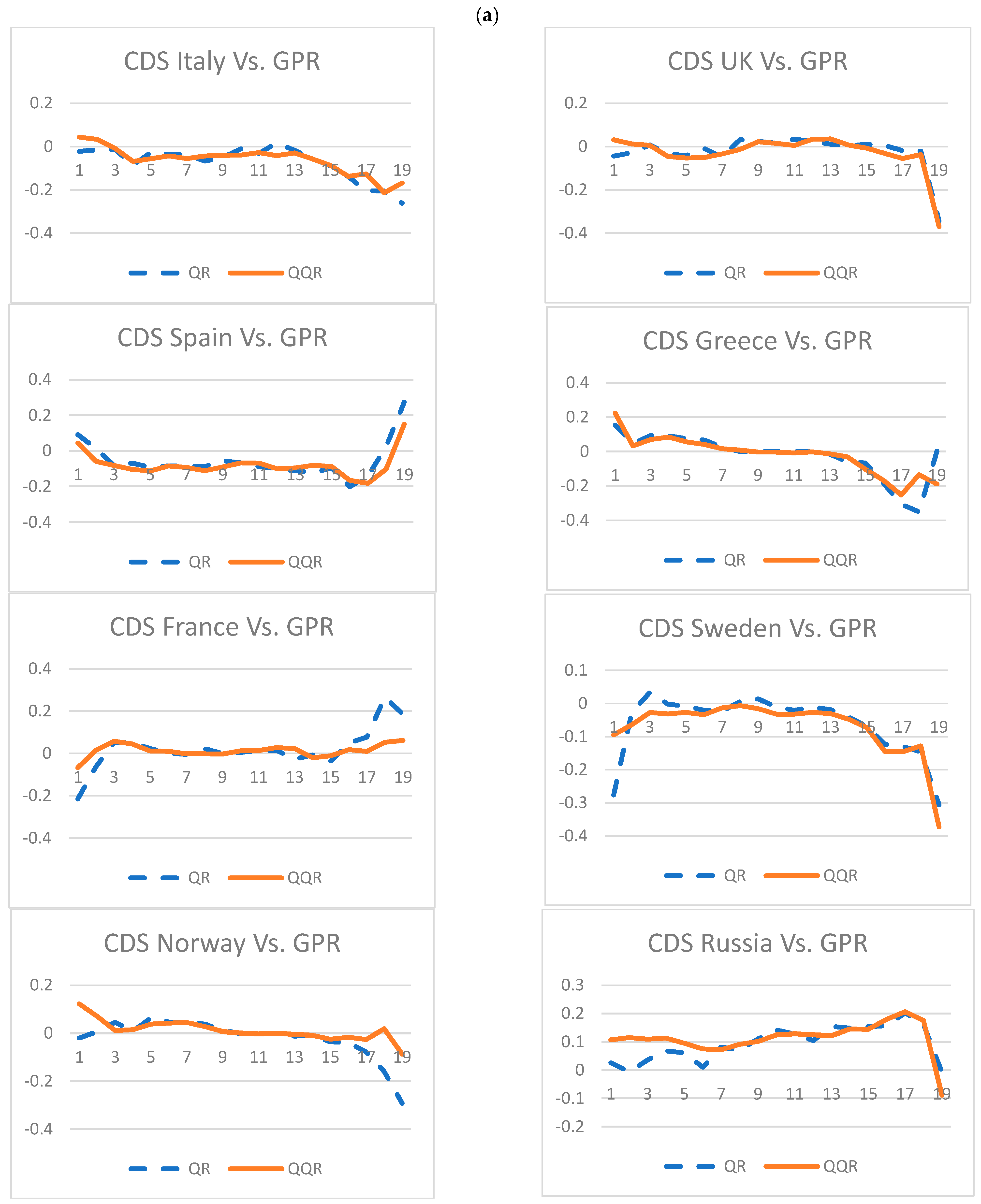
5.1. Empirical Results
5.2. Results Discussion
6. Robustness Check of QQA Findings
7. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Kernel Function is a method used to take data as input and transform it into the required form of processing data. |
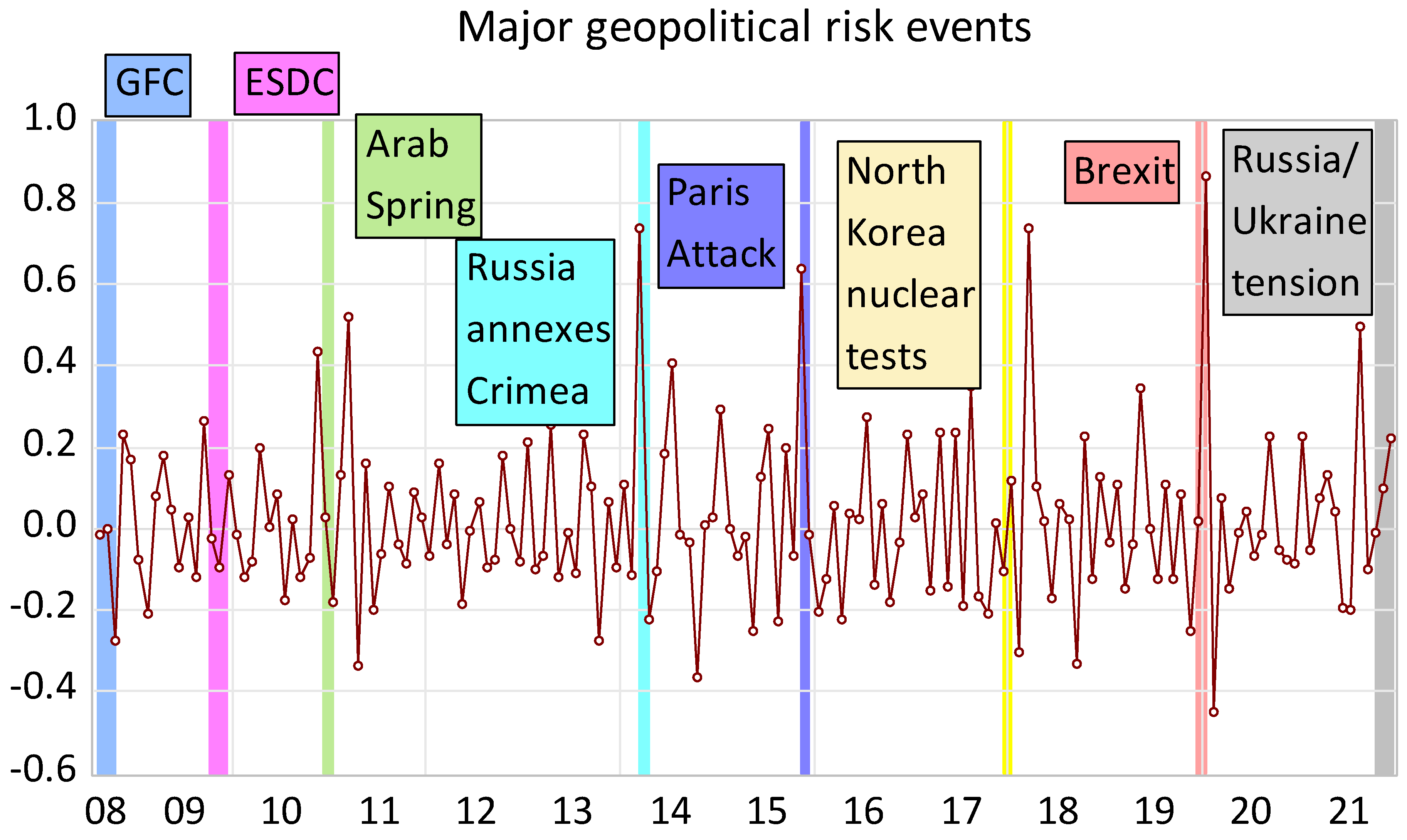
| 2 | The index was downloaded from https://www.matteoiacoviello.com/gpr.htm on 15 November 2022. The index construction is based on counting the number of articles related to adverse geopolitical events in ten newspapers for each month. |
| 3 | https://www.swfinstitute.org/fund-rankings/sovereign-wealth-fund (accessed on 22 December 2022). |
References
- Abid, Fathi, and Nader Naifar. 2006. The determinants of credit default swap rates: An explanatory study. International Journal of Theoretical and Applied Finance 9: 23–42. [Google Scholar] [CrossRef]
- Alam, Ahmed W., Reza Houston, and Ashupta Farjana. 2023. Geopolitical risk and corporate investment: How do politically connected firms respond? Finance Research Letters, 103681. [Google Scholar] [CrossRef]
- Amstad, Marlene, Eli Remolona, and Jimmy Shek. 2016. How do global investors differentiate between sovereign risks? The new normal versus the old. Journal of International Money and Finance 66: 32–48. [Google Scholar] [CrossRef]
- Arora, Nisha, and Pankaj Deep Kaur. 2020. A Bolasso based consistent feature selection enabled random forest classification algorithm: An application to credit risk assessment. Applied Soft Computing 86: 105936. [Google Scholar] [CrossRef]
- Bloom, Nicholas. 2009. The impact of uncertainty shocks. Econometrica 77: 623–85. [Google Scholar]
- Bouri, Elie, Syed Jawad Hussain Shahzad, Naveed Raza, and David Roubaud. 2018. Oil volatility and sovereign risk of BRICS. Energy Economics 70: 258–69. [Google Scholar] [CrossRef]
- Bratis, Theodore D., Georgios P. Kouretas, Nikiforos Laopodis, and Prodromos Vlamis. 2021. Sovereign Credit and Geopolitical Risks during and after the EMU Crisis. December 30. Available online: https://ssrn.com/abstract=4051483 (accessed on 4 December 2022).
- Caldara, Dario, and Matteo Iacoviello. 2022. Measuring geopolitical risk. American Economic Review 112: 1194–225. [Google Scholar] [CrossRef]
- Cheng, Chak Hung Jack, and Ching-Wai Jeremy Chiu. 2018. How important are global geopolitical risks to emerging countries? International Economics 156: 305–25. [Google Scholar] [CrossRef]
- Chuffart, Thomas, and Emma Hooper. 2019. An investigation of oil prices impact on sovereign credit default swaps in Russia and Venezuela. Energy Economics 80: 904–16. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–431. [Google Scholar]
- Eyssell, Thomas, Hung-Gay Fung, and Gaiyan Zhang. 2013. Determinants and price discovery of China sovereign credit default swaps. China Economic Review 24: 1–15. [Google Scholar] [CrossRef]
- Feng, Chaonan, Liyan Han, Samuel Vigne, and Yang Xu. 2023. Geopolitical risk and the dynamics of international capital flows. Journal of International Financial Markets, Institutions and Money 82: 101693. [Google Scholar] [CrossRef]
- Hilscher, Jens, and Yves Nosbusch. 2010. Determinants of sovereign risk: Macroeconomic fundamentals and the pricing of sovereign debt. Review of Finance 14: 235–62. [Google Scholar] [CrossRef]
- Jarrow, Robert, and Philip Protter. 2004. A short history of stochastic integration and mathematical finance: The early years, 1880–970. Lecture Notes-Monograph Series 45: 75–91. [Google Scholar]
- Kartal, Mustafa Tevfik. 2020. The Behavior of Sovereign Credit Default Swaps (CDS) Spread: Evidence from Turkey with the Effect of COVID-19 Pandemic. Available online: https://ssrn.com/abstract=3642652 (accessed on 10 January 2023).
- Lee, Jongsub, Andy Naranjo, and Stace Sirmans. 2016. Exodus from sovereign risk: Global asset and information networks in the pricing of corporate credit risk. The Journal of Finance 71: 1813–56. [Google Scholar] [CrossRef]
- Liu, Yang, and Bruce Morley. 2012. Sovereign credit default swaps and the macroeconomy. Applied Economics Letters 19: 129–32. [Google Scholar] [CrossRef]
- Longstaff, Francis A., Jun Pan, Lasse H. Pedersen, and Kenneth J. Singleton. 2011. How sovereign is sovereign credit risk? American Economic Journal: Macroeconomics 3: 75–103. [Google Scholar] [CrossRef]
- Ma, Jason Z., Xiang Deng, Kung-Cheng Ho, and Sang-Bing Tsai. 2018. Regime-switching determinants for spreads of emerging markets sovereign credit default swaps. Sustainability 10: 2730. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Naifar, Nader. 2020. What explains the sovereign credit default swap spreads changes in the GCC region? Journal of Risk and Financial Management 13: 245. [Google Scholar] [CrossRef]
- Oliveira, Luís, José Dias Curto, and João Pedro Nunes. 2012. The determinants of sovereign credit spread changes in the Euro-zone. Journal of International Financial Markets, Institutions and Money 22: 278–304. [Google Scholar] [CrossRef]
- Pan, Jun, and Kenneth J. Singleton. 2008. Default and Recovery Implicit in the Term Structure of Sovereign CDS Spreads. Journal of Finance 63: 2345–84. [Google Scholar] [CrossRef]
- Rikhotso, Prayer M., and Beatrice D. Simo-Kengne. 2022. Dependence structures between Sovereign credit default swaps and global risk factors in BRICS countries. Journal of Risk and Financial Management 15: 109. [Google Scholar] [CrossRef]
- Sim, Nicholas, and Hongtao Zhou. 2015. Oil prices, US stock returns, and the dependence between their quantiles. Journal of Banking and Finance 55: 1–8. [Google Scholar] [CrossRef]
- Simonyan, Serdar, and Sema Bayraktar. 2022. Asymmetric dynamics in sovereign credit default swaps pricing: Evidence from emerging countries. International Journal of Emerging Markets, ahead-of-print. [Google Scholar]
- Stolbov, Mikhail. 2017. Determinants of sovereign credit risk: The case of Russia. Post-Communist Economies 29: 51–70. [Google Scholar] [CrossRef]



| USA | UK | TURKEY | SWEDEN | SPAIN | |
| Mean | −0.000856 | −0.003387 | 0.018345 | −0.002852 | 0.006305 |
| Median | −0.003803 | −0.022178 | 0.006626 | −0.016751 | −0.015939 |
| Maximum | 0.457692 | 1.011656 | 0.833423 | 0.587771 | 1.160102 |
| Minimum | −0.322093 | −0.456866 | −0.362187 | −0.377613 | −0.320695 |
| Std. Dev. | 0.124701 | 0.160910 | 0.161774 | 0.133164 | 0.197209 |
| Skewness | 0.983180 | 2.184330 | 1.487338 | 1.601296 | 2.656169 |
| Kurtosis | 5.305994 | 13.93772 | 7.871133 | 9.055002 | 14.44007 |
| Jarque–Bera | 54.33971 | 820.7530 | 192.7451 | 277.6079 | 941.3193 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| ADF test | −10.70847 * | −9.346816 * | −12.76449 * | −8.565483 * | −11.51723 * |
| KSA | RUSSIA | NORWAY | MOROCCO | MEXICO | |
| Mean | 0.006280 | 0.011288 | 0.002999 | 0.002877 | 0.010310 |
| Median | −0.000242 | −0.012258 | −0.010562 | 0.000000 | −0.016317 |
| Maximum | 1.202283 | 1.215252 | 0.637081 | 0.570370 | 1.191064 |
| Minimum | −0.312242 | −0.349671 | −0.333769 | −0.215942 | −0.302280 |
| Std. Dev. | 0.171789 | 0.186493 | 0.128451 | 0.089761 | 0.167421 |
| Skewness | 3.416752 | 2.311121 | 1.778006 | 2.974467 | 2.664748 |
| Kurtosis | 21.87846 | 14.40274 | 9.897894 | 19.00920 | 18.81280 |
| Jarque–Bera | 2384.967 | 895.7095 | 356.3381 | 1725.799 | 1647.485 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| ADF test | −11.03391 * | −11.38031 * | −10.72578 * | −11.24817 * | −14.14826 * |
| FRANCE | CHINA | BRAZIL | BAHRAIN | ABU DHABI | |
| Mean | 0.006721 | 0.008506 | 0.015192 | 0.013641 | 0.001649 |
| Median | −0.028504 | −0.013722 | −0.007471 | 0.000141 | −0.015502 |
| Maximum | 1.230640 | 0.629392 | 0.966805 | 1.758141 | 1.361971 |
| Minimum | −0.397952 | −0.361098 | −0.266117 | −0.232484 | −0.267276 |
| Std. Dev. | 0.185230 | 0.156525 | 0.162857 | 0.182886 | 0.161774 |
| Skewness | 2.496679 | 0.864910 | 1.782229 | 6.376615 | 4.361900 |
| Kurtosis | 15.96265 | 4.188039 | 10.08445 | 60.04675 | 36.72696 |
| Jarque–Bera | 1141.704 | 26.05532 | 372.1273 | 20217.11 | 7180.540 |
| Probability | 0.000000 | 0.000002 | 0.000000 | 0.000000 | 0.000000 |
| ADF test | −10.61641 * | −12.76762 * | −10.80039 * | −11.22886 * | −11.32624 * |
| S. KOREA | ITALY | JAPAN | GREECE | GPR | |
| Mean | −0.001220 | 0.013828 | 0.001407 | 0.038866 | 0.019803 |
| Median | −0.025695 | −0.021359 | −0.009754 | 0.000000 | −0.004461 |
| Maximum | 0.550562 | 1.529856 | 0.742125 | 2.473361 | 0.863505 |
| Minimum | −0.362825 | −0.302794 | −0.348788 | −0.980346 | −0.451271 |
| Std. Dev. | 0.146310 | 0.211528 | 0.151064 | 0.312599 | 0.203804 |
| Skewness | 0.988031 | 3.410593 | 1.117203 | 3.866636 | 1.183766 |
| Kurtosis | 5.123337 | 22.05917 | 6.490444 | 29.88416 | 5.832712 |
| Jarque–Bera | 49.77917 | 2424.534 | 101.6233 | 4630.157 | 91.43096 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| ADF test | −9.505437 * | −12.14745 * | −12.02839 * | −11.09709 * | −11.20894 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naifar, N.; Aljarba, S. Does Geopolitical Risk Matter for Sovereign Credit Risk? Fresh Evidence from Nonlinear Analysis. J. Risk Financial Manag. 2023, 16, 148. https://doi.org/10.3390/jrfm16030148
Naifar N, Aljarba S. Does Geopolitical Risk Matter for Sovereign Credit Risk? Fresh Evidence from Nonlinear Analysis. Journal of Risk and Financial Management. 2023; 16(3):148. https://doi.org/10.3390/jrfm16030148
Chicago/Turabian StyleNaifar, Nader, and Shumokh Aljarba. 2023. "Does Geopolitical Risk Matter for Sovereign Credit Risk? Fresh Evidence from Nonlinear Analysis" Journal of Risk and Financial Management 16, no. 3: 148. https://doi.org/10.3390/jrfm16030148
APA StyleNaifar, N., & Aljarba, S. (2023). Does Geopolitical Risk Matter for Sovereign Credit Risk? Fresh Evidence from Nonlinear Analysis. Journal of Risk and Financial Management, 16(3), 148. https://doi.org/10.3390/jrfm16030148







