Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices
Abstract
1. Introduction
2. Hypotheses
3. Methodology & Data Description
4. Numerical Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VIX (CBOE) | Chicago Board Options Exchange Volatility index |
| VXN (CBOE Nasdaq 100) | CBOE Nasdaq Volatility Index |
| VXD (DJIA) | Dow Jones Industrial Average Volatility Index |
| VHSI (HSI) | Hang Seng index Volatility Index |
| KSVKOSPI (KOSPI) | Korea Composite Stock Price Index |
| GFC | Global financial crisis |
| H | Hurst exponent |
| R/S | Rescaled Range Analysis |
| AR | Autoregressive Process |
| GARCH | Generalized AutoRegressive Conditional Heteroskedasticity |
References
- Alizadeh, Sassan, Michael W. Brandt, and Francis X. Diebold. 2002. Range-based estimation of stochastic volatility models. The Journal of Finance 57: 1047–91. [Google Scholar] [CrossRef]
- Athari, Seyed Alireza, and Ngo Thai Hung. 2022. Time–frequency return co-movement among asset classes around the COVID-19 outbreak: Portfolio implications. Journal of Economics and Finance 46: 736–56. [Google Scholar] [CrossRef]
- Bhatt, S. J., H. V. Dedania, and Vipul R. Shah. 2015. Fractal Dimensional Analysis in Financial Time Series. International Journal of Financial Management 5: 46–52. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Cadenas, Erasmo, Campos-Amezcua Rafael, Rivera Wilfrido, Espinosa-Medina Marco Antonio, Méndez-Gordillo Alma Rosa, Rangel Eduardo, and Tena Jorge. 2019. Wind speed variability study based on the Hurst coefficient and fractal dimensional analysis. Journal of Energy Science and Engineering 7: 361–78. [Google Scholar] [CrossRef]
- Ceballos, Roel F., and Fe F. Largo. 2018. On The Estimation of the Hurst Exponent Using Adjusted Rescaled Range Analysis, Detrended Fluctuation Analysis and Variance Time Plot: A Case of Exponential Distribution. arXiv arXiv:1805.08931. [Google Scholar]
- Chan, Leo, and Donald Lien. 2003. Using high, low, open, and closing prices to estimate the effects of cash settlement on futures prices. International Review of Financial Analysis 12: 35–47. [Google Scholar] [CrossRef]
- Cont, Rama, and Purba Das. 2022. Rough volatility: Fact or artefact? arXiv arXiv:2203.13820v2. [Google Scholar] [CrossRef]
- Da Fonseca, Jose, and Wenjun Zhang. 2019. Volatility of volatility is (also) rough. The Journal of Futures Markets 39: 600–11. [Google Scholar] [CrossRef]
- Das, Santanu, and Ashish Kumar. 2021. Long-term dependency between sovereign bonds and sectoral indices of India: Evidence using Hurst exponent and wavelet analysis. Managerial Finance 47: 1448–64. [Google Scholar] [CrossRef]
- Decreusefond, Laurent, and Ustunel Ali Suleyman. 1998. Fractional Brownian motion: Theory and applications. Esaim: Proceedings 5: 75–86. [Google Scholar] [CrossRef]
- Di Vita, Andrea. 2021. The persistent, the anti-persistent and the Brownian: When does the Hurst exponent warn us of impending catastrophes? arXiv arXiv:2104.02187. [Google Scholar]
- Ding, Liang, Yi Luo, Yan Lin, and Yirong Huang. 2021a. Revisiting the rela- tions between Hurst exponent and fractional differencing parameter for long memory. Physica A: Statistical Mechanics and Its Applications 566: 125603. [Google Scholar] [CrossRef]
- Ding, Liang, Yi Luo, Yan Lin, and Yirong Huang. 2021b. Optimal Setting for Hurst Index Estimation and Its Application in Chinese Stock Market. IEEE Access 9: 93315–30. [Google Scholar] [CrossRef]
- Domino, Krzysztof. 2011. The use of the Hurst exponent to predict changes in trends on the Warsaw Stock Exchange. Journal Physica A: Statistical Mechanics and Its Applications 390: 98–109. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation. Econometrica 50: 987–1008. [Google Scholar] [CrossRef]
- Fukasawa, Masaaki, Tetsuya Takabatake, and Rebecca Westphal. 2019. Is Volatility Rough? arXiv arXiv:1905.04852. [Google Scholar]
- Fuss, Franz Konstantin, Yehuda Weizman, and Adin Ming Tan. 2020. The non-linear relationship between randomness and scaling properties such as fractal dimensions and Hurst exponent in distributed signals. Journal of Communications in Nonlinear Science and Numerical Simulation 96: 105683. [Google Scholar] [CrossRef]
- Gallant, Ronald, Chien-Te Hsu, and George Tauchen. 1999. Using Daily Range Data to Calibrate Volatility Diffusion and Extract the Forward Integrated Variance. Working Paper. Chapel Hill: University of North Carolina, vol. 81, pp. 617–31. [Google Scholar]
- Garcin, Matthieu. 2019. Hurst exponents and delampertized fractional Brownian motions. International Journal of Theoretical and Applied Finance 22: 1950024. [Google Scholar] [CrossRef]
- García, María de las Nieves López, and Jose Pedro Ramos Requena. 2019. Different methodologies and uses of the Hurst exponent in Econophysics. Journal of Estudios de Economía Aplicada 37: 2. [Google Scholar] [CrossRef]
- Garman, Mark B., and Michael J. Klass. 1980. On the Estimation of Security Price Volatilities from Historical Data. The Journal of Business 53: 67–78. [Google Scholar] [CrossRef]
- Ghosh, Bikramaditya, and Elie Bouri. 2022. Long Memory and Fractality in the Universe of Volatility Indices. Complexity in Financial Markets 2022: 6728432. [Google Scholar] [CrossRef]
- Gneiting, Tilmann, and Martin Schlather. 2001. Stochastic models which separate fractal dimension and Hurst effect. arXiv arXiv:physics/0109031. [Google Scholar]
- Hamza, Amjad, and Munaf Hmood. 2021. Comparison of Hurst exponent estimation methods. Journal of Economics and Administrative Sciences 27: 167–83. [Google Scholar] [CrossRef]
- Hurst, Harold E. 1951. The Long-Term Storage Capacity of Reservoirs. Transactions of the American Society of Civil Engineers 116: 770–99. [Google Scholar] [CrossRef]
- Hwang, Soosung, and Stephen E. Satchell. 2000. Market risk and the concept of fundamental volatility: Measuring volatility across asset and derivative markets and testing for the impacts of derivatives markets on financial markets. Journal of Banking and Finance 24: 759–85. [Google Scholar] [CrossRef]
- Jafari, G. R., A. Bahraminasab, and P. Norouzzadeh. 2007. Why does the Standard GARCH(1,1) model work well? arXiv arXiv:physics/0503027. [Google Scholar]
- Kondoz, Mehmet, Ilhan Bora, Dervis Kirikkaleli, and Seyed Alireza Athari. 2019. Testing the Volatility Spillover between Crude Oil Price and the U.S. Stock Market Returns. Management Science Letters 9: 1221–30. Available online: https://ssrn.com/abstract=4300741 (accessed on 5 September 2022). [CrossRef]
- Li, Yicun, and Yuanyang Teng. 2022. Estimation of the Hurst Parameter in Spot Volatility. Mathematics 10: 1619. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1967. How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science New Series 156: 636–38. [Google Scholar] [CrossRef]
- Parkinson, Michael. 1980. The extreme value method for estimating the variance of the rate of return. The Journal of Business 53: 61–65. [Google Scholar] [CrossRef]
- Rangarajan, Govindan, and Dhananjay Santb. 2004. Fractal dimensional analysis of Indian climatic dynamics. Journal Chaos, Solitons and Fractals 19: 285–91. [Google Scholar] [CrossRef]
- Rehman, S., and A. H. Siddiqi. 2009. Wavelet based hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Journal of Chaos, Solitons and Fractals 40: 1081–90. [Google Scholar] [CrossRef]
- Rehman, Shafiqur. 2009. Wavelet based hurst exponent and fractal dimensional analysis of saudi climatic parameters. The International Journal of Meteorology 34: 5. [Google Scholar]
- Rogers, L. Christopher G., and Stephen E. Satchell. 1991. Estimating variance from high, low, and closing prices. Annals of Applied Probability 1: 504–12. [Google Scholar] [CrossRef]
- Rogers, Leonard C. G., Stephen E. Satchell, and Y. Yoon. 1994. Estimating the volatility of stock prices: A comparison of methods that use high and low prices. Applied Financial Economics 4: 241–47. [Google Scholar] [CrossRef]
- Schoebel, Rainer, and Jianwei Zhu. 1999. Stochastic Volatility with an Ornstein-Uhlenbeck Process: An Extension, European Finance Review. Tübinger Diskussionsbeiträge, No. 139. Tübingen: Eberhard Karls Universität Tübingen. [Google Scholar]
- Stein, Elias M., and Jeremy C. Stein. 1991. Stock Price Distributions with Stochastic Volatility: An Analytic Approach. Review of Financial Studies 4: 727–52. [Google Scholar] [CrossRef]
- Szóstakowski, Robert. 2018. The use of the Hurst exponent to investigate the quality of forecasting methods of ultra-high-frequency data of exchange rates. Statistical Review Przeglad Statystyczny 65: 200–23. [Google Scholar] [CrossRef]
- Taylor, S. 1986. Modeling Financial Time Series. New York and Chichester: John Wiley & Sons. [Google Scholar]
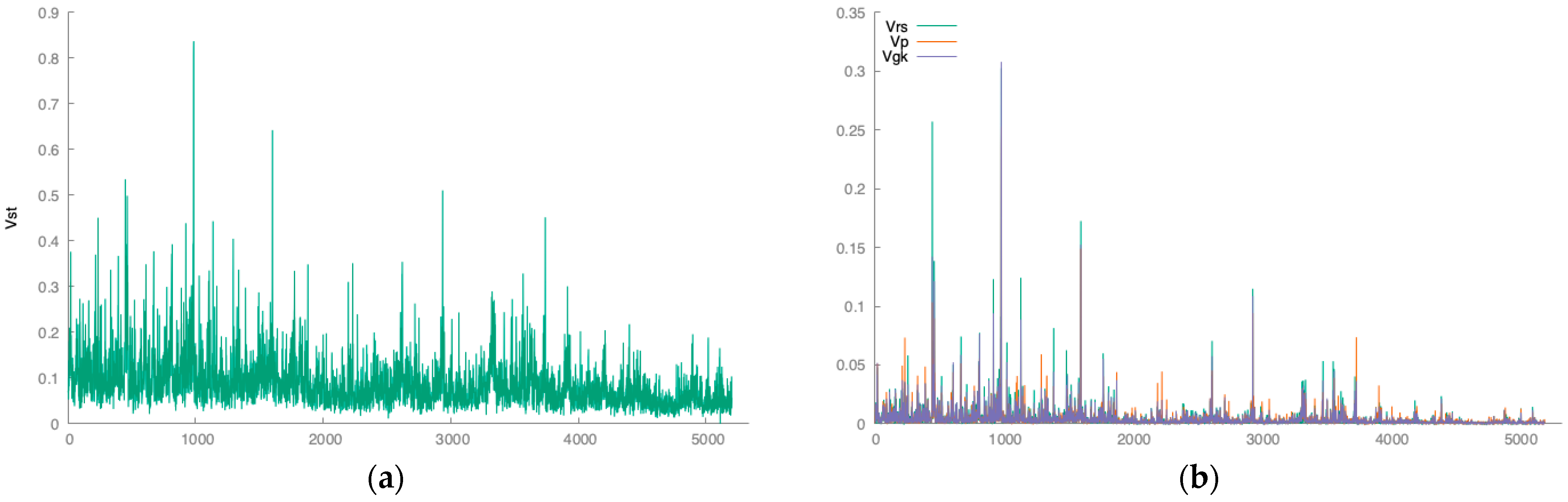
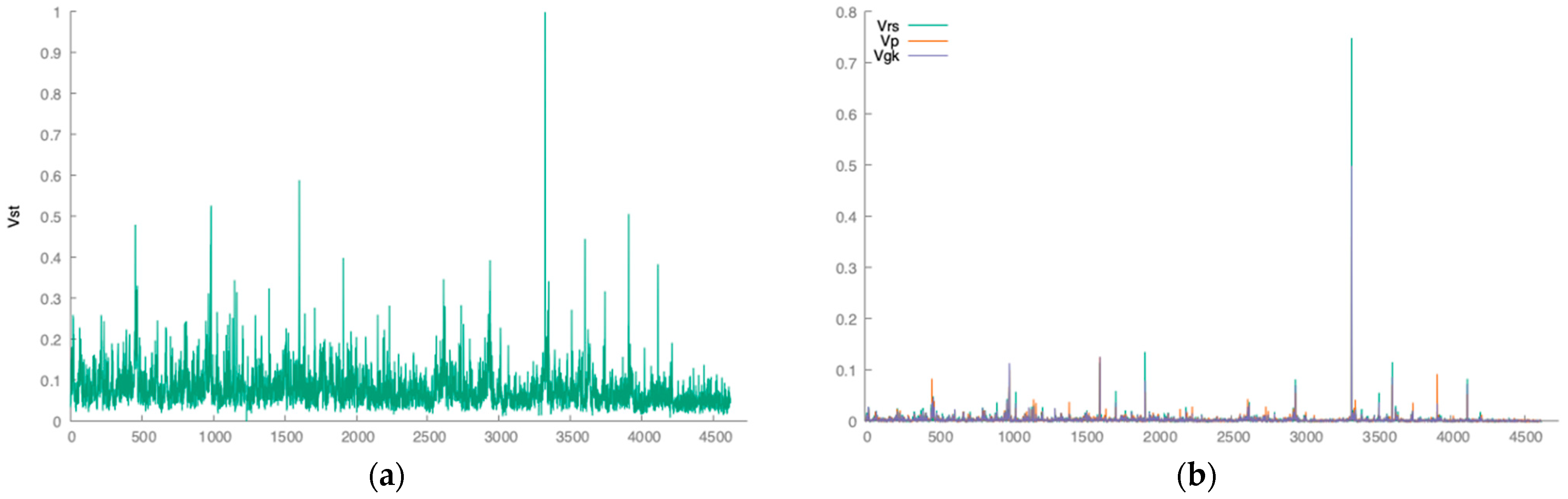


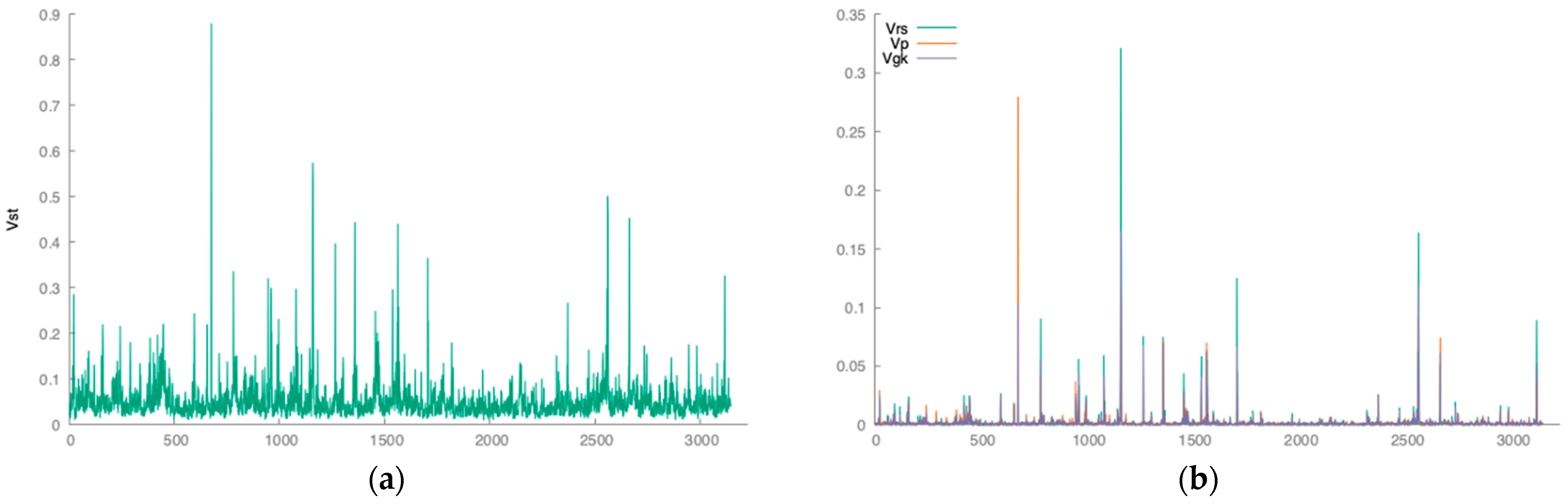
| CBOE Market Volatility Index|Price History | Close | High | Low | Open |
| Μean | 19.681 | 20.707 | 18.905 | 19.812 |
| Μedian | 17.250 | 18.080 | 16.520 | 17.340 |
| Μaximum | 82.690 | 89.530 | 72.760 | 82.690 |
| Μinimum | 9.1400 | 9.3100 | 8.5600 | 9.0100 |
| Std. Dev. | 8.9360 | 9.5939 | 8.3575 | 8.9923 |
| Skewness | 2.2932 | 2.3856 | 2.1518 | 2.2773 |
| Κurtosis | 7.9056 | 8.5988 | 6.6939 | 7.6987 |
| Jarque-Bera | 18.110 | 20.964 | 13.729 | 17.346 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 5203 | 5203 | 5203 | 5203 |
| CBOE NASDAQ 100 Volatility Index|Price History | Close | High | Low | Open |
| Μean | 24.340 | 22.880 | 21.061 | 21.968 |
| Μedian | 20.560 | 20.300 | 18.860 | 19.605 |
| Μaximum | 80.640 | 86.520 | 73.860 | 80.570 |
| Μinimum | 10.310 | 10.970 | 9.6600 | 10.310 |
| Std. Dev. | 11.067 | 9.0678 | 7.9105 | 8.4678 |
| Skewness | 1.6283 | 2.4683 | 2.2681 | 2.3566 |
| Κurtosis | 2.5228 | 9.3483 | 7.7727 | 8.4064 |
| Jarque-Bera | 3679.05 | 21.477 | 15.564 | 17.849 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 5203 | 5203 | 5203 | 5203 |
| DJIA Volatility Index|Price History | Close | High | Low | Open |
| Μean | 18.650 | 20.024 | 17.572 | 18.656 |
| Μedian | 16.120 | 17.465 | 15.170 | 16.120 |
| Μaximum | 74.600 | 80.240 | 63.250 | 74.600 |
| Μinimum | 2.7100 | 9.5600 | 2.4700 | 2.7100 |
| Std. Dev. | 8.2446 | 9.0035 | 7.7995 | 8.2493 |
| Skewness | 2.1898 | 2.1293 | 2.0826 | 2.2062 |
| Κurtosis | 6.8074 | 6.5143 | 5.9404 | 6.9090 |
| Jarque-Bera | 14.202 | 13.129 | 11.409 | 14.566 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 5202 | 5202 | 5202 | 5202 |
| HSI Volatility Index|Price History | Close | High | Low | Open |
| Μean | 21.678 | 18.931 | 17.729 | 18.341 |
| Μedian | 19.660 | 18.465 | 17.500 | 18.020 |
| Μaximum | 104.29 | 68.640 | 58.610 | 58.870 |
| Μinimum | 2.0294 | 2.0707 | 1.9985 | 2.0402 |
| Std. Dev. | 10.254 | 8.1025 | 7.1187 | 7.5525 |
| Skewness | 1.7779 | 0.68914 | 0.19054 | 0.39290 |
| Κurtosis | 6.3893 | 3.7278 | 2.1159 | 2.6870 |
| Jarque-Bera | 11.364 | 1761.31 | 515.37 | 873.569 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 2.03 × 10−185 |
| Observations | 2426 | 2676 | 2676 | 2675 |
| KSVKOSPI Volatility Index|Price History | Close | High | Low | Open |
| Μean | 16.346 | 16.912 | 15.999 | 16.465 |
| Μedian | 15.240 | 15.670 | 14.920 | 15.340 |
| Μaximum | 69.240 | 71.750 | 62.080 | 71.290 |
| Μinimum | 0.010914 | 0.011174 | 0.010879 | 0.011155 |
| Std. Dev. | 7.9787 | 8.4060 | 7.6776 | 8.0174 |
| Skewness | 0.89333 | 1.0452 | 0.76862 | 0.90655 |
| Κurtosis | 4.3562 | 5.1291 | 3.8254 | 4.5845 |
| Jarque-Bera | 2906.89 | 4022.5 | 2228.7 | 11.752 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 3147 | 3147 | 3147 | 3187.04 |
| CBOE Market Volatility Index|Price History | Vgk | Vp | Vrs | Vs |
| Μean | 0.0038030 | 0.0037981 | 0.0039638 | 0.086164 |
| Μedian | 0.0018780 | 0.0019078 | 0.0018067 | 0.072696 |
| Μaximum | 0.30795 | 0.25293 | 0.30252 | 0.83704 |
| Μinimum | 0.000000 | 0.000000 | 0.000000 | 0.0000 |
| Std. Dev. | 0.0082953 | 0.0079785 | 0.0094253 | 0.055655 |
| Skewness | 15.579 | 14.463 | 14.593 | 3.0640 |
| Κurtosis | 427.86 | 359.09 | 345.82 | 20.355 |
| Jarque-Bera | 3.98973 × 10+07 | 2.81359 × 10+07 | 2.61108 × 10+07 | 97.966 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 5203 | 5203 | 5203 | 5203 |
| CBOE NASDAQ 100 Volatility Index|Price History | Vgk | Vp | Vrs | Vs |
| Μean | 0.0029664 | 0.0030914 | 0.0031269 | 0.078422 |
| Μedian | 0.0015422 | 0.0016296 | 0.0015031 | 0.067187 |
| Μaximum | 0.49927 | 0.36051 | 0.74883 | 0.99932 |
| Μinimum | 0.0000 | 0.0000 | 0.0000 | 0.000000 |
| Std. Dev. | 0.0089028 | 0.0075764 | 0.012429 | 0.049134 |
| Skewness | 39.489 | 26.260 | 47.917 | 3.8547 |
| Κurtosis | 2111.0 | 1109.9 | 2816.0 | 38.789 |
| Jarque-Bera | 8.57543 × 10+08 | 2.37258 × 10+08 | 1.52557 × 10+09 | 300.56 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 4612 | 4612 | 4612 | 4612 |
| DJIA Volatility Index|Price History | Vgk | Vp | Vrs | Vs |
| Μean | 0.015907 | 0.012977 | 0.021436 | 0.12924 |
| Μedian | 0.0022831 | 0.0023729 | 0.0022821 | 0.081075 |
| Μaximum | 1.6846 | 1.3000 | 2.6153 | 1.8977 |
| Μinimum | −0.00013469 | 0.0000 | −0.00046366 | 0.0000 |
| Std. Dev. | 0.055918 | 0.046756 | 0.083584 | 0.13874 |
| Skewness | 13.467 | 15.625 | 15.595 | 3.7924 |
| Κurtosis | 300.86 | 355.86 | 385.30 | 25.684 |
| Jarque-Bera | 1.97765 × 10+07 | 2.76597 × 10+07 | 3.23887 × 10+07 | 155.450 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 5202 | 5202 | 5202 | 5202 |
| HSI Volatility Index|Price History | Vgk | Vp | Vrs | Vs |
| Μean | 0.0020828 | 0.0019981 | 0.0023188 | 0.059696 |
| Μedian | 0.00085300 | 0.00083030 | 0.00085529 | 0.047958 |
| Μaximum | 0.10961 | 0.086440 | 0.18831 | 0.48933 |
| Μinimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Std. Dev. | 0.0054811 | 0.0048891 | 0.0075498 | 0.044407 |
| Skewness | 9.1365 | 8.8341 | 11.524 | 3.4983 |
| Κurtosis | 111.45 | 105.41 | 189.48 | 19.140 |
| Jarque-Bera | 1.4216 × 10+06 | 1.27379 × 10+06 | 4.06097 × 10+06 | 46.304 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 2426 | 2676 | 2675 | 2676 |
| KSVKOSPI Volatility Index|Price History | Vgk | Vp | Vrs | Vs |
| Μean | 0.0015916 | 0.0016425 | 0.0017795 | 0.051696 |
| Μedian | 0.00057376 | 0.00062004 | 0.00054095 | 0.041444 |
| Μaximum | 0.16515 | 0.27974 | 0.32143 | 0.88028 |
| Μinimum | 2.8075 × 10−05 | 3.1385 × 10−05 | 0.0000 | 0.0093241 |
| Std. Dev. | 0.0064552 | 0.0071245 | 0.0096723 | 0.043337 |
| Skewness | 15.196 | 23.862 | 21.189 | 6.2728 |
| Κurtosis | 290.69 | 796.66 | 573.95 | 72.830 |
| Jarque-Bera | 1.1201 × 10+07 | 8.35198 × 10+07 | 4.34308 × 10+07 | 716.154 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 3147 | 3147 | 3147 | 3147 |
| Volatility Indices | Period 2001–2021 | Period before GFC 2001–2007 | GFC 2008–2010 | Period after GFC 2008–2021 | COVID-19 2020–2021 |
|---|---|---|---|---|---|
| CBOE Volatility Index | 0.923132 | 0.990811 | 0.97901 | 0.949799 | 0.937536 |
| CBOE NASDAQ 100 Volatility Index | 0.944038 | 1.01016 | 0.967554 | 0.951156 | 0.958043 |
| DJIA Volatility Index | 0.916349 | 0.991099 | 0.977751 | 0.943301 | 0.976587 |
| HSI Volatility Index | 0.938568 | 0.945965 | 0.978547 | 0.948096 | 1.02819 |
| KSVKOSPI Volatility Index * | 0.92346 | - | 0.972173 | 0.92346 | 1.02054 |
| Volatility Indices | Period 2001–2021 | Period before GFC 2001–2007 | GFC 2008–2010 | Period after GFC 2008–2021 | COVID-19 2020–2021 |
|---|---|---|---|---|---|
| CBOE Volatility Index | Vs: 0.738147 | Vs: 0.816659 | Vgk: 0.67335 Vp: 0.682425 Vs: 0.761437 | Vs: 0.679823 | Vgk: 0.706384 Vs: 0.748151 |
| CBOE NASDAQ 100 Volatility Index | - | Vp: 0.559094 Vs: 0.630445 | Vs: 0.63375 | Vs: 0.598392 | Vgk: 0.779025 Vp: 0.705984 Vrs: 0.775285 Vs: 0.777791 |
| DJIA Volatility Index | - | Vs: 0.700755 | Vs: 0.702298 | Vs: 0.731611 | - |
| HSI Volatility Index | Vs: 0.71753 | - | - | Vs: 0.71753 | Vp: 0.630344 Vs: 0.721309 |
| KSVKOSPI Volatility Index * | Vp: 0.530579 Vs: 0.58489 | - | Vp: 0.574546 Vs: 0.584908 | Vp: 0.530579 Vs: 0.58489 | Vs: 0.750765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zournatzidou, G.; Floros, C. Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices. J. Risk Financial Manag. 2023, 16, 272. https://doi.org/10.3390/jrfm16050272
Zournatzidou G, Floros C. Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices. Journal of Risk and Financial Management. 2023; 16(5):272. https://doi.org/10.3390/jrfm16050272
Chicago/Turabian StyleZournatzidou, Georgia, and Christos Floros. 2023. "Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices" Journal of Risk and Financial Management 16, no. 5: 272. https://doi.org/10.3390/jrfm16050272
APA StyleZournatzidou, G., & Floros, C. (2023). Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices. Journal of Risk and Financial Management, 16(5), 272. https://doi.org/10.3390/jrfm16050272








