1. Introduction
A consensus opinion expressed in the housing and real estate literature is that heterogeneity in various aspects, including price, exists in urban housing markets. Accordingly, an entire housing market should be divided into several submarkets, or market segments, to improve house price prediction accuracy. For example,
Watkins (
2001) points out that a housing market can be better analyzed as a set of distinct submarkets instead of one single homogeneous market.
Bourassa et al. (
2003) conclude that “housing submarkets matter, and location plays the major role in explaining why they matter.” A rich set of literature in the delineation of housing submarkets also reports the importance of location (e.g.,
Goodman and Thibodeau 1998,
2003;
Bourassa et al. 1999;
Hwang and Thill 2009;
Helbich et al. 2013;
Keskin and Watkins 2017). However, most empirically identified submarkets are merely based on one- or two-year pooled housing data, without serious temporal consideration (e.g.,
Goodman and Thibodeau 2007;
Wu and Sharma 2012). Thus, their results may not reflect chronological changes and can be affected by short-term fluctuations. That is, housing submarkets delineated with data for a short time period may not be reliable and consistent over time. This outcome is often attributable to either data availability constraints affiliated with a temporal dimension or the lack of appropriate and robust analytical methods to account for both spatial and temporal information.
The intrinsic significance of recognizing housing submarkets lies in the inherent heterogeneity in prices, internal characteristics, and external locations of houses.
Hwang and Thill (
2009) expound upon the following four housing submarket natures: substitutability, heterogeneity, durability, and rigidity.
Bourassa et al. (
1999) and
Pryce (
2013) define housing submarkets as a group of similar dwellings that are close substitutes for one another within, but relatively poor substitutes of those outside of, their groupings. Following this latter convention, the space–time housing submarkets in this paper have been delimited as space-constrained and time-invariant groups containing similar houses. Space means the identified submarkets are geographically constrained; time denotes the existence of consistent housing patterns over time. Because space–time data are decomposable into systematic space–time trends and small-scale stochastic variations, the focus in this paper is on consistent and reliable space–time housing patterns (i.e., trends) instead of dynamic changes (i.e., variations).
Hwang and Thill (
2009) contend that housing submarkets, at the macro-level, are durable in the sense that, once built, housing structures and locations are not going to experience dramatic changes on a large scale (i.e., historical inertia prevails) beyond age-sensitive downgrading (e.g., deterioration). Thus, uncovering reliable and stable space–time housing submarkets is vital for policymakers and urban planners when analyzing and addressing urban affairs, such as the internal structure of cities, residential mobility, residential segregation, revitalization effects, and urban development, to name a few possibilities.
Housing submarket delineation has been utilized in various arenas, including strategic housing planning policy (e.g.,
Jones 2002) and housing price forecasting (e.g.,
Chen et al. 2009). Whereas housing submarkets can be delineated based on areal units such as census tracts or school districts, use of these units is often criticized because of their ad hoc or subjective nature. Although common clustering methods, such as K-means and hierarchical, have been popularly utilized, each submarket in their delineation results commonly comprises numerous fragmented small areas scattered across a study area. Even employing methods to achieve spatially contiguous housing submarkets does not totally eliminate identifying homogeneous and spatially non-contiguous submarkets (
Keskin and Watkins 2017). Furthermore, identification of stable spatial–temporal housing submarkets increases in complexity with the addition of a temporal dimension (e.g.,
Kopczewska and Ćwiakowski 2021). Addressing this issue, this paper aims to present a novel approach to generate stable space–time housing submarkets. Specifically, the purpose of this paper is twofold. First, to summarize a method combining the random effects (RE) statistical model with spatially constrained data-driven approaches to identify stable space–time housing submarkets from a large volume of spatiotemporal housing data. Second, to investigate different ways of incorporating spatial perspectives into traditional data-driven methods by introducing two spatially constrained data-driven clustering and graph partitioning algorithms, ClustGeo and REDCAP (REgionalization with Dynamically Constrained Agglomerative clustering and Partitioning), in an empirical case study delineating housing submarkets in Franklin County, Ohio (OH).
The rest of this paper is organized as follows.
Section 2 presents a literature review about housing submarket delineations and
Section 3 discusses the research method for space–time housing submarket delineations. Then,
Section 4 describes the study area and the analysis design, and
Section 5 presents the analysis results. Finally,
Section 6 presents a discussion and conclusions.
4. The Study Area and Analysis Design
An empirical study using 19 years of house transaction data in Franklin County, OH, from 01/01/2001 to 12/31/2019 exemplifies the delineation of coterminous geographic housing submarkets. Franklin County embodies a typical mid-size private residential dwellings market, roughly equivalent to the national average. It exhibits population size stability with an annual growth rate of 1.1% during the period spanned by its empirical data (i.e., 2001–2019)
1. These housing data and variables are open records secured from the Franklin County Auditor (see
Appendix A). The dataset consists of all residential building transactions with repeat sales records, including all residential building types. The raw data size is 419,099 location and time-encoded observations. Data cleaning
2 renders 301,019 records suitable for data analysis purposes. To make house prices comparable over 19 years, transaction prices were inflation-adjusted to the base year of 2001 using the United States (US) Consumer Price Index (CPI) from the US Bureau of Labor Statistics (
https://www.bls.gov/cpi/; accessed on 30 May 2023). Franklin County is situated in the center of the Columbus MSA, with nearly 42% of its land covered by the state capital and county seat, namely the City of Columbus. According to the 2020 US Census estimates
3, Franklin County has a population of 1,323,807, making it the most populous county in OH.
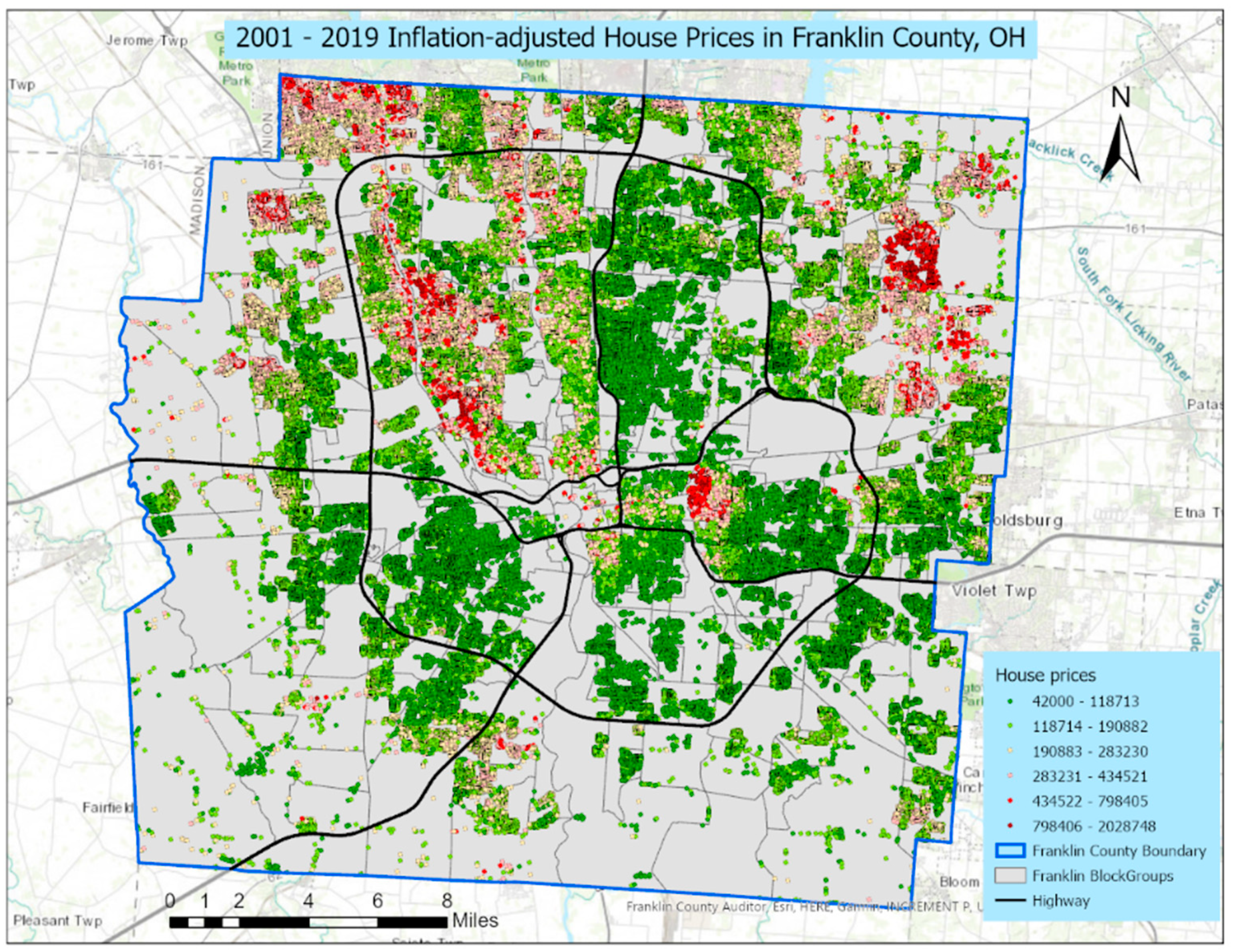
Figure 1 portrays the spatial distribution of inflation-adjusted house prices across Franklin County during the 19 studied years (2001–2019). This map includes the major highway (denoted by black) for reference purposes. House prices have an east–west geographic divider transecting the middle of the county, separating its northern and southern parts: house prices and densities in its north tend to be higher than their counterparts in its south. A prominent positive spatial autocorrelation map pattern is also observable here. More expensive houses, denoted by red or dark red, cluster together, whereas less expensive houses, denoted by green or dark green, spatially concentrate. Or, more generally, houses with similar values (high–high, moderate–moderate, low–low) tend to cluster in geographic space.
Figure 2 displays two annual time series trajectories: the 2001–2019 inflation-adjusted house prices per unit area (
Figure 2a) and the number of residential house transactions (
Figure 2b). Both graphs depict a generic V shape, demonstrating that the price values and transaction counts reached a peak during 2003–2005, dropped precipitously during and after the Great Recession (2007–2009), and then slowly bounced back during 2011–2019, which closely aligns with overall US housing market behavior statistics. As the price change due to the global factor occurred in the entire county, each submarket has the same change pattern and, hence, the RE estimation for each submarket based on the same trajectory is not expected to have a large variation.
Housing submarket boundaries delineated here utilized area aggregated spatial units (e.g., neighborhoods, school districts, zip code postal zone, census tracts, or census block groups), instead of individual housing units, for three main reasons. The first is the urban housing development process. House construction in urban areas is usually not by individuals, but rather by developers or builders in batch (which helps exploit economies of scale and minimize intermediate transport costs affiliated with agglomeration economies). It involves constructing hundreds of houses in tandem on an empty track of land, with economies of scale achieved through the utilization of similar house styles, building sizes, lot sizes, and other residential attributes, and the sharing of public infrastructure and services as well as local amenities. The second reason is that housing submarket boundaries derived from individual housing units are highly spatially fragmented. Hence, resulting submarkets barely have any practical meaning in real estate market analysis or urban policy planning. The third, and final, reason is that aggregating a large set of space–time house data into areal units and temporal intervals can compress data and significantly improve computational efficiency, which makes the submarket delineation of a large housing dataset with more than 300,000 records feasible. According to the US Census Bureau
4, railroads, roads, streets, streams, bodies of water, or other visible physical boundaries or cultural features form census block group boundaries. A census block group usually contains 600–3000 people, a smaller areal unit than a census tract, school district, or zip code area, and is relatively homogeneous and compact. Thus, it is a midpoint between a fine (e.g., a parcel occupied by an individual housing unit) and a coarse spatial resolution (e.g., zip code postal zones and census tracts that frequently encompass too much heterogeneity), and, hence, can serve as an alternative to housing neighborhood boundaries. There are 887 census block groups in Franklin County and, therefore, the individual house data are reorganized into an 887-by-76 space–time data structure as follows: in the spatial dimension, 301,204 individual house data are aggregated into and summarized for 887 census block groups; and, in the temporal dimension, data are sliced first by year and then by quarter, resulting in 76 (=19 × 4) time intervals.
4.1. Salient Housing Attribute Variables
Clustering algorithms rely heavily on calculating feature separation (mostly Euclidian distance) among observations to determine similarity. Hence, the curse of dimensionality is a common issue when dealing with a high dimension of input attributes. To ensure that any latent spatial information is adequately considered, and resulting submarkets are interpretable and meaningful, a parsimonious set of variables with three non-spatial facets and two spatial traits is chosen as input into the algorithms. Notable is that prediction or forecasting hedonic price models that others have devised—two purposes that are beyond the scope of this paper—are likely to include not just three, but many, variables (e.g.,
Li and Li 2018). The three non-spatial variables—individual unit house price, house living area, and house age—are the most crucial determinants appearing in the literature for delineating submarkets. The two spatial attributes are the (x, y) coordinates of the census block group centroids. All variables were standardized to z-scores using the z-transformation.
Table 1 tabulates summary statistics for the five raw (i.e., pre-z-score) input variables. Whereas house price, living area, and house age are at the individual house level, the block group centroid (x, y) coordinates are at the aggregated areal unit level. The minimum value of house age is −2, denoting purchases for new houses not yet built at the time of sale. These raw variables are further processed and standardized as described next. The unit house price is the per house inflation-adjusted transaction price divided by its corresponding living area. The house age is number of years old at the time of sale. The individual house price per unit, living area, and house age are aggregated quarterly by each year within each block group boundary to estimate their median value, with these medians then concatenated into an 887-by-76 space–time data structure. With repeated temporal measurements in each analysis unit, the RE models can estimate stable temporal housing patterns with varying intercepts and no covariates.
Figure 3 portrays plots of all the estimated RE terms in the study area, as well as prominent housing map patterns. Due to the presence of non-residential land-use zoning, 20 block groups with zero residential house transactions over 19 years were deleted from the study area, appearing as blank areas in the maps.
Figure 3a portrays a high house value swath in the northern part, and conspicuous low value concentrations in the central and southern parts, of the county, with some exceptions in the inner city uptown.
Figure 3b,c display an overall concentric zone pattern (i.e., the Burgess internal structure of the city spatial organization)—smaller, older buildings in the inner city, versus larger, newer edifices in the outer suburban areas.
4.2. An analytical Design for Delineating Housing Submarkets
Figure 4 presents an analytical design comprising five steps. In step 1, the 19 years of Franklin County residential housing data are split into 2 datasets using a temporally stratified random sampling scheme. A sizeable amount, 90%, of the yearly stratified random sample draws is used as a training dataset to delineate the submarkets, with the remaining 10% of annual data used for testing and comparing the resulting submarkets. In step 2, the training data are aggregated and summarized at the census block group level to construct an 887-by-76 spatial panel dataset. In step 3, the RE term is estimated conditional on the attribute variables of house price per square footage, living area, and house age as the covariates, capturing consistent temporal housing patterns. In step 4, the RE terms are introduced in conjunction with spatial information into spatially constrained data-driven algorithms to delineate the Franklin County space–time housing submarkets. In the final stage, several alternative submarkets are examined and compared based upon the following three criteria: spatial contiguity, between-cluster heterogeneity, and model performance diagnostics. A 10% temporal stratified house sample with a composite size of 30,100 supplies an independent test dataset for evaluating model fit and price prediction errors of 5 hedonic price models, with and without submarkets.
5. Results
In order for the spatially constrained algorithms to be comparable, the number of clusters is set to 10 (i.e., the same constant). Each submarket is portrayed in a different color.
Figure 5a reveals the REDCAP submarkets using Full-order constrained Ward linkage clustering (Full-Order-WLK) and
Figure 5b is the ClustGeo submarkets map with
and
. Overall, two spatially constrained data-driven clustering algorithms generated similar results. Visually, the REDCAP and ClustGeo submarkets have similar regionalization patterns, both satisfying spatial closeness and compact clustering objectives. A minor difference between the two is that the REDCAP algorithm enforces a hard spatial contiguity constraint for each submarket, whereas the ClustGeo algorithm imposes a soft contiguity constraint for formulating submarkets. A hard spatial constraint means that two similar observations must share spatial boundaries to be grouped into one submarket. In contrast, a soft spatial constraint indicates that two observations with high non-spatial attribute similarity can be grouped into one submarket even if they are not spatially contiguous, although they exhibit a certain minimal degree of geographic similarity. This is the reason why Submarkets 4 and 5 in ClustGeo have two discontinuous parts in space (see
Figure 5b).
Figure 6a,b reproduce the boxplots of three non-spatial attribute similarity variables—house price per square footage, living area, and house age—together with the between-cluster heterogeneity for REDCAP as well as ClustGeo submarkets. These 2 sets of submarkets have similar between-cluster heterogeneity values: 0.656 and 0.644, respectively. The between-cluster heterogeneity index measures the ratio of the between- and total-cluster sums of squares and is widely adopted to evaluate uncovered clusters. Linking the boxplots with their corresponding submarket maps exposes that house age successfully differentiates between Franklin County inner and outer cities.
Table 2 encapsulates the main attributes of each submarket. First, for REDCAP, low-priced, small houses in the outer city characterize Submarkets 1, 3, and 5; Submarkets 2 and 9 reflect mainly high-priced, middle-to-big sized houses in the outer city; Submarkets 6, 7, and 8 brand low-priced, small-to-mid-sized houses in the inner city; and mid-to-high-priced, big houses in the inner city stamp Submarkets 4 and 10. Second, for ClustGeo, Submarkets 1, 3, and 7 embrace primarily low-priced, small-to-mid-sized houses in the outer city; Submarkets 8 and 9 encompass high-priced, big houses in the outer city; Submarket 2 embodies mid-priced and mid-sized houses in the outer city; Submarkets 4 and 10 mostly consist of low-priced, small houses in the inner city; and Submarket 5 contains mid-priced and mid-sized houses in the inner city, Submarket 6 is labeled as high-priced, mid-sized houses in the inner city.
Figure 5c,d show the SKATER and a priori submarkets, the latter included as a reference map.
Figure 6c pictures the SKATER submarket housing characteristic boxplots. Comparing the cluster heterogeneity value and boxplot statistics confirms that the REDCAP approach performs better than the alternative SKATER algorithm in identifying distinct clusters. Thus, the REDCAP with Full-Order-WLK is superior to the SKATER approach, at least in this case, just like the author of the REDCAP method claims.
Figure 5d displays the 17 school district boundaries within Franklin County that serve as a priori submarkets
6, included here because a common traditional a priori framework practice is to demarcate with school district boundaries or municipal administrative borders. These Franklin County school district boundaries are not necessarily spatially contiguous, as is illustrated by the Columbus ISD (encoded 2503 in the map). The lack of coterminousness stems from the spatially fragmented administrative boundaries of the City of Columbus.
The 10% testing data subset was utilized to examine the performance of the 5 hedonic price models coupled with each of the 4 sets of submarkets: submarket absence (model 1), 17 a priori submarkets (model 2), SKATER submarkets (model 3), REDCAP submarkets (model 4), and ClustGeo submarkets (model 5). All submarkets are encoded with binary 0–1 dummy variables in their respective specifications. Model performance criteria consist of both the Akaike (AIC) and Bayesian information criterion (BIC), in addition to a pseudo-R-squared value (R
2) and root mean squared error (RMSE), two of the most popular goodness-of-fit measures for model comparisons (e.g.,
Wheeler et al. 2014;
Hu et al. 2022).
Table 3 reveals that the hedonic price model with REDCAP submarkets (model 4) has the best combination of overall model fit and lowest prediction error. The pseudo-R
2 value increases from 0.7382 for model 1, to 0.7734, 0.8042, and 0.8210, respectively, for models 2, 3, and 4, decreasing slightly to 0.8112 for model 5. The AIC and BIC display the same trend across these five model specifications. Furthermore, models 4 and 5, with respective REDCAP and ClustGeo submarkets, have the lowest prediction errors, as rated by their RMSE values. Levene’s test results in
Table 4 show that each set of submarkets exhibits statistically significant between-segments house price variance, with REDCAP yielding the largest F value that indicates a difference across submarkets. In other words, each submarket set contains markedly excess house price variability.
This empirical case study using a 19-year Franklin County, OH, house price dataset renders the following implications. First, all hedonic regression models with submarkets have a better model fit and lower prediction errors than a posited model with no submarket. This argues for the presence of house submarkets in Franklin County, a contention that agrees with the existing housing submarket literature. Second, in terms of three particular evaluation criteria, the spatially constrained data-driven demarcated submarkets (SKATER, REDCAP, and ClustGeo) outperform the a priori submarkets. All else being equal, the usual expectation is that a statistical model whose specification includes more subgroups will improve its model fit and reduce its prediction error. However, here, hedonic price models 3, 4, and 5 with only 10 submarkets perform better than a prevailing wisdom-based a priori submarket with 17 subgroups based upon public school districts. Third, not surprisingly, the REDCAP submarket is superior to the SKATER submarket, because SKATER is a naïve case of REDCAP. Fourth, in this empirical study, the model with REDCAP-delineated submarkets appears to excel in all five hedonic price models, capturing the highest cluster heterogeneity. However, the difference between REDCAP and ClustGeo may not be statistically significant because their statistic values are relatively close, and a visual inspection of their resulting submarket structures suggests that they appear to be similar. Therefore, overall, the proposed REDCAP and ClustGeo approaches perform equally well. Both algorithms successfully segmented the study area into inner-city and outer-city submarkets, spawning similar regionalization structures, despite some differences in their submarket boundaries. Finally, neither of the spatially constrained data-driven algorithms adopted in this study needs to specify the number of submarkets (K) beforehand, unlike K-means or DBSCAN. The arbitrariness of a choice of this K is one of the main criticisms leveled at certain popular clustering algorithms, such as K-means, the EM algorithm for a Gaussian mixture model, or DBSCAN. Due to their inherent mechanisms, different options of K can result in a given algorithm creating very different cluster structures. In contrast, both the ClustGeo and REDCAP algorithms are based upon agglomerative hierarchical clustering, meaning that clusters are hierarchically nested with varying K. In addition, these latter algorithms generate scree plots and dendrograms to uncover the finer structure within and between clusters to help choose an optimal K number of submarkets for a specific dataset.
6. Discussion and Conclusions
The study précised in this paper aimed to delineate stable and reliable space–time housing submarkets with a large spatiotemporal house sales dataset. Quantification of its temporal dimension was by extracting consistent and statistically significant patterns with RE model specifications. The spatial dimension disclosure was through implementing two spatially constrained data-driven segmentation approaches. The empirical case study using a 19-year Franklin County, OH, space–time house price dataset illustrates that these approaches perform better than non-spatial methods and a priori preset spatial boundaries.
Spatial constraints were imposed in this submarket segmentation study at three different levels. First, individual houses were aggregated into census block groups as the base unit for formulating submarkets, thus reducing computational burdens and spatial fragmentation. Second, the absolute location, the individual (x, y) coordinates of block group centroids, was included as a pair of input covariates to incorporate a reasonable proxy for spatial proximity. Third, spatial propinquity (spatial neighbors) or topology was specified in the data-driven clustering or partitioning algorithms to ensure enforcement of soft or hard spatial contiguity.
This paper contributes to the existing literature in various ways. First, it helps fill the literature gap about space–time house submarket delineation, primarily focusing on the stability of space–time submarkets. It proposes an analytical framework of combining the RE model with a spatially constrained data-driven approach to demarcate space-specific and time-invariant housing submarkets. A large quantity of spatial panel house transaction data in this study allowed for a rather comprehensive examination of this method. Second, the resulting demarcations produced practical and meaningful submarket boundaries by taking spatial closeness, spatial contiguity, and area-aggregated spatial census geography units into account. Third, the results summarized here demonstrate the superiority of the REDCAP and ClustGeo algorithms for spatial housing submarket delineation. Such applications of these two spatially constrained data-driven algorithms in housing submarket delineation are relatively novel. Although several papers already describe the use of SKATER, the naïve version of REDCAP, by itself for housing submarket delineation (e.g.,
Helbich et al. 2013), this paper presents a comparative analysis of three spatially constrained data-driven algorithms—SKATER, REDCAP, and ClustGeo. This comparison yields a practical implication that the data-driven approach can enhance spatial housing submarket demarcation. Third, this paper explores different ways of incorporating space into data-driven unsupervised (hierarchical clustering) machine learning algorithms. Accordingly, it should serve to inspire geospatial researchers to reflect on what roles space can play in machine learning methods, and encourage more data scientists to incorporate geographic locations, spatial autocorrelation, and/or spatial topology into current artificial intelligence (AI) algorithms to bring forth new spatially explicit models and bolster the cutting-edge research area of GeoAI. Finally, this paper furnishes an enhanced tool to generate housing submarkets, which is recognized as a crucial component for strategic housing investment and housing market operations (
Jones 2002;
Jones et al. 2004). This achievement can be useful for, especially, local or regional policy practitioners who are responsible for solving housing problems in relatively small areas such as a metropolitan area. Although the modeling framework articulated here can be applied to other areas, it may need selected customizing to adapt it to geographic landscape specific local characteristics.
Based upon findings summarized in this paper, some topics are worth exploring in future work. First, similar studies can also be undertaken for other coarser geographic resolution levels, such as zip code areas or census tracts. In theory, house homogeneity is harder to guarantee within coarser spatial units, but comparing the resulting submarkets derived from different aggregate areal units spanning a range of coarseness seems like a worthwhile endeavor. Second, even though this paper targets macro-level stable space–time submarkets, the investigation of housing submarket dynamics at the micro-level would be a valuable future exercise. For example, impacts of inner-city gentrification, or of a newly built highway, on house prices or submarkets. Third, the proposed method is tested only with RE. Although this component is a popular ingredient in space–time modeling, other approaches, including fixed and multi-level effects, can also provide compatible outcomes. Further investigations with a myriad of other approaches can help establish a more comprehensive understanding of housing submarket delineation.