Simulation Framework to Determine Suitable Innovations for Volatility Persistence Estimation: The GARCH Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. The GARCH Model
2.2. The fGARCH Model
2.3. The True Parameter Recovery Measure
2.4. Simulation Design
2.4.1. Aim of the Simulation Study
2.4.2. State the Research Questions
2.4.3. Method of Implementation
- Write the code: Carrying out a proper simulation experiment that mirrors real-life situations can be very demanding and computationally intensive, hence readable computer code with the right syntax must be produced. The code in this study is written to fit the true model3 to the real data to obtain the true parameter representations4 for the MCS. These true parameter values and other outputs from the fit are used in the code to generate simulated datasets that are analysed to obtain the MCS estimators. The standard errors of the estimates are also obtained in the process.
- Set the seed: Simulation code will generate a different sequence of random numbers each time it is run unless a seed is set (Danielsson 2011). A set seed initialises the random number generator (Ghalanos 2022) and ensures reproducibility, where the same result is obtained for different runs of the simulation process (Foote 2018). The seed needs to be set only once, for each simulation, at the start of the simulation session (Ghalanos 2022; Morris et al. 2019), and it is better to use the same seed values throughout the process (Morris et al. 2019).
- After setting the seed, the true parameter representations of the true sampling distribution (or true model) are then set a priori (Koopman et al. 2017; Mooney 1997).
- Next, simulated observations are generated using the true sampling distribution or the true model given some sets of (or different sets of) fixed parameters. Generation of simulated datasets through the GARCH model is carried out using the R package “rugarch”. Random data generation involving this package can be implemented using either of two approaches. The first approach is to carry out the data-generating simulation directly on a fitted object “fit” using the ugarchsim function for the simulated random data. The second approach uses the ugarchpath function, which enables simulation of desired number of volatility paths through different parameter combinations (see Ghalanos 2018, 2022; Pfaff 2016 for relevant details on the two functions and their usage).
- The generated (simulated) data are analysed, and the estimates from them are evaluated using classic methods through meta-statistics to derive relevant information about the estimators. Meta-statistics (see Chalmers and Adkins 2020) are performance measures or metrics for assessing the modelling outputs by judging the closeness between an estimate and the true parameter. A few of the frequently used meta-statistical summaries, as described below, include bias, root mean square error (RMSE) and standard error (SE). For more meta-statistics, see Chalmers and Adkins (2020); Morris et al. (2019); Sigal and Chalmers (2016).
Bias
Standard Error
RMSE
2.4.4. Discussion and Summary
3. Results: Simulation and Empirical
3.1. Practical Illustrations of the Simulation Design: Application to Bond Return Data
3.1.1. The Background
3.1.2. Aim of the Simulation Study
3.1.3. Research Questions
- Which among the assumed error distributions is the most appropriate from the fGARCH process simulation for estimating the persistence of the volatility?
- Financial data are fat-tailed (Li 2008), i.e., non-Normal. Hence, will the combined volatility estimator of the most suitable error assumption still be consistent under departure from Normal assumption?
- What type (i.e., strong, weak or inconsistent) of consistency, in terms of RMSE and SE, does the fGARCH estimator exhibit?
- How is the performance of the MCS estimator in recovering the true parameter?
3.1.4. Method of Implementation
3.2. Empirical Verification
3.2.1. Exploratory Data Analysis
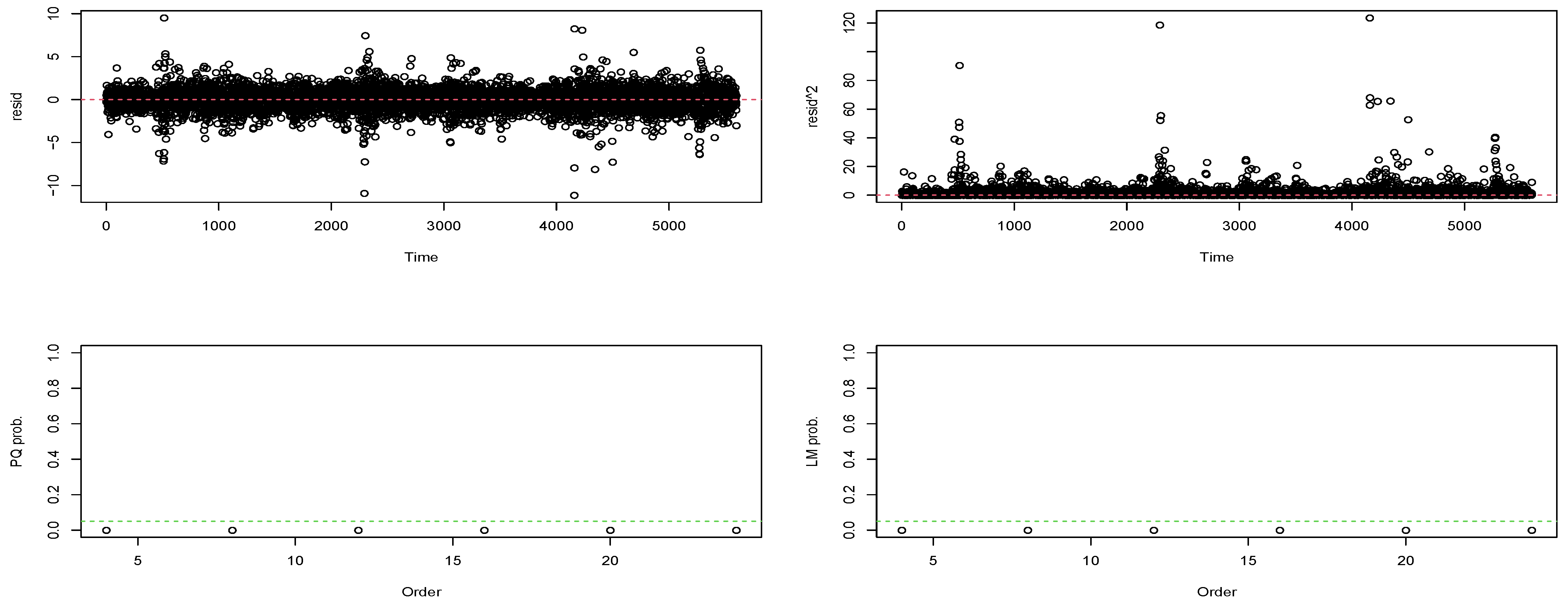
3.2.2. Tests for Serial Correlation and Heteroscedasticity
3.2.3. Selection of the Most Suitable Error Distribution
4. Discussion and Summarised Conclusions
5. Conclusions
5.1. Limitations in the Study
5.2. Future Research Interest
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCS | Monte Carlo simulation |
| SA | South Africa |
| GARCH | Generalised Autoregressive Conditional Heteroscedasticity |
| ugarchsim | Univariate GARCH Simulation |
| ugarchpath | Univariate GARCH Path Simulation |
| ARCH | Autoregressive Conditional Heteroscedasticity |
| TPR | True Parameter Recovery |
| S&P | Standard & Poor |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| i.i.d. | Independent and identically distributed |
| MLE | Maximum likelihood estimation |
| QMLE | Quasi-maximum likelihood estimation |
| fGARCH | family GARCH |
| sGARCH | simple GARCH |
| AVGARCH | Absolute Value GARCH |
| GJR GARCH | Glosten-Jagannathan-Runkle GARCH |
| TGARCH | Threshold GARCH |
| NGARCH | Nonlinear ARCH |
| NAGARCH | Nonlinear Asymmetric GARCH |
| EGARCH | Exponential GARCH |
| apARCH | Asymmetric Power ARCH |
| CGARCH | Component GARCH |
| MCGARCH | Multiplicative Component GARCH |
| Persistence | |
| DGP | Data generation process |
| RMSE | Root mean square error |
| SE | Standard error |
| GED | Generalised Error Distribution |
| GHYP | Generalised Hyperbolic |
| NIG | Normal Inverse Gaussian |
| GHST | Generalised Hyperbolic Skew-Student’s t |
| JSU | Johnson’s reparametrised SU |
| llk | log-likelihood |
| EDA | Exploratory Data Analysis |
| Quantile–Quantile | |
| LM | Lagrange Multiplier |
| PQ | Portmanteau-Q |
| WLB | Weighted Ljung–Box |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| HQIC | Hannan-Quinn information criterion |
| SIC | Shibata information criterion |
| AP-GoF | Adjusted Pearson Goodness-of-Fit |
| p-value | Probability value |
| GAS | Generalised Autoregressive Score |
Appendix A. Outcomes of Different Patterns of Seed Values for Sets S1 and S2
| () | Seed: 12345 | Seed: 54321 | Seed: 15243 | ||||||||||
| RMSE | SE | TPR (95%) | RMSE | SE | TPR (95%) | RMSE | SE | TPR (95%) | |||||
| Normal | 1000 | 0.9990 | 0.0862 | 0.0862 | 95.00% | 0.9563 | 0.0757 | 0.0625 | 90.94% | 0.9909 | 0.0801 | 0.0796 | 94.23% |
| 2000 | 0.9771 | 0.0934 | 0.0908 | 92.91% | 0.9903 | 0.0419 | 0.0410 | 94.17% | 0.9839 | 0.0490 | 0.0466 | 93.56% | |
| 3000 | 0.9727 | 0.0756 | 0.0709 | 92.50% | 0.9850 | 0.0373 | 0.0345 | 93.67% | 0.9791 | 0.0591 | 0.0557 | 93.11% | |
| 4000 | 0.9700 | 0.0693 | 0.0629 | 92.24% | 0.9846 | 0.0412 | 0.0387 | 93.64% | 0.9972 | 0.0304 | 0.0303 | 94.83% | |
| Student’s t | 1000 | 0.9990 | 0.0525 | 0.0525 | 95.00% | 0.9833 | 0.0441 | 0.0412 | 93.50% | 0.9990 | 0.0768 | 0.0768 | 95.00% |
| 2000 | 0.9902 | 0.0500 | 0.0492 | 94.16% | 0.9990 | 0.0349 | 0.0349 | 95.00% | 0.9958 | 0.0388 | 0.0386 | 94.69% | |
| 3000 | 0.9973 | 0.0327 | 0.0327 | 94.83% | 0.9977 | 0.0308 | 0.0308 | 94.87% | 0.9956 | 0.0318 | 0.0316 | 94.68% | |
| 4000 | 0.9918 | 0.0277 | 0.0267 | 94.31% | 0.9974 | 0.0258 | 0.0258 | 94.85% | 0.9963 | 0.0247 | 0.0246 | 94.74% | |
| GED | 1000 | 0.9875 | 0.0719 | 0.0710 | 93.90% | 0.9688 | 0.0499 | 0.0397 | 92.13% | 0.9899 | 0.0630 | 0.0624 | 94.13% |
| 2000 | 0.9663 | 0.0608 | 0.0512 | 91.89% | 0.9908 | 0.0336 | 0.0326 | 94.22% | 0.9847 | 0.0387 | 0.0360 | 93.64% | |
| 3000 | 0.9684 | 0.0441 | 0.0317 | 92.09% | 0.9846 | 0.0347 | 0.0315 | 93.63% | 0.9795 | 0.0385 | 0.0333 | 93.15% | |
| 4000 | 0.9692 | 0.0410 | 0.0282 | 92.16% | 0.9833 | 0.0328 | 0.0288 | 93.51% | 0.9839 | 0.0300 | 0.0259 | 93.57% | |
| GHYP | 1000 | 0.9940 | 0.0557 | 0.0555 | 94.52% | 0.9785 | 0.0437 | 0.0386 | 93.05% | 0.9897 | 0.0657 | 0.0650 | 94.12% |
| 2000 | 0.9748 | 0.0507 | 0.0446 | 92.70% | 0.9979 | 0.0328 | 0.0328 | 94.89% | 0.9871 | 0.0364 | 0.0344 | 93.87% | |
| 3000 | 0.9780 | 0.0353 | 0.0284 | 93.00% | 0.9901 | 0.0305 | 0.0292 | 94.15% | 0.9849 | 0.0325 | 0.0293 | 93.66% | |
| 4000 | 0.9776 | 0.0322 | 0.0241 | 92.97% | 0.9898 | 0.0263 | 0.0247 | 94.12% | 0.9892 | 0.0247 | 0.0226 | 94.07% | |
| () | Seed: 34567 | Seed: 76543 | Seed: 36547 | ||||||||||
| RMSE | SE | TPR (95%) | RMSE | SE | TPR (95%) | RMSE | SE | TPR (95%) | |||||
| Normal | 1000 | 0.9856 | 0.0583 | 0.0568 | 93.72% | 0.9942 | 0.0424 | 0.0421 | 94.54% | 0.9823 | 0.3888 | 0.3884 | 93.41% |
| 2000 | 0.9814 | 0.0396 | 0.0354 | 93.33% | 0.9891 | 0.0370 | 0.0357 | 94.06% | 0.9806 | 0.1419 | 0.1407 | 93.25% | |
| 3000 | 0.9845 | 0.0708 | 0.0693 | 93.62% | 0.9809 | 0.0334 | 0.0281 | 93.28% | 0.9822 | 0.0805 | 0.0787 | 93.40% | |
| 4000 | 0.9990 | 0.0397 | 0.0397 | 95.00% | 0.9778 | 0.0326 | 0.0248 | 92.98% | 0.9779 | 0.0575 | 0.0535 | 92.99% | |
| Student’s t | 1000 | 0.9971 | 0.0474 | 0.0474 | 94.82% | 0.9990 | 0.0422 | 0.0422 | 95.00% | 0.9990 | 0.0329 | 0.0329 | 95.00% |
| 2000 | 0.9789 | 0.0364 | 0.0303 | 93.08% | 0.9990 | 0.0281 | 0.0281 | 95.00% | 0.9990 | 0.0315 | 0.0315 | 95.00% | |
| 3000 | 0.9781 | 0.0326 | 0.0249 | 93.01% | 0.9975 | 0.0237 | 0.0236 | 94.86% | 0.9990 | 0.0234 | 0.0234 | 95.00% | |
| 4000 | 0.9871 | 0.0253 | 0.0223 | 93.87% | 0.9955 | 0.0218 | 0.0215 | 94.67% | 0.9946 | 0.0238 | 0.0234 | 94.58% | |
| GED | 1000 | 0.9802 | 0.0463 | 0.0423 | 93.21% | 0.9899 | 0.0389 | 0.0378 | 94.13% | 0.9986 | 0.0490 | 0.0490 | 94.96% |
| 2000 | 0.9726 | 0.0386 | 0.0282 | 92.49% | 0.9898 | 0.0280 | 0.0265 | 94.13% | 0.9879 | 0.0388 | 0.0371 | 93.94% | |
| 3000 | 0.9710 | 0.0398 | 0.0282 | 92.33% | 0.9820 | 0.0276 | 0.0218 | 93.38% | 0.9808 | 0.0303 | 0.0243 | 93.27% | |
| 4000 | 0.9800 | 0.0285 | 0.0213 | 93.19% | 0.9782 | 0.0284 | 0.0194 | 93.02% | 0.9752 | 0.0321 | 0.0215 | 92.73% | |
| GHYP | 1000 | 0.9863 | 0.0436 | 0.0417 | 93.80% | 0.9928 | 0.0383 | 0.0378 | 94.41% | 0.9990 | 0.0370 | 0.0370 | 95.00% |
| 2000 | 0.9744 | 0.0377 | 0.0285 | 92.66% | 0.9952 | 0.0265 | 0.0262 | 94.64% | 0.9990 | 0.0358 | 0.0358 | 95.00% | |
| 3000 | 0.9737 | 0.0351 | 0.0242 | 92.59% | 0.9872 | 0.0243 | 0.0213 | 93.88% | 0.9894 | 0.0256 | 0.0237 | 94.09% | |
| 4000 | 0.9810 | 0.0278 | 0.0212 | 93.29% | 0.9835 | 0.0246 | 0.0192 | 93.53% | 0.9816 | 0.0275 | 0.0213 | 93.35% | |
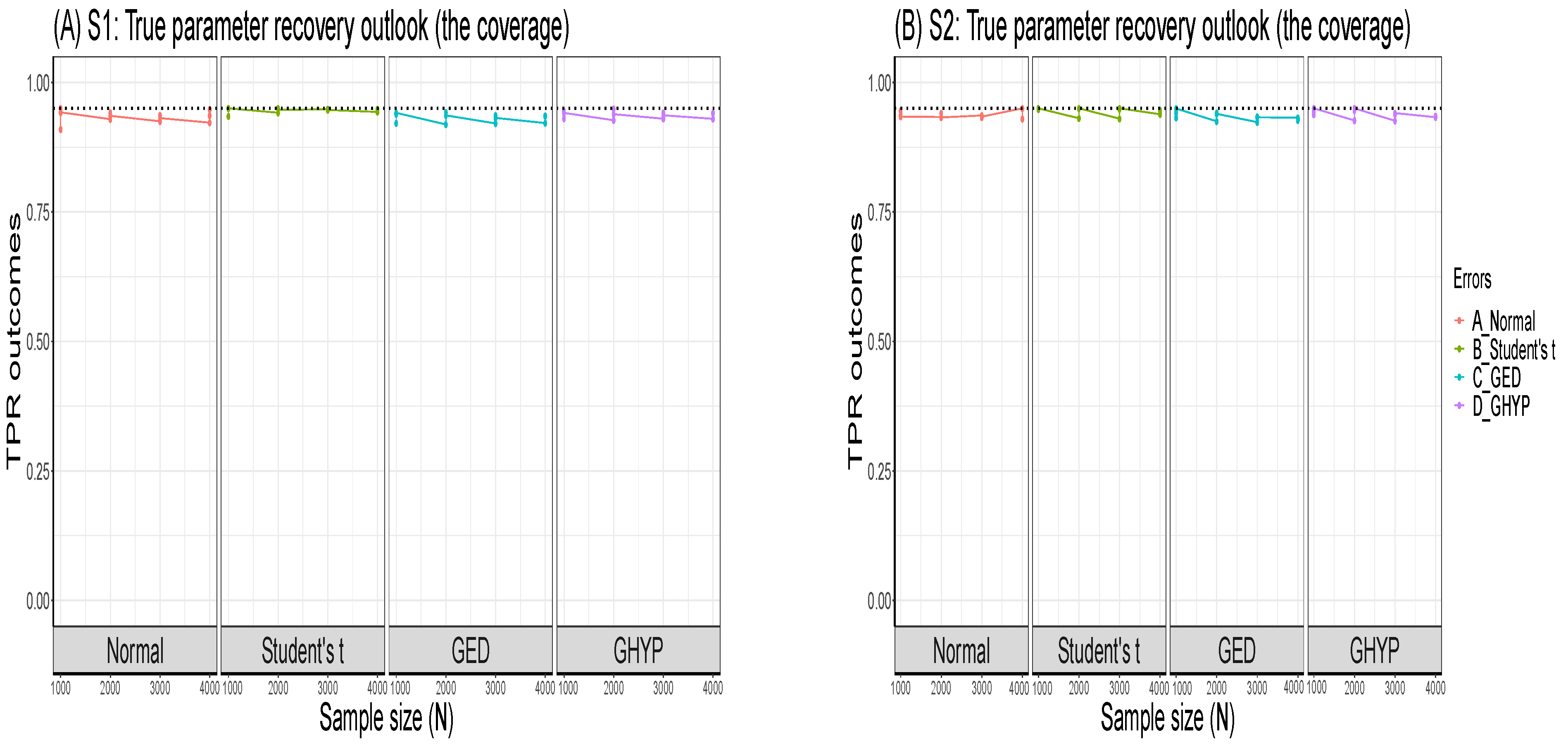
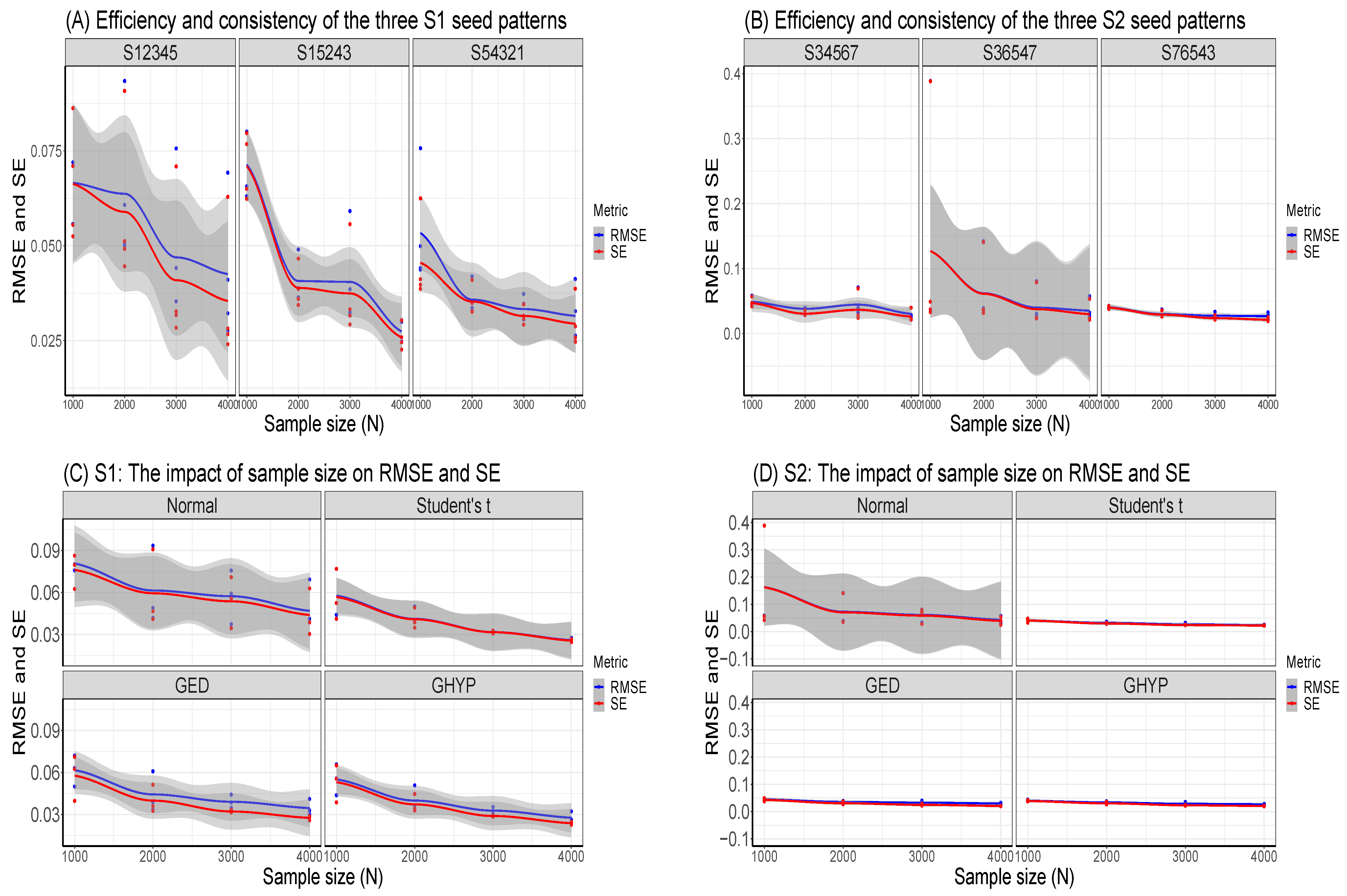
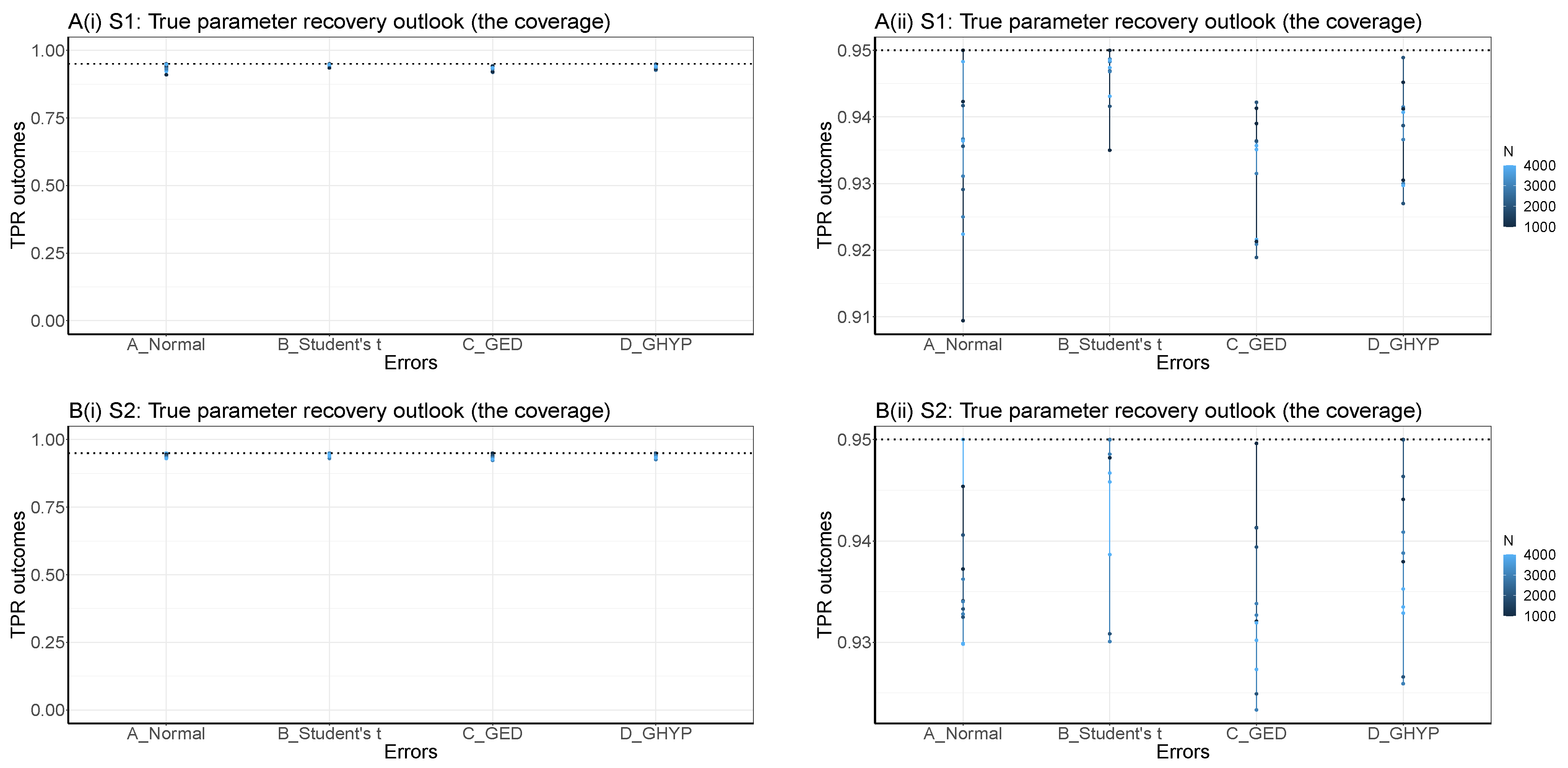
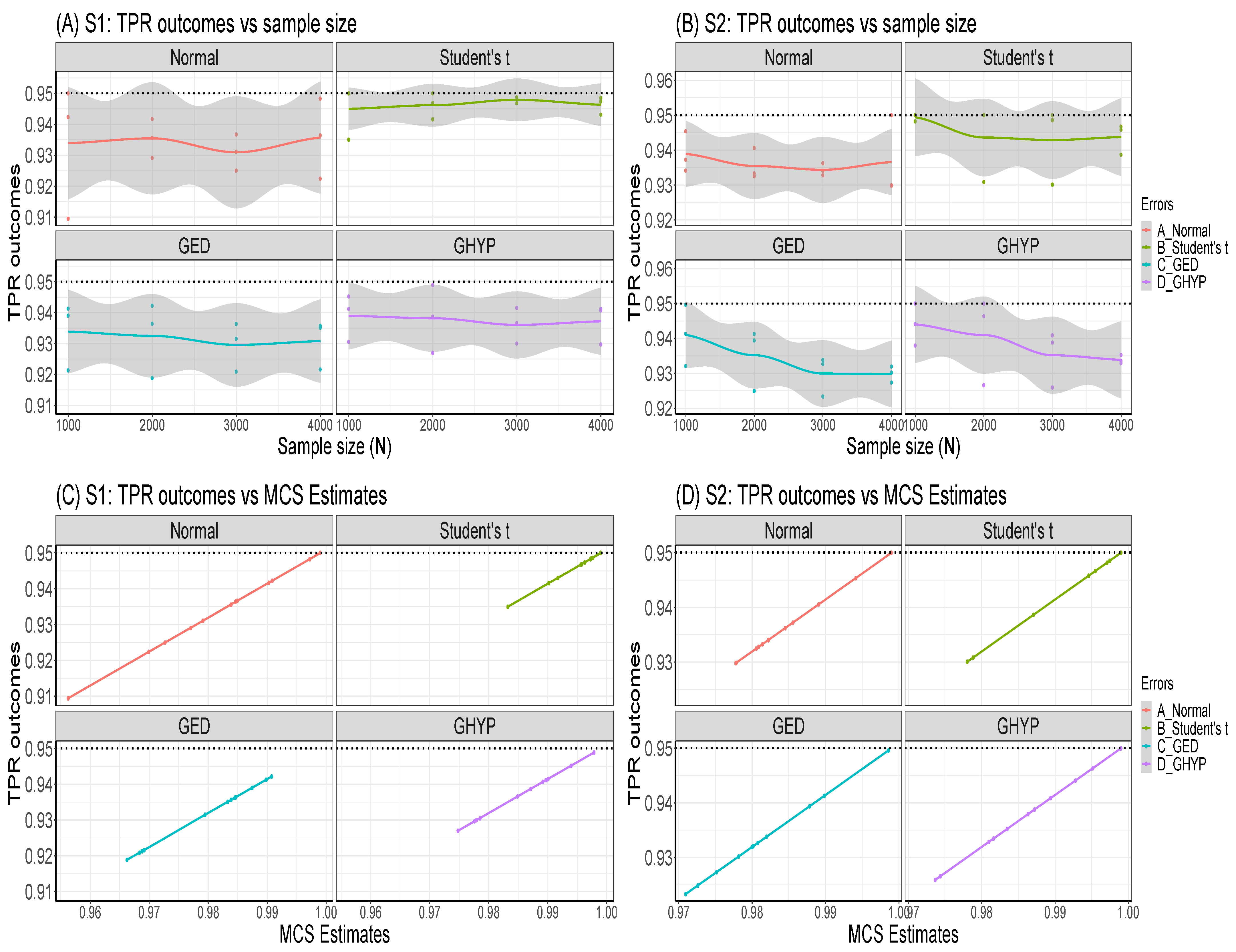
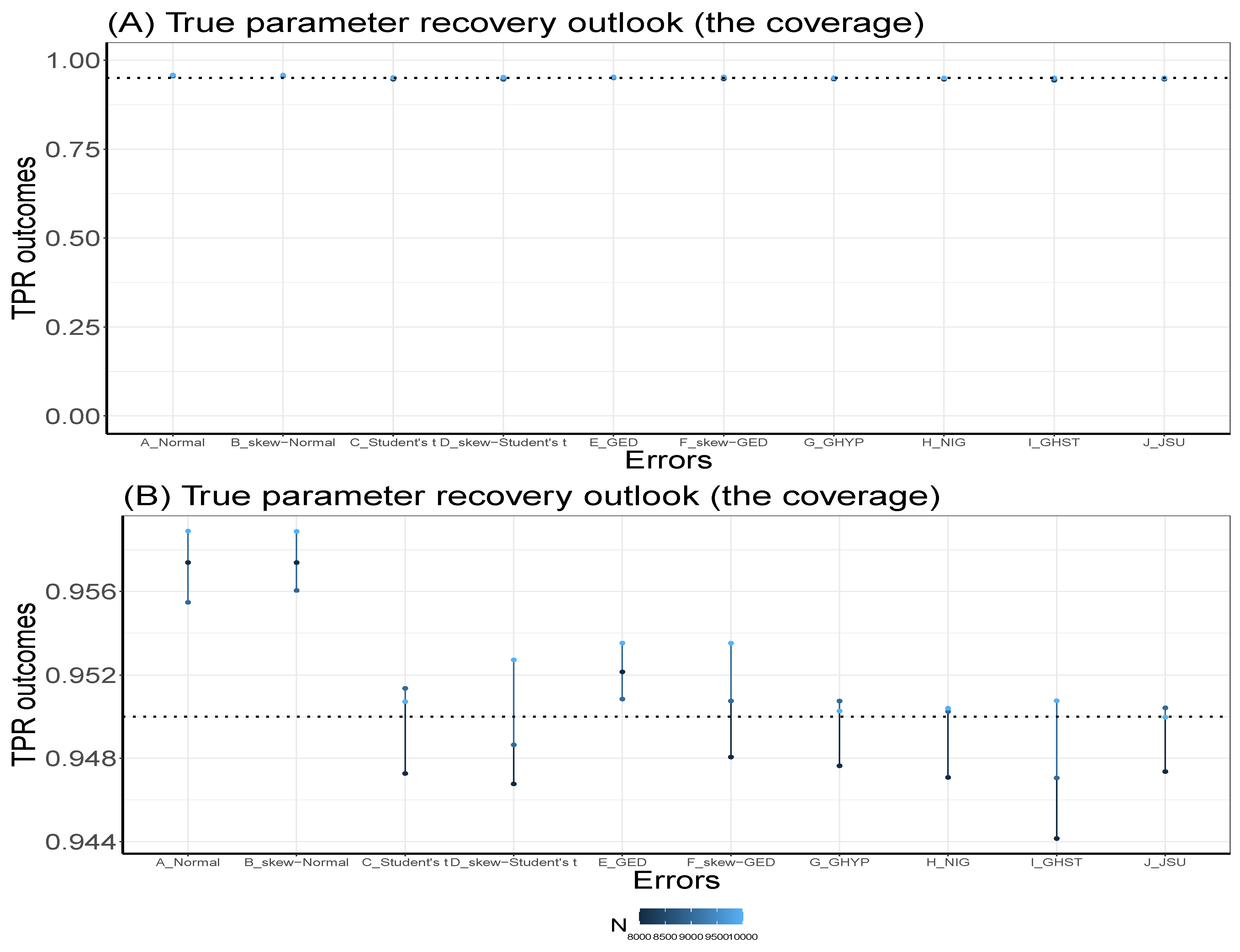
Appendix B. Further Visual Illustrations of S1 and S2 TPR Outcomes
Appendix C. The Code for DGP through the Ugarchsim Function
| Listing A1. The Code for the Method of Implementation of the MCS Experiment. | ||
| library (rugarch) | ||
| attach (BondDataSA) | ||
| BondDataSA<-as . data . frame (BondDataSA) | ||
| spec = ugarchspec (variance . model = list (model = ‘‘fGARCH’’, | ||
| garchOrder = c (1,1), | ||
| submodel = ‘‘ALLGARCH’’), | ||
| mean . model = list (armaOrder = c (1,1), | ||
| include . mean = TRUE), | ||
| distribution . model = ‘‘std’’, | ||
| fixed . pars = list (shape = 4.1)) | ||
| fit = ugarchfit (data = BondDataSA [,4, drop = FALSE], spec = spec) | ||
| fit | ||
| coef (fit) | ||
| # simulate for N = 8000 | ||
| sim = ugarchsim (fit, n . sim = 15000, n . start = 1, m. sim = 1000, | ||
| rseed = 12345, startMethod = ‘‘sample’’) | ||
| simGARCH <- fitted (sim) | ||
| simGARCH | ||
| simGARCH <- as . data . frame (simGARCH) | ||
| simGARCH | ||
| # Remove the first 7000 for initial values effect | ||
| R_simGARCH <- simGARCH[-c (1:7000), ] | ||
| R_simGARCH | ||
| # Fit ARMA(1,1)-fGARCH(1,1) to the simulated dataset R_simGARCH | ||
| # For Normal | ||
| spec <- ugarchspec (variance . model = list (model = ‘‘fGARCH’’, | ||
| garchOrder = c (1,1), | ||
| submodel = ‘‘ALLGARCH’’), | ||
| mean . model = list (armaOrder = c (1,1), | ||
| include . mean = TRUE), | ||
| distribution . model = ‘‘norm’’) | ||
| fit = ugarchfit (data = R_simGARCH, spec = spec) | ||
| show (fit) | ||
| coef (fit) | ||
| 1 | The GRETL (Baiocchi and Distaso 2003; Cottrell and Lucchetti 2023), GAS (Ardia et al. 2019) and fGARCH (Pfaff 2016; Wuertz et al. 2020) are also among the freely available and applicable software. |
| 2 | Coverage probability is the probability that a confidence interval of estimates contains or covers the true parameter value (Hilary 2002). |
| 3 | We describe the true model as the data-generating model fitted with the true sampling distribution (see Feng and Shi 2017). |
| 4 | When the true model is fitted to the real data, the estimates from the fit represent the true parameters. |
| 5 | This study only follows the authors’ trimming steps for initial values effect. The other trimming by the authors for “simulation bias” (where some initial numbers of replications are further discarded after the initial value effect adjustment) are not used here because it is observed that it sometimes distorts the estimator’s consistency. |
| 6 | See the “Synopsis of R packages” pages 125–27 in (Pfaff 2016) for relevant details on rugarch package and ugarchsim function. |
References
- Arago, Vicent, and Angeles Fernandez-Izquierdo. 2003. GARCH models with changes in variance: An approximation to risk measurements. Journal of Asset Management 4: 277–87. [Google Scholar] [CrossRef]
- Ardia, David, Kris Boudt, and Leopoldo Catania. 2019. Generalized autoregressive score models in R: The GAS package. Journal of Statistical Software 88: 1–28. [Google Scholar] [CrossRef]
- Ashour, Samir K., and Mahmood A. Abdel-hameed. 2010. Approximate skew normal distribution. Journal of Advanced Research 1: 341–50. [Google Scholar] [CrossRef]
- Azzalini, Adelchi 1985. A class of distributions which includes the normal ones. Scandinavian Journal of Statistics 12: 171–78.
- Azzalini, Adelchi, and Antonella Capitanio. 2003. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. Journal of the Royal Statistical Society. Series B: Statistical Methodology 65: 367–89. [Google Scholar] [CrossRef]
- Baiocchi, Giovanni, and Walter Distaso. 2003. GRETL: Econometric software for the GNU generation. Journal of Applied Econometrics 18: 105–1102. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Thomas Mikosch, and Sidney I. Resnick. 2013. Levy Processes: Theory and Applications. Boston: Birkhauser. New York: Springer Science+Business Media. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedastic. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. Conditionally heteroskedasticity time series model for speculative prices and rates of returns. The Review of Economic and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Jeffrey M. Wooldridge. 1992. Quasi-maximum likelihood estimation and inference in dynamic models with time-varying covariances. Econometric Reviews 11: 143–72. [Google Scholar] [CrossRef]
- Branco, Márcia D., and Dipak K. Dey. 2001. A general class of multivariate skew-elliptical distributions. Journal of Multivariate Analysis 79: 99–113. [Google Scholar] [CrossRef]
- Bratley, Paul, Bennett L. Fox, and Linus E. Schrage. 2011. A Guide to Simulation, 2nd ed. New York: Springer Science. New York: Business Media. [Google Scholar] [CrossRef]
- Buccheri, Giuseppe, Giacomo Bormetti, Fulvio Corsi, and Fabrizio Lillo. 2021. A score-driven conditional correlation model for noisy and asynchronous data: An application to high-frequency covariance dynamics. Journal of Business and Economic Statistics 39: 920–36. [Google Scholar] [CrossRef]
- Chalmers, Phil. 2019. Introduction to Monte Carlo Simulations with Applications in R Using the SimDesign Package. pp. 1–46. Available online: philchalmers.github.io/SimDesign/pres.pdf (accessed on 28 August 2023).
- Chalmers, R. Philip, and Mark C. Adkins. 2020. Writing effective and reliable Monte Carlo simulations with the SimDesign package. The Quantitative Methods for Psychology 16: 248–80. [Google Scholar] [CrossRef]
- Chib, Siddhartha. 2015. Monte Carlo Methods and Bayesian Computation: Overview. Amsterdam: Elsevier, pp. 763–67. [Google Scholar] [CrossRef]
- Chou, Ray Yeutien. 1988. Volatility persistence and stock valuations: Some empirical evidence using GARCH. Journal of Applied Econometrics 3: 279–94. [Google Scholar] [CrossRef]
- Cottrell, Allin, and Riccardo J. Lucchetti. 2023. Gnu regression, econometrics, and time-series library. In Gretl User’s Guide. Boston: Free Software Foundation, pp. 1–486. [Google Scholar]
- Creal, Drew, Siem Jan Koopman, and André Lucas. 2013. Generalized autoregressive score models with applications. Journal of Applied Econometrics 28: 777–95. [Google Scholar] [CrossRef]
- Danielsson, Jon. 2011. Financial Risk Forecasting: The Theory and Practice of Forecasting Market Risk with Implementation in R and Matlab. Chichester: John Wiley & Sons. [Google Scholar]
- Datastream. 2021. Thomson Reuters Datastream. Available online: https://solutions.refinitiv.com/datastream-macroeconomic-analysis? (accessed on 17 June 2021).
- Ding, Zhuanxin, and Clive W. J. Granger. 1996. Modeling volatility persistence of speculative returns: A new approach. Journal of Econometrics 73: 185–215. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Duda, Matej, and Henning Schmidt. 2009. Evaluation of Various Approaches to Value at Risk. Master’s thesis, Lund University, Lund, Sweden. Available online: https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=1436923&fileOId=1646971 (accessed on 28 August 2023).
- Eling, Martin. 2014. Fitting asset returns to skewed distributions: Are the skew-normal and skew-student good models? Insurance: Mathematics and Economics 59: 45–56. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedacity with estimates of variance of United Kingdom inflation. Econometrica 50: 987–1008. [Google Scholar] [CrossRef]
- Engle, Robert F., and Magdalena E. Sokalska. 2012. Forecasting intraday volatility in the US equity market. Multiplicative component GARCH. Journal of Financial Econometrics 10: 54–83. [Google Scholar] [CrossRef]
- Engle, Robert F., and Tim Bollerslev. 1986. Modelling the persistence of conditional variances. Econometric Reviews 5: 1–50. [Google Scholar]
- Engle, Robert F., and Victor K. Ng. 1993. Measuring and testing the impact of news on volatility. The Journal of Finance 48: 17749–78. [Google Scholar] [CrossRef]
- Fan, Jianqing, Lei Qi, and Dacheng Xiu. 2014. Quasi-maximum likelihood estimation of GARCH models with heavy-tailed likelihoods. Journal of Business and Economic Statistics 32: 178–91. [Google Scholar] [CrossRef]
- Feng, Lingbing, and Yanlin Shi. 2017. A simulation study on the distributions of disturbances in the GARCH model. Cogent Economics and Finance 5: 1355503. [Google Scholar] [CrossRef]
- Fisher, Thomas J., and Colin M. Gallagher. 2012. New weighted portmanteau statistics for time series goodness of fit testing. Journal of the American Statistical Association 107: 777–87. [Google Scholar] [CrossRef]
- Foote, William G. 2018. Financial Engineering Analytics: A Practice Manual Using R. Available online: https://bookdown.org/wfoote01/faur/ (accessed on 28 August 2023).
- Francq, Christian, and Jean Michel Zakoïan. 2004. Maximum likelihood estimation of pure GARCH and ARMA-GARCH processes. Bernoulli 10: 605–37. [Google Scholar] [CrossRef]
- Francq, Christian, and Le Quyen Thieu. 2019. QML inference for volatility models with covariates. Econometric Theory 35: 37–72. [Google Scholar] [CrossRef]
- Geweke, John. 1986. Comment on: Modelling the persistence of conditional variances. Econometric Reviews 5: 57–61. [Google Scholar] [CrossRef]
- Ghalanos, Alexios. 2018. Introduction to the Rugarch Package. (Version 1.3-8). Available online: mirrors.nic.cz/R/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf (accessed on 28 August 2023).
- Ghalanos, Alexios. 2022. Rugarch: Univariate GARCH Models. R Package Version 1.4-7. Available online: https://cran.r-project.org/web/packages/rugarch/rugarch.pdf (accessed on 28 August 2023).
- Gilli, Manfred, D. Maringer, and Enrico Schumann. 2019. Generating Random Numbers. Cambridge: Academic Press, pp. 103–32. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and Daviid E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hallgren, Kevin A. 2013. Conducting simulation studies in the R programming environment. Tutorials in Quantitative Methods for Psychology 9: 43–60. [Google Scholar] [CrossRef]
- Harwell, Michael. 2018. A strategy for using bias and RMSE as outcomes in Monte Carlo studies in statistics. Journal of Modern Applied Statistical Methods 17: 1–16. [Google Scholar] [CrossRef]
- Hentschel, Ludger. 1995. All in the family nesting symmetric and asymmetric GARCH models. Journal of Financial Economics 39: 71–104. [Google Scholar] [CrossRef]
- Heracleous, Maria S. 2007. Sample Kurtosis, GARCH-t and the Degrees of Freedom Issue. EUR Working Papers. Florence: European University Institute, pp. 1–22. Available online: http://hdl.handle.net/1814/7636 (accessed on 28 August 2023).
- Higgins, Matthew L., and Anil K. Bera. 1992. A class of nonlinear Arch models. International Economic Review 33: 137–58. [Google Scholar] [CrossRef]
- Hilary, Term. 2002. Descriptive Statistics for Research. Available online: https://www.stats.ox.ac.uk/pub/bdr/IAUL/Course1Notes2.pdf (accessed on 28 August 2023).
- Hoga, Yannick. 2022. Extremal dependence-based specification testing of time series. Journal of Business and Economic Statistics, 1–14. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Yeasmin Khandakar. 2008. Automatic time series forecasting: The forecast package for R. Journal of Statistical Software 27: 1–22. [Google Scholar] [CrossRef]
- Javed, Farrukh, and Panagiotis Mantalos. 2013. GARCH-type models and performance of information criteria. Communications in Statistics: Simulation and Computation 42: 1917–33. [Google Scholar] [CrossRef]
- Kim, Su Young, David Huh, Zhengyang Zhou, and Eun Young Mun. 2020. A comparison of Bayesian to maximum likelihood estimation for latent growth models in the presence of a binary outcome. International Journal of Behavioral Development 44: 447–57. [Google Scholar] [CrossRef]
- Kleijnen, Jack P. C. 2015. Design and Analysis of Simulation Experiments, 2nd ed. New York: Springer, vol. 230. [Google Scholar] [CrossRef]
- Koopman, Siem Jan, André Lucas, and Marcin Zamojski. 2017. Dynamic Term Structure Models with Score Driven Time Varying Parameters: Estimation and Forecasting. NBP Working Paper No. 258. Warszawa: Narodowy Bank Polski, Education & Publishing Department, Poland. Available online: https://static.nbp.pl/publikacje/materialy-i-studia/258_en.pdf (accessed on 28 August 2023).
- Lee, Gary J., and Robert F. Engle. 1999. A Permanent and Transitory Component Model of Stock Return Volatility. In Cointegration, Causality and Forecasting: A Festschrift in Honor of Clive W. J. Granger. New York: Oxford University Press, pp. 475–97. Available online: https://scirp.org/reference/referencespapers.aspx?referenceid=1232518 (accessed on 28 August 2023).
- Lee, Yen-Hsien, and Tung-Yueh Pai. 2010. REIT volatility prediction for skew-GED distribution of the GARCH model. Expert Systems with Applications 37: 4737–41. [Google Scholar] [CrossRef]
- Li, Qianru. 2008. Three Essays on Stock Market Volatility. All Graduate Theses and Dissertations, Spring 1920 to Summer 2023. p. 308. Available online: http://digitalcommons.usu.edu/etd/308/ (accessed on 28 August 2023).
- Lin, Chu Hsiung, and Shan Shan Shen. 2006. Can the student-t distribution provide accurate value at risk? Journal of Risk Finance 7: 292–300. [Google Scholar] [CrossRef]
- Maciel, Leandro dos Santos, and Rosangela Ballini. 2017. Value-at-risk modeling and forecasting with range-based volatility models: Empirical evidence. Revista Contabilidade e Financas 28: 361–76. [Google Scholar] [CrossRef]
- McNeil, Alexander J., and Rudiger Frey. 2000. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach. Journal of Empirical Finance 7: 271–300. [Google Scholar] [CrossRef]
- Mooney, Christopher Z. 1997. Monte Carlo Simulation, 1st ed. Thousand Oaks: SAGE Publications, vol. 116. [Google Scholar]
- Morris, Tim P., Ian R. White, and Michael J. Crowther. 2019. Using simulation studies to evaluate statistical methods. Statistics in Medicine 38: 2074–102. [Google Scholar] [CrossRef] [PubMed]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Pantula, Sastry G. 1986. Comment: Modelling the persistence of conditional variances. Econometric Reviews 5: 71–74. [Google Scholar] [CrossRef]
- Pfaff, Bernhard. 2016. Modelling Volatility. Hoboken: John Wiley & Sons, Ltd., pp. 116–32. [Google Scholar]
- Pourahmadi, Mohsen. 2007. Construction of skew-normal random variables: Are they linear combinations of normal and half-normal? Journal of Statistical Theory and Applications 3: 314–28. [Google Scholar]
- Qiu, Debin. 2015. aTSA: Alternative Time Series Analysis. Available online: https://cran.r-project.org/web/packages/aTSA/aTSA.pdf (accessed on 28 August 2023).
- Samiev, Sarvar. 2012. GARCH (1,1) with Exogenous Covariate for EUR/SEK Exchange Rate Volatility: On the Effects of Global Volatility Shock on Volatility. Master’s thesis, Umea University, Umea, Sweden. Available online: https://www.diva-portal.org/smash/get/diva2:676106/FULLTEXT01.pdf (accessed on 28 August 2023).
- Schwert, G. William. 1990. Stock volatility and the crash of ’87. The Review of Financial Studies 3: 77–102. [Google Scholar]
- Shahriari, Siroos, Sisson S. A., and Taha Rashidi. 2023. Copula ARMA-GARCH modelling of spatially and temporally correlated time series data for transportation planning use. Transportation Research Part C 146: 103969. [Google Scholar] [CrossRef]
- Sigal, Matthew J., and Philip R. Chalmers. 2016. Play it again: Teaching statistics with Monte Carlo simulation. Journal of Statistics Education 24: 136–56. [Google Scholar] [CrossRef]
- Silvennoinen, Annastiina, and Timo Teräsvirta. 2016. Testing constancy of unconditional variance in volatility models by misspecification and specification tests. Studies in Nonlinear Dynamics and Econometrics 20: 347–64. [Google Scholar] [CrossRef]
- Smith, Richard L. 2003. Statistics of extremes, with applications in environment, insurance, and finance. In Extreme Values in Finance, Telecommunications, and the Environment. Boca Raton: Chapman & Hall/CRC, pp. 20–97. [Google Scholar]
- Su, Jen Je. 2011. On the oversized problem of Dickey-Fuller-type tests with GARCH errors. Communications in Statistics: Simulation and Computation 40: 1364–72. [Google Scholar] [CrossRef][Green Version]
- Søfteland, Andreas, and IversenGlenn Stian. 2021. Applying GARCH-EVT-Copula Forecasting in Active Portfolio Management. Master’s thesis, NTNU, Trondheim, Norway. Available online: https://no.ntnu_inspera_82752696_84801861.pdf (accessed on 13 August 2023).
- Taylor, Stephen J. 1986. Modelling Financial Time Series, 2nd ed. Singapore: World Scientific Publishing Co. Pte. Ltd. [Google Scholar]
- Wang, Chao, Richard Gerlach, and Qian Chen. 2018. A semi-parametric realized joint value-at-risk and expected shortfall regression framework. arXiv arXiv:1807.02422. [Google Scholar]
- White, Halbert. 1982. Maximum likelihood estimation of misspecified models. Econometrica 50: 1–25. [Google Scholar] [CrossRef]
- Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy McGowan, Romain François, Garrett Grolemund, Alex Hayes, Lionel Henry, Jim Hester, and et al. 2019. Welcome to the Tidyverse. Journal of Open Source Software 4: 1–6. [Google Scholar] [CrossRef]
- Wuertz, Diethelm, Tobias Setz, Yohan Chalabi, Chris Boudt, Pierre Chausse, and Michal Miklovac. 2020. fGarch: Rmetrics—AutoregressivE Conditional Heteroskedastic Modelling. R Package Version 3042.83.2. Available online: https://cran.r-project.org/web/packages/fGarch/fGarch.pdf (accessed on 28 August 2023).
- Yuan, Ke Hai, Xin Tong, and Zhiyong Zhang. 2015. Bias and efficiency for SEM with missing data and auxiliary variables: Two-stage robust method versus two-stage ML. Structural Equation Modeling: A Multidisciplinary Journal 22: 178–92. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroscedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar]
- Zeileis, Achim, and Gabor Grothendieck. 2005. Zoo: S3 infrastructure for regular and irregular time series. Journal of Statistical Software 14: 1–27. [Google Scholar]
- Zhang, Yidong Terrence. 2017. Volatility Forecasting with the Multifractal Model of Asset Returns. Gainesville: University of Florida, pp. 1–24. [Google Scholar] [CrossRef]
- Zivot, Eric. 2009. Practical Issues in the Analysis of Univariate GARCH Models. Berlin and Heidelberg: Springer, pp. 113–55. [Google Scholar] [CrossRef]
- Zivot, Eric. 2013. Univariate GARCH. Available online: https://faculty.washington.edu/ezivot/econ589/univariateGarch2012powerpoint.pdf (accessed on 28 August 2023).


| Panel A: Simulation run once | ||||||||||||
| llk | RMSE | Bias | SE | RMSE | Bias | SE | RMSE | Bias | SE | |||
| 0.0931 | 0.9059 | 1000 | −2020.5 | 0.0504 | 0.0328 | 0.0383 | 0.0551 | −0.0443 | 0.0327 | 0.0719 | −0.0115 | 0.0710 |
| 2000 | −3813.8 | 0.0246 | 0.0046 | 0.0241 | 0.0462 | −0.0374 | 0.0271 | 0.0608 | −0.0327 | 0.0512 | ||
| 3000 | −5734.2 | 0.0156 | −0.0037 | 0.0152 | 0.0316 | −0.0269 | 0.0166 | 0.0441 | −0.0306 | 0.0317 | ||
| Panel B: Simulation run with 2500 replications | ||||||||||||
| 0.0931 | 0.9059 | 1000 | −2020.5 | 0.0504 | 0.0328 | 0.0383 | 0.0551 | −0.0443 | 0.0327 | 0.0719 | −0.0115 | 0.0710 |
| 2000 | −3813.8 | 0.0246 | 0.0046 | 0.0241 | 0.0462 | −0.0374 | 0.0271 | 0.0608 | −0.0327 | 0.0512 | ||
| 3000 | −5734.2 | 0.0156 | −0.0037 | 0.0152 | 0.0316 | −0.0269 | 0.0166 | 0.0441 | −0.0306 | 0.0317 | ||
| Panel C: Simulation run with 1000 replications | ||||||||||||
| 0.0931 | 0.9059 | 1000 | −2020.5 | 0.0504 | 0.0328 | 0.0383 | 0.0551 | −0.0443 | 0.0327 | 0.0719 | −0.0115 | 0.0710 |
| 2000 | −3813.8 | 0.0246 | 0.0046 | 0.0241 | 0.0462 | −0.0374 | 0.0271 | 0.0608 | −0.0327 | 0.0512 | ||
| 3000 | −5734.2 | 0.0156 | −0.0037 | 0.0152 | 0.0316 | −0.0269 | 0.0166 | 0.0441 | −0.0306 | 0.0317 | ||
| Panel D: Simulation run with 300 replications | ||||||||||||
| 0.0931 | 0.9059 | 1000 | −2020.5 | 0.0504 | 0.0328 | 0.0383 | 0.0551 | −0.0443 | 0.0327 | 0.0719 | −0.0115 | 0.0710 |
| 2000 | −3813.8 | 0.0246 | 0.0046 | 0.0241 | 0.0462 | −0.0374 | 0.0271 | 0.0608 | −0.0327 | 0.0512 | ||
| 3000 | −5734.2 | 0.0156 | −0.0037 | 0.0152 | 0.0316 | −0.0269 | 0.0166 | 0.0441 | −0.0306 | 0.0317 | ||
| N | llk | RMSE | Bias | SE | RMSE | Bias | SE | RMSE | Bias | SE | TPR | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 95% | |||||||||||||||
| Panel A | 8000 | 0.0835 | 0.9234 | 1.0069 | −13,860.4 | 0.0390 | 0.0087 | 0.0380 | 0.0377 | −0.0009 | 0.0377 | 0.0761 | 0.0078 | 0.0757 | 95.74% |
| Normal | 9000 | 0.0790 | 0.9259 | 1.0049 | −15,490.9 | 0.0297 | 0.0042 | 0.0294 | 0.0465 | 0.0015 | 0.0464 | 0.0760 | 0.0058 | 0.0758 | 95.55% |
| 10,000 | 0.0803 | 0.9281 | 1.0085 | −17,081.0 | 0.0088 | 0.0055 | 0.0069 | 0.0091 | 0.0038 | 0.0082 | 0.0178 | 0.0094 | 0.0151 | 95.89% | |
| Panel B | 8000 | 0.0834 | 0.9235 | 1.0069 | −13,860.4 | 0.0385 | 0.0086 | 0.0375 | 0.0372 | −0.0009 | 0.0372 | 0.0752 | 0.0078 | 0.0748 | 95.74% |
| skew- | 9000 | 0.0792 | 0.9262 | 1.0055 | −15,490.6 | 0.0138 | 0.0044 | 0.0131 | 0.0216 | 0.0019 | 0.0215 | 0.0352 | 0.0064 | 0.0346 | 95.61% |
| Normal | 10,000 | 0.0801 | 0.9284 | 1.0085 | −17,080.2 | 0.0085 | 0.0053 | 0.0066 | 0.0089 | 0.0041 | 0.0079 | 0.0173 | 0.0094 | 0.0145 | 95.89% |
| Panel C | 8000 | 0.0736 | 0.9226 | 0.9963 | −13,337.1 | 0.0060 | −0.0012 | 0.0058 | 0.0059 | −0.0017 | 0.0056 | 0.0118 | −0.0029 | 0.0115 | 94.73% |
| Student t | 9000 | 0.0727 | 0.9279 | 1.0006 | −14,912.0 | 0.0054 | −0.0021 | 0.0050 | 0.0056 | 0.0036 | 0.0043 | 0.0094 | 0.0014 | 0.0093 | 95.14% |
| 10,000 | 0.0735 | 0.9263 | 0.9999 | −16,428.3 | 0.0043 | −0.0013 | 0.0041 | 0.0035 | 0.0020 | 0.0028 | 0.0070 | 0.0008 | 0.0069 | 95.07% | |
| Panel D | 8000 | 0.0732 | 0.9225 | 0.9957 | −13,337.1 | 0.0084 | −0.0016 | 0.0083 | 0.0064 | −0.0018 | 0.0062 | 0.0149 | −0.0034 | 0.0145 | 94.68% |
| skew- | 9000 | 0.0715 | 0.9262 | 0.9977 | −14,912.2 | 0.0061 | −0.0033 | 0.0051 | 0.0040 | 0.0019 | 0.0036 | 0.0088 | −0.0014 | 0.0087 | 94.87% |
| Student t | 10,000 | 0.0743 | 0.9277 | 1.0020 | −16,428.4 | 0.0035 | −0.0005 | 0.0034 | 0.0041 | 0.0034 | 0.0024 | 0.0065 | 0.0029 | 0.0058 | 95.27% |
| Panel E | 8000 | 0.0770 | 0.9244 | 1.0014 | −13,386.3 | 0.0079 | 0.0022 | 0.0076 | 0.0076 | 0.0001 | 0.0076 | 0.0153 | 0.0023 | 0.0152 | 95.22% |
| GED | 9000 | 0.0734 | 0.9266 | 1.0000 | −14,966.3 | 0.0056 | −0.0014 | 0.0054 | 0.0053 | 0.0023 | 0.0048 | 0.0103 | 0.0009 | 0.0103 | 95.09% |
| 10,000 | 0.0753 | 0.9275 | 1.0028 | −16,492.3 | 0.0036 | 0.0005 | 0.0035 | 0.0042 | 0.0032 | 0.0027 | 0.0073 | 0.0037 | 0.0062 | 95.35% | |
| Panel F | 8000 | 0.0750 | 0.9221 | 0.9971 | −13,386.2 | 0.0059 | 0.0002 | 0.0059 | 0.0059 | −0.0022 | 0.0054 | 0.0115 | −0.0020 | 0.0113 | 94.81% |
| skew- | 9000 | 0.0734 | 0.9265 | 0.9999 | −14,966.0 | 0.0055 | −0.0014 | 0.0054 | 0.0054 | 0.0022 | 0.0049 | 0.0103 | 0.0008 | 0.0103 | 95.08% |
| GED | 10,000 | 0.0753 | 0.9275 | 1.0028 | −16,492.3 | 0.0035 | 0.0006 | 0.0035 | 0.0040 | 0.0031 | 0.0025 | 0.0070 | 0.0037 | 0.0060 | 95.35% |
| Panel G | 8000 | 0.0732 | 0.9234 | 0.9966 | −13,336.3 | 0.0065 | −0.0016 | 0.0063 | 0.0054 | −0.0009 | 0.0053 | 0.0119 | −0.0025 | 0.0116 | 94.76% |
| GHYP | 9000 | 0.0720 | 0.9279 | 0.9999 | −14,911.4 | 0.0057 | −0.0028 | 0.0050 | 0.0056 | 0.0036 | 0.0043 | 0.0093 | 0.0008 | 0.0093 | 95.08% |
| 10,000 | 0.0729 | 0.9265 | 0.9994 | −16,427.7 | 0.0045 | −0.0019 | 0.0040 | 0.0035 | 0.0022 | 0.0027 | 0.0067 | 0.0003 | 0.0067 | 95.03% | |
| Panel H | 8000 | 0.0731 | 0.9229 | 0.9961 | −13,343.3 | 0.0058 | −0.0017 | 0.0056 | 0.0057 | −0.0014 | 0.0055 | 0.0115 | −0.0031 | 0.0111 | 94.71% |
| NIG | 9000 | 0.0719 | 0.9275 | 0.9994 | −14,919.7 | 0.0059 | −0.0029 | 0.0052 | 0.0053 | 0.0031 | 0.0043 | 0.0095 | 0.0003 | 0.0095 | 95.03% |
| 10,000 | 0.0729 | 0.9266 | 0.9995 | −16,438.1 | 0.0045 | −0.0019 | 0.0041 | 0.0034 | 0.0023 | 0.0025 | 0.0066 | 0.0004 | 0.0066 | 95.04% | |
| Panel I | 8000 | 0.0711 | 0.9218 | 0.9930 | −13,435.0 | 0.0067 | −0.0036 | 0.0056 | 0.0070 | −0.0025 | 0.0065 | 0.0135 | −0.0062 | 0.0121 | 94.42% |
| GHST | 9000 | 0.0699 | 0.9261 | 0.9960 | −15,027.3 | 0.0071 | −0.0049 | 0.0051 | 0.0049 | 0.0018 | 0.0046 | 0.0102 | −0.0031 | 0.0097 | 94.71% |
| 10,000 | 0.0734 | 0.9266 | 0.9999 | −16,569.1 | 0.0038 | −0.0014 | 0.0035 | 0.0034 | 0.0022 | 0.0026 | 0.0061 | 0.0008 | 0.0061 | 95.08% | |
| Panel J | 8000 | 0.0731 | 0.9232 | 0.9963 | −13,337.1 | 0.0057 | −0.0017 | 0.0055 | 0.0057 | −0.0011 | 0.0055 | 0.0114 | −0.0028 | 0.0110 | 94.74% |
| JSU | 9000 | 0.0719 | 0.9277 | 0.9996 | −14,912.4 | 0.0057 | −0.0029 | 0.0050 | 0.0053 | 0.0033 | 0.0042 | 0.0091 | 0.0005 | 0.0091 | 95.04% |
| 10,000 | 0.0727 | 0.9264 | 0.9991 | −16,429.3 | 0.0045 | −0.0020 | 0.0040 | 0.0033 | 0.0020 | 0.0026 | 0.0066 | 0.0000 | 0.0066 | 95.00% |
| Panel A Normal | Panel B skew-Normal | Panel C Student’s t | Panel D skew-Student’s t | Panel E GED | |
| 0.0164 *** | 0.0078 * | 0.0387 * | 0.0177 | 0.0378 ** | |
| 0.0323 | 0.0278 | 0.0297 * | 0.0270 * | 0.0311 * | |
| 0.0701 * | 0.0670 * | 0.0690 * | 0.0661 * | 0.0700 * | |
| 0.9093 * | 0.9170 * | 0.9188 * | 0.9236 * | 0.9137 * | |
| 0.2504 * | 0.2344 * | 0.3499 * | 0.3445 * | 0.2879 * | |
| 0.2245 | 0.2209 *** | 0.0729 | 0.0943 | 0.1445 * | |
| = | 1.4550 * | 1.4233 * | 1.2362 * | 1.2058 * | 1.3436 * |
| Persistence | 0.9794 | 0.9825 | 0.9764 | 0.9792 | 0.9762 |
| WLB (5) | 0.3227 | 0.8383 | 0.9103 | 1.6060 | 1.3361 |
| p-value (5) | (1.0000) | (1.0000) | (1.0000) | (0.9955) | (0.9995) |
| ARCH LM statistic(7) | 3.0979 | 3.1854 | 3.8897 | 4.1266 | 3.4264 |
| p-value (7) | (0.4953) | (0.4793) | (0.3627) | (0.3287) | (0.4369) |
| AP-GoF | 87.2 | 64.56 | 42.32 | 18.48 | 53.68 |
| p-value | (0.0000) | (0.0000) | (0.0016) | (0.4908) | (0.0000) |
| Log-likelihood | −8909.189 | −8886.553 | −8803.012 | −8790.528 | −8825.745 |
| AIC | 3.1862 | 3.1785 | 3.1486 | 3.1445 | 3.1568 |
| BIC | 3.1969 | 3.1903 | 3.1605 | 3.1576 | 3.1686 |
| SIC | 3.1862 | 3.1785 | 3.1486 | 3.1445 | 3.1567 |
| HQIC | 3.1899 | 3.1826 | 3.1528 | 3.1491 | 3.1609 |
| Run-time (seconds) | 4.3245 | 6.6636 | 7.6463 | 11.9177 | 9.1407 |
| Panel F skew-GED | Panel G GHYP | Panel H NIG | Panel I GHST | Panel J JSU | |
| 0.0157 | 0.0156 | 0.0155 | −0.0062 | 0.0159 | |
| 0.0273 * | 0.0267 * | 0.0261 * | 0.0251 * | 0.0265 * | |
| 0.0665 * | 0.0661 * | 0.0657 * | 0.0650 * | 0.0658 * | |
| 0.9206 * | 0.9241 * | 0.9246 * | 0.9284 * | 0.9243 * | |
| 0.2823 * | 0.3370 * | 0.3341 * | 0.3202 * | 0.3378 * | |
| 0.1592 ** | 0.0942 | 0.0964 | 0.1163 ** | 0.0949 | |
| = | 1.3048 * | 1.2086 * | 1.2171 * | 1.1942 * | 1.2102 * |
| Persistence | 0.9797 | 0.9795 | 0.9800 | 0.9826 | 0.9796 |
| WLB (5) | 2.5350 | 1.5990 | 1.8260 | 2.5920 | 1.7170 |
| p-value (5) | (0.7599) | (0.9957) | (0.9822) | (0.7277) | (0.9906) |
| ARCH LM statistic(7) | 3.6331 | 4.0705 | 4.0249 | 4.2354 | 4.0750 |
| p-value (7) | (0.4026) | (0.3365) | (0.3430) | (0.3139) | (0.3359) |
| AP-GoF | 46.18 | 17.01 | 22.23 | 29.37 | 21.66 |
| p-value | (0.0005) | (0.5890) | (0.2730) | (0.0604) | (0.3013) |
| Log-likelihood | −8810.111 | −8790.079 | −8793.107 | −8800.387 | −8791.112 |
| AIC | 3.1515 | 3.1447 | 3.1454 | 3.1480 | 3.1447 |
| BIC | 3.1646 | 3.1589 | 3.1585 | 3.1611 | 3.1578 |
| SIC | 3.1515 | 3.1447 | 3.1454 | 3.1480 | 3.1447 |
| HQIC | 3.1561 | 3.1497 | 3.1500 | 3.1526 | 3.1493 |
| Run-time (seconds) | 19.0058 | 49.9461 | 20.7803 | 16.8525 | 10.6434 |
| Panel A Normal | Panel B skew-Normal | Panel C Student’s t | Panel D skew-Student’s t | Panel E GED | |
| Log-likelihood | −8910.136 | −8887.475 | −8803.200 | −8790.782 | −8826.007 |
| AIC | 3.1862 | 3.1784 | 3.1483 | 3.1443 | 3.1565 |
| BIC | 3.1957 | 3.1891 | 3.1590 | 3.1561 | 3.1671 |
| SIC | 3.1862 | 3.1784 | 3.1483 | 3.1443 | 3.1565 |
| HQIC | 3.1895 | 3.1822 | 3.1521 | 3.1484 | 3.1602 |
| Panel F skew-GED | Panel G GHYP | Panel H NIG | Panel I GHST | Panel J JSU | |
| Log-likelihood | −8810.472 | −8790.315 | −8793.329 | −8802.039 | −8791.340 |
| AIC | 3.1513 | 3.1444 | 3.1452 | 3.1483 | 3.1445 |
| BIC | 3.1631 | 3.1575 | 3.1570 | 3.1601 | 3.1563 |
| SIC | 3.1513 | 3.1444 | 3.1452 | 3.1483 | 3.1445 |
| HQIC | 3.1554 | 3.1490 | 3.1493 | 3.1524 | 3.1486 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samuel, R.T.A.; Chimedza, C.; Sigauke, C. Simulation Framework to Determine Suitable Innovations for Volatility Persistence Estimation: The GARCH Approach. J. Risk Financial Manag. 2023, 16, 392. https://doi.org/10.3390/jrfm16090392
Samuel RTA, Chimedza C, Sigauke C. Simulation Framework to Determine Suitable Innovations for Volatility Persistence Estimation: The GARCH Approach. Journal of Risk and Financial Management. 2023; 16(9):392. https://doi.org/10.3390/jrfm16090392
Chicago/Turabian StyleSamuel, Richard T. A., Charles Chimedza, and Caston Sigauke. 2023. "Simulation Framework to Determine Suitable Innovations for Volatility Persistence Estimation: The GARCH Approach" Journal of Risk and Financial Management 16, no. 9: 392. https://doi.org/10.3390/jrfm16090392
APA StyleSamuel, R. T. A., Chimedza, C., & Sigauke, C. (2023). Simulation Framework to Determine Suitable Innovations for Volatility Persistence Estimation: The GARCH Approach. Journal of Risk and Financial Management, 16(9), 392. https://doi.org/10.3390/jrfm16090392







