Tax Shields, the Weighted Average Cost of Capital, and the Appropriate Discount Rate for a Project with a Finite Useful Life
Abstract
:1. Introduction
2. The Perpetuity-Formula WACC
2.1. Firm Value and the Perpetuity-Formula WACC
2.2. Limitations of the Perpetuity-Formula WACC
3. The Finite-Life Formulas
3.1. Finite-Life Tax Shields
3.2. The Finite-Life WACC
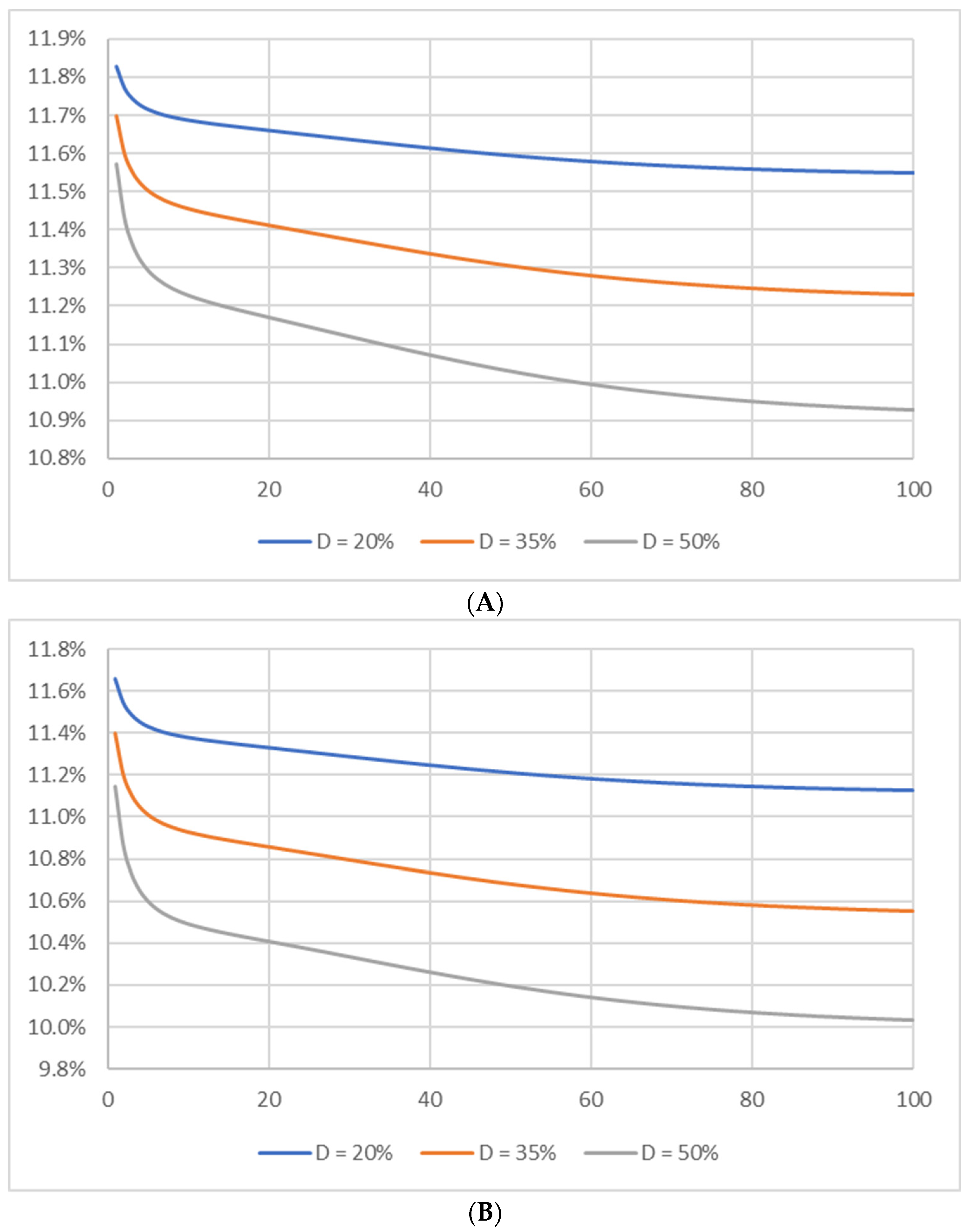
4. WACCN vs. WACC∞: Numerical Examples
- For assumed values of VU and rA,U, calculate the level-annuity, after-tax, cash flow generated by the unlevered asset (when in equilibrium: actual return = rA,U) over its N-year useful life.
- For assumed values of rD, τ, D0, and N, calculate VTS,N using Equation (5) for amortizing debt or Equation (6) for coupon bonds.
- Then, calculate the value of the levered cash flow stream, VL, using Equation (1).
- Finally, WACCN is the discount rate that sets the present value of the unlevered asset’s N-year annuity equal to VL.
4.1. Coupon Bonds
4.2. Amortizing Loans
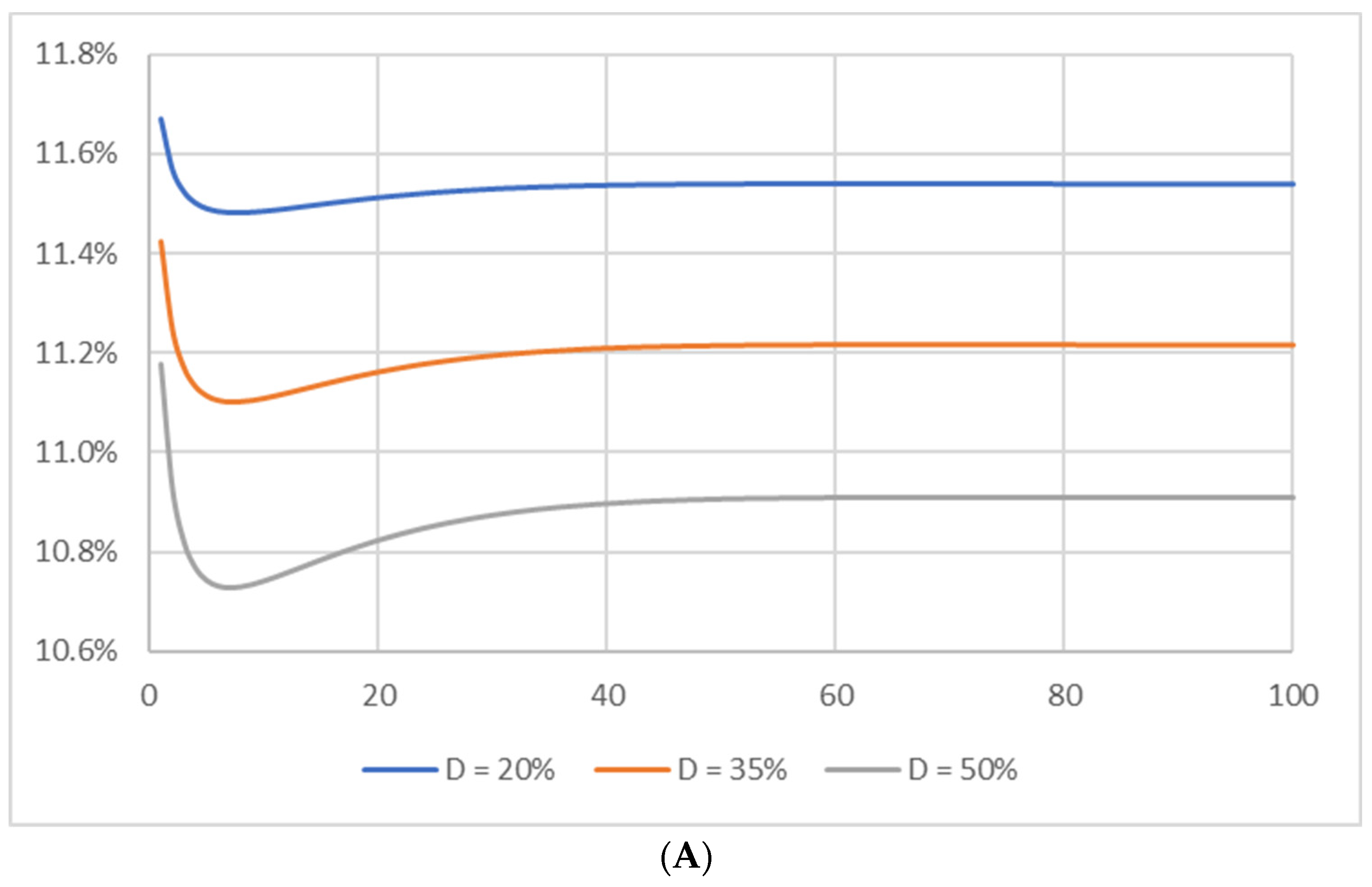
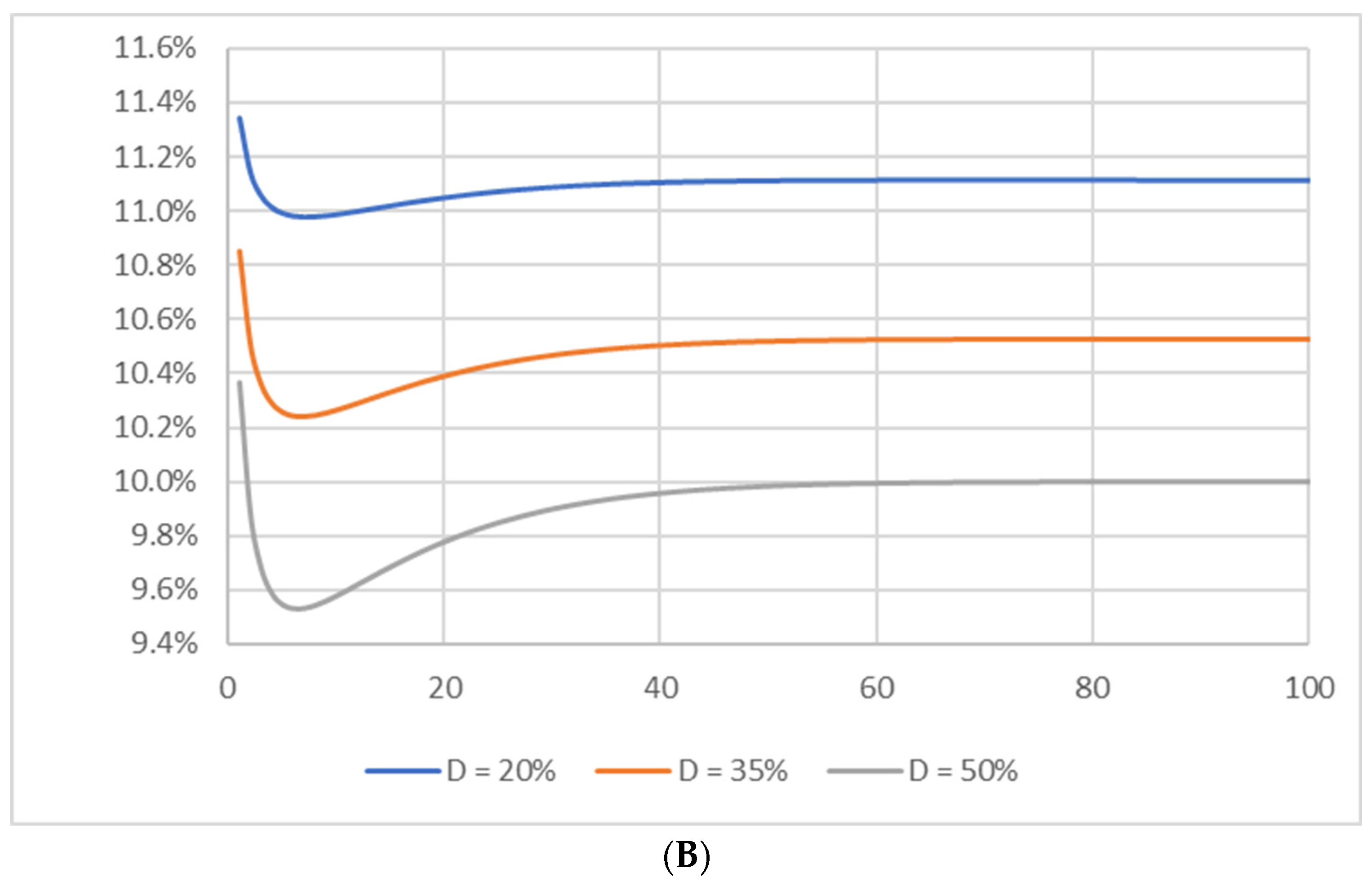
5. What Difference Does the Difference between WACCN and WACC∞ Make?
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Using the AIRR model, Magni (2010, 2013, 2016, 2020) restates the investment selection decision in terms of a project’s average economic return and its average cost of capital. Within the AIRR framework, a project is acceptable if its AIRR is equal to or in excess of the benchmark AIRR (i.e., the average cost of capital). The analysis in this paper is limited to the WACC approach to capital budgeting as presented in most finance textbooks. Within the WACC framework, a project will have a positive NPV if its internal rate of return (IRR) exceeds its WACC. |
| 2 | Alternatively, Miles and Ezzell (1980) argue that the cash flows generated by a firm’s tax shield should be discounted using the firm’s required return on assets. Farber et al. (2006) and Fernandez (2007) derive a generalized form of the WACC that allows the tax shields to be discounted using either the required return on debt or the required return on assets. Although the issue has not been resolved in the literature, this paper adopts the Modigliani and Miller (1963) and Fernandez (2004) approach and calculates the tax shield value using Equation (2). |
| 3 | |
| 4 | |
| 5 | Using the AIRR approach, Magni (2016, sct. 10) generalizes the three most prominent Modigiani and Miller results (Proposition 1, Proposition 2, and dividend irrelevance) to allow for time-varying debt, equity, and asset returns and for finite-lived assets. |
| 6 | |
| 7 | In practice, the required return on assets is unlikely to be constant over time as inflation premiums, risk premiums, and real returns can all vary in response to changing economic conditions. If the potential time series of future capital costs can be estimated, the AIRR approach, Magni (2010, 2013, 2016), provides a theoretically robust framework in which to make investment decisions. However, if future capital costs cannot be estimated with precision, the constant discount rate assumption retains value within first-cut estimates of a potential project’s NPV. |
| 8 | When WACC = 9.594%, rA,U = 10%, rD = 6%, τ = 20%, D0 = 200, VL = 1017.664, WD = D0/VL, and N = 10 are plugged into Equation (8), both sides are equal to 6.2531. |
| 9 | The value of the tax shield, using Equation (2) is 40 = (20%)200. Thus, the value of the levered firm, using Equation (1) is 1040. The WACC of 9.615% can then be calculated using Equation (3): 9.615% = 10%(1 − 20%(200/1040)). |
| 10 | When the firm issues coupon bonds, all of the estimates of WACCN satisfy Equation (8). When the firm issues amortizing loans, the estimates of WACCN do not satisfy Equation (8). |
| 11 | |
| 12 | Respondents in 12 of the 88 countries analyzed in Fernandez et al. (2021) use market risk premiums > 10%. |
| 13 | The critical value, VL = 1087.49, is the present value of a 10-year annuity of 176.98 calculated using a discount rate of 10%. |
| 14 | For WACCN to be less than WACC∞, the risk premium rA,U − rD must be sufficiently small and rD must be sufficiently large. Holding the risk premium constant at 4%, WACCN is more likely to be less than WACC∞ when rD = 8%, and less likely to be less than WACC∞ when rD = 4%. However, it is still possible for WACCN to be less than WACC∞ when rA,U = 8% and rD = 4%. For example, if VU = 1000, D0 = 500, and τ = 40%, WACC10 = 6.63% is less than WACC∞ = 6.67%. |
References
- Arditti, Fred D. 1973. The Weighted Average Cost of Capital: Some Questions on Its Definition, Interpretation and Use. Journal of Finance 28: 1001–8. [Google Scholar] [CrossRef]
- Barbi, Massimiliano. 2012. On the Risk-Neutral Value of Debt Tax Shields. Applied Financial Economics 22: 251–58. [Google Scholar] [CrossRef]
- Booth, Laurence. 2002. Finding Value Where None Exists: Pitfalls in Using Adjusted Present Value. Journal of Applied Corporate Finance 15: 95–104. [Google Scholar] [CrossRef]
- Brick, John R., and Howard E. Thompson. 1978. The Economic Life of an Investment and the Appropriate Discount Rate. Journal of Financial and Quantitative Analysis 13: 831–46. [Google Scholar] [CrossRef]
- Bruner, Robert F., Kenneth M. Eades, Robert S. Harris, and Robert C. Higgins. 1998. Best Practices in Estimating the Cost of Capital: Survey and Synthesis. Financial Practice and Education 8: 13–28. [Google Scholar]
- Brusov, Peter, Tatiana Filatova, Natali Orehova, and Nastia Brusova. 2011. Weighted Average Cost of Capital in the Theory of Modigliani-Miller, Modified for a Finite Lifetime Company. Applied Financial Economics 21: 815–24. [Google Scholar] [CrossRef]
- Campani, Carlos Heitor. 2015. On the Correct Evaluation of Cost of Capital for Project Valuation. Applied Mathematical Statistics 9: 6583–6604. [Google Scholar] [CrossRef]
- Cooper, Ian A., and Kjell G. Nyborg. 2006. The Value of Tax Shields IS Equal to the Present Value of Tax Shields. Journal of Financial Economics 81: 215–25. [Google Scholar] [CrossRef]
- Farber, André, Roland L. Gillet, and Ariane Szafarz. 2006. A General Formula for the WACC. International Journal of Business 11: 211–18. [Google Scholar]
- Fernandez, Pablo. 2004. The Value of Tax Shields is NOT Equal to the Present Value of Tax Shields. Journal of Financial Economics 73: 145–65. [Google Scholar] [CrossRef]
- Fernandez, Pablo. 2007. A General Formula for the WACC: A Comment. International Journal of Business 12: 399–403. [Google Scholar]
- Fernandez, Pablo. 2019. The Equity Premium in 150 Textbooks. Available online: https://ssrn.com/abstract=1473225 (accessed on 15 March 2023).
- Fernandez, Pablo, Sofía Bañuls, and Pablo F. Acín. 2021. Survey: Market Risk Premium and Risk-Free Rate Used for 88 Countries in 2021. IESE Business School Working Paper. Available online: https://ssrn.com/abstract=3861152 (accessed on 15 March 2023).
- Filatova, Tatiana, Brusov Peter, and Natali Orekhova. 2022. Impact of Advance Payments of Tax on Profit on Effectiveness of Investments. Mathematics 10: 666. [Google Scholar] [CrossRef]
- Haley, Charles W., and Lawrence. D. Schall. 1973. The Theory of Financial Decisions. New York: McGraw-Hill. [Google Scholar]
- Magni, Carlo Alberto. 2010. Average Internal Rate of Return and Investment Decisions: A New Perspective. The Engineering Economist 55: 150–80. [Google Scholar] [CrossRef]
- Magni, Carlo Alberto. 2013. The internal-rate-of-return approach and the AIRR paradigm: A refutation and a corroboration. The Engineering Economist 58: 73–111. [Google Scholar] [CrossRef]
- Magni, Carlo Alberto. 2016. Capital Depreciation and the Underdetermination of Rate of Return: A Unifying Perspective. Journal of Mathematical Economics 67: 54–79. [Google Scholar] [CrossRef]
- Magni, Carlo Alberto. 2020. Investment Decisions and the Logic of Valuation. Linking Finance, Accounting, and Engineering. Cham: Springer Nature Switzerland AG. [Google Scholar]
- Miles, James A., and John R. Ezzell. 1980. The Weighted Average Cost of Capital, Perfect Capital Markets, and Project Life: A Clarification. Journal of Financial and Quantitative Analysis 15: 719–30. [Google Scholar] [CrossRef]
- Miller, Richard A. 2009. The Weighted Average Cost of Capital is Not Quite Right. The Quarterly Review of Economics and Finance 49: 128–38. [Google Scholar] [CrossRef]
- Modigliani, Franco, and Merton H. Miller. 1958. The Cost of Capital, Corporation Finance and the Theory of Investment. American Economic Review 48: 261–97. [Google Scholar]
- Modigliani, Franco, and Merton H. Miller. 1963. Corporate Income Taxes and the Cost of Capital: A Correction. American Economic Review 53: 433–43. [Google Scholar]
- Myers, Stewart C. 1974. Interactions of Corporate Financing and Investment Decisions—Implications for Capital Budgeting. Journal of Finance 29: 1–25. [Google Scholar] [CrossRef]
- Pierru, Axel. 2009. The Weighted Average Cost of Capital is Not Quite Right: A Comment. The Quarterly Review of Economics and Finance 49: 1219–23. [Google Scholar] [CrossRef]
- Reilly, Raymond R., and William E. Wecker. 1973. On the Weighted Average Cost of Capital. Journal of Financial and Quantitative Analysis 8: 123–26. [Google Scholar] [CrossRef]
- Welch, Ivo. 2021. The Cost of Capital: If Not the CAPM, then What? Management and Business Review 1: 187–94. [Google Scholar]
| Balance Sheet (Initial) | Income Statement | Cash Flows | |||
|---|---|---|---|---|---|
| Working Cap. | 0 | EBITDA | 18.33 | Net Income | 7 |
| Fixed Assets | 100 | Depreciation | −5.00 | +Depr. | 5 |
| Total Assets | 100 | EBIT | 13.33 | +/− Δ in WC | 0 |
| Debt | 50 | Interest (8%) | 4.00 | −CapEx | −5 |
| Equity | 50 | EBT | 9.33 | Eq. Cash Flow | 7 |
| Total D + E | 100 | Taxes (25%) | 2.33 | Unlev. FCF | 10 a |
| Net Income | 7.00 | Cap. Cash Flow | 11 b | ||
| Useful Life (Years) | |||||
|---|---|---|---|---|---|
| rD (%) | 5 | 10 | 25 | 50 | 100 |
| Panel A: Coupon Bonds | |||||
| 2 | 0.094 | 0.180 | 0.390 | 0.628 | 0.862 |
| 4 | 0.178 | 0.324 | 0.625 | 0.859 | 0.980 |
| 6 | 0.253 | 0.442 | 0.767 | 0.946 | 0.997 |
| 8 | 0.319 | 0.537 | 0.854 | 0.979 | 0.999 |
| 10 | 0.379 | 0.614 | 0.908 | 0.991 | 0.999 |
| Panel B: Amortizing Loans | |||||
| 2 | 0.058 | 0.105 | 0.235 | 0.420 | 0.686 |
| 4 | 0.113 | 0.199 | 0.423 | 0.685 | 0.922 |
| 6 | 0.163 | 0.284 | 0.570 | 0.838 | 0.983 |
| 8 | 0.211 | 0.361 | 0.683 | 0.919 | 0.997 |
| 10 | 0.255 | 0.430 | 0.769 | 0.961 | 0.999 |
| WACCN (%) | Min. WACC | |||||||
|---|---|---|---|---|---|---|---|---|
| D0 | 1 | 10 | rE (%) | % | N | Beg N | End N | |
| Panel A: | ||||||||
| 200 | 11.83 | 11.69 | 11.54 | 13.52 | 11.54 | NA | NA | |
| 350 | 11.70 | 11.45 | 11.21 | 15.11 | 11.21 | NA | NA | |
| 500 | 11.57 | 11.23 | 10.91 | 17.33 | 10.91 | NA | NA | |
| Panel B: | ||||||||
| 200 | 11.66 | 11.38 | 11.11 | 13.09 | 11.11 | NA | NA | |
| 350 | 11.40 | 10.93 | 10.53 | 14.13 | 10.53 | NA | NA | |
| 500 | 11.15 | 10.49 | 10.00 | 15.43 | 10.00 | NA | NA | |
| WACCN (%) | Min. WACC | |||||||
|---|---|---|---|---|---|---|---|---|
| D0 | 1 | 10 | rE (%) | % | N | Beg N | End N | |
| Panel A: | ||||||||
| 200 | 11.67 | 11.48 | 11.54 | 12.76 | 11.48 | 8 | 3 | 47 |
| 350 | 11.42 | 11.11 | 11.21 | 13.56 | 11.10 | 7 | 3 | 53 |
| 500 | 11.18 | 10.74 | 10.91 | 14.67 | 10.73 | 7 | 3 | 63 |
| Panel B: | ||||||||
| 200 | 11.34 | 10.99 | 11.11 | 12.54 | 10.98 | 7 | 3 | 55 |
| 350 | 10.85 | 10.27 | 10.53 | 13.06 | 10.24 | 7 | 2 | 68 |
| 500 | 10.36 | 9.58 | 10.00 | 13.71 | 9.53 | 6 | 2 | 84 |
| WACC Value for Useful Life N (%) | |||||||
|---|---|---|---|---|---|---|---|
| D0 | 1 | 5 | 10 | 25 | 50 | 100 | |
| Panel A: | |||||||
| 200 | 11.83 | 11.82 | 11.81 | 11.76 | 11.67 | 11.57 | 11.54 |
| 350 | 11.70 | 11.68 | 11.66 | 11.58 | 11.44 | 11.27 | 11.21 |
| 500 | 11.57 | 11.55 | 11.52 | 11.41 | 11.21 | 10.99 | 10.91 |
| Panel B: | |||||||
| 200 | 11.66 | 11.64 | 11.62 | 11.53 | 11.36 | 11.18 | 11.11 |
| 350 | 11.40 | 11.37 | 11.33 | 11.19 | 10.93 | 10.63 | 10.53 |
| 500 | 11.15 | 11.11 | 11.06 | 10.86 | 10.52 | 10.13 | 10.00 |
| WACC Value for Useful Life N (%) | |||||||
|---|---|---|---|---|---|---|---|
| D0 | 1 | 5 | 10 | 25 | 50 | 100 | |
| Panel A: | |||||||
| 200 | 11.67 | 11.66 | 11.65 | 11.62 | 11.57 | 11.54 | 11.54 |
| 350 | 11.42 | 11.41 | 11.40 | 11.34 | 11.26 | 11.22 | 11.21 |
| 500 | 11.18 | 11.16 | 11.14 | 11.07 | 10.97 | 10.91 | 10.91 |
| Panel B: | |||||||
| 200 | 11.34 | 11.33 | 11.31 | 11.25 | 11.16 | 11.11 | 11.11 |
| 350 | 10.85 | 10.84 | 10.81 | 10.73 | 10.60 | 10.53 | 10.53 |
| 500 | 10.36 | 10.35 | 10.33 | 10.24 | 10.09 | 10.01 | 10.00 |
| Income Statement | Cash Flows | ||
|---|---|---|---|
| EBTD | 220 | Net Income | 72 |
| Depreciation | −100 | +Depr. | 100 |
| EBT | 120 | +/− Δ in WC | 0 |
| Taxes (40%) | 48 | −CapEx | 0 |
| Net Income | 72 | Unlev. FCF | 172 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danielson, M.G. Tax Shields, the Weighted Average Cost of Capital, and the Appropriate Discount Rate for a Project with a Finite Useful Life. J. Risk Financial Manag. 2023, 16, 398. https://doi.org/10.3390/jrfm16090398
Danielson MG. Tax Shields, the Weighted Average Cost of Capital, and the Appropriate Discount Rate for a Project with a Finite Useful Life. Journal of Risk and Financial Management. 2023; 16(9):398. https://doi.org/10.3390/jrfm16090398
Chicago/Turabian StyleDanielson, Morris G. 2023. "Tax Shields, the Weighted Average Cost of Capital, and the Appropriate Discount Rate for a Project with a Finite Useful Life" Journal of Risk and Financial Management 16, no. 9: 398. https://doi.org/10.3390/jrfm16090398
APA StyleDanielson, M. G. (2023). Tax Shields, the Weighted Average Cost of Capital, and the Appropriate Discount Rate for a Project with a Finite Useful Life. Journal of Risk and Financial Management, 16(9), 398. https://doi.org/10.3390/jrfm16090398





