Expansionary Monetary Policy and Bank Loan Loss Provisioning
Abstract
:1. Introduction
2. Institutional Background and Hypothesis Development
2.1. Role of Loan Loss Provisions
2.2. Hypothesis Development
3. Empirical Methods
3.1. Research Design
3.2. Sample Selection
3.3. Summary Statistics
4. Empirical Results
4.1. The Relationship between Monetary Policy and DLLP
4.2. The Relationship between Monetary Policy and the Timeliness of LLP
+ α5 EMPt−1 × CH_NPAt or COt + α6 CH_NPAt or COt + β Xi,t + γ Ys,t + ρ Zt
+ ∑θi + ∑μs + ∑νt + εi,t
4.3. Cross-Sectional Analyses
+ b6 EBPTt + b7 SIZEt−1 + εt
4.4. Path Analysis
4.5. Instrumental Variable (2SLS) Approach
4.6. Economic Consequences of Higher DLLPs
4.7. Economic Consequences of Banks’ Commitment to Timely Loan Loss Provisioning
4.8. Summary of Main Findings and Implications
5. Additional Analyses
5.1. Sensitivity Checks
5.2. Nonparametric, Nonlinear Tests, Sample Composite Tests, and Heterogeneous Effects
5.3. Employing Exogenous Variations in Monetary Policy as Alternative Measures
5.4. Timing of the Responses to Policy Changes
6. Conclusions and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Variable Definition
| Symbol | Definition and Data Sources | |
| LLP | = | Loan loss provisions scaled by lagged total loans from COMPUSTAT. |
| DLLP34 | = | Discretionary LLP, using the method proposed by Beatty and Liao (2014). We regress the LLP on the nondiscretionary determinants of LLP, including lagged, contemporaneous, and lead changes on nonperforming, lagged bank size, loan growth, lagged loan loss allowance, net charge-offs, and the proportion of commercial and industrial loans, consumer loans, and real estate loans. The residual is the DLLP. |
| HIGHDLLP | = | A dummy variable that equals 1 when a bank’s DLLP is above the median DLLP across all banks in the same quarter and 0 otherwise. |
| POSDLLP | = | A dummy variable that equals 1 when a bank’s DLLP is positive and 0 otherwise. |
| TIMELYt+n−1/t | = | LLP timeliness measured by incremental R2 using n-quarter rolling windows, following Beatty and Liao (2011) and Bushman and Williams (2015). It equals 1 if the bank is above the median incremental R2 and 0 otherwise. For example, TIMELYt−11/t uses a past 12-quarter rolling window, TIMELYt+11/t uses a 12-quarter forward-looking rolling window, and TIMELYt+23/t uses a 24-quarter forward-looking rolling window. |
| DELR | = | A dummy variable that equals 1 if TIMELYt−11/t equals 0. |
| DELR_strict | = | Following the construction method of TIMELYt−11/t, DELR_strict is a dummy variable that equals 1 if the bank is below the 25th percentile (instead of the median) of R2 and 0 otherwise. |
| MP | = | A general term for monetary policy; it can be proxied by the following measures of monetary policy, including BM, EMP, FFR, TRR, and RRS (as illustrated below). |
| BM | = | Narrative index of the monetary policy stance developed by Boschen and Mills (1995) based on their study of the policy records of the Federal Open Market Committee. The index is available from Weise (2008) and Lo (2015). Weise (2008) updated the index through 2000:Q4, and Lo (2015) updated the index through 2007:Q2. Applying the same technique, we extend the data from 2007:Q2 to 2010:Q4. |
| EMP | = | A dummy variable that equals 1 when the BM index in t−1 is positive and 0 otherwise. |
| FFR | = | Federal funds rate multiplied by −1, available from the Federal Reserve Bank of New York (https://apps.newyorkfed.org/markets/autorates/fed%20funds (accessed on 3 July 2021)). |
| TRR | = | Exogenous monetary policy shock generated using the Taylor rule residual obtained from a recursive rolling regression of the target federal funds rate on the deviation of CPI inflation from 2% and the difference between actual and potential GDP growth. |
| RRS | = | Exogenous monetary policy shock generated by Romer and Romer (2004) measuring the first difference in exogenous policy change. To be consistent with other regressions, we change the first differences back to levels. |
| Firm-level control variables | ||
| TIER1 | = | Tier-1 risk-adjusted capital ratio from COMPUSTAT. |
| EBTP | = | Earnings before taxes and provisions scaled by lagged total loans from COMPUSTAT. |
| LOGMV | = | The natural logarithm of the market value from COMPUSTAT. |
| MTB | = | Market to book ratio from COMPUSTAT. |
| STD_E | = | The standard deviation of earnings before taxes and provisions scaled by lagged total loans generated using 12-quarter rolling windows. |
| LOSS | = | A dummy variable that equals 1 if EBTP is negative and 0 otherwise. |
| CH_NPA | = | Changes in nonperforming assets from quarter t−1 to quarter t scaled by lagged total assets from COMPUSTAT. In particular, CH_NPA1YR is the cumulative change in nonperforming assets from quarter t to quarter t+4 (i.e., NPAt+4 + NPAt+3 + NPAt+2 + NPAt+1-NPAt) to reflect the period based on which banks are required to disclose their estimation of credit losses. |
| CH_LOAN | = | Changes in total loans scaled by lagged total assets from quarter t−1 to quarter t from COMPUSTAT. |
| CO | = | Net charge-off scaled by total loans multiplied by -1 from COMPUSTAT. |
| ALW | = | Lagged loan loss allowance scaled by lagged total loans from COMPUSTAT. |
| CON | = | The percentage of consumer loans to total loans from bank call report FR Y-9C. |
| COM | = | The percentage of commercial and industrial loans to total loans from FR Y-9C. |
| REAL | = | The percentage of real estate loans to total loans from FR Y-9C. |
| SIZE | = | The natural logarithm of book total assets. Data are available on COMPUSTAT. |
| DEPOSIT | = | The total deposits scaled by lagged total loans. Data are available on COMPUSTAT. |
| ILLIQUIDITY | = | The mean of the dollar value of stocks traded as a percentage of GDP in the current quarter. |
| BETA | = | Beta calculated using the traditional CAPM model. Data are available on CRSP. |
| VaR | = | The quarterly estimated conditional value-at-risk is at the 95th percentile of the market value of equity, following Adrian and Brunnermeier (2016). |
| CH_VaRt+4/t | = | The changes in VaR for the individual bank from t to t+4 (i.e., changes during the subsequent four quarters post-upgrading transparency). A positive number refers to increases in VaR, and vice versa. |
| CH_VaRt+1/t | = | The changes in VaR for the individual bank from t to t+1 (i.e., changes during the quarter post upgrading transparency). A positive number refers to increases in VaR, and vice versa. |
| CH_VaRt/t−1 | = | The changes in VaR for the individual bank from t−1 to t (i.e., changes during the quarter prior to upgrading transparency). A positive number refers to increases in VaR, and vice versa. |
| INST | = | The percentage holding of the firm’s outstanding shares by all institutional investors for the closest reporting quarter. Data are from the Thomson/Reuters Institutional (13f) Holdings database. |
| FD | = | A dummy variable that equals 1 for periods after the Reg FD became effective and 0 otherwise. |
| BHAR | = | Buy and hold abnormal return following Hribar et al. (2017). Data are available on CRSP. |
| ABOVE500 | = | A dummy that equals 1 if the bank’s total assets are above USD 500 million and 0 otherwise. |
| ΔσROA | = | The difference between the volatility of return on assets measured in the subsequent 8 quarters and the volatility of return on assets measured in the previous 8 quarters. |
| ΔZScore | = | The difference between the Z-score in the subsequent eight quarters and the Z-score in the previous eight quarters. Specifically, the Z-score is defined as the sum of the average return on assets and the average capital-asset ratio, divided by the period’s standard deviation of ROA. It measures the number of standard deviations a bank’s ROA has to fall before insolvency (Laeven and Levine 2009). We take the natural logarithm of Z-score due to its high skewness and multiply the log of Z-score by (−1). |
| TARGET_RATE | = | The Fed funds target rate used in rolling Taylor regression. |
| GAP | = | The percentage difference between forecasted real GDP and real potential GDP. |
| INFLATION | = | The annual percentage growth in the core consumer price index. |
| SURPRISE | = | Three-month-ahead Fed futures surprises reported in Gertler and Karadi (2015). It is constructed based on the high frequency of innovations in the Fed fund futures rate around FOMC announcements. |
| StateCharter | = | A dummy variable that equals 1 if the bank has a state charter (RSSD9055 = 0) and equals 0 otherwise. Data from FR Y-9C. |
| Strict | = | A dummy variable that equals 1 if a state’s regulatory index falls into the highest tercile and equals 0 if a state’s regulatory index falls into the lowest tercile, according to the state-level regulatory index constructed by Agarwal et al. (2014). |
| State and regional control variables | ||
| CPIt | = | The quarterly change in the consumer price index measured at the regional level from the U.S. Bureau of Labor Statistics. |
| HOUt | = | The quarterly change in house prices measured at the state level from the office of federal housing enterprise oversight/federal housing finance agency. |
| INCOMEt | = | The quarterly change in personal income measured at the state level from the U.S. Bureau of Labor Statistics. |
| UNEMPLOYt | = | The quarterly change in unemployment rate measured at the state level from the U.S. Bureau of Labor Statistics. |
| National control variables | ||
| BUSCYCLEt | = | The dating of recessions measured at each quarter from the National Bureau of Economic Research. |
| GDPGROWt | = | Real GDP growth at the national level from the U.S. Bureau of Economic Analysis. |
| DEFAULTt | = | Default spread measured as the difference between the yield to maturity on Moody’s Baa-rated and AAA-rated bonds. |
| 1 | For instance, some Federal Reserve members were worried that low rates would encourage higher risk-taking after the Fed cut interest rates to near zero during the COVID pandemic. Source: https://www.cnbc.com/2020/01/03/some-fed-members-worried-that-keeping-rates-low-would-encourage-too-much-risk-taking-minutes-show.html (accessed on 3 July 2021). |
| 2 | Claessens et al. (2018) also document that the longer the period of lower interest rates, the greater the reduction in bank profitability. |
| 3 | For example, regulators in the U.S. use a rating system called CAMELS (Capital Adequacy, Asset Quality, Management, Earnings, Liquidity, and Systematic Risk) to identify troubled banks. The CAMELS rating system is primarily based on accounting numbers from regulatory filings. |
| 4 | The capital crunch problem refers to the decline in lending by financial institutions during economic downturns. |
| 5 | We refer to banks that commit to long-term, timely LLP as banks that are timely in LLP when measured in both short-term and long-term windows (i.e., banks that are timely in LLP when measured both in an ex-post 12-quarter window and an ex-post 24- or 36-quarter window). In these tests, we measure LLP timeliness using a rolling regression model consistent with Beatty and Liao (2011). The construction of the measure is explained in detail in Appendix A. |
| 6 | Beatty and Liao (2014) use a sample of COMPUSTAT banks from 2005–2012 and measure total bank accruals as the difference between net income before extraordinary items and operating cash flows. Using the same measure in our sample period, we find that the average LLP to total accruals ratio equals 47.76% (not tabulated). We also find that the ratio does not differ much across different bank size groups. |
| 7 | For example, bank shareholders may demand conservative loan loss accounting to restrict bank managers’ excessive risk-taking incentives and to avoid potential adverse legal outcomes (e.g., Watts 2003). |
| 8 | In another speech, “Lessons of the Financial Crisis for Banking Supervision”, delivered in 2009, Ben Bernanke emphasized the Fed’s macroprudential objective to address the procyclical concern of bank capital. In addition, the then Comptroller of the Currency, John C. Dugan, delivered a speech titled ‘Loan Loss Provisioning and Pro-cyclicality’ in 2009, which stressed the important role of loan loss reserves in mitigating procyclicality issues. |
| 9 | In the single-stage procedure, we regress LLP on monetary policy stance and control for the bank-level variables that reflect the nondiscretionary determinants of LLP as well as other confounding factors. This process is equivalent to generating DLLP in the first-stage regression and then regressing the residual term generated in the first stage on monetary policy stance in the second-stage regression. Since the single-stage procedure can only be used in the reduced-form regression framework, we use the two-stage procedure in the nonparametric tests and path analysis. |
| 10 | The results are qualitatively the same if we cluster only by bank or only by quarter. |
| 11 | We use the BM index in the main test because the variation in the BM index is linear in its policy stance and because the BM index clearly distinguishes expansion from any tightening policy stances. |
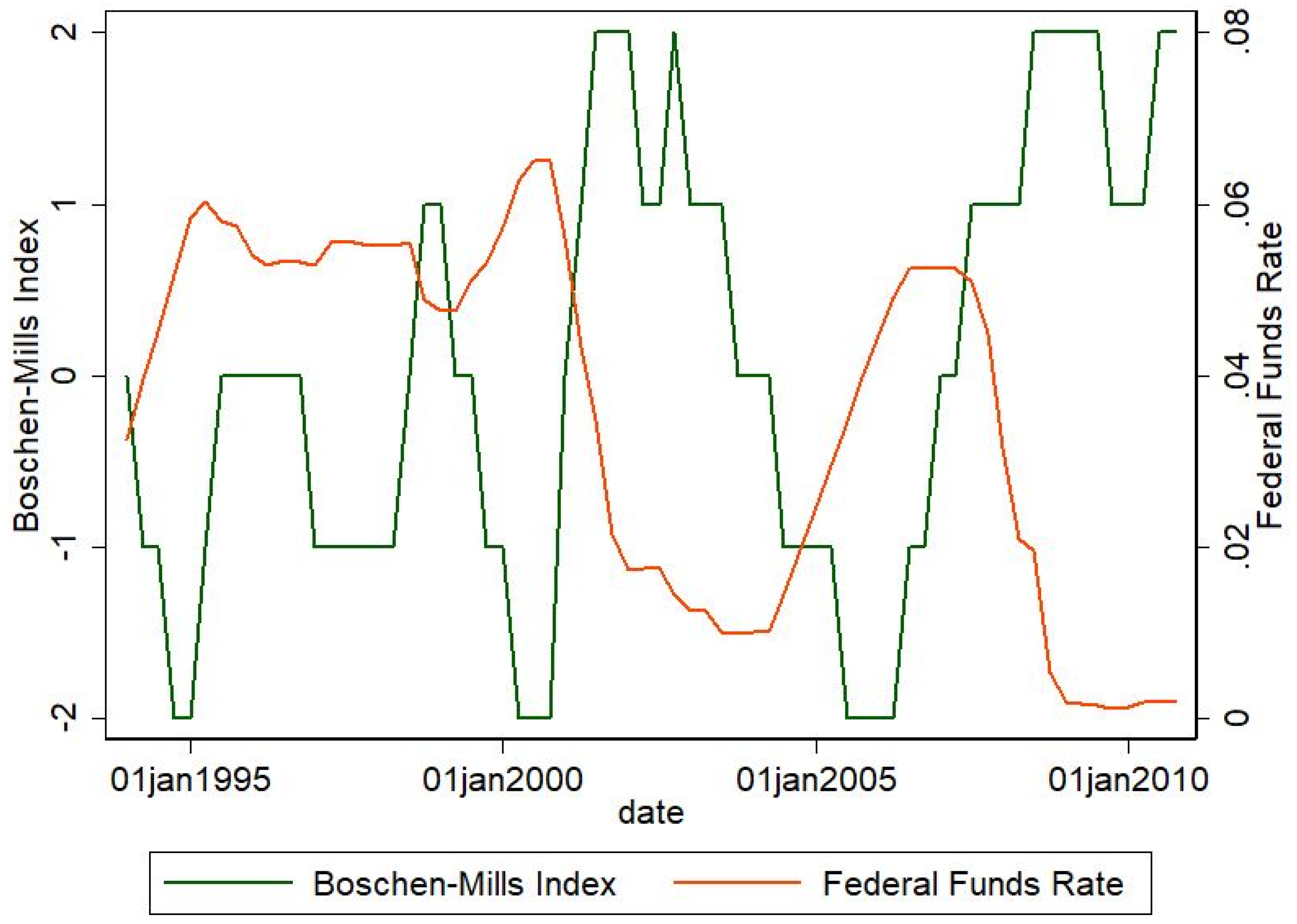
| 12 | To the extent that the BM index and federal funds rate are portraying the variation of monetary policy stances in opposite directions (i.e., a higher BM index value corresponds to a lower interest rate), we multiply the federal funds rate by −1 in all the regressions. In addition, we scale the BM index by 100 in all the regressions so that two measures have similar decimal points. |
| 13 | Our sample consists of mostly bank-holding companies. |
| 14 | Filing requirements for the FR Y-9C size threshold for bank holding companies changed in 2006. We verify that our main results remain qualitatively unchanged before and after 2006, mitigating this selection bias. |
| 15 | Lo (2015) assesses the impact of monetary policy until 2007 because of the lack of variation in monetary expansion after 2008. Similar to Lo (2015), our sample starts from 1995Q1, so we have the necessary data to construct the variables used in the models. Because there is no variation in monetary expansion after 2010 (as of January 2019), we examine banks’ responses to monetary policy until 2010Q4. |
| 16 | Our sample starts from 1995Q1 because we lack the data prior to 1995 in the COMPUSTAT database to calculate the variables needed. Our sample ends on 2010Q4 because there’s no variation in the monetary policy after that date. Since 2009, the federal funds rate has even sagged to zero or thereabouts (Borio and Gambacorta 2017). |
| 17 | The Romer and Romer (2004) exogenous shock is available until 2007. In order to maintain a reasonable amount of sample size, we choose to not drop observations with the missing Romer and Romer (2004) exogenous shock after 2007. |
| 18 | As the coefficients of BMt−1 are too small for four decimal places, we scale BMt−1 by 100 in all the regressions thereafter. This will not affect the model fit or economic or statistical significance. We multiply the federal funds rate by −1 in all the regressions to be consistent with the BM index. This applies to all regressions thereafter. |
| 19 | The focus of this paper is EMP. In order to study the effect of an EMP, we define a period as an EMP period if the BM index equals to 1 or 2, and a period as a non-EMP period (i.e., either neutral or tightening) if the BM index equals to −2, −1, or 0. |
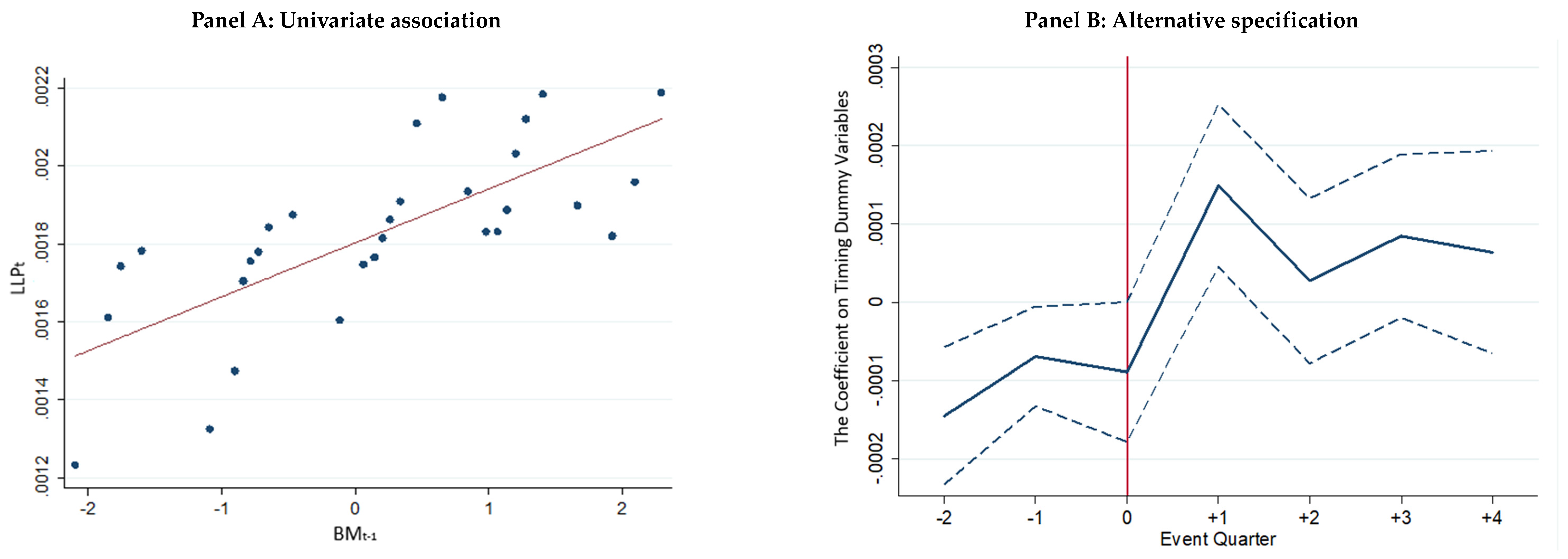
| 20 | To better visualize the data, we group all observations into 30 equally sized bins. LLP and BM are residualized by the control variables used to generate the discretionary component of LLP, including lagged, contemporaneous, and lead changes in nonperforming loans, lagged bank size, loan growth, lagged loan loss allowance, net charge-offs, and the proportions of commercial and industrial loans, consumer loans, and real estate loans (Beatty and Liao 2014). |
| 21 | It is important to note that some of the variation in coefficients does not differ statistically from zero and that readers should exercise caution when interpreting these results. |
| 22 | We multiply the federal funds rate by −1 in all regressions to be consistent with the BM index. |
| 23 | It is equal to 0.013 (standard deviation of BM) * 0.0108 (coefficient of BM)/0.0018 (mean of LLP) = 0.078. |
| 24 | It is equal to 0.0208 (standard deviation of FFR) * 0.0208 (coefficient of FFR)/0.0018 (mean of LLP) = 0.2415. |
| 25 | As Altamuro and Beatty (2010) suggest, the Federal Depository Insurance Corporation Improvement Act (FDICIA) rules that enhance internal controls would result in timelier loan loss provisioning because the improvement in internal controls increases the quality of banks’ operating activity measurement. As per FDICIA rules, banks with assets under USD 500 million are exempted from the FDICIA provisions. |
| 26 | We assign Strict = 1 if a state’s regulatory index is in the highest tercile and Strict = 0 if a state’s regulatory index is in the lowest tercile. |
| 27 | We do not use COMPUSTAT bank data because almost all the public banks are national banks. |
| 28 | We multiply the surprise by (−1), so that the higher the ‘surprise’, the more expansionary the monetary policy. |
| 29 | For example, factors such as bank portfolio composition changes and the use of collateral only tend to change with EMP, but not with previous belief updates that predict EMP. |
| 30 | As suggested by Roberts and Whited (2012), we test the strength of our instrumental variable by computing the partial F-statistic for the instrument used in the first-stage regression. The partial F-statistics are 520.43 and 786.93, which are considerably higher than the suggested minimum benchmark of 8.96 for a model with one instrument, as reported by Stock and Yogo (2005). Therefore, we conclude that our model does not suffer from a weak instrument problem. |
| 31 | The construction of the Z-score is explained in detail in Appendix A. |
| 32 | To ensure the common support assumption, we drop the treatment observations whose p-score is higher than the maximum or less than the minimum p-score of the controls. Additionally, we impose common support by dropping 10% of the treatment observations with the lowest p-score density of the control observations. We use a caliper of 0.25 for both matching procedures. |
| 33 | We thank Basil Halperin for granting us access to the Romer and Romer (2004) data. To be consistent with other variables of interest, we transform the first differences back to levels using a base level of 2% at the beginning of our sample period. The choice of base level only affects the estimates of the constant terms. |
| 34 | This variable is generated by the two-stage procedure. Since the single-stage procedure can only be used in the reduced-form regression framework, we use the two-stage procedure in the nonparametric tests, path analysis, and consequences tests. |
References
- Abadie, Alberto, and Guido W. Imbens. 2012. A martingale representation for matching estimators. Journal of the American Statistical Association 107: 833–43. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Hyun Song Shin. 2010. Liquidity and leverage. Journal of Financial Intermediation 19: 418–37. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. CoVaR. The American Economic Review 106: 1705. [Google Scholar] [CrossRef]
- Agarwal, Sumit, David Lucca, Amit Seru, and Francesco Trebbi. 2014. Inconsistent regulators: Evidence from banking. The Quarterly Journal of Economics 129: 889–938. [Google Scholar] [CrossRef]
- Alessandri, Piergiorgio, and Benjamin D. Nelson. 2015. Simple banking: Profitability and the yield curve. Journal of Money, Credit and Banking 47: 143–75. [Google Scholar] [CrossRef]
- Altamuro, Jennifer, and Anne Beatty. 2010. How does internal control regulation affect financial reporting? Journal of Accounting and Economics 49: 58–74. [Google Scholar] [CrossRef]
- Andries, Kathleen, John Gallemore, and Martin Jacob. 2017. The effect of corporate taxation on bank transparency: Evidence from loan loss provisions. Journal of Accounting and Economics 63: 307–28. [Google Scholar] [CrossRef]
- Aramonte, Sirio, Seung Jung Lee, and Viktors Stebunovs. 2022. Risk taking and low longer-term interest rates: Evidence from the US syndicated term loan market. Journal of Banking and Finance 138: 105511. [Google Scholar] [CrossRef]
- Ashbaugh, Hollis, Ryan LaFond, and Brian W. Mayhew. 2003. Do nonaudit services compromise auditor independence? Further evidence. The Accounting Review 78: 611–39. [Google Scholar] [CrossRef]
- Basu, Sudipta. 1997. The conservatism principle and the asymmetric timeliness of earnings. Journal of Accounting and Economics 24: 3–37. [Google Scholar] [CrossRef]
- Beatty, Anne, and Scott Liao. 2011. Do delays in expected loss recognition affect banks’ willingness to lend? Journal of Accounting and Economics 52: 1–20. [Google Scholar] [CrossRef]
- Beatty, Anne, and Scott Liao. 2014. Financial accounting in the banking industry: A review of the empirical literature. Journal of Accounting and Economics 58: 339–83. [Google Scholar] [CrossRef]
- Beatty, Anne L., Bin Ke, and Kathy R. Petroni. 2002. Earnings management to avoid earnings declines across publicly and privately held banks. The Accounting Review 77: 547–70. [Google Scholar] [CrossRef]
- Bergman, Nittai, David A. Matsa, and Michael Weber. 2020. Heterogeneous Labor Market Effects of Monetary Policy. Chicago Booth Research Paper, 21-02. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3757645 (accessed on 3 July 2021).
- Bernanke, Ben, and Alan S. Blinder. 1992. The federal funds rate and the transmission of monetary policy. The American Economic Review 82: 901–21. [Google Scholar]
- Bernanke, Ben S., and Alan S. Blinder. 1988. Credit, Money, and Aggregate Demand (No. w2534). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Bernanke, Ben S., and Mark Gertler. 1995. Inside the black box: The credit channel of monetary policy. Journal of Economic Perspectives 9: 27–48. [Google Scholar] [CrossRef]
- Bhat, Gauri, Stephen G. Ryan, and Dushyantkumar Vyas. 2019. The implications of credit risk modeling for banks’ loan loss provisions and loan-origination procyclicality. Management Science 65: 2116–41. [Google Scholar] [CrossRef]
- Bikker, Jacob A., and Paul AJ Metzemakers. 2005. Bank provisioning behavior and procyclicality. Journal of International Financial Markets, Institutions and Money 15: 141–57. [Google Scholar] [CrossRef]
- Borio, Claudio, and Leonardo Gambacorta. 2017. Monetary policy and bank lending in a low interest rate environment: Diminishing effectiveness? Journal of Macroeconomics 54: 217–31. [Google Scholar] [CrossRef]
- Boschen, John F., and Leonard O. Mills. 1995. The relation between narrative and money market indicators of monetary policy. Economic Inquiry 33: 24–44. [Google Scholar] [CrossRef]
- Bushman, Robert M., and Christopher D. Williams. 2012. Accounting discretion, loan loss provisioning, and discipline of banks’ risk-taking. Journal of Accounting and Economics 54: 1–18. [Google Scholar] [CrossRef]
- Bushman, Robert M., and Christopher D. Williams. 2015. Delayed expected loss recognition and the risk profile of banks. Journal of Accounting Research 53: 511–53. [Google Scholar] [CrossRef]
- Campello, Murillo. 2002. Internal capital markets in financial conglomerates: Evidence from small bank responses to monetary policy. The Journal of Finance 57: 2773–805. [Google Scholar] [CrossRef]
- Chodorow-Reich, Gabriel. 2014. Effects of Unconventional Monetary Policy on Financial Institutions (No. w20230). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Christensen, Hans B., Valeri V. Nikolaev, and Regina Wittenberg-Moerman. 2016. Accounting information in financial contracting: The incomplete contract theory perspective. Journal of Accounting Research 54: 397–435. [Google Scholar] [CrossRef]
- Claessens, Stijn, Nicholas Coleman, and Michael Donnelly. 2018. “Low-For-Long” interest rates and banks’ interest margins and profitability: Cross-country evidence. Journal of Financial Intermediation 35: 1–16. [Google Scholar] [CrossRef]
- Dang, Van Dan. 2022a. Monetary policy and bank performance: The role of business models. The North American Journal of Economics and Finance 59: 101602. [Google Scholar] [CrossRef]
- Dang, Van Dan. 2022b. Bank funding, market power, and the bank liquidity creation channel of monetary policy. Research in International Business and Finance 59: 101531. [Google Scholar] [CrossRef]
- Delis, Manthos D., and Georgios P. Kouretas. 2011. Interest rates and bank risk-taking. Journal of Banking and Finance 35: 840–55. [Google Scholar] [CrossRef]
- Dell’Ariccia, Giovanni, Luc Laeven, and Gustavo A. Suarez. 2017. Bank leverage and monetary policy’s risk-taking channel: Evidence from the United States. The Journal of Finance 72: 613–54. [Google Scholar] [CrossRef]
- Deng, Saiying, Elyas Elyasiani, and Jingyi Jia. 2013. Institutional ownership, diversification, and riskiness of bank holding companies. Financial Review 48: 385–415. [Google Scholar] [CrossRef]
- Farhi, Emmanuel, and Jean Tirole. 2012. Collective moral hazard, maturity mismatch, and systemic bailouts. The American Economic Review 102: 60–93. [Google Scholar] [CrossRef]
- Fishburn, Peter C., and R. Burr Porter. 1976. Optimal portfolios with one safe and one risky asset: Effects of changes in rate of return and risk. Management Science 22: 1064–73. [Google Scholar] [CrossRef]
- Fonseca, Ana Rosa, and Francisco Gonzalez. 2008. Cross-country determinants of bank income smoothing by managing loan-loss provisions. Journal of Banking and Finance 32: 217–28. [Google Scholar] [CrossRef]
- Gertler, Mark, and Peter Karadi. 2015. Monetary policy surprises, credit costs, and economic activity. American Economic Journal: Macroeconomics 7: 44–76. [Google Scholar] [CrossRef]
- Gomaa, Mohamed, Kiridaran Kanagaretnam, Stuart Mestelman, and Mohamed Shehata. 2019. Testing the efficacy of replacing the incurred credit loss model with the expected credit loss model. European Accounting Review 28: 309–34. [Google Scholar] [CrossRef]
- Gomaa, Mohamed, Kiridaran Kanagaretnam, Stuart Mestelman, and Mohamed Shehata. 2021. Test-bedding the new reporting standards for loan loss reserves. Journal of Economic Behavior and Organization 187: 225–45. [Google Scholar] [CrossRef]
- Gorodnichenko, Yuriy, and Michael Weber. 2016. Are sticky prices costly? Evidence from the stock market. The American Economic Review 106: 165–99. [Google Scholar] [CrossRef]
- Grimm, Maximilian, Òscar Jordà, Moritz Schularick, and Alan M. Taylor. 2023. Loose Monetary Policy and Financial Instability (No. w30958). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Heckman, James J. 1979. Sample selection bias as a specification error. Econometrica: Journal of the Econometric Society 47: 153–61. [Google Scholar] [CrossRef]
- Hribar, Paul, Samuel J. Melessa, R. Christopher Small, and Jaron H. Wilde. 2017. Does managerial sentiment affect accrual estimates? Evidence from the banking industry. Journal of Accounting and Economics 63: 26–50. [Google Scholar] [CrossRef]
- Jackson, Scott B., and Xiaotao Liu. 2010. The allowance for uncollectible accounts, conservatism, and earnings management. Journal of Accounting Research 48: 565–601. [Google Scholar] [CrossRef]
- Jiménez, Gabriel, Steven Ongena, José-Luis Peydró, and Jesús Saurina. 2012. Credit supply and monetary policy: Identifying the bank balance-sheet channel with loan applications. The American Economic Review 102: 2301–26. [Google Scholar] [CrossRef]
- Kanagaretnam, Kiridaran, Chee Yeow Lim, and Gerald J. Lobo. 2014. Influence of national culture on accounting conservatism and risk-taking in the banking industry. The Accounting Review 89: 1115–49. [Google Scholar] [CrossRef]
- Kanagaretnam, Kiridaran, Gerald J. Lobo, and Dong-Hoon Yang. 2004. Joint tests of signaling and income smoothing through bank loan loss provisions. Contemporary Accounting Research 21: 843–84. [Google Scholar] [CrossRef]
- Kanagaretnam, Kiridaran, Gerald J. Lobo, and Robert Mathieu. 2003. Managerial incentives for income smoothing through bank loan loss provisions. Review of Quantitative Finance and Accounting 20: 63–80. [Google Scholar] [CrossRef]
- Kanagaretnam, Kiridaran, Gopal V. Krishnan, and Gerald J. Lobo. 2010. An empirical analysis of auditor independence in the banking industry. The Accounting Review 85: 2011–46. [Google Scholar] [CrossRef]
- Kashyap, Anil, Jeremy Stein, and David Wilcox. 1993. The monetary transmission mechanism: Evidence from the composition of external finance. The American Economic Review 83: 78–98. [Google Scholar]
- Kashyap, Anil K., and Jeremy C. Stein. 1994. The Impact of Monetary Policy on Bank Balance Sheets (No. w4821). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Kashyap, Anil K., and Jeremy C. Stein. 2000. What do a million observations on banks say about the transmission of monetary policy? The American Economic Review 90: 407–28. [Google Scholar] [CrossRef]
- Keeley, Michael C. 1990. Deposit insurance, risk, and market power in banking. The American Economic Review 80: 1183–200. [Google Scholar]
- Kilic, Emre, Gerald J. Lobo, Tharindra Ranasinghe, and K. Sivaramakrishnan. 2013. The impact of SFAS 133 on income smoothing by banks through loan loss provisions. The Accounting Review 88: 233–60. [Google Scholar] [CrossRef]
- Kuttner, Kenneth N. 2001. Monetary policy surprises and interest rates: Evidence from the Fed funds futures market. Journal of Monetary Economics 47: 523–44. [Google Scholar] [CrossRef]
- Laeven, Luc, and Giovanni Majnoni. 2003. Loan loss provisioning and economic slowdowns: Too much, too late? Journal of Financial Intermediation 12: 178–97. [Google Scholar] [CrossRef]
- Laeven, Luc, and Ross Levine. 2009. Bank governance, regulation and risk taking. Journal of Financial Economics 93: 259–75. [Google Scholar] [CrossRef]
- Lee, Seung Jung, Lucy Qian Liu, and Viktors Stebunovs. 2022. Risk-taking spillovers of US monetary policy in the global market for US dollar corporate loans. Journal of Banking and Finance 138: 105550. [Google Scholar] [CrossRef]
- Liu, Chi-Chun, and Stephen G. Ryan. 1995. The effect of bank loan portfolio composition on the market reaction to and anticipation of loan loss provisions. Journal of Accounting Research 33: 77–94. [Google Scholar] [CrossRef]
- Liu, Chi-Chun, and Stephen G. Ryan. 2006. Income smoothing over the business cycle: Changes in banks’ coordinated management of provisions for loan losses and loan charge-offs from the pre-1990 bust to the 1990s boom. The Accounting Review 81: 421–41. [Google Scholar] [CrossRef]
- Lo, Alvis K. 2015. Accounting credibility and liquidity constraints: Evidence from reactions of small banks to monetary tightening. The Accounting Review 90: 1079–113. [Google Scholar] [CrossRef]
- Lobo, Gerald J. 2017. Accounting research in banking: A review. China Journal of Accounting Research 10: 1–7. [Google Scholar] [CrossRef]
- Maddaloni, Angela, and José-Luis Peydro. 2011. Bank risk-taking, securitization, supervision, and low interest rates: Evidence from the Euro-area and the US lending standards. Review of Financial Studies 24: 2121–65. [Google Scholar] [CrossRef]
- Ng, Jeffrey, Walid Saffar, and Janus Jian Zhang. 2020. Policy uncertainty and loan loss provisions in the banking industry. Review of Accounting Studies 25: 726–77. [Google Scholar] [CrossRef]
- Nichols, D. Craig, James M. Wahlen, and Matthew M. Wieland. 2009. Publicly traded versus privately held: Implications for conditional conservatism in bank accounting. Review of Accounting Studies 14: 88–122. [Google Scholar] [CrossRef]
- Nicoletti, Allison. 2018. The effects of bank regulators and external auditors on loan loss provisions. Journal of Accounting and Economics 66: 244–65. [Google Scholar] [CrossRef]
- Paligorova, Teodora, and Joao AC Santos. 2012. When Is It Less Costly for Risky Firms to Borrow? Evidence from the Bank Risk-Taking Channel of Monetary Policy (No. 2012-10). Ottawa: Bank of Canada. [Google Scholar]
- Rajan, Raghuram G. 2006. Has finance made the world riskier? European Financial Management 12: 499–533. [Google Scholar] [CrossRef]
- Roberts, Michael R., and Toni M. Whited. 2012. Endogeneity in empirical corporate finance. In Handbook of the Economics of Finance. Edited by George M. Constantinides, Milton Harris and René M. Stulz. Oxford: Elsevier, pp. 493–572. [Google Scholar]
- Romer, Christina D., and David H. Romer. 2004. A new measure of monetary shocks: Derivation and implications. The American Economic Review 94: 1055–84. [Google Scholar] [CrossRef]
- Soenen, Nicolas, and Rudi Vander Vennet. 2022. ECB monetary policy and bank default risk. Journal of International Money and Finance 122: 102571. [Google Scholar] [CrossRef]
- Stein, Jeremy. 2014. Incorporating Financial Stability Considerations into a Monetary Policy Framework: A Speech at the International Research Forum on Monetary Policy, Washington, DC, 21 March 2014 (No. 796). Washington, DC: Board of Governors of the Federal Reserve System (US). [Google Scholar]
- Stock, James H., and Motohiro Yogo. 2005. Testing for weak instruments in linear IV regression. In Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg. Cambridge: Cambridge University Press, pp. 80–108. [Google Scholar]
- Taylor, John B. 1993. Discretion versus policy rules in practice. In Carnegie-Rochester Conference Series on Public Policy. Amsterdam: North-Holland, vol. 39, pp. 195–214. [Google Scholar]
- Taylor, John B. 2009. The Financial Crisis and the Policy Responses: An Empirical Analysis of What Went Wrong (No. w14631). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Wahlen, James M. 1994. The nature of information in commercial bank loan loss disclosures. The Accounting Review 69: 455–78. [Google Scholar]
- Watts, Ross L. 2003. Conservatism in accounting part I: Explanations and implications. Accounting Horizons 17: 207–21. [Google Scholar] [CrossRef]
- Watts, Ross L., and Luo Zuo. 2011. Accounting Conservatism and Firm Value: Evidence from the Global Financial Crisis. Working paper. Cambridge: Massachusetts Institute of Technology. [Google Scholar]
- Weise, Charles L. 2008. Private sector influences on monetary policy in the United States. Journal of Money, Credit and Banking 40: 449–62. [Google Scholar] [CrossRef]
- Wu, Ji, Yuanyun Yan, Minghua Chen, and Bang Nam Jeon. 2022. Monetary policy, economic uncertainty and bank risk: Cross-country evidence. Journal of International Money and Finance 122: 102580. [Google Scholar] [CrossRef]
| Sample Size | |
|---|---|
| Total number of bank-quarters in COMPUSTAT in the period 1995Q1–2010Q416 Less: | 47,919 |
| Drop observations with missing required data in COMPUSTAT | (25,507) |
| Merge with commercial bank call report and bank holding company call report (Y-9C) and drop observations with missing required data | (5853) |
| Merge with CRSP database and drop observations with missing required data | (0) |
| Merge with state and national-level control variables, and exogenous shocks, including Taylor rule residual and drop observations with missing required data17 | (1310) |
| Merge with Adrian and Brunnermeier’s (2016) risk measures and drop observations with missing required data. | (626) |
| The final sample of bank-quarter observations | 14,623 |
| Variable | Non-EMP Periods (BM Index = −2, −1 or 0)18 | EMP Periods19 (BM Index = 1 or 2) | Difference in Means (t-Stat.) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N | Mean | Std Dev | Median | N | Mean | Std Dev | Median | ||
| LLP | 7930 | 0.001 | 0.001 | 0.001 | 6693 | 0.003 | 0.004 | 0.001 | −45.125 *** |
| CH_NPA | 7930 | 0.000 | 0.003 | 0.000 | 6693 | 0.002 | 0.007 | 0.000 | −24.848 *** |
| SIZE | 7930 | 7.819 | 1.614 | 7.479 | 6693 | 7.824 | 1.530 | 7.498 | −0.587 |
| CH_LOAN | 7930 | 0.034 | 0.057 | 0.024 | 6693 | 0.013 | 0.051 | 0.007 | 23.822 *** |
| CO | 7930 | 0.001 | 0.001 | 0.000 | 6693 | 0.002 | 0.003 | 0.001 | −39.699 *** |
| ALW | 7930 | 0.015 | 0.006 | 0.013 | 6693 | 0.017 | 0.008 | 0.015 | −17.648 *** |
| STD_EBIT | 7930 | 0.001 | 0.002 | 0.001 | 6693 | 0.002 | 0.003 | 0.001 | −20.310 *** |
| EBTP | 7930 | 0.008 | 0.004 | 0.008 | 6693 | 0.006 | 0.005 | 0.006 | 22.563 *** |
| CON | 7930 | 0.010 | 0.019 | 0.004 | 6693 | 0.008 | 0.016 | 0.003 | 8.807 *** |
| COM | 7930 | 0.180 | 0.118 | 0.155 | 6693 | 0.165 | 0.105 | 0.145 | 7.761 *** |
| REAL | 7930 | 0.681 | 0.181 | 0.708 | 6693 | 0.725 | 0.158 | 0.751 | −15.752 *** |
| LOSS | 7930 | 0.023 | 0.150 | 0.000 | 6693 | 0.181 | 0.385 | 0.000 | −33.179 *** |
| TIER1 | 7930 | 0.113 | 0.026 | 0.109 | 6693 | 0.113 | 0.026 | 0.110 | 0.573 |
| BHAR | 7930 | −0.001 | 0.134 | −0.011 | 6693 | −0.004 | 0.225 | −0.008 | 2.918 *** |
| MTB | 7930 | 1.975 | 0.701 | 1.874 | 6693 | 1.391 | 0.806 | 1.300 | 50.662 *** |
| LOGMV | 7930 | −2.517 | 1.812 | −2.891 | 6693 | −2.928 | 1.811 | −3.244 | 14.248 *** |
| CPI | 1604 | 0.007 | 0.007 | 0.007 | 993 | 0.004 | 0.010 | 0.004 | 20.340 *** |
| HOU | 1604 | 0.015 | 0.015 | 0.013 | 993 | 0.002 | 0.019 | 0.005 | 56.819 *** |
| INCOME | 1604 | 0.059 | 0.038 | 0.058 | 993 | 0.026 | 0.051 | 0.032 | 51.926 *** |
| UNEMPLOY | 1604 | 0.005 | 0.168 | −0.023 | 993 | 0.048 | 0.166 | 0.018 | −21.737 *** |
| DEFAULT | 40 | 0.008 | 0.001 | 0.008 | 25 | 0.014 | 0.006 | 0.012 | −80.900 *** |
| GDPGROW | 40 | 0.032 | 0.020 | 0.031 | 25 | 0.013 | 0.032 | 0.021 | 44.537 *** |
| (1) | (2) | (3) | (4) | (5) | (6) | |||||||
| Dependent Variable: | LLPt | LLPt | LLPt | LLPt | LLPt | LLPt | ||||||
| BMt−1 | 0.0092 *** | (5.91) | 0.0117 *** | (3.53) | 0.0108 *** | (3.55) | ||||||
| FFRt−1 | 0.0046 *** | (4.04) | 0.0224 *** | (4.42) | 0.0208 *** | (5.17) | ||||||
| Determinants of nondiscretionary LLP: | ||||||||||||
| CH_NPAt+1 | 0.0204 *** | (4.34) | 0.0191 *** | (4.02) | 0.0190 *** | (3.98) | 0.0223 *** | (4.67) | 0.0192 *** | (4.04) | 0.0191 *** | (3.94) |
| CH_NPAt | 0.0722 *** | (10.09) | 0.0709 *** | (10.32) | 0.0707 *** | (10.18) | 0.0738 *** | (10.27) | 0.0709 *** | (10.27) | 0.0708 *** | (10.15) |
| CH_NPAt−1 | 0.0079 | (1.24) | 0.0059 | (0.91) | 0.0063 | (0.99) | 0.0090 | (1.43) | 0.0062 | (0.97) | 0.0063 | (1.00) |
| CH_NPAt−2 | 0.0123 ** | (2.19) | 0.0101 * | (1.99) | 0.0093 * | (1.71) | 0.0132 ** | (2.31) | 0.0094 * | (1.75) | 0.0089 | (1.60) |
| SIZEt−1 | −0.0000 | (−0.44) | 0.0001 | (1.02) | 0.0001 | (1.04) | −0.0001 | (−1.47) | 0.0001 | (1.15) | 0.0001 | (1.15) |
| CH_LOANt | −0.0007 *** | (−2.83) | −0.0006 ** | (−2.25) | −0.0006 ** | (−2.34) | −0.0008 *** | (−3.46) | −0.0006 ** | (−2.33) | −0.0006 ** | (−2.36) |
| COt | 0.6861 *** | (21.77) | 0.6794 *** | (21.38) | 0.6772 *** | (21.44) | 0.6888 *** | (21.86) | 0.6779 *** | (21.46) | 0.6765 *** | (21.38) |
| ALWt−1 | −0.0493 *** | (−6.20) | −0.0503 *** | (−6.27) | −0.0505 *** | (−6.28) | −0.0514 *** | (−6.18) | −0.0516 *** | (−6.41) | −0.0515 *** | (−6.38) |
| CONt | 0.0032 | (1.56) | 0.0025 | (1.17) | 0.0025 | (1.20) | 0.0032 | (1.54) | 0.0024 | (1.15) | 0.0025 | (1.17) |
| COMt | 0.0021 *** | (3.13) | 0.0021 *** | (3.19) | 0.0021 *** | (3.21) | 0.0022 *** | (3.14) | 0.0022 *** | (3.22) | 0.0022 *** | (3.21) |
| REALt | 0.0010 * | (1.99) | 0.0011 ** | (2.17) | 0.0011 ** | (2.15) | 0.0009 * | (1.69) | 0.0011 ** | (2.16) | 0.0011 ** | (2.14) |
| Determinants of discretionary LLP: | ||||||||||||
| TIER1t−1 | 0.0020 | (1.35) | 0.0021 | (1.64) | 0.0022 * | (1.73) | 0.0015 | (1.02) | 0.0022 * | (1.72) | 0.0023 * | (1.80) |
| EBTPt | 0.0669 *** | (6.71) | 0.0678 *** | (6.93) | 0.0678 *** | (6.91) | 0.0675 *** | (6.61) | 0.0688 *** | (7.04) | 0.0683 *** | (6.97) |
| LOSSt | 0.0029 *** | (14.72) | 0.0029 *** | (14.58) | 0.0029 *** | (14.65) | 0.0029 *** | (14.67) | 0.0029 *** | (14.54) | 0.0028 *** | (14.58) |
| LOGMVt | −0.0001 | (−0.53) | −0.0001 | (−1.45) | −0.0002 | (−1.51) | −0.0000 | (−0.15) | −0.0002 | (−1.64) | −0.0002 * | (−1.67) |
| MTBt | −0.0002 *** | (−4.84) | −0.0001 *** | (−2.86) | −0.0001 *** | (−2.67) | −0.0003 *** | (−5.87) | −0.0001 *** | (−2.83) | −0.0001 ** | (−2.57) |
| STD_Et | 0.0237 | (1.56) | 0.0180 | (1.17) | 0.0169 | (1.08) | 0.0244 | (1.63) | 0.0167 | (1.07) | 0.0160 | (1.02) |
| LLPt−1 | 0.1005 *** | (4.65) | 0.0952 *** | (4.69) | 0.0952 *** | (4.70) | 0.1022 *** | (4.66) | 0.0954 *** | (4.73) | 0.0956 *** | (4.72) |
| State-wide controls: | ||||||||||||
| CPIt | −0.0028 | (−0.80) | −0.0010 | (−0.39) | −0.0030 | (−1.19) | −0.0009 | (−0.40) | ||||
| HOUt | −0.0004 | (−0.25) | 0.0004 | (0.23) | −0.0003 | (−0.25) | −0.0006 | (−0.33) | ||||
| INCOMEt | 0.0003 | (0.75) | 0.0004 | (1.26) | 0.0003 | (0.90) | 0.0003 | (1.10) | ||||
| UNEMPLOYt | −0.0003 ** | (−2.14) | −0.0001 | (−1.14) | −0.0003 *** | (−3.15) | −0.0001 | (−1.20) | ||||
| Nation-wide controls: | ||||||||||||
| BUSCYCLEt | −0.0000 | (−0.24) | 0.0000 | (0.10) | −0.0003 ** | (−2.20) | −0.0003 ** | (−2.39) | ||||
| GDPGROWt | −0.0007 | (−0.72) | −0.0006 | (−0.74) | −0.0003 | (−0.43) | −0.0010 | (−1.21) | ||||
| DEFAULTt | −0.0088 | (−0.72) | 0.0016 | (0.16) | 0.0036 | (0.34) | 0.0050 | (0.55) | ||||
| Lag Macro Controls | No | No | Yes | No | No | Yes | ||||||
| Bank FE | Yes | Yes | Yes | Yes | Yes | Yes | ||||||
| State FE | Yes | Yes | Yes | Yes | Yes | Yes | ||||||
| Year FE | No | Yes | Yes | No | Yes | Yes | ||||||
| Clustered SE | Firm and Quarter | Firm and Quarter | Firm and Quarter | Firm and Quarter | Firm and Quarter | Firm and Quarter | ||||||
| R-squared | 0.80 | 0.81 | 0.81 | 0.80 | 0.81 | 0.81 | ||||||
| N | 14,623 | 14,623 | 14,623 | 14,623 | 14,623 | 14,623 | ||||||
| Panel A: The effect of EMP on the relation between current LLP and future non-performing loans | ||||||||||||
| (1) | (2) | (3) | (4) | |||||||||
| Dependent Variable: | LLPt | LLPt | LLPt | LLPt | ||||||||
| BMt−1 | 0.0038 *** | (2.59) | 0.0056 * | (1.71) | 0.0048 | (1.60) | 0.0053 * | (1.78) | ||||
| BMt−1*CH_NPA1YR | 0.1449 *** | (2.86) | 0.1097 ** | (2.36) | 0.1023 ** | (2.15) | 0.0866 * | (1.96) | ||||
| BMt−1*CH_NPAt | 1.4046 *** | (3.30) | 1.4077 *** | (2.67) | 1.3862 ** | (2.64) | 1.4129 *** | (2.73) | ||||
| BMt−1*CH_NPAt−1 | 0.5240 | (1.21) | ||||||||||
| BMt−1*CH_NPAt−2 | 0.5174 | (1.31) | ||||||||||
| CH_NPA1YR | 0.0012 ** | (2.17) | 0.0013 ** | (2.41) | 0.0013 ** | (2.48) | 0.0013 ** | (2.49) | ||||
| CH_NPAt | 0.0500 *** | (8.39) | 0.0499 *** | (7.96) | 0.0500 *** | (8.00) | 0.0500 *** | (8.01) | ||||
| CH_NPAt−1 | −0.0032 | (−0.50) | ||||||||||
| CH_NPAt−2 | 0.0015 | (0.27) | ||||||||||
| Bank Controls | Yes | Yes | Yes | Yes | ||||||||
| Macro Controls | Yes | Yes | Yes | Yes | ||||||||
| Lagged Macro Controls | No | No | Yes | No | ||||||||
| Bank FE | Yes | Yes | Yes | Yes | ||||||||
| Year FE | No | Yes | Yes | Yes | ||||||||
| Clustered Standard Error | Bank | Bank, Quarter | Bank, Quarter | Bank, Quarter | ||||||||
| R-squared | 0.80 | 0.80 | 0.80 | 0.80 | ||||||||
| N | 13,987 | 13,987 | 13,987 | 13,987 | ||||||||
| Panel B: The effect of EMP on the relation between current LLP and future net loan charge-offs | ||||||||||||
| (1) | (2) | |||||||||||
| Dependent Variable: | LLPt | LLPt | ||||||||||
| BMt−1 | 0.0094 ** | (2.57) | 0.0045 | (1.43) | ||||||||
| BMt−1*COt+1 | 2.4782 *** | (2.94) | ||||||||||
| COt+1 | 0.0700 *** | (4.66) | ||||||||||
| BMt−1*COt+4 | 1.2594 *** | (3.86) | ||||||||||
| COt+4 | 0.0352 *** | (5.39) | ||||||||||
| BHARt+1 | −0.0003 *** | (−2.95) | ||||||||||
| BHARt+4 | 0.0002 ** | (2.49) | ||||||||||
| Bank-Level Controls | Yes | Yes | ||||||||||
| Macro-Level Controls | Yes | Yes | ||||||||||
| Bank FE | Yes | Yes | ||||||||||
| Year FE | Yes | Yes | ||||||||||
| Clustered Standard Error | Bank, Quarter | Bank, Quarter | ||||||||||
| R-squared | 0.81 | 0.81 | ||||||||||
| N | 14,623 | 13,747 | ||||||||||
| Panel A: The effect of current bank risk on the relation between LLP and monetary policy | ||||||||||||||||||||||
| (1) | (2) | (3) | ||||||||||||||||||||
| LLPt | LLPt | LLPt | ||||||||||||||||||||
| BMt−1 | 0.0077 ** | (2.31) | 0.0078 ** | (2.29) | 0.0012 | (0.25) | ||||||||||||||||
| BMt−1*STD_Et | 2.3926 *** | (3.56) | ||||||||||||||||||||
| STD_Et | −0.0032 | (−0.23) | ||||||||||||||||||||
| BMt−1*BETAt | 0.0081 *** | (3.52) | ||||||||||||||||||||
| BETAt | 0.0000 | (0.96) | ||||||||||||||||||||
| BMt−1*VaRt | 0.1840 *** | (3.25) | ||||||||||||||||||||
| VaRt | 0.0027 * | (1.92) | ||||||||||||||||||||
| Firm, state, and national controls | Yes | Yes | Yes | |||||||||||||||||||
| Bank, state and year FE | Yes | Yes | Yes | |||||||||||||||||||
| Clustered Standard Error | Firm and Quarter | Firm and Quarter | Firm and Quarter | |||||||||||||||||||
| R-squared | 0.81 | 0.81 | 0.81 | |||||||||||||||||||
| N | 14,625 | 14,625 | 14,625 | |||||||||||||||||||
| Panel B: The moderating effect of historical (past 12 quarters) informativeness of loan loss provisions on the relation between LLP and monetary policy | ||||||||||||||||||||||
| (1) | (2) | |||||||||||||||||||||
| LLPt | LLPt | |||||||||||||||||||||
| BMt−1 | 0.0117 *** | (3.09) | 0.0122 *** | (2.85) | ||||||||||||||||||
| BMt−1*DELRt−1 | 0.0041 *** | (2.71) | ||||||||||||||||||||
| DELRt−1 | 0.0001 *** | (2.99) | ||||||||||||||||||||
| BMt−1*DELR_strictt−1 | 0.0100 *** | (2.88) | ||||||||||||||||||||
| DELR_strictt−1 | 0.0001 *** | (3.55) | ||||||||||||||||||||
| Firm, state, and national controls | Yes | Yes | ||||||||||||||||||||
| Year FE | Yes | Yes | ||||||||||||||||||||
| Clustered Standard Error | Firm and Quarter | Firm and Quarter | ||||||||||||||||||||
| R-squared | 0.80 | 0.78 | ||||||||||||||||||||
| N | 9559 | 4816 | ||||||||||||||||||||
| Panel C: Testing the moderating role of institutional investors | ||||||||||||||||||||||
| (1) LLPt | (2) LLPt | (3) LLPt | (4) LLPt | (5) LLPt | (6) LLPt | |||||||||||||||||
| Monetary Policy (MP) Proxy: | EMPt−1 | EMPt−1 | FFRt−1 | EMPt−1 | FFRt−1 | EMPt−1 | ||||||||||||||||
| MPt−1 | 0.000 | (0.21) | −0.001 ** | (−2.52) | 0.007 | (0.68) | −0.001 ** | (−2.26) | 0.021 ** | (2.01) | −0.001 ** | (−2.46) | ||||||||||
| MPt−1*INSTt (*100) | 0.077 *** | (4.56) | 0.044 *** | (2.86) | 0.013 *** | (3.23) | 0.030 ** | (2.11) | 0.010 ** | (2.47) | −0.001 * | (−1.79) | ||||||||||
| MPt−1*INSTt*FDt (*100) | 0.096 *** | (3.06) | ||||||||||||||||||||
| MPt−1*CH_NPAt+1 | −0.003 | (−0.23) | −0.453 * | (−1.84) | −0.005 | (−0.39) | −0.429 * | (−1.70) | −0.006 | (−0.43) | ||||||||||||
| MPt−1*CH_NPAt | 0.032 ** | (2.35) | 0.132 | (0.43) | 0.030 ** | (2.11) | 0.160 | (0.50) | 0.029 ** | (2.00) | ||||||||||||
| MPt−1*CH_NPAt−1 | 0.008 | (0.88) | −0.107 | (−0.42) | 0.006 | (0.66) | −0.054 | (−0.21) | 0.006 | (0.65) | ||||||||||||
| MPt−1*CH_NPAt−2 | 0.011 | (1.01) | 0.093 | (0.43) | 0.008 | (0.79) | 0.097 | (0.46) | 0.008 | (0.73) | ||||||||||||
| MPt−1*SIZEt−1 | 0.000 ** | (2.32) | −0.001 | (−0.86) | 0.000 ** | (2.50) | −0.001 | (−0.63) | 0.000 *** | (2.69) | ||||||||||||
| MPt−1*CH_LOANt | −0.001 ** | (−2.10) | −0.005 | (−0.30) | −0.001 | (−1.56) | −0.002 | (−0.13) | −0.001 | (−1.66) | ||||||||||||
| MPt−1*COt | 0.255 *** | (5.68) | 4.286 *** | (4.55) | 0.251 *** | (5.48) | 4.172 *** | (4.49) | 0.248 *** | (5.47) | ||||||||||||
| MPt−1*ALWt−1 | −0.020 ** | (−2.47) | −0.649 *** | (−2.68) | −0.018 ** | (−2.23) | −0.591 ** | (−2.57) | −0.016 ** | (−2.05) | ||||||||||||
| MPt−1*CONt | −0.000 | (−0.15) | 0.046 | (1.16) | 0.000 | (0.10) | 0.062 | (1.64) | 0.000 | (0.13) | ||||||||||||
| MPt−1*COMt | 0.001 * | (1.77) | 0.009 | (0.96) | 0.001 | (1.58) | 0.008 | (0.85) | 0.001 * | (1.71) | ||||||||||||
| MPt−1*REALt | 0.001 ** | (2.38) | 0.008 | (1.04) | 0.000 | (1.66) | 0.003 | (0.37) | 0.000 | (1.56) | ||||||||||||
| INSTt | −0.000 | (−0.45) | −0.000 | (−0.51) | 0.001 *** | (2.81) | 0.000 | (0.78) | 0.001 *** | (3.01) | 0.001 ** | (2.21) | ||||||||||
| CH_NPAt+1 | 0.016 *** | (3.01) | 0.018 | (1.65) | 0.009 | (1.20) | 0.019 * | (1.70) | 0.007 | (1.02) | 0.020 * | (1.70) | ||||||||||
| CH_NPAt | 0.075 *** | (9.93) | 0.051 *** | (4.90) | 0.081 *** | (6.90) | 0.052 *** | (4.85) | 0.080 *** | (6.66) | 0.052 *** | (4.80) | ||||||||||
| CH_NPAt−1 | 0.006 | (1.19) | −0.000 | (−0.03) | 0.005 | (0.63) | 0.000 | (0.01) | 0.005 | (0.59) | 0.000 | (0.06) | ||||||||||
| CH_NPAt−2 | 0.012 ** | (2.03) | 0.004 | (0.58) | 0.015 * | (1.75) | 0.004 | (0.58) | 0.013 | (1.54) | 0.004 | (0.53) | ||||||||||
| SIZEt−1 | 0.000 ** | (2.28) | −0.000 | (−0.44) | −0.000 | (−0.74) | 0.000 | (1.60) | 0.000 * | (1.92) | 0.000 | (1.63) | ||||||||||
| CH_LOANt | 0.000 | (−1.35) | 0.000 | (0.73) | −0.001 | (−0.86) | 0.000 | (0.85) | −0.000 | (−0.53) | 0.000 | (0.80) | ||||||||||
| COt | 0.644 *** | (19.65) | 0.453 *** | (11.43) | 0.737 *** | (23.20) | 0.451 *** | (11.23) | 0.728 *** | (23.13) | 0.451 *** | (11.30) | ||||||||||
| ALWt−1 | −0.044 *** | (−5.92) | −0.035 *** | (−5.11) | −0.066 *** | (−6.62) | −0.039 *** | (−5.52) | −0.066 *** | (−7.04) | −0.041 *** | (−5.83) | ||||||||||
| CONt | 0.002 | (0.79) | 0.003 * | (1.71) | 0.004 | (1.41) | 0.002 | (1.00) | 0.004 | (1.21) | 0.002 | (0.91) | ||||||||||
| COMt | 0.002 *** | (2.9) | 0.002 ** | (2.36) | 0.002 *** | (2.78) | 0.002 ** | (2.51) | 0.002 *** | (2.82) | 0.002 ** | (2.45) | ||||||||||
| REALt | 0.001 | (1.35) | 0.000 | (0.22) | 0.000 | (0.78) | 0.000 | (0.87) | 0.001 | (0.99) | 0.000 | (0.82) | ||||||||||
| Other Bank-Level Controls | Yes | Yes | Yes | Yes | Yes | Yes | ||||||||||||||||
| Macro Controls | Yes | Yes | Yes | Yes | Yes | Yes | ||||||||||||||||
| Bank FE | Yes | Yes | Yes | Yes | Yes | Yes | ||||||||||||||||
| Year FE | Yes | No | No | Yes | Yes | Yes | ||||||||||||||||
| SE clustered in | Bank, Quarter | Bank, Quarter | Bank, Quarter | Bank, Quarter | Bank, Quarter | Bank, Quarter | ||||||||||||||||
| R-squared | 0.79 | 0.81 | 0.80 | 0.81 | 0.81 | 0.81 | ||||||||||||||||
| N | 12,281 | 12,281 | 12,281 | 12,281 | 12,281 | 12,281 | ||||||||||||||||
| Panel A: Testing the effect of the FDICIA internal control rule on the relation between EMP and DLLP | |||||||||||||||
| (1) Nearest-Neighbor Matching | (2) Nearest-Neighbor Matching | (3) Epanechnikov Kernel | (4) Epanechnikov Kernel | (5) Nearest-Neighbor Matching | (6) Linear Regression | ||||||||||
| Subsample condition: | ABOVE500 = 1 | ABOVE500 = 0 | ABOVE500 = 1 | ABOVE500 = 0 | EMPt−1 = 1 | Full Sample | |||||||||
| Outcome Var. | DLLP | DLLP | DLLP | DLLP | DLLP | LLP | |||||||||
| ABOVE500 | 0.0305 *** (t = 2.62) | ||||||||||||||
| EMPt−1 | 0.029 ** (t = 2.37) | 0.0099 (t = 0.67) | 0.28 *** (t = 7.30) | 0.0123 (t = 1.56) | |||||||||||
| EMPt−1 × ABOVE500 | 0.0148 ** (t = 2.08) | ||||||||||||||
| Bank, State, and National Control Variables | Yes | Yes | Yes | Yes | Yes | Yes | |||||||||
| Bank and Year FE | No | No | No | No | No | Yes | |||||||||
| Standard Error | AI (2006) | AI (2006) | Bootstrapped | Bootstrapped | AI (2006) | Bank, Quarter | |||||||||
| R-squared | 0.3268 | 0.1781 | 0.3268 | 0.1781 | 0.1467 | 0.7648 | |||||||||
| N | 13,105 | 1503 | 13,105 | 1503 | 6683 | 14,602 | |||||||||
| Panel B: Testing the effect of state regulatory scrutiny on the relation between EMP and DLLP | |||||||||||||||
| (1) | (2) | (3) | (4) | ||||||||||||
| LLPt | LLPt | LLPt | LLPt | ||||||||||||
| (Strict = 1) | (Strict = 0) | (Strict = 1) | (Strict = 0) | ||||||||||||
| BMt−1 | 0.0040 *** | (2.75) | 0.0032 ** | (2.29) | |||||||||||
| BMt−1*StateCharter | 0.0002 | (0.20) | −0.0027 ** | (−2.41) | |||||||||||
| FFRt−1 | 0.0139 *** | (7.99) | 0.0102 *** | (5.85) | |||||||||||
| FFRt−1*StateCharter | 0.0003 | (0.45) | −0.0023 *** | (−3.43) | |||||||||||
| StateCharter | 0.0000 *** | (2.69) | −0.0000 | (−0.15) | 0.0000 * | (1.84) | −0.0001 *** | (−2.73) | |||||||
| Comparison: | BMt−1*StateCharter | FFRt−1*StateCharter | |||||||||||||
| Chi square statistics | 3.39 | 7.47 | |||||||||||||
| p-value | 0.0657 | 0.0063 | |||||||||||||
| Bank, State, and National Control Variables | Yes | Yes | Yes | Yes | |||||||||||
| State and Year FE | Yes | Yes | Yes | Yes | |||||||||||
| R-squared | 0.69 | 0.73 | 0.69 | 0.73 | |||||||||||
| N | 150,283 | 122,346 | 154,563 | 125,285 | |||||||||||
| Coefficients | t-Stat. | |
|---|---|---|
| Direct Path | ||
| p (TRRt−1, DLLPt) | 0.008 *** | (8.17) |
| Indirect Path | ||
| p (TRRt−1, VaRt) | 0.811 *** | (32.82) |
| p (VaRt, DLLPt) | 0.007 *** | (7.02) |
| Total magnitude of the indirect effect | 0.006 *** | (6.97) |
| Percentage of the direct effect to the total effect | 57.14% | |
| Percentage of the indirect effect to the total effect | 42.85% | |
| Nation-wide and state-wide controls | Yes | |
| Firm-level controls | Yes | |
| N | 14,619 |
| (1) | (2) | (3) | (4) | |||||
| 1st Stage | 2nd Stage | 1st Stage | 2nd Stage | |||||
| Dependent Variable: | BMt−1 | LLPt | FFRt−1 | LLPt | ||||
| Pred_BMt−1 | 0.0358 *** | (3.08) | ||||||
| Pred_FFRt−1 | 0.0450 *** | (3.09) | ||||||
| SURPRISEt−2 | 0.045 *** | (22.81) | 0.035 *** | (28.05) | ||||
| CH_NPAt+1 | −0.011 | (−1.21) | 0.020 *** | (8.30) | −0.008 *** | (−1.33) | 0.020 *** | (8.31) |
| CH_NPAt | −0.009 | (−0.94) | 0.074 *** | (28.85) | −0.01 *** | (−1.58) | 0.075 *** | (28.97) |
| CH_NPAt−1 | −0.024 ** | (−2.21) | 0.008 *** | (2.70) | −0.015 *** | (−2.16) | 0.008 *** | (2.65) |
| CH_NPAt−2 | −0.016 | (−1.44) | 0.011 *** | (3.85) | 0.009 *** | (1.18) | 0.011 *** | (3.54) |
| SIZEt−1 | −0.001 *** | (−4.85) | 0.000 ** | (2.25) | −0.002 ** | (−9.12) | 0.000 ** | (2.53) |
| CH_LOANt | −0.001 | (−1.13) | −0.001 ** | (−2.20) | 0.000 ** | (−0.36) | −0.001 ** | (−2.33) |
| COt | 0.023 | (0.78) | 0.695 *** | (89.62) | 0.062 *** | (3.29) | 0.693 *** | (89.01) |
| ALWt−1 | 0.032 ** | (2.45) | −0.055 *** | (−15.70) | 0.056 *** | (6.59) | −0.056 *** | (−15.79) |
| CONt | 0.005 | (0.92) | 0.003 * | (1.81) | 0.002 * | (0.6) | 0.003 * | (1.88) |
| COMt | −0.001 | (−0.84) | 0.002 *** | (5.70) | −0.001 *** | (−0.55) | 0.002 *** | (5.67) |
| REALt | 0.000 | (−0.17) | 0.001 *** | (4.27) | 0.000 *** | (0.24) | 0.001 *** | (4.24) |
| TIER1t−1 | −0.003 | (−1.09) | 0.003 *** | (3.32) | −0.007 *** | (−3.65) | 0.003 *** | (3.56) |
| EBTPt | 0.033 * | (1.94) | 0.065 *** | (14.06) | −0.003 *** | (−0.25) | 0.066 *** | (14.45) |
| LOSSt | 0.000 | (0.44) | 0.003 *** | (46.34) | 0.000 *** | (3.18) | 0.003 *** | (45.83) |
| LOGMVt | 0.001 *** | (4.69) | −0.000 *** | (−3.71) | 0.002 *** | (11.56) | −0.000 *** | (−4.11) |
| MTBt | −0.001 *** | (−5.98) | −0.000 *** | (−3.58) | 0.000 *** | (−5.08) | −0.000 *** | (−3.89) |
| STD_Et | 0.016 | (0.62) | 0.017 ** | (2.47) | 0.057 ** | (3.43) | 0.015 ** | (2.16) |
| LLPt−1 | −0.032 | (−1.22) | 0.087 *** | (12.53) | −0.035 *** | (−2.04) | 0.088 *** | (12.62) |
| CPIt | −0.23 *** | (−30.29) | 0.006 | (1.63) | −0.114 | (−23.16) | 0.003 | (0.97) |
| HOUt | 0.046 *** | (9.01) | −0.001 | (−0.35) | 0.071 | (21.27) | −0.002 | (−1.24) |
| INCOMEt | −0.024 *** | (−19.29) | 0.001 ** | (2.47) | −0.009 * | (−11.68) | 0.001 * | (1.83) |
| UNEMPLOYt | −0.003 *** | (−6.28) | −0.000 | (−0.42) | −0.001 | (−4.32) | −0.000 | (−0.80) |
| BUSCYCLEt | 0.011 *** | (35.95) | −0.000 * | (−1.87) | 0.019 ** | (95.61) | −0.001 *** | (−2.58) |
| GDPGROWt | −0.009 ** | (−2.57) | −0.001 | (−0.77) | 0.010 | (4.13) | −0.001 | (−1.52) |
| DEFAULTt | −1.265 *** | (−38.2) | 0.034 ** | (2.03) | −0.803 * | (−37.51) | 0.025 * | (1.74) |
| Lagged Macro Controls | Yes | Yes | Yes | Yes | ||||
| Bank FE | Yes | Yes | Yes | Yes | ||||
| Year FE | Yes | Yes | Yes | Yes | ||||
| Cragg–Donald F-stat | 520.43 | 786.93 | ||||||
| R-squared | 0.06 | 0.77 | 0.06 | 0.77 | ||||
| N | 13,122 | 13,122 | 13,122 | 13,122 | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Dependent Var: | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | ΔσROAt | ΔZScoret |
| Proxy for DLLP: | n/a | HIGHDLLP | POSDLLP | DLLP | DLLP | DLLP |
| BMt−1 | 0.454 *** | 0.524 *** | 0.531 *** | 0.460 *** | 0.008 | 0.004 |
| (13.08) | (12.32) | (12.63) | (13.17) | (1.45) | (0.22) | |
| DLLP_PROXY*BMt−1 | −0.132 *** | −0.149 *** | −70.43 *** | −16.141 *** | −28.248 ** | |
| (−2.97) | (−3.39) | (−3.17) | (−3.67) | (−2.52) | ||
| DLLP_PROXY | −0.001 | −0.001 * | −0.317 | −0.225 *** | −0.465 *** | |
| (−1.38) | (−1.76) | (−0.99) | (−3.19) | (−3.31) | ||
| CONt−1 | −0.007 | −0.007 | −0.007 | −0.006 | −0.010 | 0.009 |
| (−0.42) | (−0.39) | (−0.42) | (−0.36) | (−1.26) | (0.48) | |
| COMt−1 | −0.007 | −0.008 | −0.008 | −0.007 | 0.013 * | 0.017 * |
| (−0.79) | (−0.84) | (−0.86) | (−0.73) | (1.94) | (1.65) | |
| REALt−1 | 0.007 | 0.007 | 0.007 | 0.008 | 0.008 * | 0.003 |
| (1.00) | (0.96) | (0.93) | (1.06) | (1.90) | (0.41) | |
| ROAt−1 | 0.363 *** | 0.367 *** | 0.368 *** | 0.387 *** | 0.167 *** | 0.264 *** |
| (3.95) | (3.98) | (3.98) | (4.03) | (6.29) | (5.18) | |
| DEPOSITt−1 | 0.002 | 0.002 | 0.002 | 0.002 | −0.002 ** | −0.010 *** |
| (0.56) | (0.54) | (0.54) | (0.52) | (−2.47) | (−3.61) | |
| SIZEt−1 | −0.002 | −0.002 | −0.002 | −0.002 | 0.000 | 0.003 |
| (−1.27) | (−1.34) | (−1.34) | (−1.31) | (0.31) | (1.37) | |
| CH_LOANt | 0.010 * | 0.010 * | 0.010 * | 0.009 | −0.003 * | −0.007 ** |
| (1.69) | (1.68) | (1.68) | (1.63) | (−1.94) | (−2.30) | |
| EBTPt | 0.658 *** | 0.650 *** | 0.647 *** | 0.627 *** | 0.314 *** | 0.684 *** |
| (4.36) | (4.33) | (4.31) | (4.18) | (8.33) | (7.99) | |
| TIER1t−1 | −0.066 *** | −0.065 *** | −0.065 *** | −0.063 *** | −0.026 *** | −0.055 ** |
| (−3.03) | (−3.00) | (−2.99) | (−2.88) | (−3.20) | (−2.45) | |
| BETAt | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.000 |
| (0.24) | (0.24) | (0.25) | (0.34) | (0.05) | (−0.62) | |
| ILLIQUIDITYt | −0.005 *** | −0.005 *** | −0.005 *** | −0.005 *** | −0.000 ** | −0.000 |
| (−10.61) | (−10.60) | (−10.61) | (−10.64) | (−2.19) | (−0.02) | |
| Bank FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Year FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Clustered SE | Bank | Bank | Bank | Bank | Bank | Bank |
| R-squared | 0.31 | 0.31 | 0.31 | 0.31 | 0.28 | 0.35 |
| N | 11,672.00 | 11,672.00 | 11,672.00 | 11,663.00 | 12,575.00 | 7576.00 |
| (1) | (2) | (3) | (4) | (5) | (6) | |||||||
| Dependent Variable: | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | CH_VaRt+4/t | ||||||
| Proxy for MPt−1 | BMt−1 | EMPt−1 | TRRt−1 | BMt−1 | EMPt−1 | TRRt−1 | ||||||
| Sub-Sample Condition | TIMELYt+11/t = 1 | TIMELYt+11/t = 1 | TIMELYt+11/t = 1 | TIMELYt+11/t = 1 | TIMELYt+11/t = 1 | TIMELYt+11/t = 1 | ||||||
| EMPt−1 | 0.632 *** | (9.96) | 0.036 *** | (13.83) | −0.111 *** | (−4.50) | 0.611 *** | (9.30) | 0.036 *** | (12.63) | −0.121 *** | (−5.06) |
| DLLPt | 0.008 | (1.04) | −0.008 | (−1.26) | 0.012 | (1.29) | 0.007 | (1.03) | −0.003 | (−0.59) | 0.016 | (1.62) |
| EMPt−1*DLLPt | 1.056 | (1.55) | 0.019 | (1.12) | −0.133 | (−0.54) | 0.691 | (1.52) | 0.008 | (0.59) | −0.159 | (−0.63) |
| TIMELYt+23/t | −0.001 | (−1.31) | −0.002 * | (−1.78) | 0.003 *** | (2.99) | ||||||
| TIMELYt+23/t*EMPt−1 | −0.220 *** | (−3.41) | 0.002 | (1.11) | −0.305 *** | (−8.88) | ||||||
| TIMELYt+23/t*DLLPt | −0.014 | (−1.44) | 0.005 | (0.60) | −0.001 | (−0.09) | ||||||
| TIMELYt+23/t*EMPt−1*DLLPt | −2.552 *** | (−3.02) | −0.046 ** | (−2.22) | −0.959 ** | (−2.33) | ||||||
| TIMELYt+35/t | −0.003 * | (−1.81) | −0.003 ** | (−2.06) | 0.002 | (1.60) | ||||||
| TIMELYt+35/t*EMPt−1 | −0.187 *** | (−2.85) | 0.002 | (0.84) | −0.294 *** | (−8.18) | ||||||
| TIMELYt+35/t*DLLPt | −0.015 | (−1.59) | −0.002 | (−0.26) | −0.007 | (−0.62) | ||||||
| TIMELYt+35/t*EMPt−1*DLLPt | −2.255 *** | (−3.27) | −0.034 * | (−1.77) | −0.907 ** | (−2.23) | ||||||
| CONt−1 | 0.009 | (0.30) | −0.007 | (−0.29) | 0.009 | (0.27) | 0.002 | (0.07) | −0.015 | (−0.62) | 0.010 | (0.29) |
| COMt−1 | −0.006 | (−0.37) | −0.004 | (−0.27) | −0.004 | (−0.31) | −0.006 | (−0.37) | −0.005 | (−0.31) | −0.003 | (−0.18) |
| REALt−1 | 0.005 | (0.41) | 0.001 | (0.07) | 0.004 | (0.40) | 0.004 | (0.29) | −0.001 | (−0.05) | 0.007 | (0.58) |
| ROAt−1 | 0.401 *** | (3.54) | 0.408 *** | (3.83) | 0.332 *** | (2.90) | 0.401 *** | (3.54) | 0.413 *** | (3.89) | 0.327 *** | (2.86) |
| DEPOSITt−1 | 0.001 | (0.14) | −0.000 | (−0.02) | −0.000 | (−0.05) | 0.001 | (0.17) | −0.000 | (−0.03) | −0.001 | (−0.14) |
| SIZEt−1 | −0.002 | (−0.97) | −0.003 | (−1.19) | −0.000 | (−0.09) | −0.003 | (−1.07) | −0.003 | (−1.34) | 0.000 | (0.00) |
| CH_LOANt | 0.008 | (1.01) | 0.008 | (1.04) | 0.009 | (1.14) | 0.008 | (1.05) | 0.008 | (1.00) | 0.009 | (1.10) |
| EBTPt | 0.846 *** | (3.31) | 0.937 *** | (3.80) | 0.737 *** | (3.18) | 0.839 *** | (3.29) | 0.935 *** | (3.80) | 0.733 *** | (3.17) |
| TIER1t−1 | −0.111 *** | (−3.44) | −0.118 *** | (−3.81) | −0.111 *** | (−3.51) | −0.106 *** | (−3.30) | −0.115 *** | (−3.74) | −0.110 *** | (−3.51) |
| BETAt | 0.003 *** | (2.88) | 0.002 ** | (2.27) | 0.003 *** | (3.20) | 0.003 *** | (2.99) | 0.002 ** | (2.33) | 0.003 *** | (3.26) |
| ILLIQUIDITY | −0.004 *** | (−5.27) | −0.005 *** | (−5.68) | −0.003 *** | (−4.52) | −0.004 *** | (−5.25) | −0.005 *** | (−5.66) | −0.003 *** | (−4.53) |
| MTBt | 0.001 | (0.74) | 0.001 | (0.78) | −0.000 | (−0.03) | 0.001 | (0.73) | 0.001 | (0.73) | 0.000 | (0.04) |
| Constant | 0.015 | (0.65) | 0.009 | (0.40) | 0.003 | (0.15) | 0.018 | (0.78) | 0.013 | (0.59) | 0.001 | (0.04) |
| Bank FE | Yes | Yes | Yes | Yes | Yes | Yes | ||||||
| Year FE | Yes | Yes | Yes | Yes | Yes | Yes | ||||||
| Clustered SE | Bank | Bank | Bank | Bank | Bank | Bank | ||||||
| R-squared | 0.39 | 0.44 | 0.42 | 0.39 | 0.44 | 0.42 | ||||||
| N | 5085 | 5085 | 5085 | 5085 | 5085 | 5085 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| States NOT highly correlated with U.S. economy | States highly correlated with U.S. economy | Crisis period | Non-crisis period | Periods with more bank failures | Periods with less bank failures | |
| BMt−1 | 0.0150 *** | 0.0126 *** | 0.0415 *** | 0.0121 *** | 0.0680 ** | 0.0104 *** |
| (3.55) | (3.87) | (4.46) | (3.93) | (2.81) | (4.46) | |
| Firm Level Control | Yes | Yes | Yes | Yes | Yes | Yes |
| State Level Control | Yes | Yes | Yes | Yes | Yes | Yes |
| National Level Control | Yes | Yes | Yes | Yes | Yes | Yes |
| Bank FE | Yes | Yes | Yes | Yes | Yes | Yes |
| State FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Year FE | No | No | No | No | No | No |
| Clustered Standard Error | Bank and Quarter | Bank and Quarter | Bank and Quarter | Bank and Quarter | Bank and Quarter | Bank and Quarter |
| R-squared | 0.69 | 0.67 | 0.74 | 0.68 | 0.68 | 0.52 |
| N | 9150 | 5331 | 2084 | 12,372 | 3444 | 11,030 |
| Panel A: Nonparametric and nonlinear tests | |||||||
| (1) Nearest-Neighbor Matching (N = 4) | (2) Epanechnikov Kernel | (3) Heckman Treatment Effect Model | |||||
| EMPt−1 | 0.0151 *** (3.39) | 0.0198 *** (4.00) | 0.0308 *** (7.68) | ||||
| Bank FE | No | No | No | ||||
| State FE | No | No | No | ||||
| Year FE | No | No | No | ||||
| Rho | −0.0332 | ||||||
| Standard Error | AI (2006) | Bootstrapped | Bootstrapped | ||||
| R-squared | 0.2729 | 0.719 | 0.719 | ||||
| N | 14,608 | 14,608 | 14,608 | ||||
| Panel B: Sample composite tests and heterogeneous effects | |||||||
| (1) | (2) | (3) | (4) | ||||
| Weighted by 1/Frequency of Year | Weighted by 1/Frequency of Bank | Allow macroeconomic variables to have heterogeneous effects | Allow firm characters to have heterogeneous effects | ||||
| BMt−1 | 0.0137 *** (3.21) | 0.0226 *** (4.20) | 0.0313 *** (3.87) | 0.0346 *** (2.90) | |||
| Bank FE | Yes | Yes | Yes | Yes | |||
| State FE | Yes | Yes | Yes | Yes | |||
| Year FE | Yes | Yes | Yes | Yes | |||
| Standard Error | Bank and Quarter | Bank and Quarter | Bank and Quarter | Bank and Quarter | |||
| R-squared | 0.719 | 0.719 | 0.719 | 0.719 | |||
| N | 14,623 | 14,623 | 14,623 | 14,623 | |||
| Panel A: Results of baseline regression using exogenous variations in monetary policy | ||||||||
| (1) | (2) | |||||||
| LLPt | LLPt | |||||||
| TRRt−1 | 0.0042 *** | (3.02) | ||||||
| RRSt−1 | 0.0003 *** | (4.95) | ||||||
| Firm and Macro controls | Yes | Yes | ||||||
| Bank, State, and Year FE | Yes | Yes | ||||||
| Clustered Standard Error | Firm and Quarter | Firm and Quarter | ||||||
| R-squared | 0.81 | 0.65 | ||||||
| N | 14,623 | 11,071 | ||||||
| Panel B: Timing of response to monetary policy change | ||||||||
| (1) Placebo Test | (2) Placebo Test | (3) Cumulative effect | (4) Cumulative effect | |||||
| TRRt+1 | −0.0017 | |||||||
| (−1.08) | ||||||||
| RRSt+1 | 0.0001 * | |||||||
| (1.74) | ||||||||
| 0.0193 *** (16.74) | ||||||||
| 0.0189 *** (15.16) | ||||||||
| Lagged and Current Macroeconomic | Yes | Yes | Yes | Yes | ||||
| Bank, State, and year FE | Yes | No | Yes | Yes | ||||
| Clustered Standard Error | Bank and Quarter | Bank and Quarter | Bank and Quarter | Bank and Quarter | ||||
| R-squared | 0.81 | 0.64 | 0.81 | 0.81 | ||||
| N | 14,623 | 11,071 | 14,623 | 14,623 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Jia, X.; Jin, J.Y.; Kanagaretnam, K.; Lobo, G.J. Expansionary Monetary Policy and Bank Loan Loss Provisioning. J. Risk Financial Manag. 2024, 17, 8. https://doi.org/10.3390/jrfm17010008
Guo M, Jia X, Jin JY, Kanagaretnam K, Lobo GJ. Expansionary Monetary Policy and Bank Loan Loss Provisioning. Journal of Risk and Financial Management. 2024; 17(1):8. https://doi.org/10.3390/jrfm17010008
Chicago/Turabian StyleGuo, Mengyang, Xiaoran Jia, Justin Yiqiang Jin, Kiridaran Kanagaretnam, and Gerald J. Lobo. 2024. "Expansionary Monetary Policy and Bank Loan Loss Provisioning" Journal of Risk and Financial Management 17, no. 1: 8. https://doi.org/10.3390/jrfm17010008
APA StyleGuo, M., Jia, X., Jin, J. Y., Kanagaretnam, K., & Lobo, G. J. (2024). Expansionary Monetary Policy and Bank Loan Loss Provisioning. Journal of Risk and Financial Management, 17(1), 8. https://doi.org/10.3390/jrfm17010008







