Large Drawdowns and Long-Term Asset Management
Abstract
1. Introduction
2. Materials and Methods
2.1. Definitions and Measurement
2.2. Empirical Measures of Large Drawdowns
2.3. Investor’s Problem
2.4. Methodology
2.4.1. Multivariate MS-GARCH Model
2.4.2. Minimizing the Expected Large Drawdown of a Portfolio
- 1.
- We estimate the parameters of the MS-GARCH model using daily log-returns available in quarters . The last day of the estimation period is denoted by . The next quarter, , contains days .
- 2.
- For a given estimated model, we simulate Q samples of length H of daily log-returns for the n assets: , . As the probability of being in state k at the end of period t is given by predicted probabilities , we simulate a fraction of the draws using as an initial condition for the covariance matrix in period . From the simulated daily log-returns, we compute cumulative log-returns in quarter as: for .
- 3.
- For a portfolio weight vector , we obtain daily log-values of the portfolio: , where .
- 4.
- We predict the risk measures with simulated daily log-prices of the portfolio. For each simulation q, we compute the drawdown measures using the definitions given in Section 2.2, yielding . The predictions of the drawdown measures are then given by the average over the Q simulations: , except for CED. To generate CED predictions, we rely on the MDD values obtained over all simulations and take the average of the worst MDD values as in Equation (4).
- 5.
3. Results
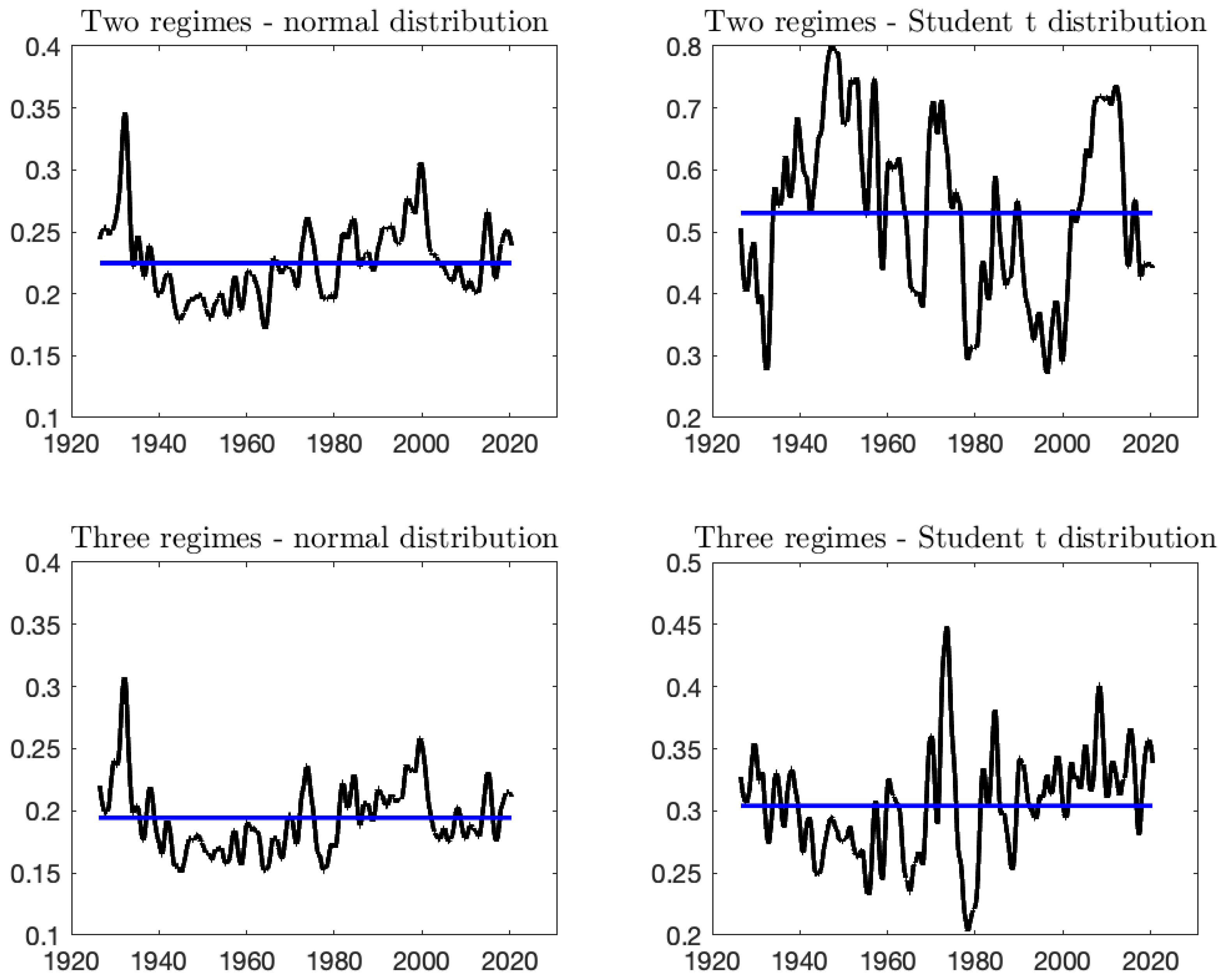
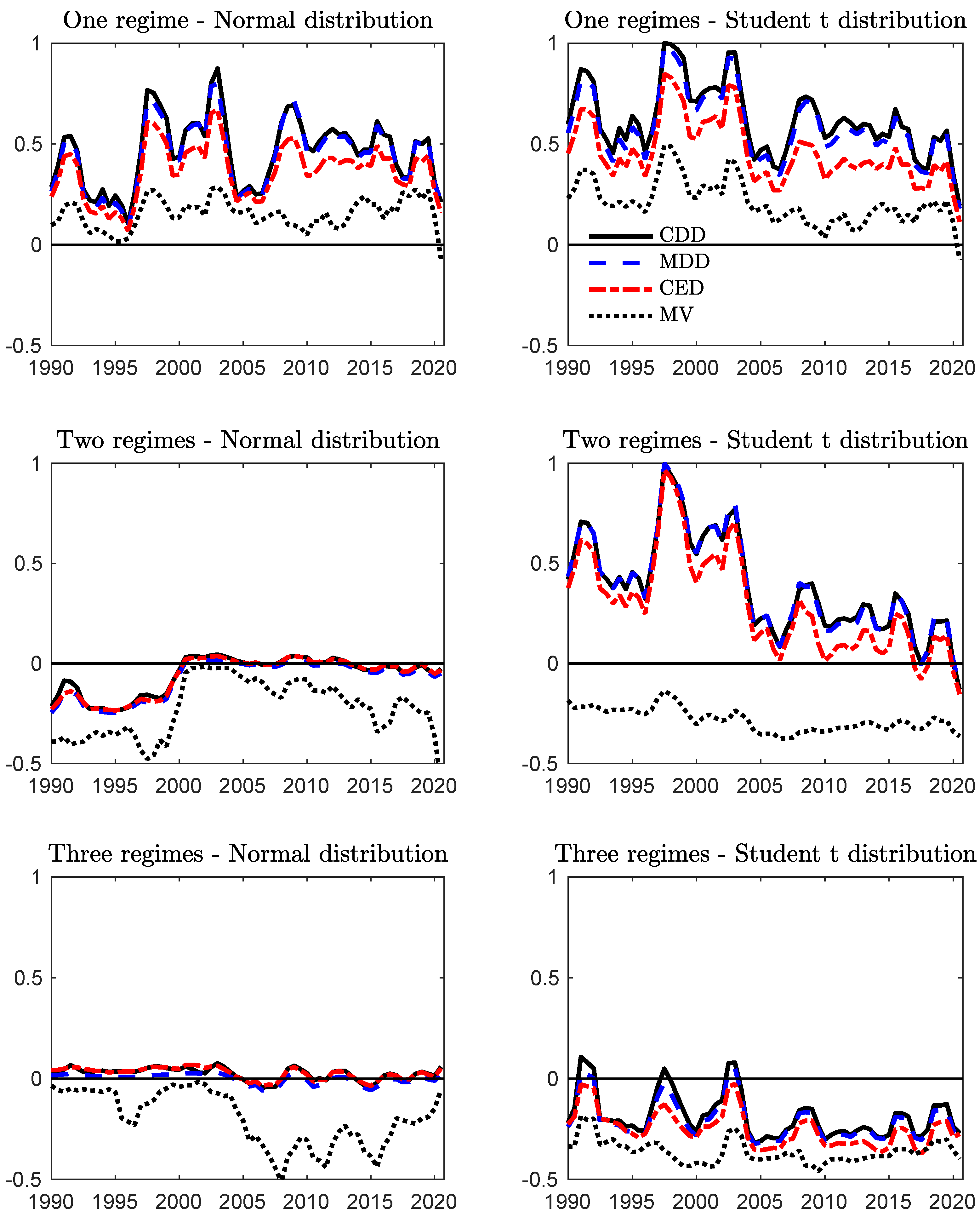
3.1. Data
3.2. Full-Sample Model Estimation
3.3. Rolling-Window Model Estimation and Adequacy Tests
3.4. Out-of-Sample Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Evolution of Model Parameters
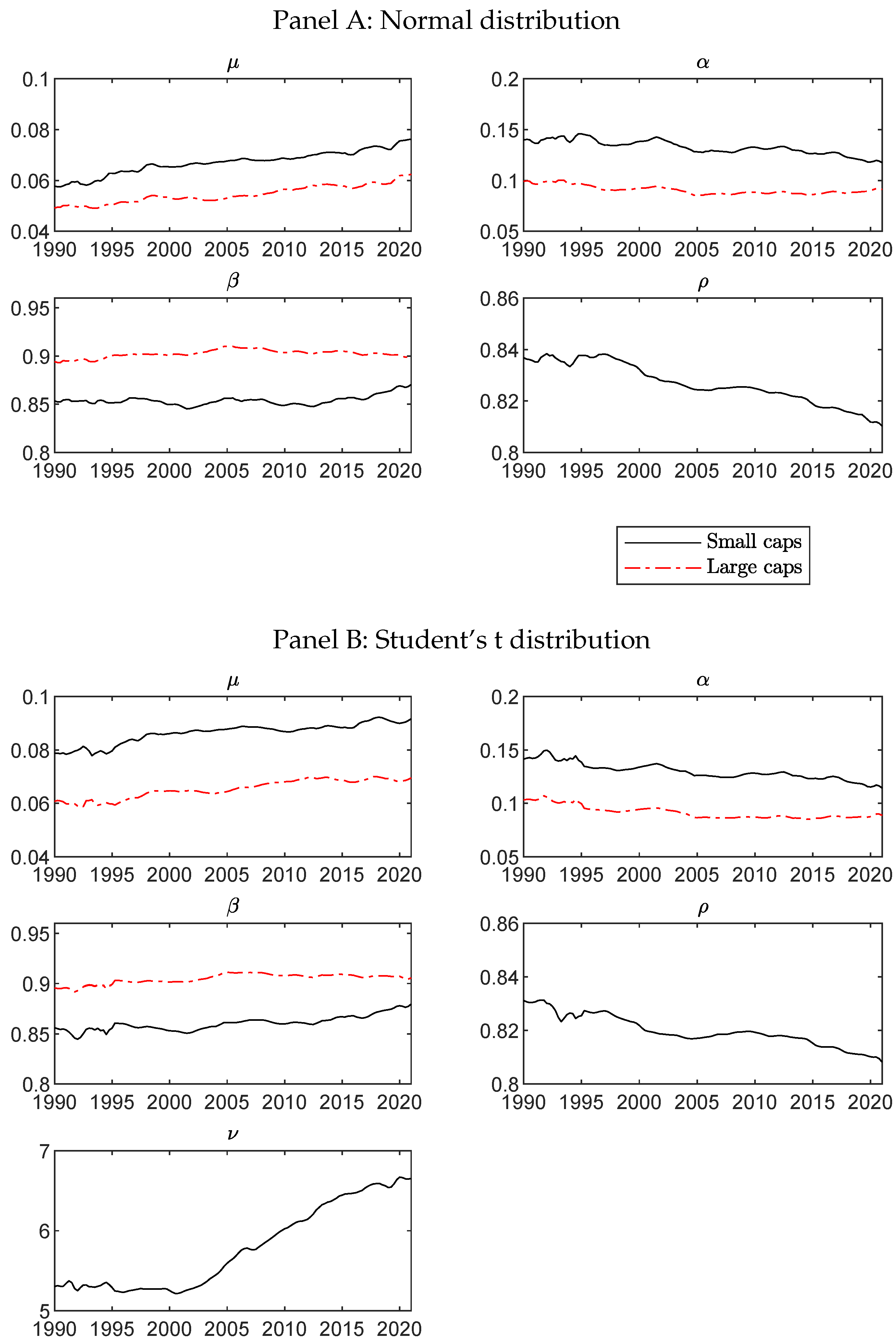
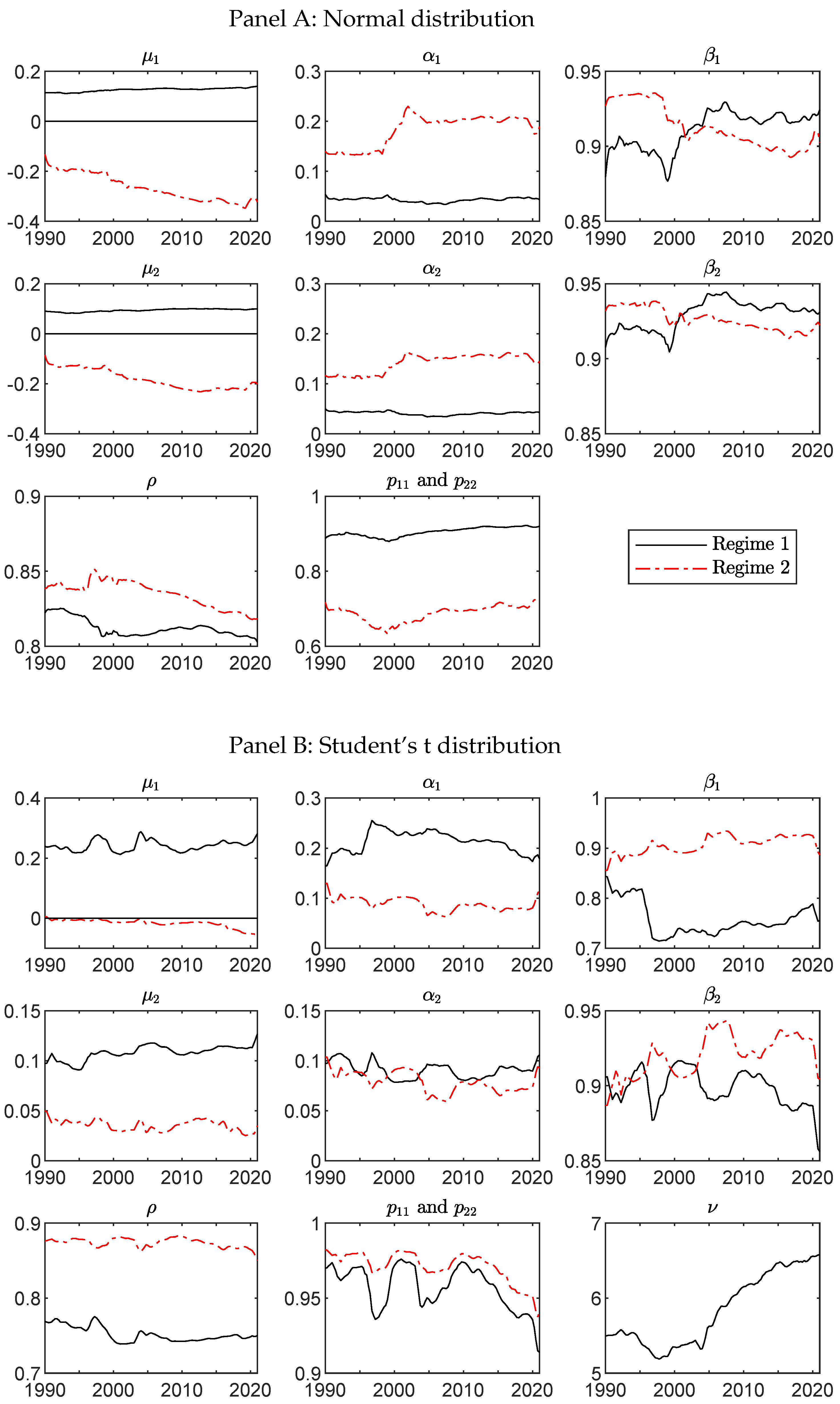
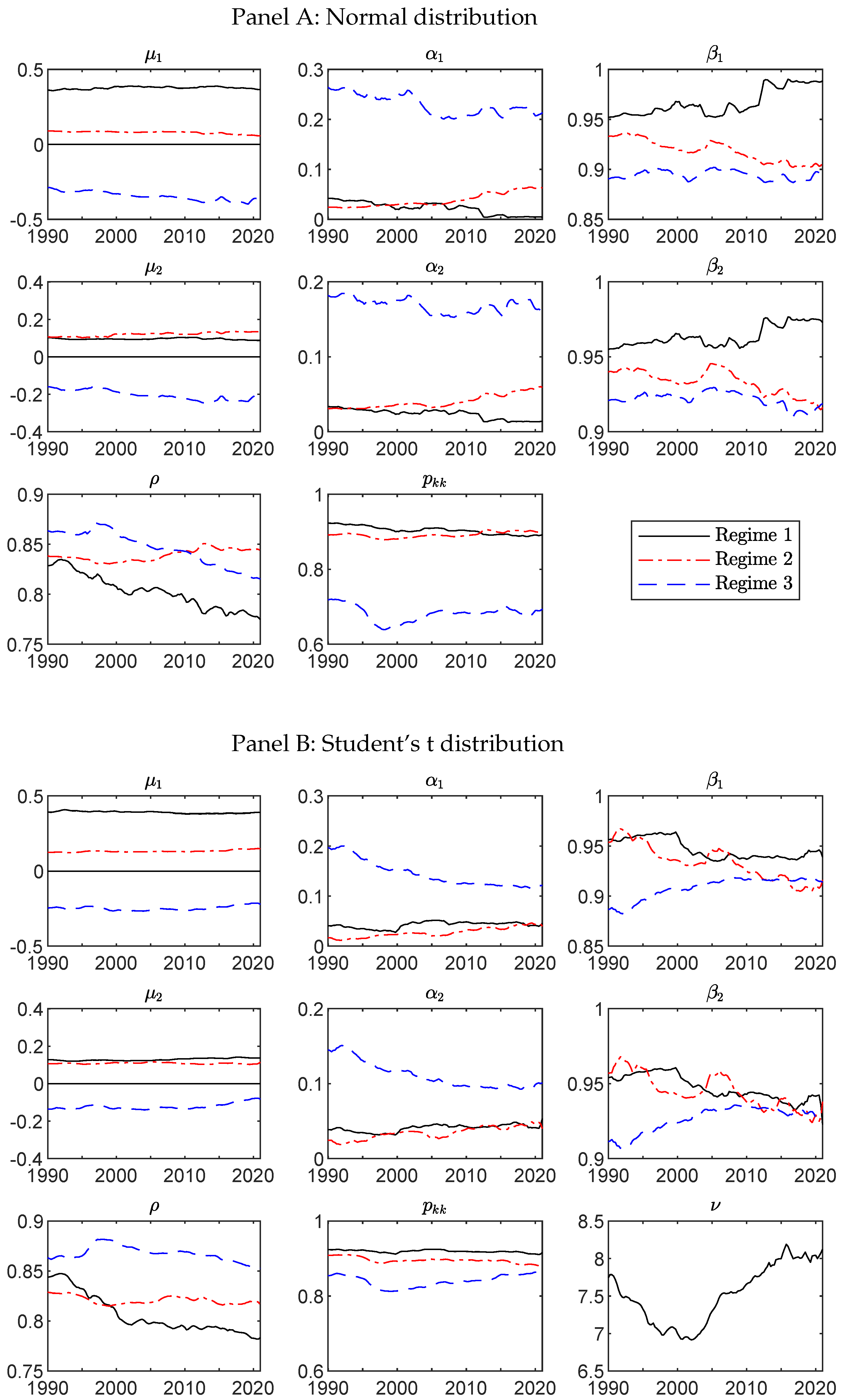
Appendix B. Adequacy Tests
Appendix B.1. Logic of the Adequacy Test
Appendix B.2. Adequacy Test Statistics
Appendix B.3. Adequacy Test Significance
- Using the model under , we simulate Q samples of log-returns for all quarters of the backtesting period: , and . The simulations are generated as in Section 2.4.2.
- We calculate the vectors of drawdowns for each simulation, , . Then, we compute Z statistic for each simulation, , . They represent the distribution of the Z statistic under the null hypothesis.
- We compute the realized Z statistic on the drawdowns .
- We estimate the significance by comparing the realized Z statistic to the distribution of the simulated Z statistics and compute the p-value of the bilateral test as: p-val .
Appendix B.4. Adequacy Test Results
| 1-Regime | 1-Regime | 2-Regime | 2-Regime | 3-Regime | 3-Regime | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Student t | Normal | Student t | Normal | Student t | |||||||
| Small | Large | Small | Large | Small | Large | Small | Large | Small | Large | Small | Large | |
| Panel A: CDD | ||||||||||||
| 1 quarter | ||||||||||||
| Nb exc. | 2597 | 1781 | 2961 | 1964 | 1490 | 1015 | 2666 | 1961 | 1512 | 1082 | 1800 | 1412 |
| Stat. | 1.693 | 0.653 | 2.310 | 0.876 | 0.052 | −0.307 | 1.693 | 0.829 | 0.039 | −0.282 | 0.308 | 0.055 |
| p-val. | (0.000) | (0.000) | (0.000) | (0.000) | (0.666) | (0.007) | (0.000) | (0.000) | (0.762) | (0.018) | (0.028) | (0.667) |
| 2 quarters | ||||||||||||
| Nb exc. | 2930 | 1938 | 3443 | 2221 | 1168 | 697 | 2967 | 2173 | 1278 | 784 | 1442 | 1124 |
| Stat. | 2.165 | 0.687 | 3.134 | 0.987 | −0.134 | −0.545 | 2.167 | 0.891 | −0.063 | −0.484 | 0.037 | -0.266 |
| p-val. | (0.000) | (0.000) | (0.000) | (0.000) | (0.210) | (0.000) | (0.000) | (0.000) | (0.367) | (0.001) | (0.396) | (0.033) |
| 4 quarters | ||||||||||||
| Nb exc. | 3163 | 1728 | 3863 | 2117 | 1037 | 510 | 3243 | 2037 | 1244 | 613 | 1193 | 683 |
| Stat. | 2.061 | 0.449 | 3.285 | 0.794 | −0.328 | −0.649 | 2.237 | 0.662 | −0.186 | −0.567 | −0.238 | −0.545 |
| p-val. | (0.000) | (0.015) | (0.000) | (0.001) | (0.066) | (0.000) | (0.000) | (0.003) | (0.218) | (0.002) | (0.138) | (0.002) |
| Panel B: MDD | ||||||||||||
| 1 quarter | ||||||||||||
| Stat. | 0.622 | 0.266 | 0.885 | 0.377 | −0.047 | −0.202 | 0.739 | 0.363 | −0.033 | −0.192 | 0.078 | −0.009 |
| p-val. | (0.000) | (0.000) | (0.000) | (0.000) | (0.327) | (0.000) | (0.000) | (0.000) | (0.538) | (0.000) | (0.176) | (0.852) |
| 2 quarters | ||||||||||||
| Stat. | 0.802 | 0.284 | 1.168 | 0.423 | −0.057 | −0.285 | 0.919 | 0.383 | −0.010 | −0.237 | −0.033 | −0.188 |
| p-val. | (0.000) | (0.000) | (0.000) | (0.000) | (0.305) | (0.000) | (0.000) | (0.000) | (0.862) | (0.000) | (0.595) | (0.002) |
| 4 quarters | ||||||||||||
| Stat. | 0.873 | 0.290 | 1.286 | 0.435 | −0.045 | −0.299 | 1.017 | 0.363 | 0.021 | −0.232 | -0.059 | −0.269 |
| p-val. | (0.000) | (0.000) | (0.000) | (0.000) | (0.503) | (0.000) | (0.000) | (0.000) | (0.773) | (0.001) | (0.404) | (0.000) |
| 1 | Disasters may include severe macroeconomic and financial crises, pandemics, wars, or extreme weather and climate conditions. |
| 2 | We use a large sample to estimate model’s parameters accurately and perform the out-of-sample analysis over a long period of time. Such a long sample would not be necessary in practice to estimate MS models and to predict subsequent large drawdowns. |
| 3 | For simplicity, we assume here a fixed number of days H per period. In the empirical analysis, we will use the actual number of days per period. |
| 4 | A drawdown may span over a short period (as for the COVID-19 crisis, with a drawdown in 24 days) or over a window of more than a year (as for the subprime crisis, with a drawdown in 355 days). |
| 5 | We note that the knowledge of the cumulated log-return at the end of the period is not sufficient to infer the large drawdown measures, as peaks and troughs are likely to occur on random days within the period. |
| 6 | The model is estimated over a long sample of daily returns, , where D is the number of days in the full sample. In contrast, large drawdown measures are computed over relatively short subsamples (e.g., one quarter or one year) with H days, which we have denoted by , in Section 2. Since we use nonoverlapping subsamples, both notations define the same sample: , where . |
| 7 | Assuming an autoregressive process would have a very limited effect for a long-term investment objective because the autocorrelation of daily returns is low. The first-order autocorrelation of the market return is equal to over the 1926–2020 period and equal to over the 1990–2020 period. |
| 8 | |
| 9 | In Section 3.2, we use simulations to demonstrate that a three-regime model with a (symmetric) Student’s t innovations can generate some asymmetry in large drawdowns, as observed in the data. |
| 10 | We note that stationarity conditions apply to the complete distribution and not regime by regime. As a consequence, usual stationarity conditions in a GARCH model might not be satisfied for some regimes. In particular, global stationarity can be obtained even when for some asset i and regime k. |
| 11 | We have also analyzed the cases of firms in the bottom and top and market capitalization, with limited impact on the main results. The data are available on the website of Kenneth French at (https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html, accessed on 2 December 2024). Other long-sample portfolios, such as value versus growth or losers versus winners portfolios, are also available. |
| 12 | Our sample ends in December 2020, slightly after the end of the COVID-19 market crash. Therefore, the impact of this episode on the financial performance of our investment strategies is reflected in the out-of-sample analysis discussed in Section 3.4. |
| 13 | Stationary (or steady-state) probabilities are defined as: . In the two-regime case, this relation boils down to . |
| 14 | This conclusion appears very robust and not driven by the choice of starting values. We experimented with several sets of starting parameter values and obtained the same parameter estimates for both models. A similar phenomenon—where the probability of remaining in the bear state is lower with normal innovations than with Student’s t innovations—was reported by Haas and Paolella (2012) and Haas and Liu (2018). |
| 15 | The finite-sample distribution of the LR statistic is obtained by simulating many samples of returns, using the estimated parameters of the -regime model and estimating, for each simulated samples, the -regime model and the n-regime model, from which we compute the LR test statistics. The finite-sample distribution of the LR test statistic is computed from the empirical distribution of the LR statistics based on the simulated samples. |
| 16 | Guidolin and Timmermann (2007) estimate MS model for U.S. small caps, large caps, and long-term bonds. In a specification with within-regime constant expected returns, volatilities, and correlations, they find that four regimes are necessary to match the data. In their model, the intermediate regime is further decomposed into a slow growth regime and a recovery regime. |
| 17 | The largest spike in the filtered probability of being in the bear state is associated with the 1973 oil crisis. The drawdown actually started in January 1973, accelerated in October with the surge in oil price and lasted until December 1974, with a drawdown of 48% over this period. A major feature of this 1973–1974 drawdown is its duration. From peak to through, the downturn lasted for almost 2 years, while the subprime crisis was associated with a 60% drawdown in slightly more than 1 year. |
| 18 | As in the models with normal innovations, one of the peaks in the filtered probability, in mid-1984, could not be associated with any particular stock market event. |
| 19 | Although we developed a similar test for CED, the number of observations was insufficient for robust conclusions. |
| 20 | We note that, even with our preferred model, i.e., the three-regime model with Student’s t distribution, the relationship between the probability of being in the bear regime (Figure 2) and the optimal small-cap weight (Figure 3) is far from perfect. The reason is that the probability of being in the bear regime predicts the state for the next day, whereas the portfolio is allocated for a long horizon (from 1 quarter to 1 year) and the regime is likely to change over this period. |
| 21 | This result of a lower small-cap weights for the MV criterion does not seem to be driven by a theoretical relation between the variance and large drawdown measures but more likely by the properties of our data. |
| 22 | |
| 23 | Note that Acerbi and Szekely (2014) assume a one-sided test in line with Basel VaR tests, which are designed to detect excesses of VaR exceptions. In our case, we assume a two-sided test, as we test whether a given model correctly predicts large drawdown measures. |
References
- Abramson, Ari, and Israel Cohen. 2007. On the stationarity of Markov-switching GARCH processes. Econometric Theory 23: 485–500. [Google Scholar] [CrossRef]
- Acerbi, Carlo, and Balazs Szekely. 2014. Backtesting Expected Shortfall. Risk 27: 76–81. [Google Scholar]
- Acerbi, Carlo, and Balazs Szekely. 2017. General Properties of Backtestable Statistics. Working Paper. New York: MSCI Inc. Available online: https://ssrn.com/abstract=2905109 (accessed on 25 February 2023).
- Ang, Andrew, and Geert Bekaert. 2002. International asset allocation with regime shifts. Review of Financial Studies 15: 1137–87. [Google Scholar] [CrossRef]
- Ang, Andrew, and Joseph Chen. 2002. Asymmetric correlations of equity portfolios. Journal of Financial Economics 63: 443–94. [Google Scholar] [CrossRef]
- Barnett, Michael, William Brock, and Lars Peter Hansen. 2020. Pricing uncertainty induced by climate change. Review of Financial Studies 33: 1024–66. [Google Scholar] [CrossRef]
- Chekhlov, Alexei, Stanislav Uryasev, and Michael Zabaranki. 2003. Portfolio optimization with drawdown constraints. In Asset and Liability Management Tools. Edited by Berndt Scherer. London: Risk Books, pp. 263–78. [Google Scholar]
- Chekhlov, Alexei, Stanislav Uryasev, and Michael Zabaranki. 2005. Drawdown measure in portfolio optimization. International Journal of Theoretical and Applied Finance 8: 13–58. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Garcia, Rene. 1998. Asymptotic null distribution of the likelihood ratio test in Markov switching models. International Economic Review 39: 763–88. [Google Scholar] [CrossRef]
- Goldberg, Lisa R., and Ola Mahmoud. 2015. On a Convex Measure of Drawdown Risk. Working Paper. Berkeley: Center for Risk Management Research. Available online: http://arxiv.org/abs/1404.7493 (accessed on 25 March 2021).
- Goldberg, Lisa R., and Ola Mahmoud. 2016. Drawdown: From practice to theory and back again. Mathematics and Financial Economics 11: 275–97. [Google Scholar] [CrossRef]
- Gray, Stephen F. 1996. Modeling the conditional distribution of interest rates as a regime-switching process. Journal of Financial Economics 42: 27–62. [Google Scholar] [CrossRef]
- Grossman, Sanford, and Zhongquan Zhou. 1993. Optimal investment strategies for controlling draw-downs. Mathematical Finance 3: 241–276. [Google Scholar] [CrossRef]
- Guidolin, Massimo, and Allan Timmermann. 2004. Value at Risk and Expected Shortfall Under Regime Switching. Working Paper. San Diego: University of California. Available online: https://ssrn.com/abstract=557091 (accessed on 1 May 2021).
- Guidolin, Massimo, and Allan Timmermann. 2007. Asset allocation under multivariate regime switching. Journal of Economic Dynamics and Control 31: 3503–44. [Google Scholar] [CrossRef]
- Guidolin, Massimo, and Allan Timmermann. 2008. International asset allocation under regime switching, skew, and kurtosis preferences. Review of Financial Studies 21: 889–935. [Google Scholar] [CrossRef]
- Haas, Markus, and Ji-Chun Liu. 2018. A multivariate regime-switching GARCH model with an application to global stock market and real estate equity returns. Studies in Nonlinear Dynamics and Econometrics 22: 1–27. [Google Scholar] [CrossRef]
- Haas, Markus, Stefan Mittnik, and Marc S. Paolella. 2004. A new approach to Markov-switching GARCH models. Journal of Financial Econometrics 2: 493–530. [Google Scholar] [CrossRef]
- Haas, Markus, and Marc S. Paolella. 2012. Mixture and regime-switching GARCH models. In Handbook of Volatility Models and Their Applications. Edited by Luc Bauwens, Christian M. Hafner and Sebastien Laurent. Hoboken: John Wiley & Sons, pp. 71–102. [Google Scholar]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 1992. The likelihood ratio test under non-standard conditions: Testing the Markov switching model of GNP. Journal of Applied Econometrics 7: S61–S82. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 1996. Inference when a nuisance parameter is not identified under the null hypothesis. Econometrica 64: 413–30. [Google Scholar] [CrossRef]
- Hansen, Peter Reinhard. 2009. In-Sample Fit and Out-of-Sample Fit: Their Joint Distribution and Its Implications for Model Selection. Working Paper. Stanford: Department of Economics, Stanford University. [Google Scholar]
- Huang, Wei, Qianqiu Liu, S. Ghon Rhee, and Feng Wu. 2012. Extreme downside risk and expected stock returns. Journal of Banking and Finance 36: 1492–502. [Google Scholar] [CrossRef]
- Karydas, Christos, and Anastasios Xepapadeas. 2019. Climate Change Financial Risks: Pricing and Portfolio Allocation. Economics Working Paper Series, No. 19/327, 327. Zurich: Center of Economic Research (CER-ETH). [Google Scholar] [CrossRef]
- Klaassen, Franc. 2002. Improving GARCH volatility forecasts with regime-switching GARCH. Empirical Economics 27: 363–94. [Google Scholar] [CrossRef]
- Pagano, Marco, Christian Wagner, and Josef Zechner. 2023. Disaster resilience and asset prices. Journal of Financial Economics 150: 103712. [Google Scholar] [CrossRef]
- Patton, Andrew. 2004. On the out-of-sample importance of skewness and asymmetric dependence for asset allocation. Journal of Financial Econometrics 2: 130–68. [Google Scholar] [CrossRef]
- Pelletier, Denis. 2006. Regime switching for dynamic correlations. Journal of Econometrics 131: 445–73. [Google Scholar] [CrossRef]
- Peng, Cheng, Young Shin Kim, and Stefan Mittnik. 2022. Portfolio optimization on multivariate regime switching GARCH model with normal tempered stable innovation. Journal of Risk and Financial Management 15: 230. [Google Scholar] [CrossRef]
- Perez-Quiros, Gabriel, and Allan Timmermann. 2000. Firm size and cyclical variations in stock returns. Journal of Finance 55: 1229–62. [Google Scholar] [CrossRef]
- Reveiz, Alejandro, and Carlos Leon. 2008. Efficient portfolio optimization in the wealth creation and maximum drawdown space. In Interest Rate Models, Asset Allocation and Quantitative Techniques for Central Banks and Sovereign Wealth Funds. Edited by Arjan B. Berkelaar, Joachim Coche and Ken Nyholm. London: Palgrave Macmillan, pp. 134–157. [Google Scholar]
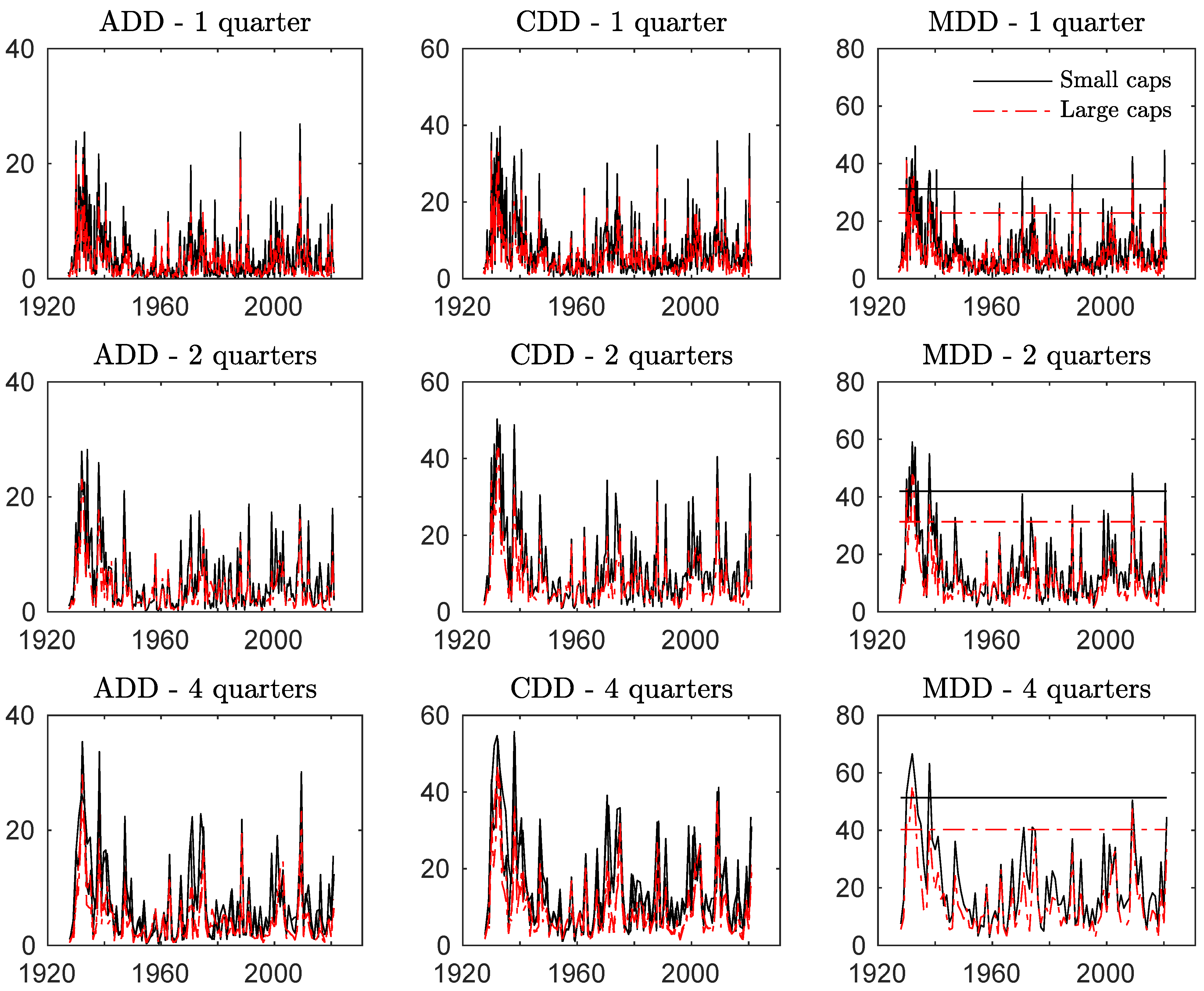
| Panel A: 1926–2020 | Panel B: 1990–2020 | |||||||
|---|---|---|---|---|---|---|---|---|
| Small Caps | Large Caps | Small Caps | Large Caps | |||||
| Daily returns | Stat. | Stat. | Stat. | Stat. | ||||
| Annualized Mean | 10.63 | 8.99 | 10.38 | 9.88 | ||||
| Annualized Std dev. | 19.50 | 17.15 | 20.36 | 18.06 | ||||
| Skewness | −0.39 | −0.48 | −0.81 | −0.40 | ||||
| Kurtosis | 23.61 | 21.83 | 13.40 | 14.03 | ||||
| Maximum | 20.42 | 14.15 | 8.02 | 11.16 | ||||
| Minimum | −16.75 | −20.94 | −14.26 | −12.57 | ||||
| VaR () | 8.53 | 6.86 | 9.01 | 7.56 | ||||
| VaR () | 3.70 | 3.11 | 3.72 | 3.26 | ||||
| VaR () | 1.82 | 1.56 | 1.97 | 1.74 | ||||
| ES () | 10.76 | 9.16 | 11.24 | 9.32 | ||||
| ES () | 5.55 | 4.64 | 5.50 | 4.76 | ||||
| ES () | 3.09 | 2.62 | 3.17 | 2.77 | ||||
| Overall MDD | 92.02 | 86.54 | 67.13 | 58.29 | ||||
| Period drawdowns | Stat. | AR(1) | Stat. | AR(1) | Stat. | AR(1) | Stat. | AR(1) |
| ADD - 1Q | 3.84 | 0.15 | 2.78 | 0.20 | 3.65 | 0.12 | 2.47 | 0.25 |
| ADD - 2Q | 5.62 | 0.29 | 3.85 | 0.42 | 5.19 | 0.00 | 3.30 | 0.35 |
| ADD - 4Q | 7.52 | 0.46 | 4.82 | 0.42 | 6.16 | −0.10 | 3.83 | 0.35 |
| CDD - 1Q | 7.75 | 0.25 | 5.76 | 0.28 | 7.28 | 0.12 | 5.27 | 0.23 |
| CDD - 2Q | 11.80 | 0.41 | 8.20 | 0.46 | 10.81 | 0.05 | 7.14 | 0.30 |
| CDD - 4Q | 16.65 | 0.45 | 10.96 | 0.43 | 13.99 | 0.01 | 8.87 | 0.33 |
| MDD - 1Q | 9.87 | 0.33 | 7.55 | 0.34 | 9.34 | 0.17 | 7.10 | 0.26 |
| MDD - 2Q | 15.05 | 0.44 | 10.93 | 0.47 | 13.99 | 0.06 | 9.93 | 0.28 |
| MDD - 4Q | 21.52 | 0.48 | 15.23 | 0.45 | 18.67 | 0.11 | 13.08 | 0.38 |
| CED - 1Q | 31.22 | 22.84 | 25.97 | 20.60 | ||||
| CED - 2Q | 41.97 | 31.35 | 35.40 | 25.41 | ||||
| CED - 4Q | 51.37 | 40.25 | 38.36 | 31.19 | ||||
| One regime—Normal distribution | One regime—Student’s t distribution | |||||||
| Small caps | Large caps | Small caps | Large caps | |||||
| param. | std err. | param. | std err. | param. | std err. | param. | std err. | |
| Expected returns | ||||||||
| () | 0.0679 | (0.006) | 0.0588 | (0.005) | 0.0865 | (0.004) | 0.0687 | (0.004) |
| Volatility dynamics | ||||||||
| () | 1.4840 | (0.201) | 0.9667 | (0.122) | 0.9902 | (0.093) | 0.7532 | (0.071) |
| 0.1298 | (0.008) | 0.0984 | (0.006) | 0.1220 | (0.007) | 0.0970 | (0.004) | |
| 0.8654 | (0.008) | 0.8962 | (0.006) | 0.8764 | (0.006) | 0.9010 | (0.004) | |
| Correlation | ||||||||
| 0.8291 | (0.003) | 0.8212 | (0.002) | |||||
| Degree of freedom | ||||||||
| – | 5.6810 | (0.154) | ||||||
| Log-lik. | −48,291.3 | −46,183.1 | ||||||
| BIC | 96.6736 | 92.4674 | ||||||
| Two regimes—Normal distribution | Two regimes—Student’s t distribution | |||||||
| Small caps | Large caps | Small caps | Large caps | |||||
| param. | std err. | param. | std err. | param. | std err. | param. | std err. | |
| Expected returns | ||||||||
| () | 0.1265 | (0.007) | 0.0965 | (0.006) | 0.2093 | (0.035) | 0.1155 | (0.012) |
| () | −0.2706 | (0.043) | −0.1771 | (0.030) | −0.0276 | (0.016) | 0.0207 | (0.010) |
| Volatility dynamics | ||||||||
| () | 0.2974 | (0.052) | 0.3132 | (0.049) | 1.2510 | (0.293) | 0.8278 | (0.140) |
| 0.0418 | (0.005) | 0.0417 | (0.004) | 0.2055 | (0.021) | 0.1309 | (0.017) | |
| 0.9209 | (0.008) | 0.9289 | (0.006) | 0.7968 | (0.020) | 0.8663 | (0.019) | |
| () | 0.1550 | (0.380) | 0.5501 | (0.279) | 0.1576 | (0.169) | 0.2482 | (0.195) |
| 0.1868 | (0.024) | 0.1463 | (0.019) | 0.0411 | (0.023) | 0.0422 | (0.021) | |
| 0.9173 | (0.011) | 0.9291 | (0.008) | 0.9563 | (0.023) | 0.9565 | (0.022) | |
| Correlation | ||||||||
| 0.8179 | (0.004) | 0.7450 | (0.014) | |||||
| 0.8334 | (0.006) | 0.8884 | (0.010) | |||||
| Transition probabilities | ||||||||
| 0.9081 | (0.009) | 0.9626 | (0.024) | |||||
| 0.6828 | (0.027) | 0.9669 | (0.019) | |||||
| Degree of freedom | ||||||||
| – | 6.2260 | (0.252) | ||||||
| Log-lik. | −45,974.7 | −45,420.1 | ||||||
| BIC | 92.1478 | 91.0507 | ||||||
| Three Regimes—Normal Distribution | Three Regimes—Student’s t Distribution | |||||||
|---|---|---|---|---|---|---|---|---|
| Small Caps | Large Caps | Small Caps | Large Caps | |||||
| param. | std err. | param. | std err. | param. | std err. | param. | std err. | |
| Expected returns | ||||||||
| () | 0.3304 | (0.022) | 0.1174 | (0.011) | 0.3194 | (0.017) | 0.1251 | (0.011) |
| () | 0.0754 | (0.008) | 0.0966 | (0.007) | 0.1193 | (0.008) | 0.1133 | (0.008) |
| () | −0.3451 | (0.024) | −0.1897 | (0.024) | −0.2316 | (0.017) | −0.1049 | (0.020) |
| Volatility dynamics | ||||||||
| () | 0.0001 | (0.191) | 0.1797 | (0.108) | 0.5529 | (0.205) | 0.4921 | (0.141) |
| 0.0403 | (0.019) | 0.0325 | (0.009) | 0.1303 | (0.022) | 0.0927 | (0.013) | |
| 0.9480 | (0.022) | 0.9534 | (0.012) | 0.8585 | (0.022) | 0.8945 | (0.013) | |
| () | 0.2705 | (0.046) | 0.3461 | (0.060) | 0.0201 | (0.200) | 0.0858 | (0.040) |
| 0.0401 | (0.005) | 0.0439 | (0.004) | 0.0122 | (0.003) | 0.0177 | (0.003) | |
| 0.9180 | (0.008) | 0.9233 | (0.006) | 0.9739 | (0.006) | 0.9691 | (0.006) | |
| () | 0.0001 | (0.640) | 0.8492 | (0.405) | 0.1357 | (0.310) | 0.6340 | (0.358) |
| 0.2262 | (0.033) | 0.1655 | (0.022) | 0.1328 | (0.031) | 0.1050 | (0.022) | |
| 0.9005 | (0.018) | 0.9246 | (0.011) | 0.9145 | (0.022) | 0.9306 | (0.017) | |
| Correlation | ||||||||
| 0.7814 | (0.025) | 0.7300 | (0.016) | |||||
| 0.8487 | (0.006) | 0.8465 | (0.009) | |||||
| 0.8462 | (0.008) | 0.8764 | (0.007) | |||||
| Transition matrix | ||||||||
| 0.9206 | 0.0169 | 0.0453 | 0.9402 | 0.0170 | 0.0266 | |||
| (0.015) | (0.003) | (0.018) | (0.009) | (0.004) | (0.007) | |||
| 0.0350 | 0.8954 | 0.2663 | 0.0165 | 0.9116 | 0.1139 | |||
| (0.016) | (0.008) | (0.026) | (0.007) | (0.011) | (0.013) | |||
| 0.0445 | 0.0877 | 0.6884 | 0.0433 | 0.0715 | 0.8595 | |||
| (0.008) | (0.006) | (0.021) | (0.008) | (0.009) | (0.014) | |||
| Degree of freedom | ||||||||
| – | 7.7750 | (0.399) | ||||||
| Log-lik. | −45,282.0 | −44,852.6 | ||||||
| BIC | 90.9244 | 90.0753 | ||||||
| Null Hypothesis | Alternative Hypothesis | dof | LR Stat. | p-Value |
|---|---|---|---|---|
| H0(N1): 1 regime—normal | Ha(N1): 1 regime—Student’s t | 1 | 4216.3 | <0.5% |
| H0(NR1): 1 regime—normal | Ha(NR1): 2 regimes—normal | 11 | 4637.0 | <0.5% |
| H0(TR1): 1 regime—Student’s t | Ha(TR1): 2 regimes—Student’s t | 11 | 1528.0 | <0.5% |
| H0(N2): 2 regimes—normal | Ha(N2): 2 regimes—Student’s t | 1 | 1107.3 | <0.5% |
| H0(NR2): 2 regimes—normal | Ha(NR2): 3 regimes—normal | 13 | 1385.3 | <0.5% |
| H0(NT2): 2 regimes—Student’s t | Ha(NT2): 3 regimes—Student’s t | 13 | 1137.2 | <0.5% |
| H0(N3): 3 regimes—normal | Ha(N3): 3 regimes—Student’s t | 1 | 859.2 | <0.5% |
| H0(NR3): 3 regimes—normal | Ha(NR3): 4 regimes—normal | 15 | 924.0 | |
| H0(NT3): 3 regimes—Student’s t | Ha(NT3): 4 regimes—Student’s t | 15 | 772.0 |
| Sample Data | 1-Regime | 1-Regime | 2-Regime | 2-Regime | 3-Regime | 3-Regime | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1926–2020) | Normal | Student t | Normal | Student t | Normal | Student t | ||||||||
| Small | Large | Small | Large | Small | Large | Small | Large | Small | Large | Small | Large | Small | Large | |
| Skewnness | −0.39 | −0.48 | 0.01 | 0.00 | 0.00 | 0.00 | −0.19 | −0.17 | 0.17 | 0.01 | −0.84 | −0.47 | −0.50 | −0.26 |
| Kurtosis | 23.92 | 21.98 | 16.65 | 10.73 | 42.01 | 36.66 | 13.43 | 13.32 | 72.30 | 28.86 | 14.70 | 14.07 | 14.04 | 13.88 |
| ADD | ||||||||||||||
| 1 quarter | 3.84 | 2.78 | 2.55 | 2.32 | 2.16 | 2.13 | 3.76 | 3.43 | 2.40 | 2.21 | 3.66 | 3.29 | 3.42 | 2.91 |
| 2 quarters | 5.62 | 3.85 | 3.42 | 3.11 | 2.68 | 2.75 | 5.62 | 5.36 | 3.14 | 2.91 | 5.34 | 4.92 | 5.33 | 4.74 |
| 4 quarters | 7.52 | 4.82 | 4.53 | 4.08 | 3.22 | 3.46 | 7.88 | 7.68 | 3.86 | 3.66 | 7.31 | 6.85 | 7.69 | 7.18 |
| CDD | ||||||||||||||
| 1 quarter | 7.75 | 5.76 | 5.41 | 4.95 | 4.72 | 4.62 | 7.93 | 7.40 | 5.20 | 4.79 | 7.74 | 7.11 | 7.58 | 6.47 |
| 2 quarters | 11.80 | 8.20 | 7.35 | 6.70 | 6.02 | 6.06 | 11.65 | 11.25 | 6.95 | 6.39 | 11.25 | 10.41 | 11.78 | 10.57 |
| 4 quarters | 16.65 | 10.96 | 10.05 | 9.01 | 7.71 | 7.94 | 16.14 | 15.80 | 8.84 | 8.27 | 15.41 | 14.40 | 16.83 | 15.68 |
| MDD | ||||||||||||||
| 1 quarter | 9.87 | 7.55 | 7.05 | 6.44 | 6.22 | 6.05 | 10.20 | 9.62 | 6.80 | 6.25 | 9.94 | 9.25 | 10.04 | 8.67 |
| 2 quarters | 15.05 | 10.93 | 9.84 | 8.92 | 8.27 | 8.18 | 14.86 | 14.41 | 9.25 | 8.51 | 14.38 | 13.46 | 15.49 | 14.13 |
| 4 quarters | 21.52 | 15.23 | 13.96 | 12.41 | 11.26 | 11.23 | 20.54 | 20.15 | 12.17 | 11.43 | 19.78 | 18.63 | 21.98 | 20.68 |
| CED | ||||||||||||||
| 1 quarter | 31.22 | 22.84 | 12.02 | 10.63 | 11.25 | 10.37 | 20.59 | 19.29 | 12.14 | 10.64 | 20.74 | 19.10 | 20.85 | 17.48 |
| 2 quarters | 41.97 | 31.35 | 17.22 | 15.06 | 15.87 | 14.74 | 27.90 | 26.86 | 16.81 | 14.83 | 27.82 | 25.75 | 29.74 | 26.97 |
| 4 quarters | 51.37 | 40.25 | 20.59 | 17.89 | 17.73 | 17.16 | 31.19 | 30.59 | 18.40 | 16.89 | 30.64 | 28.55 | 33.57 | 31.51 |
| Horizon | Statistics | 1-Regime | 1-Regime | 2-Regime | 2-Regime | 3-Regime | 3-Regime |
|---|---|---|---|---|---|---|---|
| Normal | Student t | Normal | Student t | Normal | Student t | ||
| Panel A: Minimization of CDD | |||||||
| 1 quarter | Weight | 0.44 | 0.54 | −0.11 | 0.41 | −0.17 | 0.07 |
| CDD | 5.75 | 5.90 | 5.24 | 5.66 | 5.23 | 5.27 | |
| 2 quarters | Weight | 0.46 | 0.63 | −0.06 | 0.39 | 0.02 | −0.18 |
| CDD | 8.47 | 9.16 | 7.23 | 8.30 | 7.26 | 7.15 | |
| 4 quarters | Weight | 0.51 | 0.67 | 0.42 | 0.47 | 0.87 | −0.07 |
| CDD | 11.36 | 12.66 | 11.62 | 11.34 | 14.28 | 9.22 | |
| Panel B: Minimization of MDD | |||||||
| 1 quarter | Weight | 0.43 | 0.53 | −0.12 | 0.39 | −0.17 | 0.05 |
| MDD | 7.56 | 7.71 | 7.04 | 7.40 | 7.10 | 7.02 | |
| 2 quarters | Weight | 0.44 | 0.59 | −0.08 | 0.39 | 0.00 | −0.21 |
| MDD | 11.31 | 11.95 | 10.10 | 11.14 | 10.06 | 9.92 | |
| 4 quarters | Weight | 0.48 | 0.64 | 0.09 | 0.49 | 0.18 | −0.10 |
| MDD | 16.08 | 17.15 | 14.42 | 16.16 | 14.80 | 13.82 | |
| Panel C: Minimization of CED | |||||||
| 1 quarter | Weight | 0.37 | 0.44 | −0.16 | 0.26 | −0.21 | −0.14 |
| CED | 22.25 | 22.53 | 20.69 | 21.43 | 20.30 | 20.53 | |
| 2 quarters | Weight | 0.37 | 0.47 | −0.06 | 0.30 | 0.03 | −0.25 |
| CED | 29.24 | 30.03 | 25.26 | 28.80 | 25.56 | 24.84 | |
| 4 quarters | Weight | 0.41 | 0.52 | 0.02 | 0.43 | 0.00 | −0.06 |
| CED | 35.22 | 36.40 | 33.96 | 36.51 | 33.96 | 33.56 | |
| Horizon | Statistics | 1-Regime | 1-Regime | 2-Regime | 2-Regime | 3-Regime | 3-Regime |
|---|---|---|---|---|---|---|---|
| Normal | Student t | Normal | Student t | Normal | Student t | ||
| Panel A: Expected Return—CDD criterion | |||||||
| 1 quarter | Weight | 0.47 | 0.59 | 0.12 | 1.10 | 0.17 | 0.62 |
| Criterion | −0.020 | −0.059 | 0.015 | −0.037 | 0.029 | −0.004 | |
| Opp. cost (%) | 4.87 | 8.76 | 1.43 | 6.62 | 0.00 | 3.32 | |
| 2 quarters | Weight | 0.48 | 0.64 | 0.56 | 1.40 | 0.62 | 0.29 |
| Criterion | −0.070 | −0.161 | −0.026 | −0.119 | −0.031 | −0.004 | |
| Opp. cost (%) | 6.63 | 15.70 | 2.23 | 11.53 | 2.73 | 0.00 | |
| 4 quarters | Weight | 0.54 | 0.73 | 0.48 | 1.83 | 0.50 | 0.65 |
| Criterion | −0.175 | −0.323 | −0.055 | −0.293 | −0.058 | −0.075 | |
| Opp. cost (%) | 11.66 | 26.43 | −0.30 | 23.50 | 0.00 | 1.68 | |
| Panel B: Expected Return—MDD criterion | |||||||
| 1 quarter | Weight | 0.62 | 0.85 | −0.02 | 0.85 | −0.03 | 0.31 |
| Criterion | −0.091 | −0.111 | −0.076 | −0.113 | −0.067 | −0.074 | |
| Opp. cost (%) | 2.36 | 4.40 | 0.94 | 4.57 | 0.00 | 0.67 | |
| 2 quarters | Weight | 0.68 | 1.01 | 0.43 | 1.01 | 0.60 | −0.01 |
| Criterion | −0.203 | −0.258 | −0.181 | −0.254 | −0.203 | −0.147 | |
| Opp. cost (%) | 5.57 | 11.07 | 3.42 | 10.71 | 5.64 | 0.00 | |
| 4 quarters | Weight | 0.78 | 1.28 | 0.49 | 1.42 | 0.51 | 0.50 |
| Criterion | −0.319 | −0.442 | −0.281 | −0.478 | −0.284 | −0.277 | |
| Opp. cost (%) | 4.23 | 16.49 | 0.45 | 20.14 | 0.70 | 0.00 | |
| Panel C: Expected Return—CED criterion | |||||||
| 1 quarter | Weight | 0.89 | 1.33 | −0.11 | 0.50 | −0.15 | −0.03 |
| Criterion | −0.463 | −0.481 | −0.424 | −0.460 | −0.406 | −0.409 | |
| Opp. cost (%) | 5.66 | 7.48 | 1.78 | 5.41 | 0.00 | 0.28 | |
| 2 quarters | Weight | 1.05 | 1.73 | 0.45 | 0.57 | 0.69 | −0.16 |
| Criterion | −0.648 | −0.684 | −0.616 | −0.665 | −0.681 | −0.526 | |
| Opp. cost (%) | 12.21 | 15.87 | 9.03 | 13.95 | 15.49 | 0.00 | |
| 4 quarters | Weight | 1.28 | 1.97 | 0.50 | 0.78 | 0.51 | 0.48 |
| Criterion | −0.788 | −0.850 | −0.762 | −0.889 | −0.762 | −0.789 | |
| Opp. cost (%) | 2.59 | 8.86 | 0.03 | 12.73 | 0.00 | 2.78 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jondeau, E.; Pauli, A. Large Drawdowns and Long-Term Asset Management. J. Risk Financial Manag. 2024, 17, 552. https://doi.org/10.3390/jrfm17120552
Jondeau E, Pauli A. Large Drawdowns and Long-Term Asset Management. Journal of Risk and Financial Management. 2024; 17(12):552. https://doi.org/10.3390/jrfm17120552
Chicago/Turabian StyleJondeau, Eric, and Alexandre Pauli. 2024. "Large Drawdowns and Long-Term Asset Management" Journal of Risk and Financial Management 17, no. 12: 552. https://doi.org/10.3390/jrfm17120552
APA StyleJondeau, E., & Pauli, A. (2024). Large Drawdowns and Long-Term Asset Management. Journal of Risk and Financial Management, 17(12), 552. https://doi.org/10.3390/jrfm17120552








