Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility
Abstract
1. Introduction
2. Literature Survey
3. Method
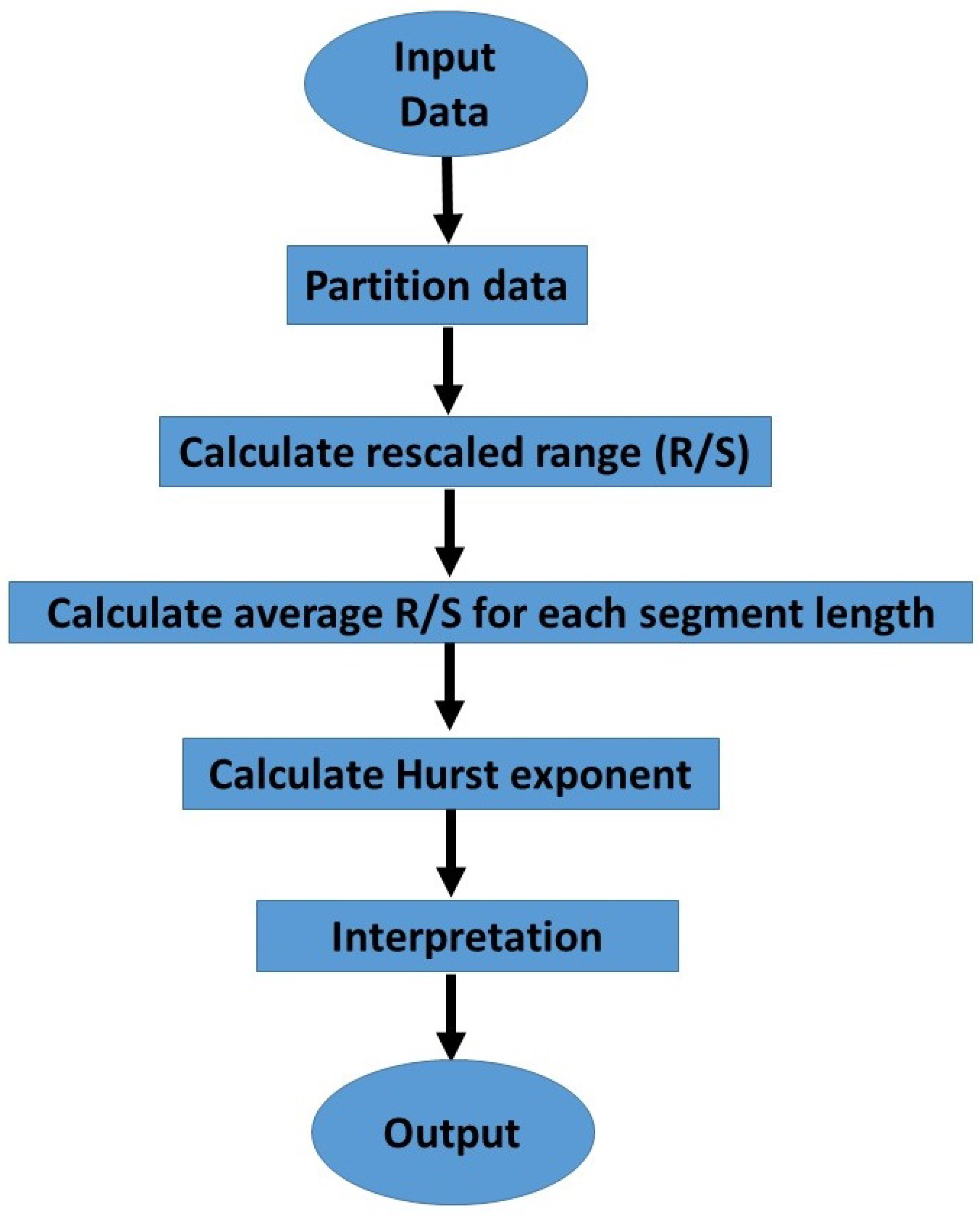
3.1. Hurst Exponent
- Step 1: Find the mean over all the sub-periods.
- Step 2: Construct a new series, , for .
- Step 3: Construct another series of cumulative deviations from step 2.
- Step 4: Calculate , for all .
- Step 5: Calculate standard deviation = of the original elements of each sub-period.
- Step 6: Calculate the rescaled range for all subperiods of fixed length n.
- Step 7: Repeat steps 1 to 6 iteratively for each length of sub-period.
3.2. Proposed Scheme
- If and , then the signal is BUY.
- If and , then the signal is SELL.
4. Results, Implementation and Validation
4.1. Evaluation Metric
- Consider a unit quantity of security under consideration for every buy or sell trade signal. The time duration for evaluation is one year. The number of buy and sell signals generated by strategies may differ in numbers.
- Separate queues for buy and sell trade signals.
- Starting with the first buy/sell signal find the complementary (sell/buy) signal and count the corresponding profit or loss.
- Keep finding pairs of complementary trades until the end of buy or sell trade signal queues.
- If there are any buy or sell trade signals that will not find their complementary trade signals after exhausting queues they are to be discarded in evaluation. In real practice, they can be carried forward to the next evaluation period using the sliding window method.
4.2. Approach and Testing
4.2.1. Strategy Implementation
4.2.2. Results
| Strategy | Buy Signals | Sell Signals | Net Result (units) |
|---|---|---|---|
| MH | 16 | 14 | +296 |
| MA | 5 | 4 | +25 |
| Strategy | Buy Signals | Sell Signals | Net Result (units) |
|---|---|---|---|
| MH | 10 | 13 | −929 |
| MA | 5 | 6 | −1498 |
| Strategy | Buy Signals | Sell Signals | Net Result (units) |
|---|---|---|---|
| MH | 11 | 13 | +8824 |
| MA | 6 | 5 | +4763 |

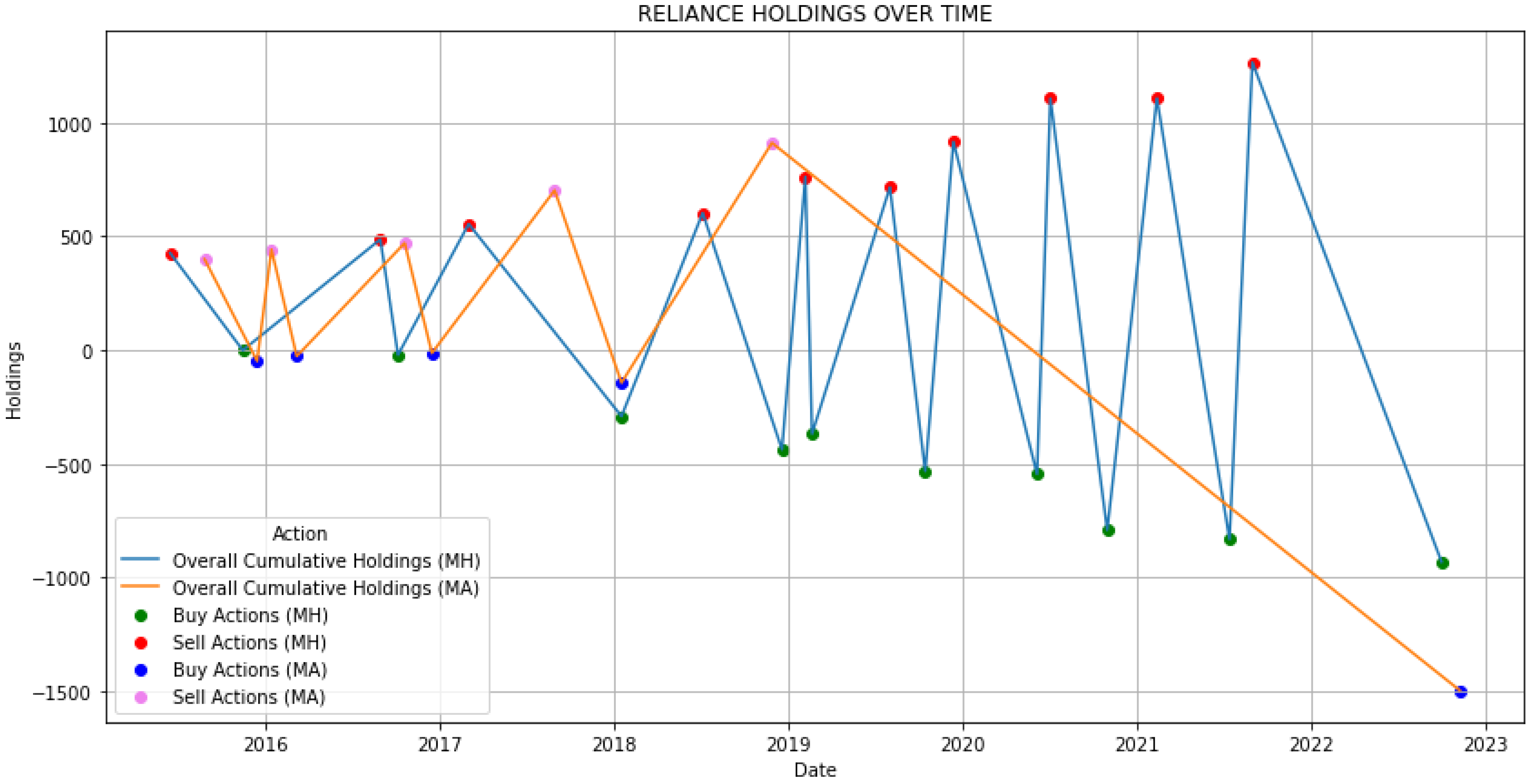
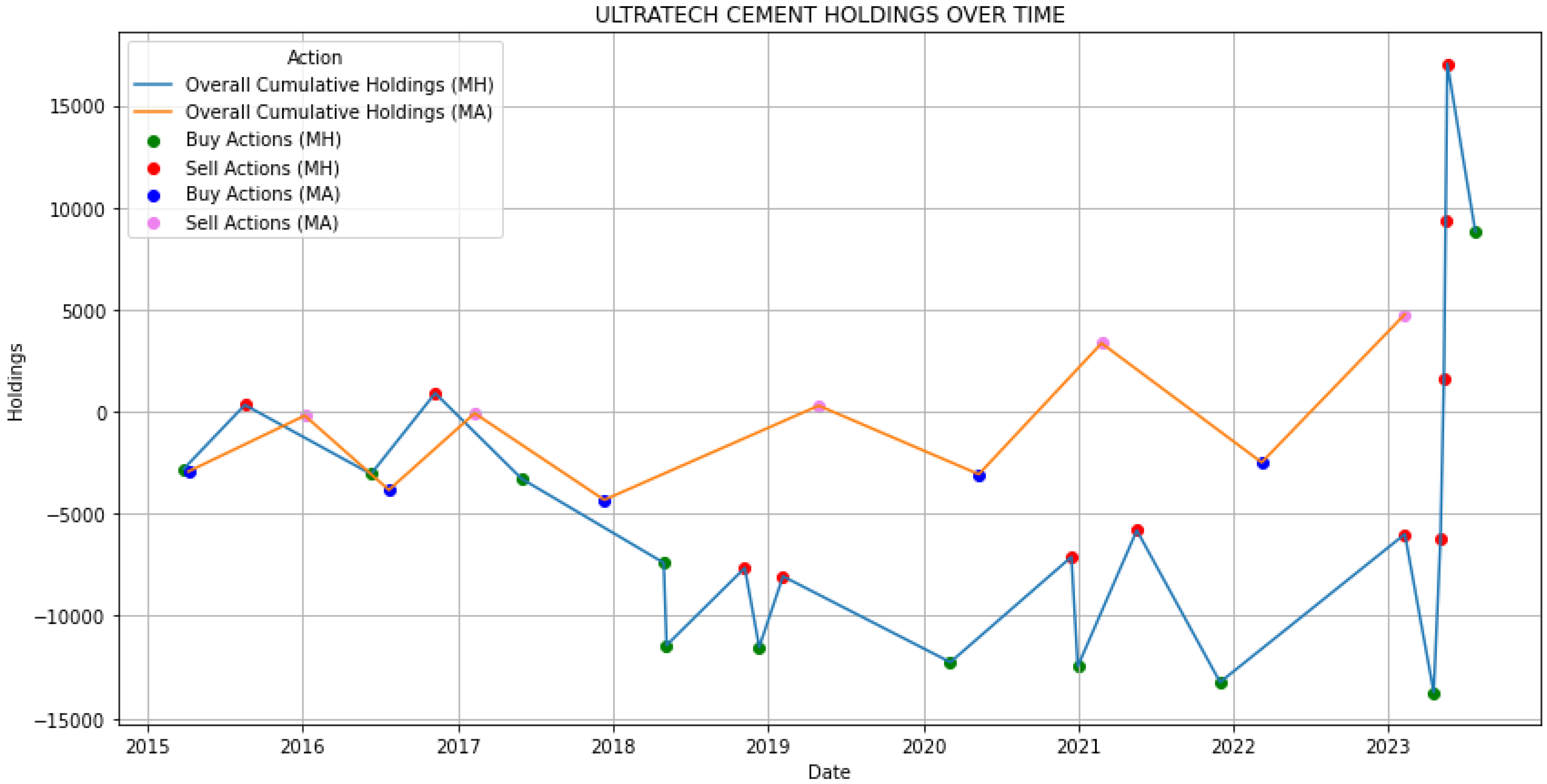
4.3. Validation via Hypothesis Testing
- (Null hypothesis): = ,
- (Alternate hypothesis): >,
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bal, Anirban, Debayan Ganguly, and Kingshuk Chatterjee. 2021. Stationarity and self-similarity determination of time series data using hurst exponent and r/s ration analysis. In Emerging Technologies in Data Mining and Information Security: Proceedings of IEMIS 2020. New York: Springer, vol. 2, pp. 601–612. [Google Scholar]
- Barunik, Jozef, and Ladislav Kristoufek. 2010. On hurst exponent estimation under heavy-tailed distributions. Physica A: Statistical Mechanics and Its Applications 389: 3844–55. [Google Scholar] [CrossRef]
- Bianchi, Sergio, and Augusto Pianese. 2018. Time-varying hurst–hölder exponents and the dynamics of (in) efficiency in stock markets. Chaos Solitons & Fractals 109: 64–75. [Google Scholar]
- Bui, Quynh, and Robert Ślepaczuk. 2022. Applying hurst exponent in pair trading strategies on nasdaq 100 index. Physica A: Statistical Mechanics and Its Applications 592: 126784. [Google Scholar] [CrossRef]
- Cho, Poongjin, and Minhyuk Lee. 2022. Forecasting the volatility of the stock index with deep learning using asymmetric hurst exponents. Fractal and Fractional 6: 394. [Google Scholar] [CrossRef]
- Couillard, Michel, and Matt Davison. 2005. A comment on measuring the hurst exponent of financial time series. Physica A: Statistical Mechanics and Its Applications 348: 404–18. [Google Scholar] [CrossRef]
- Domino, Krzysztof. 2011. The use of the hurst exponent to predict changes in trends on the warsaw stock exchange. Physica A: Statistical Mechanics and Its Applications 390: 98–109. [Google Scholar] [CrossRef]
- Eom, Cheoljun, Sunghoon Choi, Gabjin Oh, and Woo-Sung Jung. 2008. Hurst exponent and prediction based on weak-form efficient market hypothesis of stock markets. Physica A: Statistical Mechanics and its Applications 387: 4630–36. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fernández-Martínez, Sánchez-Granero, Muñoz Torrecillas, and Bill McKelvey. 2017. A comparison of three hurst exponent approaches to predict nascent bubbles in s&p500 stocks. Fractals 25: 1750006. [Google Scholar]
- Fernández-Martínez, Sánchez-Granero, Trinidad Segovia, and Román-Sánchez. 2014. An accurate algorithm to calculate the Hurst exponent of self-similar processes. Physics Letters A 378: 2355–62. [Google Scholar] [CrossRef]
- Garcin, Matthieu. 2017. Estimation of time-dependent hurst exponents with variational smoothing and application to forecasting foreign exchange rates. Physica A: Statistical Mechanics and Its Applications 483: 462–79. [Google Scholar] [CrossRef]
- Gomez-Aguila, A., J. E. Trinidad-Segovia, and M. A. Sanchez-Granero. 2022. Improvement in Hurst exponent estimation and its application to financial markets. Financial Innovation 8: 86. [Google Scholar] [CrossRef]
- Grech, Dariusz, and Grzegorz Pamuła. 2008. The local hurst exponent of the financial time series in the vicinity of crashes on the polish stock exchange market. Physica A: Statistical Mechanics and Its Applications 387: 4299–308. [Google Scholar] [CrossRef]
- Gursakal, Necmi, Zehra Berna Aydin, Sevda Gursakal, and Selim Tuzunturk. 2009. Hurst exponent analysis in Turkish stock market. International Journal of Sustainable Economy 1: 255–69. [Google Scholar] [CrossRef]
- Horta, Paulo, Sérgio Lagoa, and Luis Martins. 2014. The impact of the 2008 and 2010 financial crises on the hurst exponents of international stock markets: Implications for efficiency and contagion. International Review of Financial Analysis 35: 140–53. [Google Scholar] [CrossRef]
- Hurst, Harold Edwin. 1951. Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116: 770–99. [Google Scholar] [CrossRef]
- Kroha, Petr, and Miroslav Skoula. 2018. Hurst exponent and trading signals derived from market time series. Paper presented at the 20th International Conference on Enterprise Information Systems (ICEIS 2018), Funchal, Madeira, Portugal, March 21–24. [Google Scholar]
- Laktyunkin, Alexander, and Alexander A. Potapov. 2020. The hurst exponent application in the fractal analysis of the Russian stock market. In Advances in Artificial Systems for Medicine and Education II 2. New York: Springer, pp. 459–71. [Google Scholar]
- Peters, Edgar E. 1994. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York: John Wiley & Sons. [Google Scholar]
- Qadan, Mahmoud, and Kerem Shuval. 2022. Variance risk and the idiosyncratic volatility puzzle. Finance Research Letters 45: 102176. [Google Scholar] [CrossRef]
- Qadan, Mahmoud, Or David, Iyad Snunu, and Kerem Shuval. 2024. The vix’s term structure of individual active stocks. Finance Research Letters 61: 105036. [Google Scholar] [CrossRef]
- Qian, Bo, and Khaled Rasheed. 2004. Hurst exponent and financial market predictability. In IASTED Conference on Financial Engineering and Applications. Cambridge: IASTED International Conference, pp. 203–209. [Google Scholar]
- Sánchez-Granero, M. J., M. Fernández-Martínez, and J. E. Trinidad-Segovia. 2012. Introducing fractal dimension algorithms to calculate the Hurst exponent of financial time series. The European Physical Journal B 85: 86. [Google Scholar] [CrossRef]
- Selvaratnam, Somesh, and Michael Kirley. 2006. Predicting stock market time series using evolutionary artificial neural networks with hurst exponent input windows. In Australasian Joint Conference on Artificial Intelligence. New York: Springer, pp. 617–26. [Google Scholar]
- Sensoy, Ahmet. 2013. Generalized hurst exponent approach to efficiency in mena markets. Physica A: Statistical Mechanics and Its Applications 392: 5019–26. [Google Scholar] [CrossRef]
- Shleifer, Andrei. 2000. Inefficient Markets: An Introduction to behavioral Finance. Oxford: Oxford University Press UK. [Google Scholar]
- Tzouras, Spilios, Christoforos Anagnostopoulos, and Emma McCoy. 2015. Financial time series modeling using the hurst exponent. Physica A: Statistical Mechanics and Its Applications 425: 50–68. [Google Scholar] [CrossRef]
- Vogl, Markus. 2023. Hurst exponent dynamics of s&p 500 returns: Implications for market efficiency, long memory, multifractality and financial crises predictability by application of a nonlinear dynamics analysis framework. Chaos, Solitons & Fractals 166: 112884. [Google Scholar]
- Yahoo Finance. 2024a. Historical Prices for Cipla Pharmaceutical. New York: Yahoo Finance. [Google Scholar]
- Yahoo Finance. 2024b. Historical Prices for Reliance Industries. New York: Yahoo Finance. [Google Scholar]
- Yahoo Finance. 2024c. Historical Prices for Ultratech Cement. New York: Yahoo Finance. [Google Scholar]
- Yim, Kyubin, Gabjin Oh, and Seunghwan Kim. 2014. An analysis of the financial crisis in the kospi market using hurst exponents. Physica A: Statistical Mechanics and Its Applications 410: 327–34. [Google Scholar] [CrossRef]
- Zournatzidou, Georgia, and Christos Floros. 2023. Hurst exponent analysis: Evidence from volatility indices and the volatility of volatility indices. Journal of Risk and Financial Management 16: 272. [Google Scholar] [CrossRef]
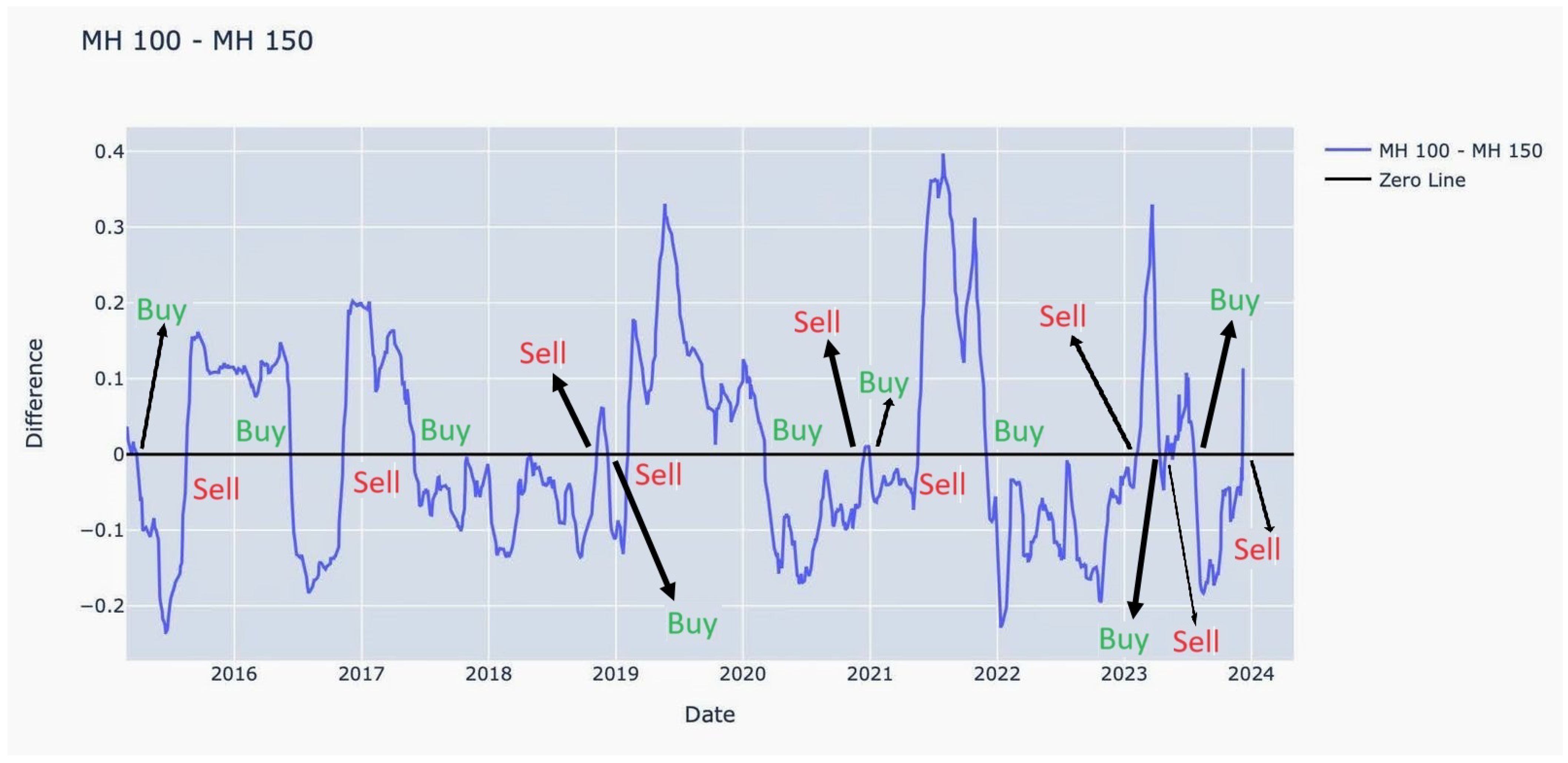
| Buy Signal Queue | Sell Signal Queue | Pair | Profit/Loss | ||||
|---|---|---|---|---|---|---|---|
| Buy Sr. No. | Date | Buy Signal | Sell Sr. No. | Date | Sell Signal | ||
| B1 | 01-01-20 | 150 | S1 | 02-02-20 | 159 | (B1, S1) | 9 |
| B2 | 15-01-20 | 155 | S2 | 03-03-20 | 162 | (B2, S2) | 7 |
| B3 | 20-02-20 | 157 | S3 | 16-03-20 | 161 | (B3, S3) | 4 |
| B4 | 15-04-20 | 164 | S4 | 18-03-20 | 160 | (S4, B4) | −4 |
| B5 | 04-05-20 | 165 | S5 | 08-04-20 | 161 | (S5, B5) | −4 |
| B6 | 14-05-20 | 161 | S6 | 29-04-20 | 162 | (S6, B6) | 1 |
| B7 | 19-05-20 | 163 | S7 | 30-05-20 | 165 | (B7, S7) | 2 |
| B8 | 23-05-20 | 165 | Unpaired | ||||
| Total Profit/Loss | 15 | ||||||
| Stock | df | p Value | h Value | Null Hypothesis () | Alternate Hypothesis () | |
|---|---|---|---|---|---|---|
| Cipla Pharmaceutical | 38 | 0.01 | 0.0006 | 1 | Rejected | Accepted |
| Reliance Industries | 33 | 0.05 | 0.0302 | 1 | Rejected | Accepted |
| UltraTech Cement | 34 | 0.03 | 0.0208 | 1 | Rejected | Accepted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, P.; Raje, A.; Shah, J. Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility. J. Risk Financial Manag. 2024, 17, 390. https://doi.org/10.3390/jrfm17090390
Shah P, Raje A, Shah J. Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility. Journal of Risk and Financial Management. 2024; 17(9):390. https://doi.org/10.3390/jrfm17090390
Chicago/Turabian StyleShah, Param, Ankush Raje, and Jigarkumar Shah. 2024. "Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility" Journal of Risk and Financial Management 17, no. 9: 390. https://doi.org/10.3390/jrfm17090390
APA StyleShah, P., Raje, A., & Shah, J. (2024). Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility. Journal of Risk and Financial Management, 17(9), 390. https://doi.org/10.3390/jrfm17090390





