The Nonsense of Bitcoin in Portfolio Analysis
Abstract
1. Introduction
2. Bitcoin and Portfolio Management
3. Bitcoin, the Lorenz, and CVaR
4. The Shapley Value of Bitcoin in a Efficient Portfolio
5. Conclusions and Implications
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Mean | Stdev | Symbol | Mean | Stdev | Symbol | Mean | Stdev |
|---|---|---|---|---|---|---|---|---|
| AAPL | 0.132% | 2.064% | CVX | 0.058% | 2.200% | NEE | 0.070% | 1.693% |
| ABBV | 0.060% | 1.775% | DE | 0.092% | 2.139% | NFLX | 0.100% | 2.971% |
| ABT | 0.065% | 1.667% | DHR | 0.084% | 1.709% | NKE | 0.065% | 2.067% |
| ACN | 0.074% | 1.783% | DIS | 0.011% | 2.048% | NOW | 0.143% | 2.731% |
| ADBE | 0.095% | 2.351% | DUK | 0.033% | 1.491% | NVDA | 0.210% | 3.320% |
| ADI | 0.083% | 2.183% | FDX | 0.025% | 2.340% | ORCL | 0.083% | 1.849% |
| ADP | 0.068% | 1.748% | GE | 0.040% | 2.682% | PEP | 0.052% | 1.364% |
| AIG | 0.037% | 2.508% | GM | 0.029% | 2.620% | PFE | 0.036% | 1.630% |
| AMAT | 0.118% | 2.894% | GOOGL | 0.083% | 1.994% | PG | 0.054% | 1.351% |
| AMD | 0.242% | 3.562% | GS | 0.047% | 2.050% | PLD | 0.076% | 1.872% |
| AMGN | 0.042% | 1.602% | HD | 0.059% | 1.793% | PM | 0.026% | 1.700% |
| AMT | 0.046% | 1.797% | HON | 0.045% | 1.686% | PNC | 0.025% | 2.165% |
| AMZN | 0.081% | 2.260% | IBM | 0.026% | 1.692% | PYPL | 0.027% | 2.702% |
| AVGO | 0.126% | 2.326% | INTC | 0.012% | 2.396% | QCOM | 0.088% | 2.584% |
| AXP | 0.071% | 2.339% | INTU | 0.103% | 2.311% | RTX | 0.043% | 2.026% |
| BA | 0.028% | 3.116% | ISRG | 0.095% | 2.272% | SBUX | 0.067% | 1.918% |
| BAC | 0.031% | 2.207% | JNJ | 0.028% | 1.294% | SCHW | 0.038% | 2.393% |
| BDX | 0.031% | 1.550% | JPM | 0.052% | 1.995% | SPGI | 0.079% | 1.859% |
| BKNG | 0.056% | 2.286% | KHC | −0.014% | 1.970% | SYK | 0.066% | 1.923% |
| BLK | 0.051% | 2.010% | KO | 0.042% | 1.325% | T | −0.003% | 1.624% |
| BMY | 0.029% | 1.502% | LIN | 0.083% | 1.700% | TFC | 0.014% | 2.461% |
| BRK-B | 0.048% | 1.432% | LLY | 0.146% | 1.860% | TGT | 0.085% | 2.152% |
| C | 0.007% | 2.402% | LMT | 0.050% | 1.659% | TMO | 0.090% | 1.767% |
| CAT | 0.058% | 2.087% | LOW | 0.090% | 2.109% | TMUS | 0.069% | 1.786% |
| CB | 0.044% | 1.764% | MA | 0.089% | 2.035% | TSLA | 0.255% | 4.107% |
| CCI | 0.031% | 1.760% | MCD | 0.059% | 1.474% | TXN | 0.069% | 2.008% |
| CI | 0.043% | 2.122% | MDLZ | 0.058% | 1.367% | UNH | 0.083% | 1.842% |
| CL | 0.019% | 1.343% | MDT | 0.025% | 1.645% | UNP | 0.054% | 1.799% |
| CMCSA | 0.024% | 1.796% | META | 0.071% | 2.773% | UPS | 0.056% | 1.880% |
| CME | 0.046% | 1.763% | MMC | 0.074% | 1.483% | USB | −0.001% | 2.178% |
| COP | 0.097% | 2.778% | MMM | −0.032% | 1.719% | V | 0.070% | 1.805% |
| COST | 0.091% | 1.518% | MO | 0.008% | 1.642% | VZ | −0.004% | 1.258% |
| CRM | 0.083% | 2.440% | MRK | 0.077% | 1.451% | WFC | 0.011% | 2.336% |
| CSCO | 0.048% | 1.806% | MS | 0.070% | 2.201% | WMT | 0.048% | 1.444% |
| CSX | 0.064% | 1.881% | MSFT | 0.124% | 1.945% | XOM | 0.060% | 2.108% |
| CVS | 0.025% | 1.796% | MU | 0.084% | 2.997% | ZTS | 0.082% | 1.755% |
| Symbol | Mean | St-Dev |
|---|---|---|
| AAPL | 0.132% | 2.064% |
| BTC | 0.149% | 4.498% |
| EEM | 0.006% | 1.437% |
| GLD | 0.032% | 0.910% |
| IXIC | 0.060% | 1.591% |
| IYE | 0.046% | 2.248% |
| JNK | 0.010% | 0.636% |
| NVDA | 0.210% | 3.320% |
| QQQ | 0.076% | 1.624% |
| SPY | 0.050% | 1.330% |
| TSLA | 0.255% | 4.107% |
| XLK | 0.090% | 1.739% |
| 1 | The utility of the mean return is greater than the mean of the utilities of the returns. |
| 2 | Since some of the the S&P100 components are added and removed by year’s end in the index, I used 108 shares to have at least 100 stocks in the sample. |
| 3 | It was suggested by a referee that one should have used Engle and Rangel (2009) method to synchronize the data. |
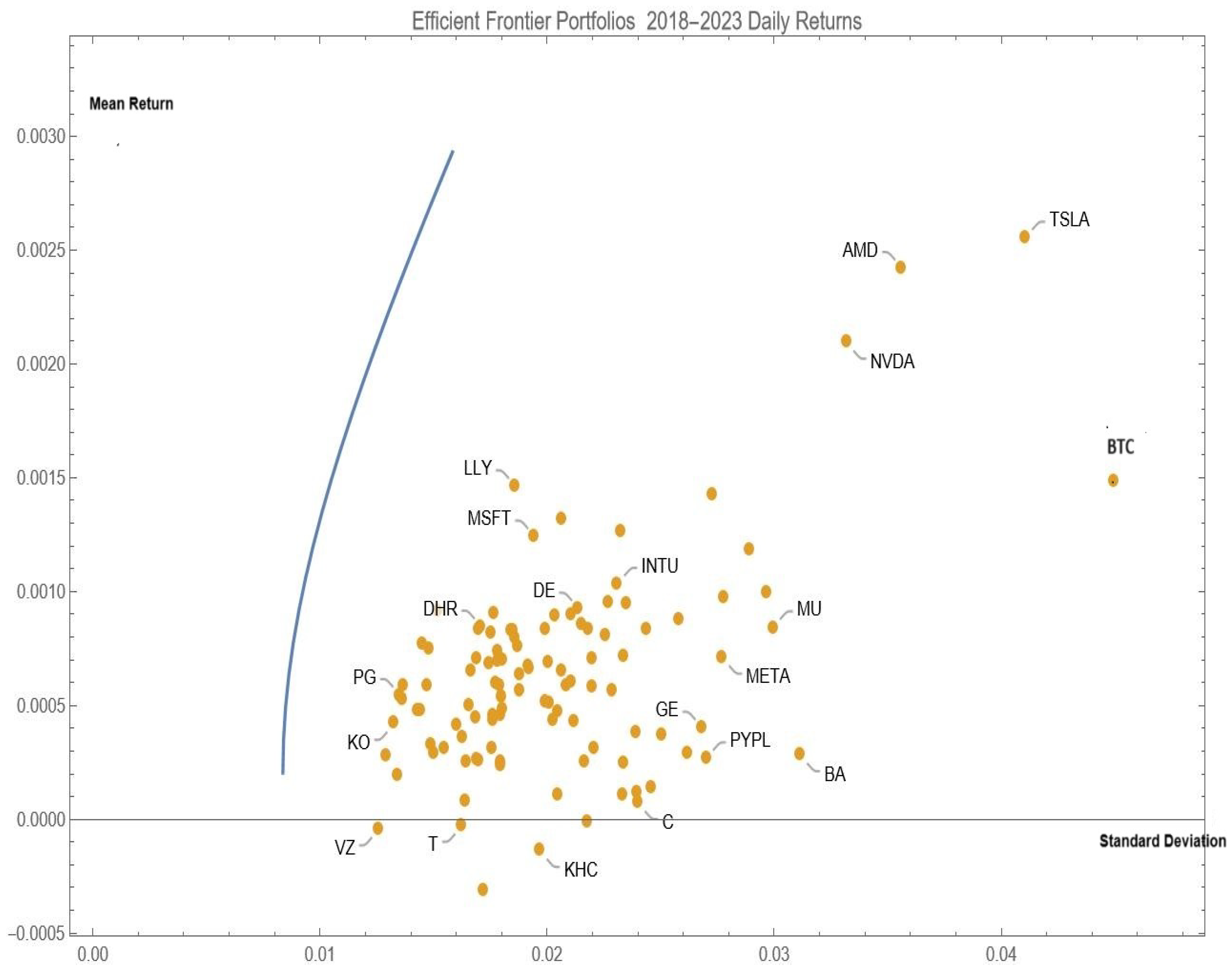
| 4 | The mean-variance frontier and 108 assets with Bitcoin are plotted in the mean–standard deviation space. |
| 5 | |
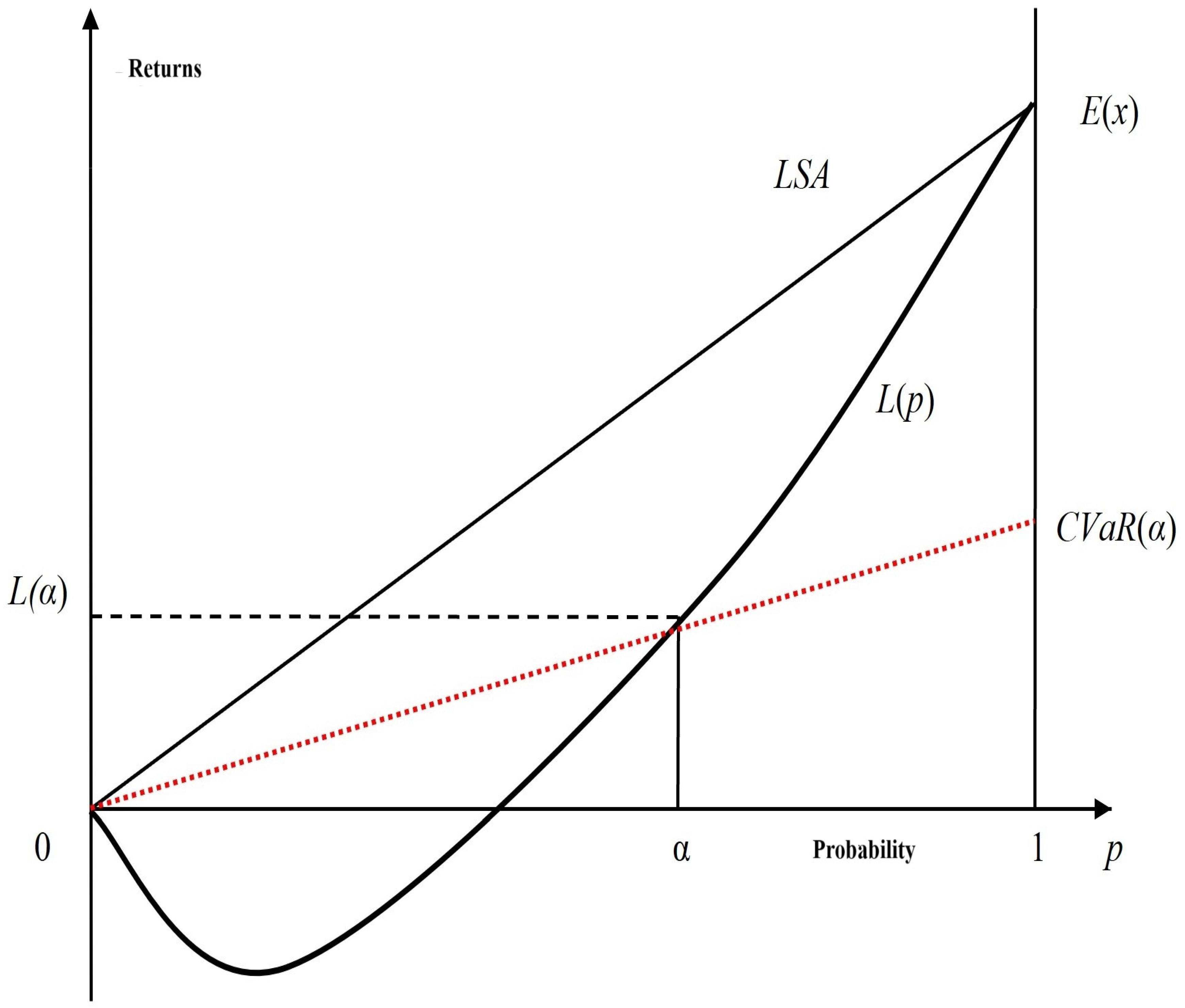
| 6 | The absolute Lorenz curve expresses the cumulative returns as a function of cumulative probabilities, with LSA being the Lorenz of a risk-free asset with identical mean return. |
References
- Akhtaruzzaman, M., Sensoyc, A., & Corbet, S. (2020). The influence of Bitcoin on portfolio diversification and design. Finance Research Letters, 37, 101344. [Google Scholar] [CrossRef]
- Artzner, P., Delbaen, F., Eber, J.-M., & Heath, D. (1999). Coherent measures of risk. Mathematical Finance, 9, 203–228. [Google Scholar] [CrossRef]
- Bakry, W., Rashid, A., Al-Mohamad, S., & El-Kanj, N. (2021). Bitcoin and porfolio diversification: A portfolio optimization approach. Journal of Risk and Financial Management, 14, 282. [Google Scholar] [CrossRef]
- Eisl, A., Gasser, S. M., & Weinmayer, K. (2015). Caveat emptor: Does bitcoin improve portfolio diversification? SSRN, 2408997. [Google Scholar] [CrossRef]
- Engle, R., & Rangel, J. (2009). The Factor-Spline-GARCH model for high and low frequency correlations. Working Papers, No. 2009-03. Banco de México, Ciudad de México. [Google Scholar]
- Foley, S., Karlsen, J. R., & Putnins, T. J. (2019). Sex, drugs, and bitcoin: How much illegal activity is financed through cryptocurrencies? The Review of Financial Studies, 32(5), 1798–1853. [Google Scholar] [CrossRef]
- Gastwirth, J. L. (1971). A general definition of the lorenz curve. Econometrica, 39, 1037–1039. [Google Scholar] [CrossRef]
- Hadar, J., & Russell, W. R. (1969). Rules for ordering uncertain prospects? American Economic Review, 59, 25–34. [Google Scholar]
- Hanoch, G., & Levy, H. (1969). The efficiency analysis of choice involving risk. Review of Economic Studies, 36, 335–346. [Google Scholar] [CrossRef]
- Huang, C.-F., & Litzenberger, R. H. (1988). Foundations for financial economics. Elsevier Science Publishing Co. [Google Scholar]
- Huberman, G., Leshno, J. D., & Moallemi, C. (2021). Monopoly without a monopolist: An economic analysis of the Bitcoin payment system. Review of Economic Studies, 88(6), 3011–3040. [Google Scholar] [CrossRef]
- Krugman, P. (2022, November 18). Is this the end game for crypto? New York Times. 15. [Google Scholar]
- Markowitz, H. (1952). Portfolio selection. Journal of Finance, 7(1), 77–91. [Google Scholar]
- Platanakis, E., & Urquhart, A. (2020). Should investors include bitcoin in their portfolios? A portfolio theory approach. The British Accounting Review, 52(4), 100837. [Google Scholar] [CrossRef]
- Rockafellar, R., & Uryasev, S. (2000). Optimization of conditional value-at-risk. Journal of Risk, 2, 21–41. [Google Scholar] [CrossRef]
- Rothschild, M., & Stiglitz, J. (1970). Increasing risk i: A definition. Journal of Economic Theory, 2, 66–84. [Google Scholar] [CrossRef]
- Shalit, H. (2014). Portfolio risk management using the Lorenz curve. Journal of Portfolio Management, 40(3), 152–159. [Google Scholar]
- Shalit, H. (2021). The Shapley value decomposition of optimal portfolios. Annals of Finance, 17(1), 1. [Google Scholar] [CrossRef]
- Shalit, H., & Yitzhaki, S. (2010). How does beta explain stochastic dominance efficiency? Review of Quantitative Finance and Accounting, 35(4), 431–444. [Google Scholar] [CrossRef]
- Shorrocks, A. F. (1983). Ranking income distributions. Economica, 50, 3–17. [Google Scholar] [CrossRef]
- Yitzhaki, S. (1982). Stochastic dominance, mean variance, and Gini’s mean difference. American Economic Review, 72(1), 178–185. [Google Scholar]


| Symbol | Mean | Gini | Symbol | Mean | Gini | Symbol | Mean | Gini | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PEP | 0.05% | 0.65% | −0.60% | ACN | 0.07% | 0.91% | −0.84% | CAT | 0.06% | 1.11% | −1.05% |
| PG | 0.05% | 0.67% | −0.61% | MO | 0.01% | 0.85% | −0.84% | ADI | 0.08% | 1.14% | −1.06% |
| KO | 0.04% | 0.66% | −0.62% | CB | 0.04% | 0.88% | −0.84% | AXP | 0.07% | 1.13% | −1.06% |
| MDLZ | 0.06% | 0.68% | −0.62% | V | 0.07% | 0.92% | −0.85% | AVGO | 0.13% | 1.19% | −1.07% |
| JNJ | 0.03% | 0.65% | −0.62% | SPGI | 0.08% | 0.93% | −0.85% | PNC | 0.03% | 1.10% | −1.07% |
| MCD | 0.06% | 0.69% | −0.63% | TMO | 0.09% | 0.94% | −0.85% | USB | 0.00% | 1.08% | −1.08% |
| WMT | 0.05% | 0.70% | −0.65% | CSCO | 0.05% | 0.91% | −0.86% | BAC | 0.03% | 1.11% | −1.08% |
| CL | 0.02% | 0.68% | −0.66% | UNP | 0.05% | 0.92% | −0.87% | ISRG | 0.09% | 1.18% | −1.08% |
| VZ | 0.00% | 0.65% | −0.66% | PLD | 0.08% | 0.95% | −0.88% | INTU | 0.10% | 1.22% | −1.11% |
| MMC | 0.07% | 0.74% | −0.67% | AMT | 0.05% | 0.92% | −0.88% | AMZN | 0.08% | 1.20% | −1.11% |
| MRK | 0.08% | 0.75% | −0.67% | SBUX | 0.07% | 0.95% | −0.88% | ADBE | 0.09% | 1.21% | −1.12% |
| BRK-B | 0.05% | 0.72% | −0.67% | CCI | 0.03% | 0.91% | −0.88% | BKNG | 0.06% | 1.18% | −1.12% |
| COST | 0.09% | 0.77% | −0.68% | CSX | 0.06% | 0.95% | −0.89% | FDX | 0.02% | 1.17% | −1.14% |
| DUK | 0.03% | 0.73% | −0.70% | MSFT | 0.12% | 1.01% | −0.89% | CRM | 0.08% | 1.25% | −1.17% |
| BMY | 0.03% | 0.78% | −0.75% | UPS | 0.06% | 0.95% | −0.89% | C | 0.01% | 1.18% | −1.17% |
| LMT | 0.05% | 0.82% | −0.77% | SYK | 0.07% | 0.96% | −0.90% | WFC | 0.01% | 1.19% | −1.18% |
| NEE | 0.07% | 0.84% | −0.77% | CVS | 0.03% | 0.93% | −0.90% | AIG | 0.04% | 1.24% | −1.20% |
| BDX | 0.03% | 0.81% | −0.78% | CMCSA | 0.02% | 0.93% | −0.91% | INTC | 0.01% | 1.21% | −1.20% |
| AMGN | 0.04% | 0.82% | −0.78% | MMM | −0.03% | 0.88% | −0.91% | SCHW | 0.04% | 1.24% | −1.20% |
| LLY | 0.15% | 0.92% | −0.78% | KHC | −0.01% | 0.91% | −0.92% | TFC | 0.01% | 1.22% | −1.21% |
| ABT | 0.06% | 0.86% | −0.80% | JPM | 0.05% | 0.99% | −0.94% | QCOM | 0.09% | 1.33% | −1.24% |
| HON | 0.04% | 0.85% | −0.80% | RTX | 0.04% | 0.99% | −0.95% | META | 0.07% | 1.35% | −1.28% |
| ADP | 0.07% | 0.87% | −0.80% | LOW | 0.09% | 1.04% | −0.95% | COP | 0.10% | 1.40% | −1.31% |
| LIN | 0.08% | 0.89% | −0.81% | TGT | 30.09% | 1.03% | −0.95% | NOW | 0.14% | 1.46% | −1.32% |
| CME | 0.05% | 0.86% | −0.81% | AAPL | 0.13% | 1.08% | −0.95% | GM | 0.03% | 1.37% | −1.34% |
| MDT | 0.03% | 0.84% | −0.81% | MA | 0.09% | 1.04% | −0.95% | GE | 0.04% | 1.41% | −1.37% |
| DHR | 0.08% | 0.90% | −0.81% | GOOGL | 0.08% | 1.05% | −0.97% | PYPL | 0.03% | 1.40% | −1.37% |
| PFE | 0.04% | 0.85% | −0.81% | BLK | 0.05% | 1.03% | −0.98% | NFLX | 0.10% | 1.51% | −1.41% |
| T | 0.00% | 0.81% | −0.81% | NKE | 0.07% | 1.05% | −0.98% | AMAT | 0.12% | 1.56% | −1.44% |
| ORCL | 0.08% | 0.90% | −0.81% | GS | 0.05% | 1.04% | −1.00% | BA | 0.03% | 1.52% | −1.49% |
| IBM | 0.03% | 0.84% | −0.82% | TXN | 0.07% | 1.07% | −1.00% | MU | 0.08% | 1.63% | −1.54% |
| PM | 0.03% | 0.85% | −0.82% | CVX | 0.06%w | 1.06% | −1.01% | NVDA | 0.21% | 1.77% | −1.56% |
| ZTS | 0.08% | 0.90% | −0.82% | DIS | 0.01% | 1.03% | −1.02% | AMD | 0.24% | 1.90% | −1.66% |
| ABBV | 0.06% | 0.89% | −0.83% | CI | 0.04% | 1.07% | −1.03% | TSLA | 0.26% | 2.16% | −1.91% |
| HD | 0.06% | 0.89% | −0.83% | DE | 0.09% | 1.12% | −1.03% | BTC | 0.15% | 2.30% | −2.16% |
| UNH | 0.08% | 0.91% | −0.83% | MS | 0.07% | 1.12% | −1.04% | ||||
| TMUS | 0.07% | 0.91% | −0.84% | XOM | 0.06% | 1.11% | −1.05% |
| Symbol | CVaR5% | CVaR10% | Symbol | CVaR5% | CVaR10% | Symbol | CVaR5% | CVaR10% |
|---|---|---|---|---|---|---|---|---|
| BTC | 28.73% | 14.30% | CVX | 13.59% | 6.76% | NFLX | 19.31% | 9.61% |
| AAPL | 13.31% | 6.62% | DE | 14.18% | 7.05% | NKE | 13.35% | 6.65% |
| ABBV | 11.38% | 5.66% | DHR | 11.28% | 5.61% | NOW | 18.39% | 9.14% |
| ABT | 11.03% | 5.48% | DIS | 13.54% | 6.74% | NVDA | 21.94% | 10.90% |
| ACN | 11.42% | 5.68% | DUK | 9.38% | 4.67% | ORCL | 11.11% | 5.53% |
| ADBE | 15.35% | 7.64% | FDX | 15.40% | 7.66% | PEP | 8.05% | 4.01% |
| ADI | 14.62% | 7.27% | GE | 18.59% | 9.25% | PFE | 11.06% | 5.50% |
| ADP | 11.01% | 5.48% | GM | 18.03% | 8.97% | PG | 8.42% | 4.19% |
| AIG | 15.98% | 7.95% | GOOGL | 13.29% | 6.62% | PLD | 12.07% | 6.01% |
| AMAT | 20.07% | 9.98% | GS | 13.61% | 6.77% | PM | 11.11% | 5.53% |
| AMD | 23.32% | 11.61% | HD | 11.35% | 5.65% | PNC | 14.33% | 7.13% |
| AMGN | 10.55% | 5.25% | HON | 10.91% | 5.43% | PYPL | 18.56% | 9.23% |
| AMT | 12.00% | 5.97% | IBM | 10.95% | 5.45% | QCOM | 16.93% | 8.42% |
| AMZN | 15.26% | 7.60% | INTC | 16.17% | 8.05% | RTX | 12.55% | 6.25% |
| AVGO | 14.90% | 7.41% | INTU | 15.39% | 7.66% | SBUX | 11.85% | 5.90% |
| AXP | 14.20% | 7.06% | ISRG | 14.84% | 7.38% | SCHW | 16.41% | 8.16% |
| BA | 19.70% | 9.81% | JNJ | 8.35% | 4.16% | SPGI | 11.74% | 5.84% |
| BAC | 14.50% | 7.21% | JPM | 12.74% | 6.34% | SYK | 12.17% | 6.05% |
| BDX | 10.64% | 5.29% | KHC | 12.16% | 6.05% | T | 10.82% | 5.38% |
| BKNG | 15.29% | 7.61% | KO | 8.36% | 4.16% | TFC | 16.06% | 7.99% |
| BLK | 13.25% | 6.60% | LIN | 11.26% | 5.60% | TGT | 12.89% | 6.41% |
| BMY | 10.18% | 5.06% | LLY | 10.97% | 5.46% | TMO | 11.99% | 5.95% |
| BRK-B | 9.21% | 4.58% | LMT | 10.31% | 5.13% | TMUS | 11.44% | 5.69% |
| C | 15.60% | 7.76% | LOW | 13.01% | 6.47% | TSLA | 26.35% | 13.11% |
| CAT | 14.41% | 7.17% | MA | 13.07% | 6.50% | TXN | 13.93% | 6.93% |
| CB | 11.32% | 5.63% | MCD | 8.59% | 4.27% | UNH | 11.36% | 5.65% |
| CCI | 11.98% | 5.96% | MDLZ | 8.46% | 4.21% | UNP | 11.89% | 5.91% |
| CI | 13.98% | 6.95% | MDT | 10.97% | 5.46% | UPS | 12.13% | 6.03% |
| CL | 8.92% | 4.43% | META | 17.34% | 8.63% | USB | 14.14% | 7.04% |
| CMCSA | 12.41% | 6.18% | MMC | 9.21% | 4.58% | V | 11.56% | 5.75% |
| CME | 11.00% | 5.47% | MMM | 12.08% | 6.02% | VZ | 8.74% | 4.35% |
| COP | 17.96% | 8.93% | MO | 11.33% | 5.64% | WFC | 15.63% | 7.78% |
| COST | 9.50% | 4.72% | MRK | 9.28% | 4.62% | WMT | 8.89% | 4.42% |
| CRM | 16.04% | 7.98% | MS | 14.37% | 7.15% | XOM | 14.41% | 7.16% |
| CSCO | 11.70% | 5.82% | MSFT | 12.41% | 6.18% | ZTS | 11.46% | 5.70% |
| CSX | 12.18% | 6.06% | MU | 21.43% | 10.66% | |||
| CVS | 12.40% | 6.17% | NEE | 10.52% | 5.23% |
| Symbol | Mean | Shapley Value |
|---|---|---|
| AAPL | 0.132% | 0.113% |
| BTC | 0.149% | 0.363% |
| EEM | 0.006% | 0.007% |
| GLD | 0.032% | −0.259% |
| IXIC | 0.060% | 0.034% |
| IYE | 0.046% | 0.126% |
| JNK | 0.010% | −0.479% |
| NVDA | 0.210% | 0.231% |
| QQQ | 0.076% | 0.040% |
| SPY | 0.050% | −0.053% |
| TSLA | 0.255% | 0.326% |
| XLK | 0.090% | 0.053% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shalit, H. The Nonsense of Bitcoin in Portfolio Analysis. J. Risk Financial Manag. 2025, 18, 125. https://doi.org/10.3390/jrfm18030125
Shalit H. The Nonsense of Bitcoin in Portfolio Analysis. Journal of Risk and Financial Management. 2025; 18(3):125. https://doi.org/10.3390/jrfm18030125
Chicago/Turabian StyleShalit, Haim. 2025. "The Nonsense of Bitcoin in Portfolio Analysis" Journal of Risk and Financial Management 18, no. 3: 125. https://doi.org/10.3390/jrfm18030125
APA StyleShalit, H. (2025). The Nonsense of Bitcoin in Portfolio Analysis. Journal of Risk and Financial Management, 18(3), 125. https://doi.org/10.3390/jrfm18030125






