Selection Rules for Resonant Longitudinal Injector-Coupling in Experimental Rocket Combustors
Abstract
:1. Introduction
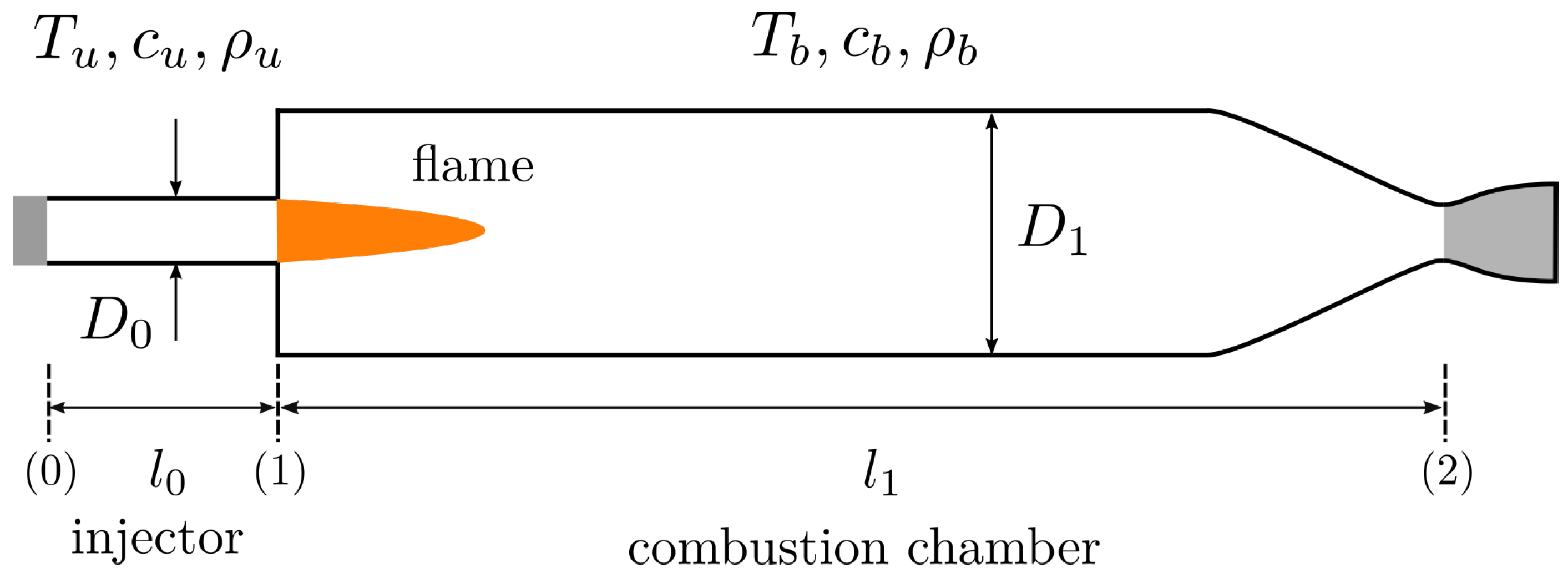
2. Acoustic Analysis of an Injector-Combustion-Chamber System
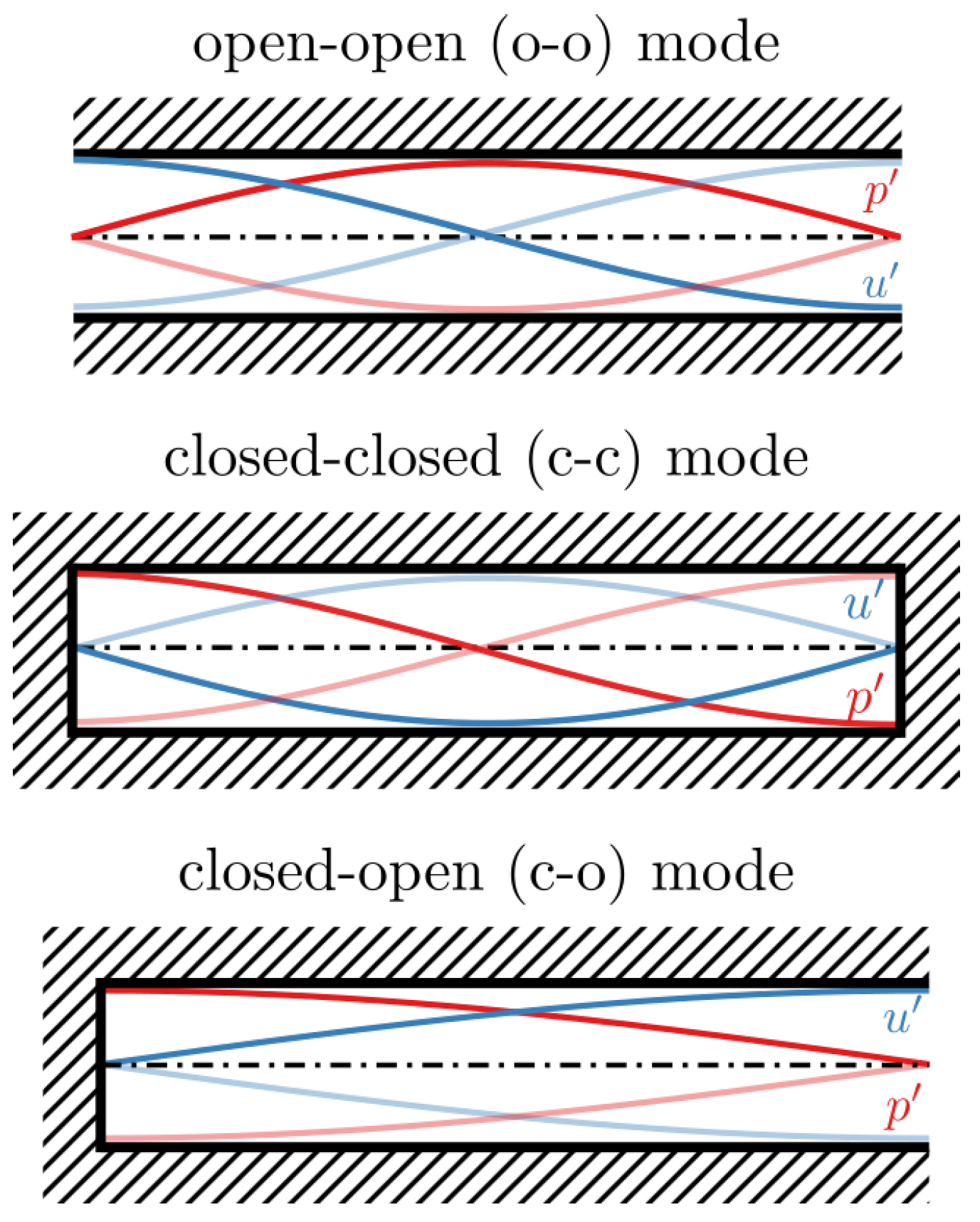
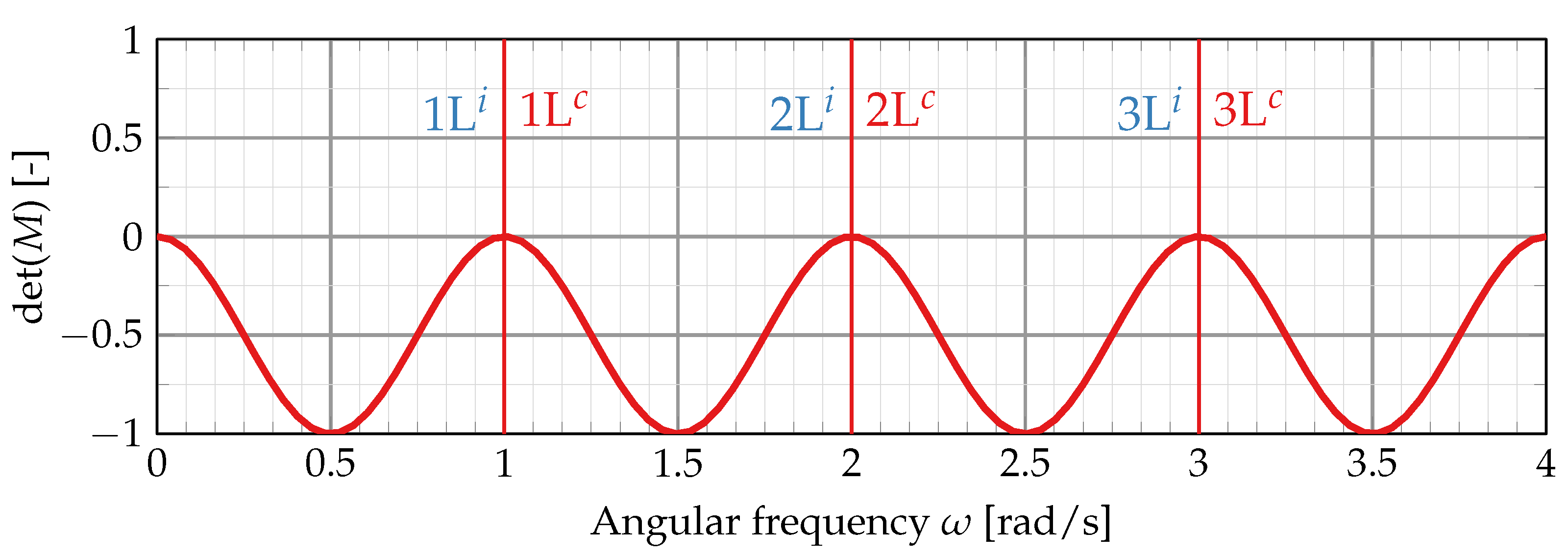
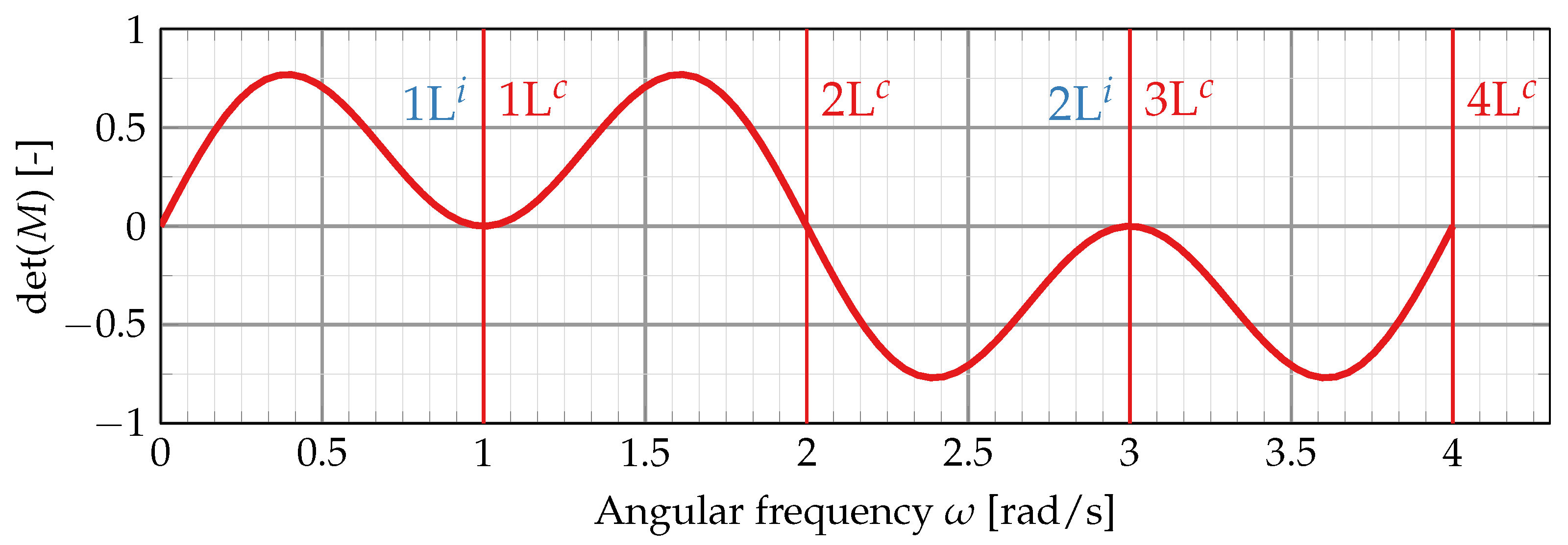
3. Derivation of Mode Selection Rules for Resonant Coupling
3.1. Resonant Mode Coupling with an Open Injector
3.2. Resonant Mode Coupling with a Closed Injector
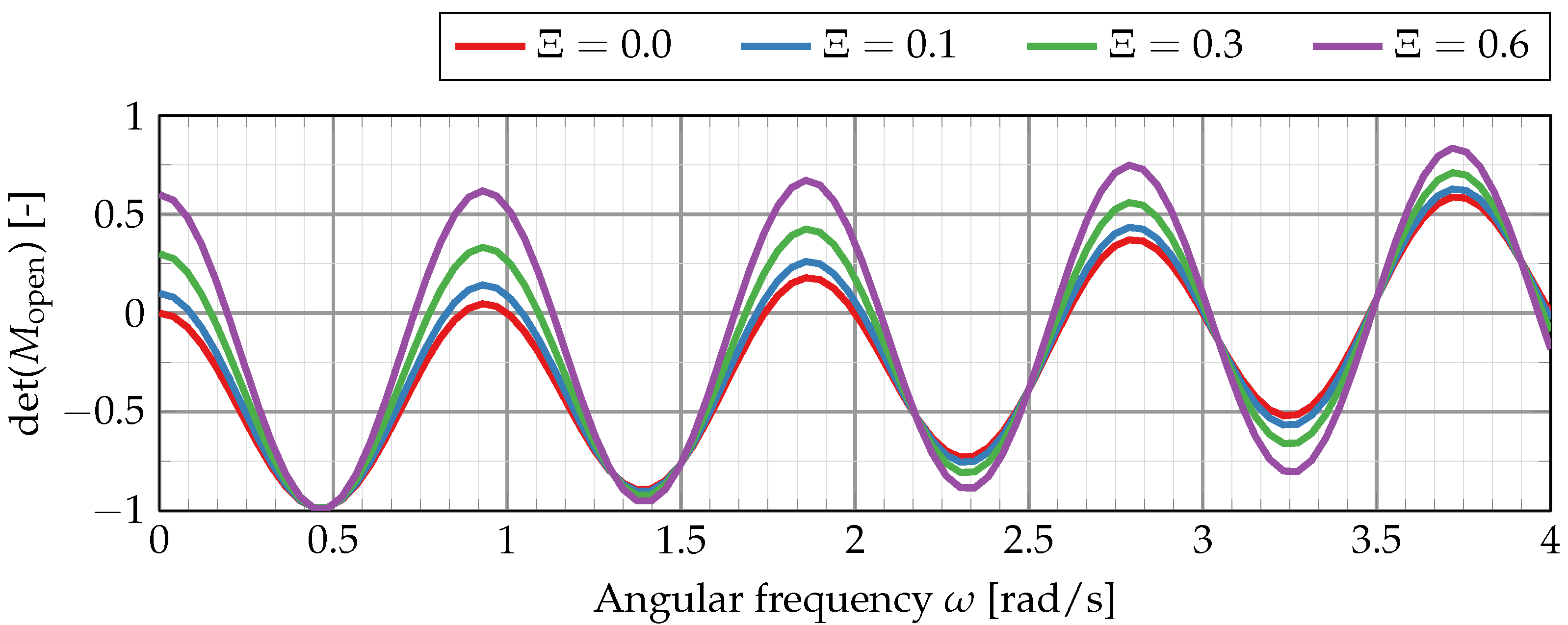
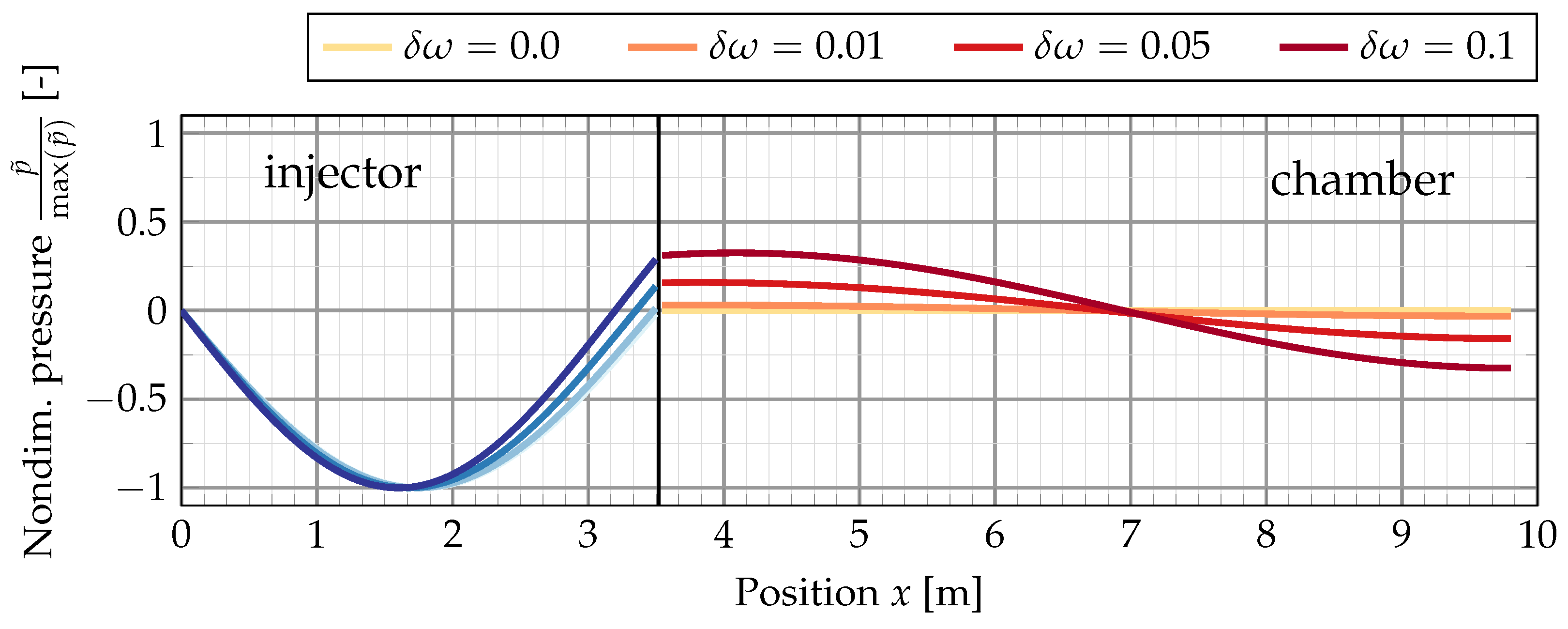
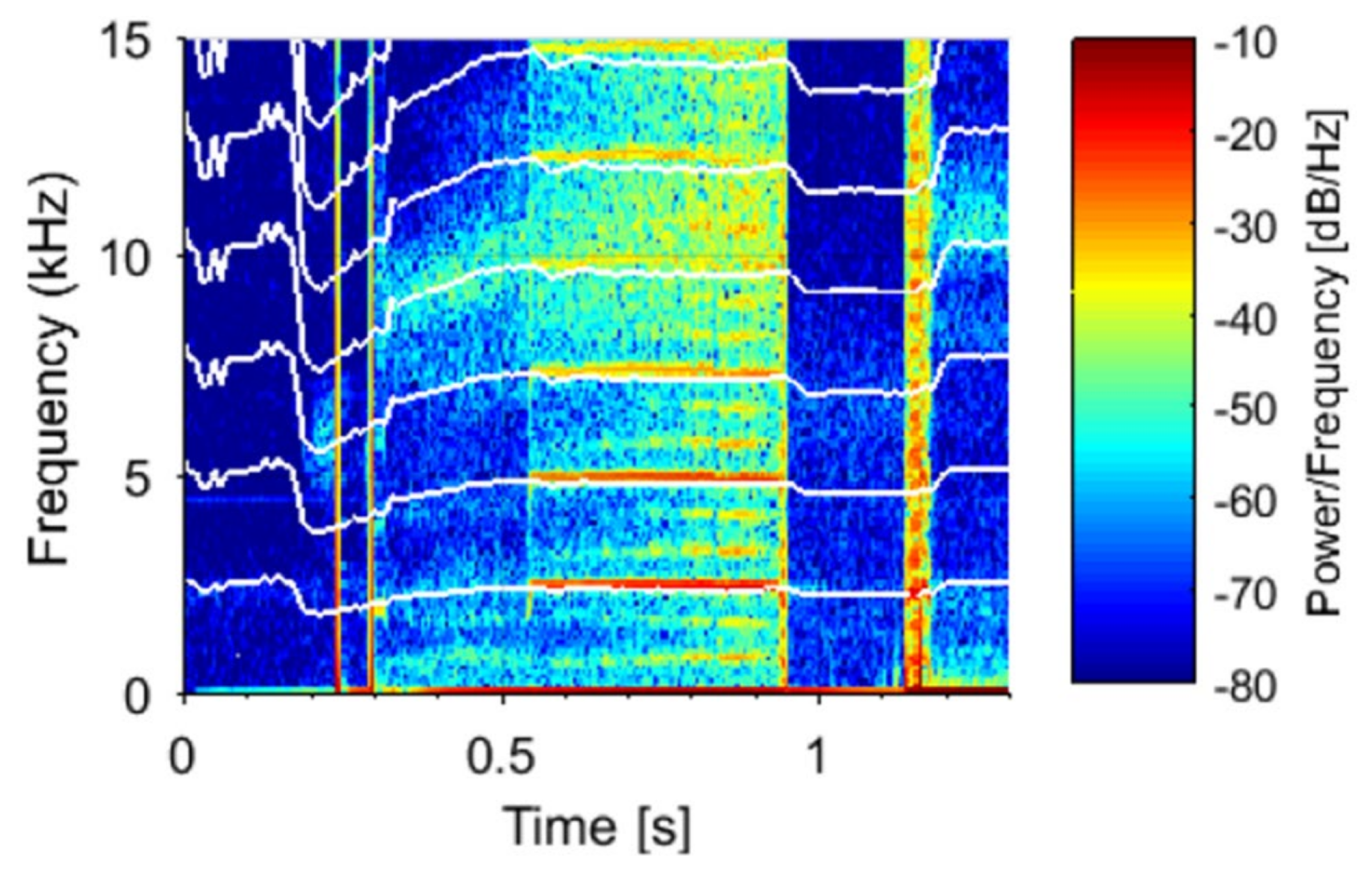
4. Results
4.1. Open Injector Coupling during Ignition Testing of a Subscale LOx-Methane Rocket Thrust Chamber
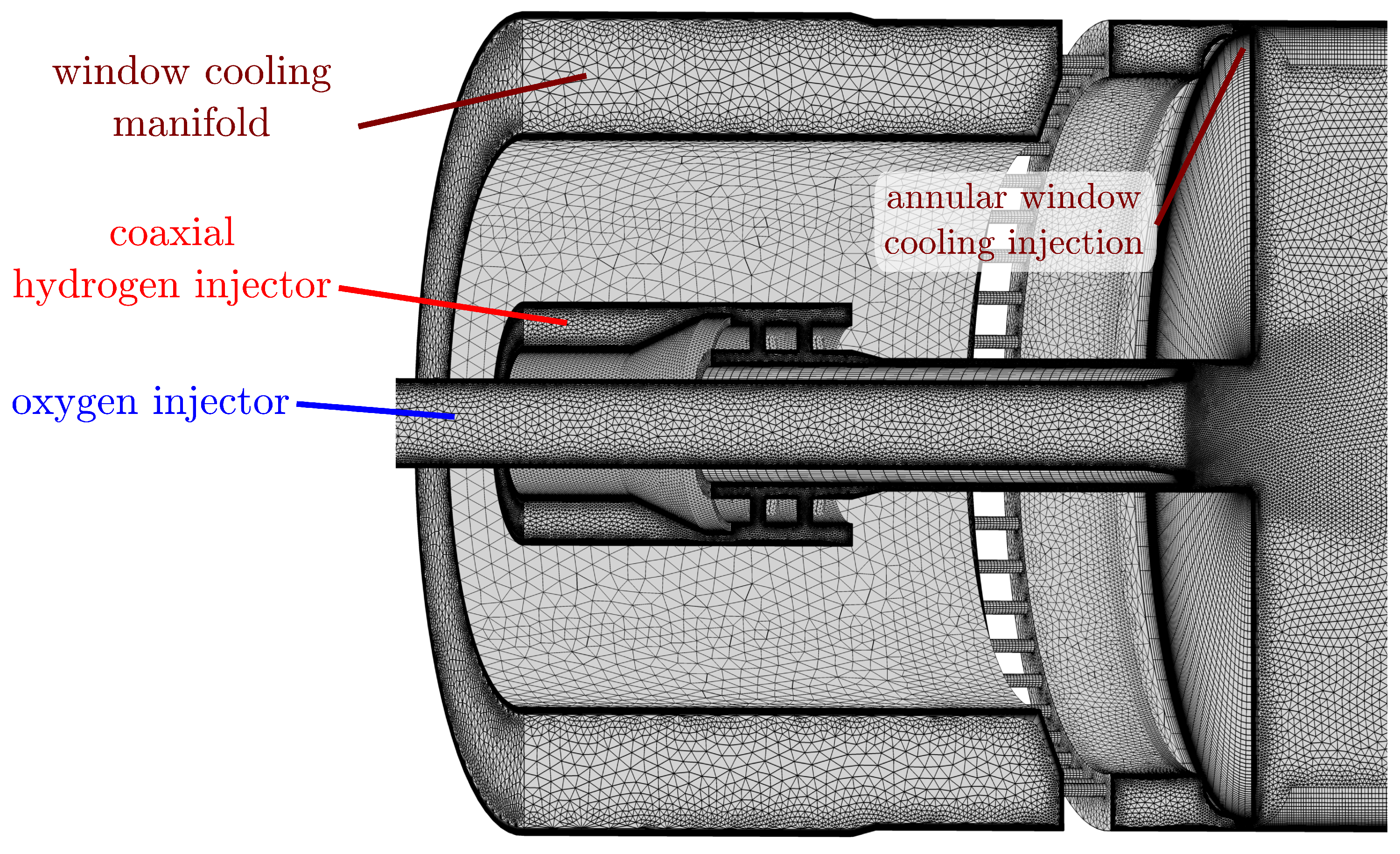
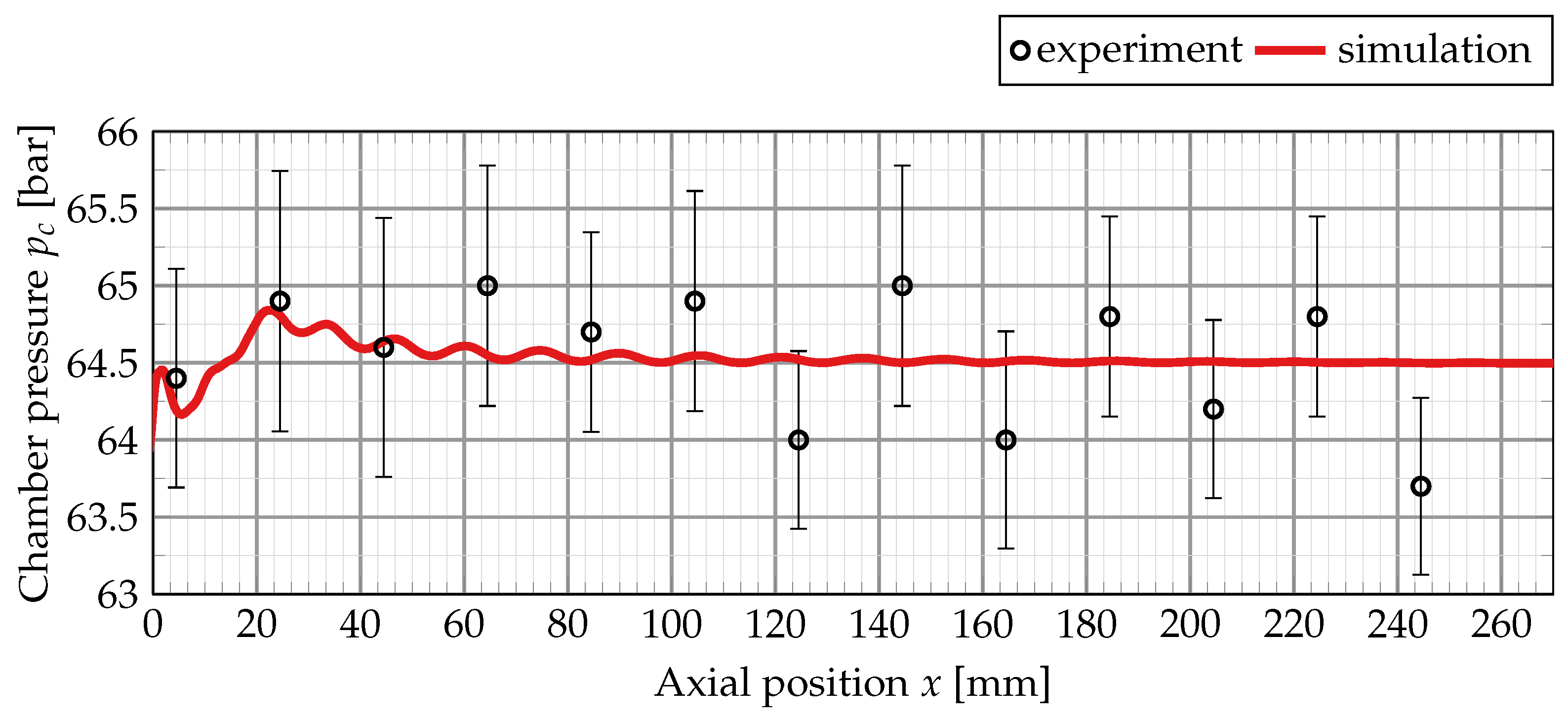
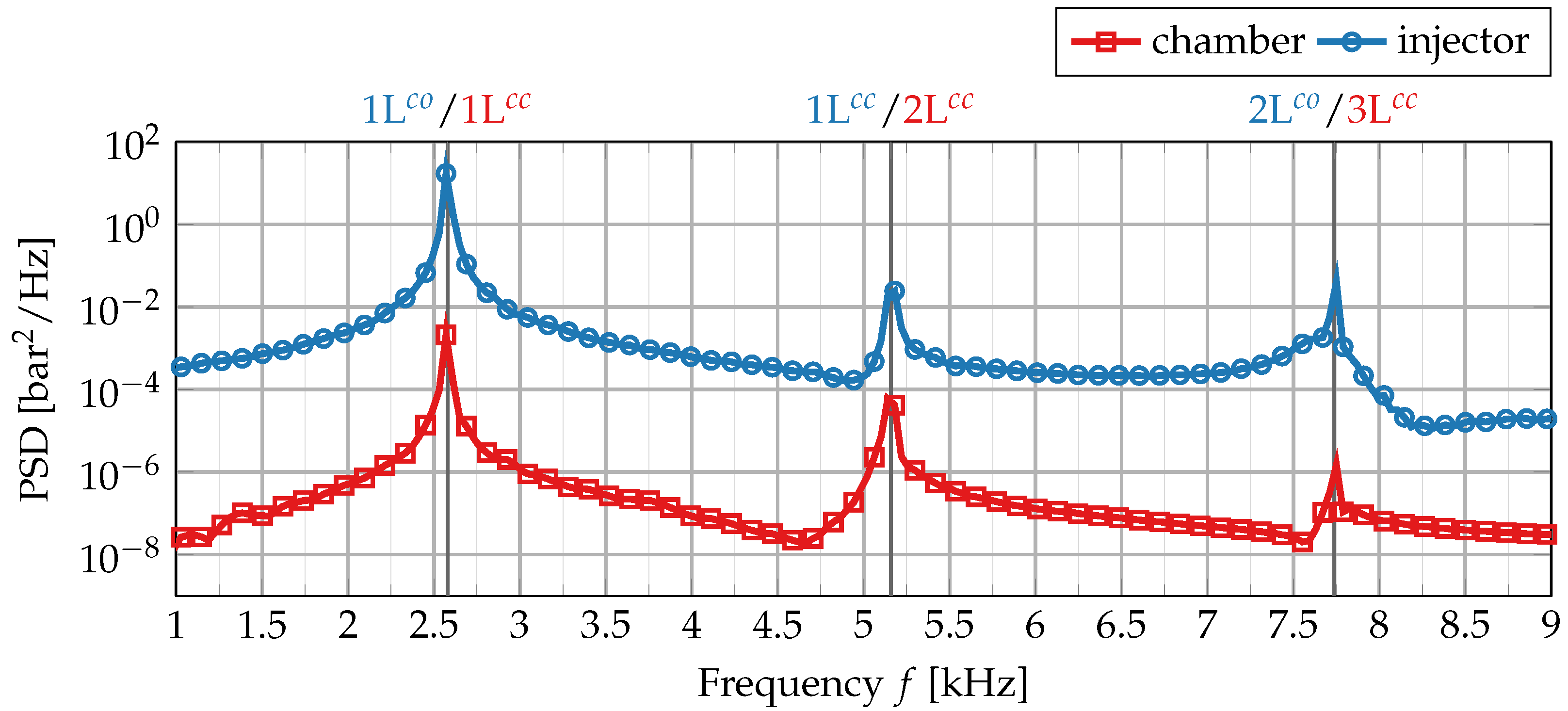
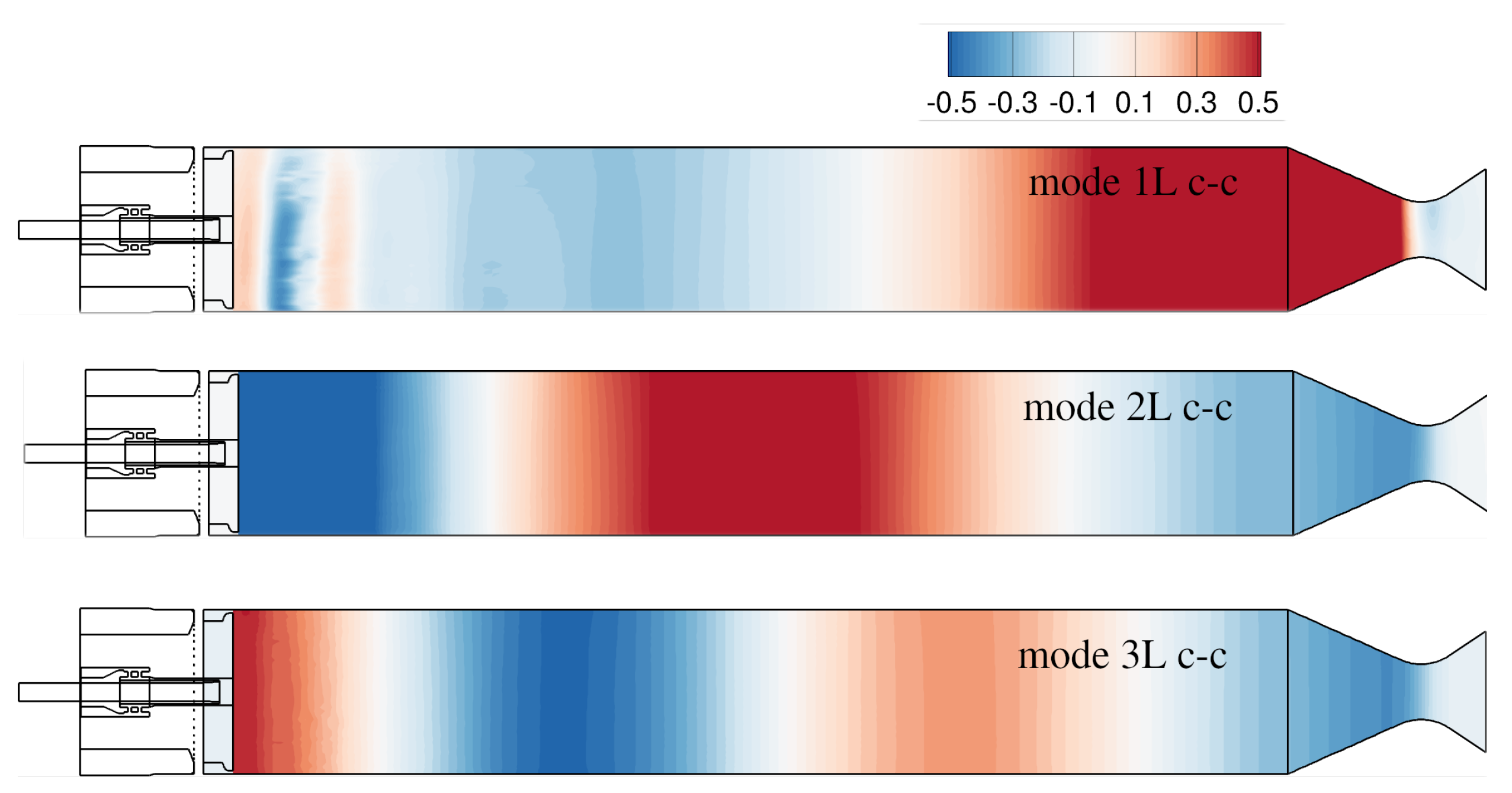
4.2. Closed Injector Coupling in Numerical Simulations of a Subscale H/O Rocket Thrust Chamber
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harrje, D.; Reardon, F. Liquid Propellant Rocket Combustion Instability; Report SP-194; National Aeronautics and Space Agency (NASA): Washington, DC, USA, 1972. [Google Scholar]
- Yang, V.; Anderson, W.E. Liquid Rocket Engine Combustion Instability; American Institute for Aeronautics and Aerospace (AIAA): Washington, DC, USA, 1995; Volume 169. [Google Scholar]
- O’Connor, J.; Acharya, V.; Lieuwen, T. Transverse combustion instabilities: Acoustic, fluid mechanic, and flame processes. Prog. Energy Combust. Sci. 2015, 49, 1–39. [Google Scholar] [CrossRef] [Green Version]
- Conrad, E.; Parish, H.; Wanhainen, J. Effect of Propellant Injection Velocity on Screech in 20,000-Pound Hydrogen-Oxygen Rocket Engine; Report TN-D-3373; National Aeronautics and Space Agency (NASA): Washington, DC, USA, 1966. [Google Scholar]
- Armbruster, W.; Hardi, J.; Oschwald, M. Impact of shear-coaxial injector hydrodynamics on high-frequency combustion instabilities in a representative cryogenic rocket engine. Int. J. Spray Combust. Dyn. 2022, 14, 118–130. [Google Scholar] [CrossRef]
- Gröning, S.; Hardi, J.S.; Suslov, D.; Oschwald, M. Injector-driven combustion instabilities in a hydrogen/oxygen rocket combustor. J. Propuls. Power 2016, 32, 560–573. [Google Scholar] [CrossRef]
- Nunome, Y.; Onodera, T.; Sasaki, M.; Tomita, T.; Kobayashi, K.; Daimon, Y. Combustion instability phenomena observed during cryogenic hydrogen injection temperature ramping tests for single coaxial injector elements. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011; p. 6027. [Google Scholar]
- Kawashima, H.; Kobayashi, K.; Tomita, T.; Kaneko, T. A Combustion Instability Phenomenon on a LOX/Methane Subscale combustor. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar] [CrossRef]
- Martin, J.; Armbruster, W.; Hardi, J. Flame-acoustic interaction in a high-pressure, single-injector LOX/H2 rocket combustor with optical access. In Proceedings of the Symposium on Thermoacoustics in Combustion: Industry meets Academia (SoTiC 2021), Garching, Germany, 6–10 September 2021. [Google Scholar]
- Gröning, S.; Hardi, J.; Suslov, D.; Oschwald, M. Influence of hydrogen temperature on the stability of a rocket engine combustor operated with hydrogen and oxygen. CEAS Space J. 2017, 9, 59–76. [Google Scholar] [CrossRef]
- Yu, Y.; Koeglmeier, S.; Sisco, J.; Anderson, W. Combustion instability of gaseous fuels in a continuously variable resonance chamber (CVRC). In Proceedings of the 44th AIAA ASME SAE ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 4657. [Google Scholar]
- Klein, S.; Börner, M.; Hardi, J.S.; Suslov, D.; Oschwald, M. Injector-coupled thermoacoustic instabilities in an experimental LOX-methane rocket combustor during start-up. CEAS Space J. 2020, 12, 267–279. [Google Scholar] [CrossRef] [Green Version]
- Schuller, T.; Durox, D.; Palies, P.; Candel, S. Acoustic decoupling of longitudinal modes in generic combustion systems. Combust. Flame 2012, 159, 1921–1931. [Google Scholar] [CrossRef]
- Candel, S. Combustion dynamics and control: Progress and challenges. Proc. Combust. Inst. 2002, 29, 1–28. [Google Scholar] [CrossRef]
- Noiray, N.; Durox, D.; Schuller, T.; Candel, S. A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 2008, 615, 139–167. [Google Scholar] [CrossRef]
- Marble, F.; Candel, S. Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
- Horchler, T.; Armbruster, W.; Hardi, J.; Karl, S.; Hanneman, K.; Gernoth, A.; De Rosa, M. Modeling Combustion Chamber acoustic using the DLR-TAU Code. In Proceedings of the Space Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Martin, J.; Armbruster, W.; Stützer, R.; General, S.; Knapp, B.; Suslov, D.; Hardi, J. Flame characteristics of a high-pressure LOX/H2 rocket combustor with large optical access. Case Stud. Therm. Eng. 2021, 28, 101546. [Google Scholar] [CrossRef]
- Schwamborn, D.; Gerhold, T.; Heinrich, R. The DLR-TAU-Code: Recent Applications in Reasearch and Industry. In Proceedings of the European Conference on Computational Fluid Dynamics (ECCOMAS), Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Jameson, A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991; p. 1596. [Google Scholar]
- Thornber, B.; Mosedale, A.; Drikakis, D.; Youngs, D.; Williams, R. An improved reconstruction method for compressible flows with low Mach number features. J. Comput. Phys. 2008, 227, 4873–4894. [Google Scholar] [CrossRef]
- Rossow, C.C. Extension of a compressible code toward the incompressible limit. AIAA J. 2003, 41, 2379–2386. [Google Scholar] [CrossRef]
- Rumsey, C. Turbulence Modeling Resource. Available online: https://turbmodels.larc.nasa.gov/ (accessed on 22 August 2022).
- Gaffney, J.R.; White, J.; Girimaji, S.; Drummond, J. Modeling turbulent/chemistry interactions using assumed PDF methods. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992; p. 3638. [Google Scholar]
- Kim, S.K.; Choi, H.S.; Kim, Y. Thermodynamic modeling based on a generalized cubic equation of state for kerosene/LOx rocket combustion. Combust. Flame 2012, 159, 1351–1365. [Google Scholar] [CrossRef]
- Horchler, T.; Fechter, S.; Hardi, J. Numerical Investigation of Flame-Acoustic Interaction at Resonant and Non-Resonant Conditions in a Model Combustion Chamber. In Proceedings of the Symposium on Thermoacoustics in Combustion: Industry meets Academia (SoTiC 2021), Garching, Germany, 6–10 September 2021. [Google Scholar]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Webster, S.; Hardi, J.; Oschwald, M. One-Dimensional Model Describing Eigenmode Frequency Shift During Transverse Excitation. In Progress in Propulsion Physics; EDP Sciences: Les Ulis Cedex A, France, 2019; pp. 273–294. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Books on Mathematics; Dover Publications Inc.: Mineola, NY, USA, 1965. [Google Scholar]





| Quantity | Value | Unit |
|---|---|---|
| Ratio oxidizer-over-fuel ROF | 4 | - |
| Chamber pressure | 64.6 | bar |
| O mass flow rate | 0.327 | kg/s |
| O injection temperature | 112 | K |
| H mass flow rate | 0.082 | kg/s |
| H injection temperature | 168 | K |
| H window film cooling | 0.199 | kg/s |
| H film cooling temperature | 168 | K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horchler, T. Selection Rules for Resonant Longitudinal Injector-Coupling in Experimental Rocket Combustors. Aerospace 2022, 9, 669. https://doi.org/10.3390/aerospace9110669
Horchler T. Selection Rules for Resonant Longitudinal Injector-Coupling in Experimental Rocket Combustors. Aerospace. 2022; 9(11):669. https://doi.org/10.3390/aerospace9110669
Chicago/Turabian StyleHorchler, Tim. 2022. "Selection Rules for Resonant Longitudinal Injector-Coupling in Experimental Rocket Combustors" Aerospace 9, no. 11: 669. https://doi.org/10.3390/aerospace9110669
APA StyleHorchler, T. (2022). Selection Rules for Resonant Longitudinal Injector-Coupling in Experimental Rocket Combustors. Aerospace, 9(11), 669. https://doi.org/10.3390/aerospace9110669






