Basics of Control of the Bow Shock Wave, Drag and Lift Forces, and Stability in a Steady Supersonic Flow Past an AD Body Using Permanently Operating Thermally Stratified Energy Deposition
Abstract
:1. Introduction
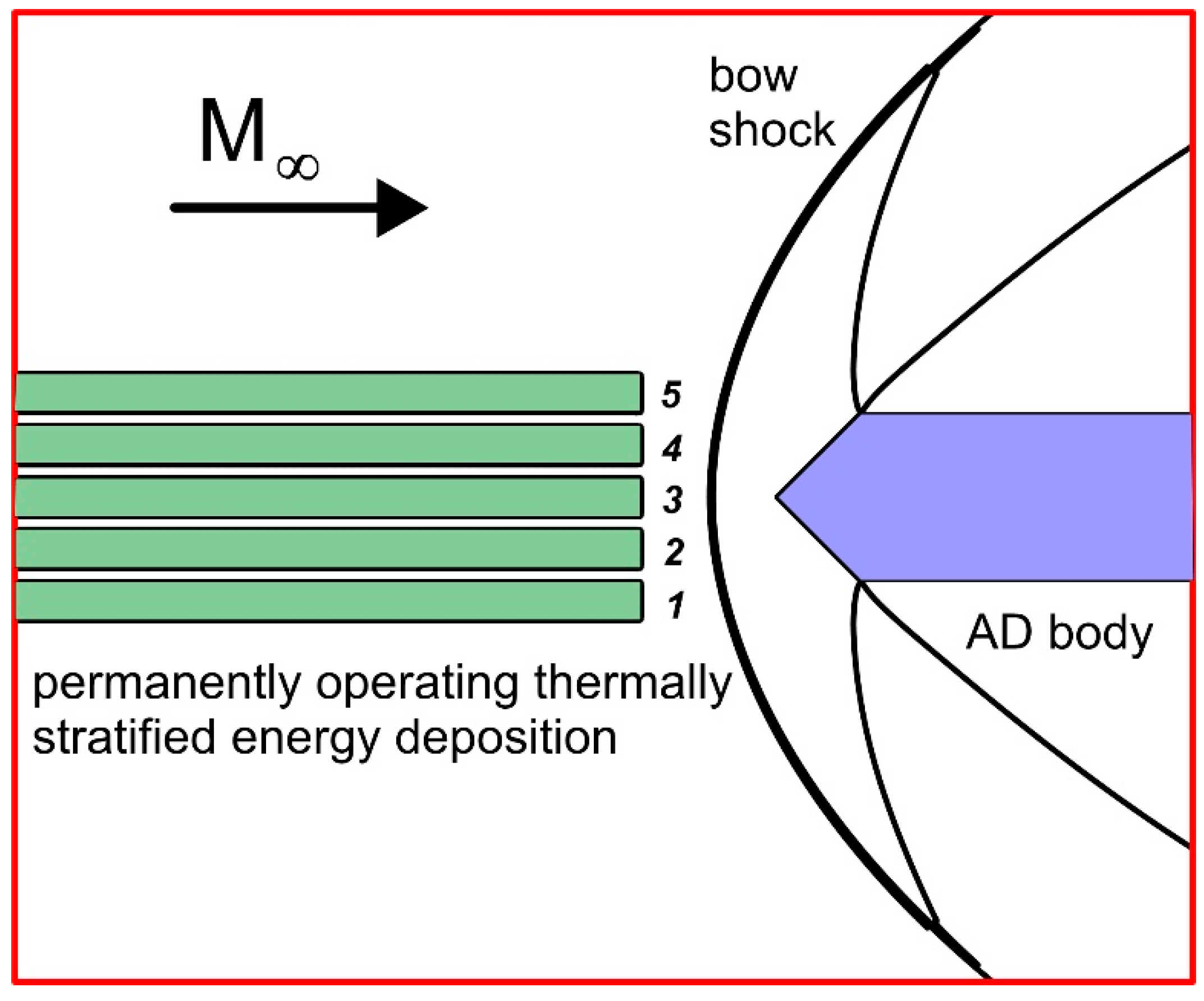
2. Statement of the Problem and Methodology
3. Analysis of the Grid Convergence
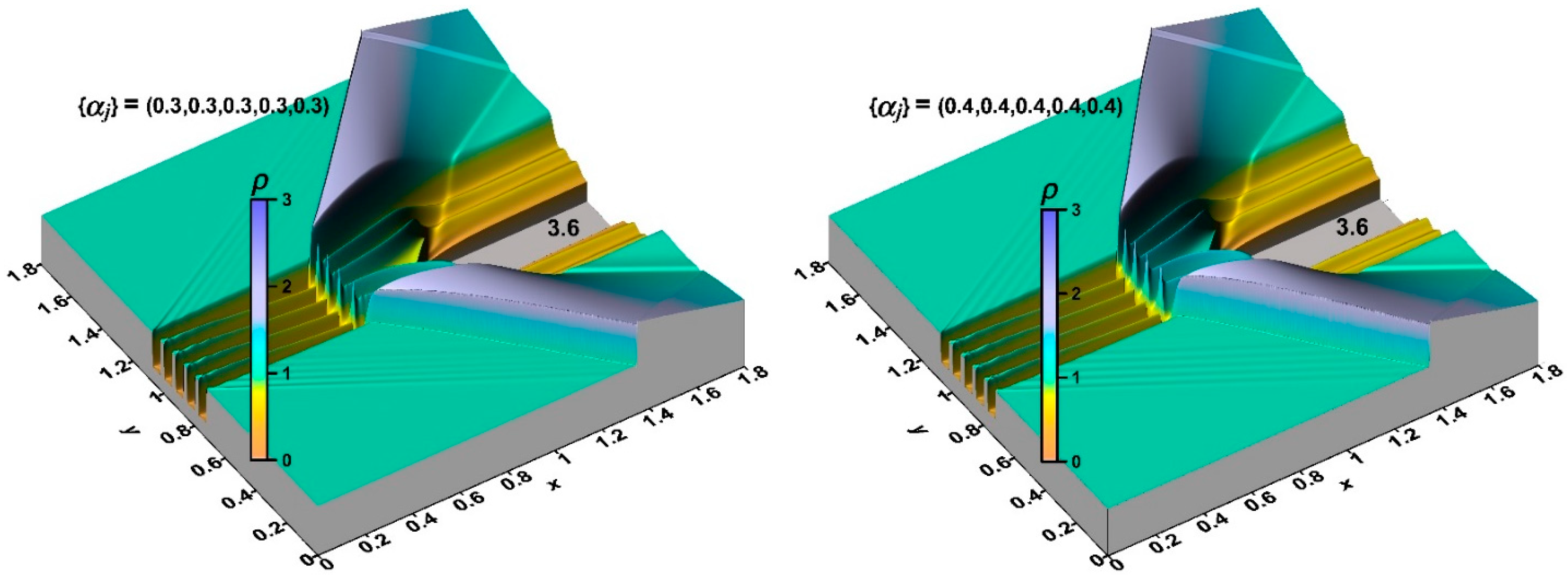
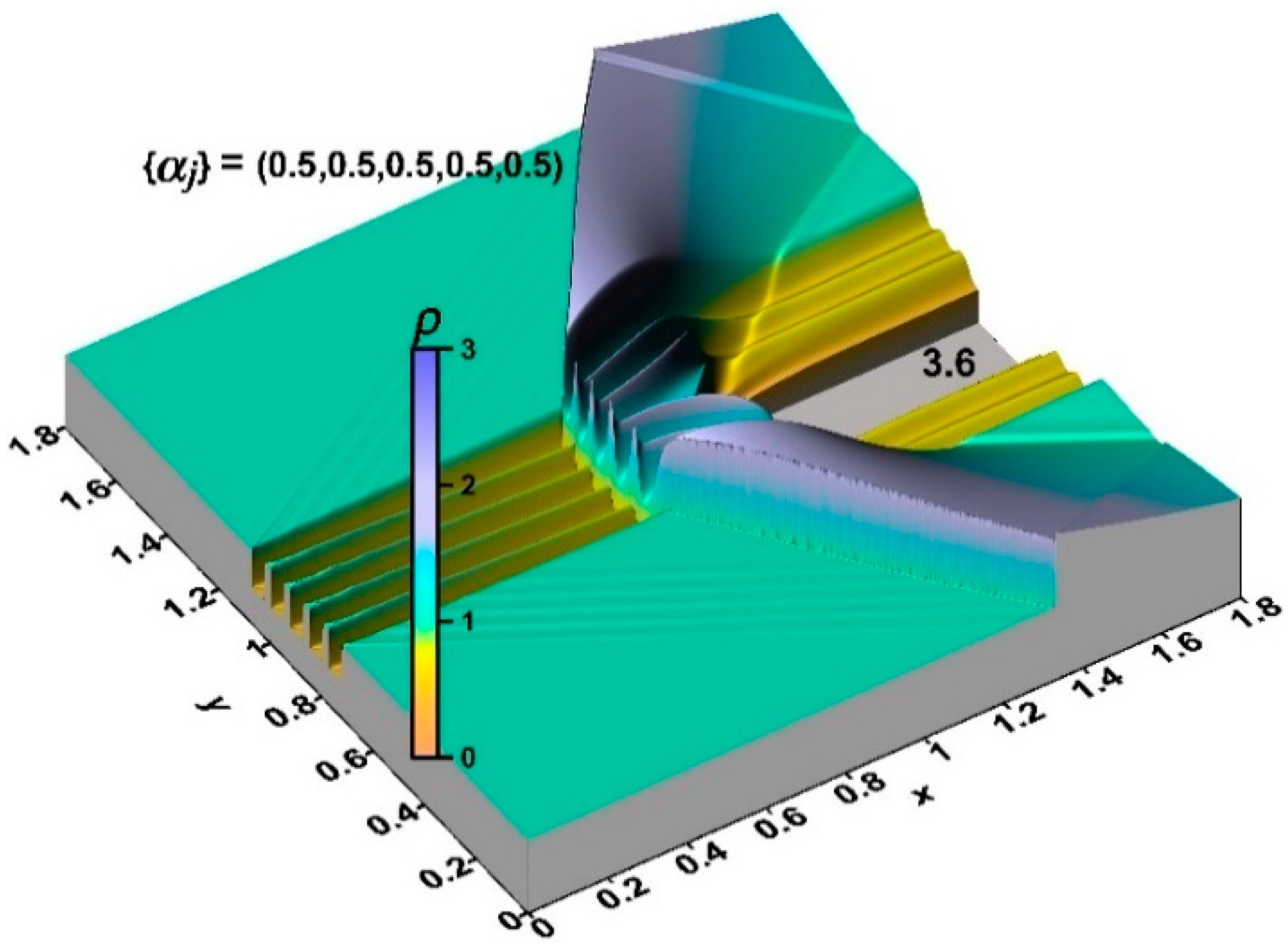
4. Analysis of the Impact of a Thermally Stratified Energy Source on a Supersonic Flow Past an AD Body for Different Symmetrical Sets {αj}
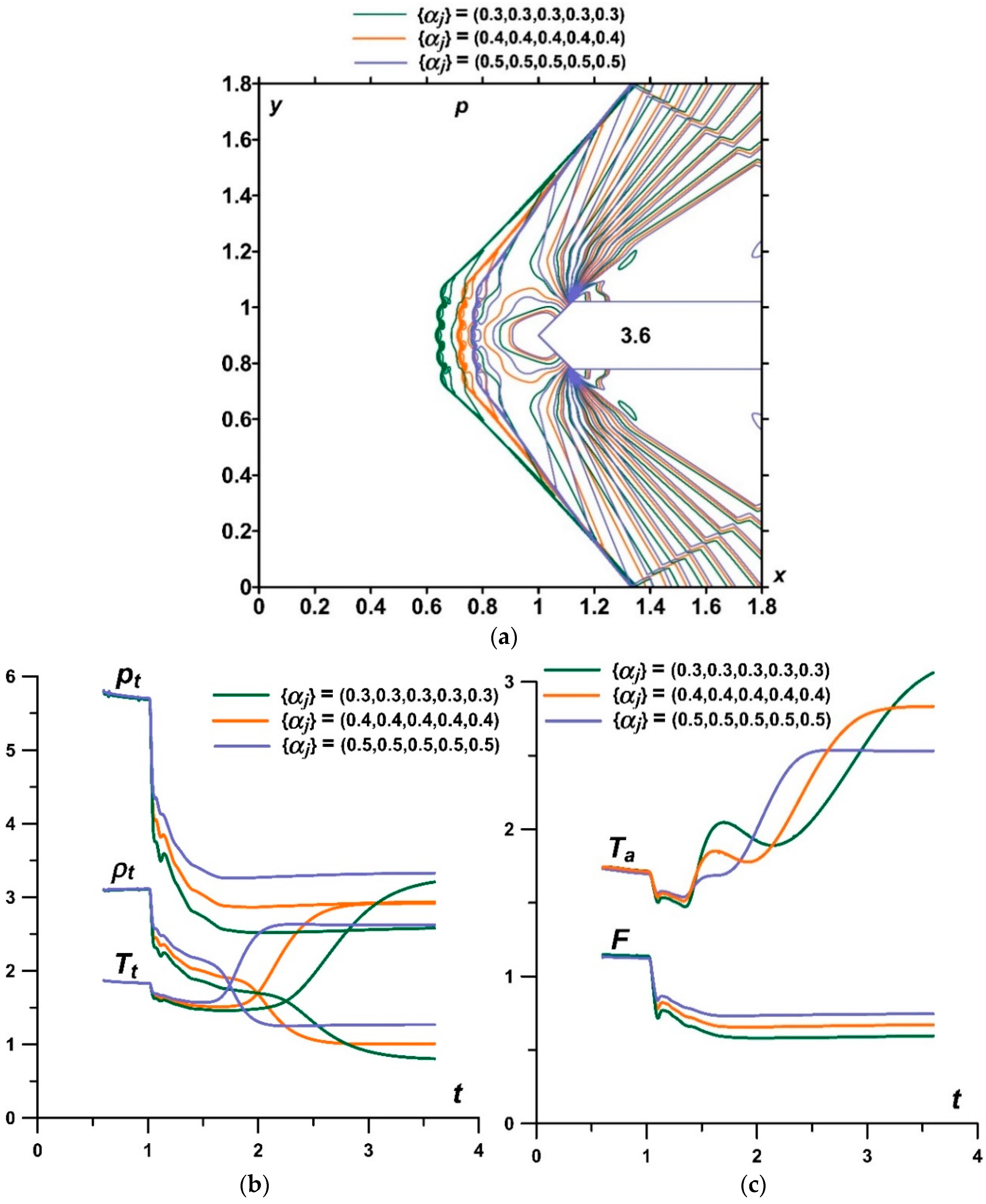
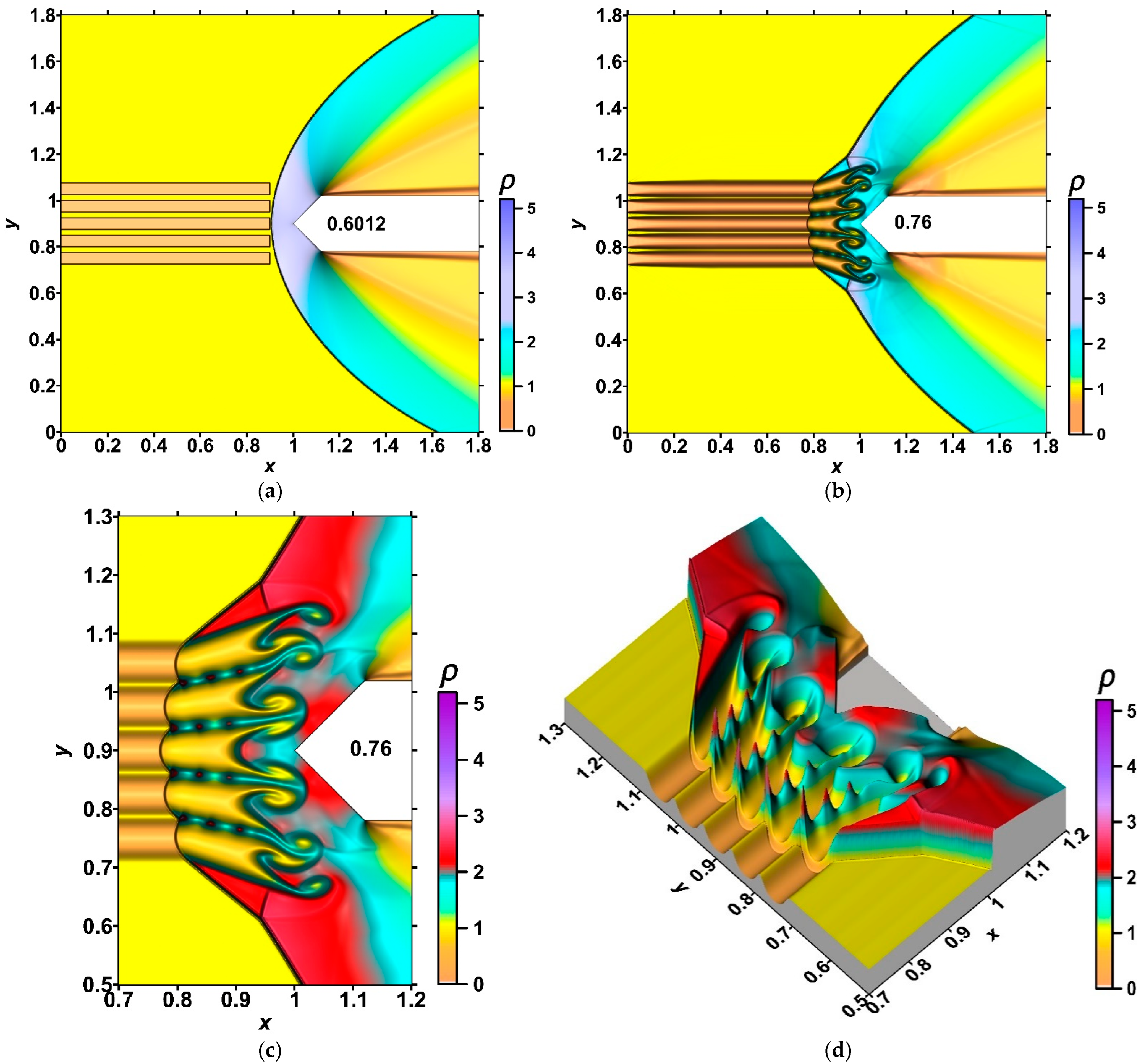
4.1. Analysis of the Flow Dynamics during the Interaction of an Energy Source with Equally Heated Layers with a Supersonic Flow Past an AD Body
4.2. Analysis of the Dynamics of the Flow Field Parameters during the Interaction of an Energy Source with Different Temperatures in the Layers with a Supersonic Flow Past an AD Body
5. Analysis of an Impact of a Thermally Stratified Energy Source on a Supersonic Flow Past an AD Body for Different Asymmetrical Sets {αj}
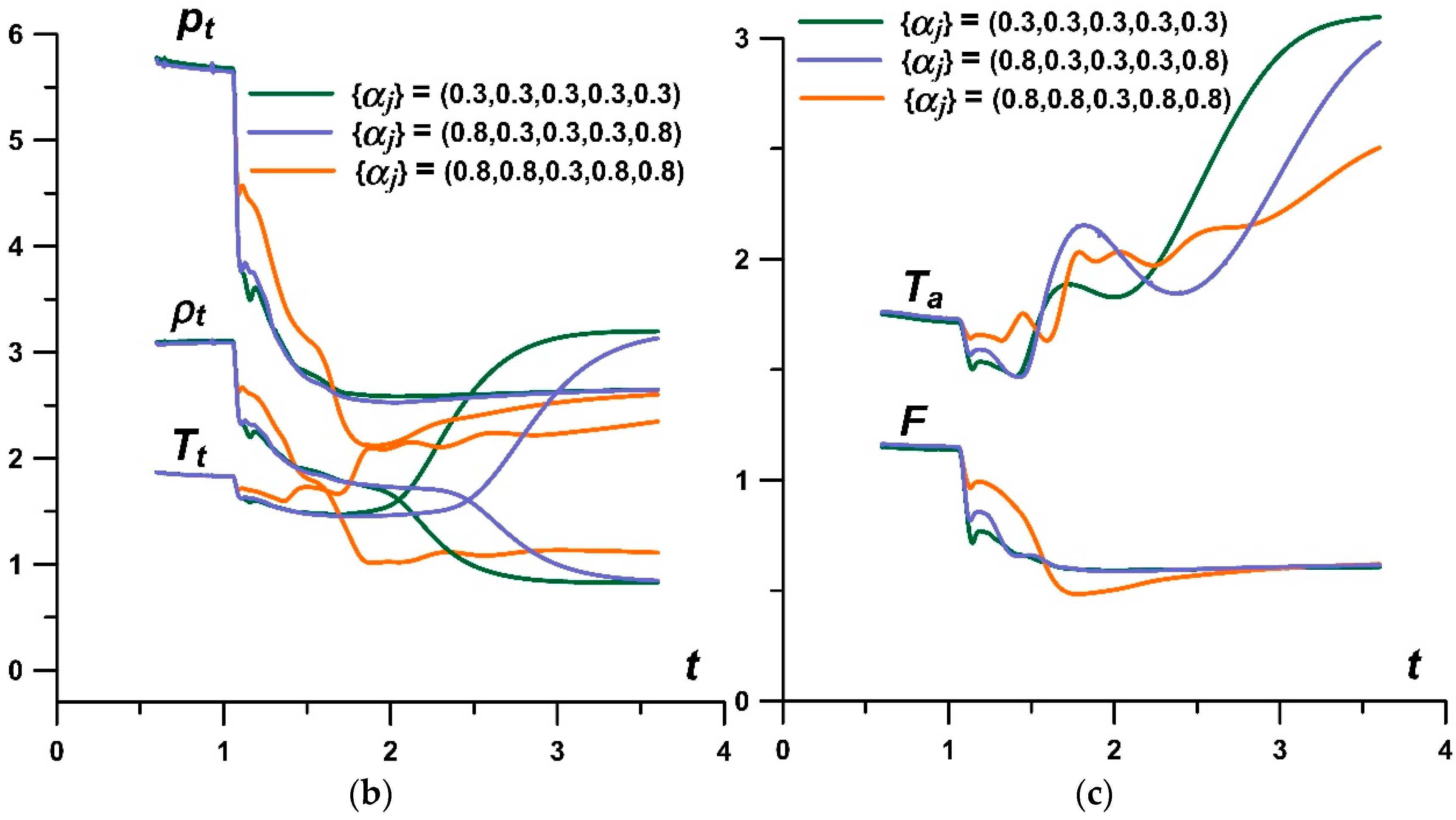
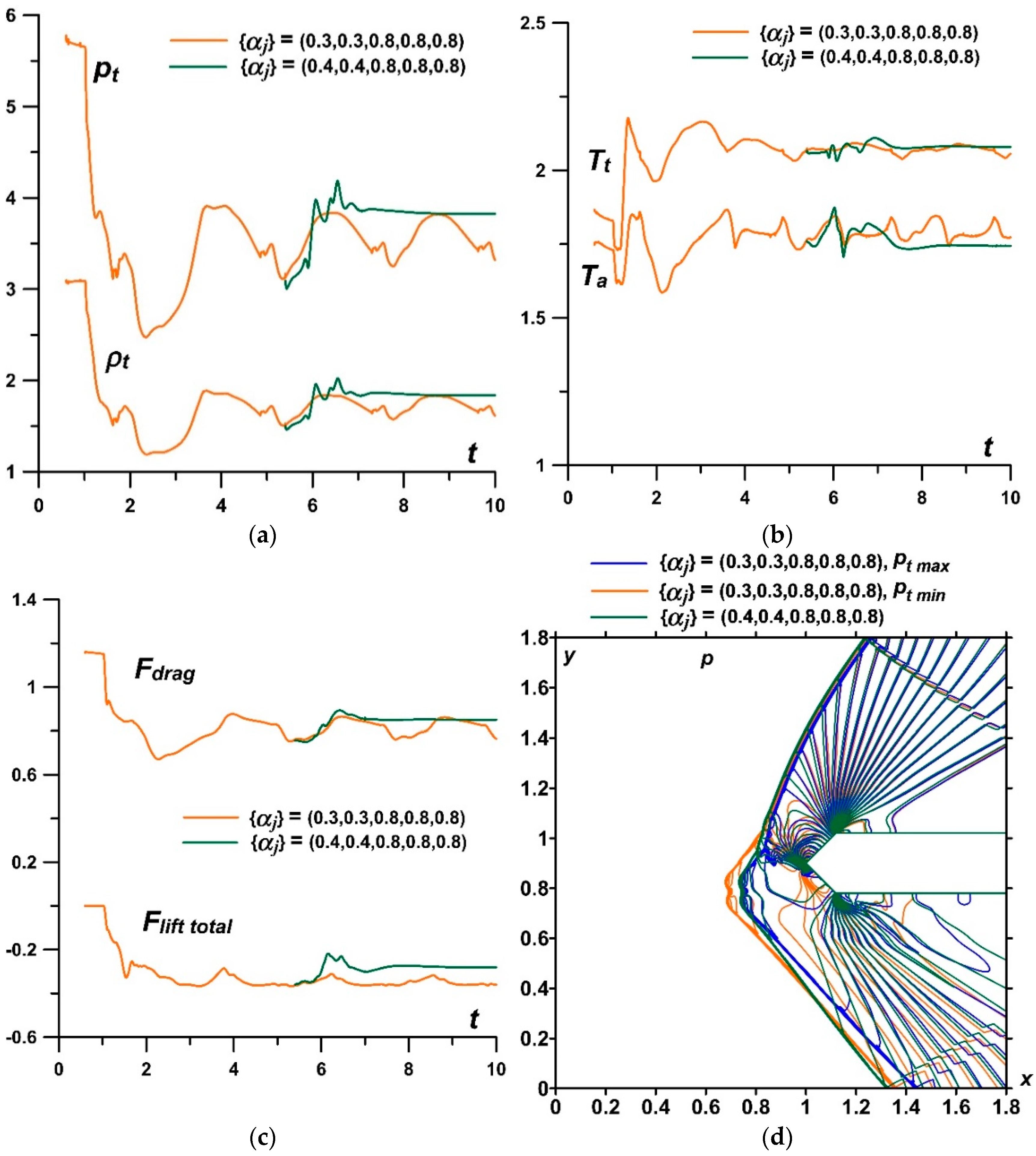
5.1. Initiation and Suppression of Flow Pulsations by Changing the Temperature in the Layers of a Stratified Energy Source
5.2. Organization of the Opposite Effect on the Front Surfaces of the Body and the Initiation of Oppositely Directed Lift (Pitch) Forces
6. Discussion
7. Conclusions
- -
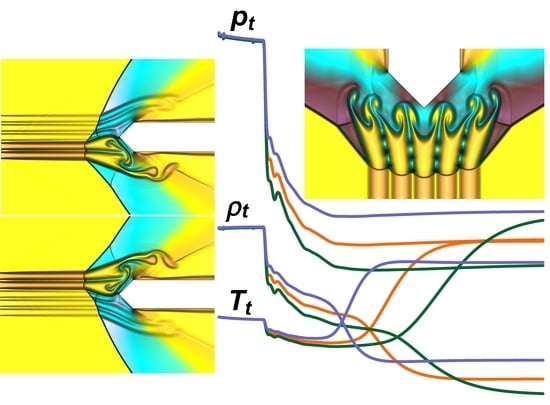
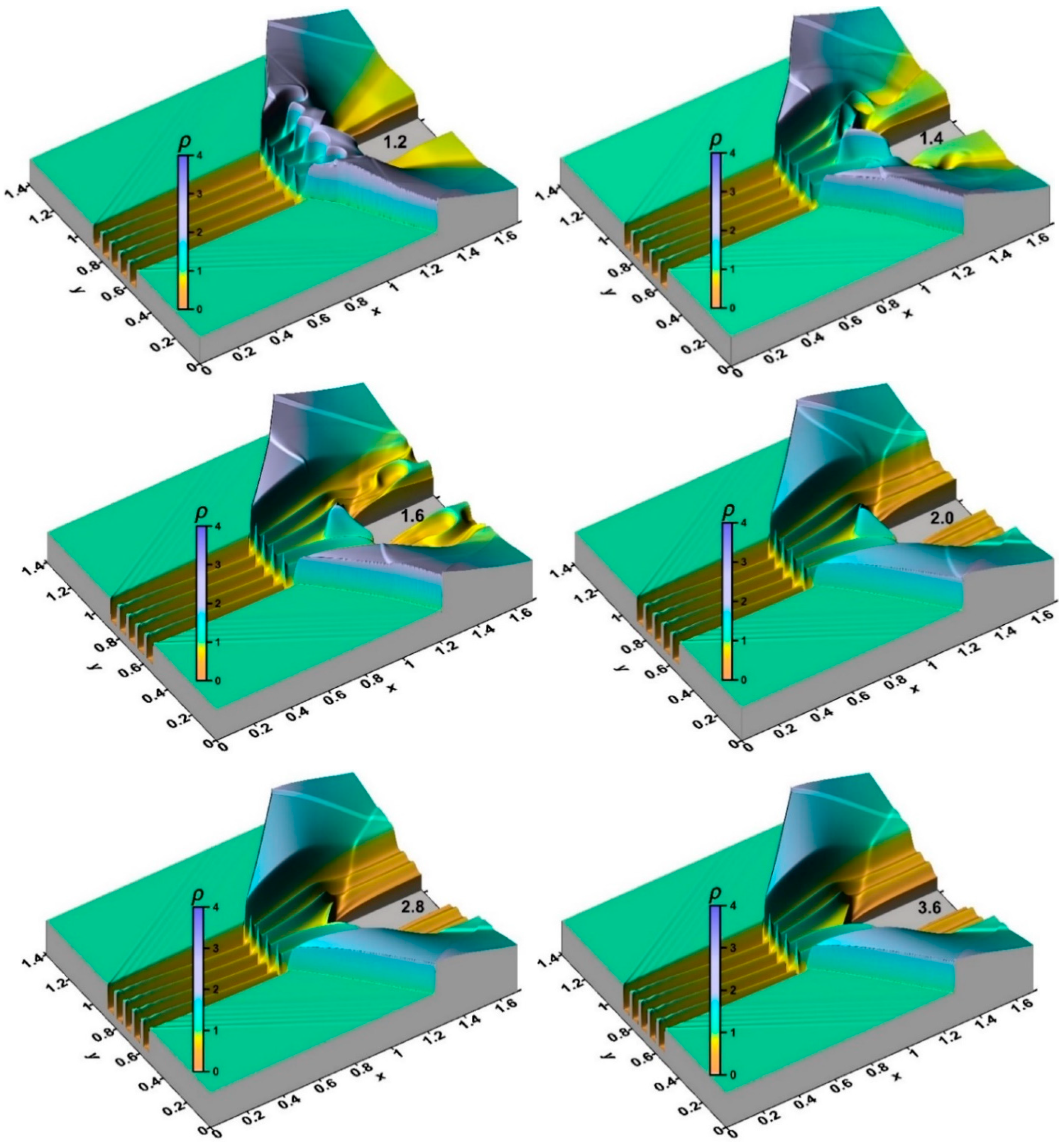
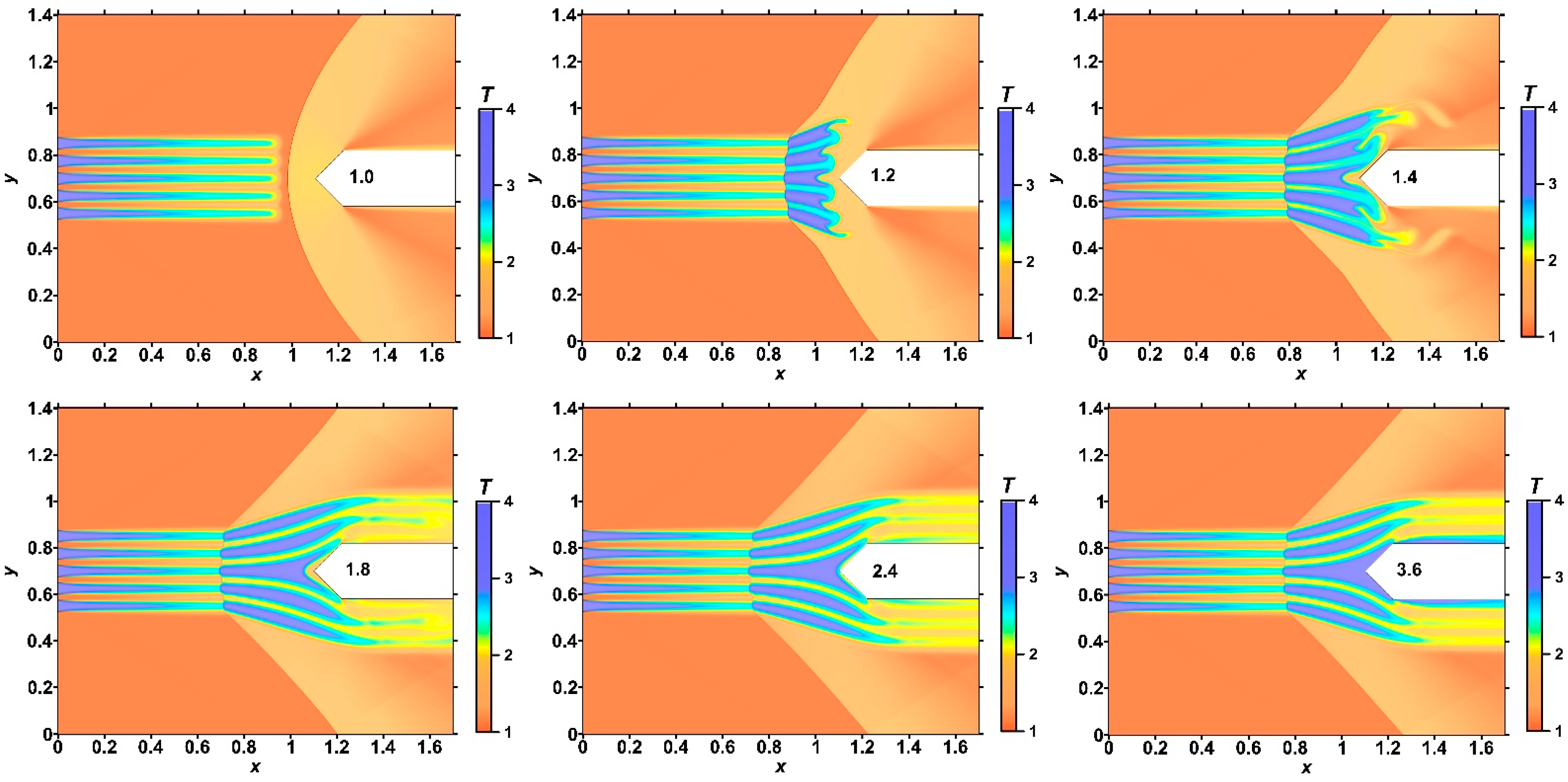
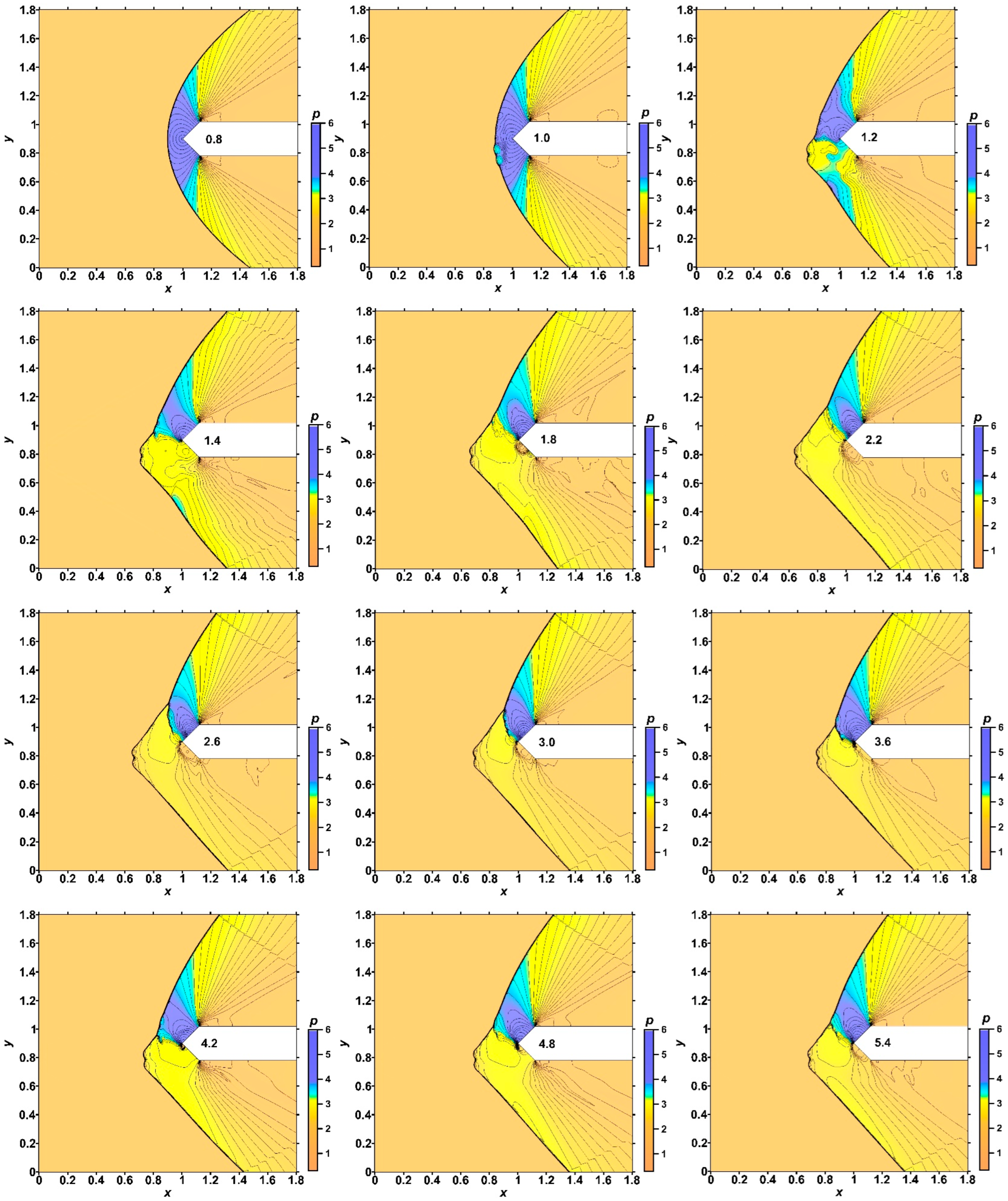
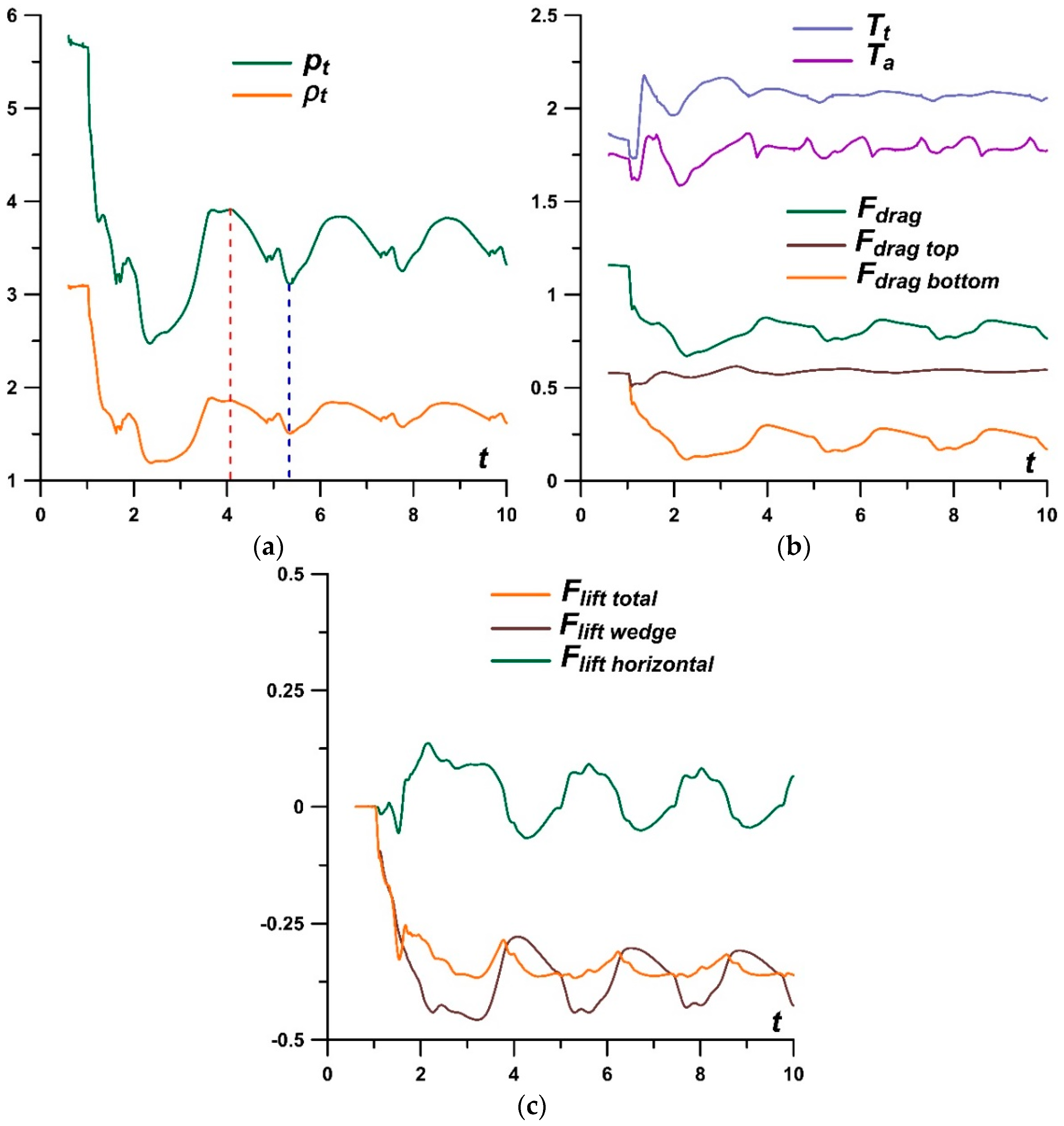
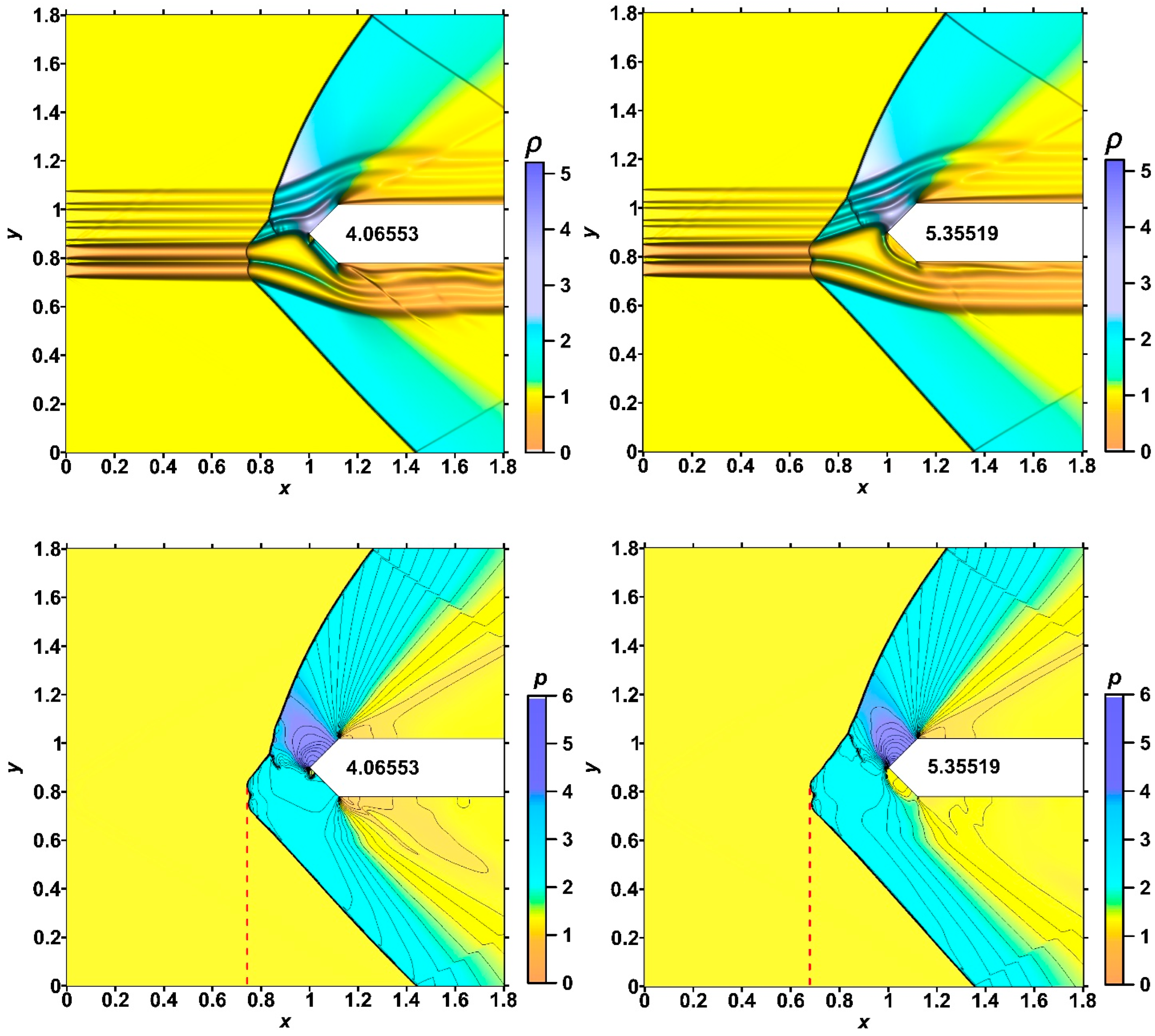
- Multiple generations of the Richtmyer–Meshkov instability were shown. A new steady flow mode was established, in which the front of the bow shock wave can be completely destroyed in the zone of the source layers. The sharp peaks accompanying the development of the Richtmyer–Meshkov instabilities were obtained, which remain in the steady flow mode established under the action of a stratified energy source. The magnitudes of the picks are greater for smaller αj (greater temperatures) in the layers of the energy source.
- -
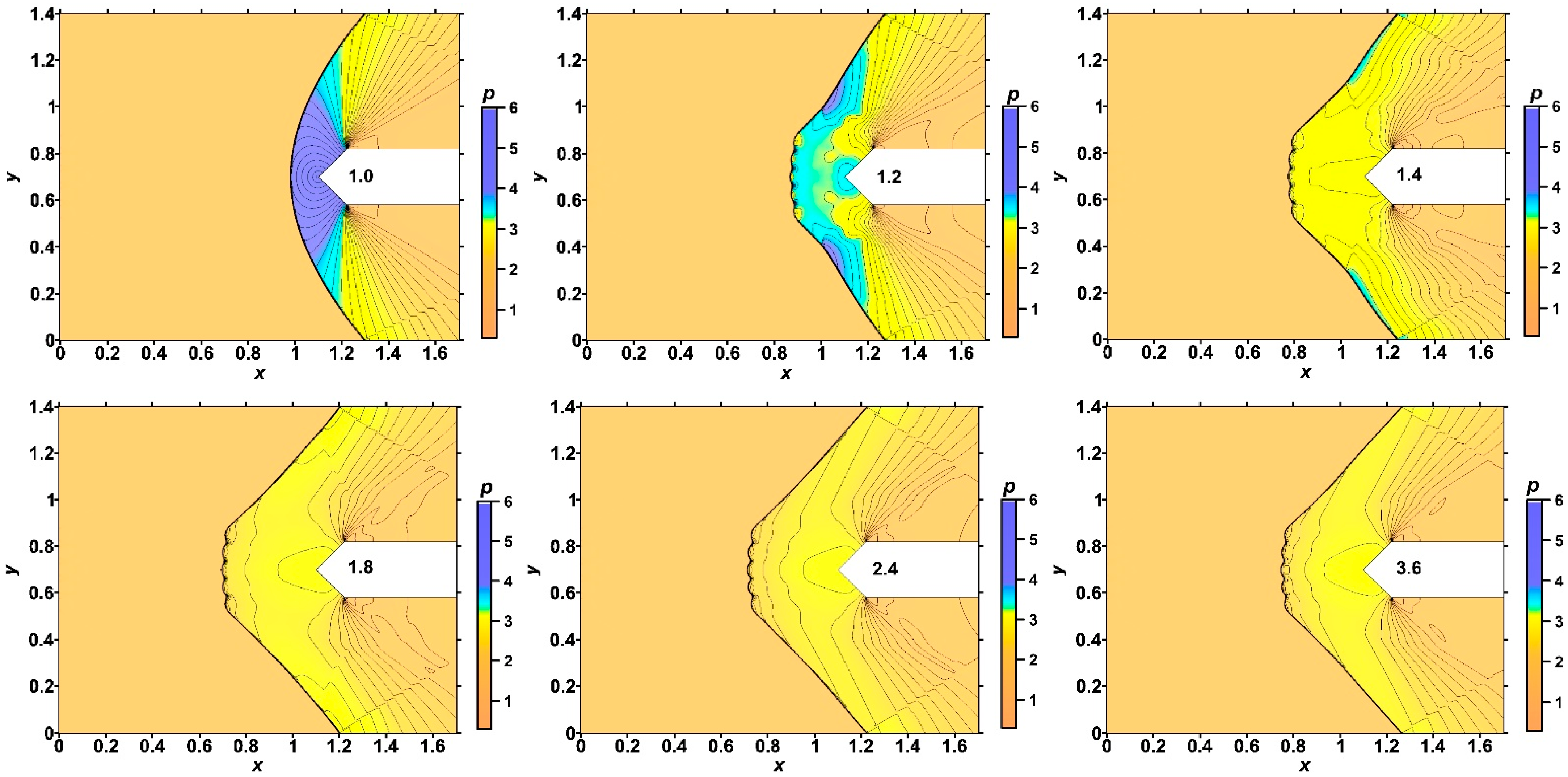
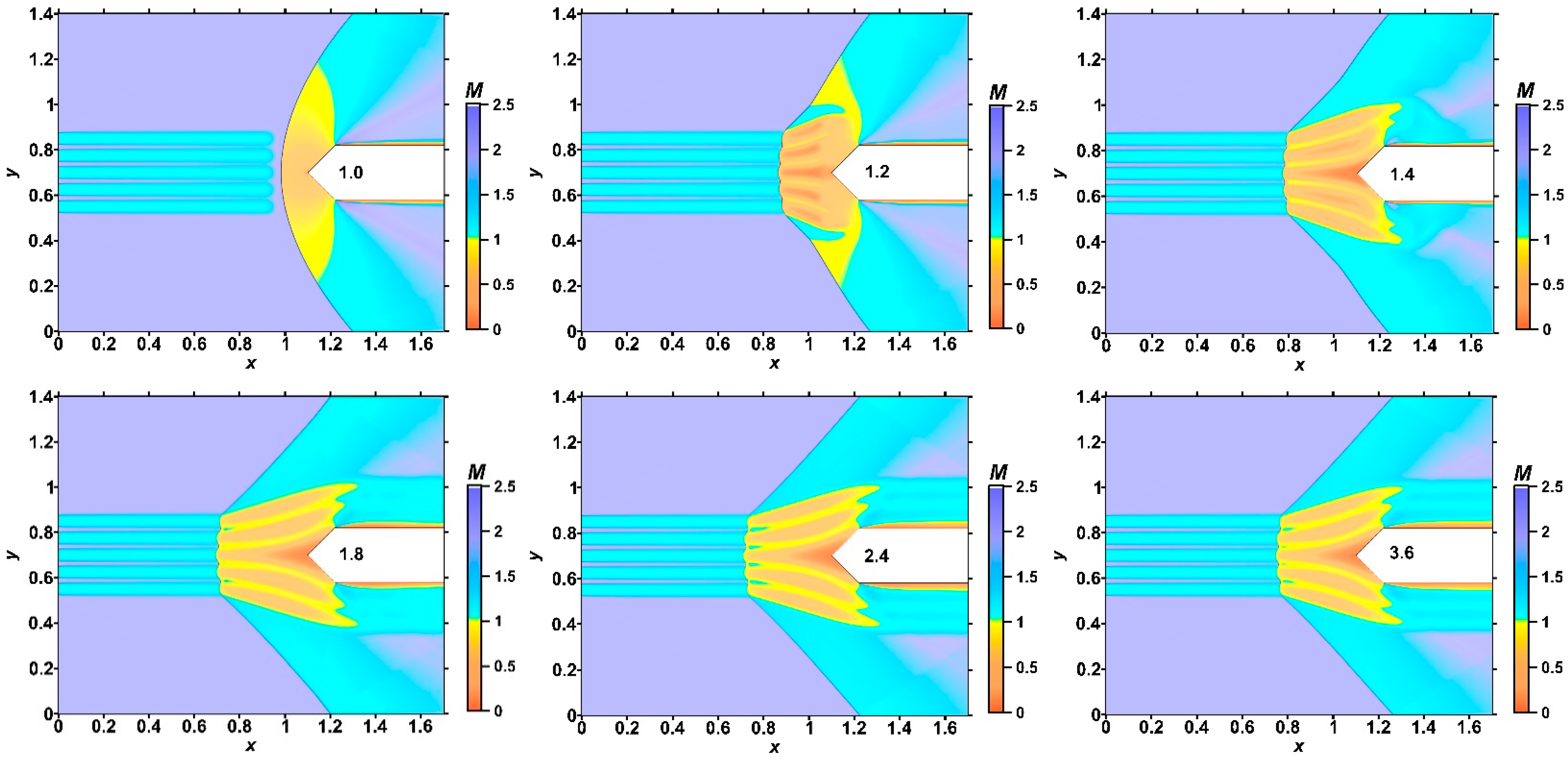
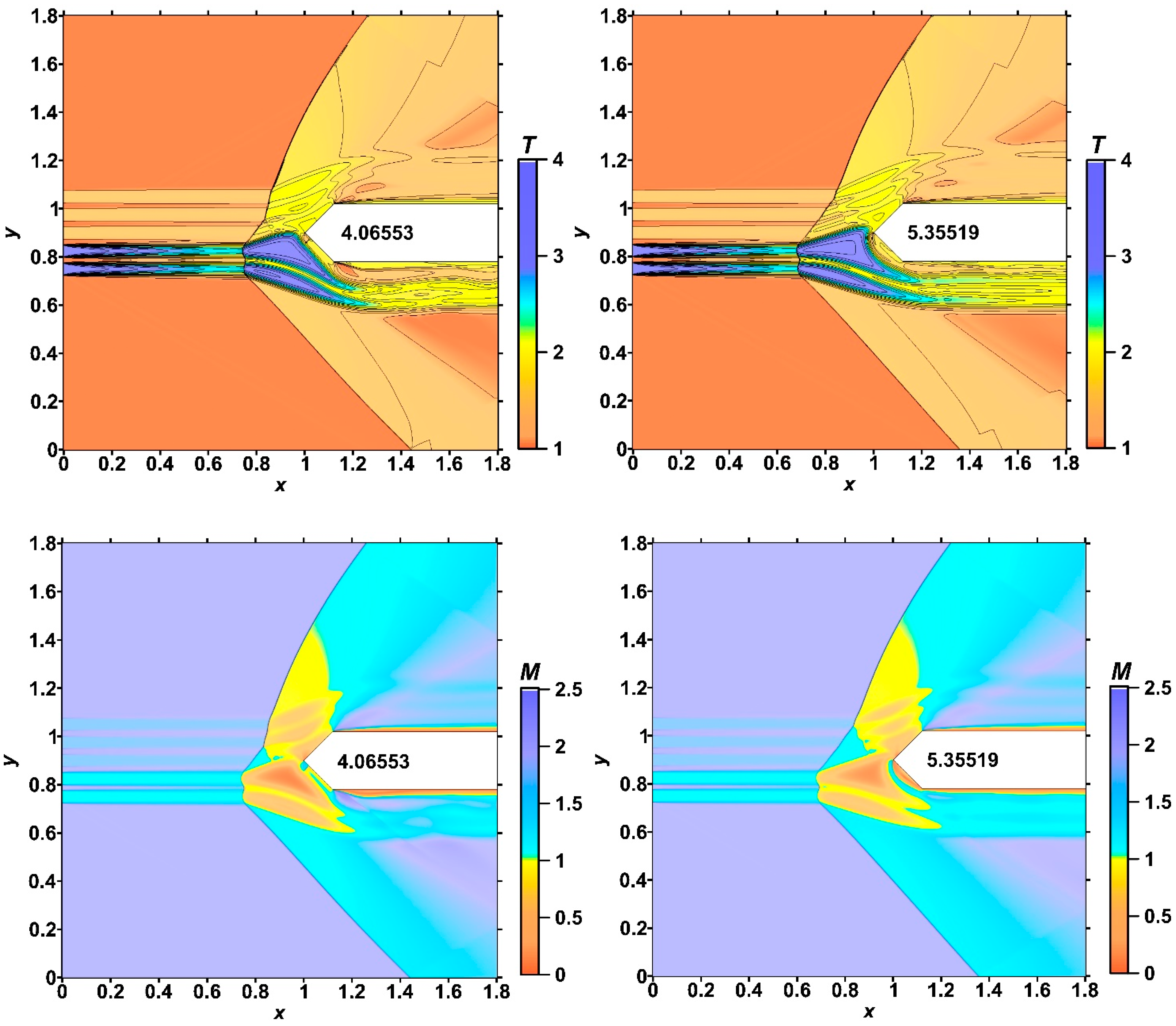
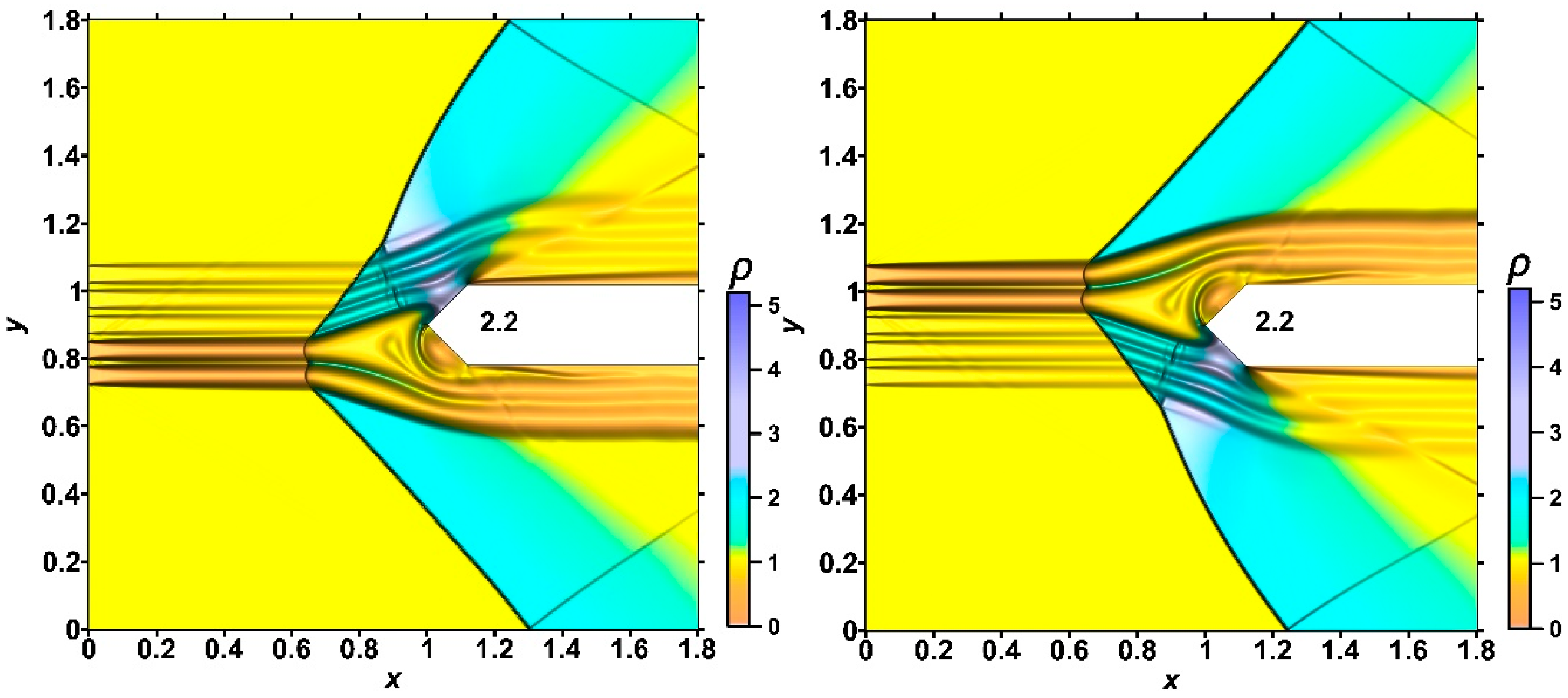
- It was shown that the front of the bow shock becomes wavy, reflecting the stratification of the energy source, and the bow shock wave standoff distance is greater for the smaller αj (greater temperatures) in the layers. In addition, the more the angle of inclination of the bow shock wave changes, the smaller the values αj in the layers. The layered nature of the fields of density, temperature, and local Mach number was also shown up to the establishment of a new steady flow mode.
- -
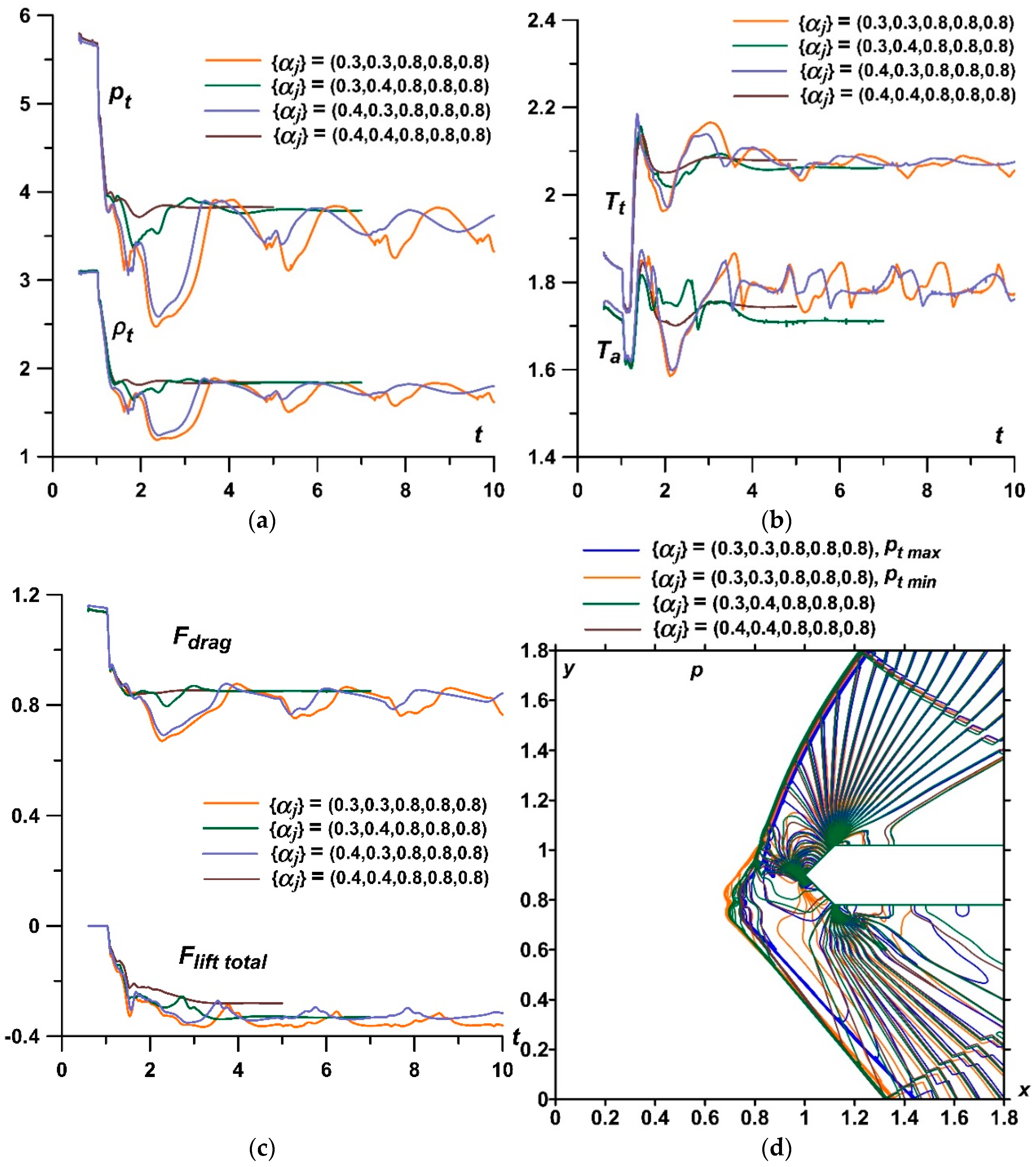
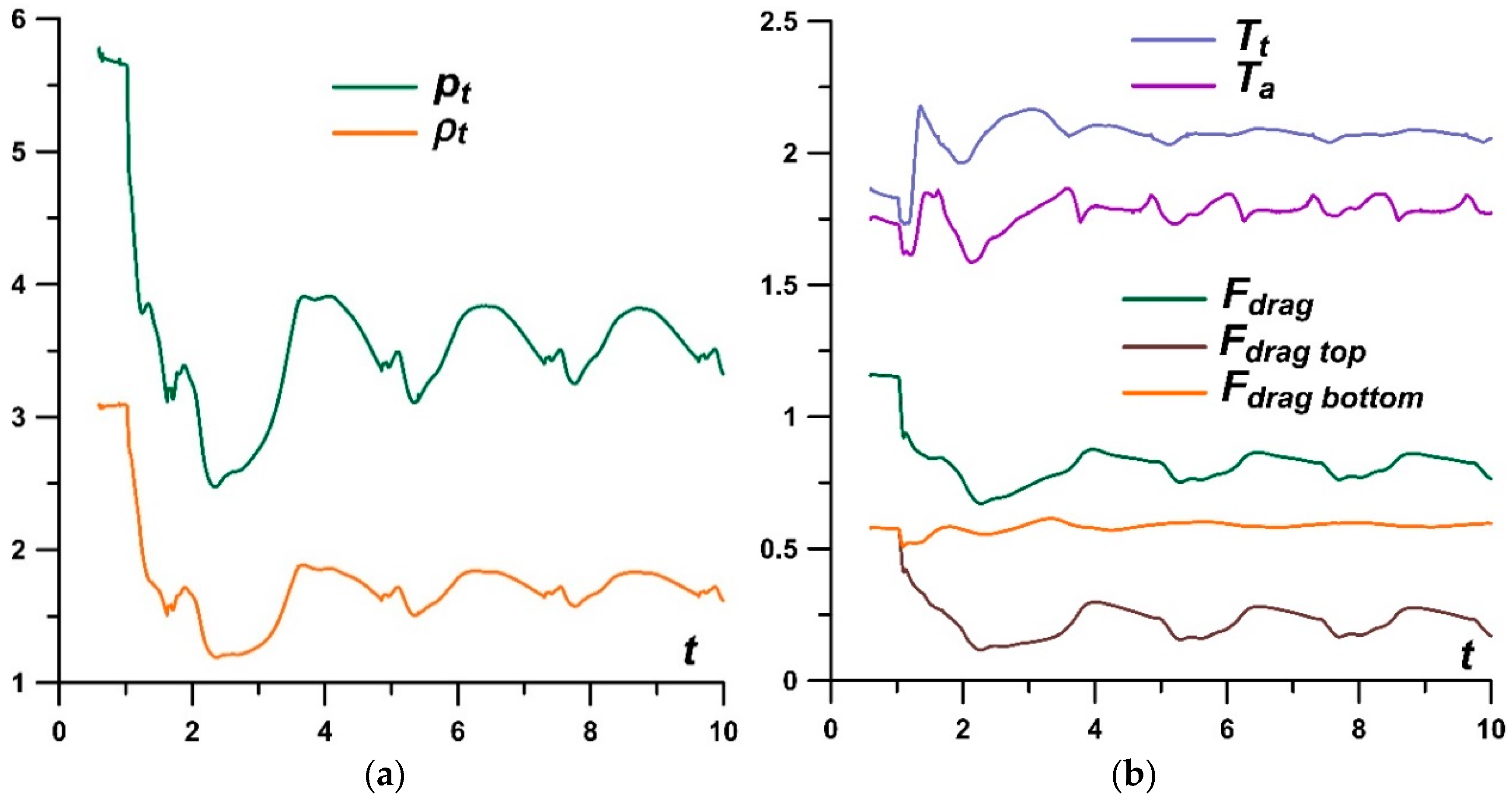
- It was shown that by changing the temperature in the layers of the stratified energy sources given by symmetrical sets {αj}, it is possible to control the defining flow parameters. For a source with the same temperatures in the layers, the pressure and density at the top of the body and the drag force of the front surface are lower for sets {αj} with smaller αj (greater temperatures). The bow shock wave is located more far from the body for the smaller αj in the layers, and the temperature at the top and the average front surface temperature are higher. It was also shown that central layers of the stratified source play a decisive role in the formation of the parameters at the top and the drag forces. In this case (for the symmetrical sets {αj}), lift forces do not arise.
- -
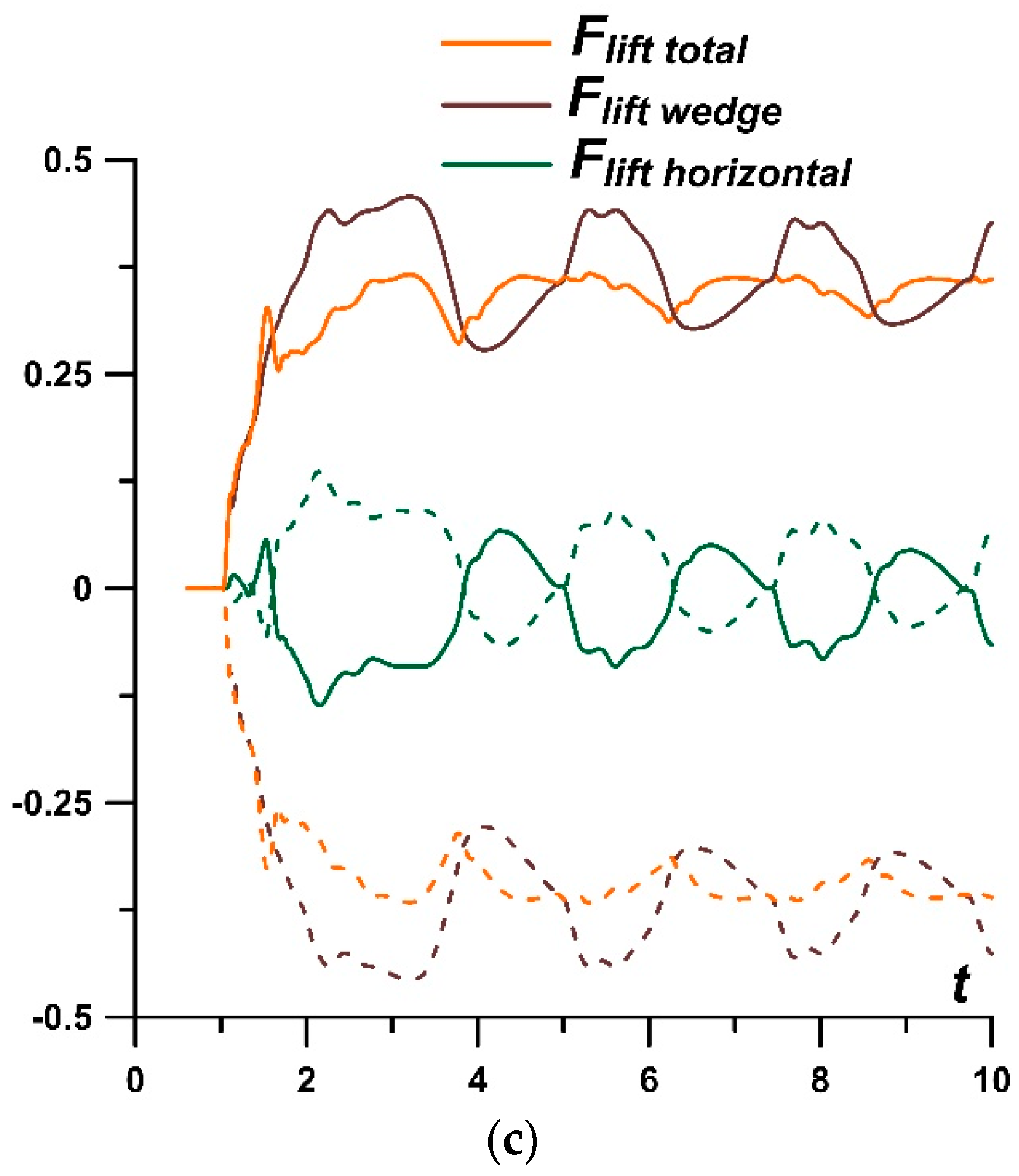
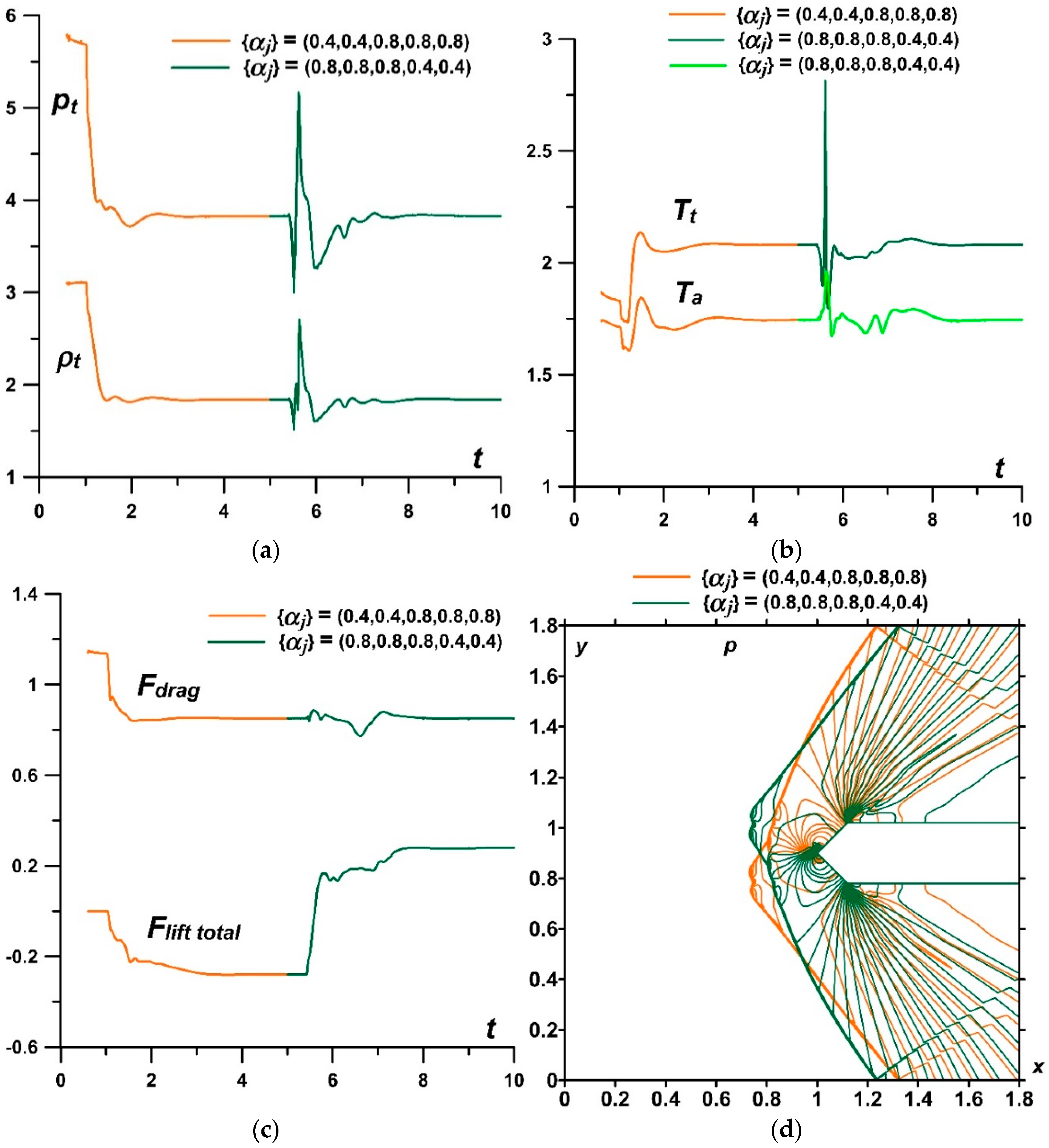
- It was established that by setting asymmetric sets {αj} in a permanently operating stratified energy source, it is possible to provoke a pulsating flow mode. The mechanism of the self-sustained flow pulsations was described. The possibility to suppress the pulsations by alternately setting lower temperatures in the layers was shown. In this case, it was shown that one can control the flow parameters and the bow shock wave during the steady flow mode establishing. In addition, it is possible to suppress the pulsations and to control the flow parameters by switching at some time the set {αj} to another one with lower temperatures in the layers.
- -
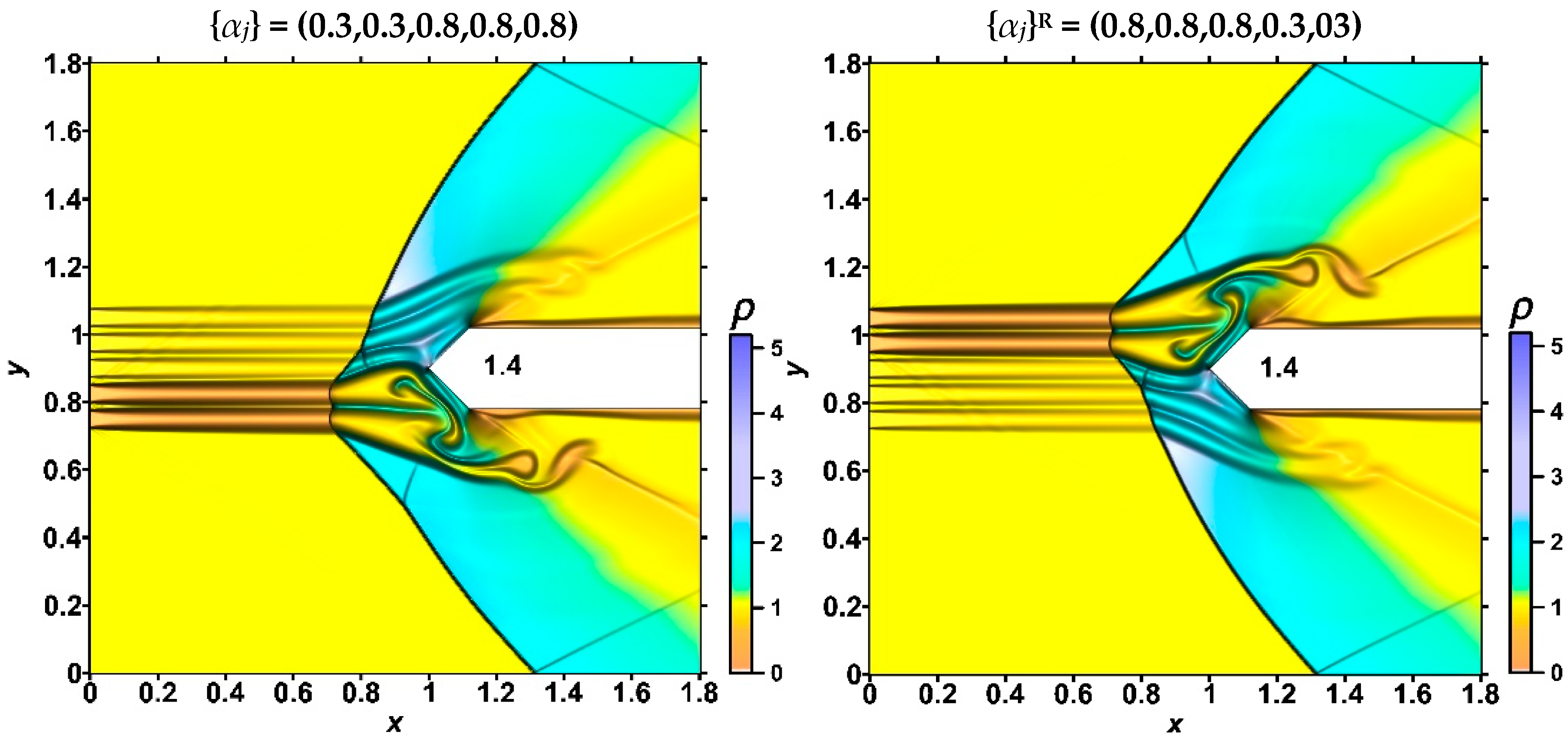
- It was obtained that for the set {αj} = (α1,α2,α3,α4,α5) and for the reverse set {αj}R = (α5,α4,α3,α2,α1) in a permanently operating stratified energy source, the flow patterns are exactly opposite due to the assumption that the axis of symmetry of the stratified source coincides with the axis of symmetry of an AD body.
- -
- It was shown that a stratified source with a reverse set {αj}R (in comparison with the source with {αj}) produces equal, in absolute value, and oppositely directed lift (pitch) forces constantly acting on the body (at zero angle of attack) and the same drag force Fdrag, the parameters at the top, and the average front surface temperature. It was also shown that a steady flow mode can be changed to another one characterized by an oppositely directed lift (pitch) force by switching at some time the set {αj} to the reverse one {αj}R. In this case, the drag force Fdrag and the parameters at the top as well as the average front surface temperature do not change.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Transverse size of the aerodynamic body |
| F | Drag force of the front surface of the aerodynamic body |
| hj | The width of the layers in the energy source |
| M∞ | The freestream Mach number |
| p, ρ, u, v, T, M | Pressure, density, velocity components, temperature, and local Mach number of the flow |
| Pr | The Prandtl number |
| Re | The Reynolds number |
| Ta | Average temperature on the front surface of the aerodynamic body |
| t | Time |
| y0 | Coordinate of the axis of symmetry of an AD body |
| αj | Rarefaction parameter in the j-layer of the stratified energy source |
| γ | Ratio of specific heats |
| ε | Specific internal energy of the gas |
| Indices | |
| j | Parameters in the layers of the stratified energy source |
| n | Normalizing parameters |
| t | Parameters at the top of the body |
| ∞ | Freestream parameters |
| AD | Aerodynamic |
References
- Knight, D.D. Energy Deposition for High-Speed Flow Control; Cambridge University Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Knight, D.D. Survey of aerodynamic drag reduction at high speed by energy deposition. J. Propuls. Power 2008, 24, 1153–1167. [Google Scholar] [CrossRef]
- Fomin, V.M.; Tretyakov, P.K.; Taran, J.-P. Flow control using various plasma and aerodynamic approaches (short review). Aerosp. Sci. Technol. 2004, 8, 411–421. [Google Scholar] [CrossRef]
- Rashid, S.; Nawaz, F.; Maqsood, A.; Salamat, S.; Riaz, R. Review of wave drag reduction techniques: Advances in active, passive, and hybrid flow control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 12, 1–83. [Google Scholar] [CrossRef]
- Ahmed, M.Y.M.; Qin, N. Forebody shock control devices for drag and aero-heating reduction: A comprehensive survey with a practical perspective. Prog. Aerosp. Sci. 2020, 112, 100585. [Google Scholar] [CrossRef]
- Starikovskiy, A.Y.; Aleksandrov, N.L. Gasdynamic flow control by ultrafast local heating in a strongly nonequilibrium pulsed plasma. Plasma Phys. Rep. 2021, 47, 148–209. [Google Scholar] [CrossRef]
- Leonov, S.B.; Adamovich, I.V.; Soloviev, V.R. Dynamics of near-surface electric discharges and mechanisms of their interaction with the airflow. Plasma Sources Sci. Technol. 2016, 25, 063001. [Google Scholar] [CrossRef]
- Leonov, S.B. Review of plasma-based methods for high-speed flow control. In Proceedings of the Sixth International Conference on Fluid Mechanics AIP Conference Proceedings, Guangzhou, China, 30 June–3 July 2011. [Google Scholar] [CrossRef]
- Russell, A.; Zare-Behtash, H.; Kontis, K. Joule heating flow control methods for high-speed flows. J. Electrost. 2016, 80, 34–68. [Google Scholar] [CrossRef] [Green Version]
- Znamenskaya, I.A. Methods for panoramic visualization and digital analysis of thermophysical flow fields. A review. Sci. Vis. 2021, 13, 125–158. [Google Scholar] [CrossRef]
- Georgievsky, P.Y.; Levin, V.A. Supersonic flow over bodies in the presence of external energy release. Pis’ma Zhurnal Teh. Phiz 1988, 14, 684–687. Available online: http://journals.ioffe.ru/articles/viewPDF/31216 (accessed on 1 October 2022). (In Russian).
- Artem’ev, V.I.; Bergel’son, V.I.; Nemchinov, I.V.; Orlova, T.I.; Smirnov, V.A.; Hazins, V.M. Changing the regime of supersonic streamlining obstacles via raising the thin channel of low density. Izv. Akad. Nauk. SSSR Meh. Židk. Gaza 1989, 5, 146–151. (In Russian) [Google Scholar]
- Nemchinov, I.V.; Artem’ev, V.I.; Bergel’son, V.I.; Hazins, V.M.; Orlova, T.I.; Rybakov, V.A. Rearrangement of the bow shock shape using a “hot spike”. Shock Waves 1994, 4, 35–40. [Google Scholar] [CrossRef]
- Kolesnichenko, Y.F.; Brovkin, V.G.; Azarova, O.A.; Grudnitsky, V.G.; Lashkov, V.A.; Mashek, I.C. Microwave energy release regimes for drag reduction in supersonic flows. Paper AIAA-2002-0353. In Proceedings of the 40th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Myrabo, L.N.; Raizer, Y.P. Laser-Induced Air Spikes for Advanced Transatmospheric Vehicles. Paper AIAA-1994-2451. In Proceedings of the 25th AIAA Plasma Dynamics and Lasers Conference, Colorado Springs, CO, USA, 20–23 June 1994. [Google Scholar]
- Tretyakov, P.K.; Fomin, V.M.; Yakovlev, V.I. New principles of control of aerophysical processes-research development. In Proceedings of the International Conference on the Methods of Aerophysical Research, Novosibirsk, Russia, 29 June–3 July 1996; pp. 210–220. [Google Scholar]
- Kim, S.; Lee, H.J. Influence of laser energy deposition conditions on the drag of a sphere in supersonic flow. Energies 2019, 12, 3914. [Google Scholar] [CrossRef] [Green Version]
- Bityurin, V.; Klimov, A.; Leonov, S.; Brovkin, V.; Kolesnichenko, Y.; Popov, N.; Van Wie, D.M. Shock waves structure and velocity at propagation through non-homogeneous plasma. AIAA Paper 2000–2571. In Proceedings of the 31st Plasmadynamics and Lasers Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar] [CrossRef]
- Ukai, T.; Kontis, K. Thermal fluctuation characteristics around a nanosecond pulsed dielectric barrier discharge plasma actuator using a frequency analysis based on schlieren images. Energies 2020, 13, 628. [Google Scholar] [CrossRef] [Green Version]
- Lapushkina, T.A. Principles of magnetohydrodynamical control of internal and external supersonic flows. Energies 2022, 15, 5641. [Google Scholar] [CrossRef]
- Lapushkina, T.A.; Erofeev, A.V. Supersonic flow control via plasma, electric and magnetic impacts. Aerosp. Sci. Technol. 2017, 69, 313. [Google Scholar] [CrossRef]
- Georgievsky, P.Y.; Levin, V.A. Transition to irregular regimes of supersonic flows over bodies initiated by energy deposition. AIAA Paper 2005-1047. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Azarova, O.A. A minimum-stencil difference scheme for computing two-dimensional axisymmetric gas flows: Examples of pulsating flows with instabilities. Comput. Math. Math. Phys. 2009, 49, 710–728. [Google Scholar] [CrossRef]
- Azarova, O.A.; Knight, D.D.; Kolesnichenko, Y.F. Pulsating stochastic flows accompanying microwave filament/supersonic shock layer interaction. Shock Waves 2011, 21, 439–450. [Google Scholar] [CrossRef]
- Azarova, O.; Knight, D.; Kravchenko, O. Lift Forces, heat fluxes and self-sustained oscillations over supersonic bodies under asymmetric energy deposition. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain, 1–4 July 2019. [Google Scholar] [CrossRef]
- Khamseh, A.P.; Kiriakos, R.M.; DeMauro, E.P. Stereoscopic particle image velocimetry of laser energy deposition on a Mach 3.4 flow field. Exp. Fluids 2021, 62, 39. [Google Scholar] [CrossRef]
- Knight, D.D.; Azarova, O.A.; Kolesnichenko, Y.F. On details of flow control via characteristics and location of microwave filament during its interaction with supersonic blunt body. AIAA Paper 2009-847. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- Azarova, O.A.; Knight, D.D.; Kolesnichenko, Y.F. Flow control via instabilities, vortices and steady structures under the action of external microwave energy release. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 1498–1515. [Google Scholar] [CrossRef]
- Leonov, S.; Carter, C.; Houpt, A.; Ombrello, T. Mitigation of reflected shock wave by streamwise plasma array. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences, Milan, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Andrews, P.; Lax, P.; Leonov, S. Triggering shock wave positions by patterned energy deposition. Energies 2022, 15, 7104. [Google Scholar] [CrossRef]
- Leonov, S.B.; Carter, C.D.; Hedlund, B.E.; Houpt, A.W.; Ombrello, T.; Firsov, A.A. Control of amplitude and position of reflected shock wave by stripwise plasma. AIAA 2018-0683. In Proceedings of the Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Leonov, S.B.; Firsov, A.A.; Houpt, A.W. Suppression of reflected oblique shock wave by multi-filamentary plasma. J. Phys. Conf. Ser. 2018, 1112, 012005. [Google Scholar] [CrossRef]
- Lapushkina, T.A.; Erofeev, A.V.; Azarova, O.A.; Kravchenko, O.V. Interaction of a plane shock wave with an area of ionization instability of discharge plasma in air. Aerosp. Sci. Technol. 2019, 85, 347–358. [Google Scholar] [CrossRef]
- Gan, T.; Wu, Y.; Sun, Z.; Jin, D.; Song, H.; Jia, M. Shock wave boundary layer interaction controlled by surface arc plasma actuators. Phys. Fluids 2018, 30, 055107. [Google Scholar] [CrossRef]
- Tang, M.; Wu, Y.; Guo, S.; Sun, Z.; Luo, Z. Effect of the streamwise pulsed arc discharge array on shock wave/boundary layer interaction control. Phys. Fluids 2020, 32, 076104. [Google Scholar] [CrossRef]
- Samimy, M.; Webb, N.; Esfahani, A. Reinventing the wheel: Excitation of flow instabilities for active flow control using plasma actuators. J. Phys. D Appl. Phys. 2019, 52, 354002. [Google Scholar] [CrossRef]
- Apazidis, N.; Sembian, S.; Liverts, M. Blast wave interaction with thermal and density inhomogeneities in air. In Proceedings of the 32nd International Symposium on Shock Waves, Singapore, 14–19 July 2019. [Google Scholar] [CrossRef]
- Sembian, S.; Liverts, M.; Apazidis, N. Plane blast wave interaction with an elongated straight and inclined heat-generated inhomogeneity. J. Fluid Mech. 2018, 851, 245–267. [Google Scholar] [CrossRef]
- Azarova, O.A. Generation of Richtmyer-Meshkov and secondary instabilities during the interaction of an energy release with a cylinder shock layer. Aerosp. Sci. Technol. 2015, 42, 376–383. [Google Scholar] [CrossRef]
- Azarova, O.A.; Kravchenko, O.V.; Lapushkina, T.A.; Erofeev, A.V. Density and temperature fluctuations behind a shock wave under the influence of a stratified energy source. Tech. Phys. Lett. 2020, 46, 649–652. [Google Scholar] [CrossRef]
- Azarova, O.A.; Krasnobaev, K.V.; Kravchenko, O.V.; Lapushkina, T.A.; Erofeev, A.V. Redistribution of energy in a viscous heat-conductive medium during the interaction of a shock wave with a temperature layered plasma region. J. Phys. Conf. Ser. 2020, 1698, 012004. [Google Scholar] [CrossRef]
- Azarova, O.A.; Lapushkina, T.A.; Krasnobaev, K.V.; Kravchenko, O.V. Redistribution of energy during interaction of a shock wave with a temperature layered plasma region at hypersonic speeds. Aerospace 2021, 8, 326. [Google Scholar] [CrossRef]
- Azarova, O.A. Supersonic flow control using combined energy deposition. Aerospace 2015, 2, 118–134. [Google Scholar] [CrossRef] [Green Version]
- Azarova, O.A.; Kravchenko, O.V. Impact of a thermally stratified energy source on the bow shock wave and aerodynamic characteristics of a body. J. Phys. Conf. Ser. 2021, 1891, 012025. [Google Scholar] [CrossRef]
- Azarova, O.A.; Kravchenko, O.V. Principles of unsteady high-speed flow control using limited in time thermally stratified energy source. Fluids 2022, 7, 326. [Google Scholar] [CrossRef]
- Roache, P.J. Computational Fluid Dynamics; Mir: Moscow, Russia, 1980. [Google Scholar]
- Azarova, O.A. Complex conservative difference schemes for computing supersonic flows past simple aerodynamic forms. J. Comput. Math. Math. Phys. 2015, 55, 2025–2049. [Google Scholar] [CrossRef]


| Description | Designation | Value |
|---|---|---|
| Freestream Mach number | M∞ | 2 |
| Ratio of specific heats | γ | 1.4 |
| Reynolds number | Re | 9500 |
| Prandtl number (20C) | Pr | 0.703 |
| Ratio of the width of an AD body to the width of the layers in the energy source | D/hj | 4.8 |
| The duration of the source action in time | L | ∞ |
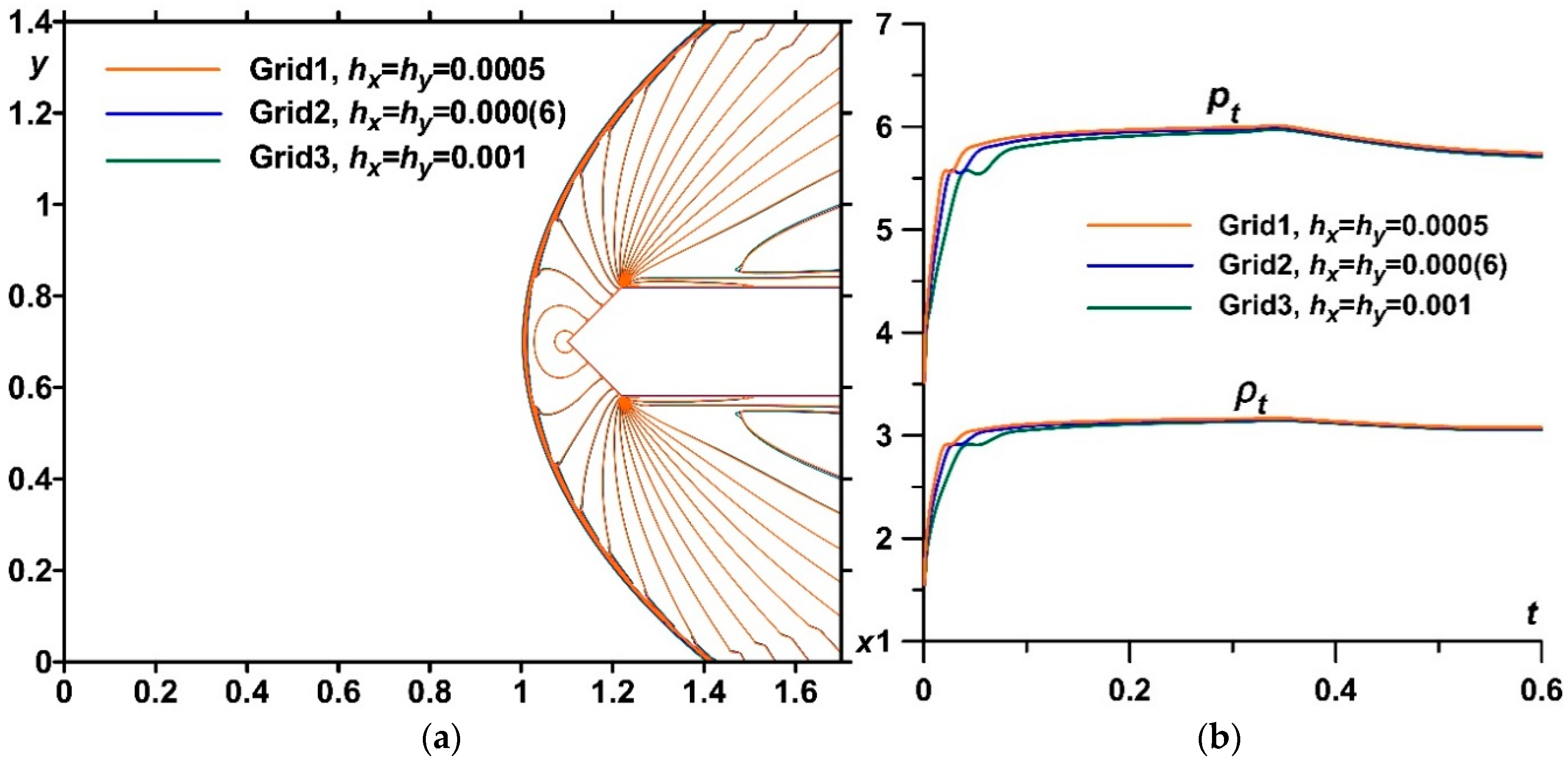
| Grid | Steps hx = hy | Sizes | Relative Error, pt | Relative Error, ρt |
|---|---|---|---|---|
| Grid1 | 0.0005 | 3400 × 2800 | 1.81% | 1.75% |
| Grid2 | 0.000(6) | 2550 × 2100 | 1.57% | 2.04% |
| Grid3 | 0.001 | 1700 × 1400 | 1.17% | 2.52% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azarova, O.A. Basics of Control of the Bow Shock Wave, Drag and Lift Forces, and Stability in a Steady Supersonic Flow Past an AD Body Using Permanently Operating Thermally Stratified Energy Deposition. Energies 2022, 15, 8627. https://doi.org/10.3390/en15228627
Azarova OA. Basics of Control of the Bow Shock Wave, Drag and Lift Forces, and Stability in a Steady Supersonic Flow Past an AD Body Using Permanently Operating Thermally Stratified Energy Deposition. Energies. 2022; 15(22):8627. https://doi.org/10.3390/en15228627
Chicago/Turabian StyleAzarova, Olga A. 2022. "Basics of Control of the Bow Shock Wave, Drag and Lift Forces, and Stability in a Steady Supersonic Flow Past an AD Body Using Permanently Operating Thermally Stratified Energy Deposition" Energies 15, no. 22: 8627. https://doi.org/10.3390/en15228627
APA StyleAzarova, O. A. (2022). Basics of Control of the Bow Shock Wave, Drag and Lift Forces, and Stability in a Steady Supersonic Flow Past an AD Body Using Permanently Operating Thermally Stratified Energy Deposition. Energies, 15(22), 8627. https://doi.org/10.3390/en15228627