The Tribo-Dynamics Performance of the Lubricated Piston Skirt–Cylinder System Considering the Cylinder Liner Vibration
Abstract
:1. Introduction
2. The Description of the Multiphysical Fields Involved in the Piston Skirt–Cylinder System
2.1. The Solid Heat Transfer Physical Field
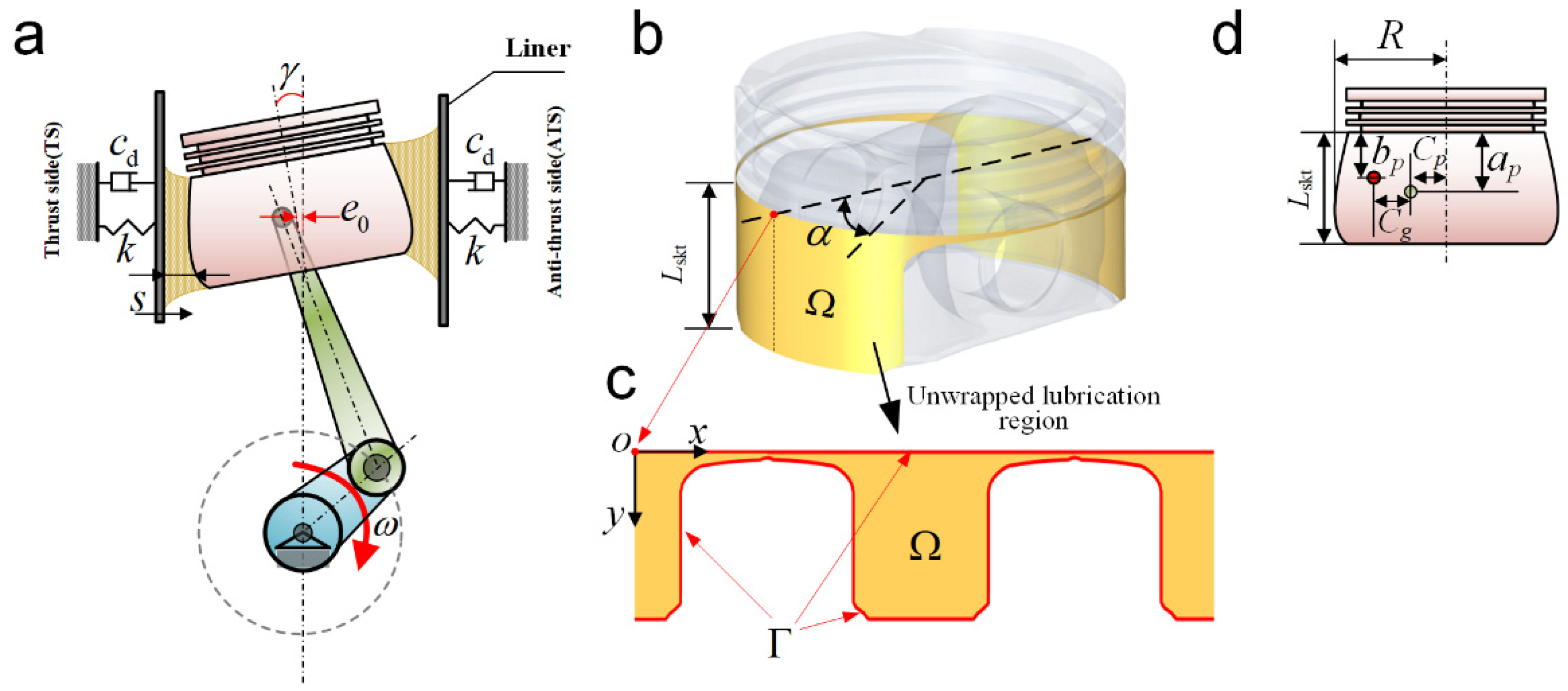
2.2. Lubrication Physical Field of the Piston Skirt–Cylinder Interface
2.2.1. Hydrodynamic Lubrication Model of Piston Skirt–Cylinder Interface
2.2.2. Rheological Relationship of the Lubricating Oil
2.2.3. Asperity Contact Model
2.3. The Solid Mechanics Physical Field for Elastic and Thermal Deformation
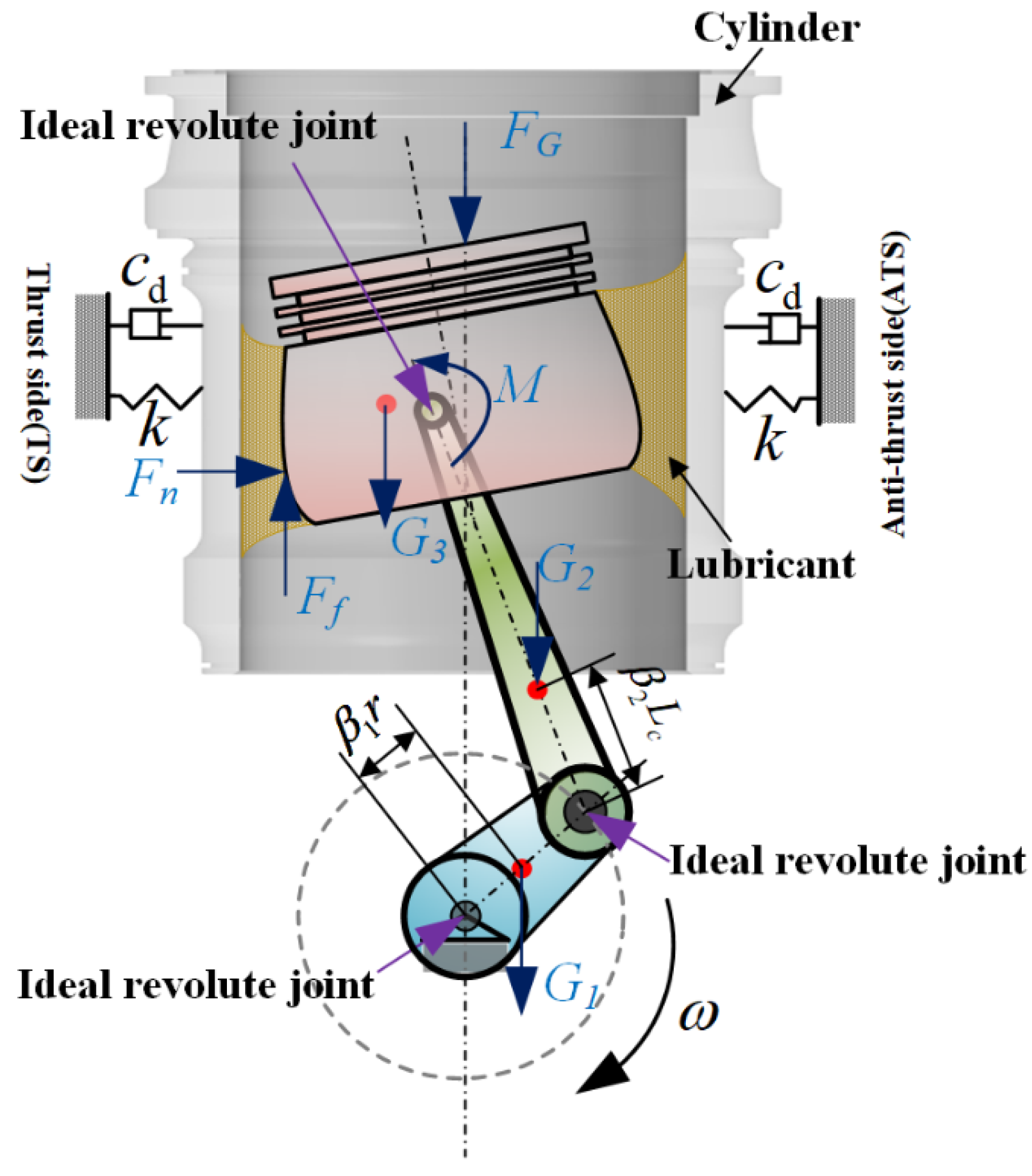
2.4. Multibody Dynamics Physical Field
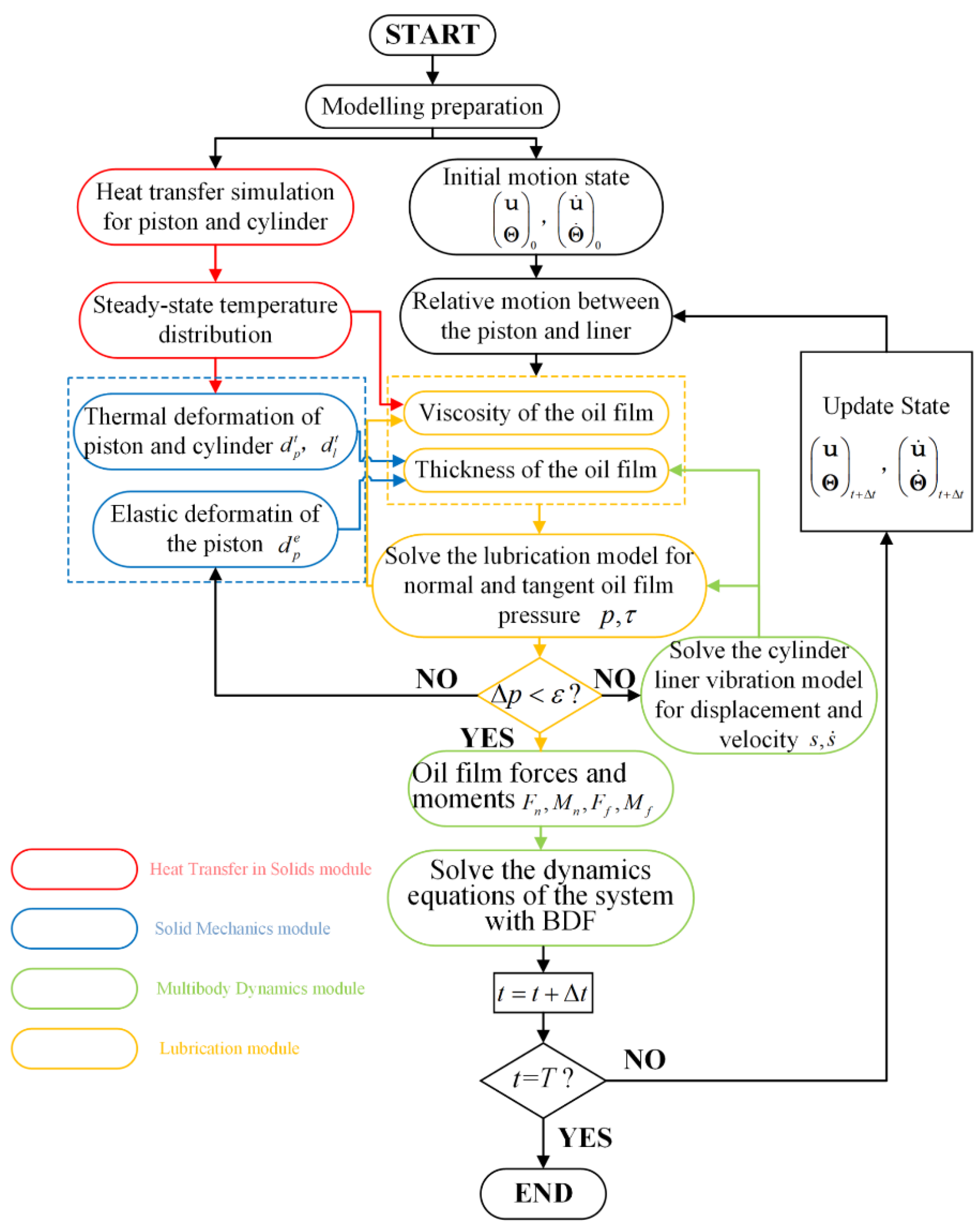
3. Computational Algorithm
4. Discussion
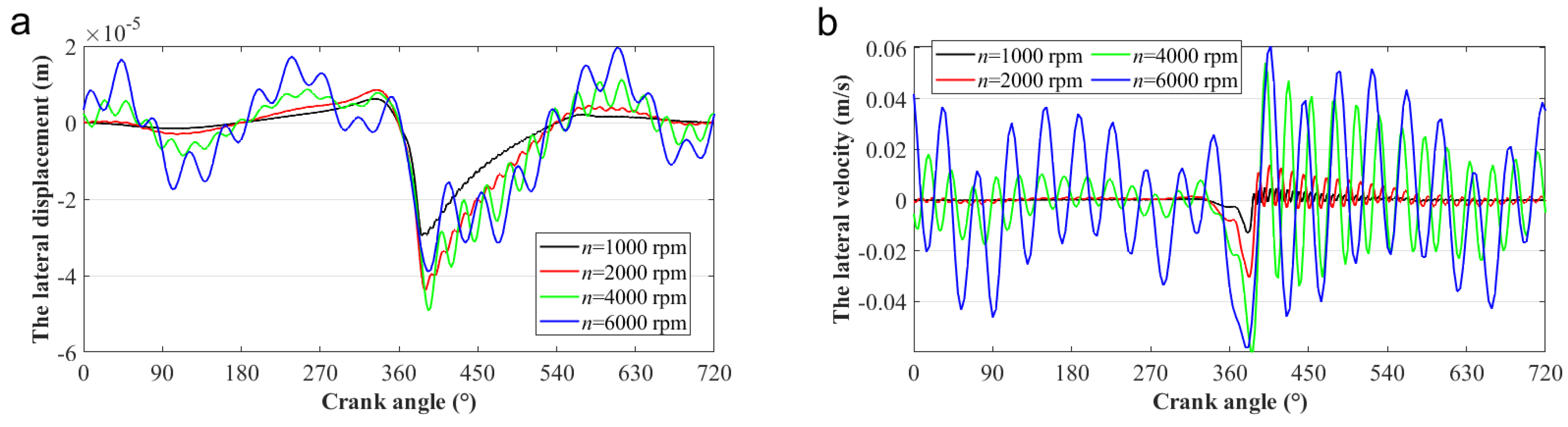
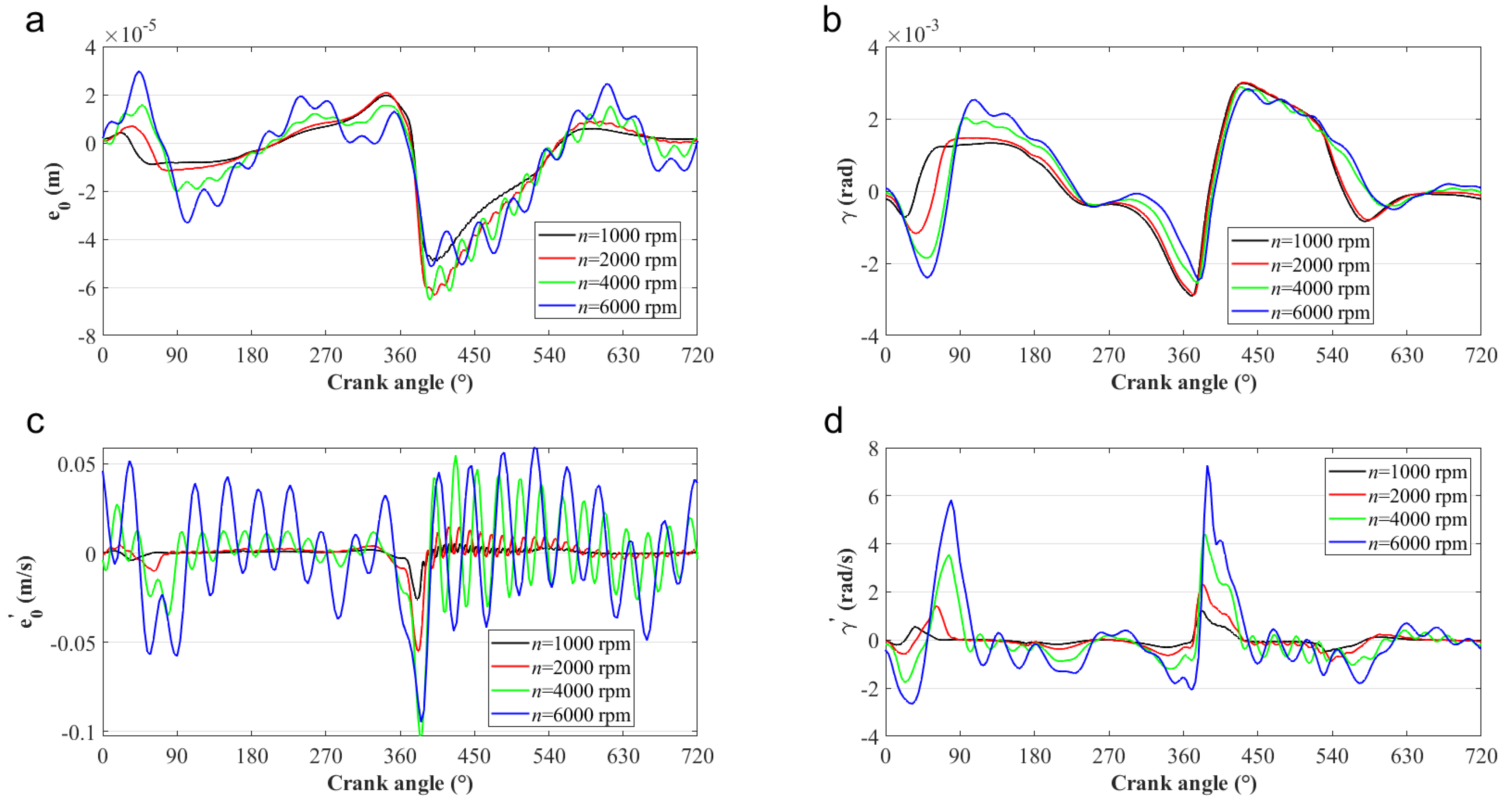
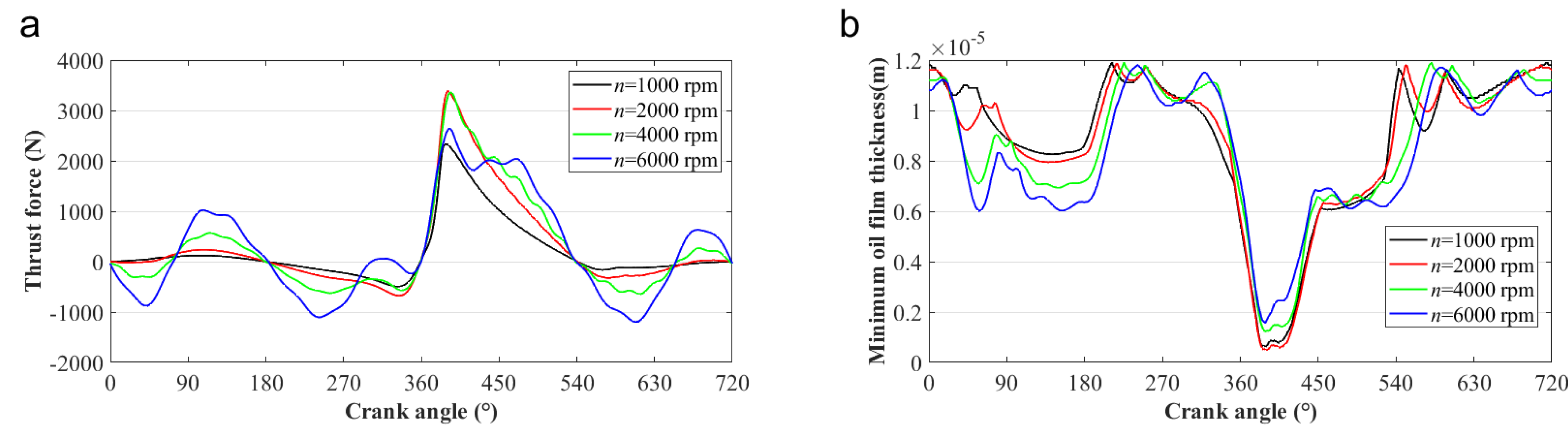
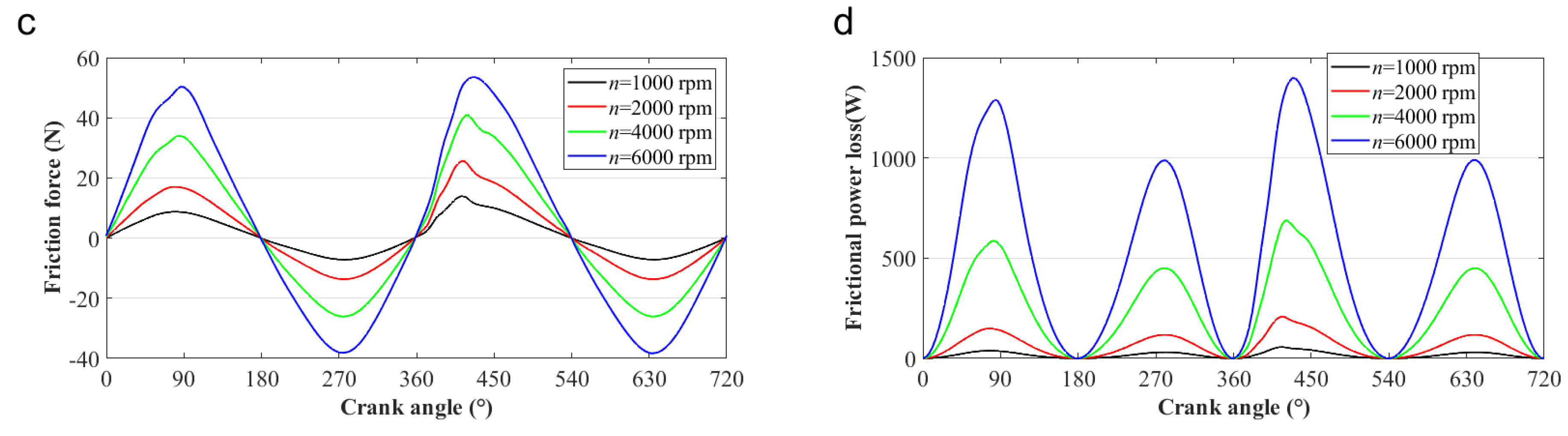
4.1. Effects of the Operation Speed on the Tribo-Dynamics Performance of the Piston–Cylinder System
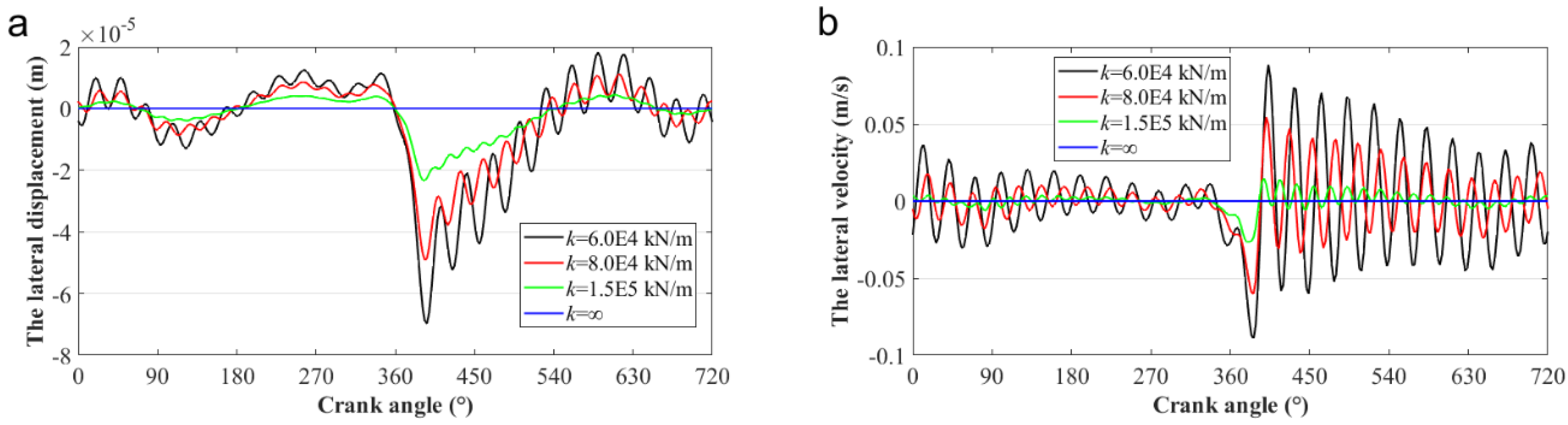
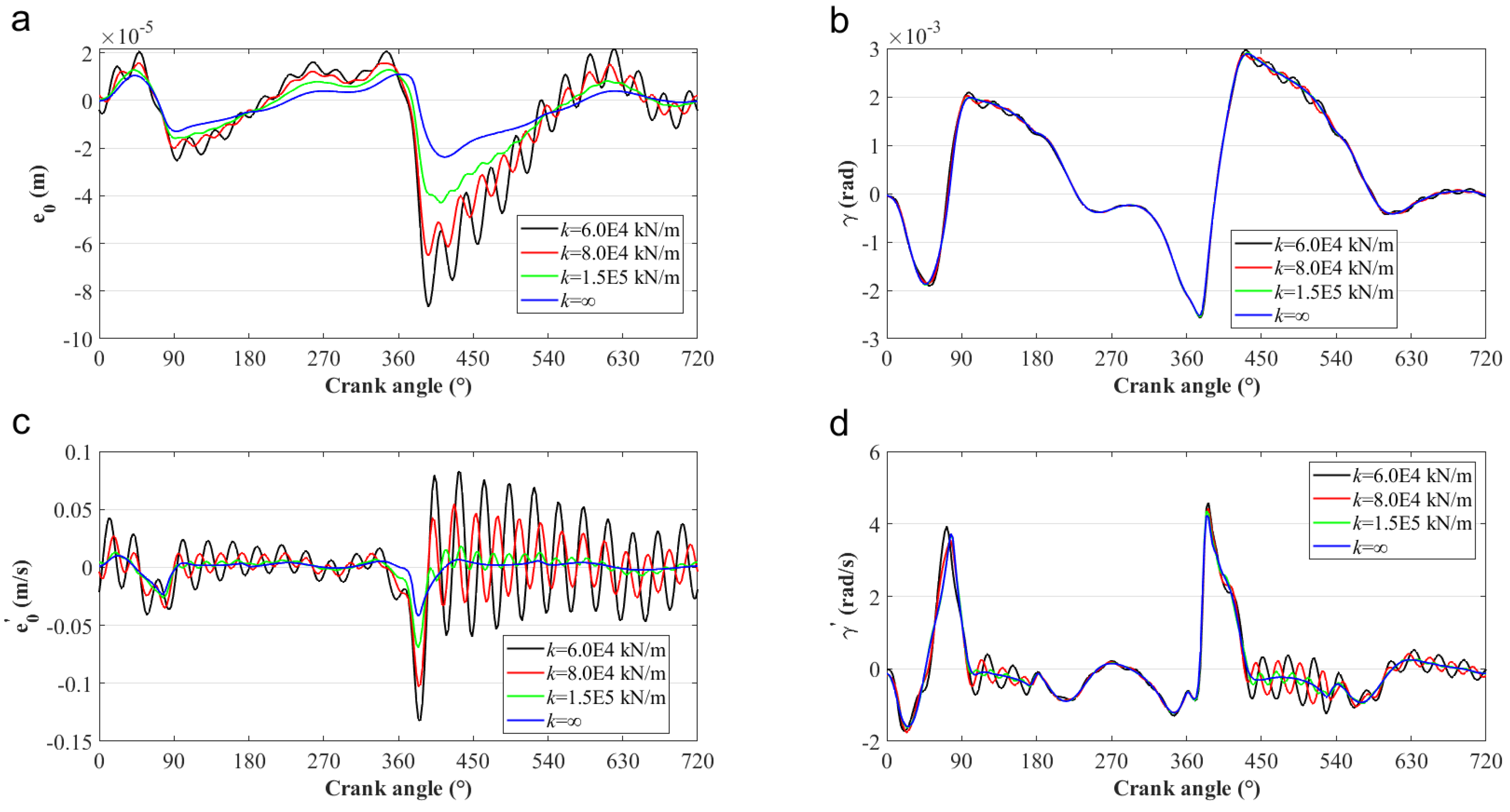
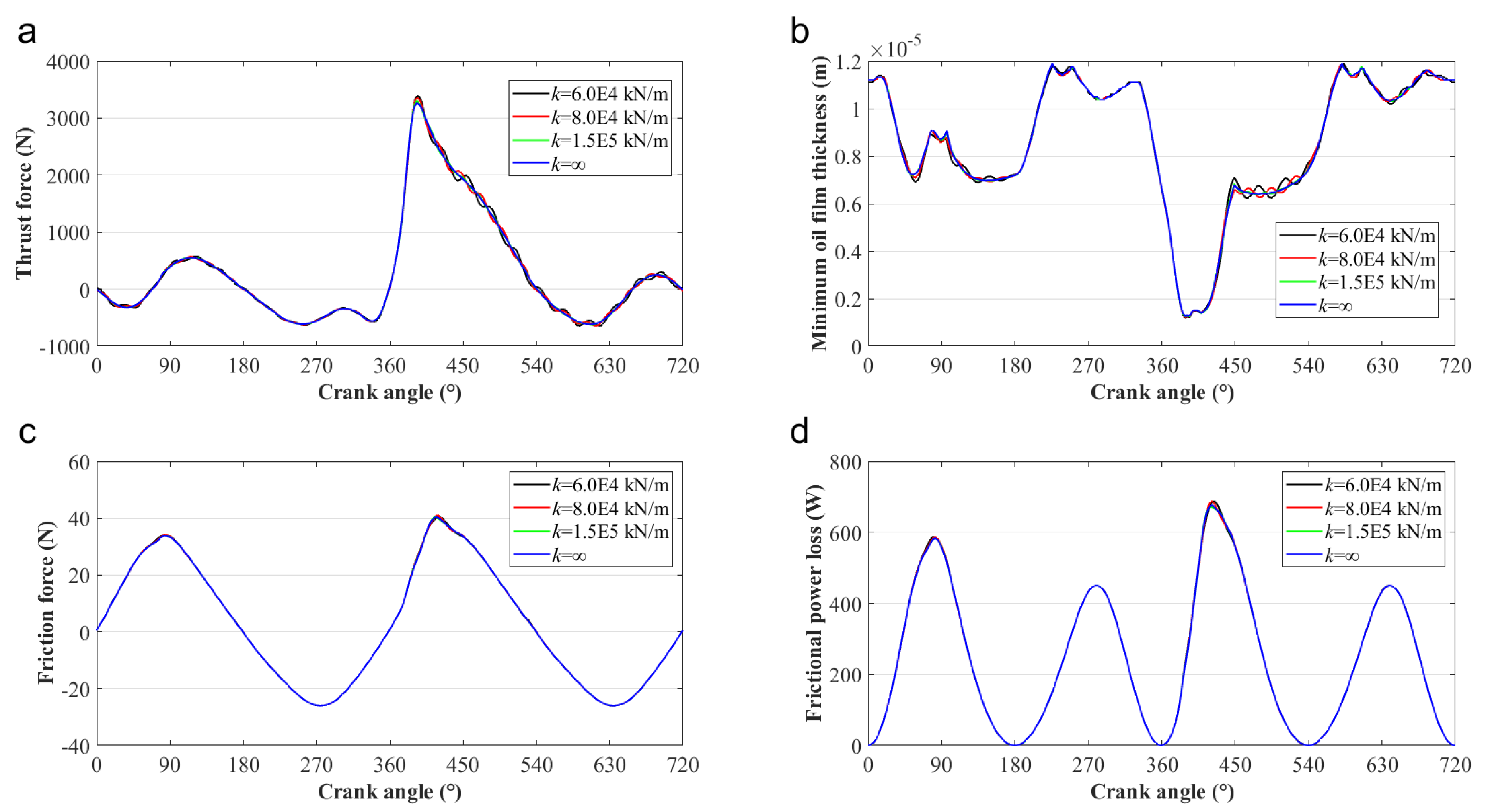
4.2. Effects of the Cylinder Stiffness Coefficient on the Tribo-Dynamics Performance of the Piston–Cylinder System
4.3. Effects of the Cylinder Damping Coefficient on the Tribo-Dynamics Performance of the Piston–Cylinder System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
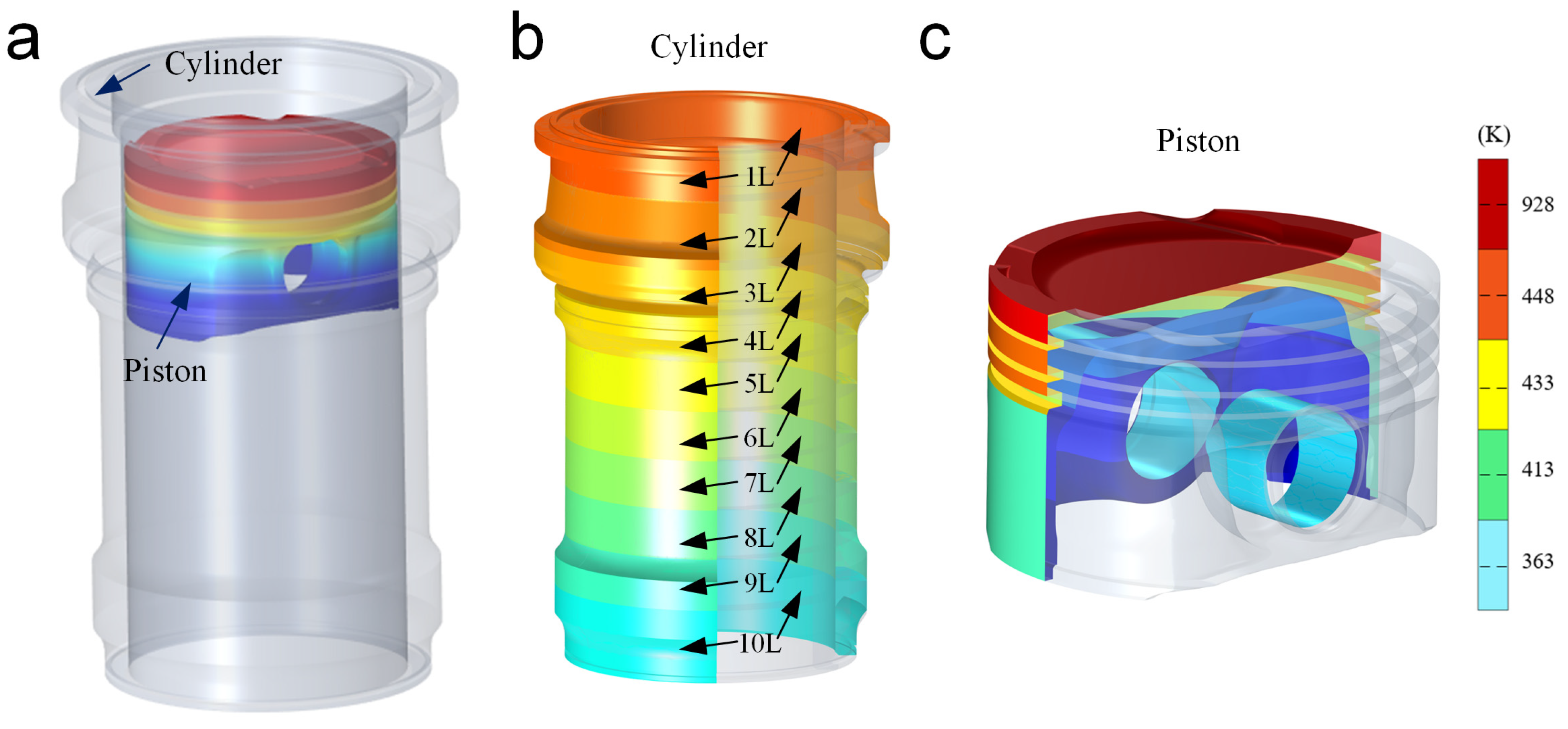
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| −1.737 mm | 1.29 × 10−4 kg m2 | 0.19 kg | |||
| 11.8 mm | 129.5 mm | 0.074 kg | |||
| 0.7 mm | 39.93 mm | 2 kg | |||
| 0.13 mm | 28 mm | 0.13 | |||
| 0.015 mm | 36.485 mm | 8 × 10−4 kN/m | |||
| 0.345 kg | 0.50 | 100 Ns/m | |||
| 9.67 × 10−4 kg m2 | 0.22 |
| Boundary Area | The Third Boundary Condition | ||
|---|---|---|---|
| Ambient Temperature (K) | Heat Convection Coefficient (W/(m2 K)) | ||
| 10 sections from the top to the bottom of the cylinder | 1 (1L) | 2600 | 500 |
| 2 (2L) | 2050 | 390 | |
| 3 (3L) | 1620 | 320 | |
| 4 (4L) | 1360 | 285 | |
| 5 (5L) | 1130 | 265 | |
| 6 (6L) | 970 | 250 | |
| 7 (7L) | 850 | 230 | |
| 8 (8L) | 790 | 200 | |
| 9 (9L) | 650 | 150 | |
| 10 (10L) | 570 | 80 | |
References
- He, Z.; Xie, W.; Zhang, G.; Hong, Z.; Zhang, J. Piston dynamic characteristics analyses based on FEM method Part I: Effected by piston skirt parameters. Adv. Eng. Softw. 2014, 75, 68–85. [Google Scholar] [CrossRef]
- Fang, C.C.; Meng, X.H.; Zhou, W.; Huang, H.C. On the tribo-dynamic interactions between piston skirt-liner system and pin assembly in a gasoline engine. Mech. Mach. Theory 2021, 166, 104497. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A. Piston dynamics, lubrication and tribological performance evaluation: A review. Int. J. Engine Res. 2020, 21, 725–741. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, X.; Li, H.; Si, X.; Dong, Q.; Zhang, Z.; Zhang, B. A new approach for modeling and analysis of the lubricated piston skirt-cylinder system with multi-physics coupling. Tribol. Int. 2022, 167, 107381. [Google Scholar] [CrossRef]
- Yasir, H.; Ali, U.; S.Kamran, A.; Cheol, W.P. Numeric based low viscosity adiabatic thermo-tribological performance analysis of piston-skirt liner system lubrication at high engine speed. Tribol. Int. 2018, 126, 166–176. [Google Scholar]
- Li, D.F.; Ezzat, H.A. An automotive piston lubrication model. ASLE Trans. 1983, 26, 151–160. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1979, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, M.S. Application of average flow model to lubrication between rough sliding surfaces. J. Tribol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, H.S.; Arai, T.; Hamai, K. A numerical analysis for piston skirts in mixed lubrication—Part I: Basic modeling. J. Tribol. 1992, 114, 553–562. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y.Z.; Cheng, H.S.; Arai, T.; Hamai, K. A numerical analysis for piston skirts in mixed lubrication—Part II: Deformation considerations. J. Tribol. 1993, 115, 125–133. [Google Scholar] [CrossRef]
- Keribar, R.; Dursunkaya, Z. A comprehensive model of piston skirt lubrication. SAE Trans. 1992, 101, 844–852. [Google Scholar]
- Wong, V.W.; Tian, T.; Lang, H.; Ryan, J.P.; Sekiya, Y.; Kobayashi, Y.; Aoyama, S. A numerical model of piston secondary motion and piston slap in partially flooded elastohydrodynamic skirt lubrication. SAE Trans. 1994, 103, 1276–1290. [Google Scholar]
- Liu, K.; Xie, Y.B.; Gui, C.L. A comprehensive study of the friction and dynamic motion of the piston assembly. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1998, 212, 221–226. [Google Scholar] [CrossRef]
- Meng, X.; Xie, Y. A new numerical analysis for piston skirtliner system lubrication considering the effects of connecting rod inertia. Tribol. Int. 2012, 47, 235–243. [Google Scholar] [CrossRef]
- Meng, X.; Ning, L.; Xie, Y.; Wong, V.W. Effects of the connecting-rod-related design parameters on the piston dynamics and the skirt-liner lubrication. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 885–898. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.P. Dynamic Analysis for Planar Multibody Mechanical Systems with Lubricated Joints. Multibody Syst. Dyn. 2004, 12, 47–74. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Song, Q.; Liu, Z.; Chen, L. Hydrodynamic lubrication analysis of two-dimensional section between piston skirt and textured cylinder wall considering slip boundary conditions. Tribol. Int. 2019, 140, 105879. [Google Scholar] [CrossRef]
- Ravn, P.; Shivaswamy, S.; Alshaer, B.J.; Hamid, M.L. Joint clearances with lubricated long bearings in multibody mechanical systems. J. Mech. Des. 2000, 122, 484–488. [Google Scholar] [CrossRef]
- Tian, Q.; Zhang, Y.; Chen, L.; Yang, J. Simulation of planar flexible multibody systems with clearance and lubricated revolute joints. Nonlinear Dyn. 2010, 60, 489–511. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, X.D.; Zhang, Z.N.; Xie, Y.B. A new numerical method for piston dynamics and lubrication analysis. Tribol. Int. 2016, 94, 395–408. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.N.; Fang, C.C.; Dai, X.D.; Xie, Y.B. Modeling and analysis of planar multibody system with mixed lubricated revolute joint. Tribol. Int. 2016, 98, 229–241. [Google Scholar] [CrossRef]
- Zhao, B.; Shen, F. A numerical coupling model for a multibody system with multiple lubricated clearance joints. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 108, p. 15006. [Google Scholar]
- Zhao, B.; Cui, Y.; Xie, Y.; Zhou, K. Dynamics and lubrication analyses of a planar multibody system with multiple lubricated joints. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 326–346. [Google Scholar] [CrossRef]
- Littlefair, B.; De, L.; Cruz, M.; Mills, R.; Theodossiades, S.; Rahnejat, H.; Dwyer-Joyce, R.; Howell-Smith, S. Lubrication of a flexible piston skirt conjunction subjected to thermo-elastic deformation: A combined numerical and experimental investigation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 69–81. [Google Scholar] [CrossRef]
- Luigi, B.; Saverio, G.B.; Valerio, M.; Matteo, G.; Gabriele, C. Influence of the thermal deformation on the lubricating performance of the piston-gudgeon pin interface in an internal combustion engine. Tribol. Int. 2022, 174, 107719. [Google Scholar]
- Oh, K.P.; Li, C.H.; Goenka, P.K. Elastohydrodynamic lubrication of piston skirts. J. Tribol. 1987, 109, 356–362. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Measurement of friction and noise from piston assembly of a single-cylinder motorbike engine at realistic speeds. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 1715–1735. [Google Scholar] [CrossRef]
- Meng, F.; Du, M.; Wang, X.; Chen, Y.; Zhang, Q. Effect of axial piston pin motion on tribo-dynamics of piston skirt-cylinder liner system. Ind. Lubr. Tribol. 2017, 70, 140–154. [Google Scholar] [CrossRef]
- Meng, F.M.; Wang, X.F.; Li, T.T.; Chen, Y.P. Influence of cylinder liner vibration on lateral motion and tribological behaviors for piston in internal combustion engine. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 151–167. [Google Scholar] [CrossRef]
- Tan, Y.C.; Ripin, Z.M. Analysis of piston secondary motion. J. Sound. Vib. 2013, 332, 5162–5176. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, X.; Xiang, P.; Dong, D. Analysis of thermal temperature fields and thermal stress under steady temperature field of diesel engine piston. Appl. Therm. Eng. 2017, 113, 796–812. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Heat Transfer Module-User’s Guide; COMSOL: Stockholm, Sweden, 2020. [Google Scholar]
- Fang, C.; Meng, X.; Kong, X.; Zhao, B.; Huang, H. Transient tribo-dynamics analysis and friction loss evaluation of piston during cold- and warm-start of a SI engine. Int. J. Mech Sci. 2017, 133, 767–787. [Google Scholar] [CrossRef]
- Ning, L.; Meng, X.; Xie, Y. Incorporation of deformation in a lubrication analysis for automotive piston skirt-liner system. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 654–670. [Google Scholar] [CrossRef]
- Wu, L.; Zheng, C. An Average Reynolds Equation for Partial Film Lubrication with a Contact Factor. Trans. ASME J. Tribol. 1989, 111, 188–191. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, B.; Zhang, K. Modelling three-dimensional soft elastohydrodynamic lubrication contact of heterogeneous materials. Tribol. Int. 2019, 129, 377–389. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ma, M.T. Incorporation of lubricant shear-thinning in a two-dimensional lubrication analysis for automotive piston-ring packs. In Proceedings of the CEC/SAE Spring Fuels & Lubricants Meeting & Exposition, Paris, France, 19–22 June 2000. SAE Technical Paper 2000-01-1786. [Google Scholar]
- Gu, C.; Meng, X.; Xie, Y.; Zhang, D. Mixed lubrication problems in the presence of textures: An efficient solution to the cavitation problem with consideration of roughness effects. Tribol. Int. 2016, 103, 516–528. [Google Scholar] [CrossRef]
- Ning, L.; Meng, X.; Xie, Y. Effects of lubricant shear thinning on the mixed lubrication of piston skirt-liner system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 1585–1598. [Google Scholar] [CrossRef]
- Greenwood, J.; Tripp, J. The contact of two nominally flat rough surfaces. Exp. Mycol. 1981, 5, 323–329. [Google Scholar] [CrossRef]
- Akalin, O.; Newaz, G.M. Piston ring-cylinder bore friction modeling in mixed lubrication regime: Part I—Analytical results. J. Tribol. 2001, 123, 211–218. [Google Scholar] [CrossRef]
- Rokad, V.; Pandya, D.H. Development of 3D improved acoustic transient model for vibro cleaner using COMSOL multiphysics. Mater. Today Proc. 2021, 44, 776–781. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Structural Mechanics Module-User’s Guide; COMSOL: Stockholm, Sweden, 2020. [Google Scholar]
- Antony, S.A.; Golbang, A.; Harkin, J.E.; Archer, E.; McIlhagger, A. Prediction of part distortion in Fused Deposition Modelling (FDM) of semi-crystalline polymers via COMSOL: Effect of printing conditions. CIRP J. Manuf. Sci. Technol. 2021, 33, 443–453. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Multibody Dynamics Module-User’s Guide; COMSOL: Stockholm, Sweden, 2020. [Google Scholar]
- Singh, N.K.; Badodkar, D.N. Modeling and analysis of hydraulic dashpot for impact free operation in a shut-off rod drive mechanism. Eng. Sci. Technol. Int. J. 2016, 19, 1514–1525. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.I. Engine friction: The influence of lubricant rheology. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1997, 211, 235–246. [Google Scholar] [CrossRef]


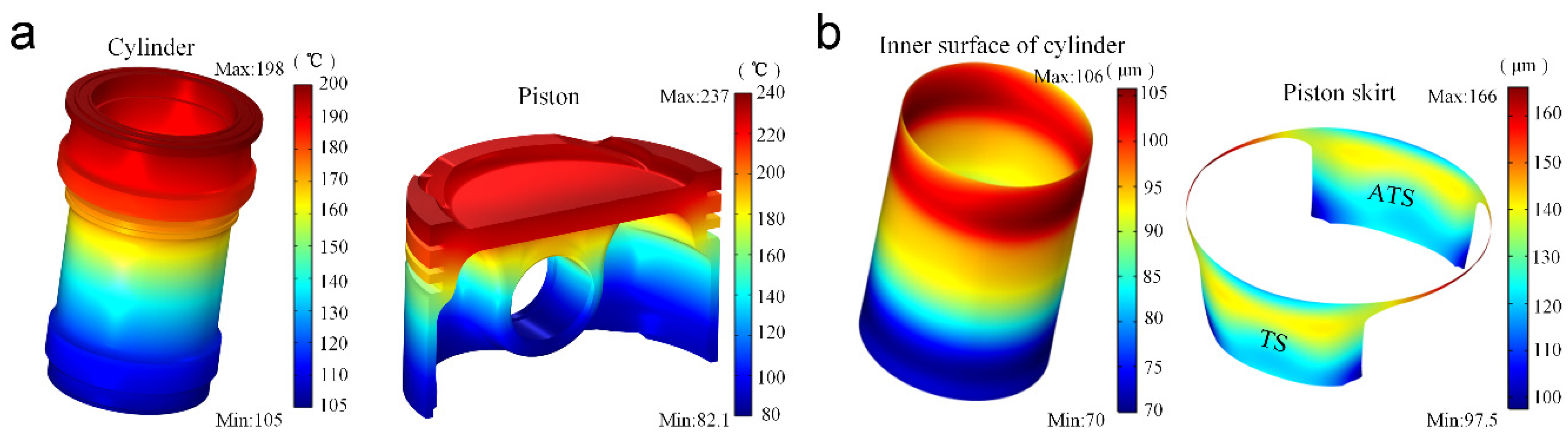


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 0.056 mPa·s | 0.0225 | ||
| 1255.5 °C | 860 kg m−3 | ||
| 117.7 °C | 6.4E−4, K−1 | ||
| 0.71 | 20 °C | ||
| 2.5 |
| Materials Properties | Values | |
|---|---|---|
| Piston | Cylinder | |
| Elastic modulus (GPa) | 165 | 165 |
| Poisson’s ratio | 0.33 | 0.27 |
| Density (kg/m3) | 2700 | 7850 |
| Thermal conductivity (W/mK) | 155 | 52 |
| Linear expansion coefficient (E−6/K) | 21.5 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Wang, S.; Xiao, P.; Xu, L.; Hu, X.; Si, X.; Liu, Y. The Tribo-Dynamics Performance of the Lubricated Piston Skirt–Cylinder System Considering the Cylinder Liner Vibration. Lubricants 2022, 10, 319. https://doi.org/10.3390/lubricants10110319
Zhao B, Wang S, Xiao P, Xu L, Hu X, Si X, Liu Y. The Tribo-Dynamics Performance of the Lubricated Piston Skirt–Cylinder System Considering the Cylinder Liner Vibration. Lubricants. 2022; 10(11):319. https://doi.org/10.3390/lubricants10110319
Chicago/Turabian StyleZhao, Bo, Shijun Wang, Peng Xiao, Lingji Xu, Xinqing Hu, Xiancai Si, and Yonghui Liu. 2022. "The Tribo-Dynamics Performance of the Lubricated Piston Skirt–Cylinder System Considering the Cylinder Liner Vibration" Lubricants 10, no. 11: 319. https://doi.org/10.3390/lubricants10110319
APA StyleZhao, B., Wang, S., Xiao, P., Xu, L., Hu, X., Si, X., & Liu, Y. (2022). The Tribo-Dynamics Performance of the Lubricated Piston Skirt–Cylinder System Considering the Cylinder Liner Vibration. Lubricants, 10(11), 319. https://doi.org/10.3390/lubricants10110319







