Next Article in Journal
Static Analysis of Underground Ant Nest Structures
Next Article in Special Issue
High-Precision Numerical Research on Flow and Structure Noise of Underwater Vehicle
Previous Article in Journal
Frequency-Domain Lifting-Line Aerodynamic Modelling for Wing Aeroelasticity
Previous Article in Special Issue
Underwater Sparse Acoustic Sensor Array Design under Spacing Constraints Based on a Global Enhancement Whale Optimization Algorithm
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 23
10.3390/app122312202
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Observing Meteorological Tides: Fifteen Years of Statistics in the Port of La Spezia (Italy)

by
Maurizio Soldani
* and
Osvaldo Faggioni
Istituto Nazionale di Geofisica e Vulcanologia, Via di Vigna Murata 605, 00143 Roma, Italy
*
Author to whom correspondence should be addressed.
Appl. Sci. 2022, 12(23), 12202; https://doi.org/10.3390/app122312202
Submission received: 24 October 2022 / Revised: 18 November 2022 / Accepted: 24 November 2022 / Published: 29 November 2022
(This article belongs to the Special Issue Advances in Applied Marine Sciences and Engineering)
Browse Figures
Versions Notes

Abstract

:
Sea level changes in coastal areas significantly influence port activities (e.g., the safety of navigation). Along Italian coastlines, sea level variations are mainly due to astronomical tides (well known, due to gravitational attraction between Earth, Moon and Sun); however, during the last fifteen years, a high number of “anomalous” tides has been observed: the study of the phenomenon has allowed to attribute its cause to variations in atmospheric pressure (the so-called meteorological tides: sea level drops when atmospheric pressure increases and vice versa); the statistical analysis of acquired data made it possible to evaluate the hydrobarometric transfer factor (a local parameter which represents the correlation between atmospheric pressure changes and consequent sea level variations): it was found that it is usually much larger within gulfs or port basins than offshore areas, where a pressure change of 1 hPa results in a sea level variation of about 1 cm; the statistical analysis described in the following, and aimed at correctly estimating the hydrobarometric transfer factor in harbors, can play a fundamental role in optimizing the management of port waters: its results allow to forecast meteorological tides and therefore future sea level (and depth) variations in a given port basin. The results of the study conducted in the port of La Spezia (North Western Italy) are presented here, together with possible applications on port activities and harbor water management.

1. Introduction

The knowledge of sea level fluctuations in coastal areas is fundamental to increasing the safety of people who work in ports or onboard ships, to best managing port activities, and to reducing economic losses and environmental damage (improving the safety of navigation, optimizing ships’ cargo and mooring, managing the refloating of stranded vessels, dimensioning maritime works, planning dredging activities, checking the chemical and physical parameters of water), as well as for civil protection purposes (mitigating the risk of flooding at the mouth of rivers) [1,2,3,4,5,6,7].
Sea level variations along Mediterranean coastlines are mostly due to astronomical tides (up and down motions caused by the gravitational attraction between the earth, moon and sun, then periodic and predictable deterministically), in particular to the diurnal and semi-diurnal components, shown in Table 1 [8,9].
However, a large number of anomalous tides have been observed over the last fifteen years inside many Italian harbors. The study of the phenomenon allowed us to associate these events to changes in atmospheric pressure above the sea basin under examination; in particular, sea level lowers/rises following an increase/decrease in atmospheric pressure (good/bad weather) and then in the weight of the overlying air column [10,11,12,13,14,15,16,17]: these low frequency oscillations, called meteorological tides, represent the geodetic adjustment (Newtonian compensation) of sea surface (induced effect), which compensates for atmospheric pressure perturbations (inducing cause), as shown in Figure 1 [18,19,20,21,22,23].
The evidence of the phenomenon was observed by means of ISPRA’s (Italian Institute for Environmental Protection and Research) meteo-mareographic station located in La Spezia harbor (Italy); for example, on 13 November 2020 at 10:15 UTC (Universal Time Coordinates) and on 8 December 2020 at 09:25 UTC, the same astronomical tide was present (nearly 20 cm), but a pressure decrease of nearly 27.1 hPa resulted in an increase of about 34 cm in the sea level acquired.
In many Italian ports, we have verified that the hydrobarometric transfer factor, a parameter that represents the correlation between the atmospheric pressure variation and the consequent change in sea level, assumes often much larger values (even double) compared with offshore areas, where, as is well known, 1 hPa (about equal to 1 mBar) of atmospheric pressure variation corresponds to approximately 1 cm of change in sea level (the so-called inverted barometer effect); so, within harbors, a few hPa of decrease/increase in atmospheric pressure can cause several cm of sea level rise/fall; in fact, a sea basin behaves in the same way as a semi-constrained domain: by hindering the horizontal movement of the water mass, it amplifies its vertical displacement. Therefore, meteorological tides can cause exceptional changes in sea level within a port basin if they occur in-phase with astronomical ones.
To be able to forecast sea level in harbors, it is therefore necessary to estimate the correlation between atmospheric pressure and sea level, represented by the hydrobarometric transfer factor; it depends on a series of local parameters (first of all the morphology of the basin examined and the atmospheric dynamics over it), so it is not described by a deterministic law valid everywhere but obtained port by port through a statistical analysis of local data acquired [24,25,26,27,28,29,30,31].
In this work, we present the analysis carried out starting from data acquired since 2006 by ISPRA’s monitoring station located inside the port of La Spezia (Eastern Ligurian Sea, Italy); based on the measurements of atmospheric pressure and sea level, the statistical analysis described below aims at estimating the hydrobarometric transfer factor in La Spezia harbor.
We also describe a prototype application developed to provide support to local authorities and port communities, in order to improve port navigation safety (obviously, the low tide hinders the port navigation, while the high tide facilitates it): based on the sea level measured or forecasted, the application updates water depths inside a port basin (“real” port bathymetric map) and detects, by means of a simple and intuitive graphic interface, hazardous areas for a certain ship moving inside the harbor at a given moment [32,33,34,35,36,37,38].

2. Materials and Methods

The starting point of this study is the monitoring of environmental parameters in the port of La Spezia, performed by means of the meteo-mareografic station working in the position 09°51′27.52″ E, 44°05′47.79″ N (see Figure 2) and belonging to the National Tidegauge Network managed by ISPRA [39,40,41,42,43,44,45].
The instrumentation used consists of a hydrometer and a barometer; the first measures the sea level on the basis of the round trip time taken by a sequence of radar pulses sent from the air towards the sea surface; since the speed of propagation of electromagnetic waves in the air, the round trip time of the pulses, and the position of the radar transducer are known, sea levels are calculated; a typical sampling interval to acquire tide data is at least 10 min.
The barometer measures the atmospheric pressure by evaluating the deformations undergone by a silicon capacitive transducer; when the atmospheric pressure changes, the distance between the two plates and therefore the electrical capacitance also varies; measurements are typically made hourly (atmospheric pressure is characterized by very slow variations).
The date and time are expressed in UTC, while the sea level refers to IGM’s (Italian Military Geographic Institute) 0 level. The data used in this work and further information about the ISPRA’s monitoring station are available on the website www.mareografico.it (data from 2006 to 2009 are not available on the website; they have been kindly provided by ISPRA) (accessed on 28 April 2022).
Atmospheric pressure and sea level measurements (one sample every hour with resolutions equal to 10−1 hPa and 1 cm, respectively) were compared with each other in order to evaluate the hydrobarometric transfer factor, a local parameter that represents the correlation between the two quantities. Figure 3 shows the signals acquired between 28 May and 7 June 2009 inside the port of La Spezia.
The sea level is the overlapping of different contributions, among which the main ones are astronomical and meteorological tides, as shown in the power spectral densities plotted in Figure 4, as regards the measurements performed in 2009: Frequency components due to diurnal and semidiurnal components are at approximately at 1.2 and 2.3 × 10−5 Hz respectively, while meteorological components are characterized by lower frequencies (slower oscillations) related to atmospheric pressure spectrum (DC components are not plotted because they do not carry useful information).
First of all, it was therefore necessary to filter acquired data in order to remove high-frequency components due to causes different than meteorological ones (there could also be a residual of the disturbance due to sea waves, although the hydrometer works inside a still-pipe): atmospheric pressure and sea level signals are subjected to low-pass filtering with an appropriate cut frequency (10−5 Hz), so that only the contributions of meteorological origin survive. Figure 5 shows the result of the low-pass filtering applied to the data shown in Figure 3.
By examining filtered signals, it is evident that a decrease Δp in atmospheric pressure equal to about 17.2 hPa causes an increase in low-frequency sea level Δh (low meteorological tide) equal to about 35.4 cm. So, for the event analyzed, the hydrobarometric transfer factor Jph can be calculated as:
J p h = Δ h Δ p = 35.4   cm 17.2   hPa = 2.1   cm * hPa − 1 ,
which is more than double the offshore case; the gradients Δh and Δp are expressed in absolute values.
The analysis just described for a single case was repeated for all the events that occurred in the port of La Spezia since 14 March 2006 (the hydrometer of ISPRA’s monitoring station has been working since 13 January 2006, but the barometer was not installed until two months later) in order to obtain an estimate of the hydrobarometric transfer factor for the water basin under examination, as described in the next paragraph.

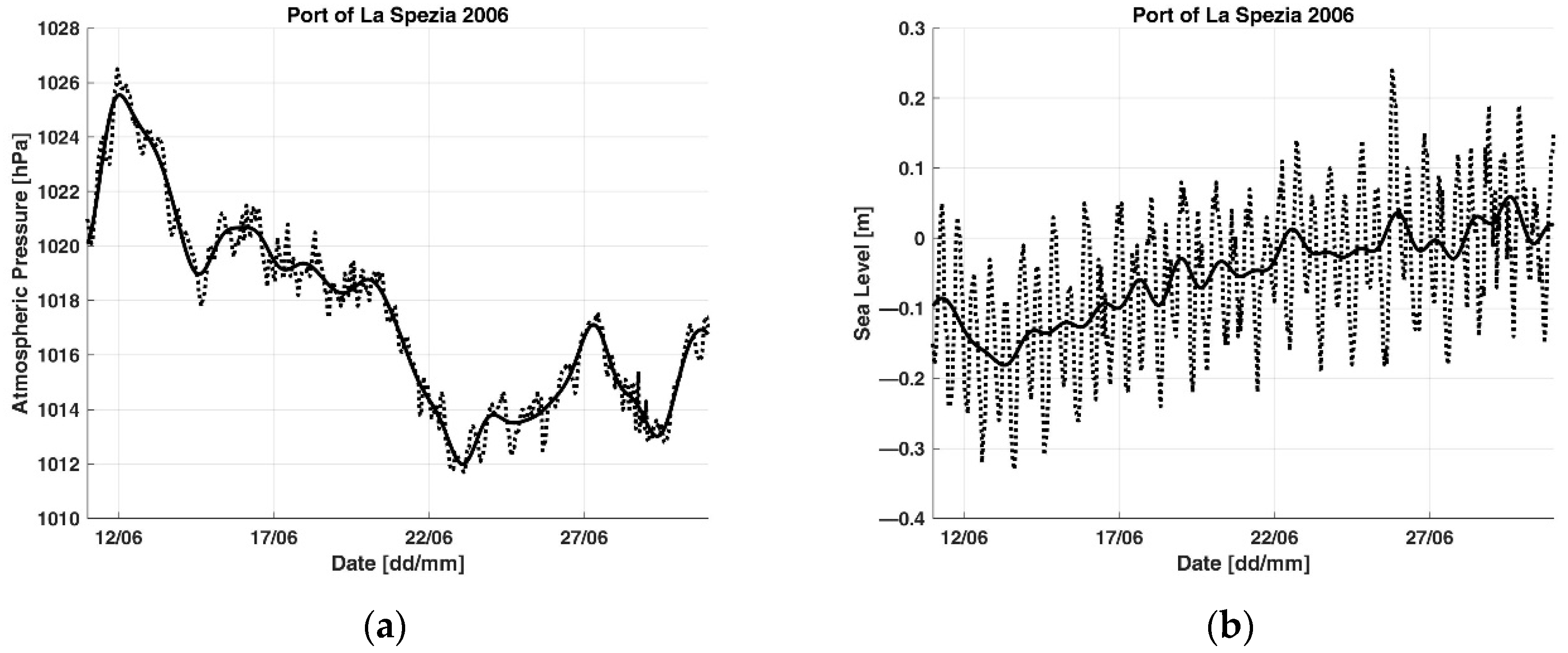
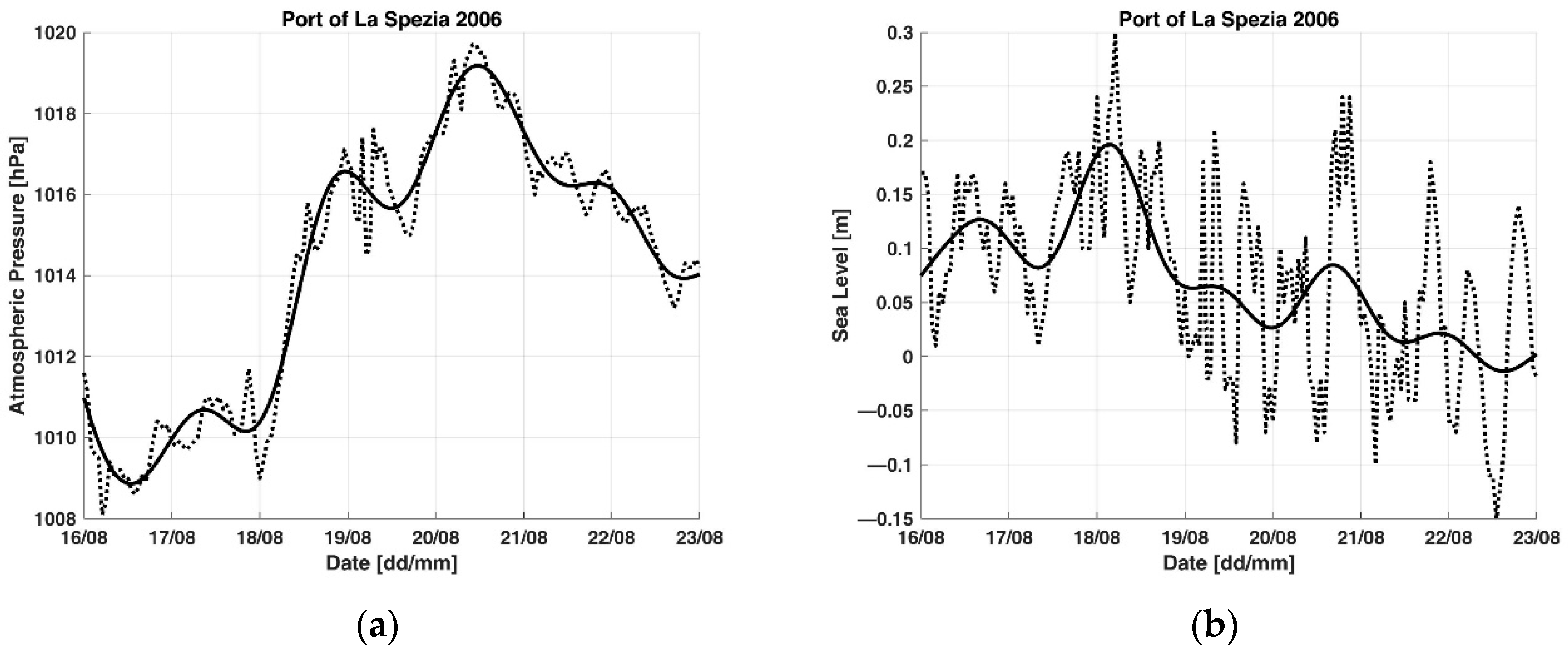
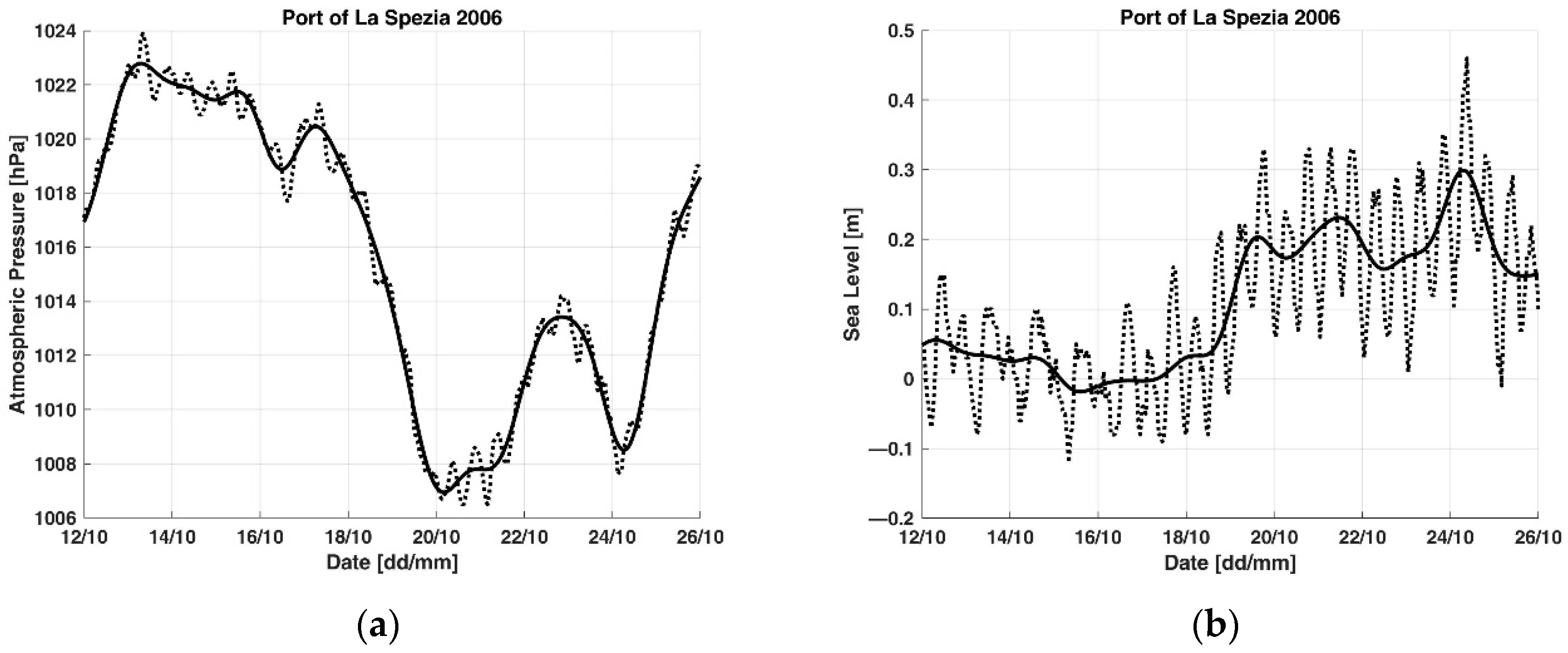
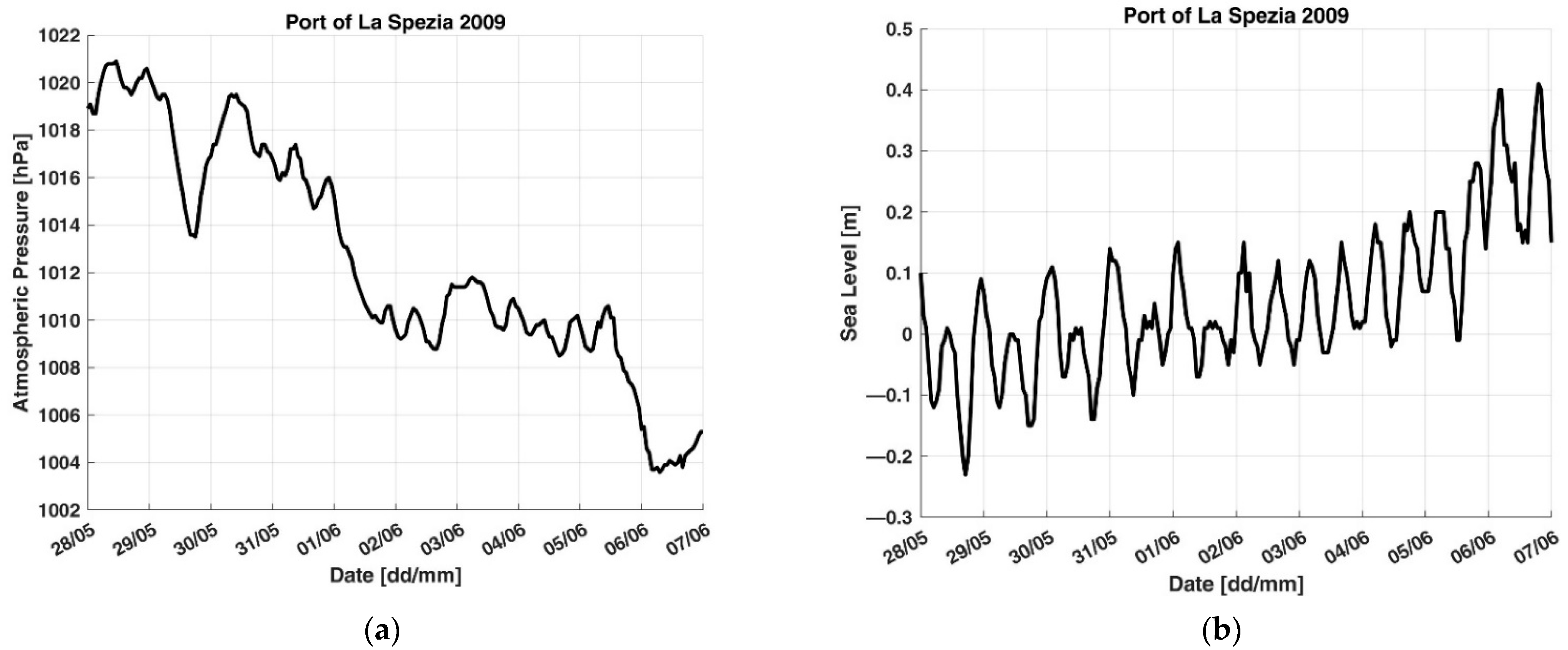
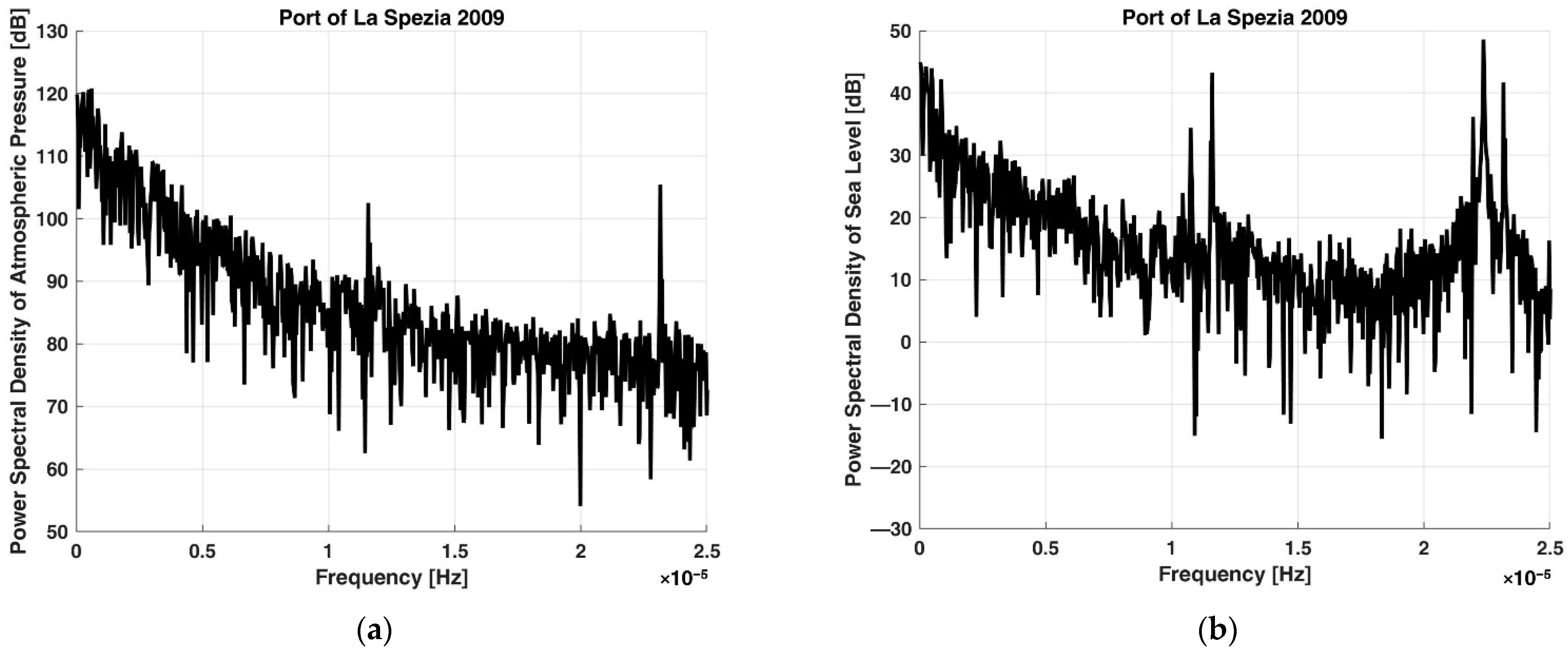
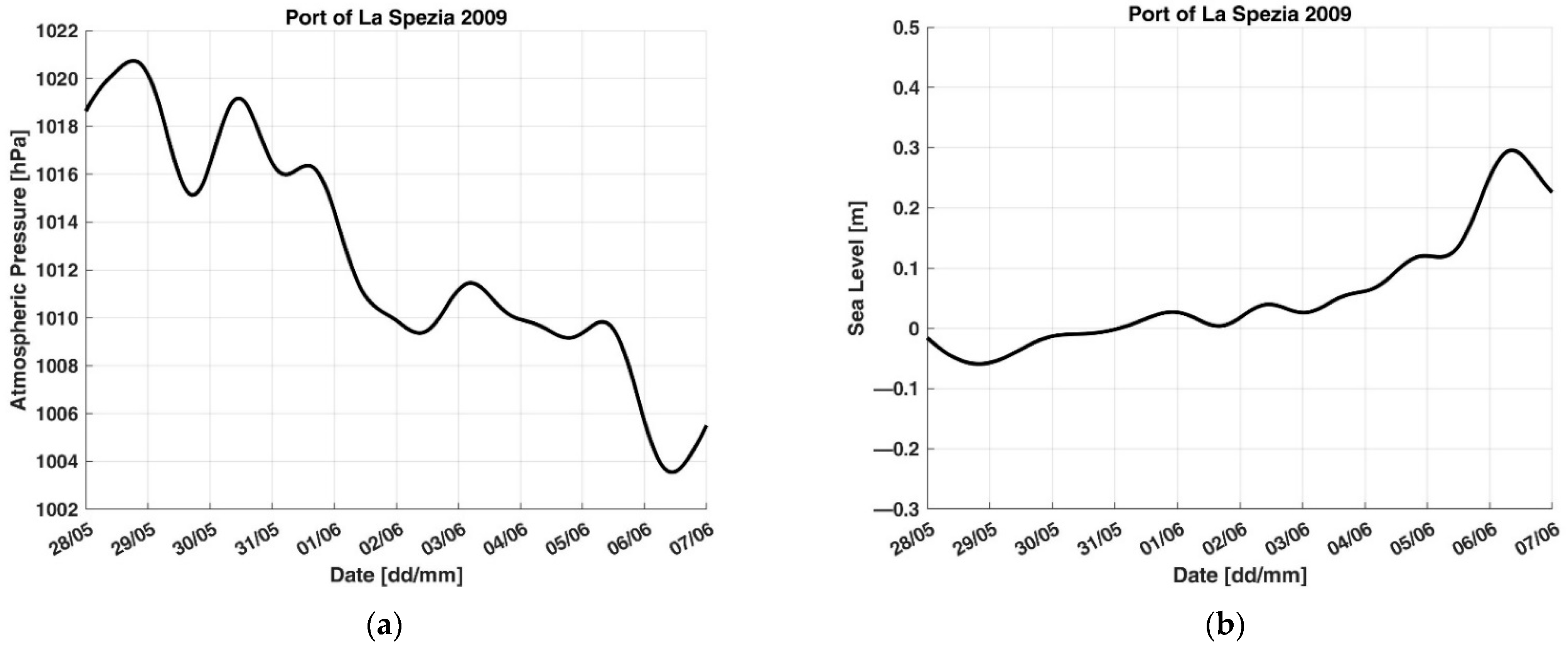
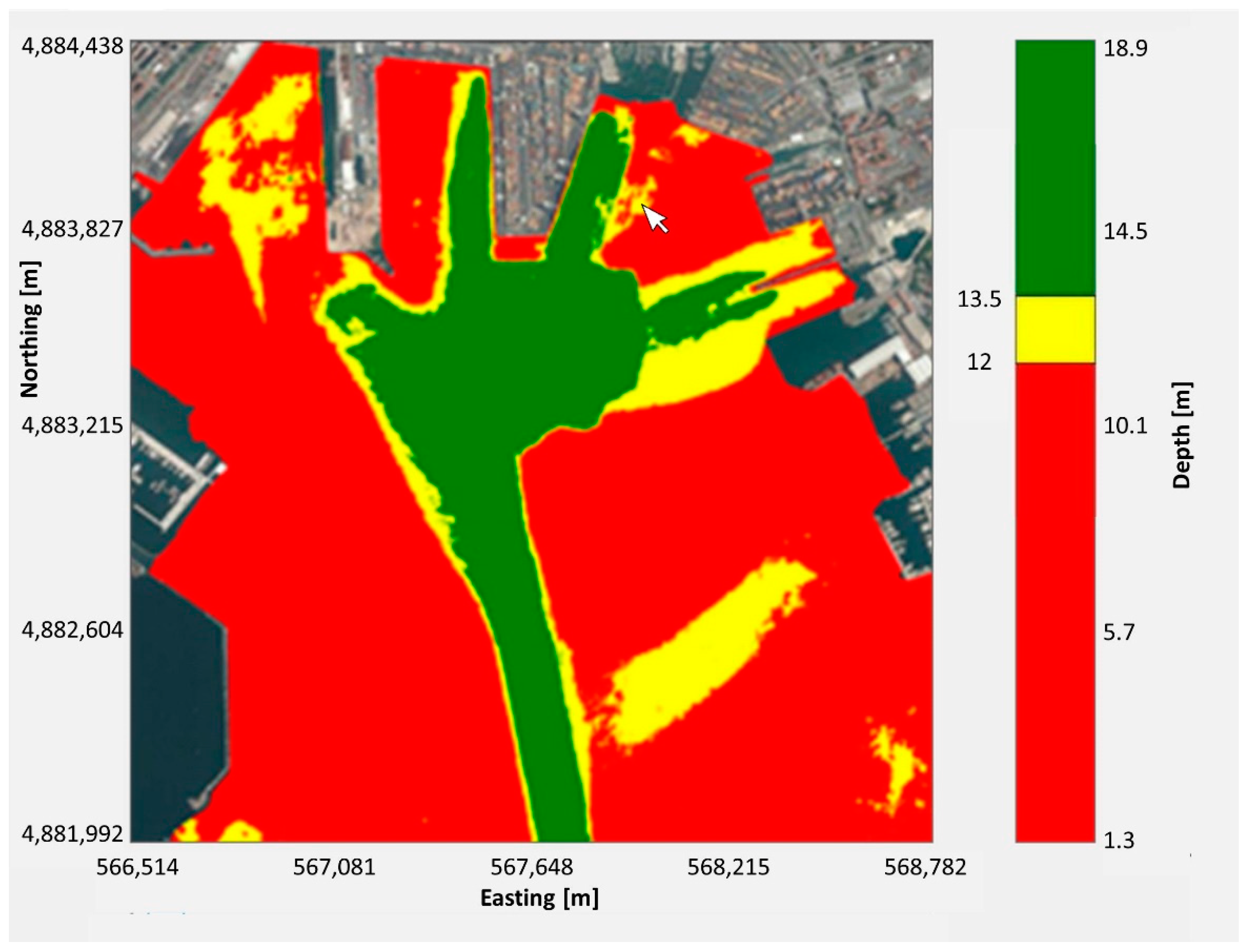
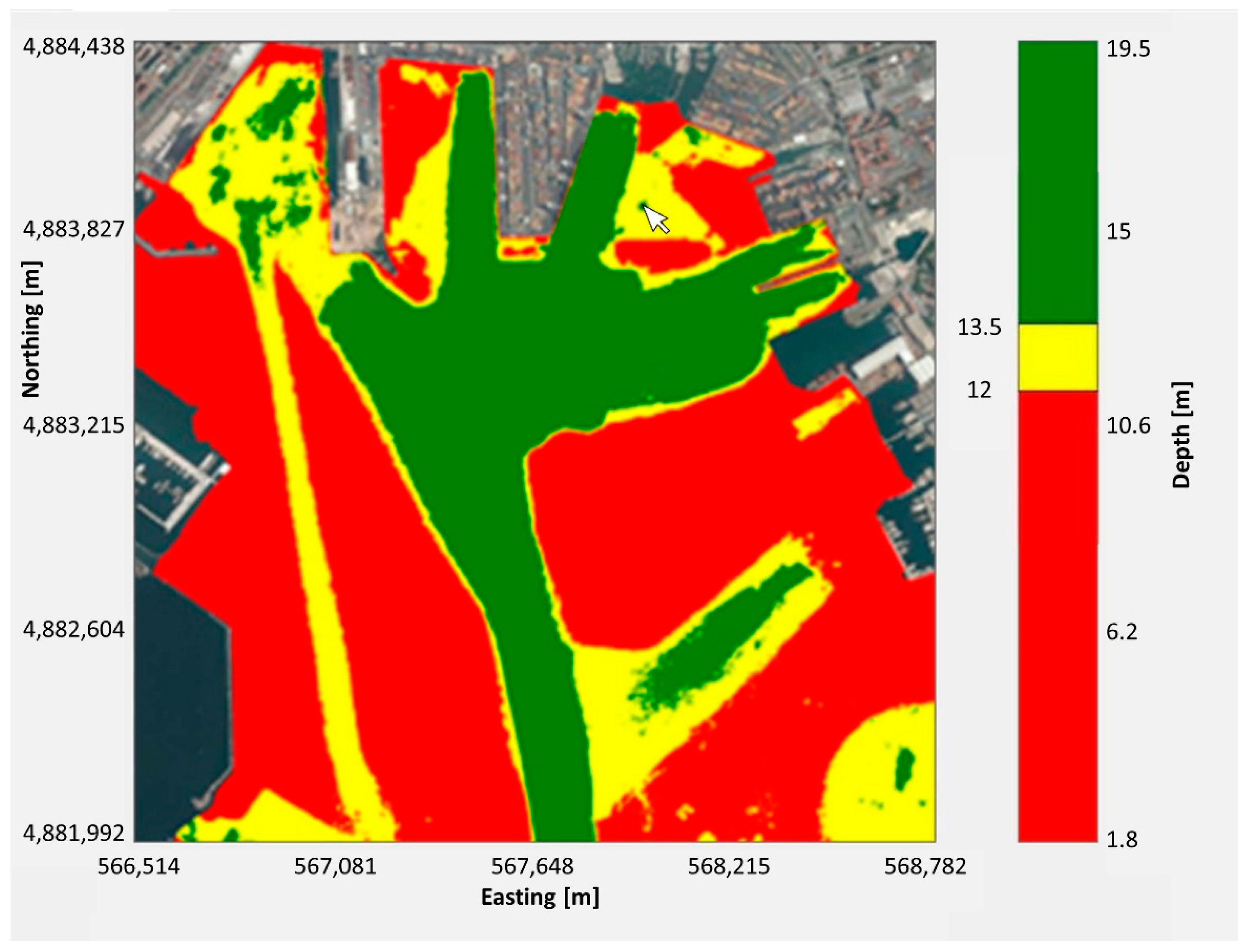
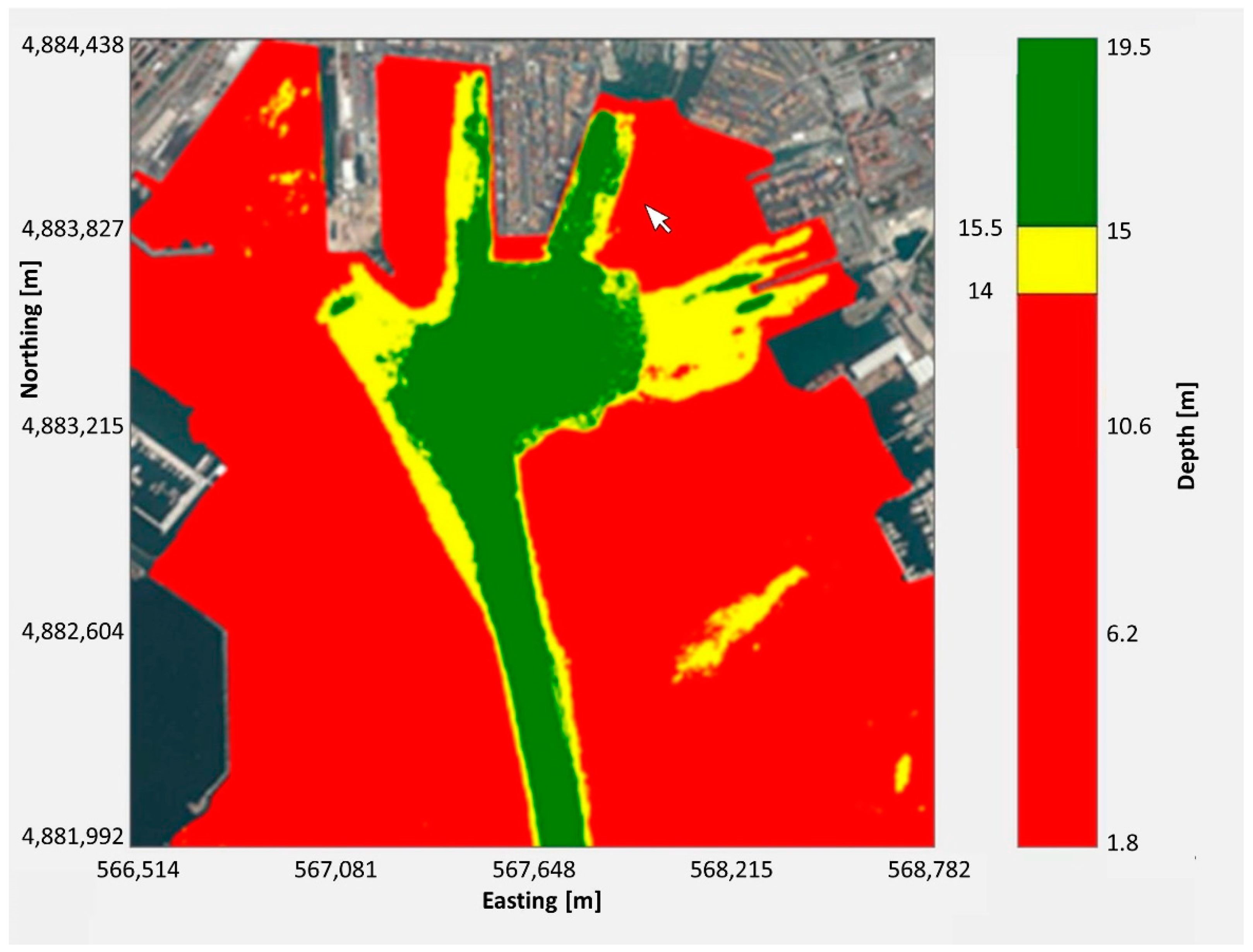
3. Results

The analysis described in the previous paragraph was replicated for every significant hydrobarometric event occurred in the port of La Spezia from March 2006 (data from 24 January 2015 to 6 March 2019 are not available) to the end of 2021, to produce a fifteen-year statistics (this study was realized starting from the installation of ISPRA’s monitoring station, in 2006).
The values of Δp, Δh and Jph estimated event by event are listed in the Appendix A, in Table A1. Only events with Δp greater than about 5 hPa are taken into account. The highest observed value of meteorological tide in this period was 52.9 cm (between 28 February and 4 March 2020).
The acquisitions related to these events are shown, in Figure A1, Figure A2, Figure A3 and Figure A4 (in the Appendix A) and Figures S1–S45 (in the Supplementary Material); events occurring in the presence of wind were not considered in the statistical analysis, in order to exclude some phenomena due to causes such as storm surges, anyway not predominant in the site examined (the anemometer to acquire wind data has been working since 30 June 2010) and then not analyzed in this work; for example, the event shown in Figure 6 (from 28 September to 5 October 2020, Δp = 20.4 hPa, Δh = 43.5 cm) has been excluded from the statistics because there was a wind coming roughly from the South East (then from the mouth of the gulf), stronger than 10 m/s and persistent for more than one day.
First, the event shown in Figure S5 was removed from the statistics because its Jph values differ from the mean value by more than 3 times the standard deviation; for this reason, it is considered outlier (rare event).
After doing that, the mean value and the standard deviation of the statistical distribution are 1.9 cm ∗ hPa−1 and 0.3 cm ∗ hPa−1, respectively.
Then, a first estimate of the hydrobarometric transfer factor for the port of La Spezia can be represented by its average: in this case the mean value is about double the offshore; after this, the mean hydrobarometric transfer factor can be used to forecast a future sea level variation Δh starting from the measured atmospheric pressure change Δp: it is sufficient to multiply Δp by Jph (taking into account that when the pressure goes up the level falls and vice versa); this corresponds to suppose a linear dependence:
Δ h = J p h *   Δ p   ,
as represented by the red straight line in Figure 7, whereas the black dots correspond to the measured pairs (Δp, Δh) listed in Table A1.
A better estimate of the relationship between atmospheric pressure and sea level gradients can be obtained by considering a non-linear law Δh = f(Δp); using the least squares method applied to the pairs (Δp, Δh) the fixed degree polynomial can be extrapolated that best fits the data cloud (the hydrobarometric transfer factor becomes a sequence of coefficients); for example, assuming a cubic dependence of Δh on Δp and imposing the passage to the origin (because Δp = 0 implies Δh = 0), this estimate of Δh is obtained:
Δ h = J p h 3 *   Δ p 3 + J p h 2 *   Δ p 2 + J p h 1 * Δ p   ,
where: Jph3 = 0.001 cm ∗ hPa−3, Jph2 = −0.05 cm ∗ hPa−2, Jph1 = 2.3 cm ∗ hPa−1, as plotted in Figure 7 (green line).
The couples (Δp, Δh) measured from 2006 to 2021 in the port of La Spezia, linear and cubic approximations are shown in Figure 7, together with the comparison with the “inverted barometer effect” of the offshore case.
Once the change in atmospheric pressure is measured or predicted, the expected sea level variation can be derived from the Equation (3).
Obviously, the two different estimates (linear and cubic) lead to two different errors between the measured value and the estimated trends: starting from data in Table A1, an average error on the expected sea level (difference between forecast and measurement) of 11.3% was obtained in the case of linear approximation, while in the case of cubic function the mean error is 9.6% (against a greater computational load), which is satisfactory for our purposes.
Therefore, the fundamental role of the hydrobarometric transfer factor consists in converting a variation of atmospheric pressure into a forecasted sea level change (meteorological component) for a given port; finally, meteorological tides will have to be added (or subctracted) to the astronomical tides (predictable by means of tide charts) to obtain the forecasted sea level in that basin.
Contributions to changes in sea level due to other causes such as, for example, seiches, storm surges or wind effects, which are not predominant in the site examined, are not taken into account in this work.
It should be emphasized that the hydrobarometric transfer factor must be updated year after year and periodically recalculated, e.g., following events that modify the topography of the basin examined (dredging operations, coastal erosion, bottom subsidence, sediment deposition).
Moreover, a multi-decade statistics is necessary to examine any changes in the hydrobarometric transfer factor due to climate change, as well as the variation over the years of occurrence frequency of events observed [46,47].

4. Discussion

As seen in the previous paragraph, the hydrobarometric transfer factor is usually much greater within port basins than in offshore areas: A few hPa of atmospheric pressure variation can cause several cm of astronomical tide that, if in phase with the astronomical one, can generate anomalous sea level variations.
The knowledge of the hydrobarometric transfer factor allows for correctly estimating expected meteorological tides in harbors and, together with the joint prediction of astronomical components from tide charts, forecasting sea level within port basins, an aspect of fundamental importance to better managing port operations.
In fact, the monitoring/forecasting of sea level (and then of water depth) in coastal areas is extremely important for managing, planning, and optimizing:
  • Maritime transport and port navigation safety (e.g., to reduce the risk of accidents or to plan the refloating of a ship and minimize the risk of environmental damages and economic losses) [48,49,50,51];
  • Ship loading (how much to load a ship in the departure port based on the expected tide in the port of arrival) [52,53,54,55];
  • Dock performances and vessel moorings;
  • Dimensioning of maritime works based on the maximum sea level expected;
  • Dredging activities;
  • The control of chemical and physical parameters of water;
as well as preventing the risk of flooding at the mouths of rivers (civil protection purposes) by providing early warning to the population involved.
For this reason, the results of this study can have important applications in coastal areas: A software tool has been developed by the research group to which the authors belong with the aim of providing useful operational support to port communities, local authorities, and decision makers; it dynamically updates the initial port bathymetric map (usually acquired through multibeam surveys and updated after changes in the harbor topography, e.g., following dredging operations) based on sea level measured or expected and, if the draught of a certain ship is known, identifies the permitted/alert/prohibited areas for that same ship at a given time. An intuitive graphical interface implements what are called “virtual traffic lights” by coloring the forbidden areas red, the alert zones yellow, and the allowed ones green, based on two thresholds that in their turn depend on the vessel draught. Red areas are those with depths less than the lower threshold (usually equal to the vessel’s draught), green areas those with depths greater than the upper threshold (much greater than the vessel’s draught); finally, yellow areas are the intermediate ones.
The application continuously recalculates the “real” bathymetry (water depth variable over time) of a harbor using sea level data acquired in real time (by downloading them from the monitoring station via an Internet connection), measured in the past and saved in a dataset (to analyze a posteriori past events of particular importance such as the stranding of ships) or forecasted in the future by means of the hydrobarometric transfer factor and tide charts, in order to signal in advance potentially dangerous areas and avoid critical situations induced by sea level changes for a given ship. It can be very useful, e.g., for supporting a certain ship in choosing the best route to follow or the best time to enter or leave a port or the most suitable quay to moor.
For example, in Figure 8, virtual traffic lights in the middle of the port of La Spezia on 30 June 2010 at 12:00 UTC are shown, when the tide gauge was measuring −0.54 m. Thresholds were chosen equal to 12 and 13.5 m, e.g., for a Panamax cargo ship, whose draught is about 12 m (areas with depth less than 12 m are prohibited, those with depth greater than 13.5 m are permitted, the others are warning areas).
Easting and northing are expressed in UTM (Universal Transverse Mercator) coordinates, zone 32T; grid spacing is 2 m; depth refers to IGM’s 0 level, depth resolution 1 cm; bathymetric data are courtesy of the Port System Authority of the Eastern Ligurian Sea, La Spezia, Italy.
Instead, Figure 9 refers to 24 November 2010 at 18:00 UTC (sea level = 0.83 m), for the same ship (and then the same thresholds).
Note how, following the rise of 1.37 m in sea level, the forbidden area narrows and many warning positions become allowed, while a yellow waterway appears in the west side of the port.
In particular, the state of the position indicated by the mouse pointer (coordinates 567,956, 4,883,930 m) in the middle top of the map switches from alert to allowed, as indicated by the color of the traffic light in Figure 8 and Figure 9, since its depth increases from 12.45 to 13.82 m.
It is worth highlighting that the increase in sea level is partly due to a 9.5 hPa fall in atmospheric pressure between 30 June 2010 at 12:00 UTC and 24 November 2010 at 18:00 UTC (from 1016.9 to 1007.4 hPa).
Obviously at the same instant, for a vessel with greater draught (for example 14 m for a container ship), thresholds would be higher, and forbidden areas would expand, as shown in Figure 10; the traffic light for the position indicated by the mouse pointer becomes red.
Therefore, this interface represents a useful tool for detecting potentially dangerous areas for a given ship at a certain moment.
Additionally other contributions due to different phenomena can be passed as input to the application, such as seiches, storm surges, or wind effects, which particularly in certain locations must be taken into account.

5. Conclusions

In Mediterranean harbors, tides are mainly due to astronomical and meteorological components; while the first ones are well known and predictable everywhere by means of a deterministic law (tide charts), the second ones (due to atmospheric disturbances) need more study: starting from monitoring environmental parameters in La Spezia harbor (Ligurian Sea, North-Western Italy), we performed a statistical analysis over the last fifteen years (starting from the installation of ISPRA’s monitoring station in 2006) to evaluate the hydrobarometric transfer factor, which represents the correlation between atmospheric pressure (cause) and sea level variations (effect) and therefore can play a fundamental role in forecasting meteorological tides in harbors.
We found that the hydrobarometric transfer factor in La Spezia harbor is larger (sometimes more than double) than in offshore areas (where 1 hPa of atmospheric pressure gradient induces nearly 1 cm of sea level rise/fall); thus, some hPa of atmospheric gradient can induce several cm of sea level rise/fall.
In particular, we found that using Jph = 1.9 cm ∗ hPa−1 results in an estimate of the average error of about 11.3%, while approximating the dependence of sea level on atmospheric pressure by means of a nonlinear (cubic) law reduces the mean error to about 9.6%. This error very rarely induces confusion between different colors along the edges of adjacent areas in the map representing virtual traffic lights described above.
Furthermore, meteorological tides can cause exceptional changes in sea level if they occur in conjunction with astronomical components: the observation of the phenomenon allowed us to highlight anomalou” tides, sea level changes that are very different from the expected astronomical tides.
The hydrobarometric transfer factor allows to forecast meteorological tides in the sea basin examined and then, simply by adding the contribution of the astronomical tides, to know in advance the sea level (and therefore water depth) expected in the near future; this can represent a useful tool for optimizing port activities and logistic operations by planning them in advance.
Since sea level changes in coastal areas affect in a relevant way the safety of port communities, a prototype application has been developed that updates the port bathymetric map based on sea level acquired in real time or forecasted, with the aim of planning and optimizing port activities or managing emergencies (it is also able to load old measurements stored in a dataset, e.g., to analyze accidents occurred in the past); the software tool classifies the port bathymetric map in forbidden (red), warning (yellow), or permitted (green) areas for a certain ship at a given moment, based on its draught (virtual traffic lights); the graphical interface is able to detect and easily signal hazardous situations in harbors in order to provide a useful support to decision makers (port authorities, coast guards), with the aim of increasing safety for people working in ports.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app122312202/s1, Figure S1. Measurements carried out between 21 and 27 February 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 10 hPa, Δh = 16 cm, Jph = 1.6 cm ∗ hPa−1). Figure S2. Measurements carried out between 25 February and 1 March 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 9.8 hPa, Δh = 16.4 cm, Jph = 1.7 cm ∗ hPa−1). Figure S3. Measurements carried out between 9 and 16 May 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 5.9 hPa, Δh = 16.1 cm, Jph = 2.7 cm ∗ hPa−1). Figure S4. Measurements carried out between 31 May and 2 June 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 4.9 hPa, Δh = 14.4 cm, Jph = 2.9 cm ∗ hPa−1). Figure S5. Measurements carried out between 1 and 4 June 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 4.9 hPa, Δh = 16.8 cm, Jph = 3.4 cm ∗ hPa−1). Figure S6. Measurements carried out between 3 and 10 August 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 12.2 hPa, Δh = 20 cm, Jph = 1.6 cm ∗ hPa−1). Figure S7. Measurements carried out between 20 and 27 October 2007 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 13.7 hPa, Δh = 27.6 cm, Jph = 2 cm ∗ hPa−1). Figure S8. Measurements carried out between 3 and 13 April 2008 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.5 hPa, Δh = 40.2 cm, Jph = 2.3 cm ∗ hPa−1). Figure S9. Measurements carried out between 10 and 17 April 2008 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 16.9 hPa, Δh = 30.8 cm, Jph = 1.8 cm ∗ hPa−1). Figure S10. Measurements carried out between 26 August and 9 September 2008 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 7.8 hPa, Δh = 19 cm, Jph = 2.4 cm ∗ hPa−1). Figure S11. Measurements carried out between 26 November and 2 December 2008 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 28.9 hPa, Δh = 51.6 cm, Jph = 1.8 cm ∗ hPa−1). Figure S12. Measurements carried out between 29 January and 9 February 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 28.2 hPa, Δh = 45.6 cm, Jph = 1.6 cm ∗ hPa−1). Figure S13. Measurements carried out between 28 May and 7 June 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.2 hPa, Δh = 35.4 cm, Jph = 2.1 cm ∗ hPa−1). Figure S14. Measurements carried out between 6 and 18 September 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 13.8 hPa, Δh = 24.6 cm, Jph = 1.8 cm ∗ hPa−1). Figure S15. Measurements carried out between 28 November and 1 December 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 20.5 hPa, Δh = 38.6 cm, Jph = 1.9 cm ∗ hPa−1). Figure S16. Measurements carried out between 18 and 20 February 2010 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 19.4 hPa, Δh = 33.9 cm, Jph = 1.7 cm ∗ hPa−1). Figure S17. Measurements carried out between 4 and 15 June 2010 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 8.2 hPa, Δh = 16.4 cm, Jph = 2 cm ∗ hPa−1). Figure S18. Measurements carried out between 7 and 16 August 2010 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 7.8 hPa, Δh = 16.5 cm, Jph = 2.1 cm ∗ hPa−1). Figure S19. Measurements carried out between 27 October and 02 November 2010 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.3 hPa, Δh = 35.7 cm, Jph = 2.1 cm ∗ hPa−1). Figure S20. Measurements carried out between 26 January and 8 February 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 18.9 hPa, Δh = 30.3 cm, Jph = 1.6 cm ∗ hPa−1). Figure S21. Measurements carried out between 18 and 28 June 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 11.3 hPa, Δh = 24.1 cm, Jph = 2.1 cm ∗ hPa−1). Figure S22. Measurements carried out between 18 September and 2 October 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 20.8 hPa, Δh = 33 cm, Jph = 1.6 cm ∗ hPa−1). Figure S23. Measurements carried out between 21 and 27 October 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 15 hPa, Δh = 33.7 cm, Jph = 2.2 cm ∗ hPa−1). Figure S24. Measurements carried out between 25 October and 3 November 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.3 hPa, Δh = 28.8 cm, Jph = 1.7 cm ∗ hPa−1). Figure S25. Measurements carried out between 28 October and 7 November 2011 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.2 hPa, Δh = 29.4 cm, Jph = 1.7 cm ∗ hPa−1). Figure S26. Measurements carried out between 12 and 20 July 2012 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 10.5 hPa, Δh = 18.1 cm, Jph = 1.7 cm ∗ hPa−1). Figure S27. Measurements carried out between 8 and 16 October 2012 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 14.2 hPa, Δh = 23.4 cm, Jph = 1.6 cm ∗ hPa−1). Figure S28. Measurements carried out between 5 and 12 May 2013 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 5.7 hPa, Δh = 17.3 cm, Jph = 3 cm ∗ hPa−1). Figure S29. Measurements carried out between 23 and 28 June 2013 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 9.3 hPa, Δh = 17.2 cm, Jph = 1.8 cm ∗ hPa−1). Figure S30. Measurements carried out between 19 and 26 January 2014 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 17.2 hPa, Δh = 35 cm, Jph = 2 cm ∗ hPa−1). Figure S31. Measurements carried out between 10 and 26 February 2014 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 23.6 hPa, Δh = 41.4 cm, Jph = 1.8 cm ∗ hPa−1). Figure S32. Measurements carried out between 12 and 16 October 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 12.3 hPa, Δh = 20.5 cm, Jph = 1.7 cm ∗ hPa−1). Figure S33. Measurements carried out between 15 and 18 October 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 9.3 hPa, Δh = 15.5 cm, Jph = 1.7 cm ∗ hPa−1). Figure S34. Measurements carried out between 17 and 21 October 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 4.8 hPa, Δh = 11.5 cm, Jph = 2.4 cm ∗ hPa−1). Figure S35. Measurements carried out between 19 and 23 October 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 6 hPa, Δh = 13.3 cm, Jph = 2.2 cm ∗ hPa−1). Figure S36. Measurements carried out between 19 and 25 November 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 12.3 hPa, Δh = 28.7 cm, Jph = 2.3 cm ∗ hPa−1). Figure S37. Measurements carried out between 27 November and 9 December 2019 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 21 hPa, Δh = 39.2 cm, Jph = 1.9 cm ∗ hPa−1). Figure S38. Measurements carried out between 28 February and 4 March 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 28.6 hPa, Δh = 52.9 cm, Jph = 1.8 cm ∗ hPa−1). Figure S39. Measurements carried out between 31 May and 8 June 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 20.3 hPa, Δh = 38.2 cm, Jph = 1.9 cm ∗ hPa−1). Figure S40. Measurements carried out between 7 and 17 June 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 6.3 hPa, Δh = 11.6 cm, Jph = 1.8 cm ∗ hPa−1). Figure S41. Measurements carried out between 21 and 31 August 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 15.3 hPa, Δh = 26.3 cm, Jph = 1.7 cm ∗ hPa−1). Figure S42. Measurements carried out between 21 and 29 June 2021 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 7.4 hPa, Δh = 1.4 cm, Jph = 1.9 cm ∗ hPa−1). Figure S43. Measurements carried out between 21 and 27 July 2021 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 8.5 hPa, Δh = 16.7 cm, Jph = 2 cm ∗ hPa−1). Figure S44. Measurements carried out between 31 July and 24 August 2021 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 14 hPa, Δh = 23.4 cm, Jph = 1.7 cm ∗ hPa−1). Figure S45. Measurements carried out between 18 and 25 September 2021 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 11 hPa, Δh = 18.8 cm, Jph = 1.7 cm ∗ hPa−1).

Author Contributions

Conceptualization, M.S. and O.F.; methodology, M.S. and O.F.; software, M.S. and O.F.; validation, M.S. and O.F.; formal analysis, M.S. and O.F.; investigation, M.S. and O.F.; resources, M.S. and O.F.; data curation, M.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S. and O.F.; visualization, M.S. and O.F.; supervision, O.F.; project administration, M.S. and O.F.; funding acquisition, M.S. and O.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded within the framework of the MENFOR Project (MEteo-tide Newtonian FORecasting) by several Italian port authorities, in particular the Port Authority of La Spezia (now named the Port System Authority of the Eastern Ligurian Sea) for what we described in this article and from the European Union and Regional Government of Liguria (Italy) by means of the Regional Plan of Innovative Actions—European Funds for the Regional Development.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Meteo-mareographic data used in this article, acquired by means of the monitoring station in La Spezia belonging to ISPRA’s National Tidegauge Network, are mostly available on the website www.mareografico.it (accessed on 28 April 2022); data from 2006 to 2009 are not available on the website; they have been kindly provided by ISPRA; additionally, archives of environmental data available on weather websites were consulted.

Acknowledgments

The authors wish to thank the Port Authority of La Spezia (now named the Port System Authority of the Eastern Ligurian Sea) for having kindly provided bathymetric data (a special thanks to D. Vetrala and I. Roncarolo) and D.A. Leoncini for his past contribution in the development of the software tool. Part of this research was carried out when the first author was at OGS—National Institute of Oceanography and Applied Geophysics (Trieste, Italy). Finally, the authors thank the anonymous reviewers whose comments and suggestions helped improve this work.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Estimated values for representative events occurred from 2006 to 2021 in the port of La Spezia.
Table A1. Estimated values for representative events occurred from 2006 to 2021 in the port of La Spezia.
StartEndΔp hPaΔh cmJph cm ∗ hPa−1Figure
11/06/200601/07/200613.5241.8A1
16/08/200623/08/200610.3212A2
12/10/200626/10/200615.831.82A3
23/10/200612/11/200623.845.31.9A4
21/02/200727/02/200710161.6S1
25/02/200701/03/20079.816.41.7S2
09/05/200716/05/20075.916.12.7S3
31/05/200702/06/20074.914.42.9S4
01/06/200704/06/20074.916.83.4S5
03/08/200710/08/200712.2201.6S6
20/10/200727/10/200713.727.62S7
03/04/200813/04/200817.540.22.3S8
10/04/200817/04/200816.930.81.8S9
26/08/200809/09/20087.8192.4S10
26/11/200802/12/200828.951.61.8S11
29/01/200909/02/200928.245.61.6S12
28/05/200907/06/200917.235.42.1S13
06/09/200918/09/200913.824.61.8S14
28/11/200901/12/200920.538.61.9S15
18/02/201020/02/201019.433.91.7S16
04/06/201015/06/20108.216.42S17
07/08/201016/08/20107.816.52.1S18
27/10/201002/11/201017.335.72.1S19
26/01/201108/02/201118.930.31.6S20
18/06/201128/06/201111.324.12.1S21
18/09/201102/10/201120.8331.6S22
21/10/201127/10/20111533.72.2S23
25/10/201103/11/201117.328.81.7S24
28/10/201107/11/201117.229.41.7S25
12/07/201220/07/201210.518.11.7S26
08/10/201216/10/201214.223.41.6S27
05/05/201312/05/20135.717.33S28
23/06/201328/06/20139.317.21.8S29
19/01/201426/01/201417.2352S30
10/02/201426/02/201423.641.41.8S31
12/10/201916/10/201912.320.51.7S32
15/10/201918/10/20199.315.51.7S33
17/10/201921/10/20194.811.52.4S34
19/10/201923/10/2019613.32.2S35
19/11/201925/11/201912.328.72.3S36
27/11/201909/12/20192139.21.9S37
28/02/202004/03/202028.652.91.8S38
31/05/202008/06/202020.338.21.9S39
07/06/202017/06/20206.311.61.8S40
21/08/202031/08/202015.326.31.7S41
21/06/202129/06/20217.4141.9S42
21/07/202127/07/20218.516.72S43
31/07/202124/08/20211423.41.7S44
18/09/202125/09/20211118.81.7S45
Figure A1, Figure A2, Figure A3 and Figure A4 (in this Appendix A) and Figures S1–S45 (in the Supplementary Material) show data acquired during the events listed in Table A1; solid lines represent low-frequency components survived the Low-Pass filtering; dashed lines represent high-frequency components removed by the Low-Pass filtering.
Applsci 12 12202 g0a1 550
Figure A1. Measurements carried out between 11 June and 01 July 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 13.5 hPa, Δh = 24 cm, Jph = 1.8 cm ∗ hPa−1).
Figure A1. Measurements carried out between 11 June and 01 July 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 13.5 hPa, Δh = 24 cm, Jph = 1.8 cm ∗ hPa−1).
Applsci 12 12202 g0a1
Applsci 12 12202 g0a2 550
Figure A2. Measurements carried out between 16 and 23 August 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 10.3 hPa, Δh = 21 cm, Jph = 2 cm ∗ hPa−1).
Figure A2. Measurements carried out between 16 and 23 August 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 10.3 hPa, Δh = 21 cm, Jph = 2 cm ∗ hPa−1).
Applsci 12 12202 g0a2
Applsci 12 12202 g0a3 550
Figure A3. Measurements carried out between 12 and 26 October 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 15.8 hPa, Δh = 31.8 cm, Jph = 2 cm ∗ hPa−1).
Figure A3. Measurements carried out between 12 and 26 October 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 15.8 hPa, Δh = 31.8 cm, Jph = 2 cm ∗ hPa−1).
Applsci 12 12202 g0a3
Applsci 12 12202 g0a4 550
Figure A4. Measurements carried out between 23 October and 12 November 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 23.8 hPa, Δh = 45.3 cm, Jph = 1.9 cm ∗ hPa−1).
Figure A4. Measurements carried out between 23 October and 12 November 2006 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level (Δp = 23.8 hPa, Δh = 45.3 cm, Jph = 1.9 cm ∗ hPa−1).
Applsci 12 12202 g0a4

References

  1. Giuffrida, N.; Stojaković, M.; Twrdy, E.; Ignaccolo, M. The Importance of Environmental Factors in the Planning of Container Terminals: The Case Study of the Port of Augusta. Appl. Sci. 2021, 11, 2153. [Google Scholar] [CrossRef]
  2. Meyers, S.D.; Luther, M.E. The impact of sea level rise on maritime navigation within a large, channelized estuary. Marit. Pol. Manag. 2020, 47, 920–936. [Google Scholar] [CrossRef]
  3. Nguyen, T.-H.; Garrè, L.; Amdahl, J.; Leira, B.J. Benchmark study on the assessment of ship damage conditions during stranding. Ships Offshore Struct. 2012, 7, 197–213. [Google Scholar] [CrossRef]
  4. Ogura, T.; Inoue, T.; Uchihira, N. Prediction of Arrival Time of Vessels Considering Future Weather Conditions. Appl. Sci. 2021, 11, 4410. [Google Scholar] [CrossRef]
  5. Petraška, A.; Čižiūnienė, K.; Jarašūnienė, A.; Maruschak, P.; Prentkovskis, O. Algorithm for the assessment of heavyweight and oversize cargo transportation routes. J. Bus. Econ. Manag. 2017, 18, 1098–1114. [Google Scholar] [CrossRef] [Green Version]
  6. Titz, M.A. Port state control versus marine environmental pollution. Marit. Pol. Manag. 1989, 16, 189–211. [Google Scholar] [CrossRef]
  7. Vandermeulen, J.H. Environmental trends of ports and harbours: Implications for planning and management. Marit. Pol. Manag. 1996, 23, 55–66. [Google Scholar] [CrossRef]
  8. Istituto Idrografico della Marina. Tavole di Marea 2022; Istituto Idrografico della Marina: Genoa, Italy, 2021.
  9. Wei, G.; Wang, Q.; Peng, W. Accurate Evaluation of Vertical Tidal Displacement Determined by GPS Kinematic Precise Point Positioning: A Case Study of Hong Kong. Sensors 2019, 19, 2559. [Google Scholar] [CrossRef] [Green Version]
  10. Allen, J.S.; Denbo, D.W. Statistical Characteristics of the Large-Scale Response of Coastal Sea Level to Atmospheric Forcing. J. Phys. Oceanogr. 1984, 14, 1079–1094. [Google Scholar] [CrossRef]
  11. Chelton, D.B.; Enfield, D.B. Ocean signals in tide gauge records. J. Geophys. Res. Solid Earth 1986, 91, 9081–9098. [Google Scholar] [CrossRef]
  12. Dickman, S.R. Theoretical investigation of the oceanic inverted barometer response. J. Geophys. Res. Solid Earth 1988, 93, 14941–14946. [Google Scholar] [CrossRef]
  13. Dobslaw, H.; Thomas, M. Atmospheric induced oceanic tides from ECMWF forecasts. Geophys. Res. Lett. 2005, 32, L10615. [Google Scholar] [CrossRef]
  14. Fu, L.-L.; Pihos, G. Determining the response of sea level to atmospheric pressure forcing using TOPEX/POSEIDON data. J. Geosphys. Res. 1994, 99, 24633–24642. [Google Scholar] [CrossRef]
  15. Moon, I.-J. Impact of a coupled ocean wave-tide-circulation system on coastal modeling. Ocean Model 2005, 8, 203–236. [Google Scholar] [CrossRef]
  16. Willebrand, J.; Philander, S.G.H.; Pacanowski, R.C. The Oceanic Response to Large-Scale Atmospheric Disturbances. J. Phys. Oceanogr. 1980, 10, 411–429. [Google Scholar] [CrossRef]
  17. Wunsch, C.; Stammer, D. Atmospheric loading and the oceanic “inverted barometer” effect. Rev. Geophys. 1997, 35, 79–107. [Google Scholar] [CrossRef]
  18. Dong, D.; Gross, R.S.; Dickey, J.O. Seasonal variations of the Earth’s gravitational field: An analysis of atmospheric pressure, ocean tidal, surface water excitation. Geophys. Res. Lett. 1996, 23, 725–728. [Google Scholar] [CrossRef] [Green Version]
  19. Faggioni, O.; Arena, G.; Bencivenga, M.; Bianco, G.; Bozzano, R.; Canepa, G.; Lusiani, P.; Nardone, G.; Piangiamore, G.L.; Soldani, M.; et al. The Newtonian approach in meteorological tide waves forecasting: Preliminary observations in the East Ligurian harbours. Ann. Geophys. 2006, 49, 1177–1187. [Google Scholar] [CrossRef]
  20. Garrett, C.; Majaess, F. Nonisostatic Response of Sea Level to Atmospheric Pressure in the Eastern Mediterranean. J. Phys. Oceanogr. 1984, 14, 656–665. [Google Scholar] [CrossRef]
  21. Merriam, J.B. Atmospheric pressure and gravity. Geophys. J. Int. 1992, 109, 488–500. [Google Scholar] [CrossRef]
  22. Spratt, R.S. Modelling the effect of atmospheric pressure variations on gravity. Geophys. J. Int. 1982, 71, 173–186. [Google Scholar] [CrossRef] [Green Version]
  23. Trenberth, K.E. Seasonal variations in global sea level pressure and the total mass of the atmosphere. J. Geophys. Res. 1981, 86, 5238–5246. [Google Scholar] [CrossRef]
  24. Bâki Iz, H. The effect of regional sea level atmospheric pressure on sea level variations at globally distributed tide gauge stations with long records. J. Geod. Sci. 2018, 8, 55–71. [Google Scholar] [CrossRef] [Green Version]
  25. Crépon, M. Influence de la pression atmosphérique sur le niveau moyen de la Méditerranée Occidentale et sur le flux à travers le détroit de Gibraltar. Cah. Oceanogr. 1965, 1, 15–32. [Google Scholar]
  26. Deser, C.; Tomas, R.A.; Sun, L. The Role of Ocean-Atmosphere Coupling in the Zonal-Mean Atmospheric Response to Arctic Sea Ice Loss. J. Clim. 2015, 28, 2168–2186. [Google Scholar] [CrossRef] [Green Version]
  27. Garrett, C.; Toulany, B. Sea level variability due to meteorological forcing in the northeast Gulf of St. Lawrence. J. Geophys. Res. 1982, 87, 1968–1978. [Google Scholar] [CrossRef]
  28. Le Traon, P.-Y.; Gauzelin, P. Response of the Mediterranean mean sea level to atmospheric pressure forcing. J. Geophys. Res. 1997, 102, 973–984. [Google Scholar] [CrossRef] [Green Version]
  29. Ponte, R.M.; Gaspar, P. Regional analysis of the inverted barometer effect over the global ocean using TOPEX/POSEIDON data and model results. J. Geosphys. Res. 1999, 104, 15587–15601. [Google Scholar] [CrossRef]
  30. Tsimplis, M.N. The Response of Sea Level to Atmospheric Forcing in the Mediterranean. J. Coast. Res. 1995, 11, 1309–1321. [Google Scholar]
  31. Tsimplis, M.N.; Vlahakis, G.N. Meteorological forcing and sea level variability in the Aegean Sea. J. Geophys. Res. 1994, 99, 9879–9890. [Google Scholar] [CrossRef]
  32. Faggioni, O.; Soldani, M. Geomatics for underwater electromagnetic harbour protection systems and Newtonian systems for coastal navigation safety—Theory. In Proceedings of the Giornate INGV sull’Ambiente Marino—INGV Workshop on Marine Environment, Rome, Italy, 26–27 June 2019; Abstract Volume. Miscellanea INGV. Sagnotti, L., Beranzoli, L., Caruso, C., Guardato, S., Simoncelli, S., Eds.; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2019; Volume 51, pp. 111–114. [Google Scholar] [CrossRef]
  33. Faggioni, O.; Soldani, M.; Piangiamore, G.L.; Ferrante, A.; Bencivenga, M.; Arena, G.; Nardone, G. harbour Water Management for port structures and sea bottom design, coast proximity navigation management, water quality control. In Proceedings of the 1st Mediterranean Days of Coastal and Port Engineering, Palermo, Italy, 7–9 October 2008; PIANC: Brussels, Belgium, 2008. [Google Scholar]
  34. Soldani, M. Geomatics for Port Safety and Security. In R3 in Geomatics: Research, Results and Review. Communications in Computer and Information Science; Parente, C., Troisi, S., Vettore, A., Eds.; Springer: Cham, Switzerland, 2020; Volume 1246, pp. 91–102. [Google Scholar] [CrossRef]
  35. Soldani, M. The contribution of Geomatics to increase safety and security in ports. Appl. Geomat. 2021, 12. [Google Scholar] [CrossRef]
  36. Soldani, M.; Faggioni, O. Geomatics for underwater electromagnetic harbour protection systems and Newtonian systems for coastal navigation safety—Applications. In Proceedings of the Giornate INGV sull’Ambiente Marino—INGV Workshop on Marine Environment, Rome, Italy, 26–27 June 2019; Abstract Volume. Miscellanea INGV. Sagnotti, L., Beranzoli, L., Caruso, C., Guardato, S., Simoncelli, S., Eds.; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2019; Volume 51, pp. 115–118. [Google Scholar] [CrossRef]
  37. Soldani, M.; Faggioni, O. A System to Improve Port Navigation Safety and Its Use in Italian harbours. Appl. Sci. 2021, 11, 10265. [Google Scholar] [CrossRef]
  38. Soldani, M.; Faggioni, O. A tool to aid the navigation in La Spezia harbour (Italy). In Geomatics for Green and Digital Transition; ASITA2022; Communications in Computer and Information Science; Borgogno-Mondino, E., Zamperlin, P., Eds.; Springer: Cham, Switzerland, 2022; Volume 1651, pp. 89–101. [Google Scholar] [CrossRef]
  39. Faggioni, O. The Information Protection in Automatic Reconstruction of Not Continuous Geophysical Data Series. J. Data Anal. Inform. Process. 2019, 7, 208–227. [Google Scholar] [CrossRef] [Green Version]
  40. Faggioni, O. Measurement and Forecasting of Port Tide Hydrostatic Component in North Tyrrhenian Sea (Italy). Open J. Mar. Sci. 2020, 10, 52–77. [Google Scholar] [CrossRef]
  41. Faggioni, O.; Soldani, M.; Leoncini, D.A. Metrological Analysis of Geopotential Gravity Field for Harbor Waterside Management and Water Quality Control. Int. J. Geophys. 2013, 2013, 398956. [Google Scholar] [CrossRef]
  42. Kanasewich, E.R. Time Sequence Analysis in Geophysics, 3rd ed.; The University of Alberta Press: Edmonton, AB, Canada, 1981. [Google Scholar]
  43. Krishnamurti, T.N. Numerical Weather Prediction. Annu. Rev. Fluid Mech. 1995, 27, 195–224. [Google Scholar] [CrossRef]
  44. Lynch, P. The origins of computer weather prediction and climate modeling. J. Comp. Phys. 2008, 227, 3431–3444. [Google Scholar] [CrossRef] [Green Version]
  45. Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar] [CrossRef]
  46. Cabos, W.; de la Vara, A.; Álvarez-García, F.J.; Sánchez, E.; Sieck, K.; Pérez-Sanz, J.-I.; Limareva, N.; Sein, D.V. Impact of ocean-atmosphere coupling on regional climate: The Iberian Peninsula case. Clim. Dyn. 2020, 54, 4441–4467. [Google Scholar] [CrossRef]
  47. El-Gindy, A.A.H.; Eid, F.M. Long-term variations of monthly mean sea level and its relation to atmospheric pressure in the Mediterranean Sea. Int. Hydrogr. Rev. 1990, 67, 147–159. [Google Scholar]
  48. Bartlett, D.; Celliers, L. (Eds.) Geoinformatics for Marine and Coastal Management, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
  49. Lam, S.Y.-W.; Yip, T.L. The role of geomatics engineering in establishing the marine information system for maritime management. Marit. Pol. Manag. 2008, 35, 53–60. [Google Scholar] [CrossRef]
  50. Palikaris, A.; Mavraeidopoulos, A.K. Electronic Navigational Charts: International Standards and Map Projections. J. Mar. Sci. Eng. 2020, 8, 248. [Google Scholar] [CrossRef] [Green Version]
  51. Weintrit, A. Geoinformatics in Shipping and Marine Transport. In Challenge of Transport Telematics: TST 2016. Communications in Computer and Information Science; Mikulski, J., Ed.; Springer: Cham, Switzerland, 2016; Volume 640, pp. 13–25. [Google Scholar] [CrossRef]
  52. Bąk, A.; Zalewski, P. Determination of the Waterway Parameters as a Component of Safety Management System. Appl. Sci. 2021, 11, 4456. [Google Scholar] [CrossRef]
  53. Ducruet, C.; Berli, J.; Bunel, M. Geography versus topology in the evolution of the global container shipping network (1977–2016). In Geographies of Maritime Transport: Transport, Mobilities and Spatial Change; Wilmsmeier, G., Monios, J., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2020; pp. 49–70. [Google Scholar] [CrossRef]
  54. Nohheman, W. Benefits of dredging through reduced tidal waiting. Marit. Pol. Manag. 1981, 8, 17–20. [Google Scholar] [CrossRef]
  55. Vidmar, P.; Perkovič, M.; Gucma, L.; Łazuga, K. Risk Assessment of Moored and Passing Ships. Appl. Sci. 2020, 10, 6825. [Google Scholar] [CrossRef]
Applsci 12 12202 g001 550
Figure 1. An increase in atmospheric pressure inducing a low meteorological tide (modified from [19]).
Figure 1. An increase in atmospheric pressure inducing a low meteorological tide (modified from [19]).
Applsci 12 12202 g001
Applsci 12 12202 g002 550
Figure 2. The position of the monitoring station (pictures from Google Earth): (a) inside the port of La Spezia; (b) within the Eastern Ligurian Sea, Italy.
Figure 2. The position of the monitoring station (pictures from Google Earth): (a) inside the port of La Spezia; (b) within the Eastern Ligurian Sea, Italy.
Applsci 12 12202 g002
Applsci 12 12202 g003 550
Figure 3. Measurements carried out between 28 May and 7 June 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level.
Figure 3. Measurements carried out between 28 May and 7 June 2009 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level.
Applsci 12 12202 g003
Applsci 12 12202 g004 550
Figure 4. Power Spectral Densities of measurements carried out in 2009 within the port of La Spezia: (a) atmospheric pressure; (b) sea level.
Figure 4. Power Spectral Densities of measurements carried out in 2009 within the port of La Spezia: (a) atmospheric pressure; (b) sea level.
Applsci 12 12202 g004
Applsci 12 12202 g005 550
Figure 5. Measurements carried out between 28 May and 7 June 2009 inside the port of La Spezia, after Low-Pass filtering: (a) atmospheric pressure; (b) sea level.
Figure 5. Measurements carried out between 28 May and 7 June 2009 inside the port of La Spezia, after Low-Pass filtering: (a) atmospheric pressure; (b) sea level.
Applsci 12 12202 g005
Applsci 12 12202 g006 550
Figure 6. Measurements carried out between 28 September and 5 October 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level; (c) wind direction, clockwise from the North; (d) wind intensity; for (a,b) solid lines represent low-frequency components survived the Low-Pass filtering; dashed lines represent high-frequency components removed by the Low-Pass filtering.
Figure 6. Measurements carried out between 28 September and 5 October 2020 inside the port of La Spezia: (a) atmospheric pressure; (b) sea level; (c) wind direction, clockwise from the North; (d) wind intensity; for (a,b) solid lines represent low-frequency components survived the Low-Pass filtering; dashed lines represent high-frequency components removed by the Low-Pass filtering.
Applsci 12 12202 g006
Applsci 12 12202 g007 550
Figure 7. Measured pairs (Δp, Δh) from 2006 to 2021 in the port of La Spezia (black dots), linear (red) and cubic (green) trends and comparison with the offshore case (black dashed line).
Figure 7. Measured pairs (Δp, Δh) from 2006 to 2021 in the port of La Spezia (black dots), linear (red) and cubic (green) trends and comparison with the offshore case (black dashed line).
Applsci 12 12202 g007
Applsci 12 12202 g008 550
Figure 8. Virtual traffic lights in the port of La Spezia on 30 June 2010 at 12:00 UTC (threshold levels 12 and 13.5 m).
Figure 8. Virtual traffic lights in the port of La Spezia on 30 June 2010 at 12:00 UTC (threshold levels 12 and 13.5 m).
Applsci 12 12202 g008
Applsci 12 12202 g009 550
Figure 9. Virtual traffic lights in the port of La Spezia on 24 November 2010 at 18:00 UTC (threshold levels 12 and 13.5 m).
Figure 9. Virtual traffic lights in the port of La Spezia on 24 November 2010 at 18:00 UTC (threshold levels 12 and 13.5 m).
Applsci 12 12202 g009
Applsci 12 12202 g010 550
Figure 10. Virtual traffic lights in the port of La Spezia on 24 November 2010 at 18:00 UTC (threshold levels 14 and 15.5 m).
Figure 10. Virtual traffic lights in the port of La Spezia on 24 November 2010 at 18:00 UTC (threshold levels 14 and 15.5 m).
Applsci 12 12202 g010
Table
Table 1. The diurnal and semi-diurnal tide components and their periods expressed in hours (from [9]).
Table 1. The diurnal and semi-diurnal tide components and their periods expressed in hours (from [9]).
NameHarmonic ConstituentPeriod/h
M2Principal lunar semi-diurnal12.4206
S2Principal solar semi-diurnal12.0000
N2Larger lunar elliptic semi-diurnal12.6583
K2Luni-solar declinational semi-diurnal11.9672
K1Luni-solar declinational diurnal23.9345
O1Principal lunar declinational diurnal25.8193
P1Principal solar declinational diurnal24.0659
Q1Lunar flowelliptic diurnal26.8680
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Soldani, M.; Faggioni, O. Observing Meteorological Tides: Fifteen Years of Statistics in the Port of La Spezia (Italy). Appl. Sci. 2022, 12, 12202. https://doi.org/10.3390/app122312202

AMA Style

Soldani M, Faggioni O. Observing Meteorological Tides: Fifteen Years of Statistics in the Port of La Spezia (Italy). Applied Sciences. 2022; 12(23):12202. https://doi.org/10.3390/app122312202

Chicago/Turabian Style

Soldani, Maurizio, and Osvaldo Faggioni. 2022. "Observing Meteorological Tides: Fifteen Years of Statistics in the Port of La Spezia (Italy)" Applied Sciences 12, no. 23: 12202. https://doi.org/10.3390/app122312202

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop