Boolean Network-Based Sensor Selection with Application to the Fault Diagnosis of a Nuclear Plant
Abstract
:1. Introduction
2. BN-Based Sensor Selection Method
2.1. Semi-Tensor Product and Logics
2.2. BN Model of Fault Propagation and Its Linear Representation
2.3. Sufficient Conditions of Fault Detectability and Discriminability
3. Application to a High Temperature Gas-Cooled Reactor Nuclear Plant
3.1. Background
3.2. Directed Graph for Fault Propagation
- (1)
- If fault f1 occurs, i.e., there is an abnormal positive or negative reactivity injection, then the neutron flux is abnormal, which further leads to abnormality in the acquired signal by s1. Since the variation of neutron flux can directly result in the variations of primary coolant temperature, fault f1 can also lead to abnormality in the acquired signal by s3. As the variation of the primary helium temperature can result in that of secondary coolant temperature, abnormality in the acquired signal by s3 can further lead to that of sensor s4.
- (2)
- If fault f2 occurs, i.e., the primary helium blower malfunctions, then there must be abnormality in the primary helium flowrate, which induces abnormality in the acquired signal by s2. Since the steam temperature is very sensitive to the helium flowrate, abnormality in the acquired signal by s2 can further lead to that of sensor s4. Because the temperature of the secondary steam/water flow can influence the primary helium temperature, abnormality in the acquired signal by s4 can induce that of s3.
- (3)
- If fault f3 occurs, i.e., the heat transfer between the two sides the OTSG will be degraded, then the thermal resistance of the OTSG becomes abnormal, which immediately leads to abnormalities of sensors s3 and s4. Here, fault f3 may be induced by the limescale inside the tubes of the OTSG.
- (4)
- Since helium is transparent to the nuclear fission reaction, i.e., it has no temperature feedback effect to neutron flux, abnormality in the signal acquired by s3 cannot directly induce that of s1.
3.3. BN Model of Fault Propagation and Its Linear Representation
3.4. Verification of Fault Detectability and Discriminability
3.5. Sensor Selection
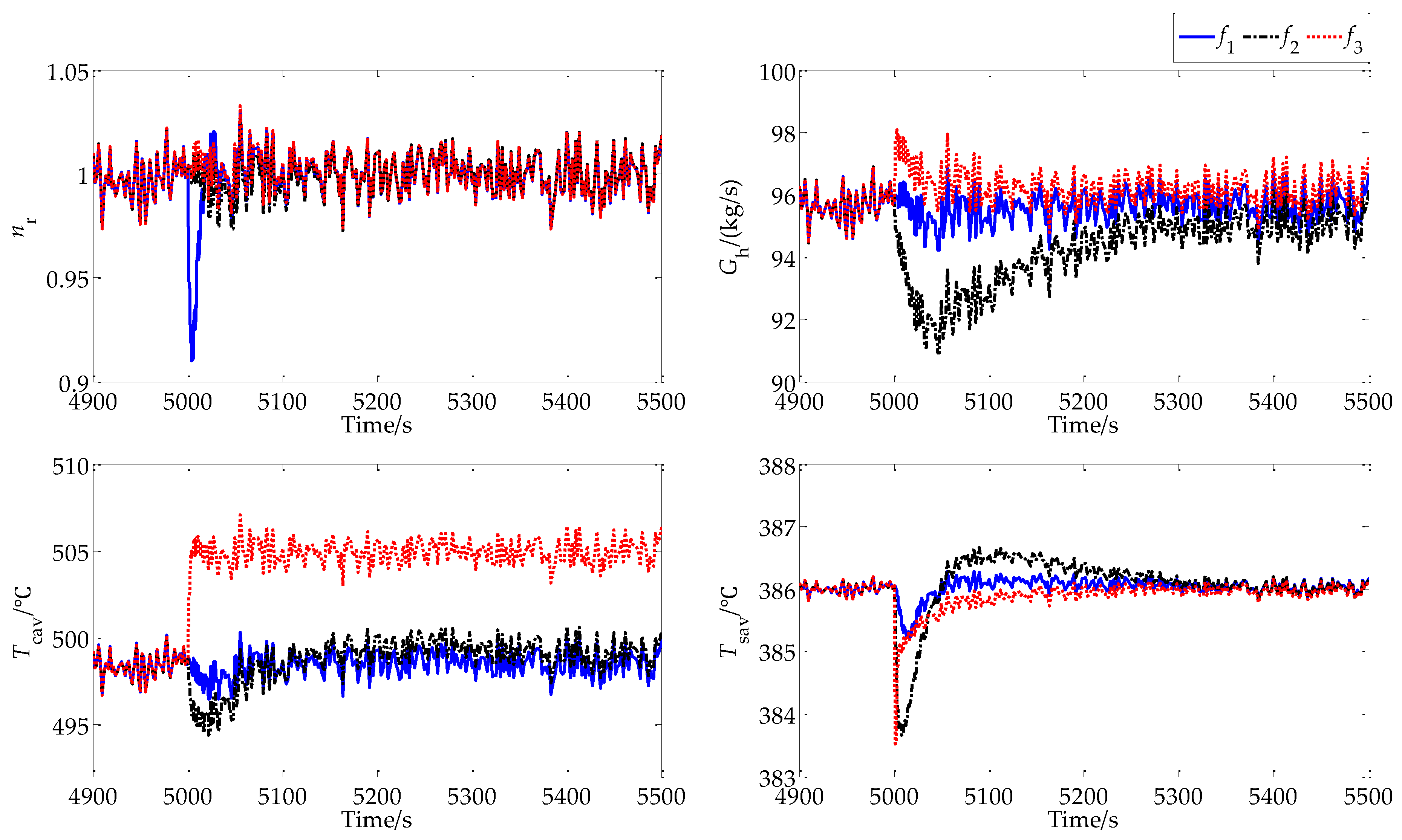
3.6. Numerical Simulation
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bagajewicz, M. Design and retrofit of sensor networks in process plants. AIChE J. 1997, 43, 2300–2306. [Google Scholar] [CrossRef]
- Bagajewicz, M. A review of techniques for instrumentation and upgrade in process plants. Can. J. Chem. Eng. 2002, 80, 3–16. [Google Scholar] [CrossRef]
- Bagajewicz, M.; Cabrera, E. New MILP formulation for instrumentation network design and upgrade. AIChE J. 2000, 48, 2271–2282. [Google Scholar] [CrossRef]
- Bagajewicz, M.; Fuxman, A.; Uribe, A. Instrumentation network design and upgrade for process monitoring and fault detection. AIChE J. 2004, 50, 1870–1880. [Google Scholar] [CrossRef]
- Bhushan, M.; Narasimhan, S.; Rengaswamy, R. Robust sensor network design for fault diagnosis. Comput. Chem. Eng. 2008, 32, 1067–1084. [Google Scholar] [CrossRef]
- Sen, S.; Narasimhan, S.; Deb, K. Sensor network design of linear processes using genetic algorithms. Comput. Chem. Eng. 1998, 22, 385–390. [Google Scholar] [CrossRef]
- Carballido, J.A.; Ponzoni, I.; Brignole, N.B. CGD-GA: A graph-based genetic algorithm for sensor network design. Inf. Sci. 2007, 177, 5091–5102. [Google Scholar] [CrossRef]
- Li, F.; Upadhyaya, B.R. Design of sensor placement for an integral pressurized water reactor using fault diagnostic observability and reliability criteria. Nucl. Technol. 2011, 173, 17–25. [Google Scholar] [CrossRef]
- Li, F.; Upadhyaya, B.R.; Perillo, S.R.P. Fault diagnosis of helical coil steam generator systems of an integral pressurized water reactor using optimal sensor selection. IEEE Trans. Nucl. Sci. 2012, 59, 403–410. [Google Scholar] [CrossRef]
- Kauffman, S.A. Metabolic stability and epigenesist in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Cheng, D.; Zhang, L. On semi-tensor product of matrices and its applications. Acta Math. Appl. Sin. 2003, 19, 219–228. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H. Controllability and observability of Boolean control networks. Automatica 2009, 45, 1659–1667. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H. A linear representation of dynamics of Boolean networks. IEEE Trans. Autom. Control 2010, 55, 2251–2258. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H. State-Space Analysis of Boolean networks. IEEE Trans. Neural Netw. 2010, 55, 2251–2258. [Google Scholar]
- Zhang, Z.; Dong, Y.; Li, F.; Zhang, Z.; Wang, H.; Huang, X.; Li, H.; Liu, B.; Wu, X.; Wang, H.; et al. The shandong shidao bay 200 MWe high-temperature-gas-cooled reactor pebble-bed module (HTR-PM) demonstration power plant: An engineering and technological innovation. Engineering 2016, 2, 112–118. [Google Scholar] [CrossRef]
- Sui, Z.; Sun, J.; Wei, C.; Ma, Y. The engineering simulation system for HTR-PM. Nucl. Eng. Des. 2014, 271, 479–486. [Google Scholar] [CrossRef]
- Dong, Z.; Pan, Y.; Song, M.; Huang, X.; Dong, Y.; Zhang, Z. Dynamic modeling and control characteristics of the two-modular HTR-PM nuclear plant. Sci. Technol. Nucl. Install. 2017, 2017, 6298037. [Google Scholar] [CrossRef]
- Dong, Z.; Pan, Y.; Zhang, Z.; Dong, Y.; Huang, X. Model-free adaptive control law for nuclear superheated-steam supply systems. Energy 2017, 135, 53–67. [Google Scholar] [CrossRef]
- Dong, Z.; Song, M.; Huang, X.; Zhang, Z.; Wu, Z. Coordination control of SMR-based NSSS modules integrated by feedwater distribution. IEEE Trans. Nucl. Sci. 2016, 63, 2682–2690. [Google Scholar] [CrossRef]
- Dong, Z.; Song, M.; Huang, X.; Zhang, Z.; Wu, Z. Module coordination control of MHTGR-based multi-modular nuclear plants. IEEE Trans. Nucl. Sci. 2016, 63, 1889–1900. [Google Scholar] [CrossRef]
- Dong, Z.; Pan, Y.; Zhang, Z.; Dong, Y.; Huang, X. Modeling and control of fluid flow networks with application to a nuclear-solar hybrid plant. Energies 2017, 10, 1912. [Google Scholar] [CrossRef]




| Nodes | Description | Unit | Range | Precision | Output Signal |
|---|---|---|---|---|---|
| s1 | reactor neutron flux | % | 0~200 | 2 | 4~20 mA |
| s2 | primary helium flowrate | kg/s | 0~200 | 2 | 4~20 mA |
| s3 | average temperature of the primary flow | °C | 300~700 | 1 | 4~20 mA |
| s4 | average temperature of the secondary flow | °C | 330~430 | 0.5 | 4~20 mA |
| Nodes | Description |
|---|---|
| f1 | abnormal reactivity injection to the reactor |
| f2 | malfunction of the primary helium blower |
| f3 | heat transfer degradation of OTSG two sides |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z. Boolean Network-Based Sensor Selection with Application to the Fault Diagnosis of a Nuclear Plant. Energies 2017, 10, 2125. https://doi.org/10.3390/en10122125
Dong Z. Boolean Network-Based Sensor Selection with Application to the Fault Diagnosis of a Nuclear Plant. Energies. 2017; 10(12):2125. https://doi.org/10.3390/en10122125
Chicago/Turabian StyleDong, Zhe. 2017. "Boolean Network-Based Sensor Selection with Application to the Fault Diagnosis of a Nuclear Plant" Energies 10, no. 12: 2125. https://doi.org/10.3390/en10122125
APA StyleDong, Z. (2017). Boolean Network-Based Sensor Selection with Application to the Fault Diagnosis of a Nuclear Plant. Energies, 10(12), 2125. https://doi.org/10.3390/en10122125




