A Method for Energy and Resource Assessment of Waves in Finite Water Depths

Abstract

This paper presents a new method for improving the assessment of energy and resources of waves in the cases of finite water depths in which the historical and some ongoing sea wave measurements are simply given in forms of scatter diagrams or the forms of (significant) wave heights and the relevant statistical wave periods, whilst the detailed spectrum information has been discarded, thus no longer available for the purpose of analysis. As a result of such simplified wave data, the assessment for embracing the effects of water depths on wave energy and resources becomes either difficult or inaccurate. In many practical cases, the effects of water depths are simply ignored because the formulas for deep-water waves are frequently employed. This simplification may cause large energy under-estimations for the sea waves in finite water depths. To improve the wave energy assessment for such much-simplified wave data, an approximate method is proposed for approximating the effect of water depth in this research, for which the wave energy period or the calculated peak period can be taken as the reference period for implementing the approximation. The examples for both theoretical and measured spectra show that the proposed method can significantly reduce the errors on wave energy assessment due to the approximations and inclusions of the effects of finite water depths.

1. Introduction

Wave energy resource assessments have been an important factor for wave energy developments in recent years, and the focus has been on the assessment and characterisation of wave energy resources [1,2,3,4,5,6,7,8,9,10,11,12,13], with the global wave energy resource assessments on the overall resources and the distributions of wave energy [3,4,5,6], and the regional and national wave energy resources on the potentials for developing wave energy [7,8,9,10,11,12,13]. As pointed out by Cahill et al. [7], the primary purpose of these studies is to examine the available potential energy at the locations of interest, and of the seasonal and annual trends in the resources. Another important issue is the identification of extreme events and wave conditions, which may be of critical importance on the operation and survival of wave energy converters (WECs). Recent global efforts on standardisation of wave resource assessments [14,15] have led to the development and publication of the International Electrotechnical Commission (IEC) technical specification [16]. An application of the IEC standard to the wave energy resources at the Irish West Coast has been published [17].

For the practical purposes and the cost of wave energy production, so far nearshore and shallow water regions have been frequently considered for deploying wave energy converters and wave farms due to their closeness to the shore and the available infrastructure for cable connection and for easy access for the operation and maintenance. Magagna et al. [18] collected the information of current and proposed wave energy deployments (see Figure 1), and it can be seen that most of the installed wave energy converters have been deployed in water depths less than 50 m, and these trends can be also seen for the proposed wave farms. Similarly, Johanning et al. [19] indicated early that wave energy converters will be very likely installed in the shallow to intermediate depths typically at the 50 m contour in the open areas for wave energy production. For such developments, the availability of wave energy resources in those regions would be important and it was confirmed by a study in Folley et al. [8] that the reduction in the net wave energy resource from a water depth = 50 m to a nearshore location of water depth = 10 m is about 10%. In this regard, the available wave resources in nearshore areas may be still good enough for promoting wave energy production. All of these considerations have been confirmed by the installed and proposed wave energy converters and wave farms (see Figure 1).

Due to the deployments of wave energy converters in relatively small water depths, it is very important to assess the wave energy and wave energy resources more accurately because the effects of finite water depths must be considered. In the cases of regular waves, the effect of water depths on wave energy can be easily calculated due to their well mathematically defined wave periods. In the cases of the sea waves (i.e., the irregular waves), it would be straightforward to assess their energy if the detailed spectra (i.e., their spectral distributions and shapes) are known, since the spectra can be regarded as a sum of many narrow bandwidths, and each narrow bandwidth corresponds to a regular wave with the given wave amplitude and frequency/period, hence its corresponding wave energy can be accurately calculated for including the effect of water depth. The sum of the energy of all the regular wave components is the wave energy for the sea wave/spectrum. However, in many practical cases, the historical and ongoing sea wave measurements are frequently given in simple forms of scatter diagrams or some statistical parameters, such as the significant wave height and statistical periods, while the important spectrum information (spectral shape and distribution) for assessing the effect of water depths on wave energy has been discarded and no longer available for analysis. As such, the effect of water depths on wave energy and resource assessments becomes difficult or inaccurate when only the significant wave heights and characteristic periods are available, and the simple option is to use the formulas for deep-water waves by ignoring the effect of water depths. Such simplification may cause large errors in the wave energy and resource assessment (up to 14% under-estimation). For improving the wave energy and resource assessment, a method is proposed in this investigation, with the inclusion of the effects of finite water depths on wave energy assessment. From the examples, it can be seen that the proposed method is capable of improving the wave energy assessment in the cases of finite water depths: for both popular theoretical spectra (Bretschneider spectrum and JONSWAP spectrum) and the measured spectra from the Irish Coast, the proposed method could reduce the errors of wave energy assessment to less than 5% for the individual sea state (from the error of more than 14% when using the deep-water formulas), and to less than 4% for wave resources (compared to the error of more than 10% using the deep-water formulas).

2. Wave Energy Assessment

2.1. Wave Equation

Linear wave theory is very well developed, and the details can be found in many standard text books [20,21,22]. For completeness and reference, some basic equations are given.

In the linear wave theory, the wave velocity potential in water depth, h, is given as

$$\varphi =\frac{gA}{\omega }\frac{\cosh k(z+h)}{\cosh kh}\sin (kx-\omega t),$$

(1)

where A is the wave amplitude, h the water depth, k the wave number (k = 2π/λ, λ is the wave length), ω the wave circular frequency. x and z are the coordinates along the x-axis (wave travel direction) and z-axis (vertical up positive with z = 0 at the calm water surface).

The wave elevation has a form as

$$\eta =A\cos (kx-\omega t),$$

(2)

with a dispersion relation as

$${\omega }^2=gk\tanh (kh).$$

(3)

2.2. Wave Energy in Deep Water

For convenience of the presentation, the formulas in deep water are given first. The deep water condition here is given when the water depth, h, is larger than half of the wave length, λ₀, i.e., h ≥ λ₀/2 (λ₀ is the wave length without seabed effect, and hereafter the subscript “0” means the parameter in deep water), though some other definitions for deep water conditions can be also seen, for instance, h ≥ λ₀/4 ([22], p. 287). However, when the deep water condition (h ≥ λ₀/2) is used, the maximal error of the wave length is about 0.36%, given by following formula:

$$err=\frac{\left|\lambda -{\lambda }_0\right|}{{\lambda }_0}\times 100\%,$$

(4)

where λ is the actual wave length at a water depth h = λ₀/2.

Similarly, when the deep water condition (h ≥ λ₀/4) is used, the maximal error in wave length is 6.67% (also for a comparison, 2.67% for h ≥ λ₀/3). It will be seen in the analysis below that the deep-water condition (h ≥ λ₀/4) may cause a large error in terms of wave energy assessment.

In deep water conditions, the wave energy of regular waves can be expressed in a popular form of wave height and period, as

$$P_{reg0}=\frac{1}{32\mathsf{\pi }}\rho g^2{H}^{2}T,$$

(5)

where H is the wave height (i.e., H = 2A).

For a given spectrum, corresponding to the frequency ω with a frequency bandwidth ∆ω, the wave power is calculated from (5), as

$$\Delta P_{irr0}=\frac{1}{32\mathsf{\pi }}\rho g^2\left[8S(\omega )\Delta \omega \right]\frac{2\mathsf{\pi }}{\omega }=\frac{1}{2}\rho g^{2}S(\omega )\frac{\Delta \omega }{\omega }.$$

(6)

Therefore, the total time averaged wave power for the given spectrum is calculated as

$$P_{irr0}=\frac{1}{2}\rho g^2{\displaystyle \underset{0}{\overset{\infty }{\int }}S(\omega )\frac{d\omega }{\omega }}.$$

(7)

For the given spectrum, the wave height is given by

$$H_s=4\sqrt{m_0},$$

(8)

and the wave characteristic/statistic periods can be defined as:

$$T_e=2\mathsf{\pi }\frac{m_{-1}}{m_0},T_{01}=2\mathsf{\pi }\frac{m_0}{m_1},T_{02}=2\mathsf{\pi }\sqrt{\frac{m_0}{m_2}},$$

(9)

where T_e, T₀₁ and T₀₂ are the energy period, the spectral mean period and the mean zero-upcrossing period, respectively, with the spectral moment being defined as

$$m_n={\displaystyle {\int }_0^{\infty }S(\omega ){\omega }^{n}d\omega },$$

(10)

where n = −2, −1, 0, 1, 2, …

Using the definitions of the significant wave height, the energy period and the spectral moments yields

$${\displaystyle \underset{0}{\overset{\infty }{\int }}S(\omega )\frac{d\omega }{\omega }}=m_{-1}=\frac{T_e}{2\pi }{m}_0=\frac{1}{32\mathsf{\pi }}{H}_s^2{T}_e.$$

(11)

Thus, the wave energy in irregular waves can be calculated as

$$P_{irr0}=\frac{1}{64\mathsf{\pi }}\rho g^2{H}_s^2{T}_e,$$

(12)

which is same as that given by Tucker and Pitt [22]. A more popular form is given in the unit of the wave power of kW/m, as

$$P_{irr0}=0.49H_s^2{T}_e.$$

(13)

It must be emphasised that this formula for the wave energy of a sea state is the only correct and universal formula for calculating wave energy in deep water. From the formula, it can be seen that the wave energy is proportional to the significant wave height squared and proportional to wave energy period. The formula has been specified in the recent international standards, the IEC technical specification (IEC 62600-101 [16]), indicating that the wave scatter diagram is given only by the significant wave height, H_s, and the energy period, T_e. It is worth mentioning that some historical and ongoing wave measurement data (or the scatter diagrams) are still given either in the spectral peak period, T_p, or the mean zero upcrossing period, T_z (note: in such cases, the relation between T_p or T_z vs. T_e must be specified so to make the data useful). A typical example is the wave data for a few locations at Irish Coast (the Irish Ocean Energy Expertise [23]), the available wave periods are only given in T_p or T_z or both, but T_e is not an option in the available data.

2.3. Waves in Finite Water Depths

From the dispersion relation (3), the wave length in a finite water depth, h, can be calculated using an iterative method (the initial wave length can be taken as the deep-water wave length, λ₀) as

$$\lambda ={\lambda }_0\tanh \left(\frac{2\mathsf{\pi }h}{\lambda }\right),$$

(14)

and the wave length in finite water depths can be seen in Figure 2.

The celerity in the finite water depth is (also see [21])

$$C=\frac{1}{2}\left(1+\frac{2kh}{\sinh (2kh)}\right)\frac{\omega }{k}=C_0\left(1+\frac{2kh}{\sinh (2kh)}\right)\frac{k_0}{k},$$

(15)

where C₀ (=ω/k₀) is the celerity of the wave in deep water.

Thus, the wave power in finite water depth is calculated as

$$P_{reg}=P_{reg0}\left(1+\frac{2kh}{\sinh (2kh)}\right)\frac{k_0}{k},$$

(16)

which indicates that the wave celerity and the wave power in finite water depth can be regarded as the celerity and wave power in deep water modified with a coefficient, defined as

$$C_h=\left(1+\frac{2kh}{\sinh (2kh)}\right)\frac{k_0}{k}.$$

(17)

From the modification coefficient curve in non-dimensional frequency shown in Figure 3, it can be seen that, for a given water depth, the modification coefficient, C_h, is a function of wave frequency, hence, it is noted as C_h(ω) hereafter. For a given spectrum in a finite water depth, the spectrum can be divided into many small bandwidths Δω, and each bandwidth corresponds to a regular wave component. For each regular wave component corresponding to the frequency ω, C_h(ω) can be calculated accurately for a given water depth. As such, the accurate wave energy assessment for the spectrum can be conducted (similar methodologies can be found in references [4,7,16,24]).

The wave power of a regular wave component in the irregular waves can be calculated as

$$\Delta P_{irr}=\frac{1}{4}\rho g\left[2S(\omega )\Delta \omega \right]\frac{\omega }{k_0}{C}_h(\omega ).$$

(18)

Therefore, the total average wave power for the given spectrum is thus

$$P_{irr}=\frac{1}{2}\rho g^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{C}_h(\omega )S(\omega )\frac{d\omega }{\omega }}.$$

(19)

The direct numerical integral of Equation (19) in the case of the available spectrum can be taken as the accurate wave power for the spectrum, denoted as $P_{irr}^0$, and the error (%) of the result from the approximation is calculated as

$$error=\frac{P_{irr}-P_{irr}^0}{P_{irr}^0}\times 100\%,$$

(20)

where P_irr is the calculated wave power using the proposed method.

Generally, the accurate integration of Equation (19) can only be possible when the spectral components are known (the corresponding C_h can be calculated accurately). However, in the case of deep water, the modification coefficient is a constant, i.e., C_h = 1.0, when the non-dimensional frequency is larger than $\sqrt{\mathsf{\pi }}$ in Figure 3. Hence, it becomes obvious that to accurately assess the wave power in finite water depth, the wave spectrum must be used.

Now, a method is proposed for solving the problem as follows. To more accurately assess the wave power in the cases of finite water depths, it is reasonable to assume that an actual wave spectrum may concentrate on a limit bandwidth of frequencies. For instance, for a Bretschneider spectrum (T_p = 8 s, H_s = 2.0 m), 50% of the energy is concentrated within a bandwidth of 0.305 rad/s around the peak period (see Figure 4). Hence, it can be suggested that C_h in the integral in Equation (19) can be approximated with a constant, the constant modification coefficient corresponding to a specific spectral characteristic frequency, ω_c, as,

$$P_{irr}\approx \frac{1}{2}\rho g^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{C}_h({\omega }_c)S(\omega )\frac{d\omega }{\omega }}.$$

(21)

With this assumption, the wave power (in kW/m) in irregular waves in finite water depths can be calculated as

$$P_{irr}=0.49H_s^2{T}_e{C}_h({\omega }_c),$$

(22)

where ω_c can be either the spectral peak frequency, ω_p (=2π/T_p), or energy frequency, ω_e (=2π/T_e). For comparison, the other statistic frequencies/periods may be used as well in the following analysis.

For convenience in the analysis, the modification factor in Equation (22) can be referred to one of the statistic periods; hence, the wave power estimation is given as

$$P_{irr}=0.49H_s^2{T}_e{C}_h(T_c),$$

(23)

where T_c can be one of the popular statistic periods, such as T_p, T_e, T₀₁ or T₀₂, and it will be seen that the first two periods may be the best choice in this regard.

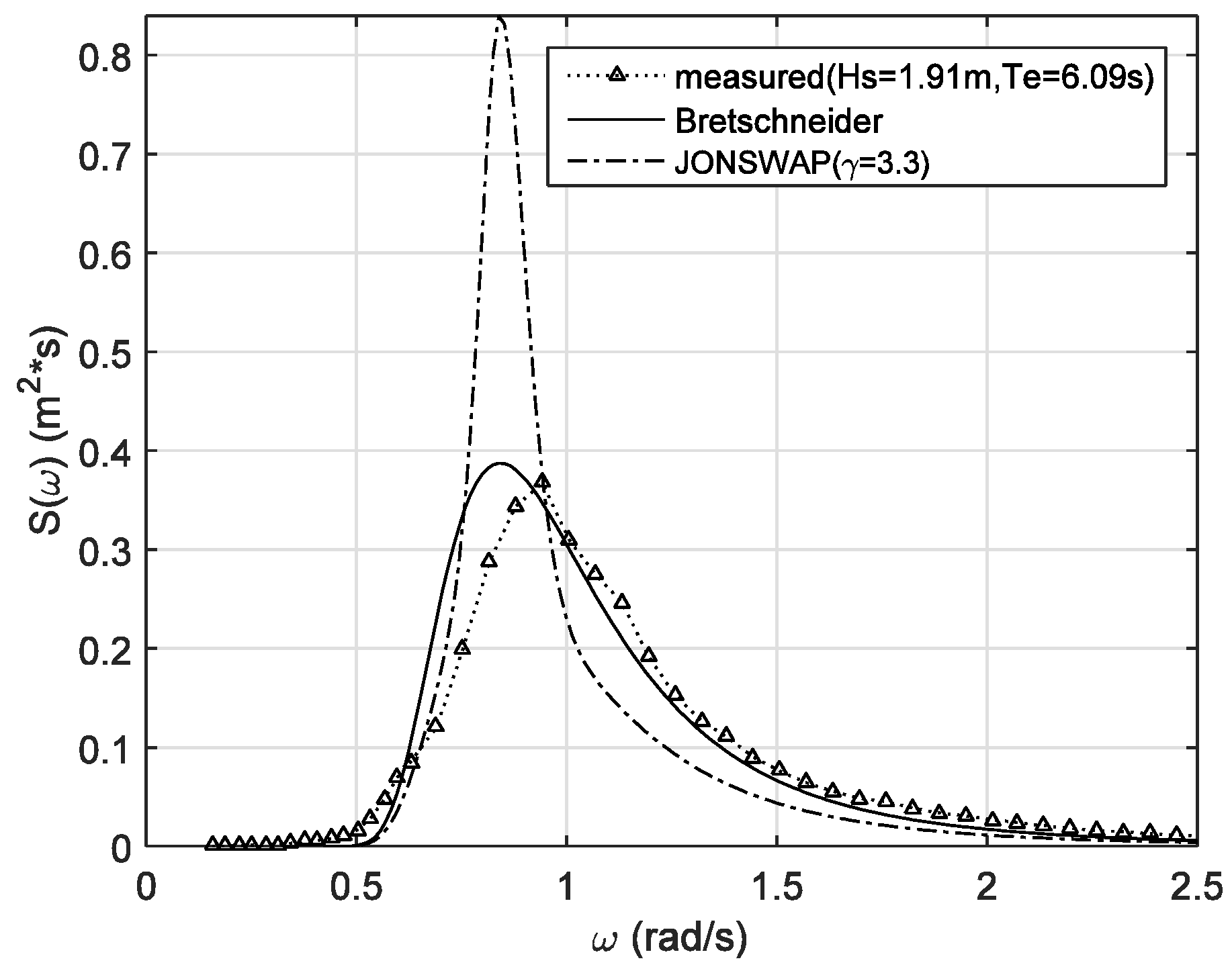
2.4. Theoretical and Measured Wave Spectra

Sea waves are irregular, meaning the wave period and wave height vary from wave to wave, thus irregular waves are often characterised by some popular and most used statistical parameters, such as the significant wave height, H_s, the characteristic wave periods: T_p (spectral peak period), T_e (energy period), T₀₁ (mean spectral period), and T₀₂ (mean zero upcrossing period). In addition, the wave spectral shape/type is an important factor in applications.

The most accepted theoretical wave spectra include the Bretschneider spectrum for the fully developed waves, and the JONSWAP spectrum for the limited developed waves. They can be expressed using a generalised JONSWAP spectrum, as

$$S(\omega )=(1-0.287\ln \gamma )\frac{5{\omega }_p^4}{16{\omega }^5}{H}_s^2{e}^{-\frac{5{\omega }_p^4}{4{\omega }^4}}{\gamma }^{\alpha },$$

(24)

with $\alpha =\exp \left(-\frac{{\left(\omega -{\omega }_p\right)}^2}{2{\omega }_p^2{\sigma }^2}\right)$ and $\sigma =\{\begin{array}{c}0.07,\omega \le {\omega }_p\\ 0.09,\omega >{\omega }_p\end{array}$. γ can take a value between 1.0–5.0 depending on the actual wave conditions and locations (see Det Norske Veritas (DNV) standard [25]), with γ = 3.3 for the standard JONSWAP spectrum, and γ = 1.0 for the Bretschneider spectrum.

As it can be seen from Equation (24), the theoretical spectrum is defined using the spectral peak frequency/period, ω_p/T_p. For measured waves, their spectra can often be spiky. Figure 5 show two measured spectra for the different measured sea states at Atlantic Marine Energy Test Site (AMETS), Belmullet, Ireland. Physically, the spectral peak period can be easily decided by simply choosing the corresponding frequency/period to the spectral peak. However, this may be very dependent on how the measured data have been recorded and analyzed; for instance, the sampling length and sampling frequency. A better choice for deciding the spectral peak period would be the calculated spectral peak period recommended by Tucker and Pitt [22] (p. 41). As such, the calculated spectral peak period has similar features as those well-defined statistical periods including T_e, T₀₁, T₀₂ (T_z) in Equation (9).

Following Tucker and Pitt [22], the calculated peak period is calculated using the relevant spectral moments, as

$$T_{pc}=2\mathsf{\pi }\frac{m_{-2}{m}_1}{m_0^2}.$$

(25)

This formula works generally well for both the Breschneider and the standard JONSWAP spectrum. However, it is also found that this formula gives a small yet a consistent over-estimation of the peak periods by 2–3%. It is therefore suggested that a slightly modified formula can be used as

$$T_{pc}=2\mathsf{\pi }\frac{m_{-2}{m}_1}{m_0^2}/1.025.$$

(26)

Formula (26) gives much better approximations for the peak period for the theoretical spectra. However, in the practical applications, especially when the wave spectrum has double peaks, such as those waves combining the swells and wind-generated waves, the formula will over-estimate the peak period very much. In that case, a limit may be applied as,

$$T_{pc}=\{\begin{array}{ll}2\mathsf{\pi }\frac{m_{-2}{m}_1}{m_0^2}/1.025,\hfill & for2\mathsf{\pi }\frac{m_{-2}{m}_1}{m_0^2}/1.025\le 1.25T_e\hfill \\ 1.25T_e,\hfill & for2\mathsf{\pi }\frac{m_{-2}{m}_1}{m_0^2}/1.025>1.25T_e\hfill \end{array}$$

(27)

Note that the coefficient 1.25 in the second equation in Equation (27) was obtained using the wave measurements in 2010 in AMETS, Ireland, and the total number of the measurements is 13,189 for two data buoys in the year of 2010.

3. Results and Analysis

In this section, the assessment of the wave energy in finite water depths will be conducted and compared. The accurate assessment of wave energy in a finite water depth is the one using the available spectra per Equation (19), which is taken as the reference in the comparison (in the figures as “Ref”), while the approximations using different C_h are identified as “Mod_Tp”, “Mod_Te”, “Mod_T01” and “Mod_T02” in the figures, denoting the modifications C_h are calculated using the peak period T_p, energy period T_e, mean spectral period T₀₁ and mean zero upcrossing period, T₀₂, respectively. In addition, the uncorrected wave energy is plotted as “DeepWater”, which is the case without including the effect of water depth on wave energy assessment.

3.1. Bretschneider Spectra (H_s = 2 m for All Cases)

Figure 6 shows the comparison of the wave energy calculations using different correction methods. It can be seen that for the small wave periods (T_e < 7.0 s), the water depth of 50 m would be considered as deep water, thus all corrections are all very small. For the long waves, the deep water condition generally under-estimate the wave energy assessment by up to 13% (see Figure 7). The correction with the peak period slightly underestimates the wave power for the short waves (similar to other corrections), and then over-estimate the wave power for the wave energy periods between 8–17 s, with the maximal error less than 5%. For other correction methods including the one with the energy period tend to under-estimate the power in short waves and then to over-estimate the wave power in the long waves. The maximal errors are 6% for “Mod_Te”, 8% for “Mod_T01” and 9% for “Mod_T02”.

In the case of water depth of 25 m, it can be seen from Figure 8 and Figure 9 that the deep water condition gives under-estimations for short waves (T_e < 15 s) with a maximal error of 13.5%. For the correction using T_p, it slightly over-estimates the wave power in the short waves (T_e < 12 s), and then under-estimates the wave power, with a maximal error about 5% (slightly larger errors in the very long waves for T_e > 16 s). For the correction using energy period, it under-estimates the wave power for short waves (T_e < 8 s), and then over-estimates the power almost constantly larger than 5% when T_e > 10 s. For the correction with T₀₁ and T₀₂, the corrected wave powers are similar to the case using the energy period, but with larger errors (maximal errors are 11% and 16%, respectively). Figure 10 shows the comparisons of the errors in different water depths (50 m and 25 m). The general trends are the same; for instance, the maximal errors are similar but occur at different wave periods. The error curves shift to longer periods in a deeper water condition. If we plot these using the non-dimensional wave energy periods, T_e^*, defined as $T_e^{*}=T_e\sqrt{\frac{g}{h}}$, the differences for the different water depths disappear (see Figure 11).

3.2. Standard JONSWAP Spectra (H_s = 2 m for All Cases)

In the cases of the standard JONSWAP spectra, it can be seen from Figure 12, Figure 13, Figure 14 and Figure 15 that similar results can be obtained to the cases of Bretschneider spectra, but with the following differences: (i) the deep water condition gives worse under-estimations of the wave power (maximal error is 14.5%); (ii) the corrections using peak period and energy period give better assessments, and the maximal errors are smaller (about 3%), even in the shallower water condition (water depth 25 m).

3.3. Spectra from Measured Waves (AMETS)

In this section, the comparison will be made for the spectra from the measured waves from seas. In getting the correct wave conditions for comparison, the measured waves are binned/grouped using the given significant wave height (H_r = 0.5 m, 1.0 m, …, representing the significant wave height bins: 0–0.5 m, 0.5–1.0 m, …) and the given reference energy periods (T_r + 0.25 s, with T_r = 6 s, 6.5 s, 7 s, …, 15 s) for the bins (bin size: 0.5 s for T_e). All the binned spectra are averaged to represent the respective wave spectra for the given wave conditions. Thus, the calculated wave significant heights and energy periods may be slightly different from the given values, but they may be very close to these given values. Figure 16 and Figure 17 show the binned average spectra for two different sea states (for a comparison, the corresponding Bretschneider and JONSWAP spectra are also plotted). In Figure 16, the spectrum corresponds to the waves of a short energy period, and it can be seen that the spectra are closer to the Bretschneider spectra (and their spectral bandwidths are closer). In the cases of a long wave period of T_e = 13.99 s, the recorded waves have double peaks, including both the locally wind-generated waves (at a higher frequency) and the swells (at a lower frequency) (see Figure 17).

Figure 18 and Figure 19 show the corrections and the corresponding errors for the wave power assessment in the water depth of 50 m. From the figures, it can be seen that the deep-water formulas under-estimate the wave power constantly, with a maximal error of 14%. The correction using the peak period over-estimates the wave power for almost all the wave periods, with a maximal error less than 5%, whilst the correction using energy period under-estimates the wave power for the waves of T_e < 11 s and then over-estimates the wave power for the long waves. The maximal error can be larger, about 10% at the longest wave period T_e = 15 s. When using T₀₁ and T₀₂ as the reference periods, the corrections for wave energy assessment in the finite water depths give larger errors than those using peak and energy periods.

4. Discussions

4.1. Peak Periods from Spectra

Spectral peak period/frequency is a very important parameter when the theoretical spectrum is defined (see Equation (24)), together with the possible requirement of the spectral peak period/frequency for wave energy assessment as shown in the previous sections, a reliable, consistent and representative spectral peak period is very desirable. As shown in the examples of the spectra from the measured sea waves in Figure 5 and Figure 17, it is easy to pick the physical spectral peak periods/frequencies from the spectral curves, but these peak spectral periods may be very subjective due to the fact that it may be very dependent on the length of the measured data and the sampling rate, as well as the method for processing the data. Generally speaking, there is no well-accepted definition for the spectral peak period, unlike other wave statistic periods, such as T_e, T₀₁ and T₀₂ in Equation (9). For solving this difficulty, Tucker and Pitt [22] proposed a so-called calculated spectral peak period T_pc, Equation (25), and it is found that the definition works very well with the theoretical spectra, but with a small and consistent over-estimation. The formula has been refined in Equation (26) for a better and more consistent calculation of the spectral peak period.

Table 1. Spectral peak period calculation for the theoretical spectra.

γ	Tp (Given)	Tp via Equation (25)	err0 (%)	Tp via Equation (26)	err1 (%)
1.0	5	5.130	2.600	5.005	0.098
	8	8.214	2.679	8.014	0.174
	10	10.269	2.692	10.019	0.188
	15	15.405	2.703	15.03	0.198
3.3	5	5.146	2.929	5.021	0.418
	8	8.239	2.986	8.038	0.474
	10	10.300	2.996	10.048	0.484
	15	15.450	3.003	15.074	0.491
5.0	5	5.137	2.731	5.011	0.226
	8	8.222	2.78	8.022	0.273
	10	10.279	2.788	10.028	0.281
	15	15.419	2.794	15.043	0.287

gives a comparison of the calculated spectral peak periods for the theoretical wave spectra, including the well-developed sea state (γ = 1.0), the standard JONSWAP spectrum (γ = 3.3) and the more peaked wave spectrum (γ = 5.0). It can be seen that the refined spectral peak period method (given by Equation (26)) predicts the spectral peak periods with much improved accuracy: the errors are less than 0.5%, whilst the Tucker and Pitt’s formula (i.e., Equation (25)) consistently over-predicts the spectral peak period by about 3%.

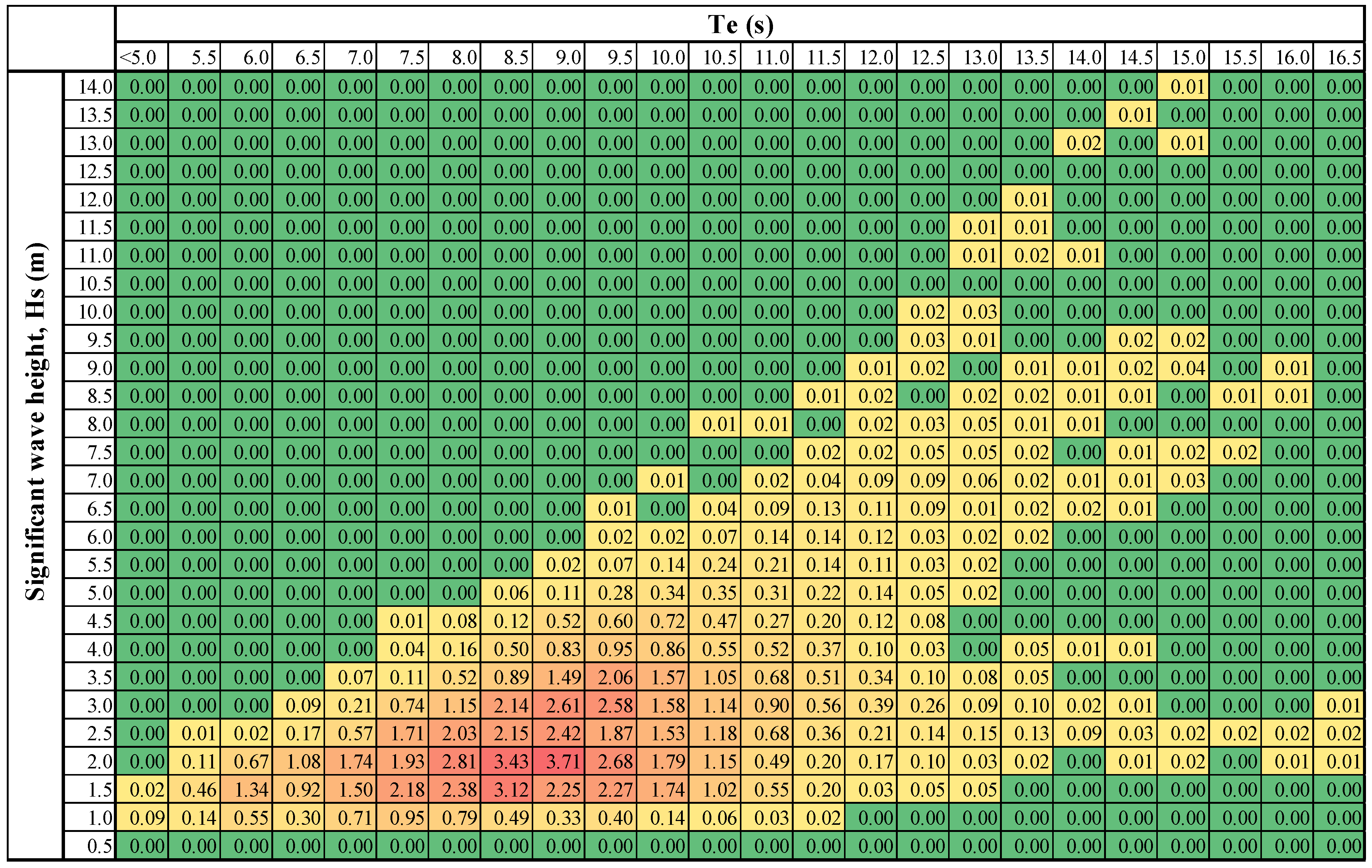
4.2. Wave Resource Assess in Finite Water Depth: Belmullet 50 m Water Depth

In the following analysis, the spectra from the sea wave measurements are same as those in Cahill et al. [7]. The total number of wave measurements is 13,189 from two data buoys in the year of 2010 in the Atlantic Marine Energy Test Site (AMETS) in the 50 m water depth (Belmullet, Ireland). The overall availability of the measured data is about 75% (the detailed availability of the data can be seen in [7]). These measured spectra are used for the following analysis and comparison.

From the available measured wave spectra, the wave energy and resource assessment can be accurately calculated using the direct numerical integration Equation (19). In addition, using these available wave spectra, a wave scatter diagram can be easily generated (Figure 20 showing the occurrence of the waves in the year in 2010), and based on which, the wave energy and resource in a water depth of 50 m (a finite water depth) will be assessed by including the effect of the water depth.

Two approximation methods are compared here: the approximation using the deep-water formula and the proposed method in this study using the water depth modification factor C_h (the results are both compared to the accurate wave energy resource, $P_{irr}^0$). From

Table 2. Wave power assessment for AMETS.

Water Depth (m)	Method	Annual Mean Power (kW/m)	Error (%)
50	Direct calculation, Equation (19)	37.41	-
	Deep water, Equation (13)	33.60	−10.18
	Correction with ωp, Equation (22)	38.76	3.86
	Correction with ωe, Equation (22)	36.86	−1.47

, it can be seen that the deep-water formula gives an under-estimation of 10.18% for the annual mean wave power. The correction method based on the spectral peak periods gives 3.86% over-estimation, and based on the energy periods gives 1.47% under-estimation. It seems that the correction with the energy period gives a better wave resource assessment, but it is caused by the under-estimation for short waves and over-estimation for long waves (Figure 19) for this particular water depth and wave condition, thus they cancel each other in the overall wave energy assessment so to give a better result, while for this particular water depth, the correction using the calculated peak period gives more consistent over-estimation of the wave energy for all waves (less than 5%).

5. Conclusions

In the paper, the effect of water depths on wave energy assessment has been studied, and a method has been proposed for improving the wave energy assessment in finite water depth for the cases of only the simple scatter diagram available. From the analyses and comparisons, the proposed method can improve the assessment of the wave energy and resource, and following conclusions can be drawn:

• For the cases of finite water depths, using the deep water formulas may under-estimate the wave power by up to 14.5% in irregular waves of interest for wave energy production.
• For the wave measurement data in simple forms of scatter diagrams, the proposed method in this investigation can improve the wave energy assessment. For both the theoretical spectra (Bretschneider and JONSWAP) and the measured spectra, the proposed method can improve the accuracy of the wave energy assessment, reducing the maximal error from about 14.5% to less than 5%.
• The proposed method using either the calculated peak period or the energy period can significantly improve the assessment of the annual mean wave power. For the AMETS data, the deep water formulas give an error more than 10%, whilst with the proposed method, the error can be reduced to less than 4% or even less.
• The calculated spectral peak period for the measured waves can be reliably calculated using Equation (27) for those wind-generated waves.